New natural garnet reference materials for determining the oxidation state of iron in garnet using the electron microprobe flank method

Abstract

The oxidation state of iron (e.g., Fe³⁺/ΣFe) in minerals is a direct proxy for the oxygen fugacity of magma and fluid, which plays a key role in the formation of various types of ore deposits. Although many techniques have been developed to determine the Fe³⁺/ΣFe ratio in minerals, the electron microprobe flank method is particularly notable for its easy accessibility and high efficiency. However, the application of this method is limited by a shortage of suitable calibration standards. In this study, we collected a series of natural, euhedral garnet grains and gem-quality garnet fragments, which were carefully crushed and separated under a binocular microscope. Following a detailed examination of their major element compositions and Mössbauer spectroscopy measurements for their Fe³⁺/ΣFe ratios, we report ten new garnet samples (three belonging to the andradite–grossular series and seven to the almandine–pyrope–grossular series) that can be used as reference materials to calibrate the Fe³⁺/ΣFe ratio of garnet using the flank method. The andradite–grossular samples are highly enriched in Fe³⁺, exhibiting Fe³⁺/ΣFe ratios ranging from 0.89 ± 0.03 to 1.00 ± 0.03, while the almandine–pyrope–grossular samples contain minimal Fe³⁺ with Fe³⁺/ΣFe ratios ranging from 0.01 ± 0.02 to 0.03 ± 0.01. One andradite sample (And1902) and one almandine sample (Ald1906) were identified as ideal for determining the flank positions for Fe L_α and Fe L_β. These two end-members, along with the other eight samples, can be employed to quantify the relationship between Fe L_β/L_α at flank positions and the Fe²⁺ or ΣFe content. The results indicate that the Fe²⁺ contents and Fe³⁺/ΣFe ratios of the ten garnet samples align with those obtained through Mössbauer spectroscopy, with an uncertainty of ±1 wt% for Fe²⁺ and ±0.05 for Fe³⁺/ΣFe, respectively. Consequently, these well-characterized natural garnet samples can serve as reliable reference materials when synthetic garnet standards are unavailable.

---

1. Introduction

Iron (Fe) is generally a major element in many mafic silicate minerals (e.g., olivine, pyroxene, garnet, amphibole, and biotite), oxides (e.g., spinel, chromite, and magnetite), and sulfides (e.g., pyrrhotite and pyrite). The oxidation state of Fe (expressed as Fe³⁺/ΣFe) in the minerals is commonly used to constrain the oxygen fugacity of magma/fluid evolution.^1–5 However, obtaining the accurate Fe³⁺/ΣFe ratio at the scale of individual mineral grains remains challenging, even though their Fe content can be easily measured.

Many techniques have been developed to determine the Fe³⁺/ΣFe ratio of minerals, including wet chemistry, Mössbauer spectroscopy, X-ray absorption near-edge structure (XANES) spectroscopy, electron energy loss spectroscopy (EELS), X-ray photoelectron spectroscopy (XPS), and electron probe microanalysis (EPMA). However, each method has its advantages and disadvantages.⁶ Wet chemistry and conventional Mössbauer spectroscopy are commonly used to determine the Fe³⁺/ΣFe ratio of powdered samples,⁷ they are inadequate for analyzing small areas (micron-scale) of individual minerals. Over the past twenty years, Mössbauer spectroscopy has significantly improved in spatial resolution with the development of “milliprobe” capabilities, achieving resolutions as small as 50 μm; however, the process of acquiring spectra remains time-consuming.^8,9In situ micro-Mössbauer and XANES techniques facilitate precise measurements of the Fe³⁺/ΣFe ratio at spatial resolutions down to a few microns.^10–13 However, these methods necessitate a synchrotron source of X-rays, which is only accessible at limited synchrotron facilities. The EELS method offers exceptional spatial resolution on the nanometer scale; however, the standards used for calibration may be inhomogeneous at this scale, and beam damage is often significant.¹⁴ XPS can provide information about the elemental and chemical states of the atoms, but a major drawback is its strong surface sensitivity, as it typically samples only the top 5 nm.⁶ The EPMA is suitable for in situ routine analysis of the Fe³⁺/ΣFe ratio in natural minerals of millimeter size; however, it necessitates multiple mineral standards for data calibration.

Höfer et al.¹⁵ conducted the pioneering study on the EPMA “flank method”, which was improved later for accurate determination of the Fe³⁺/ΣFe ratio of garnet.^16–18 This method has been successfully applied to measure the Fe³⁺/ΣFe ratio of natural garnet from metamorphic rocks,^19–22 arclogite, and deep-seated garnet pyroxenite,²³ and has been extended to amphibole and biotite,²⁴ silicate glass,^25,26 and synthetic majoritic garnet from high-pressure experiments.²⁷ The principle of this method is based on the difference in the self-absorption of Fe²⁺ and Fe³⁺ from the systematic correlation of Fe L_β/L_α at flank positions and Fe²⁺ content.¹⁷ In these studies, two synthetic pure garnet reference materials, one Fe²⁺ end-member (almandine) and one Fe³⁺ end-member (andradite), were used to identify the flank positions of Fe L_α and Fe L_β. Using multiple well-characterized garnet reference materials, a linear correlation of Fe L_β/L_α at flank positions and Fe²⁺ content of garnet can be obtained and used for determining the Fe³⁺/ΣFe ratio of unknown garnets. It is suggested that the EPMA flank method can yield an accuracy of Fe³⁺/ΣFe at ±0.04 for garnets with 10 wt% total Fe.¹⁷

The advantages of the EPMA such as easy accessibility, small spot size (micrometer) and high speed of analysis, make the EPMA flank method an ideal choice for determining Fe³⁺/ΣFe ratios of natural garnet. Garnet is widespread in metamorphic rocks, a primary constituent of the upper mantle, and is also found in some igneous rocks and sediments.²⁸ However, the application of the flank method to natural garnet is hindered by the limited availability of garnet calibration standards, which are present in only a few EPMA laboratories. In this study, we collected a series of natural, euhedral garnet grains and gem-quality garnet fragments to identify potential reference materials for the EPMA flank method. A total of ten garnet samples were ultimately selected, which can be used to determine the flank positions of Fe L_α and Fe L_β, as well as to calibrate the Fe³⁺/ΣFe ratio of unknown garnets.

2. Samples and analytical methods

2.1. Sample preparation

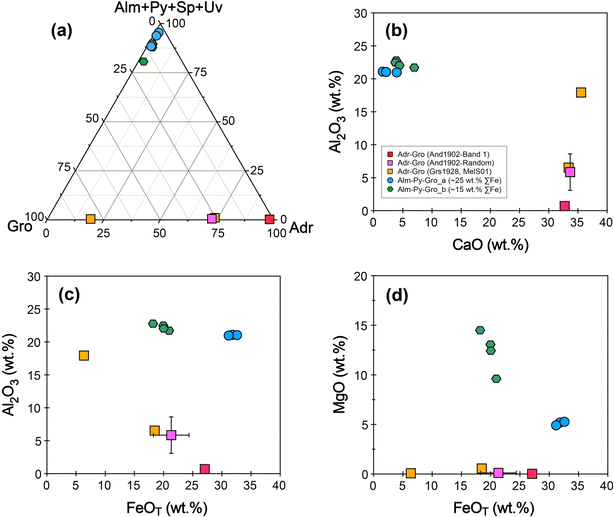
A total of twenty natural garnet samples were collected during the preparation. Three of these samples belong to the andradite–grossular series, while the remaining seventeen belong to the almandine–pyrope–grossular series (Fig. 1). These samples consist of euhedral garnet grains and gem-quality garnet fragments collected from China, Brazil, and Switzerland, all of which were purchased from online mineral retailers. The garnet samples were crushed to a particle size of 30–60 mesh. Subsequently, the garnet fragments were meticulously handpicked under a binocular microscope. Approximately 20 garnet fragments from each sample were mounted on epoxy resin and polished with diamond paste. The mounted garnet fragments were carefully examined using Raman spectroscopy to identify the phases of the garnets, while backscattered electron (BSE) images were employed to evaluate the potential zoning of the garnet grains. Finally, three samples from the andradite–grossular series (And1902, Grs1928, and MelS01) and seven samples from the almandine–pyrope–grossular series (Ald1906, Ald1915, Ald1917, Ald1905, Ald1907, Ald1925, and Ald1926) were selected (Fig. 1).

Fig. 1 Photographs of garnet collections. Abbreviations: Adr-andradite. The scale bar in all photographs is 1 cm in length.

2.2. Raman analysis

Raman spectra of natural garnet fragments were obtained using a Renishaw inVia™ Reflex (UK) confocal Raman system at the Electron Microscopy Center, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences (GIGCAS). The excitation source was a 532 nm laser (220 V) paired with a 50× objective lens to focus the excitation laser onto a spot approximately 1 μm in diameter. The laser power was set to 10 mW, and spectra were collected in the range of 50–1799 cm⁻¹ with a 3-second exposure time using a grating of 1800 grooves per mm (vis).

2.3. EPMA analysis of major elements

Major element compositions of selected garnets were determined in conjunction with flank-method measurements using a JEOL JXA-8230 EPMA equipped with five wavelength-dispersive spectrometers at the Key Laboratory of Mineralogy and Metallogeny at GIGCAS (see the Discussion section). The operating conditions of 15 kV, 60 nA, and a 5 μm beam were employed for all elements. For separate quantitative elemental analysis, we utilized 15 kV, 20 nA, and a 1 μm beam. Counting times on the peak and upper/lower background positions of elements were 20 and 10 seconds for Si, Al, Fe, Mg, and Ca; 40 and 20 seconds for Mn, Cr, and Ti; and 10 and 5 seconds for Na and K. Analytical results were processed using ZAF correction routines. Primary standards used for data calibration included chrome-diopside (Si and Ca), olivine (Mg), magnetite (Fe), almandine (Al), albite (Na), Cr₂O₃ (Cr), rutile (Ti), rhodonite (Mn), and orthoclase (K). An in-house almandine was employed as the secondary standard to monitor data accuracy and precision. Major element contents (e.g., SiO₂, MgO, FeO, Al₂O₃, and CaO) were within ±2% of preferred values, while minor element contents (<1 wt%) were within 10% of preferred values. Relative precisions were within 2% for major elements and 7% for minor elements. High-resolution elemental mapping of individual garnet fragment was conducted using the same EPMA under operating conditions of 20 kV, 100 nA, and a beam diameter of 1–1.5 μm. The dwell time for each pixel was set to 60 ms.

2.4. Mössbauer analysis of the Fe³⁺/ΣFe ratio

The Fe³⁺/ΣFe ratios of selected garnet samples were determined using Mössbauer spectroscopy. Garnet fragments of the selected samples were cleaned in an ultrasonic bath, first with ethanol for 5 minutes and then with Milli-Q water for an additional 5 minutes to remove impurities. The cleaned garnet grains were then powdered to a 200-mesh size using an agate mortar prior to Mössbauer analyses. Mössbauer spectra of the garnet powder were collected using two WSS-10 Mössbauer spectrometers at the GIGCAS (And1902, Ald1905, and Ald1906) and China University of Geosciences (Wuhan) (CUG) (Grs1928, MelS01, Ald1907, Ald1915, Ald1917, Ald1925, and Ald1926), respectively. A ⁵⁷Co source in a rhodium matrix was used at room temperature in both laboratories. Measurements were carried out in transmission geometry with a moving absorber. A standard absorber, α-Fe foil, with a thickness of 7 μm (GIGCAS) or 25 μm (CUG) was used to calibrate the velocity scale.²⁹ The Mössbauer spectra were fitted using the least squares method with the MossWinn 4.0 program, employing a Lorentzian line shape. The quality of the fits to the Mössbauer spectra indicates that the 1σ uncertainty of Fe³⁺/∑Fe is 0.01–0.04 for the different garnet samples (Table 1).

Table 1 Chemical compositions and Fe³⁺/∑Fe ratios of selected natural garnets^b

Series	Andradite–grossular								Almandine–pyrope–grossular
Sample no.	And1902-Band1		And1902		Grs1928		MelS01		Ald1906		Ald1915		Ald1917		Ald1905		Ald1907		Ald1925		Ald1926
n	20	σ	20	σ	12	σ	20	σ	20	σ	16	σ	20	σ	20	σ	20	σ	16	σ	12	σ
a The FeO and Fe2O3 contents were calculated using the total FeO and Mössbauer Fe^3+/∑Fe ratios. b bdl-below detection limit.
SiO2	34.68	0.33	36.41	0.54	38.07	0.23	34.24	0.23	37.43	0.24	37.29	0.23	37.16	0.29	40.19	0.23	39.65	0.21	38.71	0.16	39.33	0.15
TiO2	bdl	0.00	0.06	0.05	0.05	0.03	2.80	0.26	bdl	0.00	bdl	0.00	0.02	0.01	0.03	0.01	0.01	0.01	0.06	0.01	0.02	0.01
Al2O3	0.71	0.05	5.85	2.78	17.93	0.33	6.55	0.09	21.10	0.11	21.05	0.10	20.97	0.13	22.79	0.12	22.48	0.14	21.71	0.11	22.05	0.09
Cr2O3	bdl	0.00	bdl	0.00	bdl	0.00	0.01	0.00	0.01	0.01	0.01	0.01	0.05	0.01	0.02	0.01	0.01	0.00	0.07	0.01	bdl	0.00
FeO^a	bdl	0.00	bdl	0.00	0.72	0.03	0.62	0.00	31.55	0.26	30.97	0.36	30.30	0.32	17.90	0.09	19.38	0.08	19.69	0.06	18.56	0.07
Fe2O3^a	30.10	0.19	23.71	3.38	6.26	0.25	19.86	0.14	0.30	0.00	1.83	0.02	0.98	0.01	0.34	0.00	0.68	0.00	1.40	0.00	1.64	0.01
MnO	0.50	0.03	0.48	0.20	0.32	0.04	0.22	0.02	2.84	0.06	0.90	0.11	0.65	0.16	0.75	0.06	0.72	0.06	0.76	0.06	0.86	0.06
MgO	0.02	0.01	0.11	0.04	0.09	0.05	0.56	0.04	5.19	0.08	5.27	0.19	4.92	0.23	14.51	0.09	13.07	0.12	9.61	0.07	12.44	0.04
CaO	32.73	0.16	33.68	0.24	35.56	0.38	33.41	0.11	1.58	0.10	2.15	0.18	3.97	0.12	3.90	0.06	3.74	0.03	6.97	0.06	4.43	0.04
Na2O	bdl	0.01	bdl	0.01	bdl	0.00	0.01	0.01	0.01	0.01	0.01	0.01	0.01	0.01	bdl	0.01	bdl	0.00	0.01	0.01	0.01	0.01
Total	98.75		100.30		99.02		98.28		100.01		99.50		99.01		100.44		99.73		98.99		99.34
Fe^3+/∑Fe Mössbauer	1.00	0.03	1.00	0.03	0.89	0.03	0.97	0.04	0.01	0.03	0.05	0.02	0.03	0.01	0.02	0.03	0.03	0.01	0.06	0.03	0.07	0.02
Endmembers
Andradite	96.68%		71.73%		18.84%		72.06%		1.64%		1.39%		1.66%		1.90%		1.48%		2.31%		2.61%
Almandine	—		—		—		—		67.63%		69.97%		66.64%		33.68%		38.76%		41.63%		38.47%
Pyrope	0.09%		0.44%		0.34%		0.90%		20.47%		20.86%		19.52%		53.03%		48.56%		36.59%		46.60%
Grossular	1.54%		26.59%		79.42%		23.28%		2.80%		4.71%		9.52%		8.29%		8.48%		16.57%		9.31%
Spessartine	—		—		—		—		6.37%		2.03%		1.46%		1.57%		1.52%		1.65%		1.83%
Uvarovite	0.01%		0.01%		0.00%		0.02%		0.03%		0.03%		0.15%		0.06%		0.03%		0.20%		0.01%

---

3. Results

3.1. Major element compositions of garnet

The sample And1902 is identified as andradite (Fig. 2), exhibiting zoning in the BSE image, which consists of alternating dark and bright bands that correspond to variations in Fe and Al content (Fig. 3a). The MnO and MgO contents of And1902 are very low, at 0.5 wt% and 0.1 wt%, respectively (Table 1). A compositional profile across one fragment reveals opposing trends in the total FeO and Al₂O₃ contents (Fig. 4a and b). The brightest band of the fragment (Band 1) in the BSE image contains the highest total FeO content of 26.7 wt% and the lowest Al₂O₃ content of 0.62 wt% (Fig. 4b and c). Utilizing charge balance principles, the molar proportions of garnet end-members were calculated from EPMA results using an Excel spreadsheet developed by Locock.³⁰ The results show that the andradite fragment is primarily composed of 64–94% andradite (Ca₃(Fe³⁺, Ti)₂Si₃O₁₂) and 2–31% grossular (Ca₃Al₂Si₃O₁₂) end-members throughout the alternating bands (Fig. 4c and Table 2). A clear negative correlation is observed between the octahedral Fe³⁺ and Al atoms per formula unit (Fig. 4d). A random analysis of twenty points of the And1902 sample reveals an average total FeO of 21.33 wt% and Al₂O₃ of 5.85 wt%, corresponding to 72% andradite and 27% grossular end-members (Fig. 5a). The MelS01 sample is a melanite, a black Ti-bearing variety of andradite (Fig. 2). It is homogeneous and contains 17.87 wt% total FeO, 2.80 wt% TiO₂, and 6.55 wt% Al₂O₃, corresponding to 72% andradite and 23% grossular end-members (Table 1 and Fig. 5a). The Grs1928 sample exhibits a uniform composition with 5.64 wt% total FeO and 17.93 wt% Al₂O₃, comprising 79% grossular and 19% andradite end-members (Table 1 and Fig. 5a). For the andradite–grossular series samples (And1902, MelS01, and Grs1928), CaO and MgO exhibit limit variation (Fig. 5b and d), while Al₂O₃ and total FeO show large variation and a clear negative correlation (Fig. 5c).

Fig. 2 Representative Raman spectra of garnet fragments, with background correction applied. Reference spectra for andradite, grossular, and almandine are included for comparison.

Fig. 3 Backscattered electron images and high-resolution X-ray maps of Fe, Al, and Ca of selected garnet standards. (a) The andradite (And1902) fragments show clear chemical zoning of Fe and Al. (b and c) The almandine (Ald1906 and Ald1905) grains are homogeneous in both BSE images and elemental maps.

Fig. 4 Compositional profile across the representative andradite (And1902) fragment. (a) BSE image showing the analysis locations (white circles) across the bright and dark bands. (b) Variations of total FeO and Al₂O₃ contents, and (c) calculated mole percentage (%) of andradite and grossular end-members across the profile. (d) Covariation of Fe³⁺ and Al^VI atoms per formula unit (apfu) calculated on the basis of 8 cations per 12 oxygens.

Table 2 Compositional profile across the andradite grain

Sample no.	Distance (μm)	SiO2	TiO2	Al2O3	Cr2O3	FeOtot	MnO	MgO	CaO	Na2O	K2O	Total	Fe^3+	Al^VI	End-members
Oxides (wt%)													apfu	apfu	Andradite	Grossular
And1902-1	313	35.18	0.00	0.62	0.01	26.65	0.59	0.04	33.50	0.03	0.00	96.60	1.883	0.033	94.15%	1.65%
And1902-2	304	35.34	0.00	0.76	0.00	26.56	0.56	0.03	33.54	0.03	0.00	96.81	1.871	0.053	93.57%	2.65%
And1902-3	271	35.68	0.02	3.04	0.01	23.91	0.57	0.01	33.84	0.01	0.00	97.09	1.666	0.270	83.28%	13.49%
And1902-4	249	36.55	0.20	5.54	0.00	20.70	0.72	0.01	34.07	0.01	0.00	97.79	1.418	0.527	70.88%	26.37%
And1902-5	233	36.27	0.05	3.96	0.00	22.90	0.69	0.02	34.36	0.00	0.01	98.26	1.570	0.357	78.51%	17.85%
And1902-6	211	36.13	0.25	4.87	0.00	21.67	0.61	0.05	34.26	0.00	0.01	97.85	1.487	0.436	74.37%	21.80%
And1902-7	191	36.20	0.71	6.37	0.00	19.20	0.67	0.06	34.14	0.00	0.01	97.34	1.317	0.586	65.85%	29.28%
And1902-8	172	35.92	0.54	6.68	0.00	19.21	0.72	0.05	34.29	0.00	0.02	97.43	1.316	0.586	65.79%	29.29%
And1902-9	153	36.29	0.57	6.99	0.01	18.92	0.69	0.09	34.22	0.01	0.00	97.79	1.289	0.628	64.47%	31.05%
And1902-10	134	36.31	0.52	6.60	0.03	19.16	0.67	0.08	34.70	0.04	0.00	98.11	1.302	0.582	65.10%	29.12%
And1902-11	115	35.84	0.04	4.08	0.03	22.15	0.41	0.05	34.39	0.00	0.01	97.01	1.536	0.370	76.78%	18.50%
And1902-12	94	35.97	0.03	3.41	0.01	23.62	0.31	0.05	34.93	0.00	0.01	98.34	1.620	0.279	81.02%	13.97%
And1902-13	77	36.04	0.05	3.78	0.01	22.85	0.35	0.03	34.55	0.01	0.00	97.66	1.576	0.339	78.79%	16.95%
And1902-14	58	36.08	0.04	3.91	0.00	22.48	0.33	0.04	34.50	0.00	0.00	97.39	1.553	0.362	77.67%	18.10%
And1902-15	39	36.29	0.19	4.81	0.00	21.47	0.41	0.10	34.52	0.00	0.01	97.79	1.473	0.442	73.64%	22.08%
And1902-16	20	36.54	0.10	5.52	0.01	20.59	0.43	0.07	34.91	0.00	0.00	98.15	1.403	0.506	70.14%	25.31%
And1902-17	0	36.13	0.00	3.44	0.01	22.26	0.27	0.06	34.10	0.01	0.01	96.29	1.556	0.339	77.80%	16.74%

---

Fig. 5 Garnet end-members and chemical compositions of the selected garnet samples. (a) A triangular diagram of [almandine (Alm, Fe₃²⁺Al₂Si₃O₁₂) + pyrope (Py, Mg₃Al₂Si₃O₁₂) + spessartine (Sp, Mn₃Al₂Si₃O₁₂) + uvarovite (Uv, Ca₃Cr₂Si₃O₁₂)], [grossular (Gro, Ca₃Al₂Si₃O₁₂)], and [andradite (Adr, Ca₃(Fe³⁺, Ti)₂Si₃O₁₂)] end-member. (b) Binary plot of CaO versus Al₂O₃ content. (c and d) Binary plots of Al₂O₃ and MgO versus total FeO contents.

The almandine–pyrope–grossular series samples are homogeneous in the BSE images and EPMA X-ray intensity maps (Fig. 3b and c). They exhibit a large variation in FeO and MgO content, with a restricted range of Al₂O₃ (Fig. 5b–d). These samples can be divided into two groups based on their Fe content: Alm-Py-Gro_a and Alm-Py-Gro_b. Alm-Py-Gro_a (Ald1906, Ald1915, and Ald1917) contains 30.19–32.62 wt% total FeO and 4.92–5.27 wt% MgO, corresponding to 67–70% almandine (Fe²⁺₃Al₂Si₃O₁₂), 20–21% pyrope (Mg²⁺₃Al₂Si₃O₁₂), 3–10% grossular, 1–6% spessartine (Mn₃Al₂Si₃O₁₂), and 1–2% andradite. In contrast, Alm-Py-Gro_b contains lower total FeO (18.21–20.96 wt%) and higher MgO (9.61–14.51 wt%), corresponding to 34–42% almandine (Fe²⁺₃Al₂Si₃O₁₂), 37–53% pyrope (Mg²⁺₃Al₂Si₃O₁₂), 8–17% grossular, 1–2% spessartine (Mn₃Al₂Si₃O₁₂), and 1–3% andradite.

3.2. Fe³⁺/ΣFe ratio of garnet obtained by Mössbauer spectroscopy

The Mössbauer results of the Fe³⁺/ΣFe ratio of the selected garnet samples are presented in Table 1 and illustrated in Fig. 6. The And1902 sample contains nearly pure ferric iron, exhibiting a Fe³⁺/ΣFe ratio of 1.00 ± 0.03. The Grs1928 and MelS01 samples are enriched in ferric iron, with Fe³⁺/ΣFe ratios of 0.89 ± 0.03 and 0.97 ± 0.04, respectively. In contrast, the almandine–pyrope–grossular garnets contain trace amounts of ferric iron, with Fe³⁺/ΣFe ratios ranging from 0.01 to 0.07.

Fig. 6 Mössbauer spectra of the selected garnet samples and their Fe³⁺/∑Fe ratios.

4. Discussion

A comprehensive measurement procedure for the EPMA flank method was summarized by Höfer and Brey,¹⁷ encompassing two primary parts: (a) spectrometer calibration (a daily procedure) and (b) flank method measurement. To assess the reliability of the garnet samples in this study, we followed the procedures outlined by Höfer and Brey¹⁷ using the JEOL JXA-8230 EPMA at GIGCAS.

4.1. Spectrometer calibration

The reproducibility and stability of the wavelength-dispersive spectrometer in the EPMA can be affected by various factors, such as electromagnetic interference and laboratory temperature change during long-term analysis. These factors may lead to a shift in the spectrum position. Therefore, it is essential to correct the offset of the spectrometer position before conducting flank method measurements.^17,31

Höfer and Brey¹⁷ provided a daily calibration procedure for the spectrometer to correct the spectral shifts. In contrast to the calibration procedure, we performed spectrometer initialization on a thallium acid phthalate (TAP) spectrometer (slit width = 300 μm) on Day 1, prior to conducting a search for the FeKα₁ 9th order peak on the in-house Fe metal standard (Fe = 99.99 wt%). The operational conditions of 25 kV, 80 nA, and a 1 μm beam were applied to the qualitative scan using the TAP crystal in integral pulse height analysis mode. The scan range on the TAP crystal extends from 189.3 mm to 189.5 mm, with a movement step of 10 μm and a dwell time of 20 000 ms. The FeKα₁ 9th order (fe0) peak on Day 1 was recorded at 189.40 mm. Subsequently, we performed a 50 μm interval shift on both sides (fe₁ and fe₂) of the fe₀ peak to measure the counts at these two positions (Fig. 7). The fe₁ and fe₂ positions were then shifted by ±5 μm, and counts were measured at the corresponding offset positions (Fig. 7).³¹ For each of the six positions (fe₁, fe₁+5, fe₁−5, fe₂, fe₂+5, and fe₂−5), a duration of 180 seconds was allocated to obtain sufficient counts, and three repeated measurements were conducted. The averaged intensity ratio of cps fe₁/cps fe₂ was then calculated (Table 3). The resulting three ratios are plotted against the spectrometer shift of their center (−5, 0, +5) and fitted with a regression line to determine the “true” position of the peak maximum. We arbitrarily defined the cps fe₁/cps fe₂ ratio of 0.957 measured on Day 1 as the “true” spectrometer peak position. On Days 2 and 3, we conducted two runs of spectrometer calibration each day. The first run followed the same procedures as Day 1 without spectrometer initialization. In the second run, we performed spectrometer initialization followed by the routine calibration procedure. The cps fe₁/cps fe₂ ratios before spectrometer initialization measured on Days 2 and 3 was 0.898 and 0.933, respectively (Table 3), indicating a relatively large shift from the “true” position established on Day 1 (Fig. 7). In contrast, the cps fe₁/cps fe₂ ratio on Days 2 and 3 after spectrometer initialization were 0.952 and 0.945, respectively (Table 3), which are very close to the “true” position (Fig. 7). Thus, the spectrometer initialization effectively reduces the spectrometer shift. The complete spectrometer calibration procedure suggested by Höfer and Brey¹⁷ takes approximately 40 minutes in our laboratory. In contrast, the spectrometer initialization operation requires 5 minutes. Therefore, we can perform wave scans for the flank position once on the first day of each session, and the spectrometer shift can be corrected through spectrometer initialization.

Fig. 7 Comparison of the spectrometer position before and after the operation of spectrometer initialization (SPI) for 3 working days. The peak shift was accurately defined by the peak maximum of Fe FeKα₁ 9th order peak on Fe metal (see the text for details).

Table 3 Results of the spectrometer shift for 3 working days^a

Measurements	Spectrometer shift (μm)	Day 1_after SPI		Day 2_before SPI		Day 2_after SPI		Day 3_before SPI		Day 3_after SPI
		3	σ	3	σ	3	σ	3	σ	3	σ
a SPI-spectrometer initialization.
cps fe1/cps fe2	−5	0.883	0.003	0.837	0.013	0.887	0.009	0.864	0.005	0.879	0.009
cps fe1/cps fe2	0	0.957	0.005	0.898	0.009	0.952	0.006	0.933	0.008	0.945	0.024
cps fe1/cps fe2	5	1.041	0.009	0.985	0.014	1.055	0.008	1.025	0.004	1.047	0.013

---

4.2. Flank method measurement

4.2.1. Identifying the flank positions of Fe L_α and Fe L_β. The EPMA flank method is based on the Fe L-line X-ray emission spectra, which exhibit a concomitant change in both the intensity and wavelength of the soft Fe L_α and Fe L_β emission lines.¹⁷ The prerequisite for flank method measurements is the determination of the flank positions of Fe L_α and Fe L_β, which can be derived from the difference spectrum between pure garnet end-member standards (Fe²⁺ and Fe³⁺).

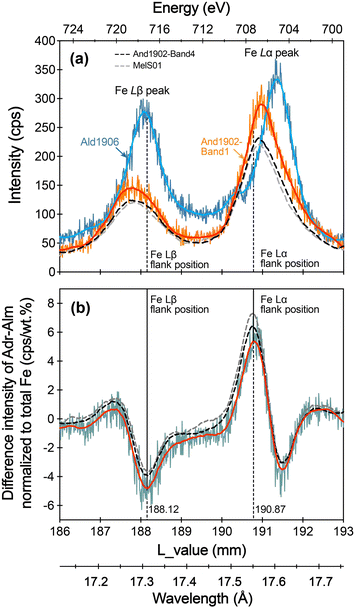
To evaluate the potential influence of chemical zoning in andradite on the determination of the Fe L_α and Fe L_β flank positions, we conducted wave scans on Band 1 and Band 4 of the And1902 sample (Fe³⁺/ΣFe = 1.00 ± 0.03). These bands exhibit different total FeO and Al₂O₃ contents, as well as varying mole percentages of calculated end-members (Fig. 4). Additionally, we scanned another andradite sample, MelS01, which has a comparable FeO content to And1902-Band 4 but a slightly lower Fe³⁺/ΣFe ratio (0.97 ± 0.04). For the Fe²⁺ garnet end-member, the Ald1906 sample (Fe³⁺/ΣFe = 0.01 ± 0.03) was selected for the wave scan.

We conducted the wave scan using an accelerating voltage of 15 kV, a probe current of 80 nA, and a beam diameter of 10 μm, employing a differential pulse height analysis mode. To achieve high intensities, we set an accumulation of twenty measurements for each garnet sample. The scanning range of the L value for the TAP spectrometer extends from 186 to 193 mm. The raw spectra of And1902-Band 1, And1902-Band 4, MelS01, and Ald1906 are presented in Fig. 8a. It shows that the Fe L_α and Fe L_β lines of Ald1906 (Fe²⁺ end-member) are shifted to a higher wavelength compared to those of the andradite samples due to self-absorption.¹⁷ And1902-Band 4 and MelS01 exhibit nearly identical peak intensities. In contrast, And1902-Band 1 displays higher peak intensities for Fe L_α and Fe L_β. Nevertheless, the peak positions of Fe L_α and Fe L_β for Band 1, Band 4 and MelS01 are nearly identical (Fig. 8a). The flank positions of Fe L_α and Fe L_β were defined in the smoothed difference spectrum, with the minimum value representing the Fe L_β flank position and the maximum value representing the Fe L_α flank position (Fig. 8b). Despite the differences in chemical compositions among And1902-Band 1, Band 4, and MelS01 their smoothed difference spectra show almost identical Fe L_α and Fe L_β flank positions (Fig. 8b). The raw spectra of these garnets, along with their difference spectrum, are comparable to those determined from synthetic garnets, as shown in Li et al.²⁴ Given that And1902-Band 1 contains a higher FeO content, which can yield greater intensity during the wave scan, the combination of And1902-Band 1 and Ald1906 is used for identifying the flank positions.

Fig. 8 The flank positions of Fe L_α and Fe L_β based on andradite and almandine samples. (a) Raw spectra of the Fe L-line of And1902-Band 1, And1902-Band 4, MelS01, and Ald1906, which were collected at 15 kV, 80 nA, and a probe diameter of 10 μm in the differential analysis mode. (b) Difference spectra between And1902-Band 1, And1902-Band4, MelS01 and Ald1906 were normalized by using their total Fe content, respectively. The flank positions of Fe L_α and Fe L_β were located by using the maximum and minimum intensities on the smoothed difference spectrum (red lines).

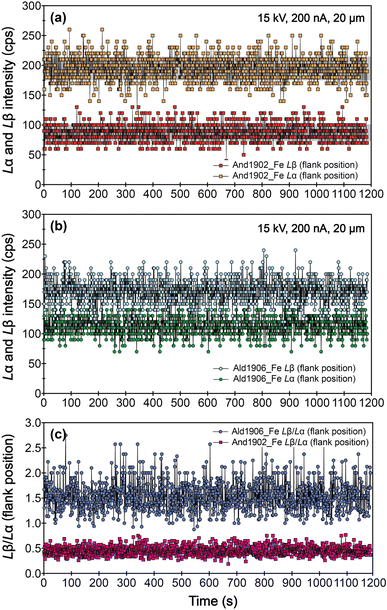
We also evaluated the robustness of the samples under prolonged beam bombardment, using an accelerating voltage of 15 kV, a probe current of 200 nA, and a beam size of 20 μm.²² The results show that the mean intensities of Fe L_β and Fe L_α at flank positions, as well as the Fe L_β/L_α ratios for And1902 and Ald1906, remain consistent for up to 1200 s (Fig. 9). This stability suggests that these garnets can withstand extended exposure to high electron beam current.

Fig. 9 Variation of intensities of Fe L_α (a) and Fe L_β (b) at flank positions, and the L_β/L_α ratios of And1902 and Ald1906 (c) as a function of time.

4.2.2. Analyses of Fe L_β and Fe L_α at the flank position. Using the flank positions of Fe L_α and Fe L_β determined from And1902-Band 1 and Ald1906, we can obtain the intensities of Fe L_β and Fe L_α at these flank positions. In this study, we added two “fake” elements at the TAP spectrometer for the flank method measurements: arsenic (As) for the Fe L_β flank position and bromine (Br) for the Fe L_α flank position. Major elements were arranged on the remaining four spectrometers. The operational conditions included an accelerating voltage of 15 kV, a probe current of 60 nA, and a beam size of 5 μm. Hezel et al.¹⁸ suggested that the mean of 9 to 16 flank method analyses per sample yields the same result as the mean of 25 analyses per sample. In this case, for each garnet sample, at least twelve points were analyzed, with a counting time of 180 s for the flank positions of Fe L_β and Fe L_α, respectively. To verify the reliability of the flank method on our EPMA, we also analyzed the Fe L_β and Fe L_α at the flank positions of nine garnet reference standards with known Fe³⁺/∑Fe ratios (0.03 to 1.01) as reported by Tao et al.²⁷ as monitor standards (provided by Dr H. Höfer), including AND1, FRA1, UA5, UA10, Mir1, Mir2, Mir13, Mir23, and Damknolle. The results of the Fe L_β/L_α ratios at the flank positions of the nine garnet reference standards are listed in Table 4.

Table 4 Chemical compositions and Fe³⁺/ΣFe ratios of garnet reference standards

Sample	AND1		FRA1		Damknolle		Mir1		Mir2		Mir13		Mir23		UA5		UA10
Measurements	10	σ	9	σ	10	σ	10	σ	10	σ	10	σ	10	σ	10	σ	14	σ
a The Fe^3+/ΣFe ratios of reference garnet standards are sourced from Tao et al.^27
SiO2	35.22	0.18	36.17	0.14	39.41	0.18	41.22	0.15	41.02	0.17	40.63	0.15	41.37	0.13	41.73	0.28	41.84	0.31
TiO2	0.01	0.01	0.00	0.00	0.34	0.01	0.40	0.01	0.34	0.01	0.45	0.01	0.41	0.02	0.69	0.03	0.06	0.01
Al2O3	0.69	0.07	19.74	0.12	21.67	0.10	22.99	0.06	22.78	0.08	22.56	0.15	23.03	0.09	19.02	0.12	19.96	0.22
Cr2O3	0.00	0.01	0.00	0.00	0.01	0.01	0.01	0.01	0.01	0.01	0.00	0.01	0.01	0.01	4.31	0.06	4.90	0.13
FeO	26.61	0.18	42.58	0.15	19.31	0.16	11.02	0.15	13.00	0.14	13.52	0.10	10.50	0.14	7.96	0.06	7.46	0.11
MnO	1.13	0.03	0.02	0.02	0.56	0.03	0.34	0.03	0.36	0.02	0.38	0.02	0.32	0.03	0.31	0.02	0.39	0.03
MgO	0.12	0.01	0.44	0.01	11.29	0.04	18.82	0.12	17.16	0.07	16.65	0.13	19.35	0.07	21.48	0.12	21.36	0.22
CaO	33.75	0.12	0.55	0.01	7.60	0.06	5.77	0.05	5.98	0.09	6.22	0.04	5.54	0.05	5.36	0.06	5.11	0.04
Na2O	0.01	0.01	0.02	0.02	0.03	0.01	0.02	0.02	0.01	0.01	0.02	0.02	0.02	0.01	0.05	0.01	0.02	0.01
Total	97.53	0.34	99.52	0.24	100.23	0.29	100.61	0.34	100.67	0.27	100.42	0.32	100.55	0.20	100.90	0.46	101.11	0.39
Fe^3+/ΣFe^a Mössbauer	1.01	—	0.03	—	0.04	—	0.05	—	0.04	—	0.04	—	0.06	—	0.13	—	0.07	—
L β/Lα (net) flank method	0.49	0.01	1.87	0.07	1.21	0.03	0.97	0.03	1.01	0.01	1.03	0.03	0.95	0.02	0.82	0.02	0.84	0.00

---

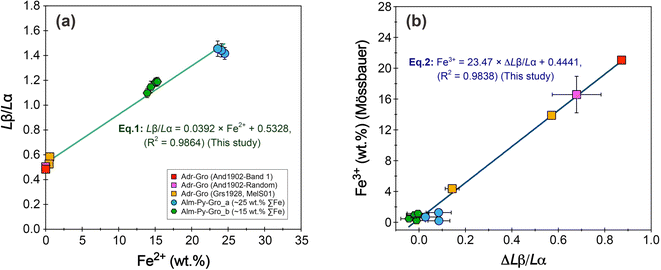
The Fe L_β/L_α ratios of the nine garnet reference standards exhibit a strong positive correlation with their Fe²⁺ contents (Fig. 10). A simple linear regression analysis of these standards yields an equation of L_β/L_α = 0.0410 × Fe²⁺ + 0.5965 (R² = 0.9835), which is comparable to the equation obtained by Tao et al.²⁷i.e., L_β/L_α = 0.0423 × Fe²⁺ + 0.5714 (R² = 0.9893). Therefore, And1902 and Ald1906 serve as reliable garnet reference materials for determining the flank positions of Fe L_α and Fe L_β.

Fig. 10 Simple linear regression of Fe L_β/L_α intensity ratios (flank ratios) against Fe²⁺ contents for nine garnet reference standards. Note that the simple linear regression for the nine garnet reference standards refer to Tao et al.²⁷

4.3. Calculation of garnet Fe²⁺ content and the Fe³⁺/∑Fe ratio

Höfer and Brey¹⁷ demonstrated that the Fe L_β/L_α ratios exhibit a linear correlation with Fe²⁺ content for garnet, with a secondary dependence on total Fe. This correlation leads to the development of a linear equation that enables the quantification of Fe²⁺ content and Fe³⁺/∑Fe in unknown garnet samples.

Ten garnet samples, with Fe²⁺ contents (calculated from the total FeO and Mössbauer Fe³⁺/∑Fe ratios) ranging from 0 to 24.5 wt%, were used as calibration standards to establish the linear equation for garnet. The Fe L_β/L_α ratios of the ten garnet samples are positively correlated with Fe²⁺ contents (Fig. 11a). A simple linear regression analysis yields an equation of

L_β/L_α = 0.0392 × Fe²⁺ + 0.5328 (R² = 0.9864) (1)

Fig. 11 (a) Simple linear regression of Fe L_β/L_α intensity ratios (flank ratios) against Fe²⁺ contents for the ten garnet samples. (b) Plot of the ΔL_β/L_α (defined as the difference of the corresponding point on the Fe³⁺/∑Fe = 0 equi-line from the measured Fe L_β/L_α ratio at a given total Fe, cf., Höfer and Brey.¹⁷) versus Fe³⁺ contents (as calculated from the EPMA analyses of total FeO and Mössbauer analyses of Fe³⁺/ΣFe ratios).

Based on eqn (1), we recalculated the Fe²⁺ content and Fe³⁺/∑Fe of each garnet from the measured Fe L_β/L_α ratios and total FeO (Table 5). The results indicate that the deviation of the calculated Fe²⁺ content and the Fe³⁺/∑Fe ratios exceeded ±1 wt% and ±0.05, respectively, for most of the samples when compared to the data obtained through Mössbauer spectroscopy (Fig. 12a and b). This discrepancy arises because the simple linear regression solely examines the relationship between Fe²⁺ contents and the Fe L_β/L_α ratios. It fails to consider the secondary self-absorption effect that results from the total Fe content, which includes a small contribution from Fe³⁺.¹⁷

Table 5 Chemical compositions and Fe³⁺/ΣFe ratios of garnet reference standards

Classification	Andradite–grossular series				Almandine–pyrope–grossular
Sample	And1902-Band1	And1902	Grs1928	MelS01	Ald1906	Ald1915	Ald1917	Ald1905	Ald1907	Ald1925	Ald1926
Measurements	20	20	12	20	20	16	20	20	20	16	12
Fe Lβ/Lα	0.485	0.504	0.584	0.526	1.417	1.442	1.455	1.098	1.185	1.190	1.147
SD	0.010	0.021	0.025	0.011	0.048	0.054	0.062	0.037	0.034	0.035	0.047
∑Fe (wt%)	21.06	16.59	4.95	14.38	24.75	25.37	24.26	14.16	15.54	16.30	15.58
Recalculated based on the Mössbauer Fe ^3+ /∑Fe ratios
Fe^2+_Moss	0.00	0.00	0.56	0.48	24.54	24.09	23.57	13.92	15.07	15.32	14.43
SD	0.00	0.00	0.02	0.00	0.20	0.28	0.25	0.07	0.06	0.05	0.06
Fe^3+_Moss	21.06	16.59	4.38	13.90	0.21	1.28	0.69	0.24	0.47	0.98	1.15
SD	0.13	2.37	0.17	0.09	0.00	0.02	0.01	0.00	0.00	0.00	0.00
Recalculated using the simple linear regression equation (eqn (1)): L β /L α = 0.0392 × Fe ^2+ + 0.5328
Fe^2+	−1.21	−0.73	1.31	−0.18	22.57	23.21	23.53	14.42	16.63	16.78	15.68
SD	0.27	0.54	0.64	0.27	1.21	1.37	1.58	0.95	0.86	0.89	1.21
Fe^3+/∑Fe	1.06	1.04	0.74	1.01	0.09	0.09	0.03	−0.02	−0.07	−0.03	−0.01
SD	0.01	0.03	0.14	0.02	0.05	0.05	0.07	0.07	0.06	0.05	0.08
Recalculated using the delta equation (eqn (2)): Fe ^3+ = 23.47 × ΔL β /L α + 0.4441
ΔLβ/Lα	0.87	0.68	0.14	0.57	0.09	0.08	0.03	−0.01	−0.04	−0.02	0.00
SD	0.01	0.10	0.03	0.01	0.05	0.05	0.06	0.04	0.03	0.03	0.05
Fe^2+	0.13	0.22	1.16	0.54	22.30	22.94	23.15	13.95	16.10	16.29	15.22
SD	0.24	0.43	0.58	0.25	1.12	1.27	1.45	0.88	0.79	0.82	1.11
Fe^3+/∑Fe	0.99	0.99	0.77	0.96	0.10	0.10	0.05	0.01	−0.04	0.00	0.02
SD	0.01	0.03	0.12	0.02	0.04	0.05	0.06	0.06	0.05	0.05	0.07
Recalculated using the multiple linear regression equation (eqn (3)): Fe ^2+ = −11.18 + 19.05 × L β /L α −0.001 × ∑Fe + 0.22 × Lβ/Lα× ∑Fe
Fe^2+	0.26	0.22	0.57	0.46	23.41	24.22	24.18	13.09	15.37	15.69	14.54
SD	0.24	0.41	0.49	0.23	1.17	1.33	1.50	0.83	0.76	0.79	1.06
Fe^3+/∑Fe	0.99	0.99	0.89	0.97	0.05	0.05	0.00	0.08	0.01	0.04	0.07
SD	0.01	0.02	0.10	0.02	0.05	0.05	0.06	0.06	0.05	0.05	0.07

---

Fig. 12 Comparison of Fe²⁺ content and Fe³⁺/∑Fe ratios of the garnet samples determined by the flank method and by Mössbauer spectroscopy. The Fe²⁺ content and Fe³⁺/∑Fe ratios obtained by the flank method in (a and b) using simple linear regression of the flank-method data and Fe²⁺ content (eqn (1)), in (c and d) using the ΔL_β/L_α-Fe³⁺ equation (eqn (2)), and in (e and f) multiple regression of the flank-method data and total Fe content (eqn (3)). The error bar is 1σ. The solid line is a 1 : 1 line. The dotted lines denote an uncertainty of ±1 wt% for Fe²⁺ and ±0.05 for the Fe³⁺/∑Fe ratio.

Höfer and Brey¹⁷ found that for a garnet with an unknown Fe³⁺ but a known total Fe content, the Fe L_β/L_α ratio of the garnet will plot below the reference line of Fe³⁺/∑Fe = 0. The magnitude of the deviation from the reference line (Δ ratio) is positively correlated with the Fe³⁺ content of the garnet. If a series of garnets with different known Fe³⁺ are available, the linear equation relating ΔL_β/L_α to the Fe³⁺ content of these garnets can be used to determine the Fe³⁺ content of unknown garnet samples.¹⁷ Based on eqn (1), we calculated the ΔL_β/L_α for ten garnet samples (Table 5). The results show that the ΔL_β/L_α is positively correlated with the Fe³⁺ contents (calculated from the total FeO by EPMA analyses and Mössbauer analyses of Fe³⁺/ΣFe ratios) (Fig. 11b), yielding a linear regression of

Fe³⁺ = 23.47 × ΔL_β/L_α + 0.4441 (R² = 0.9838) (2)

The Fe²⁺ contents and Fe³⁺/ΣFe ratios calculated using eqn (2) were plotted on a 1 : 1 line against the Mössbauer values (Fig. 12c and d). While most samples exhibit a deviation in Fe²⁺ contents of less than ±1 wt%, half of these samples show a deviation in Fe³⁺/ΣFe ratios greater than ±0.05. The almandine–pyrope–grossular samples show a larger discrepancy compared to the andradite–grossular samples, as the former contain very low Fe³⁺ content but with dispersed Fe L_β/L_α ratios, which increases the error during the calculation.

Finally, we adopted the flank-method data and total Fe content to calculate the Fe²⁺ content of these samples.¹⁷ Specifically, the equation is given as Fe²⁺ = A + B(L_β/L_α) + C∑Fe + D∑Fe × (L_β/L_α), where the coefficients A, B, C, and D can be determined through multiple regression analysis of the flank-method data, Fe²⁺ content, and the total Fe contents of the ten garnet samples. The multiple regression equation, derived from a total of 196 data points, is expressed as

Fe²⁺ = −11.18(0.737) + 19.05(0.799) × (L_β/L_α) − 0.001(0.040) × ∑Fe + 0.22(0.039) × ∑Fe × (L_β/L_α) (3)

with the numbers in parentheses representing the standard error. This equation was subsequently used to calculate the Fe²⁺ and Fe³⁺ contents of garnet samples. When compared to the results obtained from Mössbauer spectroscopy, the Fe²⁺ contents of the garnet samples exhibit a discrepancy within ±1 wt% (Fig. 12e), while the Fe³⁺/∑Fe ratios of these standards show a discrepancy within ±0.05 (Fig. 12f). Therefore, in contrast to the simple linear equation and the derived ΔL_β/L_α-Fe³⁺ equation, the multiple regression analysis of the flank-method data, Fe²⁺ and total FeO contents of these natural garnet samples provides a higher accuracy for Fe³⁺/∑Fe, particularly for garnet with low Fe³⁺ or total Fe contents.

It should be noted that the calculated Fe³⁺/∑Fe ratio of the Grs1928 sample exhibits a larger standard deviation than that of the other samples, which may be attributed to its low FeO content.²² Recent studies have demonstrated that garnet flank method measurements conducted at 80 nA and 120 nA yield improved analytical precision compared to those performed at 60 nA.^18,21,22 Therefore, a higher probe current could be utilized for garnet during the flank method measurement in the future analysis.

5. Conclusions

We report ten new natural garnets for determining the Fe oxidation state of garnet using the EPMA flank method. This collection includes three samples from the andradite–grossular series and seven samples from the almandine–pyrope–grossular series. The samples And1902 and Ald1906 can serve as primary standards for identifying the flank positions of Fe L_α and Fe L_β. All ten garnet samples can be utilized as reference materials during flank method measurements to calibrate the Fe³⁺/∑Fe ratio of unknown garnet. To determine the Fe²⁺ and Fe³⁺ with the flank method, we recommend employing multiple regression analysis of the Fe L_β/L_α at flank positions, along with Fe²⁺ content and the total Fe content of garnet. This approach yields a low uncertainty in the Fe³⁺/∑Fe ratio. Prior to conducting flank method measurement, it is advisable to initialize the spectrometer for daily calibration, as this can reduce the spectrometer shift and save time.

Data availability

Data for this article are presented in the tables.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Renbiao Tao is thanked for sharing the nine garnet reference standards and for providing valuable suggestions. Puqiu Wu and Qiuxia Wang are recognized for their assistance with the Mössbauer analysis. This study was financially supported by the National Key R&D Program of China (2018YFA0702600) and the Science and Technology Planning Project of Guangdong Province, China (2023B1212060048).

References

1. B. J. Wood and D. Virgo, Geochim. Cosmochim. Acta, 1989, 53, 1277–1291.
2. T. C. Feeley and Z. D. Sharp, Geol, 1996, 24, 1021.
3. M. Enders, D. Speer, W. V. Maresch and C. A. McCammon, Contrib. Mineral. Petrol., 2000, 140, 135–147.
4. M. C. McCanta, M. D. Dyar, M. J. Rutherford and J. S. Delaney, Am. Mineral., 2004, 89, 1685–1693.
5. A. J. Berry, G. M. Yaxley, B. J. Hanger, A. B. Woodland, M. D. De Jonge, D. L. Howard, D. Paterson and V. S. Kamenetsky, Geology, 2013, 41, 683–686.
6. C. A. McCammon, International Kimberlite Conference: Extended Abstracts, 1998, vol. 7, pp. 555–557.
7. M. D. Dyar, D. G. Agresti, M. W. Schaefer, C. A. Grant and E. C. Sklute, Annu. Rev. Earth Planet. Sci., 2006, 34, 83–125.
8. C. A. McCammon, W. L. Griffin, S. R. Shee and H. S. C. O'Neill, Contrib. Mineral. Petrol., 2001, 141, 287–296.
9. C. McCammon, in Modern Mössbauer Spectroscopy: New Challenges Based on Cutting-Edge Techniques, ed. Y. Yoshida and G. Langouche, Springer, Singapore, 2021, pp. 221–266.
10. M. Wilke, F. Farges, P.-E. Petit, G. E. Brown Jr and F. Martin, Am. Mineral., 2001, 86, 714–730.
11. A. J. Berry, H. S. C. O'Neill, K. D. Jayasuriya, S. J. Campbell and G. J. Foran, Am. Mineral., 2003, 88, 967–977.
12. E. Borfecchia, L. Mino, D. Gianolio, C. Groppo, N. Malaspina, G. Martinez-Criado, J. A. Sans, S. Poli, D. Castelli and C. Lamberti, J. Anal. At. Spectrom., 2012, 27, 1725–1733.
13. G. Marras, G. Carnevale, A. Caracausi, S. G. Rotolo and V. Stagno, Eur. J. Mineral., 2023, 35, 665–678.
14. K. D. Burgess, R. M. Stroud, M. D. Dyar and M. C. McCanta, Am. Mineral., 2016, 101, 2677–2688.
15. H. E. Höfer, G. P. Brey, B. Schulz-Dobrick and R. Oberhänsli, East. J. Med., 1994, 6, 407–418.
16. H. E. Höfer, Hyperfine Interact., 2002, 144, 239–248.
17. H. E. Höfer and G. P. Brey, Am. Mineral., 2007, 92, 873–885.
18. D. C. Hezel, H. E. Höfer and A. Fichtner, Am. Mineral., 2024, 109, 1387–1393.
19. N. Malaspina, S. Poli and P. Fumagalli, J. Petrol., 2009, 50, 1533–1552.
20. X. Li, S. Song, L. Zhang and E. H. Höfer, Sci. Bull., 2018, 63, 300–305.
21. M. Holycross, E. Cottrell, J. Ague, A. Lanzirotti and M. Newville, Chem. Geol., 2024, 647, 121937.
22. C. Wang, R. Tao, J. B. Walters, H. E. Höfer and L. Zhang, Geochim. Cosmochim. Acta, 2022, 336, 269–290.
23. M. Tang, C.-T. A. Lee, G. Costin and H. E. Höfer, Earth Planet. Sci. Lett., 2019, 528, 115827.
24. X. Li, C. Zhang, R. R. Almeev, X.-C. Zhang, X.-F. Zhao, L.-X. Wang, J. Koepke and F. Holtz, Chem. Geol., 2019, 509, 152–162.
25. C. Zhang, R. R. Almeev, E. C. Hughes, A. A. Borisov, E. P. Wolff, H. E. Höfer, R. E. Botcharnikov and J. Koepke, Am. Mineral., 2018, 103, 1445–1454.
26. E. C. Hughes, B. Buse, S. L. Kearns, J. D. Blundy, G. Kilgour, H. M. Mader, R. A. Brooker, R. Balzer, R. E. Botcharnikov, D. Di Genova, R. R. Almeev and J. M. Riker, Am. Mineral., 2018, 103, 1473–1486.
27. R. Tao, Y. Fei, E. S. Bullock, C. Xu and L. Zhang, Geochim. Cosmochim. Acta, 2018, 225, 1–16.
28. E. F. Baxter, M. J. Caddick and J. J. Ague, Elements, 2013, 9, 415–419.
29. Q. Wang, X. Ping, J. Zheng and H. Dai, Earth Sci., 2023, 48, 1217–1231.
30. A. J. Locock, Comput. Geosci., 2008, 34, 1769–1780.
31. H. E. Höfer, S. Weinbruch, C. A. Mccammon and G. P. Brey, East. J. Med., 2000, 12, 63–71.

---