 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Isotopic ratio analysis of individual sub-micron particles via spICP-TOFMS†
Sarah E.
Szakas
 and
Alexander
Gundlach-Graham
and
Alexander
Gundlach-Graham
 *
*
Department of Chemistry, Iowa State University, Ames, IA, USA. E-mail: alexgg@iastate.edu
First published on 30th May 2024
Abstract
We investigate the use of single particle inductively coupled plasma time-of-flight mass spectrometry (spICP-TOFMS) to measure isotopic ratios within individual sub-micron particles and explore the advantages and limitations of this method. Through the analysis of samarium (Sm) isotopes—147Sm and 149Sm—in individual monazite particles, and lead (Pb) isotopes—206Pb and 208Pb—in individual galena particles, we demonstrate that isotope ratios recorded by spICP-TOFMS have precision controlled by Poisson statistics. This precision depends on the signal amount measured per isotope from an individual particle: as particle size increases, more counts of each isotope are detected, and the precision improves. In monazite particles with mass amounts of Sm from 0.04 to 4 fg, recorded isotope-ratio precision (relative standard deviation, RSD) ranged from 43% to 5%. However, the average isotope ratio from a particle population is still accurate; the molar ratio determined for 149Sm/147Sm was 0.912, which is within 1% of the expected ratio. Lead isotopic composition varies widely in nature because 206Pb, 207Pb, and 208Pb are radiogenic isotopes that decay from thorium (Th) and uranium (U). In the analysis of lead isotopes from galena particles, we found that the RSD for 208Pb/206Pb ratio ranged from 32% to 2% for particles with 1.4 to 80 fg of Pb. We further explore the use of spICP-TOFMS for radiometric dating of monazite particles. Monazite is used in geochronology for radiometric dating based on 208Pb/232Th and 206Pb/238U ratios. spICP-TOFMS analyses of individual monazite particles that contain only 0.02–80 fg of Th and 0.03–30 fg of U showed radiogenic Pb-isotope signatures and a median age of 550 Ma. We also show that the spread of ages from monazite particles is broader than explainable by Poisson statistics, revealing real variation in age or depletion/enrichment of Pb, Th, and/or U in the particles. Overall, we demonstrate that spICP-TOFMS can be used for accurate isotope-ratio analysis with precisions down to a few percent; however, understanding measurement noise is critical to define the significance of isotope ratios measured from individual particles.
1 Introduction
Isotope ratio measurements obtained by inductively coupled plasma mass spectrometry (ICP-MS) are utilized in many fields such as nuclear chemistry,1,2 archeology and anthropology,3,4 geochronology and geochemistry,5,6 and environmental science.7 ICP-MS offers high sensitivity, low detection limits (usually in the low parts per trillion level), large linear dynamic range, and straight-forward sample preparation. Compared to other mass spectral techniques, such as thermal ionization mass spectrometry (TIMS) and secondary ion mass spectrometry (SIMS), ICP-MS offers similar precision and accuracy while also providing higher throughput.7,8 While precisions of ICP-MS with a quadrupole detector have been reported to have relative standard deviations (RSDs) of ≥0.1%, multi-collector (MC) ICP-MS can deliver isotope ratio RSDs down to 0.002% and lower,9,10 and so these are the ICP-MS instruments of choice for precise and accurate isotope-ratio measurements. In conventional MC-ICP-MS isotope-ratio analyses, ‘bulk’ samples are homogenized and digested, and elements of interest may be isolated through chromatographic techniques before analysis by MC-ICP-MS. While this procedure results in stable isotopic signals and good precision, an obvious drawback is that only average isotopic composition of a sample is recorded; information on isotope variation within a sample is lost. In the context of geochronology, in situ analysis via laser-ablation (LA) MC-ICP-MS has increasingly become the standard method.11,12 Many minerals important for radiometric dating (e.g. zircon, monazite) have pronounced zonation due to different growth stages, and thus can show variable ages across a single grain. The combination of mineral mapping with microscopy approaches or trace-element imaging by LA-ICP-MS, and single-spot analysis for isotope-ratio determination by LA-MC-ICP-MS allows for mineral- and zone-specific isotope-ratio dating.6,13–15 More recently, whole mineral isotope imaging with LA-ICP-MS, has emerged as an approach to perform comprehensive in situ dating of mineral samples.16,17Multi-collector ICP-MS instruments provide substantially better isotope-ratio determination precision than quadrupole-based ICP-MS instruments because isotope signals are measured simultaneously at dedicated detectors and time-dependent correlated noise sources (e.g., plasma flicker, drift, etc.) can be eliminated through signal ratioing. However, the number of mass-to-charge ratios (m/z) detectable with a MC instrument is constrained by the physical number of detectors and the available relative m/z-range of ∼15%.18 State-of-the-art MC ICP-MS instruments may be equipped with between 11–16 Faraday cup or electron multiplier detectors; the number and type of detectors used are determined based on analyte isotopes of interest and the sensitivity required to detect them.19,20 On the other hand, to detect multiple isotopes across the whole elemental mass range quasi-simultaneously, a time-of-flight (TOF) mass analyzer can be used. In previous research, ICP-TOFMS has been characterized for isotope ratio analysis in terms of mass bias and isotope fractionation for light, mid-mass, and heavy isotopes: B, Sr, and Pb.21 This study found that precision for 208Pb/206Pb was around 0.1% when a 1000 ng mL−1 solution of Pb was analyzed.21 In other work, RSD values from 0.41–0.06% were obtained for analysis of 208Pb/206Pb ratios from Pb standards with concentrations from 1 to 100 ng mL−1.22 Both previously mentioned studies used 10 s acquisition times. With extended analysis times (up to 100 s), which produce more total ion counts, isotope ratio precisions for 107Ag/109Ag and for 151Eu/153Eu have been reported as low as 0.056 and 0.02%.23,24 All mentioned studies on ICP-TOFMS isotopic analysis were carried out on dissolved samples.
In recent years, single-particle (sp) ICP-MS has emerged as powerful and high-throughput method to measure the particle number concentrations (PNCs), and element mass amounts in individual nanoparticles (<100 nm), sub-micron particles (<1000 nm), and microparticles.25–27 In spICP-MS, a dilute suspension of particles is introduced into the ICP, where the particles are vaporized, atomized, and ionized. The resulting ion clouds are transmitted into the mass analyzer and m/z-specific particle-derived ion clouds are recorded as signal spikes by the MS detector. The particle-derived signal events are typically ∼250–1000 μs in duration. With quadrupole-based mass analyzers, only one m/z can be quantitatively recorded per particle-derived signal.28,29 However, with multi-channel mass analyzers, such as multi-collector sector-field or TOF mass analyzers, signals from multiple m/z can be recorded from an individual particle.30–32 In particular, ICP-TOFMS instruments allow the collection of complete elemental mass spectra with sufficient time resolution to record single-particle events.33 spICP-TOFMS has been used extensively to analyze mixtures of nano- and micro-particles from a wide range of environmental sample types. With spICP-TOFMS, many researchers aim to detect and classify natural and anthropogenic particles based on particle-type specific multi-element signatures.34–38 Just as multi-element fingerprints allow for particle type classification, the analysis of isotope ratios of individual particles could be used to gain insights into particle origin.
To date, only a handful of researchers have reported the measurement of isotope ratios by spICP-MS. Yamashita et al. measured 30, 50, and 70 nm Pt NPs by single-particle MC-ICP-MS and demonstrated that RSD followed counting statistics and ranged from 40–10% for the smaller to larger Pt NPs. Similarly, Hendriks et al., reported 194Pt/195Pt ratios measured in 70 nm Pt NPs by spICP-TOFMS, though no isotope-ratio precision value was provided.39 von der Au et al. and Aramendía et al. independently reported the use of isotope dilution combined with spICP-TOFMS to determine the sizes of Pt NPs and Ag NPs, respectively.40,41 Montaño et al. reported Pb-isotope ratios determined by spICP-TOFMS from particles in boreal rivers in Canada.42 Manard et al. and Tian et al. each investigated 107Ag/109Ag isotope ratio accuracy and precision measured via spICP-TOFMS and found that isotopic ratio precision is well described by Poisson counting statistics.43,44 Finally, Bland et al. demonstrated that TiO2 engineered nanoparticles enriched with 47Ti could be used to track the fate and transport of anthropogenic TiO2 particles against a natural particle background in soils through measurement of the 47Ti/48Ti ratio in individual particles by spICP-TOFMS.45
Here, we characterize the expected measurement variability in isotope-ratio measurements by spICP-TOFMS through the analysis of stable isotope ratios within two mineral samples: monazite (REE(PO4)) and galena (PbS). We measure 149Sm/147Sm isotope ratios in monazite particles, 208Pb/206Pb ratios in galena particles, and explore the use of 208Pb/206Pb ratios to differentiate each mineral type. To further illustrate the capabilities of spICP-TOFMS for isotopic analysis, we measure 208Pb/232Th and 206Pb/238U ratios in the monazite particles to estimate their ages. We also developed Monte-Carlo Poisson confidence bands to account for the spread in spICP-TOFMS signal ratios due to Poisson noise. Based on these confidence bands, we can identify true isotope ratio outliers in our measured particle populations.
2 Methods and materials
2.1 Submicron particle suspensions sample preparation
Mineral samples used in this study include both monazite (REE(PO4)) and galena (PbS).46,47 The monazite sample arrived at our lab pre-ground. The original monazite sample was extracted from a rock sample containing a monazite crystal (acquired from Sieber and Sieber AG, Switzerland). Once extracted, the monazite was broken into smaller fragments, and those free of the original host rock were selected to be ball milled (4 min, Retsch Mixer Mill MM400). About 10 mg of monazite powder was diluted into 50 mL ultrapure water (18.2 MΩ PURELAB flex, Elga LabWater, United Kingdom), vortexed for 60 seconds, and water bath sonicated for 10 minutes (VWR, PA, USA). An aliquot was then pipetted into a 2 mL Eppendorf tube (Eppendorf, Germany) and ultrasonicated with a program of 10 s on, 5 s off for 60 s (100 W, VialTweeter, Hielscher UP200st, Germany). The suspension was allowed to settle for 10 minutes and aliquots were pipetted from the top for a subsequent ∼4× dilution. This procedure was done so no large particles (i.e., particles with diameters >3 μm that may not fully vaporize in the ICP) were sampled. The final particle number concentration (PNC) of the suspension used for analysis was ∼4.3 × 105 particles per mL. While only one mineral stock suspension was prepared, two replicate spICP-TOFMS measurements were run, each with ∼120 s of spICP-TOFMS data.A sample of galena was obtained via the Iowa State University Department of Geological and Atmospheric Sciences. The sample was ball milled (6 min, SPEX mixer/miller 8000M) and underwent the same sample preparation as the monazite suspension. The diluted particle suspension used for analysis had a spICP-TOFMS-determined PNC of ∼9.3 × 104 particles per mL. Three replicate measurements (each with ∼90 s of data acquisition) of the galena suspension were used for particle analysis.
All sample dilutions were prepared in ultrapure water spiked with Cs to a concentration of 5 ng mL−1, as Cs is used in our analysis as an uptake standard to calculate transport efficiency with microdroplet calibration.
2.2 Analytical instrumentation and data analysis
Online microdroplet calibration was used to obtain matrix-matched calibration, to determine mass amounts of isotopes per particles, and to determine sample-specific PNCs.48,49 Details of the online microdroplet calibration method have been reported previously.48,50,51 Two calibration solutions were used for spICP-TOFMS analysis of the two mineral types. Both solutions contain the same elements—Cs, Sm, Pb, Th, and U—but at different concentrations. Solutions were made gravimetrically from single-element standard solutions (High Purity Standards, Charleston, SC, USA) and prepared in 1% HNO3 (w/v, in-house sub-boiled nitric acid, Savillex Corp, MN, USA). Importantly, the calibration solutions used in our experiments are element standards and not isotope standards, meaning they are unverified regarding isotopic abundances. The concentrations of isotopes within the microdroplet solutions were calculated according to isotopic abundance values given by IUPAC.52 Lack of use of isotopic standards may lead to systematic errors in the accuracy of determined isotope ratios and ages; however, use of element standards does not impact the discussion of precision of spICP-TOFMS measurements. In Table S2,† we provide detailed parameters for the online microdroplet calibration measurements.
We analyzed spICP-TOFMS data with TOF-SPI (TOF Single-Particle Investigator),53 an in-house batch analysis program created in LabVIEW (LabVIEW 2018, National Instruments, TX, USA). TOF-SPI calculates the critical value (LC,sp,i) and the critical mass (XmassC,sp,i) of specified elements/isotopes (i). LC,sp,i is the count threshold criteria used to distinguish whether a signal is particle-derived or from the steady-state background. TOF-SPI background subtracts all particle data, corrects for split events, calculates absolute sensitivities, and determines PNCs and mass amounts of detected elements/isotopes within each particle. To ensure all spICP-TOFMS data are recorded within the linear working range of the ICP-TOFMS instrument, we remove all particle-derived signals with over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TofCts (summed counts from selected elements/isotopes used for analysis).54 While monazite contains many rare earth elements (Ce, La, Nd, etc.), and all were detectable within the particles, we did not quantify these elements. Sulfur and phosphorous, which are major elements in galena and monazite, respectively, were not detectable at the single-particle level with our ICP-TOFMS tune settings, which were optimized for mid-to-high m/z.
000 TofCts (summed counts from selected elements/isotopes used for analysis).54 While monazite contains many rare earth elements (Ce, La, Nd, etc.), and all were detectable within the particles, we did not quantify these elements. Sulfur and phosphorous, which are major elements in galena and monazite, respectively, were not detectable at the single-particle level with our ICP-TOFMS tune settings, which were optimized for mid-to-high m/z.
Monte Carlo Poisson confidence bands were also generated in LabVIEW. In this Monte Carlo approach, signals from two isotopes (A and B) with average rates (λA and λB), and a known signal ratio (λA/λB) are simulated. First, a series of average signal values (λA and λB) are created across a range of signal levels based on the known λA/λB ratio. Random draws (N = 105) from Poisson distributions with means of λA and λB are then taken, and the ratios of these Poisson-sampled signals are obtained. For each λA and λB, the confidence intervals are established at the 2.5% and 97.5% percentiles of the Poisson-sampled signal ratios. Confidence bands at the 95% significance level are created by compiling the confidence intervals at all simulated λA and λB values. Confidence bands generated in the signal domain are converted to the amount (i.e., mass) domain using the absolute sensitivities for measured for isotopes A and B.
3 Results and discussion
In this study, we aim to determine whether spICP-TOFMS is a viable technique to use for isotopic analysis, and to explore this method's advantages and limitations. In spICP-TOFMS analysis, the ability to accurately and precisely measure a given isotope's signal depends on its abundance within a particle, the critical mass required to detect the isotope (which depends on sensitivity and signal background levels), and detection noise. In the best-case scenario, particles will have a known size distribution, conserved isotope ratios, and Poisson noise will be the only uncorrelated noise source. In such a case, the measurement of ratios will be “Poisson-limited”. However, even with these conditions, spICP-TOFMS measures a range of isotope ratios that vary as a function of particle size. To illustrate this, in Fig. 1, we plot results from the Monte Carlo simulation of spICP-TOFMS signals from 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles with arbitrary isotopes, A and B. In our simulation, particles are modelled with a Log-Normal particle size distribution of 75*/1.5 nm,55 a particle density of 5.15 g mL−1, a conserved isotope ratio of 10/1 (A/B), absolute sensitivities of 1 × 1017 TofCts per g for both A and B, and equal critical values (LC,sp = 5 TofCts). The size and density parameters were selected to best replicate the real monazite mineral particles used in this study, and the other parameters were selected to simplify the explanation and illustration of the data treatment for these simulated particles. Fig. 1A is a graphical description of the Monte Carlo simulation for anticipated measured responses for isotopes A and B. As seen in Fig. 1A, the whole mass distribution of the lower abundance isotope B is not measurable by spICP-TOFMS because many particles have mass amounts of B below the critical mass (XmassC,sp,B).
000 particles with arbitrary isotopes, A and B. In our simulation, particles are modelled with a Log-Normal particle size distribution of 75*/1.5 nm,55 a particle density of 5.15 g mL−1, a conserved isotope ratio of 10/1 (A/B), absolute sensitivities of 1 × 1017 TofCts per g for both A and B, and equal critical values (LC,sp = 5 TofCts). The size and density parameters were selected to best replicate the real monazite mineral particles used in this study, and the other parameters were selected to simplify the explanation and illustration of the data treatment for these simulated particles. Fig. 1A is a graphical description of the Monte Carlo simulation for anticipated measured responses for isotopes A and B. As seen in Fig. 1A, the whole mass distribution of the lower abundance isotope B is not measurable by spICP-TOFMS because many particles have mass amounts of B below the critical mass (XmassC,sp,B).
Throughout the manuscript, data will follow the format presented in Fig. 1B and C. In Fig. 1B, the simulated spICP-TOFMS signals of isotopes A and B are plotted to determine their correlation. Isotope signals are not measurable below their respective LC,sp values, and the relative uncertainty (i.e., the relative spread) of the measured signal ratio decreases as the intensity of the signals in the particles increase, i.e., as the sizes of the particles increase. Since Fig. 1B is on a log–log scale, only particle events with measurable amounts of both isotopes A and B are plotted. All spICP-TOFMS particle signal data is displayed in “TOF counts” (TofCts).56 Data in the signal domain can be converted to mass, or molar, amounts using the determined isotope-specific sensitivities.
In Fig. 1C, we provide a density scatter plot of the isotope signal ratios recorded from individual particles versus the signal of the major isotope. Understanding the shape and spread of data in this scatter plot is important for assessing spICP-TOFMS isotope-ratio performance. First, as seen in Fig. 1C, no isotope ratio signals are measurable to the left of a defined boundary (TofCts A/LC,sp,B) because to the left of this line, signals of B have values below LC,sp,B, and are therefore not detectable. This low-signal cutoff indicates that the measurable isotope ratio between A and B is particle-size (or isotope-abundance) dependent. Second, as the signals from particles increase (which corresponds to a larger diameter and more mass), the isotope signal ratios converge to the known ratio (here, 10/1 for A/B). The isotope-ratio is systematically biased in smaller particles; the contribution of the minor isotope is over-determined because at counts close LC,sp, only signals from the upper tail of the signal distribution with added Poisson noise are detectable. Finally, the confidence bands in Fig. 1C show the majority of spread in the isotope-ratio data is explainable by Poisson-Normal statistics (black), but that Monte Carlo estimated Poisson confidence bands (green) provide an even better match with the spread of the isotope-ratio data. At low count rates (λ < 5), the Poisson-Normal approximation (in which confidence intervals are calculated with z-scores from Normal distribution with σ = λ1/2) fails because the distribution is highly skewed.57–59 Monte Carlo Poisson confidence bands account for this skew and thus better match the spread of our spICP-TOFMS data. For particles with conserved isotope ratios, but variable sizes, our simulations show that few outliers are expected beyond the Monte Carlo Poisson confidence bands.
3.1 Stable isotope-ratio analysis by spICP-TOFMS
In experimental spICP-TOFMS data, just as with the simulated data, conserved isotope ratios in a population of particles are expected to converge to a single value and the spread of the ratios should be within the Monte Carlo Poisson confidence bands. To evaluate this hypothesis, spICP-TOFMS analyses of two isotope pairs from two unique mineral particle types were performed: 149Sm/147Sm in monazite and 208Pb/206Pb in galena.Monazite is rich in many light rare earth elements, including Ce, La, Pr, Nd, and Sm, in addition to Th and U. For our analyses, we chose to quantify the isotope ratio of 149Sm/147Sm because these isotopes are moderately abundant in the particles and do not have any significant isobaric interferences. 149Sm is a stable isotope with a molar abundance of 13.8%; 147Sm is an extremely long-lived radio-isotope (half-life of 1.06 × 1011 years) with a natural molar abundance of 15.0%.52 In Fig. 2A, we plot the molar ratio of 149Sm to 147Sm recorded in the monazite particles. As seen, the measured molar ratio from the population of monazite particles is 0.91, which is within 1% of the expected natural 149Sm/147Sm ratio of 0.92. In Fig. 2B, we plot the signal ratios of 149Sm/147Sm vs. the signal measured for 149Sm. The 149Sm/147Sm TofCts ratio converges to 0.99, and the measured isotope-ratio population follows the same general shape as predicted by our Monte Carlo simulation (see Fig. 1C). Likewise, the Monte Carlo Poisson confidence bands predict the spread of the isotope-ratio data.
In Fig. 2C and D, we plot results from the analysis of Pb isotopes from individual galena particles. 206Pb, 207Pb and 208Pb are radiogenic isotopes that are commonly used in fields such a geology, archeology, and aerosol science for applications such as radiometric dating and source apportionment.60,61 Galena samples can have distinct Pb molar ratios of 208Pb to 206Pb based on their origin; however, the ratios of 208Pb/206Pb are expected to be close to ∼2 and are typically consistent within a single sample. The galena sample we analyzed has a stable 208Pb/206Pb molar ratio of 1.86 (mass ratio of 1.88), as shown in Fig. 2C. This molar ratio is consistent with others reported for galena.62 The density scatter plot in Fig. 2D differs slightly from the Sm isotope ratios shown in Fig. 2B in that there are multiple spots with high density. These “hot spots” could indicate a multi-modal size distribution for the galena particles. While the size distribution of this particle population was not further confirmed with other techniques, these multiple areas of overlapping data points indicate the population detected is characterized by multiple particle sizes. In our measurements, dissolved steady-state background measured in the galena samples prohibits the detection of small particles, which are expected to have higher PNCs in natural samples.63 This limits the number and size of particles detected. It could be that a large population of small galena particles is undetected in our spICP-TOFMS analysis, which would, if detectable, show high density similar to the monazite particles in Fig. 2B. Nonetheless, the spread in 208Pb/206Pb isotope-ratio data is effectively described by Monte Carlo Poisson confidence bands, which demonstrates that the isotope-ratio is constant in the galena particles.
Precision in isotopic ratio analysis is usually reported as the RSD of the ratio over multiple sample measurements. In spICP-TOFMS, each measured particle is a sample, and the RSD of the analysis depends on the particle size and isotope abundance. In Fig. 3, we plot the RSD for 149Sm/147Sm and 208Pb/206Pb as a function of the determined mass of 149Sm and 208Pb, respectively. To obtain these plots, the logarithms (base 10) of particle-signal intensities of 149Sm and 208Pb were taken and binned at increments of 0.1. Isotope ratio precisions (i.e., RSDs) from data within the log-bins were then calculated. As seen in Fig. 3A, the RSD of the 149Sm/147Sm ratio matches closely with that predicted by Poisson statistics. For the Sm isotopes, RSDs range from 43% to 5% for average TofCts from 10 to 800 for 149Sm. The best precision we achieved was 5%; for an RSD of 2%, almost 5000 counts (i.e., 12 fg) of 149Sm would be required. The initial increase in RSD for the 149Sm/147Sm ratio is an artifact in the data due to the low-signal cutoff for the ratio (i.e. TofCts 149Sm/LC,sp,147Sm) as seen in Fig. 3A (pink dashed line). This cut-off restricts the range of isotope ratios able to be recorded and thus also restricts the range of deviations possible.
Unlike the Sm isotope-ratio precision, the RSD of 208Pb/206Pb from galena (see Fig. 3B) deviates from the precision predicted by Poisson statistics, though the general trend of a lower RSD with larger particle size is followed. Deviation from the Poisson-predicted RSD could be partly caused by the low and inconsistent numbers of particles within each log-bin. The total PNC of the analyzed galena particles is ∼5× less than that of the Sm-containing monazite particles. Additionally, the high background of 206Pb and 208Pb signals could introduce non-negligible noise that is propagated during background subtraction but is not accounted for in Poisson-predicted RSDs. This background noise causes the RSDs of the ratios to be elevated compared to the Poisson-predicted RSDs. Nonetheless, the measured precision for 208Pb/206Pb in these particles ranged from 32% to 2% for particles with 1.4 to 80 fg of Pb (which correspond to estimated particle diameters from 75 to 290 nm, assuming spherical shape and a density of 7.6 g mL−1).47 For spICP-TOFMS analysis, the maximum detectable cumulative isotopic signal in a single particle event is ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TofCts; above this signal level, the detector saturates, and the isotope-ratio is no longer quantitative. Thus, the lowest isotope-ratio precision at the single-particle level is ∼1.4% (10k TofCts for each isotope). In our analysis of in situ208Pb/206Pb ratios in galena particles, the 2% RSD achieved for the largest particles is near the performance limit of spICP-TOFMS.
000 TofCts; above this signal level, the detector saturates, and the isotope-ratio is no longer quantitative. Thus, the lowest isotope-ratio precision at the single-particle level is ∼1.4% (10k TofCts for each isotope). In our analysis of in situ208Pb/206Pb ratios in galena particles, the 2% RSD achieved for the largest particles is near the performance limit of spICP-TOFMS.
3.2 Isotope-ratio fingerprinting by spICP-TOFMS
Single particle ICP-TOFMS enables the detection and quantification of multiple isotopes within individual particles and the rapid measurement of thousands of particles, making it a viable technique for isotope-fingerprinting of rare particle events. For example, this could be useful for source apportionment of aerosols,64,65 or nuclear forensics.66,67 In Fig. 4, we present TOF mass spectra from the analysis of single particles of monazite and galena. As seen, the monazite particles have a radiogenic lead signature with a much higher relative abundance of 208Pb compared to the ‘natural’ Pb isotope ratios recorded from galena particles and microdroplet standards. While the monazite particles contain detectable amounts of 206Pb, 207Pb, and 208Pb, they lack sufficient amounts of non-radiogenic 204Pb to be detected at the single-particle level. In contrast, 204Pb is detectable in ∼68% of all galena multi-metal particles.In Fig. 5, we provide scatter plots of the mass ratios of 208Pb/206Pb recorded from monazite and galena particles. While the galena particles have a 208Pb/206Pb ratio that converges to ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the 208Pb/206Pb ratio in the monazite particles is much more scattered with a ratio that converges to ∼10
1, the 208Pb/206Pb ratio in the monazite particles is much more scattered with a ratio that converges to ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. While these two minerals can be identified based on other elements present in monazite (rare earth elements), this highlights the potential use of spICP-TOFMS to find isotopic enrichment within particles (for Pb or other isotopes of interest) or for isotope fingerprinting applications. Single particle ICP-TOFMS requires low sample amounts, and particle-resolved isotope measurement provides more information than a bulk digest if mixtures of particle types are present.
1. While these two minerals can be identified based on other elements present in monazite (rare earth elements), this highlights the potential use of spICP-TOFMS to find isotopic enrichment within particles (for Pb or other isotopes of interest) or for isotope fingerprinting applications. Single particle ICP-TOFMS requires low sample amounts, and particle-resolved isotope measurement provides more information than a bulk digest if mixtures of particle types are present.
Monazite particles are rich in LREEs and Th, and can also contain significant amounts of U. The radiogenic Pb-isotope signatures detected in the monazite particles by spICP-TOFMS originate from the radioactive decay of 232Th and 238U to 208Pb and 206Pb, respectively. 208Pb has a much higher abundance than 206Pb because the monazite particles have ∼20× more Th than U (see Fig. S1†). 207Pb is also measured in the monazite particles and is the final decay product of 235U; however, 235U is not detectable in these particles, likely due to the low initial abundance of this isotope in the monazite and the shorter half-life of 235U compared to 238U. We further confirmed the presence of Pb, Th, and U in a limited number of monazite particles by SEM-EDS, which can be found in Fig. S2 and S3.† The clear radiogenic isotope signature of Pb in the monazite particles, along with the absence of non-radiogenic 204Pb, indicates that these particles may be suitable for geochronological dating using the 232Th–208Pb and 238U–206Pb systems.
3.3 Application of sp-isotopic analysis to geochronology
The decays of 232Th to 208Pb and 238U to 206Pb are commonly analyzed in monazite to determine the age of the minerals and better understand the conditions surrounding their formation.68 Monazite incorporates significant amounts of Th and U during formation, but does not tend to incorporate Pb. Monazite grains have high thermal stability (closing temperature > 800 °C) and are not very susceptible to radiation damage, which limits depletion of radiometric Pb.69 The age of a monazite sample can be estimated from first-order decay of 232Th and 238U as shown in eqn (1),70 where N is the number of atoms/moles of the parent isotope measured, N0 is the number of atoms/moles originally present in the sample, λ is the rate constant, and t is time. In our spICP-TOFMS analysis of monazite particles, we did not detect 204Pb even in particles with high mass amounts of other elements (indicating a large particle), thus we assume no “common” Pb was incorporated in the monazite grain at formation and that all 208Pb is thorogenic and all 206Pb is uranogenic. Assuming no initial amount of Pb, eqn (1) can be simplified as shown in eqn (2), using the 232Th–208Pb system as an example. The half-life (t1/2) of 232Th is around 14 billion years, whereas the half-life of 238U is around 4.5 billion years.71 | (1) |
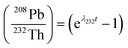 | (2) |
In our analyses, only spICP-TOFMS particle-derived signals with measurable amounts of 206Pb and 238U and/or 208Pb and 232Th were considered. Around 86% of multi-metal monazite particles contain measurable amounts of both 232Th and 208Pb; ∼47% of these particles contain measurable amounts of 238U and 206Pb. In Fig. 6, we provide density scatter plots of the Th–Pb and U–Pb ages determined for individual monazite particles with estimated diameters from 37 to 639 nm, assuming a density of 5.2 g cm−3 and an average monazite particle stoichiometry of (Ce0.44La0.14Nd0.12Pr0.08Th0.23)PO4. In Fig. S4,† we provide a histogram comparing the recorded ages in the particles; Th–Pb and U–Pb systems both yield a median age of 550 Ma. As seen in Fig. 6, while the determined single-particle Th–Pb and U–Pb ages converge to similar values, the spread of the determined ages is greater than predicted by Poisson statistics and does not match the shape expected for homogeneous isotope ratios (see Fig. 1). Particles with measured isotope ratios that fall outside the Monte Carlo Poisson confidence bands likely do not belong to the same particle population with an age that converges to ∼550 Ma. These outlier monazite particles could be the result of true age differences via zonation of monazite grains,68 or could be due to the depletion or enrichment of Pb, Th, or U from processes such as chemical weathering. For example, monazite particles with depleted Pb would appear younger, whereas particles enriched in Pb would appear older. Particles could also have “common lead” that the radiogenic Pb signal was not normalized against because 204Pb was not detectable, which would alter the ages measured. Regardless of the cause of outlier ages, our spICP-TOFMS analysis demonstrates that these outliers are not analytical artifacts and that the precision achievable for dating sub-micron particles by spICP-TOFMS is not solely limited by Poisson statistics of spICP-TOFMS measurements, but also by true heterogeneity of the particles analyzed.
4 Conclusions
We demonstrated that spICP-TOFMS can perform isotope-ratio analysis of individual sub-micron particles; however, the relatively low signals measurable from single particles caps the Poisson-limited isotope-ratio precision at ∼1.4%. For small particles with low counts of analyte isotopes, isotope-ratio precisions greater than 10% are common. With Monte Carlo simulations and the analysis of stable Sm and Pb isotopes, we demonstrate that the spread in spICP-TOFMS-determined isotope-ratios is predictable and dominated by Poisson error. For monazite particles, 149Sm/147Sm RSD ranged from 43% to 5%. Similarly, for galena particles, 208Pb/206Pb RSD ranged from 32% to 2%. The large spread in RSD highlights that isotope-ratio analyses of individual particles by spICP-TOFMS should always consider the mass amounts of the isotopes measured. When the mass amounts of isotopes of interest are low within particles, the precision of the analysis may limit the ability to determine accurate ratios and identify particles with anomalous ratios.We also demonstrate, for the first time, the radioisotope dating of individual monazite particles by spICP-TOFMS through the analysis of 208Pb/232Th and 206Pb/238U isotope ratios. We determined that the age of our sample is approximately 550 Ma. The determined age is most likely inaccurate, as we did not confirm the age through other techniques or use isotopic standards for the analysis. Nonetheless, our results show that spICP-TOFMS provides sufficient sensitivity to determine reasonable ages at the single-particle level. Since dating of individual particles requires the use of isotopic ratios, accurate spICP-TOFMS dating requires the analysis of large particles. For example, to obtain less than a 5% RSD on the predicted age of monazite particles, we would need to measure particles with at least ∼60 fg of Th. The upper limit on the precision available for spICP-TOFMS is defined by TOFMS detector saturation, and so extension of the linear dynamic range to measure more signal per isotope per particle would improve RSDs achievable.
While RSDs achievable by spICP-TOFMS are significantly higher than those reported with MC-ICP-MS, the spread around the spICP-TOFMS-determined ratios is predictable and explainable via Poisson statistics. For the analysis of monazite particles, we demonstrate that many of the determined 208Pb/232Th and 206Pb/238U ratios have variability greater than the analytical uncertainty, and thus the precision of the overall analysis is dictated by particle heterogeneity. Isotope-ratio analysis by spICP-TOFMS is a simple and rapid means of analyzing multiple isotope ratios for large populations of particles. Altogether, this could make spICP-TOFMS well suited for application in fields in which isotope ratios have large variability, such as in the source apportionment of aerosols or in nuclear forensics.
Conflicts of interest
The authors do not have any conflicts of interest to declare.Acknowledgements
The authors would like to acknowledge Iowa State University for funding through a faculty start-up grant, and funding though NSF CAREER grant CHE-2237291. We would also like to thank Dr Ralf Kaegi at EAWAG for the monazite sample, as well as the Iowa State University Department of Geological and Atmospheric Sciences for the galena mineral sample. We would like to thank Hark Karkee, Aishwarya Mantravadi, and Dr Yulia Zaikina from the Department of Chemistry at Iowa State University for ball-milling of the galena mineral. We also want to acknowledge the Iowa State University Glass Shop and Chemistry Machine Shop for fabrication of our microdroplet introduction system.References
- S. Boulyga, S. Konegger-Kappel, S. Richter and L. Sangély, J. Anal. At. Spectrom., 2015, 30, 1469–1489 RSC.
- V. C. Bradley, T. L. Spano, S. C. Metzger, B. W. Ticknor, D. R. Dunlap, N. A. Zirakparvar, B. D. Roach, C. R. Hexel and B. T. Manard, Anal. Chim. Acta, 2022, 1209, 339836 CrossRef CAS PubMed.
- E. J. Bartelink and L. A. Chesson, Forensic Sci. Res., 2019, 4, 29–44 CrossRef.
- A. M. Ghazi, Appl. Geochem., 1994, 9, 627–636 CrossRef CAS.
- B. Eglington, M. Fayek and T. K. Kyser, Applied Isotope Geochemistry, Mineralogical Association of Canada, 2019 Search PubMed.
- A. M. Cruz-Uribe, G. Craig, J. M. Garber, B. Paul, C. Arkula and C. Bouman, Geostand. Geoanal. Res., 2023, 47, 795–809 CrossRef CAS.
- V. Balaram, W. Rahaman and P. Roy, GeoGeo, 2022, 1, 100019 Search PubMed.
- J. S. Becker and H.-J. Dietze, Fresenius. J. Anal. Chem., 2000, 368, 23–30 CrossRef CAS PubMed.
- F. Vanhaecke, L. Balcaen and D. Malinovsky, J. Anal. At. Spectrom., 2009, 24, 863–886 RSC.
- K. G. Heumann, S. M. Gallus, G. Radlinger and J. Vogl, J. Anal. At. Spectrom., 1998, 13, 1001–1008 RSC.
- T. Hirata and T. Ohno, J. Anal. At. Spectrom., 2001, 16, 487–491 RSC.
- P. J. Sylvester, Geostand. Geoanal. Res., 2008, 32, 469–488 CrossRef CAS.
- D. J. Goudie, C. M. Fisher, J. M. Hanchar, J. L. Crowley and J. C. Ayers, Geochem., Geophys., Geosyst., 2014, 15, 2575–2600 CrossRef CAS.
- T. Iizuka, S. M. Eggins, M. T. McCulloch, L. P. J. Kinsley and G. E. Mortimer, Chem. Geol., 2011, 282, 45–57 CrossRef CAS.
- Y. Jiang, S. V. Hohl, X. Huang and S. Yang, Geosci. Front., 2024, 15, 101736 CrossRef CAS.
- D. M. Chew, J. A. Petrus, G. G. Kenny and N. McEvoy, J. Anal. At. Spectrom., 2017, 32, 262–276 RSC.
- D. Chew, K. Drost, J. H. Marsh and J. A. Petrus, Chem. Geol., 2021, 559, 119917 CrossRef CAS.
- N. Jakubowski, T. Prohaska, L. Rottmann and F. Vanhaecke, J. Anal. At. Spectrom., 2011, 26, 693–726 RSC.
- Thermo Fisher Scientific Inc., Neoma Multicollector ICP-MS – Illuminating the Edge of Discovery, 2020 Search PubMed.
- Nu Instruments Limited, Plasma 3 Multi-Collector ICP-MS, 2022 Search PubMed.
- A. Retzmann, S. Faßbender, M. Rosner, M. von der Au and J. Vogl, J. Anal. At. Spectrom., 2023, 38, 2144–2158 RSC.
- M. Ohata and H. Hagino, Int. J. Mass Spectrom., 2018, 430, 31–36 CrossRef CAS.
- P. P. Mahoney, S. J. Ray and G. M. Hieftje, Appl. Spectrosc., 1997, 51, 16A–28A CrossRef CAS.
- L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2017, 32, 548–561 RSC.
- M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Anal. Bioanal. Chem., 2016, 408, 5053–5074 CrossRef PubMed.
- D. Mozhayeva and C. Engelhard, J. Anal. At. Spectrom., 2020, 35, 1740–1783 RSC.
- Z. Meng, L. Zheng, H. Fang, P. Yang, B. Wang, L. Li, M. Wang and W. Feng, Processes, 2023, 11 CAS.
- M. D. Montaño, H. R. Badiei, S. Bazargan and J. F. Ranville, Environ. Sci.: Nano, 2014, 1, 338–346 RSC.
- S. Naasz, S. Weigel, O. Borovinskaya, A. Serva, C. Cascio, A. K. Undas, F. C. Simeone, H. J. P. Marvin and R. J. B. Peters, J. Anal. At. Spectrom., 2018, 33, 835–845 RSC.
- T. Hirata, S. Yamashita, M. Ishida and T. Suzuki, Mass Spectrom., 2020, 9, A0085 CrossRef CAS.
- S. Yamashita, M. Ishida, T. Suzuki, M. Nakazato and T. Hirata, Spectrochim. Acta, Part B, 2020, 169, 105881 CrossRef CAS.
- S. Yongyang, W. Wei, L. Zhiming, D. Hu, Z. Guoqing, X. Jiang and R. Xiangjun, J. Anal. At. Spectrom., 2015, 30, 1184–1190 RSC.
- A. Gundlach-Graham, in Analysis and Characterisation of Metal-Based Nanomaterials, Elsevier, 2021, pp. 69–101, DOI:10.1016/bs.coac.2021.01.008.
- A. Praetorius, A. Gundlach-Graham, E. Goldberg, W. Fabienke, J. Navratilova, A. Gondikas, R. Kaegi, D. Günther, T. Hofmann and F. von der Kammer, Environ. Sci.: Nano, 2017, 4, 307–314 RSC.
- F. Loosli, J. Wang, S. Rothenberg, M. Bizimis, C. Winkler, O. Borovinskaya, L. Flamigni and M. Baalousha, Environ. Sci.: Nano, 2019, 6, 763–777 RSC.
- K. Mehrabi, R. Kaegi, D. Günther and A. Gundlach-Graham, Environ. Sci.: Nano, 2021, 8, 1211–1225 RSC.
- T. R. Holbrook, D. Gallot-Duval, T. Reemtsma and S. Wagner, J. Anal. At. Spectrom., 2021, 36, 2684–2694 RSC.
- G. D. Bland, M. Battifarano, Q. Liu, X. Yang, D. Lu, G. Jiang and G. V. Lowry, Environ. Sci. Technol., 2022, 10, 1023–1029 Search PubMed.
- L. Hendriks, R. Bruenjes, S. Taskula, J. Kocic, B. Hattendorf, G. Bland, G. Lowry, E. Bolea-Fernandez, F. Vanhaecke, J. Wang, M. Baalousha, M. von der Au, B. Meermann, T. R. Holbrook, S. Wagner, S. Harycki, A. Gundlach-Graham and F. von der Kammer, Nanoscale, 2023, 15, 11268–11279 RSC.
- M. von der Au, S. Faßbender, M.-I. Chronakis, J. Vogl and B. Meermann, J. Anal. At. Spectrom., 2022, 37, 1203–1207 RSC.
- M. Aramendía, D. Leite, J. Resano, M. Resano, K. Billimoria and H. Goenaga-Infante, Nanomaterials, 2023, 13(17), 2392 CrossRef PubMed.
- M. D. Montaño, C. W. Cuss, H. M. Holliday, M. B. Javed, W. Shotyk, K. L. Sobocinski, T. Hofmann, F. v. d. Kammer and J. F. Ranville, ACS Earth Space Chem., 2022, 6, 943–952 CrossRef PubMed.
- B. T. Manard, V. C. Bradley, C. D. Quarles, L. Hendriks, D. R. Dunlap, C. R. Hexel, P. Sullivan and H. B. Andrews, Nanomaterials, 2023, 13, 1322 CrossRef CAS PubMed.
- X. Tian, H. Jiang, M. Wang, W. Cui, Y. Guo, L. Zheng, L. Hu, G. Qu, Y. Yin, Y. Cai and G. Jiang, Anal. Chim. Acta, 2023, 1240, 340756 CrossRef CAS PubMed.
- G. D. Bland, P. Zhang, E. Valsami-Jones and G. V. Lowry, ACS ES&T, 2022, 56, 15584–15593 Search PubMed.
- K. J. Murata, H. J. Rose and M. K. Carron, Geochim. Cosmochim. Acta, 1953, 4, 292–300 CrossRef CAS.
- Galena, https://www.mindat.org/min-563.html, accessed July, 2024.
- K. Mehrabi, D. Günther and A. Gundlach-Graham, Environ. Sci.: Nano, 2019, 6, 3349–3358 RSC.
- A. Gundlach-Graham and K. Mehrabi, J. Anal. At. Spectrom., 2020, 35, 1727–1739 RSC.
- S. Harycki and A. Gundlach-Graham, Anal. Bioanal. Chem., 2022, 414, 7543–7551 CrossRef CAS PubMed.
- L. Hendriks, B. Ramkorun-Schmidt, A. Gundlach-Graham, J. Koch, R. N. Grass, N. Jakubowski and D. Günther, J. Anal. At. Spectrom., 2019, 34, 716–728 RSC.
- J. R. d. Laeter, J. K. Böhlke, P. D. Bièvre, H. Hidaka, H. S. Peiser, K. J. R. Rosman and P. D. P. Taylor, Pure Appl. Chem., 2003, 75, 683–800 Search PubMed.
- A. Gundlach-Graham, S. Harycki, S. E. Szakas, T. L. Taylor, H. Karkee, R. L. Buckman, S. Mukta, R. Hu and W. Lee, J. Anal. At. Spectrom., 2024, 39, 704–711 RSC.
- H. Karkee and A. Gundlach-Graham, Environ. Sci. Technol., 2023, 57, 14058–14070 CrossRef CAS PubMed.
- E. Limpert, W. A. Stahel and M. Abbt, BioScience, 2001, 51, 341–352 CrossRef.
- A. Gundlach-Graham and R. Lancaster, Anal. Chem., 2023, 95, 5618–5626 CrossRef CAS PubMed.
- E. L. Crow and R. S. Gardner, Biometrika, 1959, 46, 441–453 CrossRef.
- L. Barker, Am. Stat., 2002, 56, 85–89 CrossRef.
- M. B. Swift, Commun. Stat. Theor. Methods, 2009, 38, 748–759 CrossRef.
- J. Milot, J. Blichert-Toft, M. A. Sanz, N. Fetter, P. Télouk and F. Albarède, Chem. Geol., 2021, 583, 120444 CrossRef CAS.
- J. Longman, D. Veres, V. Ersek, D. L. Phillips, C. Chauvel and C. G. Tamas, Sci. Rep., 2018, 8, 6154 CrossRef PubMed.
- X.-K. Zhu, J. Benefield, T. B. Coplen, Z. Gao and N. E. Holden, Pure Appl. Chem., 2021, 93, 155–166 CrossRef CAS.
- A. J. Goodman, A. Gundlach-Graham, S. G. Bevers and J. F. Ranville, Environ. Sci.: Nano, 2022, 9, 2638–2652 RSC.
- J. R. Graney, E. S. Edgerton and M. S. Landis, Sci. Total Environ., 2019, 654, 1293–1304 CrossRef CAS PubMed.
- S. S. Kienast, G. Winckler, J. Lippold, S. Albani and N. M. Mahowald, Global Biogeochem. Cycles, 2016, 30, 1526–1541 CrossRef CAS.
- X. Z. Zhang, F. Esaka, K. T. Esaka, M. Magara, S. Sakurai, S. Usuda and K. Watanabe, Spectrochim. Acta, Part B, 2007, 62, 1130–1134 CrossRef.
- F. Esaka, D. Suzuki and M. Magara, Anal. Chem., 2015, 87, 3107–3113 CrossRef CAS PubMed.
- M. J. Kohn and J. D. Vervoort, Geochem., Geophys., Geosyst., 2008, 9, 4 CrossRef.
- T. Yan, D. Liu, C. Si and Y. Qiao, Minerals, 2020, 10, 239 CrossRef CAS.
- B. Schoene, in Treatise on Geochemistry, ed. H. D. Holland and K. K. Turekian, Elsevier, Oxford, 2nd edn, 2014, pp. 341–378, DOI:10.1016/B978-0-08-095975-7.00310-7.
- W. L. Newman, Geologic Time, 1997 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00121d |
| This journal is © The Royal Society of Chemistry 2024 |






