Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparison and influence of 1011 and 1013 ohm resistors used for MC-ICP-MS determination of isotope ratios in highly enriched silicon†
Axel
Pramann
 * and
Olaf
Rienitz
* and
Olaf
Rienitz

Physikalisch-Technische Bundesanstalt (PTB), Bundesallee 100, 38116, Braunschweig, Germany. E-mail: axel.pramann@ptb.de
First published on 2nd May 2024
Abstract
The molar mass M and isotopic composition of a silicon material highly enriched in 28Si were measured for the first time using high ohmic (1013 Ω) resistors in the feedback loop of amplifiers connected to the Faraday detectors of a multicollector-inductively coupled plasma mass spectrometer (MC-ICP-MS). In the context of the realization and dissemination of the SI units kilogram and mole via the X-ray crystal density (XRCD) method, it is of high importance to maintain and improve the state-of-the art technique to determine M with the lowest possible associated uncertainty. The applications and influences of 1011 Ω and 1013 Ω resistors for ion detection were compared using the crystal Si28-33Pr11 exhibiting a large range (≈102) of the ratio 30Si/29Si. The low abundance of 30Si hampers the measurement and thus enlarges the uncertainty. The use of 1013 Ω resistors enables a fourfold dilution of the initial Si sample stock solutions from wx(Si) = 4536 μg g−1 down to 1134 μg g−1 preserving the MS equipment (ion lenses, slits etc.). A lower limit of wx(Si) ≈ 1134 μg g−1 for ion currents I = 3.4 fA (corresponding to U = 0.34 mV: gain corrected for R = 1013 Ω) for 30Si+ was determined still maintaining the ability to yield urel(M) = 4 × 10−9. This will also enable the use of smaller sample sizes, which will considerably reduce costs and time and thus improve this method strongly. Tau correction for 1013 Ω resistors was studied showing no significant influence in case of the continuous beam experiments.
1 Introduction
The measurement of small ion beams (≤5 mV using 1011 Ω resistors) for the determination of isotope ratios in combination with multicollector mass spectrometers (thermal ionisation mass spectrometers (TIMS) and inductively coupled plasma mass spectrometers (ICP-MS)) entered a new era with the introduction and successful application of high ohmic resistors in the feedback loop of Faraday cups used in static measurements.1–4 The amplifiers equipped with high ohmic resistors – usually with R = 1013 Ω – enable measurements of extremely small ion beams (≤5 mV corresponding to 3 × 105 counts per second (s−1)), often detected via secondary electron multipliers (SEM). A number of benefits of using 1013 Ω resistors (instead of common 1011 Ω resistors) exist: it is not necessary to use Faraday cups and SEMs in combination, avoiding the inherent problem of cross-calibration of both detector types and thus an increase in measurement uncertainty and experimental efforts. Basically, using a 1013 Ω resistor in contrast to a 1011 Ω resistor leads to a hundredfold gain while the signal to noise ratio merely decreases by a factor of ten, directly influencing the precision of the measurement, depending on the ion counting statistics and the Johnson–Nyquist noise.1In the case of the 1013 Ω resistors of amplifiers used with Faraday cups, dead-time correction and dark noise determination as in the case of an SEM are not necessary, especially when non-transient signals are measured. If respective small amounts of analytes (low concentration or mass fraction) should be detected, they are now accessible and can be measured, or on the other hand, it is possible to dilute samples further, providing a longer use of stock solutions and/or diluted aliquots. Also, some diluted aggressive matrices are less destructive toward the MS, e.g. the cones and electrostatic lens assemblies are preserved as in the current study.
Several applications of high ohmic resistors using TIMS or MC-ICP-MS have been published in the recent past.5–12 In the latest generation of the applied MC-ICP-MS (Neptune XT™, Thermo Fisher Scientific GmbH, Bremen, Germany), the gain calibration of the 1013 Ω amplifiers can be performed based on an implemented routine in the operating software. The first application of liquid sample measurements using the 1013 Ω technology within an MC-ICP-MS was reported by Pfeifer et al., who described the determination of Ta isotope ratios yielding an improved uncertainty, previously limited by the low abundance of 180Ta.13 A recent example for the applicability of the 1013 Ω technology in case of very limited and low concentration sample amounts in bio-medical cerebrospinal fluid was demonstrated by Vanhaecke and coworkers.14
In this work, we report the determination of the molar mass and isotopic composition of silicon highly enriched in 28Si using 1011 Ω and 1013 Ω amplifiers for the first time. Both performances and results were compared with respect to the associated uncertainties. The silicon sample material (crystal Si28-33Pr11) was characterized previously using a standard MC-ICP-MS routine.15 Silicon highly enriched in 28Si (x(28Si) > 0.9999 mol mol−1) was used as the material of choice for the silicon spheres applied in the context of the X-ray crystal density (XRCD) method which is the underlying primary method for the realization and dissemination of the SI base units the mole and the kilogram.15–18 A key parameter for the characterization of the respective silicon spheres is the molar mass M of this very material, which was determined with a relative associated uncertainty urel(M) < 5 × 10−9. This small uncertainty is only accessible if M is determined via the so-called Virtual-Element Isotope Dilution Mass Spectrometry (VE-IDMS) method, described in detail elsewhere.19–21 Briefly, only the isotope ratios (in a first step: intensity ratios) 30Si/29Si are determined using an MC-ICP-MS. This successful approach has been validated and reported by several national metrology institutes (NMIs) in the past.22–25
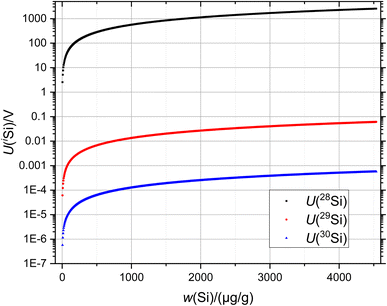
Since the silicon crystals are extremely enriched in 28Si, it is an experimental challenge to determine the isotope ratios 30Si/29Si. The silicon isotope ratios are ≈105 (28Si/29Si) and ≈107 (28Si/30Si) in this study. To symbolise this problem, Fig. 1 shows the (simulated) signal intensities (in V) of the respective Si isotopes as a function of the silicon mass fraction.
Moreover, the extremely small signal intensities of 29Si and especially 30Si are accompanied by a ratio of x(29Si)/x(30Si) ≈ 100 mol mol−1 in this crystal. The measurement of this ratio using a conventional 1011 Ω amplifier thus requires extremely high mass fractions of sample x and blend bx solutions of wx(Si) ≥ 4000 μg g−1 and wbx(Si) ≥ 1500 μg g−1 to be able to achieve a reasonable 30Si signal intensity. It is evident that these mass fractions are usually too high for MC-ICP-MS operations (clogging, surface deposition, contamination…). In this study we concentrated on several aspects: first, comparison of the molar mass and isotopic composition and their associated uncertainties as a function of the resistor connected to the amplifier. Does the use of high-ohmic (1013 Ω) resistors influence/improve the uncertainty or at least experimental issues like noise and scattering? Second, the use of highly sensitive 1013 Ω amplifiers for the 29Si and 30Si isotope detection opens up the possibility of using more diluted sample aliquots. We prepared Si sample and blend solutions by diluting the initial stock solutions of wx ≈ 4500 μg g−1 and wbx ≈ 1600 μg g−1 in order to investigate the quality of the respective isotope ratios. A reasonable lower limit was determined for wx ≈ 1100 μg g−1. Also, the influence of the blank was investigated. Measurement uncertainties were determined according to the rules of the “Guide to the Expression of Uncertainty in Measurement” (GUM).26
2. Experimental
2.1 Primary method for molar mass determination
Molar mass determinations were performed by the application of the VE-IDMS principle, described in detail elsewere.19,21 For a better understanding, only a brief description is given. In order to yield an uncertainty associated with M which is smaller than 10−8, relatively, only silicon material extremely enriched in 28Si (almost 100%, x(28Si) > 0.9999 mol mol−1) is an option. In this context, also the amount-of-substance fractions x of the “impurities” 29Si and 30Si which are present in very minor traces were determined. Due to the production of this silicon crystal material using gas centrifuges for the enrichment of 28Si in the initial SiF4 gas, not only the absolute fraction of x(29Si) and x(30Si) is different from crystal to crystal. Also important to know is the fact that the ratio of 29Si and 30Si may vary over several orders of magnitude in different crystals. In this study the crystal Si28-33Pr11 was reexamined.15 The larger this ratio, the more difficult is its measurement and the larger the uncertainty associated with the isotope ratio R and the molar mass M. Thus, using the conventional 1011 Ω technique, very high Si sample concentrations (mass fractions wx > 4000 μg g−1) have been necessary in the past. A possible technical solution for this problem is the application of high ohmic resistors (1013 Ω) as presented in this study. Using the VE-IDMS principle, the measurement of the intensity ratios 29Si/28Si and 30Si/28Si is avoided, because they are several orders of magnitude away from unity. Practically, the VE-IDMS therefore treats the two isotopes 29Si and 30Si as a “virtual element” (VE) in the matrix of an extreme excess of 28Si. Only the isotope ratios 30Si/29Si (with the index 2) were determined: in the sample (x) of the highly enriched silicon material as well as in the respective blend (bx). The latter was prepared from the sample x and a spike material y (Si highly enriched in 30Si). The respective measured intensity ratios (rx,2 and rbx,2) yield sufficiently small uncertainties. Atomic masses of the Si isotopes were taken from the literature.27 To overcome the inherent problem of mass bias (mass fractionation) when determining isotope ratios, the measured intensity ratios were corrected using calibration factors K. These were determined experimentally based on binary gravimetric mixtures of silicon parent materials having each a high enrichment in the respective isotope.20 It was necessary to determine only K factors used to correct the 30Si/29Si ratios (K2). This was done by the measurement of the respective isotope ratio rw,2 of natural silicon (w) which was properly characterized with a known “true” isotope ratio Rw,2.212.2 Materials and reagents
The samples used in this study were taken from the silicon crystal material Si28-33Pr11, reported in a previous paper.15 Thus, the measurements with the 1011 Ω resistors were used for validation purposes complemented by the new results using the 1013 Ω resistors. The general procedure for sample preparation and experimental routines is briefly outlined.The solid single crystal samples (m ≈ 500 mg each) were cleaned and etched prior to digestion with the purpose to remove any contaminations.21 All bottles and vials (made of PFA: perfluoroalkoxy alkane) were treated by applying a special protocol.21 Digestion of the etched and weighed samples was performed by dissolution in aqueous tetramethylammonium hydroxide (TMAH) at 60 °C in an ultrasonic bath using TMAH (w = 0.25 g g−1, Alfa Aesar, Thermo Fisher GmbH, Kandel, Germany) of electronic grade purity (99.9999%). The stock solutions were prepared by dilution using purified water (18 MΩ cm resistivity; water purification system: Merck Millipore™). The mass fractions of the solvent TMAH of all solutions (samples, blank) were w(TMAH) = 0.000 6 g g−1. The range of the isotopic abundance between 28Si and 30Si is extremely large and covers 7 orders of magnitude in this crystal; therefore, for the usual measurement (with 1011 Ω resistors, and as in previous measurements) it was necessary to start with very high mass fractions wx,0(Si) = 4536 μg g−1 and wbx,0(Si) = 1507 μg g−1 (in case of subsample V.2.3). The blend bx denotes the blend consisting of the sample x and spike material y. For the K factor determination material w with ww(Si) = 4 μg g−1 was used. In order to investigate the possibility of diluting the initial stock solution and blend, the starting mass fractions were diluted wx/(μg g−1): 4536 → 2268 → 1134 → 567 → 284; wbx/(μg g−1): 1507 → 754 → 377 → 188 → 94. Due to the contamination with omnipresent Si of natural isotopic composition and to correct for carry-over effects, the blank signals (measured prior to the sample or blend) were subtracted from the respective signals.
2.3 Mass spectrometry and data evaluation
The isotope ratio measurements of the enriched silicon samples were performed with a high resolution multicollector-inductively coupled plasma mass spectrometer (MC-ICP-MS) Neptune™ XT (Thermo Fisher Scientific GmbH, Bremen, Germany).13,15 Generally, the samples were measured as similar as in a previous study, where 1011 Ω resistors connected to amplifiers (in a rotating mode) were used.15 In Table 1, the typical operation conditions and in Table 2 the respective amplifier settings are shown. Since isotope ratios of silicon artificially highly enriched in 28Si and simultaneously depleted in 29Si and 30Si were determined, a sample introduction system manufactured from PFA/PEEK and an ICP torch with sapphire parts and a sapphire injector were used. Additionally, contaminations of the procedural blank introduced by the solvent were corrected for by subtracting the blank signals measured prior to the sample from the latter. This, however, might cause some trouble by blank overcorrection when the concentration of the analyte in the sample decreases. In case of the 1011 Ω amplifier configuration (see Table 2), the total measurement duration (one sequence) was approximately 2.5 hours (blank – sample (four times); blank – blend (four times); blank – nat.-Si (four times). Generally, a short sequence is preferable when measuring enriched silicon in high resolution to avoid potential mass-drift effects.28| Vacuum generation | Scroll pump, turbo pumps, jet pump (almost oil-free) |
| Sample introduction | 50 μL min−1 PFA nebulizer |
| Cyclonic and Scott chamber (PEEK/PFA) | |
| Sapphire torch and injector, sapphire bonnet, Ni X-skimmer and Ni sampler | |
| Gas flow rates (argon 5.0) | Cooling: 16 L min−1, auxiliary: 0.8 L min−1, sample: 1.0 L min−1 |
| Machine settings | Pseudo high resolution HR (M/ΔM = 8000) |
| Plasma power P(RF) = 1180 W | |
| Autosampler | CETAC ASX 110 FR |
| Sequence settings | Rinse time: 120 s |
| Take-up time: 60 s, measured samples/sequence: x, bx, w (4 times each) | |
| Blank measurement | Prior to each sample |
| 1011 Ω amplifier | 1013 Ω amplifier | |
|---|---|---|
| w x range (approx.)/(μg g−1) | 4500–4700 | 4500–4700, 2300, 1100, 550, 280 |
| Faraday detectors | C: 29Si+, H3: 30Si+ | C: 29Si+, H3: 30Si+ |
| 28Si+: detectors moved out of the beam | 28Si+: detectors moved out of the beam | |
| Amplifier no. | C: 2, H3: 8 | C: 9, H3: 10 |
| Gain | Both: 100 | Both: 10−2 |
| Tau constant/s | Ampl. 2: 0.11; ampl. 8: 0.10 | Ampl. 9: 0.61; ampl. 10: 0.53 |
| Operation mode | Static | Static |
| Rotating amplifiers | Applied/not applied | Not applied |
| Integration time/s | 4.194 | 8.389 |
| Idle time/s | 3.000 | 10.00 |
| Number of integrations | 1 | 1 |
| Number of cycles/block | 3 | 3 |
| Number of blocks | 6 | 6 |
The total measurement time increases to 3.5 hours when using the 1013 Ω amplifiers. In the latter case, the high ohmic resistors cause a slower response time of the amplifiers (so that a longer integration time (8.4 s) and idle time (10 s) are necessary).13 In case of the 1013 Ω amplifier configuration, the software-based gain calibration takes three hours.
3. Results and discussion
3.1 Statistical comparison of 1011 Ω and 1013 Ω amplifiers: isotope ratio measurements
The isotope ratios Rx = x(30Si)/x(29Si) in the sample N.2.1 (w = 4710 μg g−1) and Rbx = x(30Si)/x(29Si) in the blend bx are shown for the individual sequences and the respective amplifier settings (1011 Ω, with amplifier rotation; 1011 Ω, no amplifier rotation; 1013 Ω, no amplifier rotation) in Fig. 2. The respective raw data and calculations are given in the ESI 1† where the calculations can be retraced. In case of Rx, the data are consistent for k = 2 showing a larger scattering especially in case of the 1011 Ω setup with rotating amplifiers. Error bars denote the standard uncertainties (k = 1) without scattering contributions. For comparison of the R = 1011 Ω and the R = 1013 Ω setups at a first glance, the two setups without rotating amplifiers are more suitable. Contrary to expectations, the relative combined uncertainties associated with Rx and Rbx are twice as large in case of the R = 1013 Ω setups than in case of the R = 1011 Ω setups. Generally, uc,rel is smaller in case of Rbx compared to Rx by a factor of at least 50 due to the numerical value of Rbx which is much closer to unity.In the high concentration range of the sample (wx = 4000–5000 μg g−1), the application of 1013 Ω resistors will not improve the uncertainties in R.
However, in case of the enriched Si material, the main intention is the determination of the molar mass M and its associated uncertainty. Therefore, the impact of the different resistors on this quantity is of main interest and will be discussed in the following.
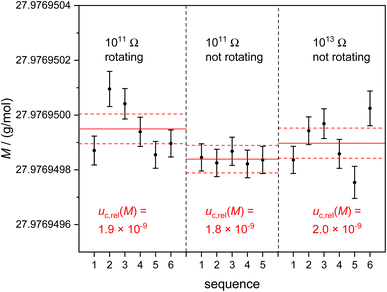
Fig. 3 shows the molar mass distribution of measurements of the subsample N.2.1 (w = 4710 μg g−1). The measurements were performed in the same way as reported previously using the 1011 Ω amplifier setting with rotating virtual amplifiers.15 Using the 1011 Ω resistors and rotating virtual amplifiers (Fig. 3 left), an average value M = 27.976949950(54) g mol−1 was obtained with urel = 1.9 × 10−9 (the last digits denote the combined uncertainty uc associated with M, k = 1).
This value is 4.2 × 10−7 g mol−1 below the value reported previously due to a long-term TMAH-leaching and new type sapphire-torch removing natural silicon even more efficiently.15 The respective measurement results without rotating amplifiers (Fig. 3 centre) yield M = 27.976 949![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839(50) g mol−1 with urel = 1.8 × 10−9.
839(50) g mol−1 with urel = 1.8 × 10−9.
This series was measured as a proof of data consistency when applying/not applying the virtual amplifier concept developed by Thermo Fisher Scientific™, which was introduced for the reduction of biases due to the gain calibration.
No significant difference in the data sets was observed within the limits of uncertainty, because main uncertainty contributions result from intensity ratios obtained from extremely different isotope abundances of the enriched material as will be outlined later. In the right part of Fig. 3 the respective molar mass results are shown using the 1013 Ω resistors connected to cups C and H3. Here, M = 27.976 949![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 898(55) g mol−1 with urel = 2.0 × 10−9 was obtained. All three measurements (1011 Ω and 1013 Ω resistors, virtual amplifier concept applied and not applied) agree within the limits of uncertainty. The underlying raw data and calculations are given in the respective Excel™ sheets of the ESI 1.†
898(55) g mol−1 with urel = 2.0 × 10−9 was obtained. All three measurements (1011 Ω and 1013 Ω resistors, virtual amplifier concept applied and not applied) agree within the limits of uncertainty. The underlying raw data and calculations are given in the respective Excel™ sheets of the ESI 1.†
Regarding the uncertainty of the molar mass of enriched silicon, no significant change was observed when using the high ohmic resistor setting. Table 3 shows representative uncertainty budgets of sample N.2.1 of a single sequence using: 1011 Ω resistors with and without rotating amplifiers as well as 1013 Ω resistors without rotating amplifiers. The uncertainty budgets were calculated using the GUM Workbench Pro™ software (version 2.4.1 392; Metrodata GmbH, Germany) according to guidelines of the GUM.26
| Amplifier setting | Quantity | Unit | Best estimate (value) | Standard uncertainty | Sensitivity coefficient | Index (%) |
|---|---|---|---|---|---|---|
| X i | [Xi] | x i | u(xi) | c i | ||
| I, II, III | M(28Si) | g mol−1 | 27.976926534940 | 540 × 10−12 | 1.0 | 0.0 |
| m yx | g | 5.611000 × 10−6 | 704 × 10−12 | 4.2 | 0.3 | |
| m x | g | 0.062474995 | 569 × 10−9 | −370 × 10−6 | 0.0 | |
| M(29Si) | g mol−1 | 28.976494669090 | 610 × 10−12 | 23 × 10−6 | 0.0 | |
| R y,3 | mol mol−1 | 1.5855 | 0.0222 | −80 × 10−9 | 0.1 | |
| I | M(30Si) | g mol−1 | 29.9737701360 | 27.0 × 10−9 | −500 × 10−9 | 0.0 |
| II | −560 × 10−9 | 0.0 | ||||
| III | −550 × 10−9 | 0.0 | ||||
| I | R y,2 | mol mol−1 | 269.04 | 5.65 | 2.0 × 10−9 | 4.3 |
| II | 4.6 | |||||
| III | 4.4 | |||||
| I | R w,2 | mol mol−1 | 0.66230 | 1.32 × 10−3 | −35 × 10−6 | 75.7 |
| II | 81.5 | |||||
| III | 76.8 | |||||
| I | r x,2 | V/V | 0.012470 | 405 × 10−6 | 50 × 10−6 | 14.2 |
| II | 0.009800 | 342 × 10−6 | 49 × 10−6 | 10.7 | ||
| III | 0.010400 | 439 × 10−6 | 49 × 10−6 | 16.5 | ||
| I | r bx,2 | V/V | 3.79034 | 1.90 × 10−3 | −6.3 × 10−6 | 5.00 |
| II | 3.80227 | 1.14 × 10−3 | −6.2 × 10−6 | 1.9 | ||
| III | 3.82259 | 1.15 × 10−3 | −6.2 × 10−6 | 1.8 | ||
| I | r w,2 | V/V | 0.6982900 | 90.8 × 10−6 | 33 × 10−6 | 0.3 |
| II | 0.702370 | 140 × 10−6 | 33 × 10−6 | 0.8 | ||
| III | 0.7050200 | 56.4 × 10−6 | 33 × 10−6 | 0.1 | ||
| I | M | g mol−1 | 27.9769499399 | 53.3 × 10−9 | ||
| II | 27.9769498685 | 51.5 × 10−9 | ||||
| III | 27.9769498590 | 52.9 × 10−9 |
The budgets are rather similar and differences can only be observed in small variations in the measured intensity ratios rx,2 (sample), rbx,2 (blend of sample x and “Si30” spike y), and rw,2 (natural Si w for K factor determination). From those, no clear indication can be derived if the high ohmic amplifiers will have a more positive impact on u(M).
An explanation will be the fact that the molar mass M is a result of the complex “Virtual-Element IDMS” principle, which is only in a minor part dependent on the intensity ratios (isotope ratios) directly, which are influenced by the kind of resistor chosen.
The influence of the 1011 Ω and 1013 Ω resistors in the case of highly enriched silicon solutions was analysed statistically by comparing the measured intensity ratios r = U(30Si)/U(29Si) in the sample solutions x, the blend solution bx, and the calibration solution w of sample N.2.1 using the initial sample concentrations (wx = 4710 μg g−1; wbx = 1510 μg g−1; ww = 4 μg g−1). For each solution, up to six sequences were measured, each yielding an average intensity ratio with an associated experimental standard deviation of the mean s according to the GUM.26 For a better comparison, the not-blank corrected ratios are discussed only. The data sets and evaluation procedures are given in the respective Excel™ sheets of the ESI 2.†Fig. 4a–c show the relative standard deviations of the mean srel of the intensity ratios r in solutions x, bx, and w, measured with 1011 Ω and 1013 Ω equipped amplifiers.
In case of the sample solution x (highly enriched Si), the relative experimental standard deviations r = U(30Si)/U(29Si) are almost equal when using the 1011 Ω or 1013 Ω setup with a small benefit of the 1011 Ω resistors. A possible reason might be the intrinsic scattering of the intensity ratios rx (≈0.01 V/V) in case of the sample material with an isotope ratio Rx ≈ 0.009 mol mol−1, two orders of magnitude away from unity, even if the absolute 30Si signal is in the lower mV range. An advantage of the 1013 Ω amplifier setup can be observed in the ratios of the blend bx with Rbx ≈ 4 mol mol−1. Here, the respective course of the relative experimental standard deviations of the mean srel is smoother and with an average of 0.0073% lower than in case of the 1011 Ω setup (0.0095%) due to the absolute ratio near unity. In case of the solution w, the impact of the setup (1011 Ω or 1013 Ω) is very similar, due to the much larger signal intensities (silicon with almost natural isotopic distribution) and an intensity ratio rw ≈ 0.7 V/V.
3.2 Comparison of 1011 Ω and 1013 Ω amplifiers: influence of sample mass fraction
However, the application of the high-ohmic resistors should enable accurate and precise measurements of lower concentrated or diluted samples. For this reason, different concentrations of the subsample V.2.3 were measured using original and diluted aliquots of x and bx (wx,0 = 4536 μg g−1; wbx,0 = 1507 μg g−1) keeping ww constant (compare Section 2.2). Fig. 5 displays the results of the molar mass determinations comparing the original measurement from 2020 (ref. 15) (wx = 4536 μg g−1 with 1011 Ω amplifiers, 6 sequences) with the recent measurements using the 1013 Ω amplifier setup. The latter were measured using the following mass fractions w: 4536 μg g−1 (6 sequences), 2268 μg g−1 (6 sequences), and 1134 μg g−1 (4 sequences due to the sample running out of stock). The average molar mass of these very samples was determined as the arithmetic mean of the two 4536 μg g−1 (1011 Ω and 1013 Ω) and the 1134 μg g−1 (1013 Ω) measurements including the contribution of data scattering. The solid black line denotes the average value M(V.2.3) = 27.97695056(14) g mol−1 (the last two digits represent the uncertainty associated with M, k = 1). This corresponds to a relative uncertainty urel(M) = 5.1 × 10−9. The data set of the 2268 μg g−1 measurement (1013 Ω, greyed out in Fig. 5) was not used for the calculation of M due to a slight offset resulting from a tentative contamination with natural silicon during dilution. The average value of M(V.2.3) agrees with the former value reported in ref. 15 within the limits of uncertainty. The data sets as well as their compilation are also available in the ESI 3.† | ||
| Fig. 5 Comparison of molar mass determinations of the sample Si28-33Pr11V.2.3: 4536 μg g−1 (black squares, 1011 Ω, 2020 (ref. 15)); 4536 μg g−1 (red circles, 1013 Ω); 2268 μg g−1 (grey triangles, 1013 Ω); 1134 μg g−1 (green triangles, 1013 Ω). The solid black line denotes the arithmetic mean of the two 4536 μg g−1 and the 1134 μg g−1 data sets. The dotted lines denote the respective upper and lower uncertainty limits (including data scattering, k = 1). | ||
The consistency of these data sets was analysed using the principle of the degrees-of-equivalence (di).
| di = Mi − M | (1) |
 | (2) |
Fig. 6 shows the di and associated uncertainties U(di) comparing the four data sets (including the scattering contribution in the respective uncertainty bars).
The data sets can be regarded as consistent if the individual di are smaller than their uncertainties. This criterion is fulfilled for almost all data points except several of the 2268 μg g−1 data. For consistency, the error bars should encompass the zero line (red line in Fig. 6). Therefore, the data set of the 2268 μg g−1 measurement was not included in the molar mass evaluation for the subsample V.2.3.
The influence of the different resistor settings was analysed by comparing the statistical impact on the relative experimental standard deviations of the mean srel of the measured intensity ratios r = U(30Si)/U(29Si) in the sample x, the blend bx, and the natural Si solution w. In case of the 1013 Ω amplifier settings, the additional dependence on the dilution of the sample x (4536, 2268, and 1134 μg g−1) is shown in Fig. 7.
Generally, the srel for rbx and rw are in a range below 0.030% which is not significantly dependent on the mass fraction w. In case of the 1013 Ω resistors, a decrease of srel(rw) can be observed by a factor of ten (<0.0050%) compared to the 1011 Ω resistors. For rbx, the range is almost constant (0.075%–0.015%) independent from the mass fraction. The 2268 μg g−1 data set also shows the statistical quality and ability of this mass fraction compared to the original 4536 μg g−1 solution.
In case of rx, the respective srel are in a higher range between 0.30% and 0.45% when using the 1013 Ω resistors, independent of the mass fraction used. Since the measurement of intensity (and isotope) ratios rx is affected by larger uncertainties, the use of 1013 Ω instead of 1011 Ω amplifiers will not significantly improve the statistical quality of the data srel(rx).
Further dilutions of samples with wx = 567 μg g−1 and wx = 284 μg g−1 could not be measured even when using 1013 Ω amplifiers, because the absolute signal intensities of 29Si and 30Si in the sample solutions were in the same range as in the blank solution. For this reason, wx = 1134 μg g−1 can be regarded as an approximate lower limit of the mass fraction for the measurement of M using the 1013 Ω amplifier set up for this special silicon crystal.
As one main result the application of high ohmic 1013 Ω resistors instead of 1011 Ω resistors is enabling the measurement of at least fourfold diluted samples (from 4536 μg g−1 down to 1134 μg g−1). To give an overview of the absolute intensities (voltages and ion currents), Table 4 lists typical data generated with sample V.2.3 using the 1011 Ω and 1013 Ω setup. The voltages in case of the 1013 Ω resistors were gain factor-corrected to enable a direct comparison with the values obtained with the 1011 Ω resistors.1 It can be observed that the overall dynamic range of the 1013 Ω resistors covers three orders of magnitude yielding in case of the 30Si+ ion an ion current of a few fA which is still sufficient for molar mass determinations.
| w x (μg g−1) | R/Ω | U/V | I/fA | |
|---|---|---|---|---|
| 4536 | 29Si+ | 1011 | 0.13542 | 1354 |
| 30Si+ | 1011 | 0.00140 | 13.96 | |
| 4536 | 29Si+ | 1013 | 0.11326 | 1133 |
| 30Si+ | 1013 | 0.00109 | 11 | |
| 2268 | 29Si+ | 1013 | 0.04050 | 405 |
| 30Si+ | 1013 | 0.00062 | 6.2 | |
| 1134 | 29Si+ | 1013 | 0.02283 | 228 |
| 30Si+ | 1013 | 0.00034 | 3.4 |
The use of high ohmic resistors is directly correlated with experimental benefits: fast clogging of the sampler and skimmer cones is avoided due to lower analyte concentrations; a more stable signal quality is generated, and the mass spectrometer can be operated in a less aggressive concentration regime. The other main outcome when using the 1013 Ω resistors is the fact, that a strongly reduced sample mass (down to m(crystal) ≈ 125 mg corresponding to w ≈ 1000 μg g−1) will be sufficient in the future for the measurement of the molar mass and isotopic composition of silicon enriched in 28Si: a mass of approximately 125 mg solid Si will yield 125 g of a solution with w ≈ 1000 μg g−1 (instead of 500 mg Si needed to prepare a solution of 125 g with w ≈ 4000 μg g−1). This will save time and costs for sample preparation and material consumption. Moreover, a smaller crystal sample (size) might enable a better space resolved sample characterization. This will improve the insight into the homogeneity of the isotopic composition of the respective crystals underpinning their ability for the use in the XRCD method.
3.3 Investigation of mass bias due to signal delay impact – tau correction
In MC-ICP-MS there are several sources for biased isotope ratios. The analogue currents, generated in the Faraday cups by release of charge create a voltage on the respective (high ohmic) resistor. These voltages are converted to frequencies using a voltage-to-frequency converter. Thus, even in a multicollector detection system very short time-offsets of the different detector outputs are generated due to different signal decays which depend on the “first-order-tau-constant” of the respective resistor.11,12,29–32 When using high ohmic resistors (e.g. 1013 Ω), this time delay between the incoming signal and detector response times (detector decay duration) might generate a bias in isotope ratios – especially in case of transient signals. A test of a potential influence of the tau correction using the 1013 Ω resistors was applied. The tau constants (symbol τ) of each amplifier – initially generated during machine installation – were taken from the software-based tau decay constants listed in the Neptune XT™ software (executive tool).29 For the test measurements, the N.2.1 subsample (w = 4710 μg g−1) was used. The C and H3 cups were operated with 1013 Ω; six sequences were measured each.For the tau corrected ion signal Icorr(ti) at the time ti, the following expression was used:
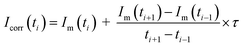 | (3) |
After measuring six sequences of the sample N.2.1 and applying tau correction, an almost identical course of the corrected molar masses Mτ and their associated uncertainties as in the case of not tau corrected measurements (Mnτ) was obtained (see Fig. 8).
 | ||
| Fig. 8 Molar mass distributions of subsample N.2.1 over six sequences. Open squares: not tau corrected data; red circles: tau corrected data. No significant difference can be observed. | ||
The absolute differences ΔM between Mnτ and Mτ are shown in Fig. 9.
The ΔM values are located in the lower 10−9 g mol−1 range (Fig. 9b). For comparison, in Fig. 9a, the area covered with the average uncertainty associated with M is bracketed by the red dashed lines. The latter covers a range approximately a factor twenty larger than ΔM. Therefore, application of tau correction in case of the 1013 Ω resistors does not influence the isotope ratios as well as the respective molar mass in the current study in any way. This is mainly based on the use of stable signal inputs (continuous ion beams) rather than transient signals as apparent when coupling the MS to a laser ablation or any kind of chromatography. Therefore, additional tau correction shows no significant advantages for the current study.
4. Conclusions
The current determination of the molar masses of different subsamples of the enriched silicon crystal Si28-33Pr11 with a large ratio 29Si/30Si > 100 using amplifier setups with 1011 Ω and 1013 Ω for the first time has produced several main outcomes: First, a direct comparison of the same sample with the original high analyte mass fraction of w > 4500 μg g−1 using 1011 Ω and 1013 Ω amplifiers shows no significant influence on the uncertainty of the molar mass and of the respective isotope ratios and measured intensity ratios. This is a consequence of the dominating mass bias of the isotope ratio Rx(30Si/29Si) in the sample which is two orders of magnitude different from unity in case of this crystal. The application and impact of tau correction in case of using 1013 Ω amplifiers can be neglected when operating with stable input signals from continuous ion beams in contrast to transient signals (e.g. as known from laser ablation). When diluting the original sample solutions (here: from w = 4536 μg g−1 down to 1134 μg g−1), the use of 1013 Ω amplifiers opens the door for the measurement of isotope ratios of enriched silicon in this concentration range maintaining the uncertainty associated with M. This study shows that a dilution of the extremely high mass fractions used in the measurements of the molar mass of enriched silicon is possible when applying the high ohmic 1013 Ω amplifier setups. This will strongly improve the experiment (reduction of clogging, increase of beam stability), enabling longer duration of measurements (sequences) and less stress toward the mass spectrometer. The main benefit of the use of 1013 Ω amplifiers is the possibility of using smaller (factor ≈ 0.25) sample sizes, enabling less sample preparation time and material costs while keeping the level of uncertainty and improving the possibility of detecting local isotopic variations. Also, in the near future silicon crystals even more depleted in 30Si will be analysed using the 1013 Ω amplifier setup.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors gratefully acknowledge the provision of silicon crystal samples by Daniela Eppers (PTB). Many thanks also to Grant Craig (Thermo Fisher Scientific Bremen GmbH) for helpful advice concerning the tau correction.References
- J. M. Koornneef, C. Bouman, J. B. Schwieters and G. R. Davies, Measurement of small ion beams by thermal ionisation mass spectrometry using new 1013 Ohm resistors, Anal. Chim. Acta, 2014, 819, 49–55 CrossRef CAS PubMed.
- A. Trinquier, Gain Calibration Protocol for 1013 Ω Resistor Current Amplifiers Using the Certified Neodymium Standard JNdi-1 on the TRITON Plus, Application Note 30285, Thermo Fisher Scientific Inc., 2014 Search PubMed.
- C. Bouman, A. Trinquier, N. Lloyd, J. Schwieters, J. Koornneef and G. Davies, New Design 1013 Ω Amplifiers for Measurement of Small Ion Beam Currents, Application Note 30282, Thermo Fisher Scientific Inc., 2015 Search PubMed.
- T. Breton, N. S. Lloyd, A. Trinquier, C. Bouman and J. B. Schwieters, Improving precision and signal/noise ratios for MC-ICP-MS, Procedia Earth Planet. Sci., 2015, 13, 240–243 CrossRef CAS.
- M. Klaver, R. J. Smeets, J. M. Koornneef, G. R. Davies and P. Z. Vroon, Pb isotope analysis of ng size samples by TIMS equipped with a 1013 Ω resistor using a 207Pb–204Pb double spike, J. Anal. At. Spectrom., 2016, 31, 171–178 RSC.
- E. Plomp, I. C. C. von Holstein, J. M. Koornneef, R. J. Smeets, L. Font, J. A. Baart, T. Forouzanfar and G. R. Davies, TIMS analysis of neodymium isotopes in human tooth enamel using 1013 Ω amplifiers, J. Anal. At. Spectrom., 2017, 32, 2391–2400 RSC.
- H. Vollstaedt, G. Craig, N. Lloyd, J. Schwieters and C. Bouman, 1013 Ω Amplifier Technology: How Low Can You Go? Smart Note SN30439, Thermo Fisher Scientific Inc., 2017 Search PubMed.
- G. Wang, H. Vollstaedt, J. Xu and W. Liu, High-Precision Measurement of 187Os/188Os Isotope Ratios of Nanogram to Picogram Amounts of Os in Geological Samples by N-TIMS using Faraday Cups Equipped with 1013 Ω Amplifiers, Geostand. Geoanal. Res., 2019, 43, 419–433 CrossRef CAS.
- M. Dellinger, R. G. Hilton and G. M. Nowell, Measurements of rhenium isotopic composition in low-abundance samples, J. Anal. At. Spectrom., 2020, 35, 377–387 RSC.
- J. B. Creech, B. F. Schaefer and S. P. Turner, Application of 1013 Ω Amplifiers in Low-Signal Plasma-Source Isotope Ratio Measurements by MC-ICP-MS: A Case Study with Pt Isotopes, Geostand. Geoanal. Res., 2020, 44, 223–229 CrossRef CAS.
- K. Yamamoto, H. Asanuma, H. Takahashi and T. Hirata, In situ isotopic analysis of uranium using a new data acquisition protocol for 1013 ohm Faraday amplifiers, J. Anal. At. Spectrom., 2021, 36, 668–675 RSC.
- J.-I. Kimura, Q. Chang, N. Kanazawa, S. Sasaki and B. S. Vaglarov, High-precision in situ analysis of Pb isotopes in glasses using 1013 Ω resistor high gain amplifiers with ultraviolet femtosecond laser ablation multiple Faraday collector inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2016, 31, 790–800 RSC.
- M. Pfeifer, N. S. Lloyd, S. T. M. Peters, F. Wombacher, B.-M. Elfers, T. Schulze and C. Münker, Tantalum isotope ratio measurements and isotope abundances determined by MC-ICP-MS using amplifiers equipped with 1010, 1012, and 1013 Ohm resistors, J. Anal. At. Spectrom., 2017, 32, 130–143 RSC.
- R. Grigoryan, M. Costas-Rodríguez, P. Santens and F. Vanhaecke, Multicollector Inductively Coupled Plasma–Mass Spectrometry with 1013 Ω Faraday Cup Amplifiers for Ultrasensitive Mg Isotopic Analysis of Cerebrospinal Fluid Microsamples, Anal. Chem., 2020, 92, 15975–15981 CrossRef CAS PubMed.
- O. Rienitz and A. Pramann, Comparison of the isotopic composition of silicon crystals highly enriched in 28Si, Crystals, 2020, 10, 500 CrossRef CAS.
- K. Fujii, H. Bettin, P. Becker, E. Massa, O. Rienitz, A. Pramann, A. Nicolaus, N. Kuramoto, I. Busch and M. Borys, Realization of the kilogram by the XRCD method, Metrologia, 2016, 53, A19–A45 CrossRef CAS.
- G. Bartl, et al. , A new 28Si single crystal: counting the atoms for the new kilogram definition, Metrologia, 2017, 54, 693–715 CrossRef CAS.
- B. Güttler, O. Rienitz and A. Pramann, The Avogadro constant for the definition and realization of the mole, Ann. Phys., 2018, 1800292 Search PubMed.
- O. Rienitz, A. Pramann and D. Schiel, Novel concept for the mass spectrometric determination of absolute isotopic abundances with improved measurement uncertainty: Part 1 – theoretical derivation and feasibility study, Int. J. Mass Spectrom., 2010, 289, 47–53 CrossRef CAS.
- G. Mana and O. Rienitz, The calibration of Si isotope-ratio measurements, Int. J. Mass Spectrom., 2010, 291, 55–60 CrossRef CAS.
- A. Pramann, K.-S. Lee, J. Noordmann and O. Rienitz, Probing the homogeneity of the isotopic composition and molar mass of the “Avogadro”-crystal, Metrologia, 2015, 52, 800–810 CrossRef CAS.
- L. Yang, Z. Mester, R. E. Sturgeon and J. Meija, Determination of the Atomic Weight of 28Si-Enriched Silicon for a Revised Estimate of the Avogadro Constant, Anal. Chem., 2012, 84, 2321–2327 CrossRef CAS PubMed.
- T. Narukawa, A. Hioki, N. Kuramoto and K. Fujii, Molar-mass Measurement of a 28Si-enriched silicon crystal for determination of the Avogadro constant, Metrologia, 2014, 51, 161–168 CrossRef CAS.
- R. D. Vocke Jr, S. A. Rabb and G. C. Turk, Absolute silicon molar mass measurements, the Avogadro constant and the redefinition of the kilogram, Metrologia, 2014, 51, 361–375 CrossRef.
- T. Ren, J. Wang, T. Zhou, H. Lu and Y.-j. Zhou, Measurement of the molar mass of the 28Si-enriched silicon crystal (AVO28) with HR-ICP-MS, J. Anal. At. Spectrom., 2015, 30, 2449–2458 RSC.
- BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, Evaluation of measurement data − Guide to the expression of uncertainty in measurement, JCGM 100:2008, 2008 Search PubMed.
- M. Wang, W. J. Huang, F. G. Kondev, G. Audi and S. Naimi, The AME2020 atomic mass evaluation, Chin. Phys. C, 2021, 45, 030003 CrossRef CAS.
- A. Pramann, J. Noordmann and O. Rienitz, Investigation of mass-scale drift effects in the milli-mass range: Influence on high mass resolution mode multicollector-inductively coupled plasma mass spectrometer isotope ratio measurements, J. Mass Spectrom., 2021, 56, e4732 CrossRef CAS PubMed.
- G. Craig, Z. Hu, A. Zhang, N. S. Lloyd, C. Bouwman and J. Schwieters, Dynamic Time Correction for High Precision Isotope Ratio Measurements, Technical Note 30396, Thermo Fisher Scientific Inc., 2019 Search PubMed.
- T. Pettke, F. Oberli, A. Audétat, U. Wiechert, C. R. Harris and C. A. Heinrich, Quantification of transient signals in multiple collector inductively coupled plasma mass spectrometry: accurate lead isotope ratio determination by laser ablation of individual fluid inclusions, J. Anal. At. Spectrom., 2011, 26, 475–492 RSC.
- A. Gourgiotis, G. Manhès, P. Louvat, J. Moureau and J. Gaillardet, Transient signal isotope analysis using multicollection of ion beams with Faraday cups equipped with 1012 Ω and 1011 Ω feedback resistors, J. Anal. At. Spectrom., 2015, 30, 1582–1589 RSC.
- A. Gourgiotis, G. Manhès, P. Louvat, J. Moureau and J. Gaillardet, Transient signal isotope analysis: validation of the method for isotope signal synchronization with the determination of amplifier first-order time constants, Rapid Commun. Mass Spectrom., 2015, 29, 1617–1622 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00066h |
| This journal is © The Royal Society of Chemistry 2024 |