Comparison of different mass bias correction procedures for the measurement of mercury species-specific isotopic composition by gas chromatography coupled to multicollector ICP-MS

Abstract

Mercury is a toxic element that can have negative effects on the environment and human health. The study of its isotopic composition provides essential information on the origin and distribution of Hg species in the environment. The determination of precise and accurate Hg species-specific isotope ratios can be carried out by coupling chromatographic techniques with multicollector ICP-MS. The preferential transmission of heavier versus lighter isotopes at the ICP-MS interface influences the isotope ratio calculation. This so-called mass bias effect must be corrected to obtain accurate and precise Hg isotope ratios. When dealing with transient signals, such as those obtained from the coupling of gas chromatography with MC-ICP-MS, mass bias has a higher impact on isotope ratio accuracy and precision than when working with continuous signals. Accuracy and precision of compound-specific isotope ratios can be improved by calculating isotope ratios from the slope of a linear regression between two isotopic signals. However, mass bias correction using this strategy needs a careful evaluation that has not been reported thus far. We demonstrate here that the classical mass bias correction based on a point-by-point isotope ratio calculation does not correct for variations of the Tl isotope ratio during Hg elution. Better internal precision in the Hg(II)-specific isotope ratios was obtained applying the mass bias correction models of Russell and Baxter and the linear regression approach for Tl isotope ratios. However, a large range of data points for Tl isotope ratios along the chromatographic peak profile must be selected to improve the internal accuracy of the Hg(II)-specific isotope ratio measurements. The standard-sample bracketing and Baxter approaches combined with the Russell and Baxter models were tested for the calculation of Hg(II)-specific delta values and did not show significant differences in terms of accuracy and precision which were evaluated with the analysis of NIST 3133 vs. NIST 3133 and NIST 8610 vs. NIST 3133, respectively.

---

Introduction

Mercury (Hg) is a global pollutant that represents a risk to the environment and human beings due to its high toxicity.¹ The measurement of Hg isotopes has emerged in recent decades as a valuable tool to understand the biogeochemical cycle of Hg and its pollution sources.² The determination of the different Hg species in a sample can be extremely helpful to understand the Hg reactivity, mobility and bioaccumulation depending on its chemical form. Hg has seven stable isotopes that can undergo mass-dependent and/or mass-independent isotopic fractionation (MDF and MIF, respectively) during different bio-geochemical processes.^3–7 MIF of odd Hg isotopes is the result of two mechanisms: the magnetic isotope effect and nuclear volume effect and has not been observed after in vivo transformations in the absence of light.⁸ Meanwhile the Hg isotope MDF provides information about the element transformations. The values associated with Hg isotope MDF and MIF are expressed in the delta notation (δ^XXXHg or Δ^XXXHg, respectively).

Accurate and precise total Hg isotope ratios (IRs) can be measured by cold vapour generation coupled to multicollector inductively coupled plasma mass spectrometry (MC-ICP-MS).⁹ The measurement of Hg species-specific isotopic ratios requires, however, the coupling of chromatographic techniques with MC-ICP-MS.¹⁰ In the case of a species-specific IR, the measurement must be performed within a short time period (2–5 s) by gas chromatography coupled to MC-ICP-MS.¹¹ Thus, the external reproducibility of Hg species-specific δ-values is affected by the transient nature of the signals, resulting in standard deviations of the IR between two to five-times higher than those obtained when measuring continuous signals.¹²

IR measurements by MC-ICP-MS are generally affected by mass bias effects that lead to deviations from the true IR in the sample.¹³ This effect results in a preferential transmission of heavier isotopes over lighter isotopes, which significantly affects the accuracy and precision of IR measurements. Mass discrimination occurs at the interface between the ICP source and the mass analyser due to nozzle and space charge effects.^14,15 Three main approaches have been traditionally described to correct for mass bias effects: (i) an external correction based on the measurement of the IR of a reference standard between samples; (ii) an internal correction based on the simultaneous IR measurement of the sample and a reference standard previously added to the sample;¹³ and, (iii) an internal correction based on the simultaneous IR measurement of the sample and a reference IR value, either from the sample itself or from a reference standard previously added to the sample.¹⁶ However, this third approach is not suitable to correct for mass bias in mercury fractionation studies. The effect caused by mass bias on the IR measurement is not constant and stable as it fluctuates throughout the analysis.¹⁷ This means that a correction of the effect is required on a continuous basis, such as the online introduction of another element of similar mass. The correction models are based on the calculation of a correction factor obtained by comparing the measured IR with the theoretical IR in a reference standard applying different mathematical correction models such as linear law, power law, exponential law, Russell's law and Russell's revised models.^18,19 Among them, the exponential and Russell's models are mostly applied for MC-ICP-MS measurements.¹⁷ Although these models have been mainly developed to correct instrumental MDF, their validity has also been studied in the correction of instrumental MIF.¹⁶ A recent study reports MIF in the measurement of the osmium IR by MC-ICP-MS.²⁰ However, when measuring a transient signal for a species-specific IR, the low number of acquisition points hinders the detection of instrumental MIF.¹⁸

Previous studies have used the point-by-point (PbP) method, which consists of measuring each IR independently along the transient signal at each point and calculates the overall IR as an average.²¹ Accuracy and precision of a species-specific IR are improved when they are calculated from the slope of a linear regression between two isotopic signals (LRS method). This strategy was first developed by Fietzke et al.²² for laser ablation coupled to MC-ICP-MS and then applied by Epov et al.¹² to measure a species-specific Hg IR by GC-MC-ICP-MS. Previous studies have reported an external reproducibility of Hg species-specific δ-values by GC-MC-ICP-MS lower than 0.5‰ (expressed as 2SD).^12,21 Typically a standard-sample bracketing (SSB) approach is applied for the calculation of the species-specific δ-values of Hg. Internal mass bias correction of Hg IR measurements is usually carried out with the continuous nebulisation of a thallium (Tl) solution for the measurement of the ^205/203Tl IR. In the case of GC-MC-ICP-MS, the nebulized Tl solution is continuously mixed with the Ar flow, transporting the gaseous analytes eluting from the GC. The elution of the sample matrix from the GC column may induce plasma instabilities affecting the mass bias in the chromatographic peak profile of Hg compounds. Previous approaches assume that on a continuous basis these instabilities equally affect Hg and Tl. Thus, the Russell model, which is the most widely used correction protocol for high precision and accuracy measurements of the Hg IR, uses the ^205/203Tl IR as a reference. This model has been revised by Baxter and coworkers,²³ following the work of Albarede et al.¹⁶ who developed a new equation in which mass bias correction is performed considering the whole data set obtained and not just the standards measured before and after the sample.

Despite the importance of mass bias correction, previously published approaches have not evaluated so far its effect on the measurement of the Hg species-specific IR using the slope of a linear regression between two different isotopic signals. This work compares different mass bias correction models to achieve the best accuracy and precision of the Hg(II)-specific IR and δ-values by GC-MC-ICP-MS. We also evaluate here two different protocols for the measurement of Hg(II)-specific δ-values: (i) the standard-sample bracketing (SSB) approach; and (ii) the bracketing procedure proposed by Baxter et al.²³ This study has been performed analysing in different measurement sessions the primary standard NIST 3133 vs. NIST 3133 and the secondary standard NIST RM-8610 (former UM-Almaden) vs. NIST 3133.

Experimental

Reagents and materials

The δ_zero standard NIST SRM-3133 and the secondary standard NIST RM-8610 (former UM-Almaden) were purchased from the National Institute of Standards and Technology (NIST, Gaithersburg, MD, USA). The thallium (Tl) standard used for the internal correction of the mass bias was obtained from Absolute Standards Inc. (Hamden, CT, USA). This standard was diluted in 2% ultrapure sub-boiled HNO₃ in ultra-pure water (≥18 MΩ cm) obtained using a Purelab Flex 3 water purification system (Elga Labwater, Lane End, UK). Sodium acetate and acetic acid (Sigma-Aldrich) were dissolved in ultra-pure water to prepare an acetic acid/sodium acetate buffer (0.1 M, pH = 4). Ethylation of Hg(II) was carried out using a sodium (tetra-n-ethyl) borate 2% (w/v) solution (LGC-Standards, Wesel, Germany) in ultrapure water. The derivatised Hg compounds were extracted in hexane purchased from Sigma-Aldrich (St. Louis, MO, USA).

Instrumentation

A multicollector inductively coupled plasma mass spectrometer Neptune Plus (Thermo Scientific, Bremen, Germany) was coupled to a gas chromatograph model Agilent 6890N (Agilent Technologies, Tokyo, Japan) fitted with a split/splitless injector and a DB-5MS capillary column from Agilent J&W Scientific (cross-linked 5% diphenyl, 95% dimethylsiloxane, 30 m × 0.53 mm i.d. × 1.0 μm). The GC-MC-ICP-MS operating conditions are shown in Table S1.† A heated metallic block was used as an interface enabling the mixing of the Ar carrier gas flow from the MC-ICP-MS and the carrier gas flow of the GC column to transfer the Hg species into the ICP source. Fig. S1† shows the experimental set-up. A PFA concentric nebulizer (700 μL min⁻¹) was employed with a cyclonic spray chamber. This assembly was connected to the GC-MC-ICP-MS through a glass Y-piece to introduce the wet aerosol of a Tl solution and mix it with the eluent from the gas chromatograph. An analytical balance Mettler Toledo MS205DU was used to weigh the samples and standards. A Basic 20 CRISON pH-meter (Alella, Barcelona, Spain) was used to adjust the pH of the buffer solution.

Sample preparation for isotope ratio measurements

Working solutions of Hg(II) were prepared in 7 mL glass vials containing 4 mL of acetic acid/acetate buffer (0.1 M, pH 4) by the addition of the appropriate amount of the standard solution to obtain a final concentration of 250 ng Hg per g in the organic phase. Hg(II) was ethylated and extracted into an organic phase by the addition of 1 mL of hexane and 200 μL of 2% sodium(tetra-n-ethyl) borate, followed by 5 minutes of manual shaking. Finally, the organic phase was transferred to a 2 mL glass vial and stored at −18 °C until analysis.

Measurement of Hg(II)-specific isotope ratios

The isotopes ¹⁹⁸Hg, ¹⁹⁹Hg, ²⁰⁰Hg, ²⁰¹Hg, ²⁰²Hg, ²⁰³Tl, and ²⁰⁵Tl were simultaneously measured in the Faraday cups L3, L2, L1, C, H1, H2, and H3, respectively. All measurements were performed in a static multicollection mode with an integration time of 0.132 s using the conventional acquisition software of the instrument. The isotopes ²⁰⁴Hg and ¹⁹⁶Hg could not be measured due to the specific Faraday cup configuration of our MC-ICP-MS instrument. ²⁰³Tl and ²⁰⁵Tl were continuously measured for mass bias correction by nebulizing a 90 ng per L Tl solution in 2% HNO₃. The concentration of the Tl solution was selected so that the voltage of ²⁰⁵Tl and the apex voltage of ²⁰²Hg matched within 10%. Before starting each measurement session, the Faraday-amplifier gains were calibrated and the mass window, lenses, torch position and Ar flows were optimized using the ²⁰⁵Tl signal. The mass accuracy of the Faraday cups was initially obtained by nebulisation of a Hg standard solution of 20 ng g⁻¹. However, in order to avoid Hg contamination in the MC-ICP-MS system due to memory effects, mass accuracy was checked and adjusted daily with the measurement of a 20 ng per g Tl solution.

Data reduction

Hg(II)-specific isotope ratio calculation and time-lag correction. The calculation of Hg(II)-specific isotope ratios was performed by the linear regression slope (LRS) approach in all cases. The LRS method is used to calculate the IR as the slope (b) of a linear regression according to eqn (1):

V^XXX = a + b × V¹⁹⁸ (1)

where V^XXX is the voltage obtained for the isotope XXX, XXX is the mass of the isotopes between ¹⁹⁹Hg and ²⁰²Hg, and a is the intercept. This equation is applied employing a range of 321 Hg acquisition points (160 acquisition points before and after the peak apex). Previous studies¹² have evaluated different chromatographic peak percentages. However, to facilitate the comparison between the different data treatment strategies applied in this work, we have evaluated the number of acquisition points of the chromatogram rather than peak percentages. The internal precision of an individual analysis is reported as 2 times the standard error of the average value of the slope. From a practical point of view, both the slope and the standard error of the slope were calculated using the function LINEST in Microsoft Excel.

Additionally, the voltages measured for the Hg transient signal were corrected for time-lag employing eqn 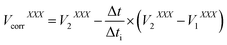(2):

In this equation V₁ and V₂ are the voltages measured for the isotope XXX by the delayed cup at the beginning and at the end of the integration time (Δt_i). All details concerning the IR calculation, time-lag values, and the correction of the voltages with respect to the time-lag can be found elsewhere.¹¹

Mass bias correction. The elution of the sample matrix from the GC column induces plasma instabilities affecting mass bias in the chromatographic peak profile of Hg compounds. To minimize this problem a Tl solution was simultaneously nebulized into the ICP source using a microconcentric nebulizer and a cyclonic spray chamber. The Tl spray was mixed through a Y-piece with the Ar flow transporting the gaseous analytes as described in Fig. S1.† The ²⁰⁵Tl/²⁰³Tl isotope ratio was also calculated using the LRS approach. In this case, as the signal for Tl is constant, the intercept of the line was assumed to be 0 and only the slope (b) was calculated according to eqn (3).²⁴ This procedure allows the determination of the residuals of the linear fit between the signals of ²⁰⁵Tl and ²⁰³Tl which would indicate possible matrix effects on mass bias occurring during the elution of the mercury peaks.

V²⁰⁵ = b × V²⁰³ (3)

The whole data reduction procedure employing eqn (1)–(3) is illustrated in Fig. S2 of the ESI.†

Then, we employed two models to correct for mass bias and to calculate delta values: the Russell model in combination with SSB and the Baxter revised model. Mass bias correction by the Russell approach was carried out using eqn (4):

In eqn (4)XXX are the Hg isotopes from 199 to 202 with the corresponding IR calculated as explained above, w is the isotopic mass of the corresponding isotope and k is the mass bias correction factor calculated employing eqn (5):

In eqn (5) we have employed a value of 2.387075 as theoretical ²⁰⁵Tl/²⁰³Tl based on the IUPAC thallium natural abundance.

For the determination of the absolute Hg isotope ratios for NIST 8610 UM-Almadén using the Russell SSB approach a correction factor (f) was calculated using the absolute abundances published by the NRCC on the NIST 3133 standard²⁵ using eqn (6)

where the expression corresponds to the average of the mass bias corrected ratios, eqn (4), measured just before and after the Almadén sample. Finally, the corrected NIST 8610 ratios were calculated using eqn (7):

On the other hand, the mass bias correction model proposed by Baxter et al.²³ determines the linear relationship between the natural logarithm of the mercury isotope ratios and the natural logarithm of the thallium isotope ratios measured for the whole calibration data set using the NIST 3133 reference standard as shown in eqn (8):

The determined values of a and b can be employed directly for the measurement of deltas as we will see below. Please note that the a and b values will vary with the measured mercury isotope ratio.

For the determination of the absolute Hg isotope ratios for NIST 8610 UM-Almadén using the Baxter approach a correction factor (f) was calculated using the absolute abundances published by the NRCC on the NIST 3133 standard²⁵ employing eqn (9):

Then, the corrected NIST 8610 ratios were calculated using eqn 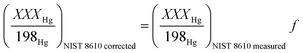(10):

The measured Tl IR for mass bias correction was calculated by using three different strategies: (1) LRS using 321 Tl acquisition points (160 acquisition points before and after the peak apex), (2) LRS using 27 Tl acquisition points (13 acquisition points before and after the peak apex), and (3) point by point (PbP) approach using 321 acquisition points. Fig. 1 gives an overview of the different strategies followed for mass bias correction and delta value calculation. The calculation by the PbP approach was only carried out using the Russell model for mass bias correction through eqn (3), since the Baxter model does not allow to correct for each individual point. The values a and b are obtained from the plotted logarithmic values of the non-corrected isotope ratio ^XXXHg/¹⁹⁸Hg of the delta zero standard NIST 3133 and the isotope ratio ²⁰⁵Tl/²⁰³Tl. Therefore, it cannot be applied to the PbP method. When applying the PbP method, the isotope ratio is calculated at each acquisition point using background corrected voltages. Then, the average of the isotope ratios measured over a certain range of acquisition points within the transient signal is calculated. More details about this protocol are detailed elsewhere.¹¹

Fig. 1 Overview of the different calculation procedures for Hg IR (internal correction) and species-specific Hg δ-values.

A correction factor (f) and thus a corrected IR were obtained for each acquisition point of the chromatogram. For the calculation of the Hg IR by LRS the corrected voltages (V_corrected^XXX) for isotopes from ¹⁹⁹Hg to ²⁰²Hg were obtained from the uncorrected V¹⁹⁸ values with eqn (11).

Calculation of Hg(II)-specific δ-values. Two different δ-value calculation strategies were used as described in Fig· S3:† (i) the traditional sample-standard bracketing (SSB) approach using the Tl-corrected isotope ratios, and (ii) the approach proposed by Baxter et al.²³ In both cases, the reference material NIST 3133 was used as the δ_zero standard. When applying the SSB approach, the δ-values were calculated as described in eqn (12):where XXX refers to the mass of the isotopes between ¹⁹⁹Hg and ²⁰²Hg. The isotope ratio of the standard NIST 3133 is calculated from the average of the Tl-corrected isotope ratios measured just before and after the sample. The concentration of the standard was adjusted to match the intensity of that of the sample within 10%.

When applying the approach proposed by Baxter et al.,²³δ-values were calculated as described in eqn (13) from the measured Hg and Tl isotope ratios in the sample:

Note that in eqn (13) the expression corresponds to the NIST 3133 value that “would have been measured” for this particular sample according to the calibration values a and b obtained from eqn (8).

Results and discussion

Evaluation of mass bias variation along the chromatographic elution profile

Mass bias correction of the Hg(II)-specific IR by GC-MC-ICP-MS is usually carried out by measuring the ²⁰⁵Tl/²⁰³Tl IR. For this purpose, a nebulised Tl solution is mixed with the Ar flow transporting the eluted compounds from the GC column. The elution of the sample matrix or even the analytes may induce plasma instabilities affecting mass discrimination in the chromatographic peak profiles. Fig. 2 shows the variation of the residuals observed when applying eqn (3) to calculate the ²⁰⁵Tl/²⁰³Tl isotope ratio along the Hg(II) elution peak. The way the residuals are calculated is illustrated in Fig. S2.† This plot shows how the residuals of the linear regression display randomly except when Hg(II) is eluted from the GC column and hence, a small variation of the mass bias factor during Hg(II) elution is observed. Consequently, the range of acquisition points of Tl selected for mass bias correction may affect the corrected IR values and the final species-specific δ-values. So, we decided to compare two ranges of Tl employed for mass bias correction: the whole profile of 321 acquisition points as selected by Queipo-Abad et al.¹¹ and a narrower range of 27 Tl data points covering only the Hg(II) elution peak profile. Additionally, we evaluate here the effect of different mass bias correction procedures (Russell with SSB and Baxter) on the accuracy and precision of the Hg(II)-specific IR and δ-values by GC-MC-ICP-MS. To facilitate the standardization and comparison of our results with those of other laboratories, δ-values and their associated uncertainties were calculated following the guidelines proposed by Blum and Bergquist,²⁶ for reporting variations in the natural isotopic composition of Hg. According to previous studies an acceptable external precision for species-specific δ-values should be lower than 0.5 as 2SD.¹¹ The whole data set consisted of 6 measurement sessions. Three of those sessions were NIST 3133 only (n = 17, n = 21 and n = 15) to evaluate the internal precision of the mercury isotope ratio measurement process and the capabilities for delta 0 measurements. Another three sessions were carried out by bracketing the n = 8 NIST RM 8610 UM-Almadén mercury standard with n = 9 NIST 3133 to evaluate both absolute mercury isotope ratios and delta values for this reference material.

Fig. 2 Distortion of ²⁰⁵Tl residuals during the elution of Hg(II). Blue dots correspond to the residuals for eqn (3) while the ²⁰²Hg peak profile is represented in red.

Evaluation of the mass bias correction procedure on the internal precision of Hg(II)-specific IR measurements by GC-MC-ICP-MS

Fig. 3 shows the ²⁰²Hg/¹⁹⁸Hg IR uncorrected and corrected for mass bias by using the Russell and Baxter correction models obtained for two independent measurement sessions of NIST RM 8610 vs. NIST 3133 (Fig. 3a and b). The IRs were corrected for mass bias either by the Russell and Baxter approach applying three different procedures detailed in the Experimental section: (i) LRS using 321 Tl acquisition points, (ii) LRS using 27 Tl acquisition points and (iii) PbP approach using 321 acquisition points (only by Russell). Table 1 summarizes the average ²⁰²Hg/¹⁹⁸Hg IR and internal precisions (expressed as 2SE) obtained from three different measurement sessions for NIST RM 8610. Table S2 of the ESI† shows all individual Hg(II)-specific IRs obtained in three different measurement sessions.

Fig. 3 ²⁰²Hg/¹⁹⁸Hg ratios calculated using Russell and Baxter correction models for mass bias, by the different calculation procedures (LRS and PbP) obtained in two analytical sessions for NIST 8610 (n = 8): (a) session 1 and (b) session 2. Uncertainties for each IR value correspond to 2SE obtained in the calculation of the IR. The secondary axis refers to the uncorrected values while the main axis refers to the values corrected for mass bias.

Table 1 ²⁰²Hg/¹⁹⁸Hg average and the internal precision expressed as ±2SE values obtained with Russell and Baxter corrections for NIST RM 8610 in three measurement sessions with three different mass bias correction approaches: (1) LRS using 321 acquisition points of Tl, (2) LRS using 27 acquisition points of Tl and (3) PbP using 321 acquisition points of Tl

Mass bias correction model	Mass bias calculation procedure with Tl	Session 1 (n = 8)	Session 2 (n = 8)	Session 3 (n = 8)
Russell	LRS-321 Tl	2.9611 ± 0.0008	2.9610 ± 0.0006	2.9612 ± 0.0014
	LRS-27 Tl	2.9605 ± 0.0018	2.9613 ± 0.0015	2.9611 ± 0.0013
	PbP-321 Tl	2.9597 ± 0.0033	2.9613 ± 0.0027	2.9608 ± 0.0032
Baxter	LRS-321 Tl	2.9611 ± 0.0003	2.9610 ± 0.0002	2.9613 ± 0.0004
	LRS-27 Tl	2.9608 ± 0.0009	2.9613 ± 0.0005	2.9611 ± 0.0005

---

According to Fig. 3, when applying Russell's correction model, the highest variability of the IR values is observed for the PbP approach. Regarding the IR corrected by using the Baxter model, only the results given by LRS will be analysed, since Baxter does not apply to the results obtained with the PbP approach, as explained in the Experimental section. Based on Table 1, for Russell and Baxter correction models the best internal precision values were obtained for LRS selecting 321 Tl acquisition points, (from 0.0002 to 0.0014 for both models). When selecting LRS with 27 Tl acquisition points the internal precision of ²⁰²Hg/¹⁹⁸Hg ranged from 0.0013 to 0.0018 when using the Russell model and from 0.0005 to 0.009 when using the Baxter model (Table 1). The rest of the isotope ratios exhibited an internal precision within 0.0005–0.0011 when using the Russell model and within 0.0002–0.0005 when using the Baxter model (Table S2†). Thus, the LRS method considering 321 Tl acquisition points using the Russell model provided in general lower 2SE values for all Hg(II)-specific IRs than when using 27 Tl acquisition points.

When applying the PbP correction method 2SE values for ²⁰²Hg/¹⁹⁸Hg ranged from 0.0027 to 0.0033 (Table 1) and 2SE values from 0.0006 to 0.0015 for the rest of Hg(II) IRs. This can be explained by the variation in the IR of Tl due to the elution of Hg as described in Fig. 2. The use of a larger number of acquisition points using the LRS method allows for improved precision and accuracy data. In this case, the selection of background points is of great importance in the calculation and reduces the impact of Hg elution on the Tl intensity. In contrast, in the PbP calculation, this variation does cause a worsening of the accuracy and precision when correcting with Tl.

Table 2 covers the mass bias corrected mercury isotope ratios for NIST RM 8610 averaged over 24 independent measurements in 3 different sessions. As can be observed, the average values for all measured isotope ratios were statistically the same using all different correction models. The 2SE values are also comparable between the Russell and the Baxter approaches and 321 data points provide the best precision values. The PbP approach shows worse performance. In summary, our results show that Russell's classical mass bias correction model with SSB gives equivalent IR results to Baxter's revised model with a similar internal precision. Also, as seen in previous work,¹¹ the selection of the adequate range of data points for the Tl IR is essential to obtain the best internal precision of the Hg(II)-specific IR.

Table 2 Overall ^XXXHg/¹⁹⁸Hg isotope ratios and the internal precision expressed as ±2SE values obtained with Russell and Baxter corrections for NIST RM 8610 after three measurement sessions (n = 24) with three different mass bias correction approaches: (1) LRS using 321 acquisition points of Tl, (2) LRS using 27 acquisition points of Tl and (3) PbP using 321 acquisition points of Tl

Mass bias correction model		Russell			Baxter
Mass bias calculation procedure with Tl		LRS-321 Tl	LRS-27 Tl	PbP-321 Tl	LRS-321 Tl	LRS-27 Tl
NIST RM 8610 (n = 24)	^199/198Hg	1.6870 ± 0.0007	1.6870 ± 0.0006	1.6869 ± 0.0007	1.6870 ± 0.0007	1.6870 ± 0.0007
	^200/198Hg	2.3043 ± 0.0009	2.3043 ± 0.0011	2.3041 ± 0.0015	2.3043 ± 0.0011	2.3044 ± 0.0011
	^201/198Hg	1.3114 ± 0.0004	1.3113 ± 0.0007	1.3112 ± 0.0012	1.3114 ± 0.0006	1.3114 ± 0.0010
	^202/198Hg	2.9611 ± 0.0010	2.9610 ± 0.0017	2.9606 ± 0.0033	2.9611 ± 0.0009	2.9610 ± 0.0018

---

Evaluation of the accuracy and external precision of mass bias corrected δ-values

The external precision or reproducibility of Hg(II)-specific δ-values was expressed as 2 times the standard deviation (2SD) of several measurements of δ-values of NIST 3133 versus the delta-zero standard NIST-3133 and NIST RM 8610 versus the delta-zero standard NIST-3133. The calculation of the delta values in this work was carried out by using two different measurement strategies: (a) SSB and (b) Baxter approaches. Based on previous studies, an optimal external precision for Hg(II)-specific δ-value measurements is equal to or below ±0.5‰ as 2SD.^11,12Fig. 4 shows the average δ^XXXHg(II) (‰) and the external precision expressed as ±2SD calculated with SSB and Baxter approaches for six independent measurement sessions for: (a) δ_zero NIST 3133 vs. NIST 3133, and (b) NIST RM 8610 vs. NIST 3133. Tables S3 and S4† show the numerical values in Fig. 4 corresponding to the average δ^XXXHg(II) (‰) and the external precision expressed as ±2SD for NIST 3133 and NIST RM 8610, respectively. The interval 0.0 ± 0.5‰ is highlighted in grey in Fig. 4a, whereas the certified δ-values (±2SD) of NIST RM 8610 are highlighted in grey in Fig. 4b. The best external precision in the calculation of delta values was obtained using SSB after mass bias correction using the Russel model and LRS with 321 Tl data points, as the external precision obtained ranged from 0.34 to 0.41‰ for NIST 3133 and from 0.34 to 0.40‰ for NIST RM 8610 (Tables S3 and S4†). When applying the Baxter model, external precision ranged from 0.35 to 0.46‰ for NIST 3133 and from 0.31 to 0.44‰ for NIST RM 8610 (Tables S3 and S4†). The external precisions for δ-values decreased significantly when 27 Tl acquisition points were selected (0.33–1.94‰) for the calculation of mass bias. A worsening of precision is also observed when calculating mass bias by the PbP approach (0.42–1.26‰) compared to the external precisions obtained by the LRS method using 321 Tl points.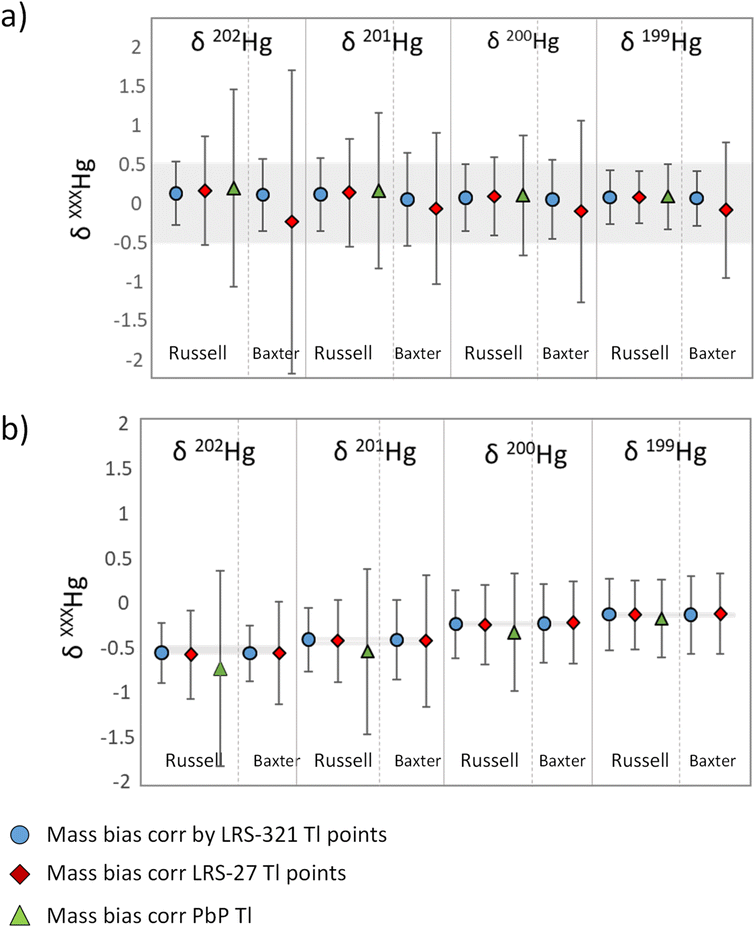

Fig. 4 δ ^XXX Hg(II) (‰) and external precision expressed as ±2SD calculated with SSB and Baxter approaches for six independent measurement sessions. (a) δ-zero values of NIST 3133 vs. NIST 3133 (n = 26). The grey line represents the ideal precision interval of 0.50‰ based on other studies,^9,18 (b) secondary standard NIST RM 8610 vs. NIST 3133 (n = 24). Grey lines represent the certified values (±2SD) for NIST RM 8610.

The evaluation of the accuracy of the δ-values was carried out comparing the reference δ-values for NIST RM 8610 with the experimental values. Table 3 and Fig. 4 show the experimental δ²⁰²Hg (‰) and external precision expressed as ±2SD for NIST RM 8610. We evaluated the mass bias correction procedures and the two measurement strategies (SSB and Baxter) and the results obtained were in agreement with those obtained in the evaluation of the internal IR precision. Overall, a better agreement was found for the LRS method considering 321 Tl points regardless of the model applied (Russell or Baxter). In contrast to the evaluation of the external precision of the delta values, the accuracy is not compromised when decreasing the number of Tl acquisition points for mass bias correction, but it is when correcting mass bias by the PbP approach. This shows that a traditional mass bias PbP correction is not a suitable method of calculation for species-specific Hg delta values.

Table 3 δ ²⁰²Hg (‰) averages and the external precision expressed as ±2SD calculated with SSB and Baxter approaches for three independent measurement sessions with three different mass bias correction approaches: (1) 321 acquisition points of Tl, (2) 27 acquisition points of Tl and (3) the PbP approach

Mass bias correction model	Mass bias calculation procedure with Tl	δ ^202 Hg NIST 3133 (‰) n = 26	δ ^202 Hg NIST RM 8610 (‰) n = 24
			Reference value	Experimental value
Russell	LRS-321 Tl	0.07 ± 0.41	−0.56 ± 0.03	−0.59 ± 0.34
	LRS-27 Tl	0.11 ± 0.70	−0.56 ± 0.03	−0.61 ± 0.49
	PbP-321 Tl	0.14 ± 1.26	−0.56 ± 0.03	−0.77 ± 1.09
Baxter	LRS-321 Tl	0.06 ± 0.46	−0.56 ± 0.03	−0.60 ± 0.31
	LRS-27 Tl	−0.29 ± 1.94	−0.56 ± 0.03	−0.60 ± 0.57

---

Conclusions

This work presents the first evaluation of different mass correction models for the measurement of compound-specific IRs in transient signals by GC-MC-ICP-MS. Until now, the Russell model was used as the default model for this type of measurement. We demonstrate here that δ^XXXHg values are affected during chromatographic elution of Hg(II) since it induces variations in the IR of Tl and hence, in the Hg(II)-specific IR and δ^XXHg values. The classical PbP correction method has been shown to be the worst option for mass bias correction in terms of precision and accuracy of Hg(II)-specific IR and δ^XXXHg values. The internal precision of absolute Hg(II)-specific ratios was better when the range of points selected for LRS is larger (321 instead of 27) regardless of the mass bias correction model (Russell or Baxter). We can therefore say that in the case of Hg(II)-specific ratios one of the critical aspects in the mass bias correction is the selection of the range of acquisition points. This may be intrinsically related to the variation of the Tl isotope ratios during the elution of the Hg peak as demonstrated in this paper. The evaluation of SSB and the bracketing procedure proposed by Baxter et al.²³ showed that both approaches provide similar accuracy and precision in δ^XXXHg. A slightly better accuracy and precision in the experimental δ^XXXHg was found applying the LRS calculation in combination with the Russell model and the SSB approach. This work highlights the importance of reviewing and evaluating different protocols for the accurate and precise measurement and calculation of species-specific IR and delta values, not only for mercury but also for other elements.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Financial support from the Spanish Ministry of Science and Innovation through project PID2021-125795NB-I00 is acknowledged. Laura Suarez-Criado is grateful to the Principality of Asturias, Spain, for their financial support through the Severo Ochoa scholarship ref. BP19-131.

References

1. J. Xu, M. Buck, K. Eklöf, O. O. Ahmed, J. K. Schaefer, K. Bishop, U. Skyllberg, E. Björn, S. Bertilsson and A. G. Bravo, Sci. Rep., 2019, 9, 518.
2. H. Hintelmann, in Mercury in the Environment: Pattern and Process, ed. M. S. Bank, Univ. Calif. Press, USA, 2012, pp. 55–72.
3. E. Young, A. Galy and H. Nagahara, Geochim. Cosmochim. Acta, 2002, 66, 1095–1104.
4. A. L. Buchachenko, J. Phys. Chem. A, 2001, 105, 9995–10011.
5. J. Bigeleisen, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 9393–9396.
6. E. A. Schauble, Geochim. Cosmochim. Acta, 2007, 71, 2170–2189.
7. J. E. Sonke, Geochim. Cosmochim. Acta, 2011, 75, 4577–4590.
8. L. Lefticariu, J. D. Blum and J. D. Gleason, Environ. Sci. Technol., 2011, 45, 1724–1729.
9. A. Rua-Ibarz, E. Bolea-Fernandez and F. Vanhaecke, Anal. Bioanal. Chem., 2016, 408, 417–429.
10. E. M. Krupp and O. F. Donard, Int. J. Mass Spectrom., 2005, 242, 233–242.
11. S. Queipo-Abad, P. Rodríguez-González and J. I. García-Alonso, J. Anal. At. Spectrom., 2019, 34, 753–763.
12. V. N. Epov, S. Berail, M. Jimenez-Moreno, V. Perrot, C. Pecheyran, D. Amouroux and O. F. Donard, Anal. Chem., 2010, 82, 5652–5662.
13. L. Yang, Mass Spectrom. Rev., 2009, 28, 990–1011.
14. D. Beauchemin, Inductively Coupled Plasma Mass Spectrometry, Anal. Chem., 2010, 82, 4786–4810.
15. C. P. Ingle, B. L. Sharp, M. S. A. Horstwood, R. R. Parrish and D. J. Lewis, J. Anal. At. Spectrom., 2003, 18, 219–229.
16. F. Albarede, P. Telouk, J. Blichert-Toft, M. Boyet, A. Agranier and B. Nelson, Geochim. Cosmochim. Acta, 2004, 68, 2725–2744.
17. J. I. García Alonso and P. Rodríguez-González, Isotope Dilution Mass Spectrometry, The Royal Society of Chemistry (RSC), 2013.
18. P. Alvarez Penanes, A. Reguera Galan, G. Huelga-Suarez, J. A. Rodríguez-Castrillón, M. Moldovan and J. I. García-Alonso, J. Anal. At. Spectrom., 2022, 37, 701–726.
19. L. Yang, S. Tong, L. Zhou, Z. Hu, Z. Mester and J. Meija, J. Anal. At. Spectrom., 2018, 33, 1849–1861.
20. Z. Zhu, J. Meija, S. Tong, A. Zeng, L. Zhou and L. Yang, Anal. Chem., 2018, 90, 9281–9288.
21. V. N. Epov, P. Rodriguez-Gonzalez, J. E. Sonke, E. Tessier, D. Amouroux, L. M. Bourgoin and O. F. X. Donard, Anal. Chem., 2008, 80, 3530–3538.
22. J. Fietzke, V. Liebetrau, D. Günther, K. Gürs, K. Hametner, K. Zumholz, T. H. Hansteena and A. Eisenhauera, J. Anal. At. Spectrom., 2008, 23, 955–961.
23. D. C. Baxter, I. Rodushkin, E. Engström and D. Malinovsky, J. Anal. At. Spectrom., 2006, 21, 427–430.
24. J. Á. Rodríguez-Castrillón, S. García-Ruiz, M. Moldovan and J. I. G. Alonso, J. Anal. At. Spectrom., 2012, 27, 611–618.
25. J. Meija, L. Yang, R. E. Sturgeon and Z. Mester, J. Anal. At. Spectrom., 2010, 25(3), 384–389.
26. J. D. Blum and B. A. Bergquist, Anal. Bioanal. Chem., 2007, 388, 353–359.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ja00356f

---