Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comparison of calibration strategies for quantitative laser ablation ICP-mass spectrometry (LA-ICP-MS) analysis of fused catalyst samples†
Ana
Rua-Ibarz‡
 a,
Thibaut
Van Acker
a,
Thibaut
Van Acker
 a,
Eduardo
Bolea-Fernandez‡
a,
Eduardo
Bolea-Fernandez‡
 a,
Marina
Boccongelli
a,
Marina
Boccongelli
 b and
Frank
Vanhaecke
b and
Frank
Vanhaecke
 *a
*a
aDepartment of Chemistry, Atomic & Mass Spectrometry – A&MS research unit, Ghent University, Campus Sterre, Krijgslaan 281-S12, 9000, Ghent, Belgium. E-mail: Frank.Vanhaecke@UGent.be
bTotal Energies OneTech Belgium, Zone Industrielle C, 7181, Feluy, Belgium
First published on 25th January 2024
Abstract
In the field of petrochemistry, the quantitative determination of trace elements in catalysts is crucial for optimizing various types of processes. Catalyst poisoning, resulting from the presence of contaminants, can lead to decreased performance and efficiency, even when these are present at trace level only. Inductively coupled plasma-mass spectrometry (ICP-MS) is a powerful technique for trace elemental analysis, but its application to catalysts is challenging due to their physicochemical characteristics challenging straightforward dissolution. Laser ablation (LA) coupled to ICP-MS (LA-ICP-MS) has emerged as a valuable approach for direct analysis of solid samples. However, developing an appropriate calibration strategy for reliable quantitative LA-ICP-MS analysis of catalyst samples remains a challenge. In this work, different calibration strategies for quantitative LA-ICP-MS analysis of fused catalyst samples were evaluated. The traditional strategy relied on external calibration against certified reference materials (CRMs) combined with internal standardization and was considered the reference approach. When using this approach, the relative bias with respect to the reference value was found to be <15%. Two novel calibration strategies were introduced and compared: a so-called multi-signal calibration approach and a solution-based calibration approach. The multi-signal calibration strategy involved varying the laser repetition rate (20, 30, 40 and 50 Hz) or laser beam diameter (10, 12, 15 and 20 μm), allowing a calibration curve to be constructed by comparing the analytical signal intensity for a single solid CRM with that for the sample, thus partially overcoming the shortage of CRMs for quantitative LA-ICP-MS analysis. The solution-based calibration approach was used for quantitative multi-element analysis without the need for any solid standard and required only minor hardware modifications to accommodate the introduction of aqueous standard solutions for calibration. Various glass certified reference materials were used for method development, calibration, and validation purposes. Furthermore, two fused alumina catalyst samples (used in the context of petroleum refining processes) were successfully analyzed as a proof-of-concept application. For both the multi-signal (matrix-matched conditions) and the solution-based calibration approaches, the average relative bias between the experimentally determined and certified/reference concentrations varied between −9% and +7%.
1. Introduction
In petrochemistry, the determination of chemical elements present at trace levels in catalysts is of particular interest because of the important economic stakes involved.1 Catalysts play a key role in various petrochemical processes, such as refining, hydrocracking, catalytic cracking and reforming. However, catalysts can be susceptible to poisoning.2 Catalyst poisoning refers to the detrimental effects exerted by the presence of certain (trace) elements or contaminants in the feedstock or reaction environment on the catalyst performance and efficiency.3 Since trace elements, even at extremely low concentration levels, can have a significant impact on catalyst activity, selectivity and lifespan, the development of suitable analytical methods allowing reliable quantitative determination of their trace elemental composition is of the utmost importance for improving the efficiency of petrochemical processes.Inductively coupled plasma-mass spectrometry (ICP-MS) is the most powerful technique for (ultra-) trace elemental and isotopic analysis in a wide variety of sample types.4 Among other advantages, ICP-MS provides high sensitivity, low limits of detection, a wide linear dynamic range, a pronounced multi-element character and the ease of combination with alternative sample introduction systems. In its standard configuration, ICP-MS is designed for analysis of liquid samples and aqueous solutions. However, direct analysis of solid material is enabled using laser ablation (LA) as a means of sample introduction (LA-ICP-MS).5,6 In LA-ICP-MS, the solid sample is placed in an air-tight ablation cell and the aerosol generated upon laser beam impact is transported out of the cell and into the ICP ion source for analysis.7,8 However, the major analytical challenge for quantitative LA-ICP-MS analysis is the development of an appropriate calibration strategy.9–11 External calibration against (a) commercially available matrix-matched certified reference material(s) (CRMs) has always been considered the reference approach,12 but the lack of suitable CRMs with a matrix composition similar to that of the samples and containing the analytes of interest at adequate concentration levels, often jeopardizes the use of this strategy. Alternatively, matrix-matched calibration standards can be prepared in-house using fused beads, pressed pellets, or sol–gel formation, aiming at a matrix composition as similar to that of the samples as possible.13–15 However, this preparation method is challenging, costly and time-consuming and the standards thus manufactured may have disadvantages such as an insufficient homogeneity. For biological samples, pseudo-matrix-matched standards, e.g., based on doped gelatin, have been used as an inexpensive and simple alternative.16 Signal normalization or internal standardization, in combination with external calibration, has been employed to enhance the accuracy of the results.17 For this purpose, a minor isotope of a matrix element or a co-nebulized standard solution may be relied on. Furthermore, various calibration strategies based on standard addition(s) or isotope dilution have also been developed over the years.18,19 The use of multiple spot ablation enables laser-induced aerosols released from different samples to be mixed within the sample chamber. Such mixing enables the use of standard addition and isotope dilution as calibration strategies.20–22 Self-evidently, the choice of method also depends on the level of accuracy and precision required.23 However, a universal approach applicable to all sample types is yet to be established, emphasizing the ongoing need for development of novel calibration strategies to facilitate straightforward quantitative LA-ICP-MS analysis.
In this work, different calibration strategies for quantitative LA-ICP-MS analysis of fused catalyst samples have been developed. A traditional method relying on external calibration against commercially available CRMs in combination with internal standardization has been considered the reference approach. The results thus obtained have been compared to those obtained by means of two newly developed calibration strategies: (1) a so-called multi-signal calibration approach, and (2) a solution-based calibration approach. The first calibration strategy relies on the monitoring of the signal intensities obtained upon variation of a specific LA setting (in this work: the laser repetition rate or beam diameter), while the second is based on adequate mixing of wet aerosol produced from aqueous calibration standards and ablated material. A multi-signal calibration approach was previously evaluated for solution-based ICP-optical emission spectroscopy (ICP-OES) and ICP-MS,24–27 while a multi-energy calibration approach was developed for the analysis of solid samples via laser-induced breakdown spectroscopy (LIBS).28,29 However, to the best of the authors' knowledge, no work to date has evaluated the use of the multi-signal calibration strategy in the context of direct analysis of solid samples via LA-ICP-MS. The second calibration approach involves the use of aqueous standards for calibration. This approach requires the simultaneous introduction of a wet aerosol and a laser-generated aerosol. The wet aerosol can be introduced either in its original state (wet plasma conditions) or after desolvation (dry plasma conditions), as described elsewhere.30–34 Recently, a solution-based calibration approach was developed by Michaliszyn et al. for the quantitative single-element determination in glass CRMs via LA-ICP-MS.35 This approach has been thoroughly revisited in this work for the analysis of fused catalyst material. After optimization and validation of the methods developed using several CRMs, the calibration strategies have been applied to the determination of Co, Mo, Ni, and V in real catalyst samples. These elements were selected because they are relevant in catalysts used for hydrotreatment in refining, or they are well-known catalyst poisons commonly found in conventional crude oils. To the best of the authors' knowledge, critical contamination levels for these elements are not well-established, and they tend to vary for each contaminant. Therefore, the development and assessment of straightforward quantitative LA-ICP-MS methods for accurate and precise determination of these target elements in catalyst samples is of paramount importance within the petrochemical industry. Moreover, the strategies developed in this study are expected to have applications beyond the analysis of catalyst samples.
2. Experimental
2.1. Instrumentation
An Analyte G2 (Teledyne Photon Machines Inc., Bozeman, MT, USA) 193 nm ArF*excimer-based LA-unit, equipped with the HelEx II two-volume ablation cell, coupled to a quadrupole-based Agilent 7900 ICP-MS instrument (Agilent Technologies Inc., Tokyo, Japan) was used for all measurements. The ICP-MS instrument was operated in “no gas” or “vented” mode, without using any collision and/or reaction gas to overcome spectral overlap. Two different sample introduction configurations were evaluated depending on the calibration strategy selected (see Fig. 1). The same setup was used for traditional external calibration and for the multi-signal calibration approaches (“dry” plasma conditions), while a different one was used for the solution-based approach (“wet” plasma conditions). It should be noted that the setups were optimized for their respective conditions, necessitating adjustments for operation under either dry or wet plasma conditions. For “dry” plasma conditions, the cell outlet (He was used as carrier gas) was connected to a low-volume laser ablation adapter (Glass Expansion, Melbourne, Australia) enabling the tangential introduction of Ar make-up gas. This setup was subsequently connected to a laser ablation mixing chamber (Glass Expansion,Melbourne, Australia) designed to provide some mixing of ablated material, thus dampening short-term signal variation (aerosol homogenization). For “wet” plasma conditions, a Peltier-cooled Scott-type spray chamber (2 °C) was used for the simultaneous introduction (via two different inlets) of the LA aerosol, previously mixed with Ar make-up gas in a glass mixing bulb, and a wet aerosol produced via pneumatic nebulization (MicroMist nebulizer, 400 μL min−1, Glass Expansion, Melbourne, Australia) of the aqueous standard solutions used for calibration. For this configuration, the carrier gas transporting the ablation-generated aerosol was introduced into the spray chamber via the make-up gas inlet, and thus, no other changes to the introduction system were required. This facilitates switching between LA-ICP-MS and pneumatic nebulization (PN) ICP-MS for other applications in routine laboratories. Table 1 shows the instrument settings and data acquisition parameters used for trace elemental analysis of glass certified reference materials and fused catalyst samples using the three different LA-ICP-MS calibration strategies. | ||
| Fig. 1 Graphical representation of the two instrument setups for: (A) external calibration and MSC approaches, and (B) the solution-based calibration approach. | ||
| External calibration | Multi-signal calibration | Solution-based calibration | |
|---|---|---|---|
| Analyte G2 LA-unit | |||
| Laser energy density (J cm−2) | 4 | 4 | 4 |
| Laser repetition rate (Hz) | 40 | 20, 30, 40, 50 | 20 |
| Laser beam diameter (μm) | 15 | 10, 12, 15, 20 | 10 |
| Dosage (shots position−1) | 25 | 25 | 5 |
| He carrier gas flow rate (L min−1) | 0.5 | 0.5 | 0.5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Agilent 7900 ICP-MS instrument | |||
| RF power (W) | 1500–1550 | 1500–1550 | 1500–1550 |
| Sampling depth (mm) | 6.5–6.9 | 6.5–6.9 | 7.5 |
| Ar plasma gas flow rate (L min−1) | 15 | 15 | 15 |
| Ar auxiliary gas flow rate (L min−1) | 0.9 | 0.9 | 0.9 |
| Ar nebulizer gas flow rate (L min−1) | — | — | 0.72–0.75 |
| Ar make-up gas flow rate (L min−1) | 1.05–1.07 | 1.05–1.07 | 0.28–0.32 |
| Nuclides monitored | 6Li, 51V, 59Co, 60Ni, 95Mo | 6Li, 51V, 59Co, 60Ni, 95Mo | 6Li, 51V, 59Co, 60Ni, 95Mo |
| Integration time per nuclide (ms) | 100 | 100 | 100 |
The X-ray Fluorescence (XRF) measurements were carried out using a wavelength-dispersive XRF (WDXRF) Axios spectrometer (Malvern Panalytical, Malvern, United Kingdom). The standards used for calibration and the catalyst samples were prepared as fused beads using a Claisse Eagon 2 fusion instrument (Malvern Panalytical, Malvern, United Kingdom). The results obtained for the two catalyst samples are shown in Table S1 of the ESI.†
2.2. Reagents, standards and samples
For “dry” plasma conditions (external and multi-signal calibration), the following glass certified reference materials (CRMs), available from NIST (National Institute of Standards and Technology, Gaithersburg, MD, USA), USGS (United States Geological Survey, Reston, VA, USA) and MPI DING (Max Planck Institute for Chemistry, Mainz, Germany), were selected for method development, calibration and validation purposes: NIST SRMs 610 and 612 (synthetic glasses), USGS GSD-1G, BHVO-2G, BIR-1G, BCR-2G and GSE-1G (basalt glasses) and MPI-DING ATHO-G (rhyolite glass) and T1G (diorite glass). Additionally, the USGS BHVO-2 powdered reference material was converted into a fused bead in the same way as the catalyst samples (see below) to be used as reference standard for the multi-signal calibration approach. For “wet” plasma conditions (solution-based calibration approach), ultra-pure water (resistivity ≥18.2 MΩ cm) was obtained from a Milli-Q Element water purification system (Millipore, Guyancourt, France). Pro analysis purity level 14 M HNO3 (ChemLab, Zedelgem, Belgium) was further purified by sub-boiling distillation. 1 g L−1 single-element standard solutions of Li, V, Co, Ni and Mo (Instrument Solutions, Nieuwegein, the Netherlands) were used to prepare the standards required for obtaining the ionic calibration curves. All standards were prepared in 0.14 M HNO3.Two alumina catalyst samples used in petroleum refining processes were analyzed as a proof-of-concept application. The catalyst samples were prepared as fused beads by mixing approximately 1 g of the sample and 10 g of a flux (Li2B4O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiBO2 – 66
LiBO2 – 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34). The mixture thus obtained was heated by using a program that slowly increases the temperature to 1100 °C in a platinum crucible. The analysis of fused beads offers specific advantages, including a reduction in the influence of sample heterogeneity on the analysis, simplified sample preparation, and compatibility with both XRF and LA-ICP-MS techniques. However, it is important to note that the high temperature applied during the fusion process can result in the loss of volatile elements, potentially leading to the underestimation of the concentration of certain elements. Additionally, contributions from alkaline materials can significantly affect the determination of some trace elements. Nonetheless, it is worth mentioning that, for the elements studied in this work, these factors were not considered limiting.
34). The mixture thus obtained was heated by using a program that slowly increases the temperature to 1100 °C in a platinum crucible. The analysis of fused beads offers specific advantages, including a reduction in the influence of sample heterogeneity on the analysis, simplified sample preparation, and compatibility with both XRF and LA-ICP-MS techniques. However, it is important to note that the high temperature applied during the fusion process can result in the loss of volatile elements, potentially leading to the underestimation of the concentration of certain elements. Additionally, contributions from alkaline materials can significantly affect the determination of some trace elements. Nonetheless, it is worth mentioning that, for the elements studied in this work, these factors were not considered limiting.
2.3. Uncertainty calculation
For each calibration strategy, the uncertainty of the results was calculated following the guidelines outlined in the ISO/IEC Guide 98-3:2008 (GUM), NIST Technical Note 1297, and EURACHEM/CITAC Guide CG 4.36–38 The uncertainty calculation was adapted for each calibration approach based on the specific experiments conducted using the principles of uncertainty propagation and metrology. For the external calibration approach, both the uncertainties on the three measurement replicates and on the certified values for the solid standards used to construct a multi-point calibration curve through linear regression analysis were considered. In the case of multi-signal calibration approaches, three measurement replicates were considered for both the sample and the solid standard used to construct the calibration curve via linear regression. The total uncertainty was estimated by taking into account the uncertainty on the slope of the regression line and the uncertainty associated with the analyte content in the reference standard. For the solution-based calibration approach, two linear regressions, one for the reference element and a second for the target analyte, were carried out. To calculate the total uncertainty, we considered both the slope and intercept of both regression lines. In this case, the uncertainty associated with the concentration of the reference element could be considered negligible.Regardless of the calibration strategy used, we conducted replicate measurements, covering a wide surface area of the solid samples to minimize the effect of potential heterogeneity typically associated with solid materials. In this regard, it is worth noting that the preparation of fused beads typically results in highly homogeneous samples, which further enhances measurement consistency.31
3. Results and discussion
3.1. External calibration approach
In this work, external calibration against matrix-matched solid standards was considered the reference approach. This calibration strategy relies on the analysis of a set of solid standards with known composition to construct a multi-point calibration curve based on linear regression analysis (best-fitting straight line through the data points). For this purpose, nine glass CRMs (see Table S2 of the ESI†) were used. The R2 values for such calibration curves were found to be between 0.976 and 0.997. To assess the accuracy of the external calibration strategy, the concentrations of the target elements in each certified reference material were calculated by using the calibration curve based on the remaining eight standards. The results are shown in Fig. 2 and in Table S3 of the ESI.† Good agreement was found between the experimentally determined concentrations and the corresponding reference values. The lowest concentrations (<20 mg kg−1) were found to deviate more from the reference values, while the error bars also indicated a higher degree of uncertainty for these results. This can be attributed to the closeness of these values to the corresponding limit of detection (LoD) and to the higher uncertainty of the reference concentrations. After assessment of the results obtained for the CRMs, the external calibration strategy was used to calculate the concentrations of the target elements in the fused catalyst samples (see Fig. 3 and Table S4 of the ESI†). As can be seen, the concentrations of all analytes investigated for the two catalysts were found to be biased low (recoveries ranging from 67 to 98%) compared to the XRF results. This discrepancy can be attributed to the use of calibration standards with a matrix composition different from that of the samples. Additionally, it is important to note that XRF analysis typically interrogates a larger sample size compared to LA-ICP-MS analysis, potentially leading to discrepancies, especially when analyzing solid materials that may exhibit some degree of heterogeneity. Furthermore, some level of inaccuracy in the XRF results cannot be ruled out either. To correct for instrumental signal drift, matrix effects and differences in ablation yield (the depth of ablation for each individual laser pulse), especially when the matrix of the standard is deviating from that of the sample, external calibration is often combined with internal standardization (see eqn (1)).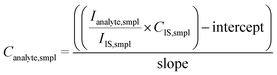 | (1) |
A suitable internal standard needs to be homogeneously distributed throughout the sample material and be present at known and relatively high concentration. In this case, Li was selected as internal standard, as its concentration is well-established in the CRMs, while this element was added under controlled conditions for the preparation of the fused beads. A comparison of the results obtained with/without Li as an internal standard is shown in Fig. 3. After internal standardization correction, the results were found to be significantly closer to the XRF data (recoveries ranging from 84 to 107%). These results demonstrate the potential of external calibration combined with the use of a suitable internal standard for obtaining accurate LA-ICP-MS results (relative bias between experimental results and reference values ranging between −15% and +7%), but this approach requires a wide range of CRMs with a matrix similar to that of the samples of interest and the presence of multiple elements in a wide range of concentrations.
3.2. Multi-signal calibration (MSC) approach
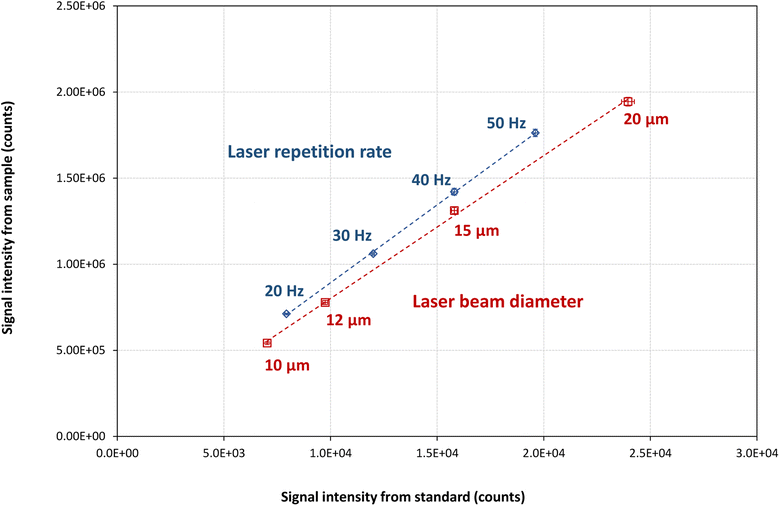
For many types of material, the use of the external calibration strategy is limited by the lack of CRMs with a matrix composition sufficiently similar to that of the samples of interest and containing all targeted analyte elements at various concentration levels. As a result, there is a pressing need to develop more streamlined and user-friendly approaches for quantitative LA-ICP-MS analysis. Multi-signal calibration (MSC) holds promise as a calibration strategy for quantitative LA-ICP-MS analysis. While such approaches have been employed in previous studies for solution-based analysis (using ICP-MS or ICP-OES) and solid sample analysis (using LIBS),29 their potential has yet to be evaluated in the context of LA-ICP-MS analysis. In these approaches, the amount of sample introduced into the ICP-MS is modulated by modifying parameters other than the analyte concentration of the calibration standards. For example, in ICP-OES, the multi-energy calibration approach is based on the use of a single concentration and multiple transition energies (wavelengths) of the same analyte, while the multi-isotope and multi-species calibration approaches in ICP-MS are based on the use of a single concentration and either multiple isotopes or multiple ionic species of the same analyte.39 In all three strategies, two measurements are required per sample: the sample itself and a mixture of the sample with a standard. In contrast, the multi-flow calibration approach is based on the use of a single standard, with multiple nebulization gas flow rates used for calibration.27 The advantage of this approach is that both the sample and the standard are measured separately, making it particularly well-suited for routine solid sample analysis. In this work, we have assessed the feasibility of applying a variant of the multi-flow calibration approach to quantitative LA-ICP-MS analysis. This novel approach relies on variation of the laser repetition rate (20, 30, 40 and 50 Hz) or of the laser beam diameter (10, 12, 15 and 20 μm). These LA settings were chosen specifically to minimize the effect on elemental fractionation (energydensity, e.g., would have a larger effect), which is a common concern in LA-ICP-MS analysis. Modifying the laser energy density would induce changes in the particle size distribution of the LA-generated aerosol potentially affecting the vaporization process and should therefore be avoided. Increasing the laser beam diameter and/or repetition rate results in a higher ablation rate, i.e., higher sample mass ablated per unit of time, increasing the mass load in the ICP. Fundamental studies have demonstrated that the energetic/thermal conditions of the ICP ion source directly influence the occurrence (degree) of elemental fractionation, as vaporization and ionization processes of the aerosol particles are dependent on the plasma temperature.40 Under sufficiently hot plasma conditions, the changes in mass load induced by varying the laser beam diameter (range: 10–20 μm) and repetition rate (range: 20–50 Hz) used in this work, will not result in “plasma-overloading” or significant mass-load dependent matrix effects, as the sample amounts are not exceeding the plasma robustness limit, as defined by Fietzke et al.41The calibration is achieved by plotting the analytical signal intensities observed for the standard against those for the sample (Fig. 4 and S1–S4 of the ESI†). The slope of the calibration curve provides the analyte concentration in the sample (see eqn (2)).
| Csample = slope × Cstandard | (2) |
This method was validated by measuring five glass CRMs: NIST SRM 610, NIST SRM 612, USGS BHVO-2G, GSD-1G, and GSE-1G. Among these, NIST SRM 610 was used as the ‘reference standard’, while the remaining four were treated as ‘samples’. The results are presented in Fig. 5 and Table S5 of the ESI.† It can be observed that also the multi-signal calibration approach demonstrates improved performance when combined with internal standardization correction. The recoveries without internal standardization ranged from 76% to 117%, while with internal standardization, they improved to a range of 90% to 110%. The internal correction resulted in accurate results for all analytes in the CRMs. Moreover, results based on modification of the repetition rate did not deviate significantly from those based on modification of the laser beam diameter, showcasing the flexibility of this calibration strategy. Additionally, this approach offers the advantage of relying on a single standard (NIST SRM 610) only, whereas the external calibration strategy requires multiple standards to construct a multi-point calibration curve.
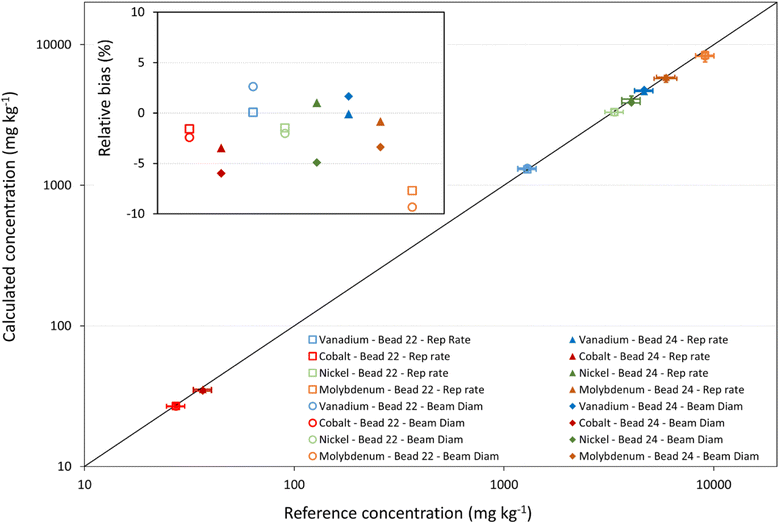
After method development and validation, the multi-signal calibration strategy was used for the analysis of the fused catalyst samples by relying on both the modification of the laser repetition rate and of the laser beam diameter. In this case, each of the five certified reference materials separately served as a ‘reference standard’ for the analysis of the catalyst beads. The recoveries without internal standardization ranged from 60% to 124%, while with internal standardization, they improved to a range of 70% to 117%. The use of internal standardization once again demonstrated an improvement of the results. It is noteworthy that the accuracy achieved with the multi-signal calibration approach closely matched that of the external calibration approach combined with internal standardization. The relative bias between the experimental results and the reference values were found to be <15% for the majority of the elements determined. For the multi-signal calibration strategy, it should also be noted that, even with internal standardization, some analytes exhibited an important bias from the XRF data when using some of the CRMs (see Fig. 6 and Table S6 of the ESI†). Additionally to the uncertainty associated with calibration versus single solid reference standards, this bias can also be attributed to differences in matrix composition between the sample and the respective standard. To further assess the accuracy of the new multi-signal calibration approach independent of matrix composition effects, one of the catalyst samples was analyzed using the other sample as the ‘reference standard’. In this case, an excellent agreement was found between the experimentally obtained results and the XRF values, with recoveries ranging from 83 to 90 and from 95 to 102% without and with internal standardization, respectively (see Table S7 of the ESI†). A relative bias ranging between −5% and +2% was observed when varying the laser repetition rate, while adjusting the laser beam diameter within the multi-signal calibration strategy resulted in a relative bias ranging between −4% and +1%. These results highlight the accuracy of the multi-signal calibration method when applied under matrix-matched conditions.
Based on the previous results, the accuracy of the calibration strategy seems to strongly depend on the level of matrix-matching between samples and standards. Therefore, an additional experiment was carried out to find a more suitable approach to produce a matrix-matched standard. A CRM available in powder form (USGS BHVO-2) was prepared as a fused bead following the same protocol as that for the catalyst samples. The lower analyte concentrations in the powder reference material were compensated by using a larger beam diameter (20, 30, 40 and 50 μm), while maintaining the repetition rate at 40 Hz. As can be seen in Fig. 7 and in Table S8 of the ESI,† accurate results were obtained when combining this approach with internal standardization, resulting in recoveries ranging between 91 and 102%. In this experiment, a slightly higher level of accuracy was achieved with the multi-signal calibration approach based on variations in the laser repetition rate (relative bias ranging between −7% and +1%) than with the approach involving variations in the laser beam diameter (relative bias ranging between −9% and +3%). Nonetheless, both approaches proved to be suitable for the analysis of fused catalyst samples. Additionally, it was observed that the fusion process did not induce changes in the elemental composition during the preparation of the fused beads for the elements of interest in this study. The suitability of powdered CRMs prepared as fused beads provides more flexibility to this methodology, as such materials with certified values for several elements at different concentration levels are more widely commercially available. This approach also opens up new possibilities for further trace elemental analysis in cases where solid calibration standards are not readily accessible.
3.3. Solution-based calibration approach
As previously mentioned, there is a significant shortage of reliable solid CRMs available for all elements across various concentration levels and with different matrix compositions. While the previous calibration strategy (MSC approach) requires one solid CRM only, it is still possible that no suitable standard meeting all the necessary requirements is available for analysis. In such cases, an alternative solution-based calibration strategy can be considered. For this purpose, a methodology involving the simultaneous introduction of ablated material (using a LA system) and wet aerosol from a standard solution (produced via pneumatic nebulization) into the ICP has been evaluated.30–34 The strategy developed in this work is based on the methodology reported by Michaliszyn et al.35 for the analysis of two commercially available CRMs (NIST SRM 610 and 612 glass samples). While their strategy was reported as a new method for SI-traceable quantification via LA-ICP-MS, it presented certain disadvantages, such as its mono-elemental nature and the significant amount of time required for analysis. In the present work, we have fully revisited this strategy for the quantitative multi-element analysis of catalyst samples prepared as fused beads. This extends the application of the method beyond its original scope and allows for a more comprehensive analysis of complex samples.The main challenges in quantitative LA-ICP-MS analysis are the significant impact of matrix effects on the accuracy of the results and the difficulty in quantifying the mass flow of ablated solid material. In this approach, matrix effects can be accounted for by introducing the ablated solid sample simultaneously with different calibration solutions. This calibration strategy is based on the principles of standard addition and can be used to improve the accuracy of the LA-ICP-MS measurement results. To address the challenge of quantifying the mass flow of the solid ablated material, a “reference element” approach was employed. In this case, Li was selected as the reference element due to its presence as a major component at known concentration in the fused beads. While the experimental setup differs from the two previously presented methodologies, we have implemented minimal hardware changes compared to traditional solution-based ICP-MS analysis. This enables a straightforward transition between different modes of operation, such as pneumatic nebulization for liquid sample analysis and laser ablation for solid sample analysis. This flexibility makes this strategy highly convenient for routine applications.
A set of five multi-element standard solutions was prepared, containing varying concentrations of Li, V, Co, Ni and Mo. The concentrations of Li in the standard solutions were 0, 5, 10, 25 and 50 μg L−1, V concentrations ranged from 0, 0.25, 0.5, 1 to 2.5 μg L−1, Co concentrations from 0, 0.1, 0.25, 0.5 to 1 μg L−1, and Ni and Mo concentrations from 0, 0.5, 1, 2.5 to 5 μg L−1. The intensity measured for each calibration standard solution corresponds to the sum of the intensity resulting from the wet aerosol generated from the aqueous solution and the intensity resulting from the ablation-generated dry aerosol, as both flows were simultaneously introduced into the ICP. All selected elements were measured along the same ablation line, and three ablation lines (replicates) were analyzed per calibration point at different areas of the solid samples. Additionally, a “gas blank” or blank measurement was performed without ablation (the laser shutter was closed) to enable blank correction at each calibration point. Using the regression line obtained from these measurements, the mass fraction of the analyte in the solid sample (wx(A)) can be calculated as follows:
 | (3) |
 | (4) |
 | (5) |
Finally, by combining eqn (3) and (5), the mass fraction of the analyte in the solid sample can be obtained:
 | (6) |
As can be seen in Fig. 8 and in Table S9 of the ESI,† accurate results were obtained for the two catalyst samples with recoveries ranging from 97 and 108%. The relative bias between the results obtained using the solution-based calibration strategy and the reference values ranged between −3% and +7%. This level of accuracy is similar to that achieved using the multi-signal calibration method when applied under matrix-matched conditions. Despite common concerns related to solution-based calibration in quantitative LA-ICP-MS analysis, arising from differences in analyte ionization behavior in the ICP between dry and wet aerosol particles, the accuracy observed for all elements in this study demonstrates the suitability of this method for the analysis of fused catalyst samples.33,34 These results open up new possibilities for quantitative LA-ICP-MS analysis where there is a scarcity of suitable solid CRMs.
4. Conclusions
In this study, different calibration strategies for quantitative bulk LA-ICP-MS analysis of fused catalyst samples were evaluated. The newly developed calibration strategies demonstrated similar or even superior performance compared to the traditional external calibration approach, while successfully overcoming most of the challenges associated with quantitative analysis of solid samples using LA-ICP-MS. The choice of the most suitable calibration strategy depends on various factors, such as the availability of appropriate CRMs, the extent of matrix effects, and the presence of a suitable “reference element” at known concentration.The external calibration approach, although commonly used and relatively simple, requires multiple CRMs with similar matrix composition and different analyte concentrations to minimize errors. It also relies on internal standardization to ensure accuracy of the results and matrix effects need to be assumed negligible or corrected for by using an internal standard.
The novel multi-signal calibration strategy, which only requires a single reference standard, demonstrated similar or better accuracy and precision compared to external calibration. However, it is limited to contexts where correcting for less severe matrix effects is needed only and still requires matrix-matching. Additionally, this approach necessitates obtaining at least three stable and sufficiently intense analytical signals, which could be achieved by modifying instrument settings such as the laser repetition rate or laser beam diameter.
The solution-based calibration approach emerged as a suitable alternative when solid CRMs are unavailable. This strategy relies on the use of aqueous standard solutions, enabling effective correction for matrix effects by using the sample itself (standard addition approach). Moreover, the use of wet plasma conditions often improves signal stability. However, this calibration strategy mandates the use of a “reference element” with a known concentration and involves a more time-consuming preparation of calibration standards and modification of the traditional LA-ICP-MS setup.
In summary, several options for achieving quantitative results in LA-ICP-MS analysis have been successfully developed. The multi-signal and solution-based calibration strategies hold potential for application in the analysis of various solid materials where the scarcity of CRMs commonly hinders accurate quantification using LA-ICP-MS. These strategies were effectively employed for the analysis of fused catalyst samples within a petrochemistry context.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
AR-I thanks European Union's Horizon 2020 research and innovation program under the Marie-Sklodowska-Curie grant agreement no. 101034288. TVA thanks the Research Foundation Flanders for support from a postdoctoral research fellowship (FWO.3E0.2022.0048.01). EB-F acknowledges financial support from the Ramón y Cajal programme – Spain – RYC2021-031093 funded by MCIN/AEI/10.13039/501100011033 and the European Union (NextGenerationEU/PRTR), the grant PID2021-122455NB-I00, funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”, and also the Aragon Government (DGA, Construyendo Europa desde Aragón, Grupo E43_20R).References
- A. Fornalczyk, J. Achiev. Mater. Manuf. Eng., 2012, 55, 864–869 Search PubMed.
- M. Yadav and Y. C. Sharma, J. Cleaner Prod., 2018, 199, 593–602 CrossRef CAS.
- C. Sievers, Y. Noda, L. Qi, E. M. Albuquerque, R. M. Rioux and S. L. Scott, ACS Catal., 2016, 6, 8286–8307 CrossRef CAS.
- T. Van Acker, S. Theiner, E. Bolea-Fernandez, F. Vanhaecke and G. Koellensperger, Nat. Rev. Methods Primers, 2023, 3, 53 CrossRef.
- J. Koch and D. Günther, Appl. Spectrosc., 2011, 65, 155–162 CrossRef PubMed.
- M. Bertini, A. Izmer, F. Vanahaecke and E. M. Krupp, J. Anal. At. Spectrom., 2013, 28, 77–91 RSC.
- R. E. Russo, X. Mao, H. Liu, J. Gonzalez and S. S. Mao, Talanta, 2002, 57, 425–451 CrossRef CAS PubMed.
- D. Günther and B. Hattendorf, TrAC, Trends Anal. Chem., 2005, 24, 255–265 CrossRef.
- N. Miliszkiewicz, S. Walas and A. Tobiasz, J. Anal. At. Spectrom., 2015, 30, 327–338 RSC.
- A. Limbeck, P. Galler, M. Bonta, G. Bauer, W. Nischkauer and F. Vanhaecke, Anal. Bioanal. Chem., 2015, 407, 6593–6617 CrossRef CAS PubMed.
- A. Villaseñor, C. Greatti, M. ÇBoccongelli and J. L. Todolí, J. Anal. At. Spectrom., 2017, 32, 587–596 RSC.
- D. B. Aeschliman, S. J. Bajic, D. p. Baldwin and R. S. Houk, J. Anal. At. Spectrom., 2003, 18, 872–877 RSC.
- D. Günther, A. von Quadt, R. Wirz, H. Cousin and V. J. Dietrich, Mikrochim. Acta, 2001, 136, 101 CrossRef.
- A. Barats, C. Pécheyran, D. Amouroux, S. Dubascoux, L. Chauvaud and O. F. X. Donard, Anal. Bioanal. Chem., 2007, 387, 1131–1140 CrossRef CAS PubMed.
- M. Martínez, C. Arnaudguilhem, R. Lobinski, B. Bouyssiere, M. Caetano and J. Chirinos, J. Anal. At. Spectrom., 2012, 27, 1007–1011 RSC.
- T. Van Acker, S. J. M. Van Malderen, M. Van Heerden, J. E. McDuffie, F. Cuyckens and F. Vanhaecke, Anal. Chim. Acta, 2016, 945, 23–30 CrossRef CAS PubMed.
- H. P. Longerich, S. E. Jackson and D. Günther, J. Anal. At. Spectrom., 1996, 11, 899–904 RSC.
- B. Wu, Y. Chen and J. S. Becker, Anal. Chim. Acta, 2009, 633, 165–172 CrossRef CAS PubMed.
- S. Compernolle, D. Wambeke, I. De Raedt and F. Vanhaecke, Spectrochim. Acta, Part B, 2012, 67, 50–56 CrossRef CAS.
- B. Fernández, F. Claverie, C. Pécheyran and O. F. X. Donard, J. Anal. At. Spectrom., 2008, 23, 367–377 RSC.
- B. Fernández, F. Claverie, C. Pécheyran, J. Alexis and O. F. X. Donard, Anal. Chem., 2008, 80, 6981–6994 CrossRef PubMed.
- Y. Makino, Y. Kuroki and T. Hirata, J. Anal. At. Spectrom., 2019, 34, 1794–1799 RSC.
- N. iliszkiewicz, S. Walas and A. Tobiasz, J. Anal. At. Spectrom., 2015, 30, 327–338 RSC.
- A. Virgilio, D. A. Gonçalves, T. McSweeney, J. A. Gomes Neto, J. A. Nóbrega and G. L. Donati, Anal. Chim. Acta, 2017, 982, 31–36 CrossRef CAS PubMed.
- A. Virgilio, J. A. Nóbrega and G. L. Donati, Anal. Bioanal. Chem., 2018, 410, 1157–1162 CrossRef CAS PubMed.
- C. B. Williams and G. L. Donati, J. Anal. At. Spectrom., 2018, 33, 762–767 RSC.
- C. B. Williams, B. T. Jones and G. L. Donati, J. Anal. At. Spectrom., 2019, 34, 1191–1197 RSC.
- A. A. C. Carvalho, L. A. Cozer, M. S. Luz, L. C. Nunes, F. R. P. Rocha and C. S. Nomura, J. Anal. At. Spectrom., 2019, 34, 1701–1707 RSC.
- L. C. Nunes, F. R. P. Rocha and F. J. Krug, J. Anal. At. Spectrom., 2019, 34, 2314–2324 RSC.
- D. Günther, H. Cousin, B. Magyar and I. Leopold, J. Anal. At. Spectrom., 1997, 12, 165–170 RSC.
- C. Pickhardt, J. S. Becker and H.-J. Dietze, Fresenius. J. Anal. Chem., 2000, 368, 173–181 CrossRef CAS PubMed.
- J. S. Becker, C. Pickhardt and H.-J. Dietze, J. Anal. At. Spectrom., 2001, 16, 603–606 RSC.
- L. Halicz and D. Günther, J. Anal. At. Spectrom., 2004, 19, 1539–1545 RSC.
- C. O'Connor, B. L. Sharp and P. Evans, J. Anal. At. Spectrom., 2006, 21, 556–565 RSC.
- L. Michaliszyn, T. Ren, A. Röthke and O. Rienitz, J. Anal. At. Spectrom., 2020, 35, 126–135 RSC.
- Joint Committee for Guides in Metrology, Evaluation of measurement data – Guide to the expression of uncertainty in measurement, available at https://www.bipm.org/en/committees/jc/jcgm/publications.
- EURACHEM/CITAC Guide: Quantifying Uncertainty in Analytical Measurement, ed. S. L. R. Ellison and A. Williams, 3rd edn, 2012, ISBN 978-0-9a48926-30-3, available from https://www.eurachem.org Search PubMed.
- NIST Technical Note 1297 1994 Edition: Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results, available at https://www.nist.gov/pml/nist-technical-note-1297.
- G. L. Donati and R. S. Amais, J. Anal. At. Spectrom., 2019, 34, 2353–2369 RSC.
- I. Kroslakova and D. Günther, J. Anal. At. Spectrom., 2007, 22, 51–62 RSC.
- J. Fietzke and M. Frische, J. Anal. At. Spectrom., 2016, 31, 234–244 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ja00271c |
| ‡ Current address: Department of Analytical Chemistry, Aragón Institute of Engineering Research (I3A), University of Zaragoza, Pedro Cerbuna 12, 50009, Zaragoza, Spain. |
| This journal is © The Royal Society of Chemistry 2024 |