Complexation of heavy metal cations with imidazolium ionic liquids lowers their reduction energy: implications for electrochemical separations

Abstract

Ionic liquids (ILs) are emerging as promising materials for the separation of heavy metals from complex feed streams through selective complexation. A predictive understanding of the coordination chemistry between ILs and targeted metal ions is critically important for enabling the rational design of efficient and selective separations. Such understanding is challenging to obtain due to the labile nature of the bonds and complicated structures formed by ILs in solution. Herein, we elucidated the complex formation of imidazolium-based ILs (i.e., 1-ethyl-3-methylimidazolium chloride, EMIMCl) with lead cations (Pb²⁺) in both the gas and aqueous phases employing a combination of experimental and theoretical methods. Gas-phase electrospray ionization mass spectrometry (ESI-MS) and negative ion photoelectron spectroscopy (NIPES) experiments suggest that Pb–Cl anions (e.g., PbCl₃⁻ and Pb₂Cl₅⁻) combine with neutral EMIMCl molecules, forming complexes of [Pb_mCl_2m+1][EMIMCl]_n⁻ (m = 1, 2, n = 1–4). These anionic complexes are shown to become less stable toward fragmentation and require more energy to dissociate an electron with an increasing number of EMIMCl molecules. In contrast, in dilute solutions, dissociated EMIM⁺ cations and Cl⁻ anions give rise to electrostatic screening of Pb–Cl bonds, resulting in the formation of distinct condensed phase complexes, such as [PbCl₅][EMIM]₂. These structures were identified by nuclear magnetic resonance (NMR) spectroscopy coupled with density functional theory (DFT) calculations. The energy gap between the highest occupied and lowest unoccupied molecular orbitals (HOMO–LUMO) of the condensed phase complexes containing EMIM⁺ was calculated to be lower compared to the Pb–Cl ionic clusters without IL, making these species more electrochemically reducible and easier to extract from solution. This study emphasizes the importance of understanding complexation between ILs and metal ions in designing efficient separation methods.

---

Introduction

Versatility of speciation, which leads to formation of distinct complexes, drives targeted reactions that have contributed to the growth of coordination chemistry over recent years.^1,2 Different chemical functional groups, stereoisomers, or other structural features affect the coordination chemistry of product complexes by altering the speciation environment, including the steric and electronic characteristics of ligands.^3–5 Speciation of ionic liquids (ILs) is a good example that has attracted broad interest due to the unique molecular capabilities of ILs to trap targeted molecules.^6,7 Due to the tunability of the chemical and physical properties of ILs through selection of various anion/cation combinations, an extraordinarily diverse combination of speciation possibilities, with potentially distinct geometric and electronic features, is feasible.⁸ Such a coordination chemistry-driven approach to metal complexation in ILs has been widely investigated in the field of separations, including the selective extraction of heavy metal ions^9–11 and rare-earth elements.^12–14 However, the ability to accurately predict and control the coordination chemistry of new species remains limited, impeding the development of effective electrochemical separation techniques.¹⁵ For example, Busato et al. combined X-ray absorption techniques and molecular dynamics simulations to reveal the coordination chemistry between Co²⁺ and Ni²⁺ cations and bistriflimide (TFSI⁻) based ILs.¹⁶ In addition, Watkins et al. demonstrated the capability of Raman spectroscopy to characterize Mg²⁺ speciation in a TFSI-based IL.¹⁷ Hence, due to the labile nature of IL-metal bonds and the multi-dimensional configurations of ILs that are possible in solution, combined experimental and theoretical approaches are generally required to accurately predict their complex structures.

Among the diverse range of ILs, imidazolium-based ILs have attracted significant attention in the field of heavy metal removal due to their strong affinity for target ions, cost-effectiveness, and ease of preparation in contrast to the other ILs.^18–22 Recently, the hydrolysis of certain imidazolium-based ILs containing fluorine in the anion, such as tetrafluoroborate (BF₄⁻) and hexafluorophosphate (PF₆⁻), was investigated, revealing their instability when exposed to moisture and the release of toxic HF and POF₃.^23–25 Consequently, questions have arisen regarding the greenness of these ILs, prompting the exploration of alternative, non-toxic, and pharmaceutically compatible anions for ILs, such as Cl⁻, Br⁻, and SO₄²⁻.²⁵ Herein, 1-ethyl-3-methylimidazolium chloride (EMIMCl) was selected as a representative IL molecule.

The electronic and geometric properties, as well as the complexation observed between EMIMCl and lead cations (Pb²⁺) are reported in both gas- and aqueous-phase environments and the implications of these findings for electrochemically-driven separations are discussed. The coordination chemistry between EMIMCl and Pb²⁺ in the gas phase is shown to be governed predominantly by Coulombic interactions between oppositely charged cation/anion pairs.²⁶ Negatively charged Pb–Cl anions (e.g., PbCl₃⁻ and Pb₂Cl₅⁻) are shown to adsorb different numbers of neutral EMIMCl molecules in the gas phase employing electrospray ionization-mass spectrometry (ESI-MS). Increasing numbers of EMIMCl molecules in these complexes are also found to result in larger electron binding energies using negative ion photoelectron spectroscopy (NIPES). In contrast, in the aqueous phase, the interaction between Pb²⁺ cations and EMIMCl molecules is found to be governed by additional intermolecular forces and thermodynamic considerations, including hydrogen bonding, van der Waals forces, and ion solvation energies. The complexation behavior between ILs and Pb²⁺ cations in the aqueous phase was characterized using nuclear magnetic resonance (NMR) and operando Raman spectroscopy coupled with density functional theory (DFT) calculations. Due to disruption of the hydrogen bonding between IL cations and anions in the presence of solvating water molecules in dilute solution,^27–29 EMIM⁺ cations are shown to introduce electrostatic screening of Pb–Cl bonds, resulting in formation of a [PbCl₅][EMIM]₂⁻ complex different from the [PbCl₃][EMIMCl]⁻ species observed in the gas phase. Calculations also indicate that complexation of condensed phase Pb–Cl ionic clusters with EMIM⁺ makes these species more reducible and easier to extract from solution. This study highlights the importance of understanding the complexation between ILs and metal cations in different speciation environments as a means of developing new separation techniques with improved efficiency and selectivity.

Experimental and theoretical methods

Electrospray ionization mass spectrometry (ESI-MS)

Details of the electrospray mass spectrometry experiments may be found in a recently published paper.³⁰ Briefly, the samples consisted of 1 mM EMIMCl, 2.5 mM PbCl₂ + 5 mM EMIMCl, and 2.5 mM PbCl₂ + 5 mM EMIMCl + 1 mM HCl solutions prepared separately in a mixture of 75 vol% methanol/25 vol% water. These solutions were individually introduced into the mass spectrometer through an atmospheric pressure ionization (API) source using a syringe pump at a flow rate of 10 μL min⁻¹. Mass spectra of charged EMIMCl clusters and EMIMCl–PbCl₂ complexes were collected in both the negative and positive ion modes using a Thermo LTQ Orbitrap XL mass spectrometer (Thermo Fisher Scientific, San Jose, CA). Mass spectrometer conditions were carefully optimized to prevent any evidence of fragmentation in the source region. Collision-induced dissociation (CID) measurements were performed by isolating individual charged complexes in the ion trap with an isolation window of Δm/z = 10 and using N₂ as an inert neutral collision partner to induce unimolecular dissociation. The mass spectra and CID data were obtained on mass-selected gas-phase ions inside the vacuum environment of the mass spectrometer where there is no influence from ambient temperature, humidity, or pressure.

Negative ion photoelectron spectroscopy (NIPES)

NIPES spectra were obtained using a magnetic-bottle time-of-flight (TOF) photoelectron spectrometer, combined with a home-made ESI source and a temperature-controlled cryogenic ion trap (RM Jordan Co., Grass Valley, CA), as described in detail elsewhere.³¹ Complexes were generated via electrospray ionization of a mixed solution consisting of EMIMCl (∼3 mM), PbCl₂ (saturated), and HCl (∼20 mM) dissolved in mixture of water/methanol (1 : 2 v/v ratio). The anions were transported by a radio-frequency quadruple ion guide and first analyzed by a quadruple mass spectrometer to optimize ESI conditions and ensure a stable and sufficiently intense ion beam. The anions were directed by a 90° bender into the cryogenic three-dimensional (3D) ion trap set at a temperature of T = 20 K where they were accumulated and cooled by collisions with cold helium buffer gas for 20–100 ms before being pulsed into the extraction zone of the TOF mass spectrometer for mass analysis. Each of the anions of interest was mass selected and decelerated before being photodetached by a 157 nm (7.866 eV, Lambda Physik CompexPro F₂) laser beam in the interaction zone of the magnetic-bottle photoelectron analyzer. Cooling of the ions in the trap and mass selection prevents any influence on the data resulting from exposure to the atmosphere, humidity, or differences in temperature. The probe laser was operated at a 20 Hz repetition rate with the anion beam off for alternating laser shots to afford real-time shot-by-shot background subtraction. The photoelectrons were collected at nearly 100% efficiency by the magnetic bottle and analyzed in a 5.2 m long electron flight tube. The recorded flight times were converted into electron kinetic energies calibrated with the known spectra of I⁻/Au(CN)₂⁻.^32,33 The electron binding energies (EBEs) were obtained by subtracting the electron kinetic energies from the photodetachment energies. The electron energy resolution (ΔE/E) was about 2% (i.e., ∼20 meV for 1 eV kinetic energy electrons).

Nuclear magnetic resonance spectroscopy (NMR)

All liquid-state NMR experiments were performed on a Varian DDRS spectrometer with an 11.7 Tesla magnet using a broad-band (BBO) probe. All NMR samples were prepared in deuterated water (D₂O, 99.9 atom %D, Sigma-Aldrich). To monitor the H/D exchange process of ¹H in EMIMCl, time-dependent ¹H spectra were acquired in intervals of an hour for 24 hours starting from the freshly prepared samples. The 90° pulse widths were 13 μs for ¹H and 20 μs for ²⁰⁷Pb. The ¹H and ²⁰⁷Pb single-pulse spectra were collected using 30° pulses with a recycling delay of 30 and 3 s, respectively, for quantitative analysis. The ¹H longitudinal (spin–lattice) (T₁) and transverse (spin–spin) (T₂) relaxation time constants were measured using inversion-recovery and Carr–Purcell–Meiboom–Gill (CPMG) methods, respectively. The ¹H diffusion coefficients were measured using bipolar pulse pair stimulated echo pulse sequence with convection compensation. The typical parameters for ¹H diffusion ordered spectroscopy (DOSY) experiments were gradient g = 1.6–34.5 G cm⁻¹, number of increments = 18, diffusion gradient duration δ = 2 ms, diffusion delay Δ = 100 ms, gradient stabilization delay = 2 ms, and number of scans = 16.

Theoretical calculations

To compute NMR shifts (ppm) and adiabatic and vertical detachment energies (ADEs and VDEs, eV) we carried out density functional theory (DFT) calculations using ORCA 5.0.3.³⁴ The Northwest Potential Energy Surface Search Engine (NWPEsSe) global optimization algorithm developed by our group³⁵ was used to accelerate the structural search for different clusters. All structural searches in NWPEsSe were performed initially with the computationally cheaper GFN2-xTB method,³⁶ followed by more accurate DFT-based geometric optimization of the GFN2-xTB structures with the lowest energies. To address the need for computing different parameters, the calculation schemes for the NMR and ADE/VDE calculations varied slightly.

For the NMR calculations, we focused on structures of PbCl_x (x = 1–6) clusters and [PbCl_m][EMIM]_n (m = 2–5 and n = 1–4) complexes. Initial structural optimizations using the GFN2-xTB method were performed in an implicit water solvent as implemented in xTB.³⁷ For each Pb–Cl and Pb–Cl–EMIM species, we searched 1000 and 100 000 structures, respectively. The optimized GFN2-xTB structure with the lowest energy in every case was then further optimized in DFT using the BP86 functional with the D3 correction³⁸ in implicit water solvent using the solvation model based on density (SMD).³⁹ The ZORA basis set and correction were considered in these calculations, which used the DFT-optimized geometries of complexes.⁴⁰ The NMR shielding was computed using the Gauge-Independent Atomic Orbitals method^41,42 as implemented in ORCA and considered both diamagnetic and paramagnetic contributions to the total shielding tensor. In addition to the DFT-optimized structures, a PbCl₉ cluster reported in a previous paper⁴³ was also considered in our NMR calculation.

For the ADE and VDE calculations, gas-phase [PbCl₃][EMIMCl]_n⁻ complexes with 0 ≤ n ≤ 4 and [Pb₂Cl₅][EMIMCl]_n⁻ with 0 ≤ n ≤ 2 were considered. For each complex, the ADE was computed as the energy difference between the neutral species and the anion, both at their respective optimized geometries. The VDE for each complex was computed as the energy difference between the neutral species and the anion, both at the optimized anion geometry. The geometries of PbCl₃ and Pb₂Cl₅ were optimized with DFT starting from a literature informed initial configuration. For complexes with n ≥ 1, we searched 1000 structures using NWPEsSe with GFN2-xTB. The geometries of the structures with the 10 lowest energies were further optimized with DFT. All DFT geometry optimizations employed the BP86 functional, a SARC-ZORA-TZVP basis set for the Pb atoms, a def2-TZVP basis set with ZORA relativistic corrections for all other atoms, a SARC/J auxiliary basis, and the D3 van der Waals correction. For each complex, the DFT-optimized geometry with the lowest energy was used in further single-point calculations to acquire the ADE and VDE values. For ADE calculations, the geometry of the neutral form of each complex was optimized again using the same level of theory as described above before single-point calculations. All single-point calculations were performed using the wB97X-V functional, a SARC-ZORA-TZVPP basis set for the Pb atoms, a def2-TZVPP basis set with ZORA relativistic corrections for all other atoms, and a SARC/J auxiliary basis. The electrostatic potential (ESP) map, and energies of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) were also evaluated based on the geometrically optimized clusters at each state.

Results and discussion

Formation and structure of EMIMCl–PbCl₂ complexes in the gas phase

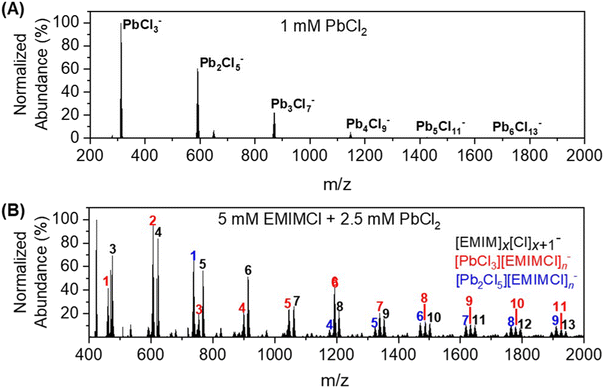
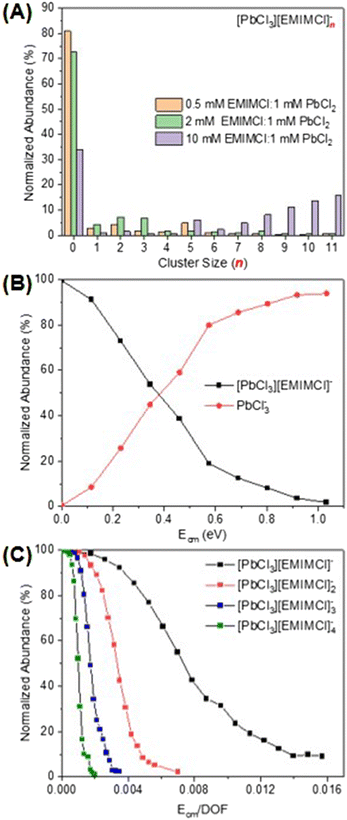
For a mixture of EMIMCl and PbCl₂ in the solid state, Coleman et al. previously revealed the existence of [PbCl_2+n] [EMIM]_n (n = 1, 2) neutral complexes and provided evidence for a dynamic structural transition from pentacoordinate PbCl₅ units at higher PbCl₂ concentrations to hexacoordinate PbCl₆ units at lower PbCl₂ concentrations, respectively.⁴⁴ In the presence of solvents (e.g., water and methanol), PbCl₂ may form solvated clusters with various stoichiometries and charge states.^44–46 In the mass spectrum presented in Fig. 1A, a series of singly charged anionic Pb_xCl_2x+1⁻ clusters containing one to six Pb²⁺ cations was observed for a solution of 1 mM PbCl₂ in 75 vol% methanol/25 vol% water. The abundance of the clusters in the mass spectrum was found to be inversely proportional to their size. After introducing EMIMCl into the PbCl₂ solution (Fig. 1B), it was found that the two most abundant clusters, PbCl₃⁻ and Pb₂Cl₅⁻, coordinated with different numbers of neutral EMIMCl molecules to form singly charged anionic complexes with the general formulas [PbCl₃][EMIMCl]_n⁻ (n = 1–11, red) and [Pb₂Cl₅][EMIMCl]_n⁻ (n = 1–9, blue). The stoichiometry of the complexes was found to be dependent on the concentration ratio of EMIMCl to PbCl₂, showing a significant increase in the abundance of species containing more EMIMCl when the EMIMCl/PbCl₂ ratio was adjusted from 0.5 to 2 (Fig. 2A). Indeed, at the highest EMIMCl concentration (EMIMCl/PbCl₂ ratio = 10), PbCl₃⁻ was found to coordinate with more EMIMCl molecules to form larger [PbCl₃][EMIMCl]_n⁻ (n = 5–11) complexes. The fragmentation of these gas-phase complexes was also investigated by performing energy-resolved collision-induced dissociation (CID) measurements using the mass spectrometer. For example, as the collision energy in the center-of-mass reference frame (E_cm) was systematically increased, the relative abundance of the representative [PbCl₃][EMIMCl]⁻ precursor anion decreased while the abundance of the PbCl₃⁻ product anion increased (Fig. 2B). This result indicates that the [PbCl₃][EMIMCl]⁻ complex fragmented via unimolecular dissociation of a neutral EMIMCl molecule according to eqn (1).

[PbCl₃][EMIMCl]⁻ → PbCl₃⁻ + EMIMCl (1)

Fig. 1 Representative negative ion mode ESI-MS spectra of gas-phase (A) Pb_xCl_2x+1⁻ (top) and (B) [EMIM]_x[Cl]_x+1⁻ (black, bottom), [PbCl₃][EMIMCl]_n⁻ (red, bottom), and [Pb₂Cl₅][EMIMCl]_n⁻ (blue, bottom) complexes. The resolution of the mass spectra (m/Δm) is approximately 60 000. The number above each peak in the spectra presents the x or n value for each species.

Fig. 2 (A) Distribution of gas-phase cluster sizes observed for different concentration ratios of EMIMCl to PbCl₂ in solution. (B) Fragmentation curve for the representative mass-selected [PbCl₃][EMIMCl]⁻ precursor ion. (C) Survival curves for mass-selected [PbCl₃][EMIMCl]_n⁻ (n = 1–4) precursor ions.

By performing kinetic energy-resolved CID measurements on other selected [PbCl₃][EMIMCl]_n⁻ (n = 2–4) complexes, we constructed the precursor anion survival curves presented in Fig. 2C. These curves summarize the abundance of each complex as a function of the kinetic energy of the collisions between the mass-selected precursor anions and the inert collision partner (N₂). The survival curves provide qualitative insight into the relative stability of the complexes toward unimolecular dissociation in the gas phase. For example, to have 50% abundance of the precursor anion remaining during CID experiments, the fragmentation energy for [PbCl₃][EMIMCl]⁻ (∼0.007) is nearly seven times higher than that needed for [PbCl₃][EMIMCl]₄⁻ (∼0.001), indicating an inverse relationship between the size of complexes and their stability toward unimolecular dissociation in the gas phase. To account for the influence of the different number of vibrational degrees of freedom (n_VDOF) of various size ions on the kinetic energy required to fragment them, the normalized abundance of each mass-selected precursor anion was plotted as a function of E_cm/n_VDOF. As n increases in larger complexes, the number of VDOF into which the internal energy obtained from collisions with N₂ may be redistributed also increases. When E_cm is normalized to the n_VDOF of each complex, therefore, the survival curves, represent qualitative differences in the energetics and dynamics of fragmentation of the IL complexes. The ESI-MS spectra associated with the CID experiments provide valuable insight into the composition, stability, and dissociation pathways of complexes formed in aqueous EMIMCl–PbCl₂ solution.

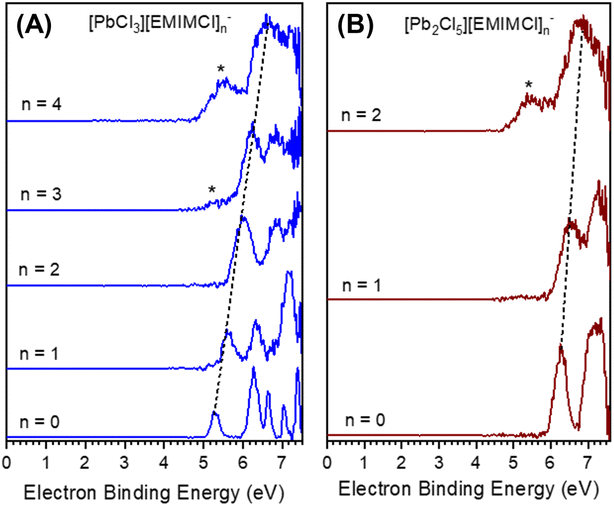
To obtain insight into the size-, stoichiometry-, and charge-dependent electronic structure of the gas-phase EMIMCl–PbCl₂ complexes we performed negative ion photoelectron spectroscopy (NIPES) experiments at T = 20 K and a photodetachment wavelength of 157 nm on [PbCl₃][EMIMCl]_n⁻ (n = 0–4) and [Pb₂Cl₅][EMIMCl]_n⁻ (n = 0–2) (Fig. 3). For PbCl₃⁻, five distinct bands were observed within the photon energy range, corresponding to transitions from the ground anionic state to various neutral ground and excited states. The experimental ADE and VDE of the PbCl₃⁻ anion were determined, respectively, from the onset threshold and the peak maximum of the lowest electron-binding-energy (EBE) band, to be 5.10 and 5.26 eV (Table 1). With the addition of one EMIMCl molecule, the electron photodetachment spectrum of [PbCl₃][EMIMCl]⁻ blue shifted to higher EBE and only exhibited three bands, with an ADE of 5.40 eV and a VDE of 5.58 eV (Table 1). It is notable that the ADEs measured here only represent an estimated upper limit of the true value since the 0–0 transitions that represent actual ADE values may have negligible intensities due to large changes in geometry following photodetachment. Stepwise ADE (upper limit)/VDE blue shifts were also observed for [PbCl₃][EMIMCl]₂⁻ and [PbCl₃][EMIMCl]₃⁻, both of which exhibit two bands in the spectral EBE range (Fig. 3). The observed ADE (upper limit)/VDE values further shift to 5.65/5.96, 5.84/6.25, and 6.10/6.51 eV for the [PbCl₃][EMIMCl]₂⁻, [PbCl₃][EMIMCl]₃⁻, and [PbCl₃][EMIMCl]₄⁻ anions, respectively (Table 1). In addition, there is an extra feature that appears at lower EBE starting from the [PbCl₃][EMIMCl]₃⁻ anion and becoming more pronounced for [PbCl₃][EMIMCl]₄⁻ (marked with “*” in Fig. 3A). This low EBE feature is assigned to less abundant coexisting doubly charged [PbCl₃]₂[EMIMCl]₆²⁻ and [PbCl₃]₂[EMIMCl]₈²⁻ species having degenerate mass to charge ratios to the corresponding singly charged anions [PbCl₃][EMIMCl]₃⁻ and [PbCl₃][EMIMCl]₄⁻. The coexistence of both singly- and doubly-charged complexes has been observed for similar systems before^47,48 and may be confirmed through comparison with the spectra of doubly-charged complexes with odd numbers of EMIMCl molecules (Fig. S1†). The ADEs (upper limit)/VDEs of the [PbCl₃]₂[EMIMCl]₆²⁻, [PbCl₃]₂[EMIMCl]₇²⁻, [PbCl₃]₂[EMIMCl]₈²⁻, and [PbCl₃]₂[EMIMCl]₉²⁻ complexes are estimated to be 4.9/5.4, 4.9/5.4, 4.9/5.5, and 4.9/5.5 eV, respectively (Table S1†).

Fig. 3 T = 20 K NIPES spectra of gas-phase (A) [PbCl₃][EMIMCl]_n⁻ (n = 0–4) and (B) [Pb₂Cl₅][EMIMCl]_n⁻ (n = 0–2) complexes recorded at a photodetachment wavelength of 157 nm. The features marked with a “*” are attributed to coexisting doubly-charged [PbCl₃]₂[EMIMCl]_2n²⁻ (n = 3, 4) and [Pb₂Cl₅]₂[EMIMCl]₄²⁻ complexes. The dashed lines indicate the trend in the blue shift of the VDEs. The estimated energy resolution (ΔE/E) is about 20 meV at 1 eV.

Table 1 Theoretically calculated and experimentally measured ADEs and VDEs for gas-phase [PbCl₃][EMIMCl]_n⁻ (0 ≤ n ≤ 4) and [Pb₂Cl₅][EMIMCl]_n⁻ (0 ≤ n ≤ 2) complexes

Complex	Structures^a	ADE calculated/measured (eV) % error	VDE calculated/measured (eV) % error
a Brown: Pb atom; Green: Cl atom; Black: C atom; Blue: N atom; White: H atom. b Derived from the low EBE * band. The error for all experimental ADEs and VDEs is 0.1 eV.
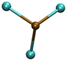
PbCl3^−		4.85/5.10	5.30/5.26
		4.90	0.76
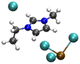
[PbCl3][EMIMCl]^−		4.39/5.40	5.25/5.58
		18.70	5.91
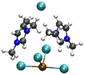
[PbCl3][EMIMCl]2^−		4.54/5.65	5.36/5.96
		19.65	10.07
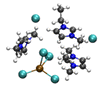
[PbCl3][EMIMCl]3^−		4.79/5.84 (4.9)^b	5.57/6.25 (5.4)^b
		17.98 (2.2)^b	10.88 (3.1)^b
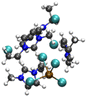
[PbCl3][EMIMCl]4^−		4.75/6.10 (4.9)^b	5.67/6.51 (5.5)^b
		22.13 (3.1)^b	12.90 (3.1)^b
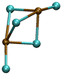
Pb2Cl5^−		5.31/6.00	6.34/6.26
		11.50	1.28
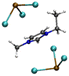
[Pb2Cl5][EMIMCl]^−		6.00/6.08	6.25/6.48
		1.32	3.55
[Pb2Cl5][EMIMCl]2^−		4.66/6.18 (4.9)^b	5.62/6.70 (5.4)^b
		24.60 (4.9)^b	16.12 (4.1)^b

---

In comparison to PbCl₃⁻, the larger Pb₂Cl₅⁻ anion possesses higher ADE (upper limit)/VDE values of 6.00/6.26 eV (Fig. 3B and Table 1). The electronic structure of Pb₂Cl₅⁻ is further stabilized by addition of one and two EMIMCl molecules, resulting in an ADE upper limit of 6.08 eV and a VDE of 6.48 eV for [Pb₂Cl₅][EMIMCl]⁻ and 6.18 and 6.70 eV for [Pb₂Cl₅][EMIMCl]₂⁻. The doubly charged [Pb₂Cl₅]₂[EMIMCl]₃²⁻ complex was also observed (Fig. S2†) and the [Pb₂Cl₅][EMIMCl]₂⁻ NIPES spectrum exhibited a significant contribution from the coexisting doubly charged [Pb₂Cl₅]₂[EMIMCl]₄²⁻ anion (Fig. S2†). The ADEs (upper limit)/VDEs are estimated as 4.8/5.5 and 4.9/5.4 eV for [Pb₂Cl₅]₂[EMIMCl]₃²⁻ and [Pb₂Cl₅]₂[EMIMCl]₄²⁻, respectively. Overall, the ADE and VDE values derived from the NIPES experiments reveal a linear trend (R² = 0.99) of increasing EBE with sequential addition of EMIMCl molecules to both PbCl₃⁻ and Pb₂Cl₅⁻, which is consistent with greater electronic stability and reduced Coulombic repulsion in the larger species.

The theoretically calculated ADEs and VDEs for the Pb–EMIMCl complexes, along with the corresponding structures are also shown in Table 1 alongside the experimental values. For the smaller species, the DFT-calculated values are in reasonably good agreement with experiment. With increasing size, however, the agreement between the experimental and calculated values deteriorates. The experimental electron detachment energies increase with complex size, similar to the trends observed previously for [EMIM]_x[Cl]_x+1⁻_.^30,48 In comparison, the calculated ADE values of [PbCl₃][EMIMCl]_n⁻ decrease from n = 0 to 1 and then increase from n = 2 to 4 while the values of [Pb₂Cl₅][EMIMCl]_n⁻ increase from n = 0 to 1 and then decrease from n = 1 to 2. The agreement between the experimental and theoretically calculated VDEs of [PbCl₃][EMIMCl]_n⁻ was better than the ADEs with both values showing increasing EBE with the addition of EMIMCl molecules. It is worth noting that the calculated VDEs of [PbCl₃][EMIMCl]₄⁻ and [Pb₂Cl₅][EMIMCl]₂⁻ are approximately 1 eV smaller than the experimental values derived from the main bands but agree excellently with those estimated from the low EBE bands (marked with *) (Table 1). According to the computed structures, these two clusters contain [PbCl₄]²⁻ and [Pb₂Cl₇]³⁻ subunits and may be better described as [PbCl₄][EMIM][EMIMCl]₃⁻ and [Pb₂Cl₇][EMIM]₂⁻, respectively. It is likely that the low EBE band (*) has contributions from these highly coordinated metal chloride species when more EMIMCl molecules are available, a point that parallels the findings from the aqueous phase study described later. As expected, both the measured and calculated VDEs of the complexes are higher than their ADEs. The difference between the VDE and ADE values is also found to increase for the larger complexes. This observation may be explained by more substantial structural relaxation of the larger complexes upon electron photodetachment. The predicted gas-phase structures and dissociation data for [PbCl₃][EMIMCl]_n⁻ complexes indicate a trend of decreasing structural stability toward fragmentation as additional EMIMCl molecules are attached to PbCl₃⁻. At the same time, the ADE/VDE values for [PbCl₃][EMIMCl]_n⁻ and [Pb₂Cl₅][EMIMCl]_n⁻ complexes indicate electronic stabilization with increasing numbers of EMIMCl. These findings imply that PbCl₃ coordinated with a lower number of EMIMCl molecules may require more energy to be desolvated and release Pb²⁺ cations for subsequent adsorption or reduction at a working electrode during electrochemical separations. In addition, partial vs. full solvation with EMIMCl may modulate the reduction potential of Pb²⁺ at the electrode interface. It is imperative, therefore, to understand how the presence of water molecules influences the steady-state formation of EMIMCl–PbCl₂ complexes in solution and their diffusion and migration properties.

Emergence of EMIMCl–PbCl₂ complexes in the aqueous phase

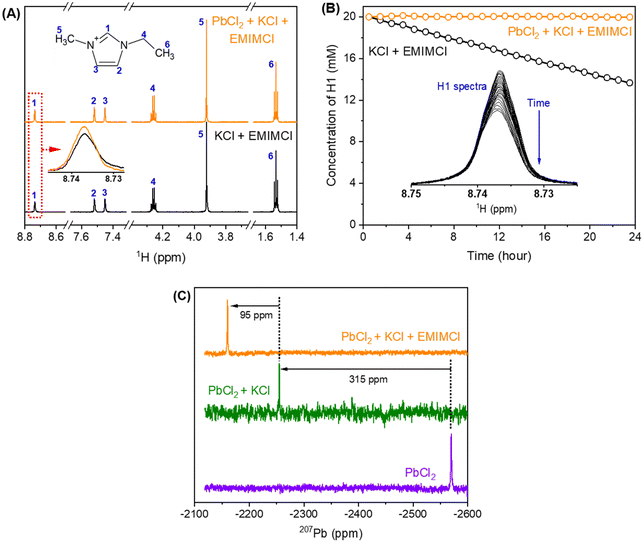
Mixtures of PbCl₂, KCl, and EMIMCl in water were prepared to investigate the formation of EMIMCl–PbCl₂ complexes in aqueous solution using NMR techniques. As shown in the ¹H NMR spectra presented in Fig. 4A, introducing 10 mM PbCl₂ to a mixture of 40 mM KCl and 20 mM EMIMCl in D₂O had little effect on the chemical shifts of the protons in EMIM⁺. Nevertheless, the most acidic proton (H1, Fig. 4A) exhibited a slightly lower intensity in the original KCl + EMIMCl solution compared to the PbCl₂ + KCl + EMIMCl solution due to exchange of H and D. A plot showing the change in the concentration of H1 with time, estimated using the integrated ratios from the ¹H NMR spectra, is shown in Fig. 4B. The estimated H/D exchange rate of H1 is 0.25 mM per hour in the original solution at pH 5 which is reduced to zero with the addition of PbCl₂ at the same pH. This observation suggests that PbCl_x^(2−x)+ species interact with EMIM⁺ in a way that prevents H/D exchange. ¹H NMR relaxation and diffusion measurements were also performed to further understand the influence of Pb²⁺ on EMIM⁺. The measured ¹H spin–lattice relaxation constants (T₁) and spin–spin relaxation constants (T₂) of EMIM⁺ are shown in Table S2.† The T₁ values of all the protons in EMIM⁺ do not show a statistically significant difference between the two solutions, but the T₂ values of H1 and H2 exhibit a noticeable change (44%). In dilute D₂O solutions, while ¹H T₁ is usually determined by rotational motions at a frequency that matches the proton Larmor frequency (750 MHz), the main relaxation mechanisms for ¹H T₂ include chemical exchange and tumbling reorientations. As observed in Fig. 4B, H1 of EMIM⁺ experiences relatively slow chemical exchange with deuterium from D₂O in the KCl + EMIMCl solution, which is consistent with the smallest ¹H T₂ value measured for H1. With the addition of PbCl₂, the chemical exchange between H and D is prohibited, which increases H1 T₂. At the same time, the tumbling motion of H1 in EMIM⁺ is restricted due to the proximity of PbCl_x^(2−x)+, which decreases H1 T₂. Therefore, the overall H1 T₂ value increases by 15% in the presence of Pb²⁺. On the other hand, H2 does not experience chemical exchange. The significant decrease in H2 T₂ by 44%, therefore, is primarily caused by the restriction of the H2 tumbling reorientation, indicating that the major interaction sites of EMIM⁺ with PbCl_x^(2−x)+ are H1 and H2. The diffusion measurements (Table S3†) show a subtle decrease in diffusion coefficients for both H₂O and EMIM⁺ with Pb²⁺, but the change may be within experimental error. Combined with the unaltered ¹H chemical shifts, we conclude that PbCl_x^(2−x)+–EMIM⁺ complexes formed in aqueous solution at the conditions described herein are short-lived and loosely associated.

Fig. 4 (A) ¹H NMR spectra of 40 mM KCl + 20 mM EMIMCl at pH 5 (black) and 10 mM PbCl₂ + 40 mM KCl + 20 mM EMIMCl (orange) at pH 5, (B) evolution of the H1 concentration with time, comparing the two solutions containing KCl + EMIMCl (black) and PbCl₂ + KCl + EMIMCl (orange), (C) ²⁰⁷Pb NMR spectra of the three solutions consisting of PbCl₂ (purple), PbCl₂ + KCl (green), and PbCl₂ + KCl + EMIMCl (orange). The estimated resolution of the NMR spectra is 0.002 ppm.

The ²⁰⁷Pb NMR spectra exhibit a single resonance for all the solutions containing PbCl₂, suggesting that all PbCl_x^(2−x)+ species experience fast ligand exchange (faster than the NMR time scale [<1 ms]) in solution. The downfield shift of 95 ppm observed after adding EMIMCl to the mixture of PbCl₂ and KCl indicates a lower electron density on the metal centers in the presence of EMIM⁺, further supporting the formation of PbCl_x^(2−x)+–EMIM⁺ ion complexes. To identify the local environmental changes occurring around Pb in different solutions at an atomistic level, we performed searches for the low energy structures of different Pb–Cl–EMIM complexes and used DFT calculations to predict the corresponding Pb NMR shifts. The DFT-calculated Pb NMR shifts for different Pb–Cl clusters are provided in Fig. 5A. For the experimental Pb NMR measurement (−2570 ppm) of the PbCl₂ solution (Fig. 4C), simplified modeling of PbCl₂ (−2502 ppm) and PbCl₃⁻ (−2547 ppm) shows the best agreement. Therefore, this Pb²⁺ has mostly two or three local Cl⁻ neighbors in aqueous solution. After KCl was added to the solution of PbCl₂, the experimental NMR showed a shift of 315 ppm (Fig. 4C). The magnitude of the DFT-calculated shift, compared to the experimental values, suggests that adding KCl increases the local concentration of Cl⁻ neighbors of Pb²⁺ from 2–3 to 4–5, consistent with Le Chatelier's principle of dynamic equilibrium.

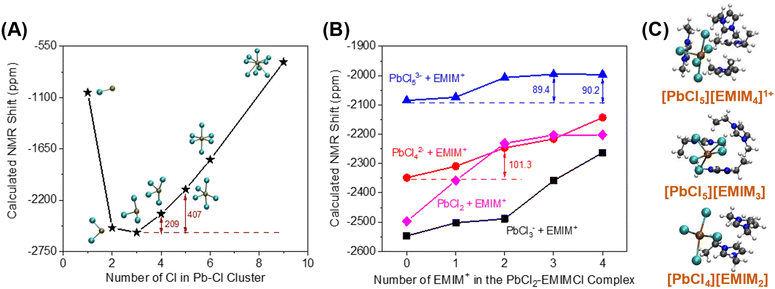Fig. 5 Calculated Pb NMR shifts of different aqueous-phase (A) Pb–Cl clusters, (B) EMIMCl–PbCl₂ complexes, and (C) Calculated structures of three proposed candidate EMIMCl–PbCl₂ complexes.

We theoretically explored local structures where different amounts of EMIM⁺ were added to the Pb–Cl system. The results are illustrated in Fig. 5B. To provide a better overall picture, we calculated the Pb NMR shifts of all the PbCl_n (n = 2–5) complexes with EMIM⁺ cations. In general, the addition of EMIM⁺ further positively shifted the Pb NMR spectra regardless of the amount of Cl⁻ in the local environment of Pb. When we compared the experimentally measured shift (95 ppm) with the results of our calculations, we identified 3 candidate structures (Fig. 5C) that show the best match to the experimental value: (1) PbCl₄²⁻ with 2 EMIM⁺, (2) PbCl₅³⁻ with 3 EMIM⁺, and (3) PbCl₅³⁻ with 4 EMIM⁺, which have differences in their NMR shifts of 101.3, 89.4, and 90.2 ppm, respectively, in comparison to the samples without EMIM⁺. Since each of these calculated shifts is consistent with the experimental value, the existence of different species in the liquid phase is likely. In summary, DFT calculations suggest that adding KCl to the PbCl₂ solution increases the coordination of Pb²⁺ as interpreted through the positive shift of Pb NMR peaks observed in experiments (Fig. 4C). Further addition of EMIMCl leads to an additional positive shift of the Pb NMR peaks in the experimental measurements (Fig. 4C) due to introduction of neighboring EMIM⁺ cations that stabilize these Pb–Cl clusters. The Pb NMR shift of 315 ppm observed when KCl was added to the solution and the weaker shift of 95 ppm when EMIMCl was added (Fig. 4C) indicate direct interactions between cationic Pb and anionic Cl while the presence of EMIM⁺ cations introduces electrostatic screening to these ionic bonds. Furthermore, such coordination between EMIM⁺ and Pb–Cl clusters was observed to be endothermic, as evidenced by temperature-dependent operando Raman measurements in Fig. S3.† As the temperature gradually increased from room temperature to T = 75 °C, the intensity of the Pb–Cl feature belonging to PbCl₂ dramatically decreased, whereas the intensity of the Pb–Cl_b, referring to the bridging bond in the complex increased.

Predicted Reactivity of EMIMCl–PbCl₂ Complexes in the Gas and Condensed Phases

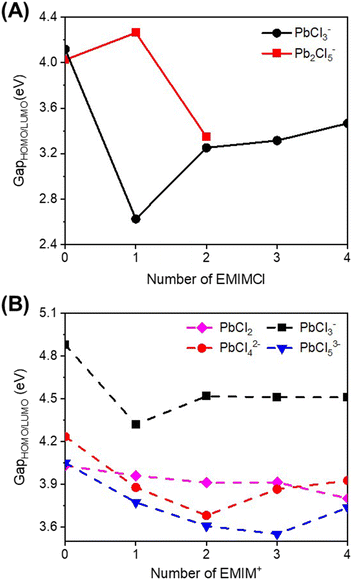
To gain a deeper understanding of the reactivity of Pb–Cl clusters when exposed to EMIMCl molecules, additional computations were performed. We first calculated the energies of the HOMO and LUMO (Fig. S4–S6†) along with the corresponding energy gaps (Fig. 6 and Tables S4, S5†) for the complexes. Additionally, electrostatic potential (ESP) maps were generated to visualize the distribution of charge in the complexes (Fig. S7–S9†).

Fig. 6 Calculated HOMO–LUMO gaps for optimized (A) PbCl₃⁻ and Pb₂Cl₅⁻ clusters and complexes with EMIMCl in the gas phase and (B) PbCl₂, PbCl₃⁻, PbCl₄²⁻ and PbCl₅³⁻ clusters and complexes with EMIM⁺ in the aqueous phase.

Generally, the predicted HOMO–LUMO gaps of the complexes were found to be higher in the aqueous phase compared to the gas phase (Fig. 6). This observation suggests that the presence of solvent molecules (i.e., water) stabilizes the formation of clusters. Therefore, desolvation of water molecules is a key barrier to overcome to facilitate chemical reactions. Furthermore, in both the gas and aqueous phases, addition of EMIMCl molecules reduces the HOMO–LUMO gap of these complexes (Fig. 6). The decrease in the HOMO–LUMO gap may be attributed to a decrease in the difference in the oxidation and reduction potentials of these complexes, making them more electrochemically reversible and reactive.^49,50 Overall, this finding suggests a potentially sustainable pathway for the electrochemical adsorption and deposition of Pb, a toxic heavy metal ion, using environmentally friendly green IL molecules.^51,52

Compared to bare Pb–Cl clusters, visualization of the calculated HOMOs and LUMOs of the EMIMCl–PbCl₂ complexes (Fig. S4–S6†) revealed interesting insights. Specifically, in the gas-phase EMIMCl–PbCl complexes, the HOMO is predominantly located on the σ orbital of the Cl⁻ anion, while the LUMO is primarily situated on the π orbitals of EMIM⁺ cations. This spatially separated and delocalized (in the case of the LUMO) orbital arrangement likely contributes to the decreased HOMO–LUMO gaps observed in the gas phase EMIMCl–PbCl₂ complexes. In comparison, in the aqueous phase, the HOMO is delocalized over the PbCl_x subunit of the complexes. The less spatially separated and more delocalized nature of the HOMO and LUMO in the aqueous phase may underlie the larger calculated HOMO–LUMO gaps of these complexes compared to those in the gas phase.

The calculated ESP maps (Fig. S7 and S8†) provide further support for the enhanced reactivity of PbCl₃⁻ in the gas phase due to the presence of additional EMIMCl molecules. Specifically, the ESP maps of PbCl₃⁻ revealed an increased abundance of electronically negative regions on the surface of the complexes with an increasing number of EMIMCl molecules, indicating a higher susceptibility to reaction with electrophilic species like metal cations. However, the impact of additional IL molecules on the ESP of Pb₂Cl₅⁻ was found to be less pronounced (Fig. S8†). In comparison to the gas-phase complexes, the ESP maps of the aqueous-phase Pb–Cl complexes revealed the formation of spatially segregated regions of positive and negative charge (Fig. S9†) and increasing negative charge with the addition of EMIMCl.

Conclusions

In this study, we investigated the speciation of Pb²⁺ cations in EMIMCl IL, covering electrostatically-driven complex formation in the gas phase as well as coordination in the aqueous phase. In the gas phase, ESI-MS measurements revealed that PbCl₃⁻ and Pb₂Cl₅⁻ anions form complexes with different numbers of neutral EMIMCl molecules leading to two series of singly charged species [PbCl₃][EMIMCl]_n⁻ (n = 1–11) and [Pb₂Cl₅][EMIMCl]_n⁻ (n = 4–9). Energy-resolved CID experiments revealed that the gas phase complexes fragment predominately through the loss of neutral EMIMCl molecules. In addition, as the number of EMIMCl molecules in each of the complexes increases, the bonds become less stable toward unimolecular dissociation, requiring less kinetic energy to produce an equivalent yield of product anions. Gas-phase NIPES experiments demonstrated that each EMIMCl molecule added to the PbCl₃⁻ and Pb₂Cl₅⁻ anions further stabilized their electronic structure, resulting in larger measured EBEs. DFT calculations predicted the geometric structures and ADE/VDE values of these complexes which were found to be reasonably consistent with the experimental results. The calculations further suggest new speciation with high coordination numbers of Pb chlorides formed in the gas phase when more EMIMCl molecules are attached.

In contrast, coordination of Pb²⁺ cations and EMIMCl molecules was found to be different in the aqueous phase, where the EMIM⁺ cations were solvated with water molecules and isolated from the solvated Cl⁻ anions in dilute solution. NMR measurements revealed that site-specific proton exchange on EMIM⁺ was prohibited by complex formation with Pb–Cl ions, leading to a significant shift in the NMR peak of Pb²⁰⁷. Based on the NMR results, DFT calculations identified several candidate complexes and their structures (e.g., [PbCl₅][EMIM]₃) that exhibited Pb²⁰⁷ NMR shifts consistent with the experimental results. These species were likely formed through an endothermic coordination reaction, as demonstrated by operando temperature-resolved Raman spectroscopy measurements.

Further computational analysis of the HOMO–LUMO gaps in both the gas- and condense-phases highlights that introduction of EMIMCl reduces the HOMO–LUMO gaps of PbCl_x complexes, thereby making them more electrochemically reactive than bare PbCl₂ within the potential range limited by water oxidation–reduction. This molecular-level understanding of the coordination chemistry occurring between ILs and metal ions in different speciation environments provides insight into the factors controlling the properties of IL complexes. This insight opens up new opportunities for ILs to be applied in the efficient and selective separation of heavy metal ions and rare earth elements.

Author contributions

The manuscript was written through the contributions of all authors. S. Tan prepared the samples, performed operando Raman spectroscopy measurements, and wrote the original draft. D. Zhang and B. Helfrecht performed the theoretical calculations, including DFT, ESP, and HOMO–LUMO. Y. Chen conducted the NMR measurements. E. Baxter performed the ESI-MS and CID experiments. W. Cao and X.-B. Wang performed the NIPES measurements. V. Prabhakaran, G. Johnson, and M.-T. Nguyen established and guided the research plan and contributed to the interpretation of the data and writing of the manuscript. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, Field Work Proposal (FWP) 81462 (Interfacial Structure and Dynamics in Separations). The NIPES work was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Condensed Phase and Interfacial Molecular Science program, FWP 16248. PNNL is a multiprogram national laboratory operated by Battelle for the U.S. DOE under Contract DE-AC05-76RL01830. Computer resources were provided by Research Computing at PNNL, and the National Energy Research Scientific Computing Center (NERSC), a U.S. DOE Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.

References

1. X. Gao, X. Liu, A. Mariani, G. A. Elia, M. Lechner, C. Streb and S. Passerini, Energy Environ. Sci., 2020, 13, 2559–2569.
2. S. Jiang, Y. Liu, L. Wang, Z. Chai and W. Q. Shi, Chem. – Eur. J., 2022, 28(60), e202201145.
3. A. D. Wilson, H. Lee and C. Stetson, Commun. Chem., 2021, 4, 1–8.
4. K. H. Yim, C. T. Yeung, M. R. Probert, W. T. K. Chan, L. E. Mackenzie, R. Pal, W. T. Wong and G. L. Law, Commun. Chem., 2021, 4, 2–11.
5. J. Bai, L. Zhang, Z. Shi and X. Jiang, Chem. Mater., 2022, 34, 10172–10180.
6. P. Nockemann, B. Thijs, K. Lunstroot, T. N. Parac-Voet, C. Görller-Walrand, K. Binnemans, K. Van Hecke, L. Van Meervelt, S. Nikitenko, J. Daniels, C. Hennig and R. Van Deun, Chem. – Eur. J., 2009, 15, 1449–1461.
7. A. P. Abbott, G. Frisch and K. S. Ryder, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2008, 104, 21–45.
8. R. F. Higgins, K. P. Ruoff, A. Kumar and E. J. Schelter, Acc. Chem. Res., 2022, 55, 2616–2627.
9. Q. Luo and E. Pentzer, ACS Appl. Mater. Interfaces, 2020, 12, 5169–5176.
10. S. Imdad and R. K. Dohare, Chem. Eng. Process. – Process Intensif., 2022, 173, 108812.
11. A. Misra, C. Zambrzycki, G. Kloker, A. Kotyrba, M. H. Anjass, I. Franco Castillo, S. G. Mitchell, R. Güttel and C. Streb, Angew. Chem., Int. Ed., 2020, 59, 1601–1605.
12. M. Khodakarami and L. Alagha, Sep. Purif. Technol., 2020, 232, 115952.
13. P. Sun, K. Huang, W. Song, Z. Gao and H. Liu, Ind. Eng. Chem. Res., 2018, 57, 16934–16943.
14. X. Li, J. J. M. M. Van De Ven, Z. Li and K. Binnemans, Ind. Eng. Chem. Res., 2022, 61, 5927–5935.
15. A. Sorgho, M. Bougouma, G. De Leener, J. Vander Steen and T. Doneux, Electrochem. Commun., 2022, 140, 107327.
16. M. Busato, A. Lapi, P. D'Angelo and A. Melchior, J. Phys. Chem. B, 2021, 125, 6639–6648.
17. T. Watkins and D. A. Buttry, J. Phys. Chem. B, 2015, 119, 7003–7014.
18. S. Muhammad, M. N. Javed, K. A. Gill, F. I. Ali, W. Henderson, A. Bari, S. G. Musharraf, J. A. Baig and I. A. Hashmi, J. Cleaner Prod., 2022, 344, 131119.
19. U. Domańska and A. Rękawek, J. Solution Chem., 2009, 38, 739–751.
20. A. P. De Los Ríos, F. J. Hernández-Fernández, F. J. Alguacil, L. J. Lozano, A. Ginestá, I. García-Díaz, S. Sánchez-Segado, F. A. López and C. Godínez, Sep. Purif. Technol., 2012, 97, 150–157.
21. B. Ekka, L. Rout, M. K. Sahu Aniket Kumar, R. K. Patel and P. Dash, J. Environ. Chem. Eng., 2015, 3, 1356–1364.
22. S. Tan, M.-T. Nguyen, D. Zhang, L. Zhong, Z. Cheng, S. China, G. E. Johnson and V. Prabhakaran, ACS Appl. Mater. Interfaces, 2023, 15(37), 44469–44481.
23. A. Fortunati, F. Risplendi, M. Re Fiorentin, G. Cicero, E. Parisi, M. Castellino, E. Simone, B. Iliev, T. J. S. Schubert, N. Russo and S. Hernández, Commun. Chem., 2023, 6(84), 1–13.
24. M. G. Freire, C. M. S. S. Neves, I. M. Marrucho, J. A. P. Coutinho and A. M. Fernandes, J. Phys. Chem. A, 2010, 114, 3744–3749.
25. R. P. Swatloski, J. D. Holbrey and R. D. Rogers, Green Chem., 2003, 5, 361–363.
26. C. A. Schalley, Mass Spectrom. Rev., 2001, 20, 253–309.
27. S. V. J. Yuvaraj, R. K. Zhdanov, R. V. Belosludov, V. R. Belosludov, O. S. Subbotin, K. Kanie, K. Funaki, A. Muramatsu, T. Nakamura and Y. Kawazoe, J. Phys. Chem. B, 2015, 119, 12894–12904.
28. A. A. Niazi, B. D. Rabideau and A. E. Ismail, J. Phys. Chem. B, 2013, 117, 1378–1388.
29. T. C. Schutt, G. A. Hegde, V. S. Bharadwaj, A. J. Johns and C. M. Maupin, J. Phys. Chem. B, 2017, 121, 843–853.
30. J. Zhang, E. T. Baxter, M. T. Nguyen, V. Prabhakaran, R. Rousseau, G. E. Johnson and V. A. Glezakou, J. Phys. Chem. Lett., 2020, 11, 6844–6851.
31. Q. Yuan, W. Cao and X.-B. Wang, Int. Rev. Phys. Chem., 2020, 39, 83–108.
32. X.-B. Wang, Y. L. Wang, J. Yang, X. P. Xing, J. Li and L. S. Wang, J. Am. Chem. Soc., 2009, 131, 16368–16370.
33. D. Leimbach, S. Rothe, J. Sundberg and D. Hanstorp, J. Phys. B: At., Mol. Opt. Phys., 1992, 25, 1773.
34. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
35. J. Zhang, V. A. Glezakou, R. Rousseau and M. T. Nguyen, J. Chem. Theory Comput., 2020, 16, 3947–3958.
36. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
37. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, 1–49.
38. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
39. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
40. D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919.
41. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
42. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
43. F. Alkan and C. Dybowski, Phys. Chem. Chem. Phys., 2015, 17, 25014–25026.
44. F. Coleman, G. Feng, R. W. Murphy, P. Nockemann, K. R. Seddon and M. Swadźba-Kwaśny, Dalton Trans., 2013, 42, 5025–5035.
45. Y. Luo and F. J. Millero, Geochim. Cosmochim. Acta, 2007, 71, 326–334.
46. I. F. Burshte and A. L. Poznyak, Crystallogr. Rep., 2002, 47, 62–64.
47. S. H. M. Deng, X. Y. Kong and X.-B. Wang, J. Chem. Phys., 2015, 142, 024313.
48. E. T. Baxter, J. Zhang, S. Tan, M. T. Nguyen, D. Zhang, Q. Yuan, W. Cao, X.-B. Wang, V. Prabhakaran, V. A. Glezakou and G. E. Johnson, Chem. Mater., 2022, 34, 2612–2623.
49. P. Peljo and H. H. Girault, Energy Environ. Sci., 2018, 11, 2306–2309.
50. J. L. Bredas, Mater. Horiz., 2014, 1, 17–19.
51. A. P. Abbott, G. Frisch, J. Hartley and K. S. Ryder, Green Chem., 2011, 13, 471–481.
52. P. C. Marr and A. C. Marr, Green Chem., 2015, 18, 105–128.

---

Footnote

† Electronic supplementary information (ESI) available: Operando Raman experimental methods and data, NIPES data, and visualizations of calculated HOMO–LOMO and ESP maps of EMIMCl–PbCl₂ complexes. See DOI: https://doi.org/10.1039/d3gc03713d

---