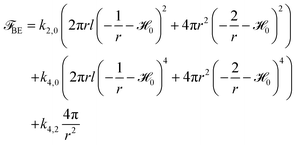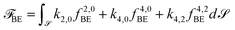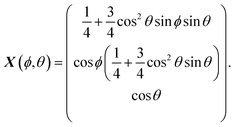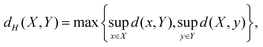Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The influence of higher order geometric terms on the asymmetry and dynamics of membranes†
Jan Magnus Sischka a,
Ingo Nitschkea and
Axel Voigt
a,
Ingo Nitschkea and
Axel Voigt *abc
*abc
aFaculty Mathematics, TU Dresden, 01062 Dresden, Germany. E-mail: axel.voigt@tu-dresden.de
bCenter for Systems Biology Dresden (CSBD), Pfotenhauerstr. 108, 01307 Dresden, Germany
cCluster of Excellence, Physics of Life, TU Dresden, Arnoldstr. 18, 01307 Dresden, Germany
First published on 3rd February 2025
Abstract
We consider membranes as fluid deformable surfaces and allow for higher order geometric terms in the bending energy related to the Gaussian curvature squared and the mean curvature minus the spontaneous curvature to the fourth power. The evolution equations are derived and numerically solved using surface finite elements. The two higher order geometric terms have different effects. While the Gaussian curvature squared term has a tendency to stabilize tubes and enhance the evolution towards equilibrium shapes, thereby facilitating rapid shape changes, the mean curvature minus the spontaneous curvature to the fourth power destabilizes tubes and leads to qualitatively different equilibrium shapes but also enhances the evolution. This is demonstrated in axisymmetric settings and fully three-dimensional simulations. We therefore postulate that not only surface viscosity but also higher order geometric terms in the bending energy contribute to rapid shape changes which are relevant for morphological changes of cells.
1 Introduction
Membranes are ubiquitous and essential in biology; they compartmentalize biomaterials, separate the cell from its exterior and organelles from the cytoplasm, dynamically remodel and change conformation. Geometric properties of the membrane have been identified as key players for such processes.1–3 As the typical thickness of a membrane is orders of magnitude smaller than its lateral extension, treating the membrane as a two-dimensional surface embedded in a three-dimensional space is a reasonable approximation. This separation of length scales allows for a mesoscopic modeling where details related to membrane molecular structure are considered in effective material parameters and geometric quantities and led to the success of the classical Canham–Helfrich model,4,5 which builds on a bending energy with mean curvature
with mean curvature ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , Gaussian curvature
, Gaussian curvature ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , bending rigidity parameters k2,0 and k2,1, a spontaneous curvature
, bending rigidity parameters k2,0 and k2,1, a spontaneous curvature ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 and additional (local or global) area and volume constraints. For definitions see Section 2.1. Assuming constant values of k2,1, the second term reduces to a topological measure and thus a constant as long as the topology does not change. We will therefore neglect this term.
0 and additional (local or global) area and volume constraints. For definitions see Section 2.1. Assuming constant values of k2,1, the second term reduces to a topological measure and thus a constant as long as the topology does not change. We will therefore neglect this term.
Equilibrium shapes, resulting from minimizing the bending energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE, have been extensively studied, see ref. 6 for a review. For
BE, have been extensively studied, see ref. 6 for a review. For ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 = 0 and wide ranges of the reduced volume, which is the ratio of the volume and the volume of an equivalent sphere with the same area, they are dominated by prolate and oblate shapes.7 The spontaneous curvature
0 = 0 and wide ranges of the reduced volume, which is the ratio of the volume and the volume of an equivalent sphere with the same area, they are dominated by prolate and oblate shapes.7 The spontaneous curvature ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0, which accounts for the asymmetry of the membrane, is able to modify these shapes.7 A wealth of studies also aims to produce tubes as minimizing shapes. Tubes are ubiquitous in membranes and play crucial roles in trafficking, ion transport, and cellular motility. For idealized situations this is rather simple as
0, which accounts for the asymmetry of the membrane, is able to modify these shapes.7 A wealth of studies also aims to produce tubes as minimizing shapes. Tubes are ubiquitous in membranes and play crucial roles in trafficking, ion transport, and cellular motility. For idealized situations this is rather simple as ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE = 0 if
BE = 0 if ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0, which is achieved for an infinite tube of radius r and
0, which is achieved for an infinite tube of radius r and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 = −1/r. However, this solution is not unique, a sphere of radius 2r also leads to
0 = −1/r. However, this solution is not unique, a sphere of radius 2r also leads to ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE = 0. More realistic situations with finite volume and area require further considerations, e.g., introducing a spontaneous curvature deviator.8–10 Also, various ideas have been proposed to consider higher order geometric terms in the bending energy
BE = 0. More realistic situations with finite volume and area require further considerations, e.g., introducing a spontaneous curvature deviator.8–10 Also, various ideas have been proposed to consider higher order geometric terms in the bending energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE to enforce the stability of tubes.2,11–14 For example, fourth order terms proportional to
BE to enforce the stability of tubes.2,11–14 For example, fourth order terms proportional to ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 2 seem plausible as
2 seem plausible as ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) = 0 for tubes.
= 0 for tubes.
Most of these studies only focus on equilibrium shapes, comparing the bending energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE of different configurations and addressing their stability. But the dynamic evolution of the membrane and associated shape changes are also of interest, e.g. in the context of the formation of bulges with pinch-offs, which can be associated with endocytosis and exocytosis15–17 or shape changes associated with cell motility.18–20 All these processes require additional phenomena, which are not considered in the Canham–Helfrich model. But there is growing interest in the role of membranes in these processes. One striking example where membranes at least participate are frequently forming and retracting filopodia.21 This process requires rapid shape changes in cells and according to ref. 22 the membrane and the underlying cortex act as an integrated system to globally coordinate such changes in cell shape. To facilitate these rapid morphological changes, cells maintain an excess of membrane that is organized in membrane reservoirs and is available to the cell on the order of seconds.23 To understand such processes thus not only requires unveiling the secretes of equilibrium shapes but also to consider the flow of membranes which facilitates the rapid shape changes. To model such processes is a different story and even if various models for the cellular cortex exist24–27 and also first attempts to couple them with membrane models to form the mentioned integrated system have been proposed,22,28 we here refrain from such couplings and only aim first for a minimal model of the membrane alone, which facilitates rapid shape changes.
BE of different configurations and addressing their stability. But the dynamic evolution of the membrane and associated shape changes are also of interest, e.g. in the context of the formation of bulges with pinch-offs, which can be associated with endocytosis and exocytosis15–17 or shape changes associated with cell motility.18–20 All these processes require additional phenomena, which are not considered in the Canham–Helfrich model. But there is growing interest in the role of membranes in these processes. One striking example where membranes at least participate are frequently forming and retracting filopodia.21 This process requires rapid shape changes in cells and according to ref. 22 the membrane and the underlying cortex act as an integrated system to globally coordinate such changes in cell shape. To facilitate these rapid morphological changes, cells maintain an excess of membrane that is organized in membrane reservoirs and is available to the cell on the order of seconds.23 To understand such processes thus not only requires unveiling the secretes of equilibrium shapes but also to consider the flow of membranes which facilitates the rapid shape changes. To model such processes is a different story and even if various models for the cellular cortex exist24–27 and also first attempts to couple them with membrane models to form the mentioned integrated system have been proposed,22,28 we here refrain from such couplings and only aim first for a minimal model of the membrane alone, which facilitates rapid shape changes.
Surface viscosity has been identified as a key player29 and considering membranes as fluid deformable surfaces30–33 opened new perspectives on the description of the dynamics of membranes. Fluid deformable surfaces can be viewed as two-dimensional viscous fluids with bending elasticity. Due to this solid–fluid duality, any shape change contributes to tangential flow, and vice versa, any tangential flow on a curved surface induces shape deformations. This tight coupling between shape and flow makes curvature a natural element of the governing equations. As demonstrated by numerical studies of the equations for fluid deformable surfaces, surface hydrodynamics can significantly speed up the evolution34,35 and can enhance bulging and furrow formation in membranes.17
Combined with higher order geometric terms in the bending energy, models for fluid deformable surfaces has the potential to enable the rapid shape changes in the release and formation of membrane reservoirs and the formation and retraction of filopodia. We computationally explore the effect of these terms on the equilibrium shapes and the dynamics to reach them and analyze their impact to facilitate rapid shape changes. Any coupling with the cortex,22 interaction with proteins that induce curvature36 or to forces exerted on the membrane37,38 are not considered. We also neglect any interaction with the surrounding bulk phases. This results from the theoretical interest in exploring the membrane properties without any additional influence and the limit of a large Saffman–Delbrück number. This number describes the relation between the viscosities of the membrane and the typically less viscous bulk fluid and if large allows the decoupling of surface and bulk flows.39
The rest of the paper is structured as follows. In Section 2 we introduce the full model and briefly mention the considered numerical approach. More details on the derivation of the model and on the numerical approach including convergence studies are provided in Appendices (Model derivation, Numerical method and Validation). Computational results are described in Section 3. They contain axisymmetric and full three-dimensional computations addressing the dynamic evolution and the equilibrium shapes. In Section 4 we draw conclusions and mention possible directions to extend the described model to enable simulations of rapid morphological changes of cells.
2 Model
2.1 Notation
The considered mesoscale model requires basic notation from differential geometry and geometric partial differential equations. Besides classical mathematical text books in these fields we refer to ref. 2 for an introduction in the context of membranes. We follow the same notation as in ref. 17 which is here repeated for convenience. We consider a time dependent smooth and oriented surface![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) =
= ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (t) without boundary, embedded in
(t) without boundary, embedded in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. The enclosed volume is denoted by Ω = Ω(t). We denote by ν the outward pointing surface normal, the surface projection is P = I − ν⊗ν, with I the identity matrix, the shape operator is
3. The enclosed volume is denoted by Ω = Ω(t). We denote by ν the outward pointing surface normal, the surface projection is P = I − ν⊗ν, with I the identity matrix, the shape operator is ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = −∇Pν, the mean curvature
= −∇Pν, the mean curvature ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = tr
= tr![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) , and the Gaussian curvature
, and the Gaussian curvature  . We consider time-dependent Euclidean-based n-tensor fields in Tn
. We consider time-dependent Euclidean-based n-tensor fields in Tn![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) . We call T0
. We call T0![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = T0
= T0![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) the space of scalar fields, T1
the space of scalar fields, T1![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = T
= T![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) the space of vector fields, and T2
the space of vector fields, and T2![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) the space of 2-tensor fields. Important subtensor fields are tangential n-tensor fields in Tn
the space of 2-tensor fields. Important subtensor fields are tangential n-tensor fields in Tn![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ≤Tn
≤Tn![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) . Let p ∈ T0
. Let p ∈ T0![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) be a continuously differentiable scalar field, u ∈ T
be a continuously differentiable scalar field, u ∈ T![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) a continuously differentiable
a continuously differentiable ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3-vector field, and σ ∈ T2
3-vector field, and σ ∈ T2![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) a continuously differentiable
a continuously differentiable ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3×3-tensor field defined on
3×3-tensor field defined on ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) . We define the different surface gradients by ∇P p = P∇pe, ∇P u = P∇ueP and ∇C σ = ∇σeP, where pe, ue and σe are arbitrary smooth extensions of p, u and σ in the normal direction and ∇ is the gradient of the embedding space
. We define the different surface gradients by ∇P p = P∇pe, ∇P u = P∇ueP and ∇C σ = ∇σeP, where pe, ue and σe are arbitrary smooth extensions of p, u and σ in the normal direction and ∇ is the gradient of the embedding space ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. The corresponding divergence operators for a vector field u and a tensor field σ are divP u = tr(∇P u) and divC (σP) = tr∇C (σP), where tr is the trace operator. The relations to the covariant derivatives ∇
3. The corresponding divergence operators for a vector field u and a tensor field σ are divP u = tr(∇P u) and divC (σP) = tr∇C (σP), where tr is the trace operator. The relations to the covariant derivatives ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) and the covariant divergence div
and the covariant divergence div![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) on
on ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , with Δ
, with Δ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = div
= div![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ·∇
·∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) the Laplace–Beltrami operator, read ∇P p = ∇
the Laplace–Beltrami operator, read ∇P p = ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) p and divP u = div
p and divP u = div![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (Pu) − (u·ν)
(Pu) − (u·ν)![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , respectively.
, respectively.
2.2 Governing equations
The material velocity u ∈ T![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) can be decomposed into u = uNν + uT, with uN = u·ν and uT = Pu, the normal and the tangential part, respectively. The pressure p ∈ T0
can be decomposed into u = uNν + uT, with uN = u·ν and uT = Pu, the normal and the tangential part, respectively. The pressure p ∈ T0![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) serves as Lagrange multiplier for the inextensibility constraint. The governing equations for these unknowns read
serves as Lagrange multiplier for the inextensibility constraint. The governing equations for these unknowns read
 | (1) |
| divPu = 0 | (2) |
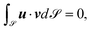 | (3) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ui,w), i = 1, 2, 3, with w = u − ∂tX is the relative velocity and X a parameterisation of
ui,w), i = 1, 2, 3, with w = u − ∂tX is the relative velocity and X a parameterisation of ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ,
,  is the rate of deformation tensor, Re > 0 is the Reynolds number, γ ≥ 0 is a friction coefficient, λ ∈
is the rate of deformation tensor, Re > 0 is the Reynolds number, γ ≥ 0 is a friction coefficient, λ ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) is a Lagrange multiplier to ensure a constant enclosed volume, and b denotes a bending force, defined by
is a Lagrange multiplier to ensure a constant enclosed volume, and b denotes a bending force, defined by
 | (4) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 is a spontaneous curvature and k2,0,k4,0,k4,2 ∈
0 is a spontaneous curvature and k2,0,k4,0,k4,2 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) are bending rigidity parameters. The system of equations considers a model for fluid deformable surfaces. Such models consist of incompressible surface Navier–Stokes equations with bending forces and a constraint on the enclosed volume. The highly nonlinear model accounts for the tight interplay between surface evolution, surface curvature and surface hydrodynamics and allows for the modelling of membranes with surface viscosity. For derivations of the model (with k4,0 = k4,2 = 0) we refer to ref. 17, 31, 34, 40 and 41. They consider different principles and build on a nonlinear Onsager formalism,31 thin film limits from three-dimensional models34,40 and a Lagrange–D’Alembert approach.17,41 For a comparison of derivations for b = 0 and without the constraint on the enclosed volume we refer to ref. 42–44.
are bending rigidity parameters. The system of equations considers a model for fluid deformable surfaces. Such models consist of incompressible surface Navier–Stokes equations with bending forces and a constraint on the enclosed volume. The highly nonlinear model accounts for the tight interplay between surface evolution, surface curvature and surface hydrodynamics and allows for the modelling of membranes with surface viscosity. For derivations of the model (with k4,0 = k4,2 = 0) we refer to ref. 17, 31, 34, 40 and 41. They consider different principles and build on a nonlinear Onsager formalism,31 thin film limits from three-dimensional models34,40 and a Lagrange–D’Alembert approach.17,41 For a comparison of derivations for b = 0 and without the constraint on the enclosed volume we refer to ref. 42–44.
The mentioned solid–fluid duality of these models, which leads to a tight coupling between shape and flow, and lets any shape change contribute to tangential flow, and vice versa, can best be seen by rewriting eqn (1)–(3) as coupled equations for uN = u·ν and uT = Pu.34,42,43 One out of several of the resulting coupling terms results from eqn (2), which leads to divPu = uN![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) + divPuT = 0 and explicitly demonstrates the relation between the mean curvature and the tangential velocity.
+ divPuT = 0 and explicitly demonstrates the relation between the mean curvature and the tangential velocity.
Considering the overdamped limit, formally letting γ → ∞, leads to the classical dynamic equations
u = −∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) p − p p − p![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ν + b − λν ν + b − λν
| (5) |
| divPu = 0 | (6) |
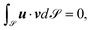 | (7) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) p + p
p + p![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 2 + λ = b·ν
2 + λ = b·ν![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) and corresponds to previous models, if b only contains second order geometric terms.45–49 Further relaxing the constraint on inextensibility leads to the classical Canham–Helfrich models with area and volume constraints.48
and corresponds to previous models, if b only contains second order geometric terms.45–49 Further relaxing the constraint on inextensibility leads to the classical Canham–Helfrich models with area and volume constraints.48
In contrast to previous approaches for fluid deformable surfaces17,31,34,35,50 the bending force b also contains higher order geometric terms.
2.3 Bending forces
The bending force eqn (4) results from the bending energy
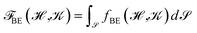 | (8) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 leading to
0 leading toin terms of geometric orders n ≤ N ∈
![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) for different bending rigidity parameters kn,α ∈
for different bending rigidity parameters kn,α ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) . This expression corresponds to the generalized form of the classical Canham–Helfrich energy (n = 2) introduced in ref. 11 and also considered in ref. 2, 12 and 13 if gradient terms are neglected. It can be simplified assuming certain properties of the bending energy: as we are interested in variations of the energy, we can omit the constant contribution k0,0. We will further not allow for topological changes, thus, we can omit the k2,1
. This expression corresponds to the generalized form of the classical Canham–Helfrich energy (n = 2) introduced in ref. 11 and also considered in ref. 2, 12 and 13 if gradient terms are neglected. It can be simplified assuming certain properties of the bending energy: as we are interested in variations of the energy, we can omit the constant contribution k0,0. We will further not allow for topological changes, thus, we can omit the k2,1![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) term, applying Gauss–Bonnet’s theorem. Furthermore, we only allow for terms which guarantee boundedness from below. This excludes all odd geometric orders as well as k4,1. Considering these points and only contributions up to geometric order N = 4 leads to the following bending energy density
term, applying Gauss–Bonnet’s theorem. Furthermore, we only allow for terms which guarantee boundedness from below. This excludes all odd geometric orders as well as k4,1. Considering these points and only contributions up to geometric order N = 4 leads to the following bending energy density fBE(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , ,![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ) = k2,0( ) = k2,0(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − − ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0)2 + k4,0( 0)2 + k4,0(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − − ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0)4 + k4,2 0)4 + k4,2![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 2, 2, |
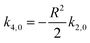 with k4,2 not determined. We here restrict the parameter space to k2,0 > 0, k4,0 ≥ 0 and k4,2 ≥ 0. We would like to remark that more general parameter combinations are possible, still leading to well-posed bending energies and stable solutions. However,
with k4,2 not determined. We here restrict the parameter space to k2,0 > 0, k4,0 ≥ 0 and k4,2 ≥ 0. We would like to remark that more general parameter combinations are possible, still leading to well-posed bending energies and stable solutions. However, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) = 0 is a property of a tube and thus k4,2
= 0 is a property of a tube and thus k4,2![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 2 seems to be the most plausible higher order extension in the bending energy to stabilize tubular structures. k4,0(
2 seems to be the most plausible higher order extension in the bending energy to stabilize tubular structures. k4,0(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) −
− ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0)4 is considered for completeness. In any case the bending force b is derived as the negative of the variational derivative of the bending energy (8)
0)4 is considered for completeness. In any case the bending force b is derived as the negative of the variational derivative of the bending energy (8)A detailed derivation of the bending force is done in the Appendix: Model derivation.
2.4 Numerical approach
The numerical approach extends the approach used in ref. 17 and 35 which is based on surface finite elements51,52 and builds on a Taylor–Hood element for the surface Navier–Stokes equations, higher order surface parametrizations, appropriate approximations of the geometric quantities, mesh redistribution, a semi-implicit discretization in time and an iterative approach to deal with the non-local constraint on the enclosed volume. Additional challenges emerge from the higher order geometric terms. In the Appendix: Numerical method we provide a detailed description and in Appendix: Validation convergence studies for these terms. The implementation is done in DUNE/AMDiS.53,54 Throughout the paper we consider Re = 1.0 and γ = 0 and only vary![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0, k2,0, k4,0 and k4,2. Numerical parameters, such as mesh size h and time step τ are chosen to resolve the highest curvature values and to meet stability constraints, following ref. 35.
0, k2,0, k4,0 and k4,2. Numerical parameters, such as mesh size h and time step τ are chosen to resolve the highest curvature values and to meet stability constraints, following ref. 35.
3 Results
3.1 Axisymmetric simulation without surface viscosity
We begin by describing the membrane using cylindrical coordinates (r, θ, z) and consider a rotational symmetric tube with periodic boundary conditions. With
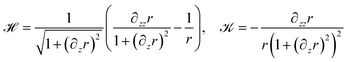 | (9) |
the bending energy density fBE(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ,
,![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ) can be reformulated and considered as a function of r(z, t), the radial distance of the axisymmetric membrane from the cylindrical symmetry axis, where z measures the coordinate along that axis and t is time. For the evolution we consider the corresponding equations to eqn (5)–(7) but drop the constraints on inextensibility and volume. The resulting equation to solve reads
) can be reformulated and considered as a function of r(z, t), the radial distance of the axisymmetric membrane from the cylindrical symmetry axis, where z measures the coordinate along that axis and t is time. For the evolution we consider the corresponding equations to eqn (5)–(7) but drop the constraints on inextensibility and volume. The resulting equation to solve reads
 | (10) |
with b = b·ν. While lengthy if fully written down, the resulting model can be solved using standard approaches. We again use finite elements in space, a semi-implicit discretization in time, smoothing of the geometric properties and consider DUNE/AMDiS53,54 for the realization. Fig. 1 shows the time evolution of a periodically perturbed tube for different values of k4,2 and k4,0 together with the evolution of the bending energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE over time. For k4,2 = 0 and k4,0 = 0 this is a well studied problem of the stability of a tube.55–57 The parameters are chosen to remain within the stability region. The results clearly indicate a stronger damping of the perturbations for increasing values of k4,2 and k4,0. However, the behaviour slightly differs with respect to the damping of the perturbations and adjustment of r(z). This difference is also seen in the decrease of the bending energy.
BE over time. For k4,2 = 0 and k4,0 = 0 this is a well studied problem of the stability of a tube.55–57 The parameters are chosen to remain within the stability region. The results clearly indicate a stronger damping of the perturbations for increasing values of k4,2 and k4,0. However, the behaviour slightly differs with respect to the damping of the perturbations and adjustment of r(z). This difference is also seen in the decrease of the bending energy.
Results of a linear stability analysis58 for the case of k4,2 = 0 and k4,0 = 0 but considering surface viscosity using a Stokes approximation of eqn (1) indicate a similar stability region as in the overdamped limit and we assume this holds also for k4,2 > 0 and k4,0 > 0 and the full problem.
3.2 Equilibrium shape of tubular cell
The shape of a tubular cell can be approximated by a cylinder with hemispherical caps, as shown in Fig. 2. For this simple shape, we can compute the bending energy aswhere r is the radius and l the length of the cylinder. For
 , the energy of the cylindrical part vanishes and the energy simplifies to
, the energy of the cylindrical part vanishes and the energy simplifies to | ||
| Fig. 2 (a) As initial surface we consider a cylinder with hemispherical caps. (b) The geometry is determined by the length of the cylinder l and the radius r of the cylinder and hemispherical caps. | ||
Note that this energy is independent of the length of the cylinder. We consider this shape as the initial configuration and the energy as a quantity for comparison.
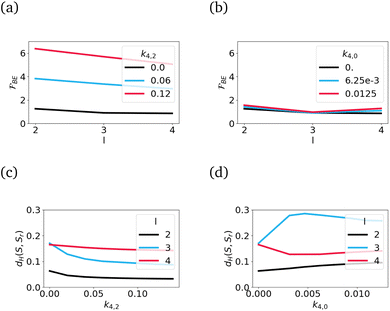
Fig. 3 shows the final configurations achieved by solving the full problem, eqn (1)–(3), for three different values l. In all cases, the shape deviates from the initial configuration. For k4,2 = 0 and k4,0 = 0 the resulting shapes correspond to the equilibrium prolate shapes in ref. 7. However, for k4,2 > 0 and k4,0 > 0, these shapes deviate. For k4,2 > 0 the bending energy is reduced by increasing l and the Hausdorff distance dH(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ,
,![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 0) to the idealized initial shape of a cylinder with hemispherical caps
0) to the idealized initial shape of a cylinder with hemispherical caps ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 0 is reduced by increasing k4,2, see Fig. 4. The Hausdorff distance is a measure of the distance between sets of points, in our case the discretization points of the equilibrium shape and the initial shape. For a mathematical definition and implementation issues see Appendix: Hausdorff distance. The observed trends are far from being general. This can also not be expected due to the highly nonlinear coupling of the geometric terms and the considered constraints on volume and inextensibility. However, they confirm the intuition of the potential impact of k4,2
0 is reduced by increasing k4,2, see Fig. 4. The Hausdorff distance is a measure of the distance between sets of points, in our case the discretization points of the equilibrium shape and the initial shape. For a mathematical definition and implementation issues see Appendix: Hausdorff distance. The observed trends are far from being general. This can also not be expected due to the highly nonlinear coupling of the geometric terms and the considered constraints on volume and inextensibility. However, they confirm the intuition of the potential impact of k4,2![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 2 in the bending energy on the emerging equilibrium shapes. The effect of k4,0 > 0 differs. The increased tendency to enforce
2 in the bending energy on the emerging equilibrium shapes. The effect of k4,0 > 0 differs. The increased tendency to enforce ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 leads to undulations with a wavelength related to −2/
0 leads to undulations with a wavelength related to −2/![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0. How well this can be achieved strongly depends on the length l. Therefore also the Hausdorff distance dH(
0. How well this can be achieved strongly depends on the length l. Therefore also the Hausdorff distance dH(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ,
,![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 0) to the idealized initial shape of a cylinder with hemispherical caps
0) to the idealized initial shape of a cylinder with hemispherical caps ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 0 does not decrease but leads to a non-monotonic behaviour if considered as a function of l. The dependency of l on the bending energy
0 does not decrease but leads to a non-monotonic behaviour if considered as a function of l. The dependency of l on the bending energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE is negligible for the considered parameters. To summarize, within the stability region of the classical Canham–Helfrich model, higher order geometric terms related to k4,2
BE is negligible for the considered parameters. To summarize, within the stability region of the classical Canham–Helfrich model, higher order geometric terms related to k4,2![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 2 seem to stabilize tubular shapes and terms related to k4,0(
2 seem to stabilize tubular shapes and terms related to k4,0(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) −
− ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0)4 seem to destabilize these shapes.
0)4 seem to destabilize these shapes.
3.3 Dynamic evolution
In order to further explore the influence of the higher order geometric terms related to k4,2![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 2 and k4,0(
2 and k4,0(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) −
− ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0)4 on the dynamics, we consider an initial surface
0)4 on the dynamics, we consider an initial surface ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 0 as a perturbed unit sphere
0 as a perturbed unit sphere
 | (11) |
 | (12) |
with spherical harmonics Yml and Legendre polynomials Pml and the case l = 5, m = 3 and r0 = 0.5. The velocity field is initialized with u0 = 0. The initial surface has non-zero mean and Gaussian curvature and is out of equilibrium. It serves as a prototypical example to study the rapid shape changes featuring moderate geometric properties of a cell with membrane reservoirs. The resulting bending force induces shape deformations in the normal direction. However, the curvature terms also induce tangential flows, which also contribute to shape deformations. This coupling between tangential flow and shape deformations is well understood and shown to enhance the evolution towards equilibrium shapes.35 Here, we explore the evolution for different values of k4,2 and k4,0, which are k4,2 = 0, 0.06 and 0.12 and k4,0 = 0, 0.00625 and 0.0125, respectively. Fig. 5 and 6 show snapshots of the evolutions. The color coding corresponds to shape deformations (red – movement outwards, blue – movement inwards) and the arrows indicate the tangential velocity, where the length scales with the magnitude. Furthermore, the energy contributions are shown over time. Here, the bending energy is split into the different contributions ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE =
BE = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0 +
2,0 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,0 +
4,0 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,2 and the total energy
4,2 and the total energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) =
= ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE +
BE + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) K is the sum of the bending energy and the kinetic energy
K is the sum of the bending energy and the kinetic energy 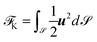 . All evolutions converge to an equilibrium shape, which for the cases k4,2 = 0 and k4,0 = 0 correspond to the associated Seifert shape,7 which here corresponds to an oblate. For k4,2 > 0 the equilibrium shapes only slightly differ. The difference in orientation might result from the different dynamics. However, due to the decoupling from the surrounding bulk phases and the considered parameter γ = 0, force-free rigid body rotations are also possible.59 While the equilibrium shapes are similar, significant changes can be observed in the dynamics. The close coupling between the bending energy
. All evolutions converge to an equilibrium shape, which for the cases k4,2 = 0 and k4,0 = 0 correspond to the associated Seifert shape,7 which here corresponds to an oblate. For k4,2 > 0 the equilibrium shapes only slightly differ. The difference in orientation might result from the different dynamics. However, due to the decoupling from the surrounding bulk phases and the considered parameter γ = 0, force-free rigid body rotations are also possible.59 While the equilibrium shapes are similar, significant changes can be observed in the dynamics. The close coupling between the bending energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE and the kinetic energy
BE and the kinetic energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) K can be observed and related to significant shape changes. But their appearance differs. The plateau in
K can be observed and related to significant shape changes. But their appearance differs. The plateau in ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE =
BE = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0 for k4,2 = 0 between t ≈ 2 and t ≈ 6 is reduced for k4,2 = 0.06 and 0.12 and already ends at t ≈ 4.5 and t ≈ 3, respectively. It should be noted that the absolute values of the energies cannot be directly compared as k4,2 varies by definition. The situation changes for k4,0 > 0. The equilibrium shapes are prolate shapes. Besides this difference in the long time behavior, the short time evolution also changes. We observe similar behavior as for k4,2 > 0 with an enhanced influence of the kinetic energy and a faster evolution towards intermediate shapes. The final convergence towards the equilibrium shape at late times probably results form similar values for the local minima on the oblate and prolate branch as also known for the classical Canham–Helfrich model.6 Again, the absolute values of the energies cannot be directly compared as k4,0 varies in the definition.
2,0 for k4,2 = 0 between t ≈ 2 and t ≈ 6 is reduced for k4,2 = 0.06 and 0.12 and already ends at t ≈ 4.5 and t ≈ 3, respectively. It should be noted that the absolute values of the energies cannot be directly compared as k4,2 varies by definition. The situation changes for k4,0 > 0. The equilibrium shapes are prolate shapes. Besides this difference in the long time behavior, the short time evolution also changes. We observe similar behavior as for k4,2 > 0 with an enhanced influence of the kinetic energy and a faster evolution towards intermediate shapes. The final convergence towards the equilibrium shape at late times probably results form similar values for the local minima on the oblate and prolate branch as also known for the classical Canham–Helfrich model.6 Again, the absolute values of the energies cannot be directly compared as k4,0 varies in the definition.
 | ||
Fig. 5 Evolution of a perturbed sphere considering parameters k2,0 = 0.125, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 = 0 and different values of k4,2. (a)–(c) Time instances for the evolution for k4,2 = 0, 0.06 and 0.12, respectively. The color coding indicates movement in the normal direction (red – movement outwards, blue – movement inwards) and the arrows indicate the tangential velocity. The time evolves from left to right; the time instances except for the last one are equal and are depicted in (d). (d) Evolution of the different energy contributions: 0 = 0 and different values of k4,2. (a)–(c) Time instances for the evolution for k4,2 = 0, 0.06 and 0.12, respectively. The color coding indicates movement in the normal direction (red – movement outwards, blue – movement inwards) and the arrows indicate the tangential velocity. The time evolves from left to right; the time instances except for the last one are equal and are depicted in (d). (d) Evolution of the different energy contributions: ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0 and 2,0 and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,2 are the energies linked to the corresponding bending terms, 4,2 are the energies linked to the corresponding bending terms, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) K is the kinetic energy. The bending energy is K is the kinetic energy. The bending energy is ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE = BE = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0 + 2,0 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,2 and the total energy 4,2 and the total energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE + BE + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) K. Shown is the evolution for k4,2 = 0, 0.06 and 0.12 (from left to right). Corresponding videos to the evolution in (a)–(c) are provided in the SI† using a LIC filter for visualization of the tangential flow. K. Shown is the evolution for k4,2 = 0, 0.06 and 0.12 (from left to right). Corresponding videos to the evolution in (a)–(c) are provided in the SI† using a LIC filter for visualization of the tangential flow. | ||
 | ||
Fig. 6 Evolution of a perturbed sphere considering parameters k2,0 = 0.125, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 = 0 and different values of k4,0. (a)–(c) Time instances for the evolution for k4,0 = 0, 0.00625 and 0.0125, respectively. The color coding indicates movement in the normal direction (red – movement outwards, blue – movement inwards) and the arrows indicate the tangential velocity. The time evolves from left to right; the time instances except for the last one are equal and are depicted in (d). (d) Evolution of the different energy contributions: 0 = 0 and different values of k4,0. (a)–(c) Time instances for the evolution for k4,0 = 0, 0.00625 and 0.0125, respectively. The color coding indicates movement in the normal direction (red – movement outwards, blue – movement inwards) and the arrows indicate the tangential velocity. The time evolves from left to right; the time instances except for the last one are equal and are depicted in (d). (d) Evolution of the different energy contributions: ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0 and 2,0 and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,0 are the energies linked to the corresponding bending terms, 4,0 are the energies linked to the corresponding bending terms, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) K is the kinetic energy. The bending energy is K is the kinetic energy. The bending energy is ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE = BE = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0 + 2,0 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,0 and the total energy 4,0 and the total energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) BE + BE + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) K. Shown is the evolution for k4,0 = 0, 0.00625 and 0.0125 (from left to right). Corresponding videos to the evolution in (a)–(c) are provided in the SI† using a LIC filter for visualization of the tangential flow. K. Shown is the evolution for k4,0 = 0, 0.00625 and 0.0125 (from left to right). Corresponding videos to the evolution in (a)–(c) are provided in the SI† using a LIC filter for visualization of the tangential flow. | ||
Qualitatively the higher order geometric terms further enhance the evolution and lead to alternative pathways to dissipate energy. This is most pronounced in the inlets highlighting the initial evolution; the drastic decrease of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,2 and
4,2 and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,0 is associated with large fluctuation of
4,0 is associated with large fluctuation of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) K. This behavior increases with increasing values of k4,2 and k4,0. Furthermore, while
K. This behavior increases with increasing values of k4,2 and k4,0. Furthermore, while ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,2 is roughly one order of magnitude smaller than
4,2 is roughly one order of magnitude smaller than ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0, the influence on the dynamics is dramatic. This is less pronounced for
2,0, the influence on the dynamics is dramatic. This is less pronounced for ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 4,0, which is at the same order as
4,0, which is at the same order as ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 2,0. We expect these fast shape changes to be even enhanced for less regular real geometries of membrane reservoirs, due to the appearance of larger curvature gradients.
2,0. We expect these fast shape changes to be even enhanced for less regular real geometries of membrane reservoirs, due to the appearance of larger curvature gradients.
4 Conclusions
Motivated by rapid shape changes of cells, where an excess of membrane that is organized in membrane reservoirs is made available to the cell on the order of seconds,23 we formulated a minimal mesoscopic membrane model which helps to facilitate this behavior. This, on the one side, includes an extension of the classical Canham–Helfrich model towards higher order geometric terms, and on the other side, includes the explicit treatment of the fluid properties of the membrane by considering membranes as fluid deformable surfaces. The first aspect adds to the classical bending energy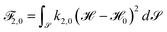 , terms proportional to the Gaussian curvature squared,
, terms proportional to the Gaussian curvature squared,  , and the mean curvature minus the spontaneous curvature to the fourth power,
, and the mean curvature minus the spontaneous curvature to the fourth power, 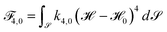 . The effects of these higher order terms are different. While the one related to the Gaussian curvature squared not only helps to damp perturbations of tubes, it also has a tendency to stabilize them, the term related to the mean curvature minus the spontaneous curvature to the fourth power has a tendency to destabilize tubes. Both effects have been considered in idealized rotational symmetric and full three-dimensional situations by analyzing the evolution and the emerging equilibrium shapes. If combined with the second aspect, which takes the surface viscosity of the membrane into account and combines the bending in the normal direction with the properties of an inextensible surface fluid, as a fluid deformable surface, the dynamic drastically changes. Already for the classical bending energy
. The effects of these higher order terms are different. While the one related to the Gaussian curvature squared not only helps to damp perturbations of tubes, it also has a tendency to stabilize them, the term related to the mean curvature minus the spontaneous curvature to the fourth power has a tendency to destabilize tubes. Both effects have been considered in idealized rotational symmetric and full three-dimensional situations by analyzing the evolution and the emerging equilibrium shapes. If combined with the second aspect, which takes the surface viscosity of the membrane into account and combines the bending in the normal direction with the properties of an inextensible surface fluid, as a fluid deformable surface, the dynamic drastically changes. Already for the classical bending energy 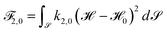 an enhanced evolution towards the equilibrium shape has been observed if the effects of surface viscosity are taken into account.35 With the higher order geometric terms this is further enhanced. The considered numerical experiments for the relaxation of a perturbed sphere showed alternative pathways to dissipate energy and strong tangential flows inducing fast shape changes. However, besides enabling rapid shape changes, the evolution and also the emerging equilibrium shapes qualitatively differ for the considered higher order terms. While the model with the Gaussian curvature squared term also converges to similar oblate-like shapes as the corresponding Seifert shapes6 for the classical Canham–Helfrich model, the model with the mean curvature minus the spontaneous curvature to the fourth power term converges to prolate-like shapes.
an enhanced evolution towards the equilibrium shape has been observed if the effects of surface viscosity are taken into account.35 With the higher order geometric terms this is further enhanced. The considered numerical experiments for the relaxation of a perturbed sphere showed alternative pathways to dissipate energy and strong tangential flows inducing fast shape changes. However, besides enabling rapid shape changes, the evolution and also the emerging equilibrium shapes qualitatively differ for the considered higher order terms. While the model with the Gaussian curvature squared term also converges to similar oblate-like shapes as the corresponding Seifert shapes6 for the classical Canham–Helfrich model, the model with the mean curvature minus the spontaneous curvature to the fourth power term converges to prolate-like shapes.
However, the focus of this paper is not to classify the increased phase space of equilibrium shapes resulting from the higher order terms, but to address additional mechanisms which facilitate rapid shape changes. While certainly more research is needed to fully explore the potential of the higher order geometric terms, e.g., with respect to the stability of tubes extending the analysis in ref. 58 the numerical studies already clearly indicate the potential for rapid shape changes. Even if only passive contributions of a homogeneous membrane are considered, and a full model for morphological changes of a cell requires the taking of inhomogeneities, active processes of the underlying cortex, adhesion between the membrane and the cortex and probably even more phenomena into account, the study contributes to identifying underlying general mechanical principles which might help to predict and control the dynamics of cells.20 Surface viscosity and higher order geometric terms in the bending energy provide mechanical cues and probably support active processes to enable rapid shape changes of cells.
A full model able to address the mentioned example of frequently forming and retracting filopodia and the associated fast shape changes of membrane reservoirs will require the coupling of models for the cellular cortex24–27 with membrane models of the considered type, which requires additional modeling and numerical efforts. One intermediate step to link this research closer to biology could be efforts to resolve the dynamics of membrane reservoirs and compare them with simulations of the proposed model.
Data availability
Data are available from Zenodo at https://doi.org/10.5281/zenodo.14503545.Conflicts of interest
There are no conflicts to declare.Appendices
Model derivation
We here compute the variational derivatives of the higher order geometric terms in the bending energy. We therefore write the bending energy aswith bending density components fn,αBE = (
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) −
− ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0)n−2α
0)n−2α![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) α. The corresponding forces bn,α ∈ T
α. The corresponding forces bn,α ∈ T![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) are given by
are given byfor all W ∈ T
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) . The result for f2,0BE is well known
. The result for f2,0BE is well knownFor the remaining terms we use the deformation derivative ðW60 and obtain the deformation formula
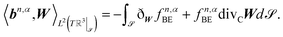 | (13) |
P(ðW![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) )P = ∇ )P = ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (ν·∇CW) − (ν·∇CW) − ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ∇CW, ∇CW,
| (14) |
ðW![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = tr(P(ðW = tr(P(ðW![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) )P) = div )P) = div![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (ν·∇CW) − (ν·∇CW) − ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∇CW ∇CW
| (15) |
Another application of integrations by parts w.r.t. ∇C, yields
divC(σP) = div![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (PσP) − ν·σ (PσP) − ν·σ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) + (div + (div![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (ν·σP) + (ν·σP) + ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ)ν σ)ν
| (16) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3|
3|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) .41,60 Therefore, the tangential part of b4,0 cancels out and we obtain
.41,60 Therefore, the tangential part of b4,0 cancels out and we obtainWith (14) and (15), the deformation derivative of
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) = 2(
= 2(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 2 − ‖
2 − ‖![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ‖2) reveals
‖2) revealsAs a consequence, the deformation formula (13), integrations by parts, and
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 2 =
2 = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) −
− ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) P, result in
P, result inSince div
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (
(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) P −
P − ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ) = 0 holds, integrations by parts yields
) = 0 holds, integrations by parts yieldsUsing (16), the tangential part of b4,2 cancels out and we obtain
b4,2 = −(2div![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (( ((![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) P − P − ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) )∇ )∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ) + ) + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 2)ν. 2)ν. |
Numerical method
We consider a surface finite element method (SFEM)51,52 to solve the highly nonlinear set of geometric and surface partial differential equations (1)–(3), using the approaches in ref. 17 and 35.We combine the system (1)–(3) with a mesh redistribution approach.61 These are equations for the parametrization
| ∂tX·ν = u·ν | (17) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ν = ΔCX, ν = ΔCX,
| (18) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) . We consider a discrete k-th order approximation
. We consider a discrete k-th order approximation ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) kh of
kh of ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , with h the size of the mesh elements, i.e. the longest edge of the mesh. We use the DUNECurvedGrid library62 and consider each geometrical quantity like the normal vector νh, the shape operator
, with h the size of the mesh elements, i.e. the longest edge of the mesh. We use the DUNECurvedGrid library62 and consider each geometrical quantity like the normal vector νh, the shape operator ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) h, the Gaussian curvature
h, the Gaussian curvature ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) h, and the inner products (·,·)h with respect to the
h, and the inner products (·,·)h with respect to the ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) kh. In the following, we will drop the index k. We define the discrete function spaces for scalar functions by Vk(
kh. In the following, we will drop the index k. We define the discrete function spaces for scalar functions by Vk(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h) = {ψ ∈ C0(
h) = {ψ ∈ C0(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h)|ψ|T ∈
h)|ψ|T ∈ ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) k(T)} and for vector fields by Vk(
k(T)} and for vector fields by Vk(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) [h]) = [Vk(
[h]) = [Vk(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) [h])]3. Within these definitions T is the mesh element and
[h])]3. Within these definitions T is the mesh element and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) k are the polynomials of order k. We consider uh,X ∈ V3(
k are the polynomials of order k. We consider uh,X ∈ V3(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h),
h), ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) h ∈ V3(
h ∈ V3(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h), and ph ∈ V2(
h), and ph ∈ V2(![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h), which leads to an isogeometric setting for the velocity and a
h), which leads to an isogeometric setting for the velocity and a ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 3 −
3 − ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 2 Taylor-Hood element for the surface Navier–Stokes-like equations. We discretize in time using constant time stepping with step size τ. In each time step we solve the surface Navier–Stokes-like equations and the mesh redistribution together. We define a discrete surface update variable Yn = Xn − Xn−1, which is considered as unknown instead of the surface parametrization Xn. The system to solve reads:
2 Taylor-Hood element for the surface Navier–Stokes-like equations. We discretize in time using constant time stepping with step size τ. In each time step we solve the surface Navier–Stokes-like equations and the mesh redistribution together. We define a discrete surface update variable Yn = Xn − Xn−1, which is considered as unknown instead of the surface parametrization Xn. The system to solve reads:
Find (unh,pnh,![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nh,Yn) ∈ [V3×V2×V3×V3](
nh,Yn) ∈ [V3×V2×V3×V3](![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) n−1h) such that:
n−1h) such that:
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) n−1h), where
n−1h), where 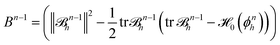 .
.
In the above formulation we used the identity (−∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) pnh − pnh
pnh − pnh![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nhνh,νh)h = (pnh,divPνh)h. Note that the Lagrange multiplier λ is unknown, which leads to an underdetermined system. To resolve that problem, we follow the approach introduced in ref. 35. In order to fulfill the volume constraint, λ has to be chosen such that
nhνh,νh)h = (pnh,divPνh)h. Note that the Lagrange multiplier λ is unknown, which leads to an underdetermined system. To resolve that problem, we follow the approach introduced in ref. 35. In order to fulfill the volume constraint, λ has to be chosen such that
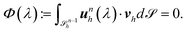 | (19) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) nh needs to be computed by updating the parametrization Xn = Xn−1 + Yn, lifting the solutions unh, pnh and
nh needs to be computed by updating the parametrization Xn = Xn−1 + Yn, lifting the solutions unh, pnh and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nh to the new surface and computing the remaining geometric quantities νnh,
nh to the new surface and computing the remaining geometric quantities νnh, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) nh, ∇
nh, ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nh,
nh, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) nh and ∇
nh and ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) nh for the new surface. While this approach showed the (expected) optimal order of convergence,35 with respect to computational and numerical analysis results for the underlying surface Stokes equations on stationary surfaces63,64 for bending terms up to second order, the approach is not sufficient if higher order geometric terms are included.
nh for the new surface. While this approach showed the (expected) optimal order of convergence,35 with respect to computational and numerical analysis results for the underlying surface Stokes equations on stationary surfaces63,64 for bending terms up to second order, the approach is not sufficient if higher order geometric terms are included.
We therefore introduce a smoothing step of the surface quantities ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nh, ∇
nh, ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nh,
nh, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) nh and ∇
nh and ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) nh. For each surface quantity or its components ah =
nh. For each surface quantity or its components ah = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nh, [∇
nh, [∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nh]i,
nh]i, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) nh and [∇
nh and [∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) nh]i, i = 1, 2 we solve one time step of the diffusion equation
nh]i, i = 1, 2 we solve one time step of the diffusion equation
as − εΔ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) as = ah, as = ah, |
Validation
Instead of a full convergence study of the numerical approach we only test the smoothing of surface quantities. We consider a surface for which the surface quantities can be computed analytically. The surface is parametrized by X : [0,2π) × [0,π) →![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2,
2,We compute the L2-error of the surface quantities
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ,
, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , ∇
, ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) and ∇
and ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) for different grid widths h. The smoothing parameter ε is chosen experimentally such that it shows optimal results. Fig. 7 shows that for this test case the surface quantities converge with the optimal orders and that the additional smoothing step for all quantities improves the approximation. Together with the convergence studies in ref. 17 and 35 these results provide enough confidence in the numerical approach for the full problem including the higher order geometric terms. They require an appropriate resolution of
for different grid widths h. The smoothing parameter ε is chosen experimentally such that it shows optimal results. Fig. 7 shows that for this test case the surface quantities converge with the optimal orders and that the additional smoothing step for all quantities improves the approximation. Together with the convergence studies in ref. 17 and 35 these results provide enough confidence in the numerical approach for the full problem including the higher order geometric terms. They require an appropriate resolution of ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) and ∇
and ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , which is achieved in O(h2) and O(h), respectively. This motivated the considered discrete function spaces.
, which is achieved in O(h2) and O(h), respectively. This motivated the considered discrete function spaces.
Hausdorff distance
For two sets X, Y ⊂![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, we consider the Hausdorff distance given by
3, we consider the Hausdorff distance given bywhere d(x, M) = supm∈M‖x − m‖ and ‖·‖ is the Euclidean norm. In the implementation we use the VTK Hausdorff distance point set filter65 with the target distance method point to cell.
Acknowledgements
We acknowledge fruitful discussions with Patrick Zager (UCSF) and Veit Krause (TUD). This work was funded by DFG within FOR3013 “Vector- and tensor-valued surface PDEs”. We further acknowledge computing resources at FZ Jülich under Grant No. MORPHO and at ZIH under Grant No. WIR.References
- H. T. McMahon and J. L. Gallop, Nature, 2005, 438, 590–596 CrossRef CAS PubMed.
- M. Deserno, Chem. Phys. Lipids, 2015, 185, 11–45 Search PubMed.
- R. Lipowsky and R. Dimova, Soft Matter, 2021, 17, 214–221 RSC.
- W. Helfrich, Z. Naturforsch. C., 1973, 28, 693 CrossRef CAS PubMed.
- P. Canham, J. Theor. Biol., 1970, 26, 61 CrossRef CAS PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A:At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS PubMed.
- N. Bobrovska, W. Góźdź, V. Kralj-Iglič and A. Iglič, PLoS One, 2013, 8, e73941 CrossRef PubMed.
- N. Walani, J. Torres and A. Agrawal, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062715 CrossRef PubMed.
- A. Mahapatra and P. Rangamani, Soft Matter, 2023, 19, 4345–4359 RSC.
- M. D. Mitov, C. R. Acad. Bulg. Sci., 1978, 31, 513–515 Search PubMed.
- J. B. Fournier and P. Galatola, Europhys. Lett., 1997, 39, 225 Search PubMed.
- R. Capovilla, J. Guven and J. A. Santiago, J. Phys. A: Math. Gen., 2003, 36, 6281 CrossRef.
- T. Shemesh, A. Luini, V. Malhotra, K. N. Burger and M. M. Kozlov, Biophys. J., 2003, 85, 3813–3827 Search PubMed.
- M. Kaksonen and A. Roux, Nat. Rev. Mol. Cell Biol., 2018, 19, 313–326 Search PubMed.
- S. C. Al-Izzi, P. Sens and M. S. Turner, Phys. Rev. Lett., 2020, 125, 018101 Search PubMed.
- E. Bachini, V. Krause, I. Nitschke and A. Voigt, J. Fluid Mech., 2023, 977, A41 CrossRef CAS.
- M. Arroyo, L. Heltai, D. Millán and A. DeSimone, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17874–17879 CrossRef CAS PubMed.
- B. Winkler, I. S. Aranson and F. Ziebert, Commun. Phys., 2019, 2, 82 CrossRef.
- R. K. Sadhu, A. Iglič and N. S. Gov, J. Cell Sci., 2023, 136, jcs260744 Search PubMed.
- V. T. Ruhoff, N. Leijnse, A. Doostmohammadi and P. M. Bendix, Trends Cell Biol., 2024, 35, 129–140 CrossRef PubMed.
- H. De Belly and O. D. Weiner, Curr. Opin. Cell Biol., 2024, 89, 102392 Search PubMed.
- H. De Belly, S. Yan, H. B. da Rocha, S. Ichbiah, J. P. Town, P. J. Zager, D. C. Estrada, K. Meyer, H. Turlier and C. Bustamante, et al., Cell, 2023, 186, 3049–3061 CrossRef PubMed.
- S. R. Naganathan, S. Fürthauer, M. Nishikawa, F. Jülicher and S. W. Grill, eLife, 2014, 3, e04165 CrossRef PubMed.
- A.-C. Reymann, F. Staniscia, A. Erzberger, G. Salbreux and S. W. Grill, eLife, 2016, 5, e17807 CrossRef PubMed.
- H. B. da Rocha, J. Bleyer and H. Turlier, J. Mech. Phys. Solids, 2022, 164, 104876 CrossRef.
- A. Bhatnagar, M. Nestler, P. Gross, M. Kramar, M. Leaver, A. Voigt and S. W. Grill, Curr. Biol., 2023, 33, 5096–5108 CrossRef CAS PubMed.
- T. Itoh and K. Tsujita, Curr. Opin. Cell Biol., 2023, 81, 102173 CrossRef CAS PubMed.
- H. A. Faizi, R. Dimova and P. M. Vlahovska, Biophys. J., 2022, 121, 910–918 CrossRef CAS PubMed.
- M. Arroyo and A. DeSimone, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031915 CrossRef PubMed.
- A. Torres-Sánchez, D. Millán and M. Arroyo, J. Fluid Mech., 2019, 872, 218–271 CrossRef.
- A. Voigt, J. Fluid Mech., 2019, 878, 1–4 CrossRef CAS.
- S. C. Al-Izzi and R. G. Morris, Semin. Cell Dev. Biol., 2021, 120, 44–52 CrossRef PubMed.
- S. Reuther, I. Nitschke and A. Voigt, J. Fluid Mech., 2020, 900, R8 CrossRef CAS.
- V. Krause and A. Voigt, J. Comput. Phys., 2023, 486, 112097 CrossRef.
- M. Simunovic, G. A. Voth, A. Callan-Jones and P. Bassereau, Trends Cell Biol., 2015, 25, 780–792 CrossRef CAS PubMed.
- I. Derényi, F. Jülicher and J. Prost, Phys. Rev. Lett., 2002, 88, 238101 CrossRef PubMed.
- A. Roux, G. Cappello, J. Cartaud, J. Prost, B. Goud and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5394–5399 CrossRef CAS PubMed.
- P. G. Saffman and M. Delbrück, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113 CrossRef CAS PubMed.
- I. Nitschke, S. Reuther and A. Voigt, Phys. Rev. Fluids, 2019, 4, 044002 CrossRef.
- I. Nitschke and A. Voigt, Adv. Differ. Equ., 2025, 30, 335–420 Search PubMed.
- S. Reuther and A. Voigt, Multiscale Model. Simul., 2015, 13, 632–643 CrossRef.
- S. Reuther and A. Voigt, Multiscale Model. Simul., 2018, 16, 1448–1453 CrossRef.
- P. Brandner, A. Reusken and P. Schwering, Interface. Free Bound., 2022, 24, 533–563 Search PubMed.
- T. Biben and C. Misbah, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031908 CrossRef CAS PubMed.
- Y. Kim and M.-C. Lai, J. Comput. Phys., 2010, 229, 4840–4853 CrossRef CAS.
- D. Salac and M. J. Miksis, J. Fluid Mech., 2012, 711, 122–146 CrossRef.
- F. Haußer, W. Marth, S. Li, J. S. Lowengrub, A. Rätz and A. Voigt, Int. J. Biomath. Biostat., 2013, 2, 19–48 Search PubMed.
- S. Aland, S. Egerer, J. Lowengrub and A. Voigt, J. Comput. Phys., 2014, 277, 32–47 CrossRef PubMed.
- V. Krause and A. Voigt, J. R. Soc. Interface, 2024, 21, 20240056 CrossRef CAS PubMed.
- G. Dziuk and C. M. Elliott, Acta Numer., 2013, 22, 289–396 CrossRef.
- M. Nestler, I. Nitschke and A. Voigt, J. Comput. Phys., 2019, 389, 48–61 CrossRef.
- S. Vey and A. Voigt, Comput. Visualization Sci., 2007, 10, 57–67 CrossRef.
- T. Witkowski, S. Ling, S. Praetorius and A. Voigt, Adv. Comput. Math., 2015, 41, 1145–1177 CrossRef.
- T. R. Powers, Rev. Mod. Phys., 2010, 82, 1607–1631 CrossRef.
- R. E. Goldstein, P. Nelson, T. Powers and U. Seifert, J. Phys. II, 1996, 6, 767–796 CrossRef CAS.
- S. C. Al-Izzi, G. Rowlands, P. Sens and M. S. Turner, Phys. Rev. Lett., 2018, 120, 138102 CrossRef CAS PubMed.
- M. Janssen, S. Liese, S. C. Al-Izzi and A. Carlson, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2024, 109, 044403 CrossRef CAS PubMed.
- M. Nestler and A. Voigt, Proc. Appl. Math. Mech., 2023, 23, e202300044 CrossRef.
- I. Nitschke, S. Sadik and A. Voigt, IMA Journal of Applied Mathematics, 2023, 88, 917–958 CrossRef.
- J. W. Barrett, H. Garcke and R. Nurnberg, SIAM J. Sci. Comput., 2008, 31, 225–253 CrossRef.
- S. Praetorius and F. Stenger, Archive of Numerical Software, 2022, 6, 1–27 Search PubMed.
- P. Brandner, T. Jankuhn, S. Praetorius, A. Reusken and A. Voigt, SIAM J. Sci. Comput., 2022, 44, A1807–A1832 CrossRef.
- H. Hardering and S. Praetorius, IMA Journal of Numerical Analysis, 2023, 43, 1543–1585 CrossRef.
- F. Commandeur, J. Velut and O. Acosta, VTK Journal, 2011 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00202d |
| This journal is © The Royal Society of Chemistry 2025 |