Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Integration of generative machine learning with the heuristic crystal structure prediction code FUSE
Christopher M. Collins *ab,
Hasan M. Sayeed
*ab,
Hasan M. Sayeed c,
George R. Darling
c,
George R. Darling a,
John B. Claridge
a,
John B. Claridge a,
Taylor D. Sparks
a,
Taylor D. Sparks *c and
Matthew J. Rosseinsky
*c and
Matthew J. Rosseinsky *ab
*ab
aDepartment of Chemistry, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK. E-mail: rossein@liverpool.ac.uk; c.m.collins@liverpool.ac.uk
bLeverhulme Research Centre for Functional Materials Design, Materials Innovation Factory, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK
cDepartment of Materials Science and Engineering, University of Utah, 122 Central Campus Dr, Salt Lake City, Utah 84112, USA. E-mail: sparks@eng.utah.edu
First published on 30th May 2024
Abstract
The prediction of new compounds via crystal structure prediction may transform how the materials chemistry community discovers new compounds. In the prediction of inorganic crystal structures there are three distinct classes of prediction: performing crystal structure prediction via heuristic algorithms, using a range of established crystal structure prediction codes, an emerging community using generative machine learning models to predict crystal structures directly and the use of mathematical optimisation to solve crystal structures exactly. In this work, we demonstrate the combination of heuristic and generative machine learning, the use of a generative machine learning model to produce the starting population of crystal structures for a heuristic algorithm and discuss the benefits, demonstrating the method on eight known compounds with reported crystal structures and three hypothetical compounds. We show that the integration of machine learning structure generation with heuristic structure prediction results in both faster compute times per structure and lower energies. This work provides to the community a set of eleven compounds with varying chemistry and complexity that can be used as a benchmark for new crystal structure prediction methods as they emerge.
1 Introduction
In inorganic materials chemistry, the discovery of new materials can be guided by crystal structure prediction (CSP). The use of CSP in the discovery of new compounds allows for experimental researchers to focus their efforts only on those compositions which are likely to yield new crystalline phases, greatly accelerating the speed with which they can be found.1,2 There are three main approaches to the crystal structure prediction problem. Firstly, well established codes based on heuristic algorithms which evolve crystal structures from a starting point, such as FUSE,3 which is based on a basin hopping algorithm, or USPEX4 based upon genetic algorithms. Also within this class of structure search is the particle swarm optimisation method CALYPSO.5 Related to this are random structure search methods which use randomly generated structures, constrained with a set of chemical rules, such as the code AIRSS.6A second, recently emerging approach to the prediction of crystal is through the use of machine learning (ML) models. ML structure generation making use of now well-curated structure databases, such as the Materials Project7 or ICSD,8 to train models to rapidly generate plausible crystal structures for inorganic solids. These models include the use of graph neural networks,9 diffusion models10 or large language models.11 ML models have reached the point where they can efficiently generate large numbers of plausible crystal structures for a target composition. However, when such models are used far from their training data, or for non-trivial compositions they frequently fail to produce the correct structure, or a structure which can be relaxed into the ground state with a conventional chemistry calculation, for example with density functional theory (DFT). A final, newly emerging approach is that of mathematical optimisation, where the structure prediction problem is constructed as a series of linear equations, which can then be solved. Within the constraints of how the problem is formulated, this then provides a guarantee that the global minimum structure has been located.12
The types of heuristic methods for crystal structure prediction mentioned above are all dependent on an algorithm to generate initial structure(s) with an element of randomness that then evolve in some specified way. The initial structures can be produced using simple rules, for example randomly selecting a unit cell then populating it with atoms with minimum inter-atomic distance constraints, or with more complex rule sets based upon knowledge of inorganic chemistry, as used, e.g., in FUSE having structures assembled from randomly generated blocks using rules based on how such blocks connect in known compounds. Hereafter, we refer to all of these methods to generate trial crystal structures as “random structure generation”, in contrast to structures generated by ML models. Once structures are generated, they are optimised into their nearest energy minimum according to the forces acting on the atoms calculated using well-established chemistry methods, such as the Density Functional Theory (DFT) code VASP,13 referred to here as local optimisation. The vast majority of the computational costs of heuristic crystal structure prediction methods lie in these local optimisation steps, with the total cost very closely aligned with how close the initially generated structures are to local minima on the potential energy surface.
In this work we demonstrate a new hybrid approach to CSP: to use ML models to generate initial crystal structures for a given composition in place of the conventional random structure generation. We integrate this ML model into the heuristic CSP code FUSE, and demonstrate usage across eleven compounds: eight known compounds, and three hypothetical. We hypothesise that the inclusion of ML generated crystal structures can yield two potential benefits to CSP:
1. As ML generated structures should be close to plausible crystal structures, they should be closer to minima on potential energy surfaces and so reduce the computational cost per structure.
2. ML generation models will on average produce structures which are closer to ground state structures and so will reduce the energy of the global minimum structure located by FUSE within a similar amount of compute time when compared to using random structure generation.
2 Methods
2.1 Generative machine learning model
In this section, we delve into the intricacies of the retrained machine learning model, adapted from the original paper,9 specifically designed for crystal structure prediction utilizing a graph network (GN) in conjunction with an optimization algorithm (OA). The original framework comprised three essential components: a database, a GN model, and an OA for accelerated crystal structure search.The crystal graph used in the original GN was defined by nodes (vi), edges connecting nodes (ek), and global attributes (u), representing atoms, pairs, and macroscopic attributes, respectively. The crystal graph was numerically represented by G({vi}i=1,nv,{ek}k=1:ne,u), where vi and ek are elemental and pair attributes, and nv and ne are the number of atoms and pairs in the cell. The GN model is equipped with elemental embeddings and pair features, which are learned during the training process on two benchmark databases: the open quantum materials database (OQMD)14,15 and Matbench (MatB).16 An embedding layer and a matrix were added to accommodate atomic attributes and pair connectivity, respectively. The GN model consisted of MEGNet17 layers and set2set layers to update the elemental and pair matrices. The GN model, trained separately on OQMD and MatB, resulted in two models, GN(OQMD) and GN(MatB), with the latter demonstrating superior performance in CSP despite having slightly higher mean absolute error (MAE) during training.
Two benchmark datasets, OQMD and MatB, were employed for GN model training and evaluation. Data cleaning was performed to ensure reliability and comparability, and the datasets were split into training, validation, and test sets following a consistent ratio. The trained GN models, GN(OQMD) and GN(MatB), were selected based on hyperparameter optimization to minimize errors between GN-predicted and density functional theory (DFT)-calculated formation enthalpies (ΔH) on the test set.
To enhance the efficiency of CSP, a symmetry constraint was incorporated, taking into account the observed prevalence of symmetry in experimental crystal structures, particularly at low temperatures. Additional structural features, crystal symmetry S and the occupancy of Wyckoff position Wi, were incorporated, allowing for CSP with symmetry constraints. Symmetry operations were chosen from the 229 space groups after P1, and Wyckoff positions were selected accordingly. The procedure ensured the generation of symmetrical crystal structures during CSP.
Three optimization algorithms (OAs) – random searching (RAS), particle-swarm optimization (PSO), and Bayesian optimization (BO) – were adopted for CSP. BO, specifically implemented with a Gaussian mixture model based on the tree of Parzen estimators, demonstrated superior performance in efficiently exploring the structural space. The GN-OA approach iteratively generated and evaluated crystal structures until convergence, with BO demonstrating superior performance due to its effective balance between exploitation and exploration.
Given its superior performance, we opted to retrain the GN(MatB)-BO model specifically for our use case. An illustration of the model architecture that was chosen to be trained is shown in Fig. 1. The retraining process involved the direct adoption of the GN model from the original paper, with no hyperparameter tuning. The training, conducted on a “Tesla A100” GPU with 2 GPU devices per node and utilizing 80 GB global memory, proceeded until the 479th iteration step, achieving a validation MAE of 0.034786 eV per atom. The original model was directly adopted without additional evaluation, aligning with the reported results from the original paper.
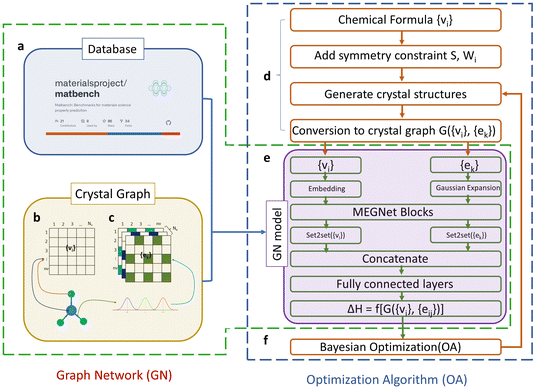 | ||
| Fig. 1 (a) The GN model was trained using the MatBench benchmark dataset. The input atomic feature for the crystal graph is (b) embedded atomic number (1 to Nv) for each compositional atom (1 to nv) and the input pair feature is (c) Gaussian-expanded distance (1 to Ne) for each pair connecting atom i (1 to nv) and atom j (1 to nv). (d) The structural generation phase encompasses adding symmetry constraints, generating structures, and converting them into crystal graphs. (e) The GN model integrates embedded atomic numbers, Gaussian-expanded pair distances, MEGNet blocks, set2set layers for atomic numbers and pair distances, a concatenation layer, and a fully connected layer to derive the correlation model between a crystal and its formation enthalpy. (f) A Bayesian Optimization block is included. This figure was adapted from ref. 9. | ||
In the next section, we discuss the integration of this ML model with FUSE, elucidating how this combination enhances overall performance.
2.2 New implementation of the FUSE method
For clarity, we refer to version 1 of the code as the original implementation, which functions as detailed in ref. 3. FUSE predicts crystal structures by assembling them from small blocks containing 0–4 atoms, which are in turn assembled into layers (referred to as modules), that are stacked to construct a full crystal structure. In the original implementation of the code, the sub-modules are generated according to a pre-designed set of eight possible motifs, with defined options for the angles of the sub-module, which are dependent on the Bravais lattice type for the assembled structure (itself, selected at random), allowing FUSE to assemble sub-modules and therefore whole structures with flexible unit cell angles. The size of the sub-module in Angstroms is based upon the sum of the atomic radii of the elements in the system: Ip = 2(RCat + RAn) where RCat is the mean cation radii and RAn is the mean anion radii. If oxidation states are not supplied, the code uses Ip = 4Rat where Rat is the mean atomic radius. The size of the sub-module is then set to be equal to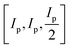 .
.
For FUSE to be able to use the output of generative ML models in place of randomly generated structures, the code required altering such that it is possible to decompose any arbitrary crystal structure into a set of constituent sub-modules that can then be used in the code's basin hopping routine. The ability to do this for any arbitrary crystal structure will greatly increase the flexibility of the sub-modules that FUSE is able to use.
The new implementation of the code (written in python 3) starts by computing the size of a sub-module based upon the atomic radii within the composition as described above. Then along each of the three unit cell axes, FUSE calculates the nearest integer number of sub-modules along each direction. The resulting sub-modules are then populated by extracting atoms from the starting structure according to their fractional atomic co-ordinates. The angles for the sub-module are inherited from the unit cell of the structure being broken down. The stacking direction is taken as c axis of the parent crystal structure. For example, as shown in Fig. 2, FUSE calculates the size of a sub-module for Ca3Al2Si3O12 (ref. 18) to be 4.24 × 4.24 × 2.12 Å. This sub-module size equates to the full structure being broken down into 54 sub-modules, in a 3 × 3 × 6 grid. Corresponding to the structure being broken down into 6 modules, with each module comprising of 3 × 3 × 1 sub-modules.
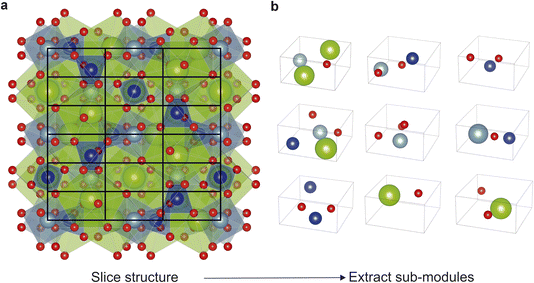 | ||
| Fig. 2 (a) Example of FUSE2 selecting a module shape to slice the known garnet compound Ca3Al2Si3O12,18 based upon creating sub-modules with the lattice parameter 4.24 × 4.24 × 2.12 Å, derived from atomic radii as outlined in Methods. FUSE2 slices the structure with a grid of 3 × 3 × 6, yielding a total of 54 sub-modules within the structure. (b) The first nine sub-modules extracted from the structure of Ca3Al2Si3O12, illustrating the diversity of sub-modules when compared to those in the previous version of FUSE, restricted to one of only eight possible motifs. Atoms coloured as follows: Ca (green), Al (cyan), Si (blue), O (red). | ||
Therefore when FUSE is extracting a sub-module with the position x, y, z on the grid for the above, it will use all atoms with the fractional co-ordinates within the range: 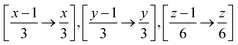 . The crystal structure now broken down into the constituent sub-modules can then be evolved using a basin hopping routine similar to that in the original implementation of the code. The flowchart for the new implementation of FUSE is shown in Fig. 3.
. The crystal structure now broken down into the constituent sub-modules can then be evolved using a basin hopping routine similar to that in the original implementation of the code. The flowchart for the new implementation of FUSE is shown in Fig. 3.
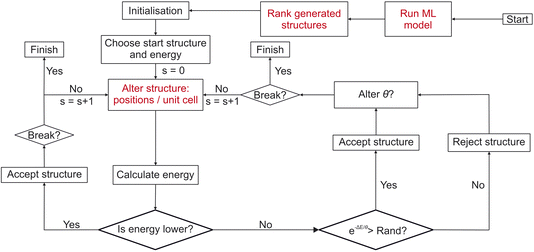 | ||
| Fig. 3 Flowchart detailing the workflow of FUSE2 as presented in this work. Red sections indicate where FUSE has been modified for this work. “Run ML model”: the trained gn-boss model presented in this work is run for the given composition, to generate potential crystal structures for use in the main CSP search. “Rank generated structures”: in order to remove non-physical structures which are generated (as a result of noise in the model), the generated structures are re-ranked using a statistical proxy potential19 (see Methods), structures are then fed into the initial population for FUSE2 using this re-ranking, remaining structures from the ML generated population may then be used later in the “Alter structure” stage. “Alter structure: positions/unit cell”: here the basin hopping move which would generate a random new structure is replaced by using remaining structures from those generated using the ML model, if none remain, FUSE2 reverts back to using the original version of the random structure generator. | ||
In the new implementation of FUSE, at the start of a structure prediction run, the code will run the ML model, outlined in Section 2.1 generating a user specified number of crystal structures for each number of formula units specified by the use in the input file, using the specified optimizer and range of space groups. To remove un-physical structures generated by the ML models (generated as a result of noise within the model), an option to re-rank the generated structures has been included. In this work, ML generated structures are re-ranked using universal, statistical inter-atomic proxy potentials19 (SPP), derived from all ordered crystal structures within the ICSD. The structures which can be successfully computed at the ranking stage are then compiled into a pool of structures which the basin hopping routine can access. Once structures have been generated and ranked, in order to proceed with the basin hopping search routine used in FUSE, the code needs to assemble the initial population of structures. The population is assembled by taking the top x structures (where x is a user defined initial population) from the ML generated pool, which are then broken down into their sub-modular structures as outlined above, and their energies calculated using the user chosen method. If the ML generator fails to produce x structures which FUSE is able to rank, it will revert to generating additional structures using the original structure generation algorithm to complete the initial population. With the new implementation of FUSE, all crystal structures can now be symmetrised prior to any geometry optimisation using the python spglib library, as this reduces the occurrence of crystal structures with very flat shapes, which can be slow to compute with computational chemistry codes. After the structure has been parsed by spglib (if used), the calculation proceeds with no symmetry imposed during the local optimisation in P1 symmetry. The basin hopping routine then progresses in the same manner as per the original implementation, with the following move types written to work with this implementation (presented in order in which they are in the code), the probability of the code using each move is definable by the user, by default there is an equal probability of using each:
1. Swap the position of two atoms: locate two atoms of different species within the crystal structure and swap their positions, this move is not used if the composition is elemental.
2. Swap an atom into a vacant space within the structure: first choose an atom in the structure, then locate a space within the crystal structure which is more than x Å from any other atom, and move it into this space. Where x is a user specified distance used within the code as a threshold for atom–atom contacts which are too short, the default value is 1 Å.
3. Swapping the position of i atoms, where n > i > 2 where n is the total number of atoms within the structure. This move is not used if the composition is elemental, or the structure contains fewer than 4 atoms.
4. Swapping the positions of i atoms, where n > i > 2, as with move 3. But allowing atoms to move into vacant spaces within the structure as defined in move 2.
5. Swap the positions of all of the atoms within the structure, this move is not used if the composition is elemental.
6. Swap the positions of all of the atoms within the structure, allowing for atoms to be moved into vacant positions as outlined in move 2.
7. Swap the position of two sub-modules: swap the location of two sub-modules from within the crystal structure.
8. Swap the position of two modules within the structure.
9. Generate a new unit cell shape for the sub-modules within the current structure. This move reshapes the sub-modules of the current structure into a new unit cell shape, with the shape randomly determined according to the original implementation of FUSE.
10. Mutation of the structure: inspired by genetic algorithms, the code selects a sub-module from the current structure and modifies the positions of the atoms within it. Currently, the only option, is for the code to select a sub-module with <5 atoms, and move their fractional co-ordinates to match one of the original sub-module motifs from the original implementation of FUSE.
11. Double the current structure along one axis. Providing the current structure is ≤ half the maximum number of atoms permitted from the input file, the structure will be doubled along one randomly selected crystallographic axis. For the new part of the crystal structure there is an even chance to: repeat the structure, translate the structure by 0.5 fraction co-ordinates in the plane perpendicular to the direction chosen, invert the atomic co-ordinates, about the centre of the plane through which the structure has been doubled or mirror the structure through a mirror plane in the face through which the structure has been doubled.
12. Triple the crystal structure along one axis. Providing the number of atoms within the current structure is ≤ than one third of the maximum atoms permitted in the input file, the code will triple the current structure along one crystallographic axis. When the structure is tripled, there is an equal probability to: repeat the structure along the chosen axis or to translate the atomic co-ordinates of each new set of atoms by one third in the plane perpendicular to the direction in which the structure is being extended.
13. Generate a random new structure up to the size of the current structure. The current structure is replaced by a new random structure, with an equal probability to select a structure from the pool of ML generated structures if unused structures are available, or to generate a new structure using the algorithm used in the original implementation of FUSE.
14. Generate a random new structure up to the maximum size permitted from the input file. An identical copy of move 13, with the maximum number of atoms raised to be equal to the maximum number of atoms within the input file.
This new implementation of FUSE is hereafter referred to as FUSE2.
3 Results
3.1 Calculation setup
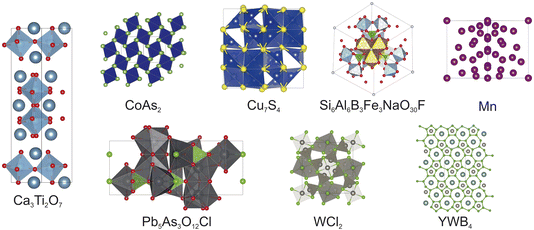
The experiments outlined below were designed to test FUSE2 with both a range of different chemistries and varying complexity. In order to do this, all of the compositions have been chosen with system sizes and target crystal structures which are non-trivial for FUSE2 to calculate, therefore it is unlikely to predict the precise crystal structures within the compute time available. This is a result of the combination of the range of number of formula units available in the search space and the complexity of the target crystal structures. For our first test, we explored a range of eight compounds, with known experimentally reported ordered crystal structures: Ca3Ti2O7,20 CoAs2,21 Cu7S4,22 Mn,23 Pb5As3O12Cl,24 Si6Al6B3Fe3NaO30F,25 WCl2,26 and YWB4,27 the target crystal structures are shown in Fig. 4. Each of the reported crystal structures has a primitive unit cell which consists of 50 atoms or fewer. To ensure that any benefits observed using ML structure generation are not from the model purely recalling structures from training data, the same experiments detailed above were performed for three hypothetical compounds which have been studied previously: Li2Sn2S3Cl4, Li3Si3O5Cl5 and Li4OBrCl.19 In practice, FUSE is used to rapidly predict approximate probe structures2 for a range of compositions which can be used to predict the energy landscape of compositional phase fields, without explicitly predicting the exact ground state structure. When used in this way, using DFT as the energy calculator, the formula units and number of atoms are typically limited to 20–30 atoms.For each of the compositions tested in this work, the same set of four experiments with FUSE2 have been performed:
1. “fgen”: as our baseline experiment, FUSE2 is run without using the ML model outlined in Section 2.1, all crystal structure are therefore generated as in the original version of the code, using the original random unit cell selection and sub-module motifs to populate the unit cell. Local optimisation is then only performed using VASP. This experiment is similar to structure prediction runs using the original implementation of FUSE.
2. “mlgen”: the initial population of crystal structures is generated using the ML model in 2.1. The ML generated structures are ranked using SPPs and the top x structures selected and broken down into their sub-modules. The remaining ML structures which do not form the initial population of structures then form a pool of structures which may be introduced into the search via moves 13 and 14 outlined above. Local optimisation is then only performed using VASP.
3. “fgen-SPP”: as experiment 1, but local optimisation is performed in two stages: (1) structures are locally optimised using SPPs and (2) the SPP optimised structure is then re-optimised using VASP, with the final energy taken from VASP.
4. “mlgen-SPP”: as experiment 2, but local optimisation is performed in two stages: (1) structures are locally optimised using SPPs and (2) the SPP optimised structure is then re-optimised using VASP, with the final energy taken from VASP.
For each of the experiments performed in this work, the same approximate quantity of computing time has been allocated; note that this means that due to the differences in the compute time required per structure (see below), each experiment will not have explored the same number of individual crystal structures. In total, for the experiments below approximately 1.5M core hours were used, equally distributed among all experiments, with all experiments for a given composition performed on the same high performance computing cluster to ensure a fair comparison between experiments. For all of the timings discussed below where the ML structure generation is used, the computational cost of running the ML model for the initial structure generation is not factored in, as this a constant value and the amount this contributes towards the overall runtime is minimal. In this work, the ML structure generation and ranking for each run of the code uses between 2–16 core hours (approximately 600 core hours in total), compared to the total CPU time budget of 1.5M core hours.
For each of the compositions described below (see Tables 1 and 3), a maximum limit of 50 atoms per structure was used, with an initial population of 25 structures. For each experiment, three independent runs of FUSE2 were performed, replicating a typical use case, and the lowest energy from the combined results of each experiment is reported. For timings, the run times across all three runs are aggregated, along with the total number of structures to produce a mean run time. For all but one of the FUSE2 experiments described below, where ML generated structures were used, 5000 structures were generated per formula unit, using the Bayesian optimisation search which is integrated into the ML model (see Section 2.1) with only triclinic symmetries used. For each composition, the ML model was run for up to 8 formula units, or the highest number of formula units which is less than the set limit of 50 atoms. In the case of Si6Al6B3Fe3NaO30F, where only one formula unit could be used, 7500 structures were generated.
Where SPPs are used in both the ranking and pre-optimising structures prior to optimisation with DFT, all structures were relaxed to their nearest minimum, with forces optimised until the normalised gradient of the forces was < than 0.1, computed using GULP.28 DFT calculations were performed for all structures within searches, using the density functional theory code VASP13 with conventional PBE pseudo-potentials,29 for a total of 220 steps or until the forces are below 0.03 eV Å−1, Γ-centred k-point grids are generated using the “KSPACING” setting in VASP, with the value at the final step of the calculation of 0.3. The plane-wave cutoff was set for each composition to be 1.3× the maximum plane wave energy from the pseudo-potentials.
For each of the four experiments described above, two key performance metrics were used: the mean time taken to obtain an energy for each individual structure and the lowest energy obtained from any run of each experiment.
3.2 Results
For six of the eight compounds tested, Ca3Ti2O7, Cu7S4, Mn, Pb5As3O12Cl, Si6Al6B3Fe3NaO30F and WCl2, the mlgen-SPP configuration proved to be the fastest in time per structure, with the fastest speed-up relative to the baseline fgen experiment for WCl2 of 8.3, and the slowest speed up is for Mn of 1.5 (Table 1). The mlgen experiment was fastest for CoAs2, with a speed increase of 3.9. For Cu7S4 the mlgen experiment had the same speed up factor as for the mlgen-SPP experiment above. For the compound YWB4, none of the experiments tested here were able to provide a speed up relative to the fgen experiment, where the mlgen was the slowest, decreasing the time per structure by a factor of 10.| Composition | fgen-SPP | mlgen | mlgen-SPP |
|---|---|---|---|
| Ca3Ti2O7 | 1.3 | 1.4 | 2.9 |
| CoAs2 | 0.4 | 3.9 | 2.0 |
| Cu7S4 | 0.5 | 1.9 | 1.9 |
| Mn | 1.4 | 0.9 | 1.5 |
| Pb5As3O12Cl | 3.3 | 2.2 | 5.3 |
| Si6Al6B3Fe3NaO30F | 2.1 | 1.8 | 3.3 |
| WCl2 | 1.5 | 2.2 | 8.3 |
| YWB4 | 0.7 | 0.1 | 0.5 |
The second metric used to compare the different experiments is the lowest energy which was obtained from each experiment as shown in Table 2. For all eight compositions, the lowest energies were obtained from experiments starting from crystal structures generated using the ML model. For two compositions Cu7S4 and Mn both the mlgen and mlgen-SPP experiments obtained the same energy, and for Pb5As3O12Cl and CoAs2 the lowest energies were obtained by the mlgen experiment. For the compositions Ca3Ti2O7, Si6Al6B3Fe3NaO30F and WCl2 the lowest energy was obtained by the mlgen-SPP experiment. For YWB4, both the baseline fgen and mlgen-SPP experiments have obtained equal energies.
| Composition | fgen | fgen-SPP | mlgen | mlgen-SPP |
|---|---|---|---|---|
| Ca3Ti2O7 | −7.69 | −7.64 | −7.69 | −7.73 |
| CoAs2 | −5.55 | −5.43 | −5.62 | −5.57 |
| Cu7S4 | −3.97 | −4.01 | −4.03 | −4.03 |
| Mn | −8.93 | −8.92 | −8.93 | −8.93 |
| Pb5As3O12Cl | −5.31 | −5.55 | −5.59 | −5.56 |
| Si6Al6B3Fe3NaO30F | −7.03 | −7.09 | −7.01 | −7.37 |
| WCl2 | −5.94 | −6.12 | −6.03 | −6.14 |
| YWB4 | −8.14 | −8.12 | −7.79 | −8.14 |
For each of the three hypothetical compounds tested in this work, which are un-reported experimentally, the mlgen-SPP experiment showed the fastest speed-up, with the smallest speedup being for Li2Sn2S3Cl4 with a speed up factor of 3.7 (Table 3). The fastest speedup was for the composition Li4BrOCl, with a speedup factor of 6.3. For two of the compositions in this section, the lowest energy structure was obtained by one of the experiments using ML generated structures. For the two compositions Li2Sn2S3Cl4 and Li3Si3O5Cl5 the lowest energy structure was obtained by the mlgen-SPP experiment. The lowest energy structures from the mlgen-SPP experiments are shown in Fig. 5. For Li4OBrCl, the lowest energy was obtained by all four experiments (Table 4).
| Composition | fgen-SPP | mlgen | mlgen-SPP |
|---|---|---|---|
| Li2Sn2S3Cl4 | 1.0 | 2.3 | 3.7 |
| Li3Si3O5Cl5 | 1.5 | 3.1 | 5.0 |
| Li4OBrCl | 5.3 | 4.6 | 6.3 |
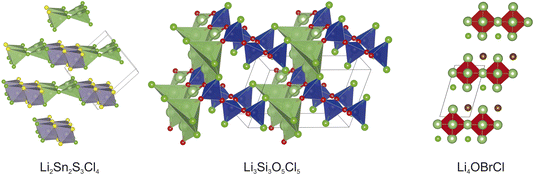 | ||
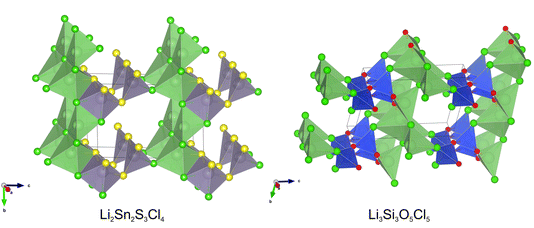
| Fig. 5 The minimum energy structures obtained for the three hypothetical compounds tested in this work, obtained from the mlgen-SPP experiment. | ||
| Composition | fgen | fgen-SPP | mlgen | mlgen-SPP |
|---|---|---|---|---|
| Li2Sn2S3Cl4 | −3.66 | −3.73 | −3.78 | −3.80 |
| Li3Si3O5Cl5 | −5.20 | −4.85 | −5.50 | −5.55 |
| Li4OBrCl | −4.05 | −4.05 | −4.05 | −4.05 |
3.3 Implementation of machine learnt inter-atomic potential ChgNET
The creation of well-curated databases of density functional theory calculations such as those used above to train the gnboss model has also led to the development of a number of machine learnt inter-atomic potentials. In FUSE2, we have implemented an energy calculator using the readily available ChgNET potential.30 This calculator can be used in the same fashion as either of the other energy calculators within FUSE2: they can be used in isolation, or as part of a tiered approach to calculations as with the SPP potentials in the previous sections, using any combination of potentials implemented in GULP, ChgNET and VASP. In this section, we demonstrate the use of ChgNET within FUSE2, in the same fashion as SPP potentials above, using DFT to obtain final energy rankings. Experiments were performed on the two putative compositions Li3Si3O5Cl5 and Li2Sn2S3Cl4, two additional experiments have been performed for each of the two compositions, using ChgNET v.3.2, with the experiments using the original FUSE structure generator and the ML structure generation referred to as fgen-ChgNET and mlgen-ChgNET respectively. The composition Li4OBrCl was omitted as in the previous section all of the experiments agree on the same ground state, and was trivial to locate.For these four experiments, 24.6K CPU hours of compute time was used, with each generator using the same amount of CPU time within each composition. For the ChgNET part of the structure relaxations, the structure was relaxed until the maximum force acting on the atoms was less than 0.05 eV Å−1, or 2000 ionic steps had passed. The resulting structures were then re-optimized using VASP as outlined above. The remaining setup of the experiment then remained the same as for the fgen-SPP and mlgen-SPP experiments listed above, with the exception that ranking the ML generated structures. Only single point calculations were used with ChgNET, as a result of preliminary testing, where attempting relaxations on ML generated structures failed due to isolated atoms within some structures (defined within ChgNET as having a distance of greater than 6 Å to its nearest neighbour), with this failure often resulting in ChgNET crashing and making FUSE2 runs unstable. In future versions of FUSE we will include filters prior to structures being passed to ChgNET to avoid this issue, allowing for ML generated structures to be optimised at this stage. The results for these experiments are shown in Table 5. It was observed that in both cases the mlgen-ChgNET increases the speed of optimising crystal structures by 5 and 1.7 times for the Li2Sn2S3Cl4 and Li3Si3O5Cl5 compositions relative to the fgen-ChgNET experiments respectively. It was also observed that all four of the experiments using ChgNET to pre-optimise structures resulted in lower energy structures (structures shown in Fig. 6). This result, when combined with the observations in the previous section, continue to demonstrate that the use of ML based structure generation with heuristic structure prediction methods, results in a significant increase in the speed of calculations. Our observations with using both a data driven potential (SPPs) and machine learnt potential (ChgNET), additionally suggest that the speed increases are generally complementary to each other rather than in competition.
| Composition | mlgen-ChgNET speed-up | fgen-ChgNET energy | mlgen-ChgNET energy |
|---|---|---|---|
| Li2Sn2S3Cl4 | 5.0 | −3.79 | −3.80 |
| Li3Si3O5Cl5 | 1.7 | −5.57 | −5.58 |
 | ||
| Fig. 6 The lowest energy structures obtained in experiments running FUSE2 using ChgNET30 in place of SPPs, combined with VASP for the compositions Li2Sn2S3Cl4 and Li3Si3O5Cl5. | ||
4 Discussion and conclusion
When the results for both experiments listed above are combined, it is observed that replacing the random structure generation within FUSE with structures generated from ML models provides a significant advantage in the majority of the experiments tested within this work. Firstly, the structures generated require considerably less computational time to optimise into the nearest minimum. When comparing only the structure generators (fgen vs. mlgen experiments), the mean speedup across the whole suite of tests is a factor of 2.2 times faster. This speed up factor still applies in the case when comparing the two experiments where as generated structures are pre-optimized using our SPPs (fgen-SPP vs. mlgen-SPP) where the mean speed up between the two structure generators is a factor of 2. Equally, when comparing both structure generation methods, using SPPs to pre-optimise structures, we still observe a speed up for six of the eight known compounds and all three of the hypothetical compounds, with a mean speed up of 2.3, with the fastest acceleration observed for CoAs2. However, for the compound YWB4, we observe a dramatic slowdown, being an order of magnitude slower than the fgen experiment. An explanation for this slowdown is that when the ML generated structures are ranked using SPPs, that ranking guides the initial population towards structures which are actually very far from the DFT local minima and so are very slow to converge, and we hypothesise that this composition could benefit from learning a SPP which is more aligned with this specific chemistry, over using the generic SPPs. When the combined use of the ML structure generation with our SPPs is compared against our baseline experiment (fgen vs. mlgen-SPP), we observe a mean speed up of a factor of 3.8. However, with the fgen vs. mlgen-SPP comparison, we note that the fastest speed up is up to 8.3 times faster. We do however, observe that specifically for the composition YWB4 that the original random structure generation routine remains superior to the ML generation when considering the total time taken to optimise crystal structures.Examining the results of the experiments in terms of the energies obtained, for the majority of experiments, the lowest energy structure was obtained by an experiment using the ML structure generation. This is with the exception of the composition YWB4, where both the fgen and mlgen-SPP experiments were tied and Li4OBrCl where all four experiments obtained the same energy minimum. The largest difference comes for the composition Si6Al6B3Fe3NaO30F, where the mlgen-SPP experiment obtains an energy 338 meV per atom lower than obtained by the baseline fgen experiment.
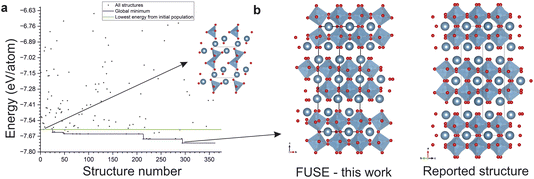
The experiments using the ML structure generation in this work demonstrate the benefits of integrating ML structure generation to create a combined CSP method which is superior to using purely ML structure prediction or heuristic methods. In 58 out of the 66 calculations making up the main mlgen based experiments in the Results section (11 compositions, with 6 mlgen experiments per composition) the lowest energy structure is not obtained in the starting generation of structures generated with ML, it is arrived at by the basin hopping within FUSE2, demonstrating the benefits of combining ML structure generation with heuristic CSP to obtain lower energy structures for a given composition (Table 6). Of all 66 runs, the mean improvement over the ML generated starting structures is 155 meV per atom, with a standard deviation of 209 meV per atom. The large standard deviation comes from the wide range of improvements, from the 8 runs where the improvement is zero, and the largest improvement is for one run of WCl2 in the mlgen-SPP experiment, where the basin hopping improved the energy from the initial population by 969 meV per atom. This is demonstrated by the composition Ca3Ti2O7 in the mlgen-SPP experiment, where the lowest energy structure from the initial population generated by ML has an energy of −7.61 eV per atom, during the basin hopping routine, FUSE2 is then reduces the energy to −7.73 eV per atom, a reduction of 112 meV per atom shown in Fig. 7. We have implemented the recently developed machine learnt potential ChgNET, demonstrating that the speed advantage between the two structure generation methods presented in this work is maintained, using our ML structure generation and ChgNET, we obtained lower energies than were obtained in the main study in this work, demonstrating the advantages of combining both ML structure generation, data derived potentials and heuristic CSP methods.
| Composition | mlgen mean difference | mlgen-SPP mean energy difference |
|---|---|---|
| Ca3Ti2O7 | −34 | −92 |
| CoAs2 | −191 | −150 |
| Cu7S4 | −3 | −4 |
| Mn | −29 | −207 |
| Pb5As3O12Cl | −198 | −225 |
| Si6Al6B3Fe3NaO30F | −22 | −214 |
| WCl2 | −182 | −928 |
| YWB4 | 0 | −224 |
| Li2Sn2S3Cl4 | −54 | −70 |
| Li3Si3O5Cl5 | −213 | −340 |
| Li4OBrCl | −22 | −19 |
In conclusion, we have demonstrated how data driven approaches to materials modelling can be integrated with conventional heuristic CSP methods to create a new implementation of our CSP method FUSE. Our results overall demonstrate that the integration of ML structure generation with heuristic CSP results in a speed up of up to 8 times vs. our baseline experiment and is able to obtain lower energy structures. As part of our demonstration, we have curated a set of eleven compounds (eight known, three hypothetical), which present a challenge to modern CSP methods, and so can be used as a benchmark set for the wider structure prediction community. We have demonstrated that FUSE2, provides a CSP platform to use both data driven structure generation and derived potentials, written in python, creating an open platform where researchers can readily integrate new models. As FUSE2 is developed in the future, we envision the development of better ML models to generate our initial structures either through tuning the existing model, or the adoption or development of new ML structure generators, as well as the implementation of new ML interatomic potentials as they become available. Additional improvements are envisioned to the core code through both the development of new move options for the basin hopping routine and through the implementation of reinforcement learning to guide the code on the weights to use for each of the available move types, as we have recently implemented for the original version of the code,31 and the integration of mathematical optimisation to contribute to the construction of structures and determine when to stop a calculation.12 FUSE2 will enable accelerated CSP across solid state inorganic chemistry, which will only continue to improve as new and better data driven ML models for inorganic chemistry are created alongside future development of the code.
Data availability
FUSE2 (version 2.02) is available on GitHub here: https://github.com/lrcfmd/FUSE-stable, this version of the code includes a copy of the pre-trained ML model used for the structure generation in this work, alongside a library of the SPPs used within this work. Example input scripts and the output structures for all of the experiments presented in this work are also provided.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
We thank the Leverhulme Trust for funding through the Leverhulme Research Centre for Functional Materials Design (RC-2015-036). Computer time was provided via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431 and EP/X035859), this work used the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/T022213 and EP/W032260) using the YOUNG service. Computer time was also provided by the EPSRC's Cirrus service, funded by EPSRC (grant EP/V026887/1). M. R., J. C. and G. D. thank EPSRC for funding through the grant EP/V026887/1. We thank the University of Liverpool for additional computing resources. Images of crystal structures were generated using the VESTA visualisation software.32References
- C. M. Collins, et al., Discovery of a low thermal conductivity oxide guided by probe structure prediction and machine learning, Angew. Chem., Int. Ed., 2021, 60, 16457–16465, DOI:10.1002/anie.202102073.
- C. Collins, et al., Accelerated discovery of two crystal structure types in a complex inorganic phase field, Nature, 2017, 546, 280–284, DOI:10.1038/nature22374.
- C. Collins, G. R. Darling and M. J. Rosseinsky, The Flexible Unit Structure Engine (FUSE) for probe structure-based composition prediction, Faraday Discuss., 2018, 211, 117–131, 10.1039/C8FD00045J.
- A. R. Oganov and C. W. Glass, Crystal structure prediction using ab initio evolutionary techniques: Principles and applications, J. Chem. Phys., 2006, 124, 244704, DOI:10.1063/1.2210932.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A method for crystal structure prediction, Comput. Phys. Commun., 2012, 183, 2063–2070, DOI:10.1016/j.cpc.2012.05.008.
- C. J. Pickard and R. J. Needs, Ab initio random structure searching, J. Phys.: Condens. Matter, 2011, 23, 053201, DOI:10.1088/0953-8984/23/5/053201.
- A. Jain, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002, DOI:10.1063/1.4812323.
- Crystallographic databases edited by F. H. Allen, G. Gergerhoff and R. Sievers. Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 680, DOI:10.1107/S0108768188099641.
- G. Cheng, X.-G. Gong and W.-J. Yin, Crystal structure prediction by combining graph network and optimization algorithm, Nat. Commun., 2022, 13, 1492, DOI:10.1038/s41467-022-29241-4.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, Crystal diffusion variational autoencoder for periodic material generation, arXiv, 2022, preprint, arXiv:2110.06197, DOI:10.48550/arXiv.2110.06197.
- L. M. Antunes, K. T. Butler and R. Grau-Crespo, Crystal structure generation with autoregressive large language modeling, arXiv, 2023, preprint, arXiv:2307.04340, DOI:10.48550/arXiv.2307.04340.
- V. V. Gusev, et al., Optimality guarantees for crystal structure prediction, Nature, 2023, 619, 68–72, DOI:10.1038/s41586-023-06071-y.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD), JOM, 2013, 65, 1501–1509, DOI:10.1007/s11837-013-0755-4.
- S. Kirklin, et al., The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1, 15010, DOI:10.1038/npjcompumats.2015.10.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm, npj Comput. Mater., 2020, 6, 138, DOI:10.1038/s41524-020-00406-3.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph networks as a universal machine learning framework for molecules and crystals, Chem. Mater., 2019, 31, 3564–3572, DOI:10.1021/acs.chemmater.9b01294.
- S. C. Abrahams and S. Geller, Refinement of the structure of a grossularite garnet, Acta Crystallogr., 1958, 11, 437–441, DOI:10.1107/S0365110X5800116X.
- D. Antypov, et al., Statistically derived proxy potentials accelerate geometry optimization of crystal structures, ChemPhysChem, 2024, e202400254, DOI:10.1002/cphc.202400254.
- M. M. Elcombe, et al., Structure determinations for Ca3Ti2O7, Ca4Ti3O10, Ca3.6Sr0.4Ti3O10 and a refinement of Sr3Ti2O7, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 305–314, DOI:10.1107/S0108768190013416.
- A. Kjekshus, Properties of binary compounds with CoSb2 type crystal structure, Acta Chem. Scand., 1971, 25, 411, DOI:10.3891/acta.chem.scand.25-0411.
- K. Koto and N. Morimoto, The crystal structure of anilite, Acta Crystallogr., Sect. B: Struct. Sci., 1970, 26, 915–924, DOI:10.1107/S0567740870003370.
- J. A. Oberteuffer and J. A. Ibers, A refinement of the atomic and thermal parameters of α-manganese from a single crystal, Acta Crystallogr., Sect. B: Struct. Sci., 1970, 26, 1499–1504, DOI:10.1107/S0567740870004399.
- N. J. Calos, C. H. L. Kennard and R. L. Davis, Crystal structure of mimetite, Pb5(AsO4)3Cl, Z. Kristallogr., 1990, 191, 125–129, DOI:10.1524/zkri.1990.191.1-2.125.
- R. Barton Jnr, Refinement of the crystal structure of buergerite and the absolute orientation of tourmalines, Acta Crystallogr., Sect. B: Struct. Sci., 1969, 25, 1524–1533, DOI:10.1107/S0567740869004286.
- H. Schäfer, et al., Neue untersuchungen über die chloride des molybdäns, Z. Anorg. Allg. Chem., 1967, 353, 281–310, DOI:10.1002/zaac.19673530510.
- C. Benndorf, et al., 11B and 89Y solid state MAS NMR spectroscopic investigations of the layered borides YTB4 (T = Mo, W, Re), Dalton Trans., 2019, 48, 1118–1128, 10.1039/C8DT04444A.
- J. D. Gale and A. L. Rohl, The General Utility Lattice Program (GULP), Mol. Simul., 2003, 29, 291–341, DOI:10.1080/0892702031000104887.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- B. Deng, et al., CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nat. Mach. Intell., 2023, 5, 1031–1041, DOI:10.1038/s42256-023-00716-3.
- E. Zamaraeva, et al., Reinforcement learning in crystal structure prediction, Digital Discovery, 2023, 2, 1831–1840, 10.1039/D3DD00063J.
- K. Momma and F. Izumi, VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276, DOI:10.1107/S0021889811038970.
| This journal is © The Royal Society of Chemistry 2024 |