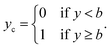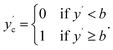Are we fitting data or noise? Analysing the predictive power of commonly used datasets in drug-, materials-, and molecular-discovery

Abstract

Data-driven techniques for establishing quantitative structure property relations are a pillar of modern materials and molecular discovery. Fuelled by the recent progress in deep learning methodology and the abundance of new algorithms, it is tempting to chase benchmarks and incrementally build ever more capable machine learning (ML) models. While model evaluation has made significant progress, the intrinsic limitations arising from the underlying experimental data are often overlooked. In the chemical sciences data collection is costly, thus datasets are small and experimental errors can be significant. These limitations of such datasets affect their predictive power, a fact that is rarely considered in a quantitative way. In this study, we analyse commonly used ML datasets for regression and classification from drug discovery, molecular discovery, and materials discovery. We derived maximum and realistic performance bounds for nine such datasets by introducing noise based on estimated or actual experimental errors. We then compared the estimated performance bounds to the reported performance of leading ML models in the literature. Out of the nine datasets and corresponding ML models considered, four were identified to have reached or surpassed dataset performance limitations and thus, they may potentially be fitting noise. More generally, we systematically examine how data range, the magnitude of experimental error, and the number of data points influence dataset performance bounds. Alongside this paper, we release the Python package NoiseEstimator and provide a web-based application for computing realistic performance bounds. This study and the resulting tools will help practitioners in the field understand the limitations of datasets and set realistic expectations for ML model performance. This work stands as a reference point, offering analysis and tools to guide development of future ML models in the chemical sciences.

---

1 Introduction

Machine learning (ML) models are widely used tools in the fields of chemistry, drug discovery, molecular science, and materials-discovery.^1–4 These models aid the development of quantitative structure activity relations (QSAR) or quantitative structure property relations (QSPR), which can be used to predict various properties such as bioactivity, physicochemical characteristics, reaction data, or quantum mechanical properties.^5–9 The focus of the ML community and literature is often on state-of-the-art algorithms. However, the recent and past successes of ML models in biology and chemistry are not only due to algorithmic advancements, but also because of increasing amounts of data, either deposited to databases or laboriously curated from existing literature.^10–13 Assessing the variability in experimental data is important,¹⁴ but ML applications in chemistry are also often limited by the high cost and presence of experimental noise in the data. This challenge is recognised but not always accounted for when evaluating ML model performance and uncertainty.¹⁵

The ML literature distinguishes two types of uncertainty: aleatoric and epistemic.^16–18 Aleatoric uncertainty arises due to random or systematic noise in the data. ML models are capable of fitting noise perfectly,¹⁹ therefore it is important to consider the aleatoric limit, a maximum performance limit of ML models due to noise in the underlying data. The aleatoric limit primarily refers to the evaluation or test set data: it has been shown that performance of ML models trained on noisy data can potentially surpass the expected performance due to noise in the training set, if evaluated on a noise-free dataset.¹⁸ Nonetheless, in practice, training and test datasets usually have comparable noise levels, and this effect most likely remains hidden. Epistemic uncertainty, on the other hand, is uncertainty due to limited expressiveness of a model, known as model bias; and suboptimal parameter choice, often referred to as model variance.¹⁷

In this study, we specifically focus on how aleatoric uncertainty, or experimental noise, can limit ML model performance. We extend the method by Brown et al. to define performance bounds for common datasets in chemistry and materials, distinguishing between experimental noise (σ_E) and prediction noise (σ_pred). Assuming a perfect model (σ_pred = 0), we obtain the aleatoric limit or maximum performance bound. When incorporating non-zero model prediction noise σ_pred, which could arise from model bias, model variance, or noise in the training dataset, we also identify a realistic performance bound.

The method of Brown derives performance bounds by computing performance metrics between a set of data points and the same set with added noise. If the added noise matches the size of the underlying experimental error, the method reveals limits of model accuracy that should not be surpassed.

We investigate the impact of data range, experimental error, and dataset size on these performance bounds. We then examine nine ML datasets from biological, chemical, and materials science domains, estimate performance bounds based on experimental errors, and compare to reported performance of leading ML models.

2 Results and discussion

In Section 2.1, we analyse the general influence of dataset properties, such as the data range, the size of experimental errors, and the number of data points on the maximum and realistic performance bounds of datasets used for ML models. Utilising synthetic datasets, we specifically investigate how Gaussian noise, applied at one and two levels, affects these bounds. This analysis is the foundation for Section 2.2, where we compare estimated performance bounds of nine real-world ML datasets to reported performance of leading ML models. This allows us to distinguish between datasets where ML models have reached the limit of performance due to experimental error, and datasets where there is still room for ML model improvement.

2.1 Impact of data range, experimental error, and number of datapoints on realistic and maximum performance bounds

In the following, we investigate the effect of data range, magnitude of experimental error, and dataset size on performance bounds using the method developed by Brown et al.²⁰ described in detail in Section 4.1 and extended by us to classification datasets. We define two types of performance bounds: a maximum performance bound where we only assume presence of an experimental error σ_E, and a realistic performance bound, which also considers model prediction error σ_pred. The maximum performance bounds consider an intrinsic predictive limitation when evaluating ML models, based on the experimental uncertainty present in the datasets alone. For the realistic performance bounds, we assumed a prediction error σ_pred equal to the experimental error σ_E, which we assume to be reasonable for most ML models.

Our analysis uses synthetic datasets uniformly distributed in the range [0,1]. For regression tasks, we use both the Pearson correlation coefficient R and the coefficient of determination r² as evaluation metrics. To obtain maximum performance bounds, we add noise to the dataset labels and compute the evaluation metrics between the original dataset labels and the noisy labels. For the realistic performance bounds, instead of the original dataset labels, we consider a second set of noisy prediction labels, which simulate a model evaluation. Repeating this procedure multiple times yields distributions for each performance metric, from which we can estimate standard deviations or confidence intervals of the performance bounds.

Additionally, we compute a maximum performance bound for binary classification tasks obtained from regression datasets, for which we use the Matthews correlation coefficient MCC, as well as the Area Under the Receiver Operating Characteristic Curve ROC-AUC as performance metrics. Details of this method are described in Section 4.1.

The performance bounds can be computed for different noise distributions. Here, we exclusively consider Gaussian noise: first, we add Gaussian noise of a single level across all data points to identify general trends. Next, we mirror real-world data complexities by considering different noise levels depending on the label size. We study how the presence of two noise levels changes performance bounds relative to Gaussian noise of a single level. In principle, performance bounds could also be derived for other noise distributions, such as uniform, bimodal, or cosh distributed noise.

2.1.1 Gaussian noise of one level. First, we consider adding Gaussian noise with standard deviations σ, which we present in % relative to the dataset range [0,1] of the synthetic datasets: a noise level of 10% corresponds to Gaussian noise drawn from a normal distribution with μ = 0 and standard deviation σ = 0.1. Fig. 1 shows maximum performance bounds (σ_E) for regression (Fig. 1a and d), realistic performance bounds (σ_pred = σ_E) for regression (Fig. 1b and e), and maximum performance bounds (σ_E) for classification (Fig. 1c and f) for different dataset size and noise levels. As expected, increased noise levels reduced the maximum and realistic performance bounds of a dataset. For regression tasks, noise levels of σ_E ≤ 15% yielded maximum Pearson correlation coefficients of R > 0.9. Noise levels of σ_E ≤ 10% yielded r² scores of r² > 0.9. To increase performance bounds of a dataset, one therefore needs to reduce noise levels or increase the range of the data.

Fig. 1 Shown are the distributions of different performance metrics for regression (a, b, d and e) and classification (c and f) of synthetic datasets as heatmaps. The mean values of the performance metrics are shown in the heatmaps, the standard deviations are overlayed as black contour lines. The synthetic datasets vary in sample size as shown on the x-axes and noise levels σ, given in relative units to the data range on the y-axes. For cases (a), (d), (c) and (f), we only considered experimental noise σ_E; for cases (b) and (e), we considered experimental noise σ_E and predictor noise σ_pred = σ_E. The range for all datasets is [0,1], with datapoints distributed uniformly over the whole range. For the classification datasets, the regression datasets were divided into 0 (inactive) for values < 0.5, and 1 (active) for values ≥ 0.5. This was done before and after addition of noise, such that noise can lead to misclassification of datapoints.

What is the impact of dataset size on these bounds? Increasing the dataset size at constant noise levels did not improve the maximum or realistic performance bounds of the datasets. However, the standard deviations of the observed performance metrics reduced. Thus, the predictive power of a dataset of larger size can be more confidently defined. This effect is similar to what is observed for significance testing, when comparing two distributions.³ The performance bounds considered here do not assess how well or efficiently a ML model might learn from a given dataset. The maximum performance bounds consider an intrinsic predictive limitation when evaluating models, based on the experimental uncertainty present in the datasets alone. The realistic performance bounds also consider a prediction error σ_pred. It is important to point out that σ_pred will likely depend on the specific ML model and contributions of model bias, model variance, as well as how well the model can deal with experimental noise in the training data. In principle, models trained on datasets with noise-levels of σ_E can achieve higher predictive performance (i.e. σ_pred < σ_E), if evaluated on a test set with noise < σ_E.¹⁸ A future avenue of research could be to train ML models on abundant noisy data, while evaluation could be performed on smaller high-quality datasets. Thus, models with high predictive power could be obtained, even if the performance bounds of the training data sets are lower.

2.1.2 Gaussian noise of two levels in a single dataset. For some experimental measurements, error sizes can vary with the absolute size of the quantity measured. Size dependent errors were seen in the Rzepiela dataset,²¹ one of the nine datasets we study in more detail in Section 2.2. Here, we simulate this effect for a synthetic dataset of N = 100 of range [0,1], by adding Gaussian noise with σ_E,1 = 0.2 to the lower half of the dataset (< 0.5), and a second noise level of σ_E,2 = 0.05 to the other half of the dataset (≥ 0.5). We compute maximum performance bounds and directly compare this case to adding Gaussian noise of σ_E = {0.05, 0.1, 0.2} to the whole dataset.

As can be seen in Fig. 2, the dataset with σ_E = 0.1 had a higher maximum performance bound relative to the dataset with the two noise levels. Furthermore, the performance bound was more sharply defined, i.e. had a lower standard deviation σ_R. For comparison, the resulting distributions of Pearson correlation R for single noise levels of σ_E = 0.05 and σ_E = 0.2 are also plotted. Therefore, noise of two levels (high and low) is worse than a moderate noise level for all datapoints. This hints at a wider ranging conclusion: presence of a few outliers or datapoints with high noise in an otherwise low-noise dataset can degrade performance disproportionately. We exemplarily show this by varying the location of the noise barrier, as shown in Fig. 2c, which is equivalent to changing the fraction of the dataset that is exposed to high noise levels. The maximum expected performance bound decreased steadily with increasing fraction of datapoints experiencing high noise levels. Therefore, datapoints with high noise levels should be excluded, if possible, to maximise predictive performance of a given dataset.

Fig. 2 (a) Synthetic dataset of size N = 100 with Gaussian noise of two levels added (σ_E,1 for [0, 0.5), σ_E,2 for [0.5,1]) is shown in blue. The same synthetic dataset with Gaussian noise of σ_E = 0.1 is shown in red. (b) Shown are the distribution of Pearson correlation R for the two different scenarios as histograms. As can be seen, the maximum expected performance for a dataset with the two levels of low and high noise (blue) is worse than the single level of moderate noise (red). For comparison, the low and high noise levels are also shown when applied to the whole dataset (see black dashed/dotted lines, respectively). (c) Variation of mean and standard deviation of the Pearson correlation R with the noise barrier location of a uniform synthetic dataset. Varying the noise barrier location corresponds to varying the fraction of the dataset that experiences high noise addition. At a barrier location of 0, Gaussian noise with σ_E,1 = 0.05 is added to the entire dataset (dashed line in (b)). If the barrier location is 1.0, the entire dataset experiences Gaussian noise with σ_E,2 = 0.2 (dotted line in (b)). The barrier location of 0.5 corresponds to the blue case in (b).

2.2 Are we fitting data or noise? Assessing performance bounds of application datasets and comparison to ML model performance

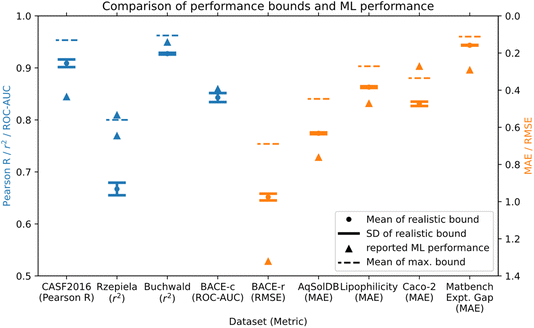
The maximum and realistic performance bounds for a total of nine datasets from drug discovery, materials discovery, and molecular discovery applications, that were used for building ML models are shown in Table 1 and Fig. 3. We used error estimates in the following order of preference as available: (1) reported experimental standard deviations for datapoints, (2) reported standard deviation for the specific experimental assay, (3) standard deviation estimated from duplicate values via pairwise comparison (see Section 4.4 for details), (4) standard deviation obtained from inter-lab comparison studies of the general method. Table 1 shows a detailed overview of the datasets used, the experimental error estimates, and the resulting maximum and realistic performance bounds for Pearson R/MCC, as well as the performance bounds in the evaluation metric of the best performing ML models from the literature. Fig. 3 shows a direct comparison of the performance bounds with the reported ML performance for all datasets considered. For three out of the nine datasets, ML model performance exceeded or was at the maximum performance bound, and thus the reported ML performance seems unrealistically high given the error estimates made here. An additional ML model exceeds the realistic performance bound but is below the maximum performance bound. The other five datasets have ML models that are below the performance bounds. We discuss the individual datasets in more detail as follows.

Fig. 3 Performance bounds for different datasets compared to reported ML performance from the literature. Metrics that have best performance at a value of 1.0 are shown in blue (left axis), error-metrics with the best performance at values of 0 are shown in orange (right axis). For each dataset, the mean and standard deviation of the realistic performance bounds (σ_E = σ_pred), as well as the mean of the maximum performance bounds are shown, if defined. The reported ML model performances for the BACE classification dataset (BACE-c), the Caco-2, and the Rzepiela datasets seem unrealistically high, given the estimated experimental error. For most other datasets, reported ML model performance remains below the realistic performance bounds, indicating further room for ML model improvement.

Table 1 Maximum and realistic performance bounds for chemical datasets, compared to leading ML models

Dataset name/range	No. of datapoints	Assay/experimental method	Experimental error estimate σE	Mean of maximum (realistic) performance bound: Pearson R (regression), MCC (classification)	Mean of maximum performance bound in ML eval. metric	Mean of realistic performance bound in ML eval. metric	Best ML model performance/model name/data split
a Not defined for the classification case.b Estimated by us, based on pairwise estimate of repeats performed in the original assay literature.c Estimated by us, based on pairwise error estimate via duplicates in raw data.d Rzepiela et al. report two different models. Bold ML performance metric values indicate models exceeding the estimated maximum performance bounds.
Drug binding
CASF 2016 (PDBBind 2016 core set)/9.75 log units	285	Binding affinity, multiple targets log Ki	0.69 pKi units^24	0.95 (0.91)	R: 0.95	R: 0.91	R: 0.845/ΔLin_F9XGB ^34/—
BACE regression/6.0 log units	1513	Binding affinity, single target log Ki	0.69 pKi units^24	0.89 (0.79)	RMSE: 0.69	RMSE: 0.98	RMSE: 1.32/RF ^35/scaffold
BACE classification/{0,1}	1513	Binding affinity converted to binary classes: 0,1	0.69 pKi units^24	MCC: 0.69 (—)	ROC-AUC: 0.84	—^a	ROC-AUC: 0.86/Uni-Mol/scaffold
Drug pharmacokinetics/molecular
Lipophilicity AstraZeneca (MolNet, TDC)/6.0 log units	4200	Lipophilicity assay log-ratio	0.34^b log units	0.96 (0.93)	MAE: 0.27	MAE: 0.38	MAE: 0.47/Chemprop-RDKit ^36/scaffold
AqSolDB (TDC)/15.3 log units	9982	Solvation assay log (S)	0.56^c log units	0.97 (0.95)	MAE: 0.45	MAE: 0.63	MAE: 0.76/Chemprop-RDKit ^36/scaffold
Caco-2 permeability (Wang) (TDC)/4.3 log units	906	Caco-2 permeability assay (log (Papp))	0.42 log units^30	0.88 (0.77)	MAE: 0.34	MAE: 0.47	MAE: 0.27/MapLight ^37/scaffold
Rzepiela dataset/3.5 log units	4367	Pampa permeability assay (log (Papp))	0.2 log units for high-perm., 0.6 log units for low perm^21	0.91 (0.83)	r^2: 0.80	r^2: 0.66	r^2: 0.81/0.77^d/Rzepiela QSPR ^21/random
Buchwald–Hartwig HTE/0–100%	3955	Chemical reaction yields, obtained via high-throughput screening (%)	5.3^b %	0.98 (0.96)	r^2: 0.96	r^2: 0.93	r^2: 0.95/yield-BERT ^38/random
Materials
Matbench: matbench_expt_gap/11.7 eV	4604	Experimentally measured band gaps (eV)	0.14^c eV	1.0 (0.99)	MAE: 0.11	MAE: 0.16	MAE: 0.29/Darwin ^39/random (NCV)

---

2.2.1 Drug binding tasks. Both the CASF2016 (ref. 22) and the BACE²³ datasets (BACE-c: classification, BACE-r: regression) report measured binding affinities. The CASF2016 (also sometimes referred to as PDBBind 2016 core set) covers multiple targets, the BACE dataset is a set of inhibitors of human β-secretase 1 (BACE-1) with both quantitative (IC₅₀) labels (here: BACE-r) and qualitative binary labels (here: BACE-c). CASF2016 has a range of 9.75 log units, while BACE-r only covers 6 log units. Since both datasets originate from different laboratories and do not necessarily use the exact same experimental protocol, we estimated the experimental error σ_E = 0.69 log units. This estimate is based on a systematic study of duplicate values in the ChEMBL database.^12,24 Owing to the greater range, the maximum and realistic performance bounds of CASF2016 are higher than that of BACE-r, even though the experimental error estimate is the same. For both BACE-r and CASF2016, development of improved ML models seems possible, given the dataset performance bounds. Conversion of the BACE dataset into a classification task (BACE-c) leads to a ML model that exceeds the maximum predictive performance of the classification dataset. This suggests that the classification task simplified the bioactivity prediction task, however, the model might also fit to noise in the dataset.

2.2.2 Drug pharmacokinetics and molecular ML tasks. Next, we consider properties relevant in both molecular and drug discovery settings: chemical reaction yields via the Buchwald–Hartwig HTE dataset,²⁵ physicochemical properties such as aqueous solubility and lipophilicity, as well as in vitro (PAMPA) and in vivo (Caco-2) permeability assays.

The AqSolDB dataset²⁶ is an aggregation of aqueous solubility measurements. We estimated the experimental error as σ_E = 0.56 log units via reported duplicates in the raw data that were removed in the compiled dataset. Since the range of the AqSolDB dataset is large (15.3 log units) relative to the error estimate (0.56 log units), performance bounds are high. The best reported ML model performance does not reach the performance bounds.

The lipophilicity dataset²⁷ has a smaller range of 6.0 log units compared to some of the previous datasets, however, estimated performance bounds are still high. This is because all datapoints are from the same assay with an estimated experimental error of σ_E = 0.32 log units of the assay.²⁸ Reported ML models have not reached the performance bounds of the dataset.

The Rzepiela dataset (ref. 21) is a collection of PAMPA permeability measurements, all performed via the same assay. In the publication, the authors report experimental error estimates that are different for high and low permeability compounds. We have simulated the effect of two levels of noise in Section 2.1 for a synthetic dataset and apply the same method here. We used a value of σ_E,1 = 0.2 log units for values of log P_eff > −7.6, and a value of σ_E,2 = 0.6 log units for values of log P_eff ≤ −7.6. As already seen for the synthetic dataset, performance bounds are decreased due to the higher noise levels of some of the data points. The ML model performance reported exceeds the performance bounds estimated here. It could be that the reported experimental error is too large, or the ML model might be fitting to noise in the dataset. The authors applied 10-fold cross-validation with random splits to generate training and test data sets and evaluate ML model performance. The dataset contained 48 topologically different macrocyclic scaffolds, so there might have been structurally similar compounds in the train and test set, and it would be interesting to see how performance of the reported QSPR models would change for e.g. a scaffold-based split.

The Caco-2 dataset²⁹ is a collection of Caco-2 permeability measurements with a range of 4.25 log units, aggregated from different publications. We used an error estimate of σ_E = 0.42 log units from an inter-lab comparison study for Caco-2 assays.³⁰ The reported ML model performance is higher than the maximum performance bounds, indicating potential issues with fitting to noise.

Finally, we investigated a dataset of reaction yields (range of 0–100%) of Buchwald–Hartwig reactions from a high throughput experiment.²⁵ We estimated a noise level of σ_E = 5.3%, which is based on repeat measurements performed as part of validating the original experimental protocol.³¹ The best reported ML models have high reported r² scores and are between the realistic and maximum performance bounds. This could indicate a high-quality ML model, but since the dataset was split randomly, some fitting of noise cannot be ruled out.

2.2.3 Materials science datasets. Many of the common materials science ML datasets have computational rather than experimental endpoints. This avoids the issue of experimental noise and allows construction of accurate ML models. We chose a dataset of experimentally measured band gaps³² reported as part of the Matbench suite³³ of materials science benchmarks. However, only non-zero values were measured experimentally. We estimated the experimental noise as σ_E = 0.14 eV from the unprocessed dataset that contained duplicate values. The estimated performance bounds are high, since the noise value is small relative to the range of the dataset (11.7 eV) and further ML model improvements seem possible.

2.2.4 ML model performances exceeding performance bounds. Out of the nine datasets studied, four datasets surpassed the estimated realistic performance bounds. Three out of these four cases also reached or surpassed the estimated maximum performance bounds. Why do certain ML models surpass our calculated performance bounds? two of the flagged models (Rzepiela, Buchwald) were evaluated using random data splits, which might lead to inflated performance estimates due to overfitting to noise, memorisation, and overlap between train and test sets.

The Rzepiela and Caco-2 permeability datasets and ML models were both flagged. The underlying datasets are complex permeability endpoints with a narrow data range relative to the estimated error, resulting in relatively low performance bounds.

The BACE classification ML model also exceeded the performance bounds estimated.

Our findings highlight the need to carefully consider noise when building ML models based on experimental data, since several ML models report performances that seem unlikely given the estimated experimental error of the underlying data. Future studies and novel ML algorithms should consider the easy to calculate performance bounds when evaluating model performance, to ensure that advancements in ML models are genuine and do not result from overfitting to experimental noise.

3 Conclusions

This study has investigated the impact of experimental noise on predictive performance of commonly used experimental ML datasets. Based on the work of Brown et al., we define maximum and realistic performance bounds. Maximum bounds only consider experimental noise in the dataset used for evaluation, while realistic performance bounds also consider the estimated ML model performance uncertainty. In general, increasing the dataset size leads to higher confidence in the value of the performance metrics, but does not yield increases in the performance bounds themselves. The value of the maximum and realistic performance bounds is determined by the size of the experimental noise relative to the data range. The here defined performance bounds can serve as a quantitative evaluation metric to assess if models fit to noise. This could also be applied during model training: evaluating ML models on a validation dataset and ensuring that performance bounds are not exceeded could serve as an alternative, quantitative metric to avoid over-fitting. As part of this study, we identified 9 commonly used ML datasets from drug-, molecular-, and materials-discovery and derived a systematic protocol to estimate realistic experimental errors. We show that for some datasets, reported ML model performance exceeds or is close to what we believe to be an upper performance limit. High ML performance is encouraging, but only if the model evaluation was rigorous. ML model performance that is at the performance bounds or even higher suggests that some ML models may be fitting to noise. This is a significant issue because these models will likely underperform in application scenarios. For some of the datasets investigated, ML model performance has not yet reached the maximum performance that could theoretically be achieved with the underlying datasets. This highlights the need for further efforts relating to model and algorithm development, e.g. for ligand binding affinity predictions.

ML model evaluations themselves are still a debated topic, but efforts such as the therapeutic data commons (TDC) that include pre-defined datasets, data-splits and standardised evaluation metrics are a step in the right direction. However, the commonly reported tabular benchmarks of ML models are not enough, and more thorough evaluations based on statistical tests should be used to convincingly claim performance advances of new algorithms.³ When generating evaluation datasets, we recommend increasing the data range, or reducing the experimental error if possible. Additionally, the use of low-noise data points as test sets should be considered, if data of varying quality is available.

Datasets with computational endpoints are often used in materials science applications. Such datasets do not have experimental noise, and use of these synthetic datasets is a promising path forward if experimental data is scarce or impossible to acquire. For synthetic datasets and corresponding ML models, it will be interesting to further study the addition of artificial noise of varying levels to see how different ML models deal with noise, and if they can surpass the noise levels given in training datasets when evaluated on noise-free or low-noise test sets.¹⁸ When constructing synthetic datasets of experimentally measurable endpoints, e.g. via physics-based simulations, addition of noise to the same levels as observed in experiments should be considered. Further, one should ensure to mirror the data range of experimental assays with the synthetic datasets. Otherwise, the performance bounds will be artificially increased, the task is effectively simplified, and models should not be expected to transfer well to predicting the underlying experimental tasks.

4 Methods

4.1 Addition of Gaussian noise and estimation of performance metric bounds

For a dataset of size N, with range [y_min, y_max], and labels y we draw N random samples from a normal (Gaussian) distribution with mean μ = 0 and standard deviation σ equal to the desired experimental noise level via the NumPy package.⁴⁰ The probability density for the Gaussian distribution is

We obtain the noisy labels y′ by adding noise to the labels y (see Fig. 4 for several examples of synthetic datasets with different noise levels). Given an original label y_i, a noise sample n_i, we obtain a noisy label via:

Fig. 4 Uniformly distributed synthetic datasets of size N = 50, with no added noise (a), Gaussian noise added with standard deviations of σ_E = 0.1 (b), σ_E = 0.25 (c), and σ_E = 0.5 (d). If we consider the classification case, the boundary b is shown as a vertical dashed line. Resulting false negatives (fn) and false positives (fp) due to addition of noise are colour coded. Predictor noise σ_pred = 0 for all cases.

We can then compute regression metrics, such as the Pearson correlation coefficient R, coefficient of determination r², etc., directly between the original dataset labels y, and the noisy labels y′ to obtain maximum performance bounds, since we do not consider any predictor noise. For estimating a realistic performance bound, we draw a second set of noisy labels , with noise from a Gaussian with mean μ = 0 and standard deviation σ_pred. We then compute the relevant metrics between y′ and , which effectively simulates evaluation of a ML model.

To simulate effects of noise when converting regression datasets to binary classification datasets, we add noise as described to the labels y to obtain noisy labels y′. Then, with a sharply defined class boundary b, which serves to split the dataset into binary classes {0,1}, we obtain the noise-free class labels y_c via

The noisy classification labels are then equivalently defined as

We can then compute classification metrics, such as Matthews correlation coefficient MCC, or ROC-AUC, etc. between y_c and . For both classification and regression performance bound estimates, we independently repeat the noise addition and performance bound computation 1000 times if not specified otherwise. This yields a distribution of values for each metric considered, of which we report the mean and standard deviation.

We also performed addition of Gaussian noise of two different levels. For this, we split the dataset along a boundary b′. To obtain the noisy labels y′, we add Gaussian noise of σ₁ to all values of y that are below b′; for values above b′ we add Gaussian noise of σ₂. The estimation of the performance bounds is then performed as described above.

4.2 Synthetic dataset generation

Synthetic datasets were generated via the NumPy package.⁴⁰ All synthetic datasets are of range [0,1] with datapoints distributed uniformly over the full range. After generating a uniformly distributed dataset of size N, we draw N random samples from a normal (Gaussian) distribution with μ = 0 and σ equal to the desired noise level as described in the previous section. This noise is then added to the datapoints as described in Section 4.1 to obtain y′ or . Fig. 4 shows an example synthetic dataset with N = 50 with various levels of experimental noise added in (b), (c), (d).

4.3 Experimental dataset selection and dataset details

We selected datasets that were used for ML modelling from drug discovery, materials science, and molecular science applications. We can distinguish datasets based on the following attributes:

• Labels: experimental or computational observable.

• Source: single source and assay or aggregate of multiple sources or assays.

• Task: regression task, or classification task (or regression converted to classification).

Every dataset has the following properties: (1) range of labels or number of classes in the classification context, (2) size of experimental error, which is often unknown or not reported, and (3) number of datapoints. When estimating performance bounds, selection of a realistic estimate of the experimental noise is key. In the following, we detail the selected datasets and how error estimates were obtained.

4.3.1 Drug binding datasets. The CASF 2016 dataset²² (also referred to as PDBbind 2016 core set, N = 285) is a commonly used evaluation dataset for ML/DL scoring functions for the prediction of protein ligand binding affinities.⁴¹ Experimental error of binding affinity data depends on the specific binding assay method, error estimates range from around 0.2 log units for industrial drug research up to 0.69 log units for public affinity data from various sources, as applicable for PDBbind.^15,24 The data was obtained from https://www.pdbbind.org.cn/casf.php. The experimental error estimate used was 0.69 log units, as derived in Kramer et al. This is based on 2540 systems with 7667 measurements.

The BACE dataset²³ (N = 1513) is part of the MoleculeNet benchmark suite.⁴² As the BACE dataset originates from various sources, we assume an experimental error of 0.69 log units, identical to the CASF 2016 dataset. Since the BACE dataset has been used for both regression and classification, we also derive performance bounds for the classification task. The BACE dataset was obtained from https://moleculenet.org/datasets-1 on March 21, 2024.

4.3.2 Drug pharmacokinetics and molecular datasets. The AstraZeneca lipophilicity dataset²⁷ (N = 4200), as deposited to ChEMBL¹² and listed in the Therapeutic Data Commons repository^43,44 and MoleculeNet,⁴² is a dataset of experimental octanol/water distribution coefficients (log D at pH 7.4). All data points were measured via a single, well-defined shake-flask method,²⁸ and we estimated an experimental standard deviation of 0.34 log units (RMSE: 0.46 log units). This value was based on a pairwise comparison of reported assay values to the 22 reference literature values as reported in the assay publication.²⁸ This includes six compounds for which the reported assay values were outside of the assay range, <−1.5 or >4.5; we set those values to be equal to −1.5 or 4.5, respectively. The assay publication lists an RMSE of 0.2 log units (corresponding standard deviation of 0.16 log units), which can be obtained if the six ‘out-of-range’ datapoints are excluded. The experimental range of the assay is 6.0 log units. The lipophilicity dataset was obtained via the Therapeutic Data Commons python package, as described at https://tdcommons.ai/single_pred_tasks/adme/#lipophilicity-astrazeneca on March 20, 2024.

The Wang Caco-2 permeability dataset²⁹ (N = 906) is another of the datasets listed in the Therapeutic Data Commons repository. The dataset is an aggregate of Caco-2 permeability measurements from different sources. Caco-2 cells are used as an in vitro model to simulate the human intestinal tissue. Since this dataset was compiled from different sources, we estimated the experimental error based on a quantitative inter-lab comparison study to be 0.42 log units.³⁰ This is based on 10 compounds, measured in seven different laboratories, yielding 169 value pairs that were used to estimate the standard deviation. The Wang dataset was obtained via the Therapeutic Data Commons python package on March 20, 2024, as described at https://tdcommons.ai/single_pred_tasks/adme/#caco-2-cell-effective-permeability-wang-et-al.

The Rzepiela dataset²¹ (N = 3600) is a single source, single-assay dataset of macrocycle PAMPA measurements (parallel artificial membrane permeability assay). Different to many other datasets encountered, the authors provide an uncertainty estimate depending on the permeability value. Experimental error was higher for low permeability values (0.6 log units for permeabilities of (−log Peff ∼ 7.6)). At higher permeability values (−log Peff ∼ 5.8), the standard error of PAMPA measurement is only ∼0.2 log units. To estimate performance bounds, we applied noise levels σ_E,1 = 0.6 log units for values > 6.7; and σ_E,2 = 0.2 log units for values ≤ 6.7. The Rzepiela dataset was obtained from the original publication supplementary data.

The AqSolDB dataset²⁶ (N = 9982) is an aggregate of a total of 9 different datasets of experimental aqueous solubility measurements (log S). When merging the 9 datasets, the authors attempted to select the most reliable values if duplicates were present. Some of the datapoints have an associated standard deviation if duplicates were measured. We estimated the experimental error via pairwise computation of the standard deviation based on duplicate values using the method of Kramer²⁴ and as defined in Section 4.4. This yields an overall experimental standard deviation of σ_E = 0.56 log units. The AqSolDB dataset was obtained via the Therapeutic Data Commons python package, as described at https://tdcommons.ai/single_pred_tasks/adme/#solubility-aqsoldb, on March 20, 2024.

The Buchwald–Hartwig HTE dataset²⁵ (N = 3955) is a single source, high-throughput experimentation-based dataset of reaction yield measurements of a palladium-catalysed Buchwald–Hartwig cross-coupling reaction. To the best of our knowledge, no experimental uncertainties were recorded as part of the dataset directly. The high-throughput experimental protocol was developed in the Merck Research Laboratories for nanomole-scale experimentation in 1536-well plates.³¹ In the original protocol publication, 64 reactions were run twice as part of an experiment. We used these 64 reactions to estimate an experimental standard deviation based on the pairwise method defined in Section 4.4. This yields an experimental standard deviation of the high-throughput protocol of σ_E = 5.3%, which we used as an approximate error for the Buchwald–Hartwig HTE dataset. The Buchwald dataset was obtained from https://github.com/rxn4chemistry/rxn_yields on March 21, 2024.

4.3.3 Materials science datasets. The Matbench_expt_gap dataset³³ (N = 4604) as listed in the MatBench repository is a dataset linked to the materials project, and lists experimentally determined band gaps in units of eV of inorganic materials. Only non-zero values were measured experimentally. As part of the MatBench curation process, duplicates were removed. Accessing the original data source³² allowed us to use the duplicate values to estimate possible experimental error via pairwise estimation of errors. We obtain an experimental standard deviation of σ_E = 0.14 eV. The MatBench expt gap dataset was obtained via the MatBench python package, as described at https://matbench.materialsproject.org/How-To-Use/1install/ on March 21, 2024.

4.4 Noise estimation for experimental datasets

To obtain an estimate of experimental noise, we relied on the following order of preference: (1) reported experimental standard deviations for datapoints, (2) the reported standard deviation for the specific experimental assay (if a single well-defined assay was performed for the entire dataset), (3) standard deviation estimated from duplicate values via pairwise comparison, (4) inter-lab comparison studies of the general method used.

None of the datasets considered here had individually reported standard deviations for all datapoints (1). For datasets that originated from a single, well-defined assay, we used the reported standard deviation of that assay as a noise estimate.

For datasets that are aggregates of multiple studies or methods performed by different labs, we went back to the raw data before de-duplication, if available, and estimated the standard deviation based on pairwise deviations according to the method described by Kramer et al.²⁴ and briefly summarised here: The estimated experimental standard deviation σ_E is computed from all possible m pairs of measured duplicate values (the pair i has the measured values y_pub,i,1, y_pub,i,2):

If no duplicate raw data was available, we looked for quantitative inter-lab comparison studies of the specific methods to obtain a noise estimate. For classification datasets, it is more difficult to find reliable noise estimates. For the BACE classification task, we went back to the original regression data, added noise to the regression labels, while maintaining the same class boundary as used for conversion to the classification task. We then derived noisy classification labels, which we compared to the true classification labels as described in Section 4.1 to obtain estimates of the classification performance metrics.

Data availability

The Python package NoiseEstimator and all data and code to reproduce this study are available at https://github.com/d-cru/NoiseEstimator and forked at https://github.com/bigginlab/NoiseEstimator (release v0.0.2) We also provide a web-based application hosted at https://noiseestimator.bioch.ox.ac.uk to aid computation of maximum and realistic performance bounds for other experimental ML datasets. The code and data are also archived on Zenodo and can be accessed at https://doi.org/10.5281/zenodo.11397227.

Author contributions

Daniel Crusius: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization. Flaviu Cipcigan: conceptualization, investigation, writing – review & editing, supervision, project administration. Philip C. Biggin: conceptualization, investigation, writing – review & editing, supervision, project administration, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Matt Warren for helpful discussion related to binding affinity prediction. DC is supported by the University of Oxford Medical Science Division and IBM/EPSRC. Flaviu Cipcigan recognises support by the Hartree National Centre for Digital Innovation, a collaboration between STFC and IBM.

Notes and references

1. J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K. R. Muller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872.
2. A. C. Mater and M. L. Coote, J. Chem. Inf. Model., 2019, 59, 2545–2559.
3. A. Nicholls, J. Comput.-Aided Mol. Des., 2016, 30, 103–126.
4. P. Walters, Practical Cheminformatics, 2019.
5. A. Cherkasov, E. N. Muratov, D. Fourches, A. Varnek, I. I. Baskin, M. Cronin, J. Dearden, P. Gramatica, Y. C. Martin, R. Todeschini, V. Consonni, V. E. Kuz'min, R. Cramer, R. Benigni, C. Yang, J. Rathman, L. Terfloth, J. Gasteiger, A. Richard and A. Tropsha, J. Med. Chem., 2014, 57, 4977–5010.
6. A. Tropsha, P. Gramatica and V. K. Gombar, QSAR Comb. Sci., 2003, 22, 69–77.
7. L. D. Hughes, D. S. Palmer, F. Nigsch and J. B. Mitchell, J. Chem. Inf. Model., 2008, 48, 220–232.
8. J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, npj Comput. Mater., 2019, 5, 83.
9. J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. Zhao, Nat. Rev. Drug Discovery, 2019, 18, 463–477.
10. D. Crusius, J. Schnell, F. Cipcigan and P. Biggin, Digital Discovery, 2023, 2, 1163.
11. H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242.
12. B. Zdrazil, E. Felix, F. Hunter, E. J. Manners, J. Blackshaw, S. Corbett, M. de Veij, H. Ioannidis, D. M. Lopez, J. F. Mosquera, M. P. Magarinos, N. Bosc, R. Arcila, T. Kiziloren, A. Gaulton, A. P. Bento, M. F. Adasme, P. Monecke, G. A. Landrum and A. R. Leach, Nucleic Acids Res., 2024, 52, D1180–D1192.
13. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1.
14. G. A. Ross, C. Lu, G. Scarabelli, S. K. Albanese, E. Houang, R. Abel, E. D. Harder and L. Wang, Commun. Chem., 2023, 6, 222.
15. G. A. Landrum and S. Riniker, J. Chem. Inf. Model., 2024, 64, 1560–1567.
16. S. C. Hora, Reliab. Eng. Syst. Saf., 1996, 54, 217–223.
17. E. Hüllermeier and W. Waegeman, Mach. Learn., 2021, 110, 457–506.
18. E. Heid, C. J. McGill, F. H. Vermeire and W. H. Green, J. Chem. Inf. Model., 2023, 63, 4012–4029.
19. C. Zhang, S. Bengio, M. Hardt, B. Recht and O. Vinyals, Commun. ACM, 2021, 64, 107–115.
20. S. P. Brown, S. W. Muchmore and P. J. Hajduk, Drug Discovery Today, 2009, 14, 420–427.
21. A. A. Rzepiela, L. A. Viarengo-Baker, V. Tatarskii, R. Kombarov and A. Whitty, J. Med. Chem., 2022, 65, 10300–10317.
22. M. Su, Q. Yang, Y. Du, G. Feng, Z. Liu, Y. Li and R. Wang, J. Chem. Inf. Model., 2019, 59, 895–913.
23. G. Subramanian, B. Ramsundar, V. Pande and R. A. Denny, J. Chem. Inf. Model., 2016, 56, 1936–1949.
24. C. Kramer, T. Kalliokoski, P. Gedeck and A. Vulpetti, J. Med. Chem., 2012, 55, 5165–5173.
25. D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190.
26. M. C. Sorkun, A. Khetan and S. Er, Sci. Data, 2019, 6, 143.
27. M. Wenlock and N. Tomkinson, Experimental in vitro DMPK and physicochemical data on a set of publicly disclosed compounds, 2016,  DOI:10.6019/CHEMBL3301361.
28. M. C. Wenlock, T. Potter, P. Barton and R. P. Austin, J. Biomol. Screening, 2011, 16, 348–355.
29. N. N. Wang, J. Dong, Y. H. Deng, M. F. Zhu, M. Wen, Z. J. Yao, A. P. Lu, J. B. Wang and D. S. Cao, J. Chem. Inf. Model., 2016, 56, 763–773.
30. J. B. Lee, A. Zgair, D. A. Taha, X. Zang, L. Kagan, T. H. Kim, M. G. Kim, H. Y. Yun, P. M. Fischer and P. Gershkovich, Eur. J. Pharm. Biopharm., 2017, 114, 38–42.
31. A. Buitrago Santanilla, E. L. Regalado, T. Pereira, M. Shevlin, K. Bateman, L. C. Campeau, J. Schneeweis, S. Berritt, Z. C. Shi, P. Nantermet, Y. Liu, R. Helmy, C. J. Welch, P. Vachal, I. W. Davies, T. Cernak and S. D. Dreher, Science, 2015, 347, 49–53.
32. Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, J. Phys. Chem. Lett., 2018, 9, 1668–1673.
33. A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, npj Comput. Mater., 2020, 6, 138.
34. C. Yang and Y. Zhang, J. Chem. Inf. Model., 2022, 62, 2696–2712.
35. W. Ahmad, E. Simon, S. Chithrananda, G. Grand and B. Ramsundar, arXiv, preprint, arXiv:2209.01712, 2022,  DOI:10.48550/arXiv.2209.01712.
36. K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 3370–3388.
37. J. H. Notwell and M. W. Wood, arXiv, preprint, arXiv:2310.00174, 2023, DOI:  DOI:10.48550/arXiv.2310.00174.
38. P. Schwaller, A. C. Vaucher, T. Laino and J.-L. Reymond, Mach. Learn.: Sci. Technol., 2021, 2, 015016.
39. T. Xie, Y. Wan, W. Huang, Y. Zhou, Y. Liu, Q. Linghu, S. Wang, C. Kit, C. Grazian, W. Zhang and B. Hoex, arXiv, peprint, arXiv:2304.02213, 2023, DOI:  DOI:10.48550/arXiv.2304.02213.
40. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. Del Rio, M. Wiebe, P. Peterson, P. Gerard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
41. R. Meli, G. M. Morris and P. C. Biggin, Front. bioinform., 2022, 2, 885983.
42. Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530.
43. K. Huang, T. Fu, W. Gao, Y. Zhao, Y. Roohani, J. Leskovec, C. W. Coley, C. Xiao, J. Sun and M. Zitnik, Nat. Chem. Biol., 2022, 18, 1033–1036.
44. K. Huang, T. Fu, W. Gao, Y. Zhao, Y. Roohani, J. Leskovec, C. W. Coley, C. Xiao, J. Sun and M. Zitnik, arXiv, preprint, arXiv:2102.09548, 2021, DOI:  DOI:10.48550/arXiv.2102.09548.

---