Magnetic study and DFT analysis of a doubly carboxylato-bridged Co(II) derivative anchored with a ‘scorpionate’ precursor as a potential electrocatalyst for heterogeneous H₂ evolution

Abstract

A new doubly carboxylato-bridged Co(II) dinuclear complex, [Co(bdtbpza)(NCS)]₂ (1), was obtained in a satisfactory yield by employing a ‘scorpionate’-type precursor, bdtbpza {bis-(3,5-di-tert-butylpyrazol-1-yl)acetate}, and was then structurally characterized. Single-crystal X-ray diffraction analysis revealed that, in 1, each Co(II) is penta-coordinated, leading to a distorted trigonal–bipyramidal geometry within the coordination environment of N₃O₂. Weak antiferromagnetic coupling within the Co(II) ions in 1 was found based on the isotropic spin Hamiltonian H = −J(S₁·S₂) for the S_i = 3/2 system. For evaluating the spin density distribution and the mechanism for the magnetic exchange coupling, DFT analysis was performed, with the calculated result agreeing the experimental magnetic data. A study into electrochemical H₂ evolution, involving cyclic voltammetry (CV), controlled potential electrolysis (CPE), and gas chromatographic (GC) analyses of the graphite electrode modified with the cobalt complex in a neutral aqueous solution revealed the high catalytic activity of the complex with a low overpotential toward H₂O reduction. The faradaic efficiency of the catalyst was found to be 83.7% and the di-cobalt catalyst-modified electrode displayed quite an interesting H₂-evolution activity compared with that of bare electrodes. These results are encouraging for the future potential application of 1 in water splitting.

---

Introduction

The consequential climate change and incessant global warming due to the massive emission of greenhouse gasses (such as CO₂) pose an urgent challenge to the sustainable development of natural systems and humans.¹ It is of grave concern that the greenhouse gas concentration reached as high as 407 ppm in 2017, the highest level of the past 800 000 years. This has directed research efforts towards the development of renewable and carbon neutral fuels.² Electrochemical hydrogen evolution from the reduction of water or proton sources using cheap and earth-abundant transition metal complexes as catalysts is a potentially attractive and sustainable route for future hydrogen supply.³ Organic precursors with metals such as Co, Ni, Fe, and Cu as central and active parts of the catalyst for hydrogen generation have been intensively studied.^4–7 In recent decades, cobalt complexes of various macrocyclic ligands such as polypyridines, porphyrins, Schiff bases, phthalocyanines, and other macrocycles have been investigated and employed as efficient electrocatalysts for molecular hydrogen evolution.⁸ Since the central metal ions play a significant role in catalysis, the presence of more than one metal center in the catalyst contributes to its better activity. Although metal complexes of Schiff bases have already been used as electrocatalysts for H₂ evolution,⁹ research is ongoing, mainly focused on mononuclear molecular catalysts to work in organic solvents upon the addition of H₂O or acid as a proton source. Moreover, there are a few studies in the literature about heterogenous catalysis in neutral aqueous solutions employing dinuclear metal complexes,¹⁰ but the reported metal derivatives are not anchored with pyrazole-based ligand systems.

Turning our focus to sterically bulky bis(pyrazolyl)acetate precursors,¹¹ we synthesized a new dinuclear Co(II) derivative, [Co(bdtbpza)(NCS)]₂ (1), in a satisfactory yield, whose structure was elucidated through X-ray diffraction analysis on single crystals. The dinuclear cobalt complex was deposited onto an electrode surface by continuous sweeping during cyclic voltammetry and used for electrochemical H₂ evolution in a neutral aqueous solution. Our catalytic activity study using CV and CPE showed unprecedented catalytic activity and low overpotential when compared with the control experiment with bare electrodes. The evolution of H₂ gas was detected by gas chromatographic (GC) techniques employing a TCD detector and its amount was determined using the calibration curve of standard hydrogen. Different spectroscopic techniques, such as infrared spectroscopy (IR), ultraviolet–visible (UV–Vis), and electron paramagnetic resonance (EPR), were employed for the characterization of the dinuclear Co(II) derivative 1. DFT study was performed to gain insights for a theoretical interpretation of the temperature-dependent magneto–structural correlations of complex 1.

Results and discussion

Synthesis and characterization

The ‘scorpionate’-type precursor bdtbpza was derived according to a literature procedure.¹¹ Here, the treatment of two equivalents of 3,5-di-tert-butylpyrazole and an excess of potassium hydroxide, potassium carbonate, and a small amount of benzyltriethylammonium chloride, acting as the phase-transfer catalyst, in dichloromethane yielded bis-(3,5-di-tert-butylpyrazol-1-yl)methane (bdtbpzm). Later, the combination of bdtbpzm and nBuLi in tetrahydrofuran under a CO₂ source gave the desired product (bdtbpza), which was washed in pentane. A mixture of bdtbpza, CoCl₂·6H₂O, and NaSCN in MeOH/H₂O solution furnished the dinuclear Co^II derivative (1) (see Scheme 1).

Scheme 1 Formation of complex 1.

Complex 1 was isolated in good yield with perfect purity and characterized by different spectroscopic analyses. The IR spectra of the ligand and of the metal derivative were measured in the range of 4000–400 cm⁻¹ (as KBr pellets). The carboxylate group could be easily detected by infrared spectroscopy because of its strong, characteristic absorbance, which disappears upon conversion to the acid form.¹² The strong band at 2970 cm⁻¹ in both the ligand and complex 1 could be attributed to the ν_C–H stretching of the –CH–COOH moiety. The sharp band at 1740 cm⁻¹, corresponding to the asymmetric stretching vibration of ν_as(COO) in the free ligand, was shifted considerably to much lower frequency at 1646 cm⁻¹, indicating coordination between the metal ion and the carboxylic moiety.¹³ The symmetric stretching band ν_sym(COO) observed at 1366 cm⁻¹ remained almost unchanged in 1 compared with the band for the free ligand. The fact that the asymmetric bond decreased significantly with the increase in bond length (due to the coordination to cobalt), whereas the symmetric C=O band remained invariant, is an indication that only one O atom of the –COO group participated in bonding, bridging two metal ions, while the other C=O remained uncoordinated. Other intense bands were found in the region of 1530–1540 cm⁻¹, which corresponded to ν_(C=N)Pz.¹⁴ The strong sharp band at 2065 cm⁻¹ was attributed to the stretching vibration ν_(SCN).

Crystal structure

The molecular structure of 1 in the solid state was elucidated through X-ray diffraction analysis on single crystals. It consisted of a centrosymmetric, dimeric complex with the general formula [Co(bdtbpza)(NCS)]₂ [bdtbpza = bis(3,5-di-t-butylpyrazol-1-yl)acetate] that crystallizes in the monoclinic space group P21/c (see Fig. 1). Its asymmetric unit comprises one Co(II) cation, one mono-negative ligand bdtbpza, and one isothiocyanate anion.

Fig. 1 Molecular structure of 1 with a partial labeling scheme of the atoms belonging to the asymmetric unit. The symmetry code to generate the whole complex is −x, −y + 1, −z + 1. The H atoms of the tert-butyl groups have been omitted for clarity.

Each Co(II) is penta-coordinated showing a distorted trigonal–bipyramidal geometry, with a τ₅ value of 0.84 (where τ₅ = 0 represents a perfect square pyramid and τ₅ = 1 represents a perfect trigonal bipyramid), following the classification introduced by Addison and coworkers.¹⁵ For the cobalt center Co1, the axial positions are occupied by the nitrogen atom N 1S of one isothiocyanate anion and by the acetate oxygen atom O1ⁱ (i = −x, −y + 1, −z + 1) of the symmetry-related bdtbpza ligand, which, along with O1, bridges the two metal centers Co1 and Co1ⁱ at a distance of 3.522(1) Å. The atoms O1 (acetate), N2ⁱ, and N4ⁱ (imidazole) complete the coordination in the equatorial positions. Overall, bdtbpza acts as a tetradentate bridging ligand forming two five-membered chelation rings (O1–C1–C2–N3–N4 and N2–N1–C2–N3–N4) at an angle of 65.44(3)° with respect to each other. The bond distances and angles are in the normal range for this type of compounds (see Table 1 for selected geometrical parameters).

Table 1 Selected bond lengths [Å] and angles [°] for 1

Symmetry code: (i) −x, −y + 1, −z + 1.
Co1—N1S	1.975 (3)	N1S—Co1—N4^i	100.60 (11)
Co1—N2^i	2.041 (2)	O1—Co1—N4^i	125.06 (9)
Co1—N4^i	2.057 (2)	N2^i—Co1—N4^i	97.48 (10)
Co1—O1	1.980 (2)	N1S—Co1—O1^i	175.84 (10)
Co1—O1^i	2.327 (2)	O1—Co1—O1^i	70.57 (9)
N1S—Co1—O1	113.33 (10)	N2^i—Co1—O1^i	77.77 (9)
N1S—Co1—N2^i	98.81 (11)	N4^i—Co1—O1^i	77.66 (9)
O1—Co1—N2^i	117.21 (9)

---

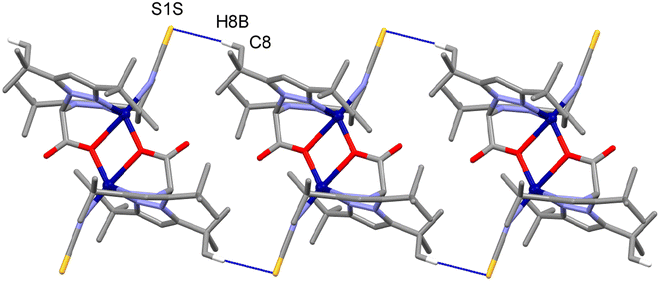
In the crystal, the main supramolecular contacts directing the packing are C8–H8B⋯S1S(−x + 1,−y + 1,−z + 1) interactions, which give rise to chains running along the a-axis direction of the unit cell [C8–H8B⋯S1S: 3.840(4) Å and 171.1(2)°], held together by dispersion forces (see Fig. 2 and 3).

Fig. 2 View of the supramolecular chains formed by 1 along the a-axis direction of the unit cell. The C–H⋯S interactions are represented as blue dotted lines. For clarity, only the H atoms involved in the interactions are shown.

Fig. 3 Crystal packing of 1 viewed down the crystallographic a axis, highlighting different chains held together by dispersion forces. H atoms have been omitted for clarity. The b and c axis are represented in green and blue, respectively.

A search in the Cambridge Structural Database (CSD, Version 5.38, update August 2018)¹⁶ for dimeric complexes containing the ligand bdtbpza yielded three hits with the ref. codes BEDLAY,¹⁷ CUMNOP, and CUMNUV.¹⁸ BEDLAY and CUMNUV are a Fe(II) and a Co(II) complex, respectively; the coordination mode of bdtbpza is analogous to the one displayed in the title compound, but with chloride (BEDLAY) or nitrate (CUMNUV) instead of isothiocyanate as counter ions completing the coordination sphere of the metal, which has a distorted trigonal–bipyramidal geometry. In the case of CUPNOV, which is a copper coordination compound, the binding mode of bdtbpza is different, and involves both oxygen atoms of the acetate moiety bridging the two metal centers, yielding a square-pyramidal coordination completed by the nitrate anion acting as a monodentate ligand.

Electronic spectra

The UV–Vis absorption spectrum of complex 1 was recorded in HPLC grade methanol in the region of 200–800 nm (see Fig. 4). The free ligand showed mainly a strong band at 230 nm (probably due to π → π* transitions) along with other weak bands around 260 nm.¹⁹ The metal complex exhibited high energy bands at 214 and 281 nm, which are analyzed below and were shifted with respect to the ligand due to complexation. In the spectrum, a much weaker, less well-defined and broad band originated at lower energy regions (470 and 520 nm) associated with transitions involving the metal orbitals. This is a specific indication of a Co(II) derivative with the metal in a five-coordination environment.²⁰

Fig. 4 Electronic spectrum of complex 1, measured in methanol; inset shows an enlargement of the 400–700 nm region.

TD-DFT calculations, detailed in the ESI,† were conducted to investigate the bands in complex 1. The full analysis is available in the ESI,† with key findings discussed here. The first significant band according to the TD-DFT calculations was found at 579 nm with an oscillator strength of 0.0033, which aligns reasonably with the experimental band observed at 520 nm. This band, characterized as S₀ → S₁₂ excitation, involves transitions primarily from HOMO → LUMO+3 and HOMO−1 → LUMO+2, among others. Given that the HOMO and HOMO−1 are delocalized across both metal and ligand, while the LUMOs are localized at the metal centers, this band exhibited characteristics of both ligand–metal charge transfer (LMCT) and metal–metal charge transfer (MMCT). Plots of the relevant molecular orbitals are provided in the ESI, Fig. S2 and Table S1.† Other significant bands at 296 (f = 0.0344) and 292 (f = 0.0269) nm from the TD-DFT matched an experimental band at 281 nm, corresponding to S₀ → S₂₈ and S₀ → S₂₉ excitations. This band involved multiple transitions: HOMO−5 → LUMO+3, HOMO−4 → LUMO+2, HOMO−1 → LUMO+3, and HOMO → LUMO+2, featuring a mix of LMTC and MMCT characteristics, as detailed in the ESI.† The highest energy band predicted at 214 nm was not observed in the TD-DFT analysis, likely because it exceeded the upper limit of the calculated states, capped at the S₄₀ state.

EPR spectra

The EPR spectra were recorded on a polycrystalline powder of 1 as a function of the temperature. The spectra measured at 298, 180, and 77 K are shown in Fig. 5. The spectrum at room temperature was almost silent with only a weak absorption at 1576 Gauss (as indicated by the arrow in Fig. 5). This weak resonance could be attributed to the “forbidden” ΔM_S = ±2 resonance, often observed in the case of dinuclear metal complexes (e.g., with Cu^II) in a doublet spin state.²¹ The small distance between the two Co^II ions would support the magnetic interaction between the two paramagnetic centers. With decreasing temperature, a broad absorption centered at g_eff ∼ 4.2 was revealed. Superimposed to the signal, ΔM_S = ±2 resonance at 1572–1574 Gauss was also detected.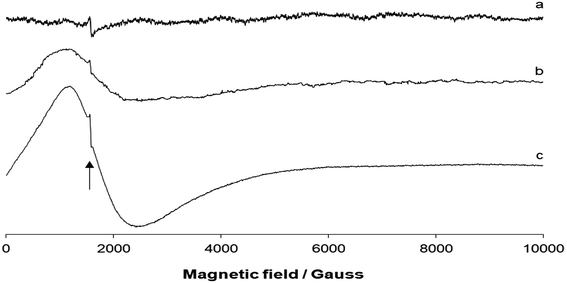

Fig. 5 X-band EPR spectra of the polycrystalline powder of 1: (a) at 298 K, (b) 180 K, and (c) 77 K. The position of the “forbidden” ΔM_S = ±2 resonance is indicated by the black arrow.

The EPR theory predicts g = 4.33 for high-spin octahedral Co^II complexes,²² and an intense band in the range of 6.3–6.7 for trigonal–bipyramidal Co^II species.²³ Overall, the lack of the signal at 298 K,²⁴ the “forbidden” ΔM_S = ±2 resonance, and the appearance of the broad signal between g_eff ∼ 7 and g_eff ∼ 3 were features indicative of a dinuclear high-spin Co^II complex.

Magnetic property

The analysis of magnetic properties of complex 1 in the form of a χ_MT vs. T plot (where χ_M is the molar magnetic susceptibility for two Co²⁺ ions) is shown in Fig. 6. The value of χ_MT at 300 K was 4.40 cm³ mol⁻¹ K, slightly higher than that expected for two isolated spin-only ions (χ_MT = 3.75 cm³ mol⁻¹ K for two isolated S = 3/2 ions). This indicates a g factor higher than 2.0, which was probably due to the effects of the magnetic anisotropy associated with each high-spin Co(II) ion. When lowering the temperature, the χ_MT product continuously decreased and reached a minimum of 2.45 cm³ mol⁻¹ K at 2 K.

Fig. 6 Plot of χ_MT vs. T for complex 1. The solid line corresponds to the best fit (see text). The inset shows the plot of the reduced magnetization M/Nβ vs. applied field H at 2 K.

The shape of this curve can be caused by either the spin–orbit coupling (SOC) of each Co(II) ion, antiferromagnetic exchange between the two Co(II) ions, or both.²⁵ It is well known that orbital angular momentum is totally or partially quenched depending on the ligand field symmetry,²⁶ and its effect is strongly related to the symmetry around the metal ion. To the best of our knowledge, from a magnetic point of view there are only a few cases of studies on Co(II) either with a trigonal–bipyramidal symmetry (TBP) or square-pyramidal symmetry (SP),²⁷ contrary to octahedral or tetrahedral Co(II) complexes, which have been intensively studied.²⁸ The magnetism of high-spin Co(II) complexes of a TBP or SP symmetry can be divided into two classes: (a) a regular SP or TBP symmetry where the ground term has an orbital angular momentum, and the spin–orbit treatment is valid; (b) a highly distorted lower symmetry case, where the spin–orbit coupling effect is dissipated for both of them. However, slight distortion can cause a non-completely quenched SOC.²⁹ Based on the comments above, the magnetic susceptibility data for 1 were analyzed first by using a conventional isotropic spin Hamiltonian H = −J (S₁·S₂) for the S_i = 3/2 system. All attempts to fit the magnetic data by using the PHI program³⁰ failed, and no satisfactory fits were achieved by considering the crystal-field effects. Indeed, the only successful fit was based upon an isotropic exchange J in the dinuclear unit taking into account the SOC effects (S = 3/2 and L = 1). The best fit of the experimental data gave the following parameters J = −0.43 cm⁻¹, g = 2.05, and λ (spin–orbit parameter) = −39.3 cm⁻¹ with an error R = 6.637 × 10⁻⁵, where R = ∑[(χ_MT)_exp − (χ_MT)_cal]²/∑(χ_MT)_exp². In the fitting process, the orbital reduction factor σ was fixed as 1.1.³⁰ The reduced molar magnetization (M/Nß) per Co(II) dinuclear unit tended to 3.6 electrons for 1 (inset Fig. 6). This value is less than that expected for two isolated Co(II) ions not coupled (5–6Nß). This feature agrees with the weak antiferromagnetic coupling within the Co(II) ions. The small exchange coupling parameter found (J) could be related to the poor overlap between the equatorial (short distance: 1.980 Å) and axial (long distance: 2.327 Å) orbitals that participate in the magnetic pathway leading, in this way, to almost negligible coupling.

DFT calculations

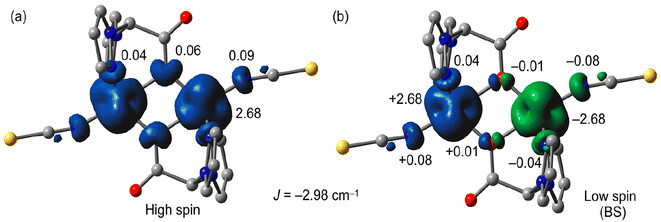
We used B3LYP/6-31+G* calculations (broken-symmetry approach, see theoretical methods) to evaluate the magnetic coupling constant J in 1. The theoretical value of J (−2.98 cm⁻¹) was in reasonable agreement with the experimental one (−0.43 cm⁻¹) and confirmed the weak antiferromagnetic coupling. To investigate the mechanism for the magnetic exchange coupling, the spin density distribution was analyzed. The atomic spin population values on the Co metal centers and the donor atoms of the ligands are included in Fig. 7 along with the spin density plots for the high-spin and low-spin (broken-symmetry) configurations. For the high-spin (HS) configuration (see Fig. 7a), the Mulliken spin population data showed that some of the spin (ca. 0.32 e) was delocalized through the ligands, and the rest (2.68 e) was supported by the Co ions in both the “broken-symmetry” wave function and the high-spin state for complex 1 (α and β spin states are represented by blue and green signs, respectively). The broken-symmetry spin population values at the magnetic centers were ±2.68 e and ∼10% of the spin was delocalized to the ligand framework. The spin on the acetate O-atoms was 0.06 e in the HS state and ±0.01 e in the broken-symmetry state of complex 1, consequently, the bridging oxygen atoms mediate the magnetic exchange. The low spin density observed in the bridging O atoms of the HS state agreed with the small experimental exchange coupling.

Fig. 7 Spin density (contour 0.004 e Å⁻³) plots in the high-spin (a) and low-spin (b) configurations of complex 1. Positive spin is represented in blue and negative spin in green. Spin density at selected atoms is also given. The tbutyl groups and H atoms have been omitted for the sake of clarity.

Plots of the magnetic orbitals are given in Fig. 8 showing the main contribution of the d atomic orbitals of the Co atoms along with an almost negligible contribution of the p orbitals of the bridging O atoms, thus revealing a minimum overlap of the orbitals that participate in the magnetic pathway.

Fig. 8 Magnetic orbitals (a–f) and energies retrieved from the broken symmetry solution of complex 1; t-Butyl groups and H-atoms omitted for the sake of clarity. Isosurface value for plotting orbitals is 0.04 a.u.

Electrochemical characterization

The electrochemical redox properties of the compound were studied by cyclic voltammetry (CV) in DMSO using graphite as the working electrode, Pt as the counter electrode, and Ag wire as the reference electrode at RT and at scan rate of 0.1 V s⁻¹. The results (as shown in Fig. 9) indicated the reversible redox process at E_1/2 = −0.68 V vs. NHE, which was assigned to the reduction couple Co²⁺/Co⁺¹. Moreover, a weak irreversible oxidation peak was observed at E_1/2 = −0.2 V vs. NHE, which was due to the possible oxidation of Co(II) to Co(III). The ligand as well as the cobalt salt were electrochemically silent in the potential range where the metal–ligand complex showed redox peaks. Thus, the redox potential peaks observed were due to the metal ion (as explained above), and not due to the ligand or free metal salt.

Fig. 9 CV plot of 1 mM catalyst in DMSO using graphite as the working electrode, Pt as the counter electrode, and Ag wire as the reference electrode at RT and at a scan rate of 0.1 V s⁻¹.

The catalytic-type irreversible reduction current at E_1/2 = −1.2 V vs. NHE may be due to catalytic reduction of the residual proton of the solvent by the metal complex. This finding suggests the potential application of complex 1 for the electrochemical reduction of protons/H₂O to generate molecular hydrogen.

Catalytic hydrogen-evolution study in aqueous solution

Inspired by the promising catalytic current of the complex in an organic solvent, a hydrogen-evolution catalysis study was conducted in neutral aqueous solution by using a catalyst-modified graphite electrode as the working electrode, Pt as the counter electrode, and Ag wire as the reference electrode, at RT and at a scan rate of 0.1 V s⁻¹ (Fig. 10). The catalyst-modified electrode was obtained by using continuous swiping techniques of the electrode in a solution of the catalyst in which it was swept for 100 cycles in the potential window from +1.25 to −1.25 V vs. NHE. The modified electrode was then taken out and immersed in DMSO and then water for 5 m in each solvent to remove any loosely attached catalyst. Then, taking the catalyst-modified electrodes, cyclic voltammetry (CV) and CPE (controlled potential electrolysis) experiments were performed. As can be seen from Fig. 10, the catalyst-modified electrode showed enhanced catalytic current with reduced overpotential (black curve) when compared with the control experiment (bare electrode, red curve).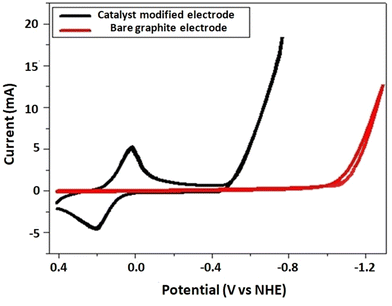

Fig. 10 CV plot in 2 M Kpi using graphite as the working electrode, Pt as the counter electrode, and Ag wire as the reference electrode at RT and at a scan rate of 0.1 V s⁻¹.

Thus, the reduction catalytic peak was sharply amplified at E_1/2 = −0.48 V vs. NHE for a catalyst-modified electrode. For the bare electrode, the catalytic current started to grow at E_1/2 = −1.05 V vs. NHE, with an overpotential of 530 mV, indicating a tremendous catalytic current enhancement at lower potential for the catalyst-modified electrode in neutral aqueous solution. To further explore the catalytic activity of the modified electrode, we conducted a controlled potential electrolysis at −1.4 V vs. NHE for 30 m. The amount of charge accumulated/current passing through the system was higher for the catalyst-modified electrode when compared with the control experiment with bare electrode (Fig. 11).

Fig. 11 CPE plot in 2 M Kpi at pH 7, using graphite as the working electrode, Pt as the counter electrode, and Ag wire as the reference electrode at RT and at an applied potential of −1.4 V vs. NHE.

The electrolysis was carried out in an air-tight electrochemical system at −1.4 V vs. NHE, producing 61.8C of charge after 30 m. Since 1 mol of electron is equal to 1 F or 96 485C, the charge produced after 30 m (61.8C) is equal to 639 μmol of electrons. To generate 1 mol of H₂, two moles of electrons are required (2H⁺ + 2e⁻ = H₂). Accordingly, assuming under 100% faradaic efficiency, 639 μmol of electrons are equivalent to 319.5 μmol of H₂. Following controlled potential electrolysis, the headspace of the reaction was analyzed by GC, as shown in Fig. 12.

Fig. 12 GC chromatogram of the headspace gas before and after bulk electrolysis at different time intervals. The headspace gas was analyzed following the controlled potential electrolysis of the catalyst-modified glassy carbon electrodes in 2 M potassium phosphate buffer solution (pH 7), at room temperature.

The amount of H₂ was measured using the calibration curve equation for standard H₂. After 30 m of electrolysis, a GC chromatogram with a peak area of 6000 was obtained and the amount of H₂ from GC (practical yield) was estimated to be 267.5 μmol of H₂. Hence, the faradaic efficiency of the catalysis was 83.7%. Since it is difficult to evaluate the amount of catalyst loaded onto the electrode surface, we could not determine the TON/TOF of the catalyst in this study.

Conclusion

A new di-carboxylato-bridged Co(II) derivative incorporating the precursor bdtbpza {bis-(3,5-di-tert-butylpyrazol-1-yl)acetate} was furnished and several spectral studies were executed for its characterization. The magnetic study revealed that there was a weak antiferromagnetic interaction between the two Co(II) centers, which was also evidenced by density functional theory calculations. Successively, we investigated the electrochemical hydrogen generation of a graphite electrode modified with the complex (which was based on a cheap and earth-abundant metal) in aqueous solution. The enhanced high catalytic current with a low overpotential for the catalyst-modified electrode showed the quantitative evolution of hydrogen and a promising potential application of the complex to be used as an electrocatalyst for water splitting. Following the encouraging results for electrochemical H₂ generation, in our laboratory we are currently planning to work on photo-electrochemical CO₂ reduction by employing different metal complexes with porphyrin moieties.

Experimental section

Materials

All the experiments were carried out under aerobic conditions. All solvents were of reagent grade and used without further purification. CoCl₂·6H₂O and sodium thiocyanate were purchased from Aldrich Chemicals. 3,5-Di-tert-butylpyrazol, KOH, K₂CO₃, and benzyltriethylammonium chloride were purchased from Showa Chemicals. The ligand bis-(3,5-di-tert-butylpyrazol-1-yl)acetic acid (bdtbpza) was prepared according to a literature procedure.¹¹

Physical measurements

Microanalytical data (C, H, and N) were collected on a PerkinElmer 2400 CHNS/O elemental analyzer. FTIR spectra were recorded on a PerkinElmer RX-1 spectrophotometer in the range of 4000–400 cm⁻¹ as KBr pellets. EPR spectra were recorded from 0 to 10 000 Gauss as a function of an organic solution on an X-band Bruker EMX spectrometer equipped with a HP 53150A microwave frequency counter. The microwave frequency was 9.40 or 9.41 GHz, the microwave power was 20 mW (below the saturation limit with the ER4119 HS resonator), the time constant was 81.92 ms, the modulation frequency was 100 kHz, the modulation amplitude was 0.4 mT, and the resolution was 8192 points. Magnetic measurements were carried out at “Servei de Magnetoquímica (Universitat de Barcelona)” on a polycrystalline sample (30 mg) with a Quantum Design SQUID MPMS-XL magnetometer apparatus working in the range of 2–300 K under a magnetic field of approximately 5000 G. The diamagnetic corrections were evaluated from Pascal's constants.

Synthesis of the ligand

Synthesis of bis(3,5-di-tert-butylpyrazol-1-yl)methane (bdtbpzm). 3,5-Di-tert-butylpyrazol (3.00 g, 16.64 mmol), KOH (3.60 g, 64.16 mmol), K₂CO₃ (9.00 g, 65.12 mmol), and benzyltriethylammonium chloride (0.5 g) were dissolved together in dichloromethane (100 mL) and refluxed for 5 h. After removing the salts by filtration, the filtrate was concentrated in vacuo to dryness. The white residue was dissolved in water and extracted with pentane (2 × 150 mL). The organic layer was dried over CaSO₄ and the solvent removed in vacuo. The white residue was recrystallized from pentane to give the desired product (bdtbpzm) as a white powder, which was dried again in vacuo. Yield 2.40 g (77%).

Synthesis of bis(3,5-di-tert-butylpyrazol-1-yl)acetic acid (bdtbpza). A solution of bis(3,5-di-tert-butylpyrazol-1-yl)methane (bdtbpzm) (2.30 g, 6.17 mmol) in tetrahydrofuran (50 mL) was treated with nBuLi (1.6 M solution in hexane, 4 mL, 6.40 mmol) at −70 °C. The solution was allowed to warm to −45 °C under a CO₂ source during a period of 4 h and finally poured into 200 g of crushed dry ice. After reaching room temperature, the solvent was removed in vacuo and the white residue was dissolved in water (100 mL). The aqueous solution was acidified with half concentrated HCl to pH 1 and extracted with diethyl ether (3 × 100 mL). The combined organic layers were dried (Na₂SO₄) and concentrated in vacuo to give a honey-like yellow oil. The product was crystallized within two days when stored at room temperature under air. The white crystalline substance was washed with pentane to remove unreacted bis(3,5-di-tert-butylpyrazol-1-yl)methane (bdtbpzm), which gave bdtbpza as a colorless powder. Yield 2.2 g (77%).

Synthesis of complex (1). To a methanol solution (10 mL) of CoCl₂·6H₂O (0.237 g, 1 mmol), bdtbpza (1 mmol) in 15 mL of methanol was added under constant stirring. The resulting green solution was kept boiling for 10 m. After that and still under heat, a 10 mL water solution of NaSCN (0.081 g, 1 mmol) was added under constant stirring and then, the mixture was kept undisturbed in a refrigerator. Dark-brown rectangular-shaped single crystals of 1 were generated after one week. These were separated by filtration and air-dried before X-ray diffraction analysis. Yield: 0.64 g. Anal. calc. for C₅₀H₇₈O₄N₁₀S₂Co₂: C, 56.33; H, 7.38; N, 13.14. Found: C, 56.67; H, 7.17; N, 12.89%.

X-Ray crystallography

The crystal structure of complex 1 was determined by X-ray diffraction methods. Intensity data and cell parameters were recorded at 293(2) K on a Bruker ApexII diffractometer (MoKα radiation λ = 0.71073 Å) equipped with a CCD area detector and a graphite monochromator. The raw frame data were processed using the programs SAINT and SADABS to yield the reflection data files.³¹ The structure was solved by Direct Methods using the SIR97 program³² and refined on F_o² by full-matrix least-squares procedures, using the SHELXL-2014/7 program³³ in the WinGX suite v.2014.1.³⁴ All non-hydrogen atoms were refined with anisotropic atomic displacements; the carbon-bound H atoms were placed in calculated positions and refined isotropically using the riding model with C–H ranging from 0.93 to 0.98 Å and U_iso(H) set to 1.2–1.5U_eq(C). The weighting scheme used in the last cycle of the refinement was w = 1/[σ²F_o² + (0.0113P)² + 1.2694P], where P = (F_o² + 2F_c²)/3. The crystal data and experimental details for the data collection and structure refinement are reported in Table S2.† Crystallographic data for the structure reported have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication no. CCDC 2337161.†

Theoretical methods

The magnetic properties of compound 1 were computed using the Gaussian 09 package³⁵ using density functional theory (DFT) combined with the broken-symmetry approach.³⁶ We used the hybrid B3LYP³⁷ functional and the 6-31+G* basis set,³⁸ because it is a good compromise between the size of the systems and the accuracy of the method. We used the solid-state geometry of the complex and we optimized the positions of the hydrogen atoms. The α-HOMOs and β-HOMOs in the BS state were considered as the magnetic orbital. For the TD-DFT calculations, the MeOH solvent was simulated using the PCM method³⁹ and the first 40 excited states were considered.

Conflicts of interest

We wish to assure that our manuscript does not contain any “conflicts of interest”.

Acknowledgements

KD expresses her appreciation to the SERB (Science and Engineering Research Board, India) Grant (PDF/2016/002832) for financial assistance. AD and CHH would like to acknowledge the Ministry of Science and Technology, Taiwan for financial assistance.

References

1. (a) K. R. Gurney, D. L. Mendoza, Y. Zhou, M. L. Fischer, C. C. Miller and S. Geethakumar, Environ. Sci. Technol., 2009, 43, 5535–5541; (b) K. R. Gurney, Y. Song, J. Liang and G. Roest, Environ. Sci. Technol., 2020, 54, 9896–9907.
2. (a) C.-C. Lee and J. Hussain, Innov. Green Dev., 2022, 1, 100002; (b) H. Feng, Front. Environ. Sci., 2022, 10, 1–16; (c) D. Broadstock, Q. Ji, S. Managi and D. Zhang, Resour., Conserv. Recycl., 2021, 169, 105472.
3. (a) S. Aralekallu, L. K. Sannegowda and V. Singh, Int. J. Hydrogen Energy, 2023, 48, 16569–16592; (b) M. Drosou, F. Kamatsos and C. A. Mitsopoulou, Inorg. Chem. Front., 2020, 7, 37–71; (c) T. Wang, H. Xie, M. Chen, A. D'Aloia, J. Cho, G. Wu and Q. Li, Nano Energy, 2017, 42, 69–89; (d) K. E. Dalle, J. Warnan, J. J. Leung, B. Reuillard, I. S. Karmel and E. Reisner, Chem. Rev., 2019, 119, 2752–2875; (e) V. R. Bakuru, M. E. Dmello and S. B. Kalidindi, ChemPhysChem, 2019, 20, 1177–1215; (f) C. Zhang, E. Prignot, O. Jeannin, A. Vacher, D. Dragoe, F. Camerel, Z. Halime and R. Gramage-Doria, ACS Catal., 2023, 13, 2367–2373; (g) V. A. Larson and N. Lehnert, ACS Catal., 2024, 14, 192–210.
4. (a) J. Li, S. Zhang, J. Wang, X. Yin, Z. Han, G. Chen, D. Zhang and M. Wang, Molecules, 2022, 27, 1399–1404; (b) D. Dolui, S. Khandelwal, P. Majumder and A. Dutta, Chem. Commun., 2020, 56, 8166–8181; (c) S. Khandelwal, A. Zamader, V. Nagayach, D. Dolui, A. Q. Mir and A. Dutta, ACS Catal., 2019, 9, 2334–2344.
5. (a) J. P. Cao, T. Fang, L. Z. Fu, L. L. Zhou and S. Z. Zhan, Int. J. Hydrogen Energy, 2014, 39, 10980–10986; (b) M. L. Helm, M. P. Stewart, R. M. Bullock, M. R. DuBois and D. L. DuBois, Science, 2011, 333, 863–866.
6. (a) A. D. Nguyen, M. D. Rail, M. Shanmugam, J. C. Fettinger and L. A. Berben, Inorg. Chem., 2013, 52, 12847–12854; (b) F. Quentel, G. Passard and F. Gloaguen, Energy Environ. Sci., 2012, 5, 7757–7761; (c) M. E. Carroll, B. E. Barton, T. B. Rauchfuss and P. J. Carroll, J. Am. Chem. Soc., 2012, 134, 18843–18852.
7. (a) L. L. Zhou, T. Fang, J. P. Cao, Z. Zhu, X. Su and S. Z. Zhan, J. Power Sources, 2015, 273, 298–304; (b) A. Datta, K. Das, B. B. Beyene, E. Garribba, M. J. Gajewska and C.-H. Hung, Mol. Catal., 2017, 439, 81–90; (c) J. P. Cao, T. Fang, L. Z. Fu, L. L. Zhou and S. Z. Zhan, Int. J. Hydrogen Energy, 2014, 39, 13972–13978; (d) J. P. Cao, T. Fang, Z. Q. Wang, Y. W. Ren and S. Z. Zhan, J. Mol. Catal. A: Chem., 2014, 391, 191–197.
8. (a) S. Natesakhawat, J. W. Lekse, J. P. Baltrus, P. R. Ohodnicki, B. H. Howard, X. Deng and C. Matranga, ACS Catal., 2012, 2, 1667–1676; (b) H.-B. Cui, J.-H. Li, X. Zhang, M. Zhou, Z.-Z. Huang, Y.-C. Lai, J.-X. Qiu, Y.-J. Ren and H.-X. Zhang, Int. J. Hydrogen Energy, 2023, 48, 10891–10902; (c) J. Liu, R.-Z. Liao, F. W. Heinemann, K. Meyer, R. P. Thummel, Y. Zhang and L. Tong, Inorg. Chem., 2021, 60, 17976–17985; (d) Y. Sun, J. P. Bigi, N. A. Piro, M. L. Tang, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2011, 133, 9212–9215; (e) A. E. King, Y. Surendranath, N. A. Piro, J. P. Bigi, J. R. Long and J. C. Chang, Chem. Sci., 2013, 4, 1578–1587.
9. (a) S. Khandelwal, A. Zamader, V. Nagayach, D. Dolui, A. Q. Mir and A. Dutta, ACS Catal., 2019, 9, 2334–2344; (b) C.-B. Li, P. Gong, Y. Yang and H.-Y. Wang, Catal. Lett., 2018, 148, 3158–3164; (c) B. B. Beyene, K. Das, B. A. Kerayu, A. Datta and C.-H. Hung, Catal. Commun., 2019, 119, 111–114; (d) K. Das, B. B. Beyene, A. W. Yibeltal, S. Goswami, C. Massera, E. Garribba, A. Datta and C.-H. Hung, Catal. Lett., 2020, 150, 2200.
10. (a) T. H. To, D. B. Tran, V. T. T. Ha and P. D. Tran, RSC Adv., 2022, 12, 26428–26434; (b) L. Tong, L. Duan, A. Zhou and R. P. Thummel, Coord. Chem. Rev., 2020, 402, 213079; (c) M. G. Papanikolaou, A. Elliott, J. McAllister, J. K. Gallos, A. D. Keramidas, T. A. Kabanos, S. Sproules and H. N. Miras, Dalton Trans., 2020, 49, 15718–15730.
11. A. Beck, B. Weibert and N. Burzlaff, Eur. J. Inorg. Chem., 2001, 521–527.
12. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Theory and Applications in Inorganic Chemistry, John Wiley and Sons, Inc., New York, 5th edn, 1997.
13. R. C. Mehrotra and R. Bohra, Metal Carboxylates, Academia Press, London, UK, 1983.
14. A. Beck, A. Barth, E. Hubner and N. Burzlaff, Inorg. Chem., 2003, 42, 7182–7188.
15. A. W. Addison, N. T. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356.
16. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
17. A. Beck, A. Barth, E. Hubner and N. Burzlaff, Inorg. Chem., 2003, 42, 7182–7188.
18. B. Kozlevčar, K. Jakomin, M. Počkaj, Z. Jagličić, A. Beyer, N. Burzlaff and N. Kitanovski, Eur. J. Inorg. Chem., 2015, 3688–3693.
19. A. B. P. Lever, Inorganic electronic spectroscopy, Elsevier Science, New York, 1984.
20. G. Dyer and D. W. Meek, J. Am. Chem. Soc., 1967, 89, 3983–3987.
21. T. D. Smith and J. R. Pilbrow, Coord. Chem. Rev., 1974, 13, 173–278.
22. A. Abragam and M. H. L. Pryce, Proc. R. Soc. London, A, 1951, 206, 173–191.
23. C. Benelli and D. Gatteschi, Inorg. Chem., 1982, 21, 1788–1790.
24. (a) A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, 1970; (b) R. S. Drago, Physical Methods in Chemistry, W. B. Saunders Company, Philadelphia, 1977; (c) L. Banci, A. Bencini, C. Benelli, D. Gatteschi and C. Zanchini, in Structures versus Special Properties, Springer, Berlin, 1982, pp. 37–86; (d) A. Bencini and D. Gatteschi, in Transition Met. Chem. (London), ed. G. A. Melson and B. N. Figgis, Marcel Dekker, New York, 1982, vol. 8, pp. 1–178.
25. (a) O. Kahn, Molecular Magnetism, VCH Publishers, New York, 1993; (b) R. L. Carlin, Magnetochemistry, Springer, Berlin, 1986; (c) F. E. Mabbs and D. J. Machin, Magnetism and Transition MetalscComplexes, Chapman and Hall, London, 1973.
26. B. N. Figgis and M. A. Hitchman, Ligand Field Theory and its Application, Wiley-VCH, New York, 2000.
27. (a) B. Kozlevcar, K. Jakomin, M. Pockaj, Z. Jaglicic, A. Beyer, N. Burzlaff and N. Kitanovski, Eur. J. Inorg. Chem., 2015, 3688–3693; (b) M. Sarkar, R. Clérac, C. Mathonier, N. C. R. Hearns, V. Bertolasi and D. Ray, Eur. J. Inorg. Chem., 2009, 4675–4685; (c) X. Hou, X. Wang, X. Liu, J. Wang, L. Tang and P. Ju, New J. Chem., 2018, 42, 8583–8590.
28. (a) F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445 and references therein; (b) M. Fondo, N. Ocampo, A. M. García-Deibe, M. Corbella, M. Salah El Fallah, J. Cano, J. Sanmartín and M. R. Bermejo, Dalton Trans., 2006, 4905–4913.
29. J. Ribas, Coordination Chemistry, Wiley-VCH, Weinheim, 2008.
30. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
31. SADABS Bruker AXS, Madison, Wisconsin, USA, 2004; SAINT, Software Users Guide, Version 6.0, Bruker Analytical X-ray Systems, Madison, WI, 1999; G. M. Sheldrick, SADABS v2.03: Area-Detector Absorption Correction, University of Göttingen, Germany, 1999.
32. A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 32, 115–119.
33. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
34. L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta Jr, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
36. (a) L. J. J. Noodleman, Chem. Phys., 1981, 74, 5737–5743; (b) L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143; (c) L. Noodleman, C. Y. Peng, D. A. Case and J. M. Mouesca, Coord. Chem. Rev., 1995, 144, 199–244.
37. A. D. J. Becke, Chem. Phys., 1993, 98, 5648–5652.
38. R. Ditchfield, W. J. Hehre and J. A. Pople, Chem. Phys., 1971, 54, 724–728.
39. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2337161. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00807c

---