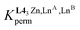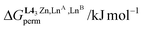Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Programming heterometallic 4f–4f′ helicates under thermodynamic control: the circle is complete†
Charlotte
Egger
a,
Laure
Guénée
b,
Neel
Deorukhkar
a and
Claude
Piguet
 *a
*a
aDepartment of Inorganic and Analytical Chemistry, University of Geneva, 30 quai E. Ansermet, CH-1211 Geneva 4, Switzerland. E-mail: Claude.Piguet@unige.ch
bLaboratory of Crystallography, University of Geneva, 24 quai E. Ansermet, CH-1211 Geneva 4, Switzerland
First published on 1st March 2024
Abstract
Three non-symmetrical segmental ligand strands L4 can be wrapped around a linear sequence of one Zn2+ and two trivalent lanthanide cations Ln3+ to give quantitatively directional [ZnLn2(L4)3]8+ triple-stranded helicates in the solid state and in solution. NMR speciations in CD3CN show negligible decomplexation at a millimolar concentration and the latter helicate can be thus safely considered as a preorganized C3-symmetrical HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ platform in which the thermodynamic properties of (i) lanthanide permutation between the central N9 and the terminal N6O3 binding sites and (ii) exchange processes between homo- and heterolanthanide helicates are easy to access (Ln = La, Eu, Lu). Deviations from statistical distributions could be programmed by exploiting specific site recognition and intermetallic pair interactions. Considering the challenging La3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eu3+ ionic pair, for which the sizes of the two cations differ by only 8%, a remarkable excess (70%) of the heterolanthanide is produced, together with a preference for the formation of the isomer where the largest lanthanum cation lies in the central N9 site ([(La)(Eu)]
Eu3+ ionic pair, for which the sizes of the two cations differ by only 8%, a remarkable excess (70%) of the heterolanthanide is produced, together with a preference for the formation of the isomer where the largest lanthanum cation lies in the central N9 site ([(La)(Eu)]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [(Eu)(La)] = 9
[(Eu)(La)] = 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). This rare design and its rational programming pave the way for the preparation of directional light-converters and/or molecular Q-bits at the (supra)molecular level.
1). This rare design and its rational programming pave the way for the preparation of directional light-converters and/or molecular Q-bits at the (supra)molecular level.
Introduction
The lack of radial node characterizing the atomic orbitals having n − l = 1 (n and l are the principal and azimuthal quantum numbers, respectively), often referred to as the primogenic effect,1 significantly contributes to the inner-shell pseudo-atomic character of the valence 4f orbitals in the trivalent lanthanides Ln3+ ([Xe]4fn, n = 0–14).2–4 The main consequence for chemistry results in a (very) similar reactivity of Ln3+ along the complete lanthanide series, which is only smoothly modulated by the stepwise 1% contraction of the ionic radii between adjacent elements.5–8 The molecular recognition of specific Ln3+, beyond the standard electrostatic trend,5–8 is therefore mainly lacking for coordination complexes in solution.9 This prevents the planned design of heterometallic polynuclear f–f′ assemblies in solution under thermodynamic control, except for some rare reports of deviations from statistical distributions in solution.10–14 Consequently, the planned implementation of pure heterometallic f–f′ molecular complexes in solution mainly relies on multistep strategies which exploit the kinetic inertness provided by the complexation of Ln3+ within rigid, highly preorganized and often anionic receptors (Fig. A1-1 in Appendix 1, see ESI†).15–26 By broadening the perspective, one realizes that energy barriers, responsible for kinetic inertness, thermodynamic stability and selectivity, may greatly benefit from long-range stacking interactions accompanying crystallization processes,27–29 and serendipitous pure f–f′ assemblies are therefore reported in crystalline materials (Fig. A1-2 in Appendix 1, see ESI†).30,31–40 The use of statistical doping has made it possible to temporarily circumvent these limits and myriads of doped ionic solids,41 nanoparticles,42,43 metal–organic frameworks30,44,45 or solid-state molecular aggregates and clusters46–49 have been prepared and explored for improving lighting and optical signaling in materials. However, the recent recognition35 that the (very) minor magnetic coupling operating between two different lanthanide Kramer's ions in non-statistical molecular heterometallic f–f′ entities represents a keystone for the design of basic information units in quantum computers, that is Q-bits,50 reactivates the efforts aiming at the preparation of pure (i.e. non-statistical) heterometallic lanthanide molecular complexes under thermodynamic control. With this in mind, Aromi and coworkers have developed some remarkable and versatile scaffolds consisting of fused didentate β-diketonate and tridentate 2,6-dipicolinate units for the formation of different binding pockets, which display size discriminating effects along the lanthanide series in the solid state, when three ligands are wrapped around two (Scheme 1)35–37 or more trivalent cations (Fig. A1–2d in Appendix 1, see ESI†).38–40 | ||
Scheme 1 a) Permutation (eqn 1-L1) and exchange (eqn 2-L1) equilibria proposed for the heterometallic HHT-[(L1)3LnALnB(NO3)(H2O)(pyridine)] complexes and (b) associated gas-phase DFT-computed energy changes.36 corresponds to the difference of nine-coordinate lanthanide ionic radii in the considered metallic pair.51 The linear trendlines are only a guide to the eye. (c) Crystal structure of HHT-[(L1)3LaEr(NO3)(H2O)(pyridine)].35 corresponds to the difference of nine-coordinate lanthanide ionic radii in the considered metallic pair.51 The linear trendlines are only a guide to the eye. (c) Crystal structure of HHT-[(L1)3LaEr(NO3)(H2O)(pyridine)].35 | ||
Focusing on HHT-[(L1)3LnALnB(NO3)(H2O)(pyridine)],36 impressive deviations (1 ≤ EA,Bperm ≤ 11 kJ mol−1 and −120 ≤ ΔHA,Bexch ≤ −14 kJ mol−1, Scheme 1b) from the expected statistical distributions (ΔGA,B, statperm = 0 kJ mol−1 for eqn 1-L1 and ΔGA,B, statexch = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(4) = −3.4 kJ mol−1 for eqn 2-L1) could be predicted by gas-phase DFT calculations assuming that the molecular structures observed in the crystalline state (Scheme 1c) are pertinent to initiate gas-phase modelling.36
ln(4) = −3.4 kJ mol−1 for eqn 2-L1) could be predicted by gas-phase DFT calculations assuming that the molecular structures observed in the crystalline state (Scheme 1c) are pertinent to initiate gas-phase modelling.36
To the best of our knowledge, related experimental thermodynamic data are available only for homometallic/heterometallic exchange eqn (2-L2) operating in the triple-stranded [(L2)3(LnA)(2−n)(LnB)n]6+ helicates (n = 0, 1, 2) in acetonitrile (Scheme 2a).10 One can note that the measured free energy changes −6 ≤ ΔGA,Bexch ≤ −14 kJ mol−1 in solution (Scheme 2b) drastically differ from the optimistic gas-phase DFT-predictions reported for HHT-[(L1)3LnALnB(NO3)(H2O)(pyridine)] (Scheme 1b).36
 | ||
Scheme 2 a) Thermodynamic exchange equilibria (eqn 2-L2) and (b) associated free energy changes of the triple-stranded [(L2)3(LnA)(2−n)(LnB)n]6+ helicates (x = 0, 1, 2) in CD3CN at room temperature.10 Only the HHH isomer is shown, but mixtures of HHH and HHT isomers exist in solution.  corresponds to the difference of nine-coordinate lanthanide ionic radii in the metallic pair.51 The dashed linear trendline is only a guide to the eye. (c) Crystal structure of HHH-[(L2)3LaEu](ClO4)6.10 corresponds to the difference of nine-coordinate lanthanide ionic radii in the metallic pair.51 The dashed linear trendline is only a guide to the eye. (c) Crystal structure of HHH-[(L2)3LaEu](ClO4)6.10 | ||
The unavoidable ligand permutation, which interconverts C3-symmetrical HHH-[(L2)3(LnA)(2−n)(LnB)n]6+ with its C1-symmetrical HHT-[(L2)3(LnA)(2−n)(LnB)n]6+ counterpart, severely limits further thermodynamic analysis and the target (trivial) lanthanide exchange process involving two well-defined and different binding sites proposed by Aromi in eqn (1-L1) for HHT-[(L1)3LnALnB(NO3)(H2O)(pyridine)] (Scheme 1) escaped quantification in solution with L2.
Connecting the three strands to a non-labile tripod seems to be the obvious choice for avoiding ligand scrambling and permutation, but structural constraints imposed by the helical wrapping of the strands required considerable synthetic efforts and delicate chemical design, which have been only approached once for the preorganized heterometallic dinuclear C3-symmetrical [L3LaLu]6+ podate (Scheme 3a).52–55 The free energy change estimated for the searched La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lu permutation summarized in eqn (1-L3) amounts to ΔGLa, Luperm = 12.1(1) kJ mol−1 (CD3CN at room temperature), but it entirely relies on the assumption that the mixing rule ΔEmix1–2 = ΔELa, Lu1–2 − ½(ΔELa, La1–2 + ΔELu, Lu1–2) = 0 is obeyed.56
Lu permutation summarized in eqn (1-L3) amounts to ΔGLa, Luperm = 12.1(1) kJ mol−1 (CD3CN at room temperature), but it entirely relies on the assumption that the mixing rule ΔEmix1–2 = ΔELa, Lu1–2 − ½(ΔELa, La1–2 + ΔELu, Lu1–2) = 0 is obeyed.56
 | ||
| Scheme 3 a) Thermodynamic permutation equilibrium (eqn 1-L3) estimated for [(L3)LaLu]6+ in CD3CN at room temperature.52 (b) Removal of HHH/HHT isomerism in the dinuclear-lanthanide triple-stranded helicates HHH-[(L43Zn)(LnA)(LnB)]8+ by using [Zn(pyridine-benzimidazole)3] as a preorganized non-covalent tripod.57 | ||
Rejuvenated by the challenge of preparing pure f–f′ complexes under thermodynamic control, which are required for the preparation of molecular magnetic Q-bits,36 we have re-engaged the fight with the use of a terminal non-covalent HHH-[Zn(pyridine-benzimidazole)3] tripod which preorganizes the three strands for their concomitant efficient binding around two successive Ln3+ guests in two well-defined and different coordination sites. We therefore propose in this work to close the loop with a novel and efficient preparation of the segmental ligand L4 so that one can access the thermodynamically self-assembled HHH-[(L43Zn)LnALnB]8+ helicates for which both lanthanide permutation eqn (1-L4) and lanthanide exchange eqn (2-L4) can be deciphered in solution (Scheme 3b).57
Results and discussion
Preparation and structures of L4 and its homolanthanide triple-helical complexes HHH-[(L43Zn)Ln2](CF3SO3)8 (Ln = La, Eu, Lu)
Taking advantage of previous synthetic efforts,57 the strategy for preparing the segmental didentate–tridentate–tridentate ligand L4 has been optimized (Scheme A2-1 in Appendix 2). L4 could be thus efficiently prepared in seven steps with a global yield of 5.6% from commercially available 2,5-lutidine (1a), together with previously synthesized 4,4′-methylenebis(N-methyl-2-nitroaniline) (2c),58 6-(diethylcarbamoyl)picolinic acid (3d)59 and N2,N2-diethyl-N6-methyl-N6-(4-(4-(methylamino)-3-nitrobenzyl)-2-nitrophenyl)pyridine-2,6-dicarboxamide (8).59 The 1H-NMR of the free ligand L4 shows a total of 32 signals accounting for the 55 protons, which confirms an average Cs-symmetry on the NMR timescale (Fig. S1†). The absence of NOE correlations between the pyridine meta-protons and the benzimidazole methyl groups implies anti conformations of the donor N-atoms of the α,α′-diimine units, which are typical of unbound polyaromatic benzimidazole-pyridine segments in solution,59–61 a trend further confirmed in the crystal structure of L4·C3H8O (Fig. S2, S3 and Tables S1–S3†). The subsequent reaction of the segmental ligand L4 (3.0 eq., 15 mM) with stoichiometric amounts of Zn(CF3SO3)2 (1.0 eq., 5 mM) and Ln(CF3SO3)3 (2.0 eq., 10 mM, Ln = La(III), Eu(III), Lu(III)) in CDCl3/CD3CN (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) quantitatively affords the target homolanthanide HHH-[(L43Zn)Ln2]8+ triple-stranded helicates within a few hours according to global equilibrium 3 (Fig. S4–S6†).
2) quantitatively affords the target homolanthanide HHH-[(L43Zn)Ln2]8+ triple-stranded helicates within a few hours according to global equilibrium 3 (Fig. S4–S6†). | (3) |
The final 1H-NMR spectra of HHH-[(L43Zn)Ln2]8+ show the exclusive (>98%) formation of a single C3-symmetrical helicate in solution for each assembly process (Fig. 1 and S7–S15†). A consequence of the close vicinity of the three wrapped strands is highlighted in the diamagnetic complexes HHH-[(L43Zn)Ln2]8+ (Ln = La, Lu) by the unusually low chemical shifts (4.95 ≤ δ ≤ 5.85 ppm) recorded for the aromatic protons 8, 12, 20 and 24 which are located in the shielding region of a benzimidazole ring of an adjacent strand (Fig. 1 and S7†).
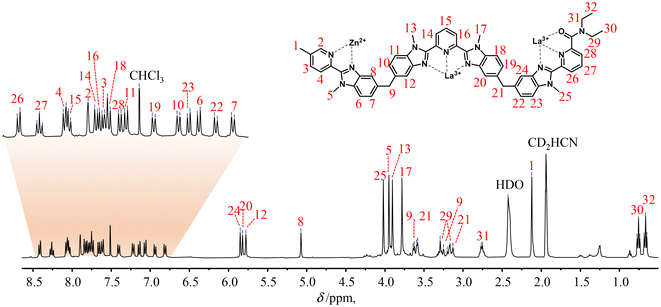 | ||
Fig. 1
1H-NMR spectrum of the HHH-[(L43Zn)La2]8+ complex (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 CD3CN/CDCl3, 400 MHz, 298 K). The aromatic region was expanded for clarity. 1 CD3CN/CDCl3, 400 MHz, 298 K). The aromatic region was expanded for clarity. | ||
One further notes that the small ionic radius of Lu(III) leads to a tighter wrapping of the ligand strands, which shifts the 1H-NMR signals of the benzimidazole protons 8, 12, 20 and 24 from 5.07 ≤ δ ≤ 5.85 ppm in HHH-[(L43Zn)La2]8+ toward 4.95 ≤ δ ≤ 5.34 ppm in HHH-[(L43Zn)Lu2]8+ (Fig. S16 and Table S4†). The replacement of the diamagnetic La3+ or Lu3+ cations with fast-relaxing paramagnetic Eu3+ in HHH-[(L43Zn)Eu2]8+ results in the expected11,59 downfield shifts of the singlet signals of the benzimidazole protons 12, 20 and 24 (12.00 ≤ δ ≤ 14.62 ppm) which are located close to the Eu3+ paramagnetic centers in the final complex (Table S5 and Fig. S8†). Additional proof for the formation of the desired complex is provided by the high-resolution ESI-TOF spectra recorded in acetonitrile, which display peaks corresponding to the series of triflate adducts HHH-{[(L43Zn)Ln2](CF3SO3)n}(8−n)+ (n = 2, 4, 5; Ln = La, Eu), although only at low relative intensities (Fig. S17 and S19†). The theoretical isotopic patterns nicely match the experimental peaks (Fig. S18 and S20†). The rest of the peaks, which have been assigned by their isotopic patterns, correspond to partial dissociation of one or more ligand strands and/or of one or more metal ions (Tables S6 and S7†). Due to the complete lack of 1H-NMR evidence supporting significant decomplexation of HHH-[(L43Zn)Ln2]8+ complexes (Ln = La, Eu, Lu) at millimolar concentrations in solution, the dissociation observed in the HR-MS spectra are assigned to the gas-phase reaction accompanying the ESI process.
Considering the labile character of both Zn(II) and Ln(III) (Ln = La, Eu, Lu) in solution, the formation of the desired trinuclear homolanthanide helicates within a few hours contrasts sharply with the fast (within seconds) self-assembly of the analogous dinuclear dimetallic [ZnLa(6)3]5+ complex, where the shorter segmental ligand 6 (Fig. A2–1 in Appendix 2, see ESI†) corresponds to L4 after the removal of the central tridentate 2,6-bis(benzimidazole)pyridine unit.59 The elongation of the ligand strand in L4 increases the complexity of the supramolecular system, which in turn increases the number of possible intermediates and reversible steps required before converging toward the thermodynamic products.62,63 An ultra-simplistic consideration of the whole self-assembly process as being modeled with equilibrium (3) predicts a negligible dissociation rate constant 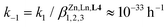 since (i) k1 can be estimated around 1000 M−6 h−1 when one takes into account a characteristic time constant of 2 hours for the formation of 50% of the final HHH-[(L43Zn)Ln2]8+ helicate in solution at a millimolar concentration and (ii)
since (i) k1 can be estimated around 1000 M−6 h−1 when one takes into account a characteristic time constant of 2 hours for the formation of 50% of the final HHH-[(L43Zn)Ln2]8+ helicate in solution at a millimolar concentration and (ii)  for HHH-[(L43Zn)Lu2]8+ in acetonitrile.57
for HHH-[(L43Zn)Lu2]8+ in acetonitrile.57
Slow diffusion of isopropanol and diethyl ether, respectively, into solutions of HHH-[(L43Zn)Eu2]8+ and HHH-[(L43Zn)La2]8+ in acetonitrile yielded single crystals of [(L43Zn)Eu2](CF3SO3)8·12(C3H8O) and [(L43Zn)La2](CF3SO3)8·7.25(CH3CN) of suitable quality for X-ray diffraction analysis (Fig. 2 and S21–S28, Tables S8–S25†). The X-ray structure of analogous [(L43Zn)Lu2](CF3SO3)8 was reported previously,57 but the limited quality of the datasets collected at this time (despite using a synchrotron radiation source) did not allow a detailed analysis of the structure.
The crystal structures unambiguously confirm the formation of the desired homolanthanide d–f–f triple-stranded helicates, showing the three metal ions almost linearly aligned along the pseudo-C3 axis (average Zn–Lnc–Lnt angle 176(2)°, Fig. 2a and Table S26†) and the three ligand strands helically wrapped around them in a head-to-head-to-head fashion (Fig. 2b). The intermetallic distances between adjacent cations average to 8.7(2) Å (Table S26†) lie within the range of distances previously reported in a number of polynuclear lanthanide helicates based on similar oligo-pyridyl-benzimidazole scaffolds (Scheme 2c and Fig. 3).10,59,64–68 The tighter wrapping of the ligand strands around the smallest lanthanide ions, previously mentioned when discussing the large upfield shift of the 1H-NMR signals of the benzimidazole protons in HHH-[(L43Zn)Lu2]8+ (Fig. S16†), leads to increasingly longer intermetallic distances as the size of the coordinated lanthanide ions reduces (entries 1 and 2 in Table S26†). While the average helical pitches (14.1–14.4 Å) do not vary significantly between the three complexes (entry 8 in Table S26†), and closely mirror those measured for previous homolanthanide helicates (Fig. S29†), a detailed analysis of each helical portion defined by eight almost parallel facial planes F1–F8 (Fig. S22, S23 and S25–S28†) showed significant local variations of the wrapping mode (Table S25†). In all three helicates, the tight rotations observed around each binding site alternate with severely relaxed helical twists associated with the diphenylmethane linkers. The helicity within the terminal [LntN6O3] binding site is the most irregular out of the three coordinating units due to the difference in angular rotation caused by the carboxamide-pyridine moiety on one side, and by the pyridine-benzimidazole motif on the other side.59
 | ||
| Fig. 3 Variation of the average bond valences νLn-donor calculated with eqn (4) for (a) Ln(III)c in the central N9 binding site and (b) Ln(III)t in the terminal N6O3 site as a function of the inverse of the nine-coordinate lanthanide ionic radii51 in HHH-[(L43Zn)Ln2]8+ (Ln = La(III), Eu(III), and Lu(III)). Standard deviations of the averages are shown with vertical error bars. The dashed traces are only a guide to the eye. | ||
The geometries of the coordination spheres around the three cations were analyzed with the software SHAPE,69–71 the final scores of which point toward a pseudo-octahedral arrangement for the [ZnN6] units (Table S26, entries 11 and 12†). Due to the poor stereochemical preferences of the lanthanide ions,72,73 comparable SHAPE scores are obtained for various geometries of the nine-coordinate Ln3+ sites. At the more flexible terminal [LntN6O3] sites, the lowest scores for all three lanthanides point to the tricapped trigonal prism geometry (Table S26, entries 20 and 21†). In the central [LncN9] sites, a tricapped trigonal prism geometry is adopted by the largest La(III) cation, while a spherical capped square antiprism geometry is observed around the smaller Eu(III) and Lu(III) cations (Table S26, entries 15 and 16†). One finally notices that the Zn–N bond distances do not vary significantly in the different HHH-[(L43Zn)Ln2]8+ helicates (Ln = La, Eu, Lu; Fig. S30†). This implies sufficient flexibility within the wrapped strands for overcoming significant structural constraints accompanying the lanthanide contraction along the 4f-series.
As expected for the flexible scaffold found in HHH-[(L43Zn)Ln2]8+, the Ln–N and Ln–O bond distances mirror the lanthanide contraction along the series (Fig. S30†),51,74,75 but a more detailed analysis of the Ln–N and Ln–O bond strengths, corrected for the lanthanide contraction, can be assessed by calculating the bond valences νij with eqn (4), where Rij is the bond valence parameter associated with a given set of metal ion i and donor atom j,76–78dij is the distance between the i–j pair, and b = 0.37 is a universal scaling constant (Fig. 3 and Table S27†).79
| νij = e[(Rij−dij)/b] | (4) |
The largest bond valences, diagnostic of the strongest metal–ligand affinities, were found between the lanthanides and the O-donors in the terminal N6O3 site (Fig. 3b). Interestingly, a sharp decrease of the Lnt–O bond valence observed when going from La(III) to Eu(III) is compensated by an increase of the Lnt–Nbz and Lnt–Npy interactions. The resulting concave trend detected for both Lnt–Nbz and Lnt–Npy bond valences in the terminal N6O3 site is not reproduced in the central N9 site (Fig. 3a), where the average Lnc–Nbz interaction decreases regularly throughout the series while the Lnc–Npy interaction remains roughly constant. Altogether, the terminal N6O3 site exhibits a weak preference for binding mid-range Ln3+ while the central N9 site penalizes the binding of the smaller lanthanides in HHH-[(L43Zn)Ln2]8+, a tendency previously established for the related [LnN9] and [LnN6O3] sites found in the homolanthanide D3-symmetrical [(L5)3Ln2]6+ and [(L6)3Ln2]6+ helicates (Fig. S29†).80
Formation and speciation of heterolanthanide triple-helical complexes HHH-[(L43Zn)LnALnB]8+ in solution (LnA, LnB = La, Eu, Lu)
The reaction of the segmental ligand L4 (3.0 eq.) with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Zn(CF3SO3)2 (1.0 eq.), La(CF3SO3)3 (1.0 eq.) and Eu(CF3SO3)3 (1.0 eq.) in a 1
1 mixture of Zn(CF3SO3)2 (1.0 eq.), La(CF3SO3)3 (1.0 eq.) and Eu(CF3SO3)3 (1.0 eq.) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of CDCl3/CD3CN was followed by 1H-NMR until the equilibrium was reached (Fig. S31†). The comparison of the 1H-NMR spectrum of the final mixture with those of the free ligand L4 and the previously characterized homolanthanide complexes HHH-[(L43Zn)La2]8+ and HHH-[(L43Zn)Eu2]8+ demonstrates the formation of a single major new species displaying the characteristic features of a C3-symmetric triple-stranded helicate (Fig. S32†). The rest of the (minor) signals correspond to the homolanthanide complexes, with no trace of the free ligand (Fig. 4). One of the two possible heterolanthanide isomers strongly dominates the speciation (Table 1, second column), thus confirming that the two different lanthanide binding sites exhibit size-discriminating effects. With the help of correlation and NOE spectroscopy (Fig. S33†), the 1H-NMR spectrum of the main product could be fully assigned to HHH-[(L43Zn)LaEu]8+, where specific paramagnetic-induced chemical shifts (Fig. S34†) ascertain that the Eu(III) cation occupies the terminal N6O3 binding site in the major heterolanthanide isomer (Fig. 4). As expected, the high-resolution ESI-TOF spectrum of the mixture confirmed the co-existence of both the homo- and heterolanthanide complexes in the gas-phase (Fig. S35†).
2 mixture of CDCl3/CD3CN was followed by 1H-NMR until the equilibrium was reached (Fig. S31†). The comparison of the 1H-NMR spectrum of the final mixture with those of the free ligand L4 and the previously characterized homolanthanide complexes HHH-[(L43Zn)La2]8+ and HHH-[(L43Zn)Eu2]8+ demonstrates the formation of a single major new species displaying the characteristic features of a C3-symmetric triple-stranded helicate (Fig. S32†). The rest of the (minor) signals correspond to the homolanthanide complexes, with no trace of the free ligand (Fig. 4). One of the two possible heterolanthanide isomers strongly dominates the speciation (Table 1, second column), thus confirming that the two different lanthanide binding sites exhibit size-discriminating effects. With the help of correlation and NOE spectroscopy (Fig. S33†), the 1H-NMR spectrum of the main product could be fully assigned to HHH-[(L43Zn)LaEu]8+, where specific paramagnetic-induced chemical shifts (Fig. S34†) ascertain that the Eu(III) cation occupies the terminal N6O3 binding site in the major heterolanthanide isomer (Fig. 4). As expected, the high-resolution ESI-TOF spectrum of the mixture confirmed the co-existence of both the homo- and heterolanthanide complexes in the gas-phase (Fig. S35†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of CDCl3/CD3CN, 298 K)
2 mixture of CDCl3/CD3CN, 298 K)
The formation of the HHH-[(L43Zn)LaEu]8+ complex as the main product of the self-assembly of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Zn(CF3SO3)2, La(CF3SO3)3, and Eu(CF3SO3)3 with 3.0 eq. of L4 is consistent with the stereochemical preference of the central N9 site for larger lanthanide ions and that of the terminal N6O3 site for smaller ones.10,11,80 In this context, replacing La(III) with Lu(III) in the mixture should make the coordination of the Eu(III) cation now more favorable in the central N9 site made of three wrapped bis(benzimidazole)pyridine segments while the terminal N6O3 site should preferentially accommodate the smaller Lu(III), hence yielding HHH-[(L43Zn)EuLu]8+ as the major heterolanthanide isomer in solution. The latter prediction was confirmed by following the reaction of L4 (3.0 eq., 15 mM) with a 1eq
1 mixture of Zn(CF3SO3)2, La(CF3SO3)3, and Eu(CF3SO3)3 with 3.0 eq. of L4 is consistent with the stereochemical preference of the central N9 site for larger lanthanide ions and that of the terminal N6O3 site for smaller ones.10,11,80 In this context, replacing La(III) with Lu(III) in the mixture should make the coordination of the Eu(III) cation now more favorable in the central N9 site made of three wrapped bis(benzimidazole)pyridine segments while the terminal N6O3 site should preferentially accommodate the smaller Lu(III), hence yielding HHH-[(L43Zn)EuLu]8+ as the major heterolanthanide isomer in solution. The latter prediction was confirmed by following the reaction of L4 (3.0 eq., 15 mM) with a 1eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1eq
1eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1eq mixture of Zn(CF3SO3)2, Eu(CF3SO3)3 and Lu(CF3SO3)3 in a 1
1eq mixture of Zn(CF3SO3)2, Eu(CF3SO3)3 and Lu(CF3SO3)3 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of CDCl3/CD3CN with the help of 1H-NMR techniques. The 1H-NMR spectrum recorded at equilibrium (after 24 hours, Fig. S36†) showed non-negligible amounts of the homolanthanide helicates HHH-[(L43Zn)Eu2]8+ and HHH-[(L43Zn)Lu2]8+ together with one major set of unidentified peaks that corresponded to the heterolanthanide HHH-[(L43Zn)EuLu]8+ isomer (Fig. S37–S39,† column 3 in Table 1).
2 mixture of CDCl3/CD3CN with the help of 1H-NMR techniques. The 1H-NMR spectrum recorded at equilibrium (after 24 hours, Fig. S36†) showed non-negligible amounts of the homolanthanide helicates HHH-[(L43Zn)Eu2]8+ and HHH-[(L43Zn)Lu2]8+ together with one major set of unidentified peaks that corresponded to the heterolanthanide HHH-[(L43Zn)EuLu]8+ isomer (Fig. S37–S39,† column 3 in Table 1).
Finally, the reaction of L4 (3.0 eq., 15 mM) with a 1 eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 eq
1 eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 eq mixture of Zn(CF3SO3)2, La(CF3SO3)3 and Lu(CF3SO3)3 was the fastest to reach the equilibrium, showing little to no evolution in the 1H-NMR spectrum after only a few hours at room temperature (Fig. S40†). Similarly to the previous mixtures, two homolanthanide helicates HHH-[(L43Zn)La2]8+ and HHH-[(L43Zn)Lu2]8+ are formed, along with only one of the two possible heterolanthanide isomers (Fig. S41–S42,† column 4 in Table 1). The absence of the open-shell Eu(III) probe in the mixture makes the assignment of the 1H-NMR spectrum of the heterolanthanide HHH-[(L43Zn)LaLu]8+ complex harder since the chemical shifts of the protons surrounding the central and the terminal sites are not as different as with the paramagnetic helicates. However, the size difference between La(III) and Lu(III) has been shown to affect the tightness of the wrapping of the ligand strands (Fig. S16†), which results in 1H-NMR signals for the central isolated benzimidazole singlets which are diagnostic for the binding of the largest La(III) cation in the central N9 site, while Lu(III) lies in the terminal site in HHH-[(L43Zn)LaLu]8+ (Fig. S42†). The permutated HHH-[(L43Zn)LuLa]8+ isomer could not be detected in the final mixture and its mole fraction was thus set at the limit of accuracy (x ≤ 0.05) estimated for our 1H-NMR experimental setup (Table 1).
1 eq mixture of Zn(CF3SO3)2, La(CF3SO3)3 and Lu(CF3SO3)3 was the fastest to reach the equilibrium, showing little to no evolution in the 1H-NMR spectrum after only a few hours at room temperature (Fig. S40†). Similarly to the previous mixtures, two homolanthanide helicates HHH-[(L43Zn)La2]8+ and HHH-[(L43Zn)Lu2]8+ are formed, along with only one of the two possible heterolanthanide isomers (Fig. S41–S42,† column 4 in Table 1). The absence of the open-shell Eu(III) probe in the mixture makes the assignment of the 1H-NMR spectrum of the heterolanthanide HHH-[(L43Zn)LaLu]8+ complex harder since the chemical shifts of the protons surrounding the central and the terminal sites are not as different as with the paramagnetic helicates. However, the size difference between La(III) and Lu(III) has been shown to affect the tightness of the wrapping of the ligand strands (Fig. S16†), which results in 1H-NMR signals for the central isolated benzimidazole singlets which are diagnostic for the binding of the largest La(III) cation in the central N9 site, while Lu(III) lies in the terminal site in HHH-[(L43Zn)LaLu]8+ (Fig. S42†). The permutated HHH-[(L43Zn)LuLa]8+ isomer could not be detected in the final mixture and its mole fraction was thus set at the limit of accuracy (x ≤ 0.05) estimated for our 1H-NMR experimental setup (Table 1).
Thermodynamic rationalization of the formation of heterolanthanide triple-helical complexes HHH-[(L43Zn)LnALnB]8+ in solution (LnA, LnB = La, Eu, Lu)
In the absence of significant complex dissociation at millimolar concentrations, as demonstrated for the stoichiometric mixing of L4 (3.0 eq.) with Zn(CF3SO3)2 (1.0 eq.), LnA(CF3SO3)3 and LnB(CF3SO3)3 (1.0 eq.) in solution, the four interconverting helicates HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ (n = 0, 1, 2) are related by the generic thermodynamic permutation equilibrium (1) (eqn 1-Lk in Schemes 1–3, further generalized below as eqn (5)) and exchange equilibrium (2) (eqn 2-Lk in Schemes 1–3, further generalized below as eqn (6)), where HHH-[(L43Zn)]2+ is considered as a rigid platform for the complexation of LnA and LnB in the two appended and preorganized N9 and N6O3 binding sites (Scheme 4). The equilibrium concentrations are written between double vertical bars | | in eqn (5) and (6). | (5) |
 | (6) |
 | ||
Scheme 4 Microscopic thermodynamic formation constants  for HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ (n = 0, 1, and 2) and their modeling with the site binding model.81,82 See main text for the definitions of fLnji and uLni1–2, Lnj. for HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ (n = 0, 1, and 2) and their modeling with the site binding model.81,82 See main text for the definitions of fLnji and uLni1–2, Lnj. | ||
Focusing on HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+, 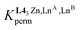 (eqn (5)) and
(eqn (5)) and  (eqn (6)) can be modeled with the help of microscopic formation constants
(eqn (6)) can be modeled with the help of microscopic formation constants  to give eqn (7) and (8) within the frame of the site binding model, where fiLnj is the intermolecular microscopic affinity of the nine-coordinate site i for the entering lanthanide Lnj in the preorganized HHH-[(L43Zn)]2+ receptor and
to give eqn (7) and (8) within the frame of the site binding model, where fiLnj is the intermolecular microscopic affinity of the nine-coordinate site i for the entering lanthanide Lnj in the preorganized HHH-[(L43Zn)]2+ receptor and  is the Boltzmann factor measuring the intermetallic pair interactions
is the Boltzmann factor measuring the intermetallic pair interactions 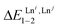 operating between adjacent Lni and Lnj cations in [(Lni)(Lnj)] (Scheme 4).81,82
operating between adjacent Lni and Lnj cations in [(Lni)(Lnj)] (Scheme 4).81,82
 | (7) |
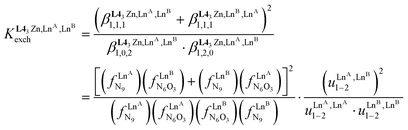 | (8) |
The last term of eqn (8) corresponds to the square of  , which is related to the mixing energy ΔEmix1–2 in eqn (9).56
, which is related to the mixing energy ΔEmix1–2 in eqn (9).56
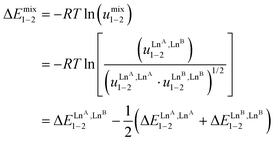 | (9) |
 , which corresponds to a non-cooperative behavior and results in a random distribution of the two different metal ions among the coordination sites.56 Deviations from the mixing rule can be assigned to either cooperative processes (ΔEmix1–2 > 0), which are characterized by the clustering of identical metals along the strands, or anti-cooperative processes (ΔEmix1–2 < 0), which correspond to an alternation of the different metals.56,81,82
, which corresponds to a non-cooperative behavior and results in a random distribution of the two different metal ions among the coordination sites.56 Deviations from the mixing rule can be assigned to either cooperative processes (ΔEmix1–2 > 0), which are characterized by the clustering of identical metals along the strands, or anti-cooperative processes (ΔEmix1–2 < 0), which correspond to an alternation of the different metals.56,81,82
The experimental permutation energies (orange markers) and exchange energies (blue markers) obtained for HHH-[(L43Zn)(LnA)(LnB)]8+ (entries 7 and 9 in Table 1) are summarized in Fig. 5. One immediately notices the systematic positive permutation energies 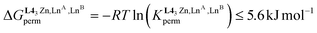 (top of Fig. 5), which reflect the preferred formation of the heterolanthanide isomer where the larger cation lies in the central N9 binding site and the smaller cation occupies the terminal N6O3 binding site (
(top of Fig. 5), which reflect the preferred formation of the heterolanthanide isomer where the larger cation lies in the central N9 binding site and the smaller cation occupies the terminal N6O3 binding site ( , eqn (7)). The combination of eqn (7) and (8), pertinent to
, eqn (7)). The combination of eqn (7) and (8), pertinent to  and
and  , provides an elegant experimental access to the balance of the intermetallic pair interactions as measured by umix1–2 in eqn (10), and consequently to the associated mixing energies −0.8 ≤ ΔEmix1–2 ≤ 1.9 kJ mol−1 operating in HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ (n = 0, 1, 2; Table 1, entry 11).
, provides an elegant experimental access to the balance of the intermetallic pair interactions as measured by umix1–2 in eqn (10), and consequently to the associated mixing energies −0.8 ≤ ΔEmix1–2 ≤ 1.9 kJ mol−1 operating in HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ (n = 0, 1, 2; Table 1, entry 11).
 | (10) |
 | ||
Fig. 5 Free energies for permutation (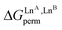 in eqn (5), orange markers) and for exchange ( in eqn (5), orange markers) and for exchange (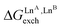 in eqn (6), blue markers) observed in solution at room temperature for HHH-[(L43Zn)(LnA)(LnB)]8+ (Table 2) as a function of the difference of the nine-coordinate lanthanide ionic radii (ΔRA, BCN=9).51 The full traces correspond to statistical behaviours. in eqn (6), blue markers) observed in solution at room temperature for HHH-[(L43Zn)(LnA)(LnB)]8+ (Table 2) as a function of the difference of the nine-coordinate lanthanide ionic radii (ΔRA, BCN=9).51 The full traces correspond to statistical behaviours. | ||
When the two different lanthanide cations are larger than Gd3+ (= belong to the first half of the lanthanide series), as illustrated in HHH-[(L43Zn)(La)(2−n)(Eu)n]8+ (n = 0, 1, 2), then ΔELa, Eu1–2 < ½(ΔELa, La1–2 + ΔEEu, Eu1–2) and the associated value of umix1–2 = 1.4(2) boosts the formation of the heterolanthanide HHH-[(L43Zn)(La)(Eu)]8+ complexes to reach  , which lies much beyond the statistical value of ΔGstatexch = −RT
, which lies much beyond the statistical value of ΔGstatexch = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(4) = −3.4 kJ mol−1 (bottom of Fig. 5, blue trace). As soon as one lanthanide cation of the pair belongs to the second part of the lanthanide series, as exemplified in heterolanthanide [(Eu)(Lu)] and in [(La)(Lu)] helicates, the reverse situation occurs with
ln(4) = −3.4 kJ mol−1 (bottom of Fig. 5, blue trace). As soon as one lanthanide cation of the pair belongs to the second part of the lanthanide series, as exemplified in heterolanthanide [(Eu)(Lu)] and in [(La)(Lu)] helicates, the reverse situation occurs with 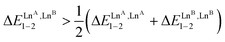 and the balance of pair interactions tend to discard the formation of heterolanthanide HHH-[(L43Zn)(LnA)(LnB)]8+ complexes.
and the balance of pair interactions tend to discard the formation of heterolanthanide HHH-[(L43Zn)(LnA)(LnB)]8+ complexes.
The origin of the latter driving force is far from being obvious, but it can be traced back to related trends observed for the thermodynamic self-assemblies of symmetrical dinuclear [(L53)(LnA)(2−n)(LnB)n]6+ (n = 0, 1, 2)65 and [(L63)(LnA)(2−n)(LnB)n]6+ (n = 0, 1, and 2),66,83 trinuclear [(L73)(LnA)(3−n)(LnB)n]9+ (n = 0, 1, 2, 3)11 and tetranuclear [(L83) (LnA)(3−n)(LnB)n]12+ (n = 0, 1, 2, 3, and 4)12 helicates (Fig. S29†) based on the segmental ligands L5–L8 (Scheme 5, see Appendices 3–4 for a comprehensive thermodynamic analysis, see ESI).
 | ||
| Scheme 5 Chemical structures of segmental ligands used for the self-assemblies of heterometallic dinuclear [(L53)(LnA)(2−n)(LnB)n]6+ (n = 0, 1, 2)65 and [(L63)(LnA)(2−n)(LnB)n]6+ (n = 0, 1, 2),66,83 trinuclear [(L73)(LnA)(3−n)(LnB)n]9+ (n = 0, 1, 2, 3)11 and tetranuclear [(L83) (LnA)(4−n)(LnB)n]12+ (n = 0, 1, 2, 3, and 4)12 helicates. | ||
The two adjacent N6O3 binding units found in [(L63)(LnA)(2−n)(LnB)n]6+ are not able to induce deviations from statistical mixtures in solution (Fig. A3-1a in Appendix 3, see ESI†) and one systematically obtains umix1–2 = 1 for any lanthanide pairs (ΔEmix1–2 = 0 in Table S29†). In contrast, the two connected N9 sites implemented in [(L53)(LnA)(2−n)(LnB)n]6+ induce positive mixing energies 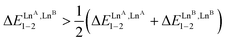 (Fig. A3-1b and ΔEmix1–2 > 0 in Table S28†), which favor homometallic matching beyond statistical distributions, as long as at least one lanthanide of the metallic pairs belongs to the second half of the lanthanide series. Moving from two adjacent identical nine-coordinated binding sites, as found in [(L53)(LnA)(2−n)(LnB)n]6+ (N9–N9) or in [(L63)(LnA)(2−n)(LnB)n]6+ (N6O3–N6O3), toward two different connected N9 and N6O3 sites in HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ brings a novel dimension to the size discriminating process. Firstly, due to the presence of the central constrained N9 site,84 the mixing rule ΔE1–2mix > 0 discards the formation of the heterolanthanide HHH-[(L43Zn)(LnA)(LnB)]8+ isomers as soon as the small Lu3+ cation is considered as a member of the lanthanide pair in [(La)(Lu)] and [(Eu)(Lu)]. Secondly, the non-zero permutation energies provided by the existence of the two different binding sites (N9–N6O3) may partially compensate for the latter detrimental effect, and the formation of the heterolanthanide HHH-[(L43Zn)(LnA)Lu]8+ isomers still represents 40–50% of the speciation in solution (Table 1, entries 4 and 5). Finally, when two large lanthanides are bound in HHH-[(L43Zn)LaEu]8+, both the balance of the intermetallic interactions (ΔEmix1–2 < 0) and site selectivity
(Fig. A3-1b and ΔEmix1–2 > 0 in Table S28†), which favor homometallic matching beyond statistical distributions, as long as at least one lanthanide of the metallic pairs belongs to the second half of the lanthanide series. Moving from two adjacent identical nine-coordinated binding sites, as found in [(L53)(LnA)(2−n)(LnB)n]6+ (N9–N9) or in [(L63)(LnA)(2−n)(LnB)n]6+ (N6O3–N6O3), toward two different connected N9 and N6O3 sites in HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ brings a novel dimension to the size discriminating process. Firstly, due to the presence of the central constrained N9 site,84 the mixing rule ΔE1–2mix > 0 discards the formation of the heterolanthanide HHH-[(L43Zn)(LnA)(LnB)]8+ isomers as soon as the small Lu3+ cation is considered as a member of the lanthanide pair in [(La)(Lu)] and [(Eu)(Lu)]. Secondly, the non-zero permutation energies provided by the existence of the two different binding sites (N9–N6O3) may partially compensate for the latter detrimental effect, and the formation of the heterolanthanide HHH-[(L43Zn)(LnA)Lu]8+ isomers still represents 40–50% of the speciation in solution (Table 1, entries 4 and 5). Finally, when two large lanthanides are bound in HHH-[(L43Zn)LaEu]8+, both the balance of the intermetallic interactions (ΔEmix1–2 < 0) and site selectivity  contribute favorably and synergistically to a large deviation of statistics with the formation of up to 70% of the heterolanthanide HHH-[(L43Zn)LaEu]8+ and HHH-[(L43Zn)EuLa]8+ in solution, which exist moreover in a |[(La)(Eu)]|/|[(Eu)(La)]| = 9
contribute favorably and synergistically to a large deviation of statistics with the formation of up to 70% of the heterolanthanide HHH-[(L43Zn)LaEu]8+ and HHH-[(L43Zn)EuLa]8+ in solution, which exist moreover in a |[(La)(Eu)]|/|[(Eu)(La)]| = 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (Table 1 and Fig. 5).
1 ratio (Table 1 and Fig. 5).
Conclusions
Puzzled by preliminary, partial and explorative studies reported for [(L1)3LnALnB(NO3)(H2O)(pyridine)] (Scheme 1),36 [(L2)3(LnA)(2−n)(LnB)n]6+ (Scheme 2)10 and [(L3)LaLu]6+ (Scheme 3),52 which claimed for some selective lanthanide recognition to form f–f′ complexes under thermodynamic control in solution, one realizes that any pertinent discriminating effects, if they exist, should be quantitatively addressed with the help of two simple free energy descriptors measuring (i) the intermolecular affinity of a given preorganized binding site i for the entering lanthanide Lnj (ΔGLnjaff, i = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(fLnji)) and (ii) the balance of the intermetallic interactions operating within adjacent pairs of lanthanides
ln(fLnji)) and (ii) the balance of the intermetallic interactions operating within adjacent pairs of lanthanides  .56 Although a direct access to these two crucial thermodynamic descriptors proved to be (very) difficult,80 an indirect approach appears to be possible since the experimentally accessible permutation equilibrium (eqn (7)), which accompanies the distribution of the various heterolanthanide isomers, and the exchange equilibrium (eqn (8)), which measures the amounts of homo- versus heterolanthanide complexes formed, reflect these thermodynamic parameters in solution. With this in mind, the lack of reliable and complete speciations addressed for the non-symmetrical [(L1)3LnALnB(NO3)(H2O)(pyridine)],36 [(L2)3(LnA)(2−n)(LnB)n]6+ (Table 2, entry 1)10 and [(L3)LaLu]6+ (Table 2, entry 2)52 complexes limits further rational thermodynamic analysis. In contrast, the detailed solution studies reported for the symmetrical dinuclear triple-stranded [(L53)(LnA)(2−n)(LnB)n]6+ and [(L63)(LnA)(2−n)(LnB)n]6+ helicates in solution can be used to initiate the thermodynamic exploration.80 The strict statistical behavior observed for the loading of pairs of lanthanide cations in [(L63)(LnA)(2−n)(LnB)n]6+ indicates that the sequence of two adjacent semi-flexible N6O3 binding sites is not able to induce any significant recognition along the lanthanide series (Table 2, entry 3). The same behaviour characterizes the binding of the two large La3+ and Eu3+ cations in [(L53)(La)(2−n)(Eu)n]6+ (Table 2, entry 4). However, when at least one lanthanide of the pairs is smaller than Gd3+, the two adjacent N9 binding sites in the latter complexes [(L53)(LnA)(2−n)(LnA)n]6+ show a global preference for the formation of homometallic complexes due to cooperative intermetallic mixing energies ΔEmix1–2 ≈ 2 kJ mol−1 (Table 2, entry 5). The symmetrical trinuclear [(L73)(LnA)(3−n)(LnB)n]9+ (N6O3–N9–N6O3, Table 2 entry 6) and tetranuclear [(L83)(LnA)(4−n)(LnB)n]12+ (N6O3–N9–N9–N6O3, Table 2 entry 7) helicates confirm these trends with the appearance of sizeable unbalanced intermetallic interactions (i.e. ΔEmix1–2 ≠ 0) only when a sequence of two adjacent N9 site binding sites exists.
.56 Although a direct access to these two crucial thermodynamic descriptors proved to be (very) difficult,80 an indirect approach appears to be possible since the experimentally accessible permutation equilibrium (eqn (7)), which accompanies the distribution of the various heterolanthanide isomers, and the exchange equilibrium (eqn (8)), which measures the amounts of homo- versus heterolanthanide complexes formed, reflect these thermodynamic parameters in solution. With this in mind, the lack of reliable and complete speciations addressed for the non-symmetrical [(L1)3LnALnB(NO3)(H2O)(pyridine)],36 [(L2)3(LnA)(2−n)(LnB)n]6+ (Table 2, entry 1)10 and [(L3)LaLu]6+ (Table 2, entry 2)52 complexes limits further rational thermodynamic analysis. In contrast, the detailed solution studies reported for the symmetrical dinuclear triple-stranded [(L53)(LnA)(2−n)(LnB)n]6+ and [(L63)(LnA)(2−n)(LnB)n]6+ helicates in solution can be used to initiate the thermodynamic exploration.80 The strict statistical behavior observed for the loading of pairs of lanthanide cations in [(L63)(LnA)(2−n)(LnB)n]6+ indicates that the sequence of two adjacent semi-flexible N6O3 binding sites is not able to induce any significant recognition along the lanthanide series (Table 2, entry 3). The same behaviour characterizes the binding of the two large La3+ and Eu3+ cations in [(L53)(La)(2−n)(Eu)n]6+ (Table 2, entry 4). However, when at least one lanthanide of the pairs is smaller than Gd3+, the two adjacent N9 binding sites in the latter complexes [(L53)(LnA)(2−n)(LnA)n]6+ show a global preference for the formation of homometallic complexes due to cooperative intermetallic mixing energies ΔEmix1–2 ≈ 2 kJ mol−1 (Table 2, entry 5). The symmetrical trinuclear [(L73)(LnA)(3−n)(LnB)n]9+ (N6O3–N9–N6O3, Table 2 entry 6) and tetranuclear [(L83)(LnA)(4−n)(LnB)n]12+ (N6O3–N9–N9–N6O3, Table 2 entry 7) helicates confirm these trends with the appearance of sizeable unbalanced intermetallic interactions (i.e. ΔEmix1–2 ≠ 0) only when a sequence of two adjacent N9 site binding sites exists.
| Helicate | Binding sites | ΔGstatperm (kJ mol−1) | ΔEmix1–2 (kJ mol−1) | ΔGstatexch (kJ mol−1) | Condition | Favoured speciesa | Ref. | ||
|---|---|---|---|---|---|---|---|---|---|
| a Homo resp. hetero = preference for homometallic, resp. heterometallic lanthanide complexes; statistical = no preference. b The triple-stranded helicates exist as variable mixtures of HHH (N9–N6O3) and HHT (N8–N7O2) isomers. c R represents an organic tripod. d The mixing energy is arbitrarily fixed to ΔEmix1–2 = 0. | |||||||||
| [(L2)3(LnA)(2−n)(LnB)n]6+ | N9–N6O3/N8–N7O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | 0 | — | −14.1 to −6.4 | −3.4 | — | Hetero | 10 |
| [(L3)3(La)(2−n)(Lu)n]6+ | R–N9–N6O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
12.1 | 0 | 0d | — | −3.4 | — | — | 52 |
| [(L6)3(LnA)(2−n)(LnB)n]6+ | N6O3–N6O3 | 0 | 0 | −0.6 to 0.4 | −3.5 to −3.3 | −3.4 | — | Statistical | 83 |
| [(L5)3(LnA)(2−n)(LnB)n]6+ | N9–N9 | 0 | 0 | 0 | −3.4 | −3.4 | R LnA ≥ RGd and RLnB ≥ RGd | Statistical | 65 |
| [(L5)3(LnA)(2−n)(LnB)n]6+ | N9–N9 | 0 | 0 | 1.6 to 2.3 | −0.2 to 1.2 | −3.4 | R LnA < RGd or RLnB < RGd | Homo | 65 |
| [(L7)3(LnA)(3−n)(LnB)n]9+ | N6O3–N9–N6O3 | 2.2 to 4.2 | 3.34 | −0.6 to 0.2 | −10.8 to −5.4 | −5.4 | — | Hetero | 67 |
| [(L8)3(La)(4−n)(Lu)n]12+ | N6O3–N9–N9–N6O3 | — | — | −2 | −47.5 | −22.2 | — | Hetero | 12 |
| [(L43Zn)(LnA)(2−n)(LnB)n]8+ | [ZnN6]–N9–N6O3 | 3.0 to 5.4 | 0 | 1.2 to 1.9 | −3.6 to −0.4 | −3.4 | R LnA < RGd or RLnB < RGd | Homo | This work |
| [(L43Zn)(LnA)(2−n)(LnB)n]8+ | [ZnN6]–N9–N6O3 | 5.4 | 0 | −0.8 | −7.5 | −3.4 | R LnA ≥ RGd and RLnB ≥ RGd | Hetero | This work |
When a constrained sequence of two adjacent N6O3 and N9 binding sites is ensured via the connection of the ligand strands to a covalent sulfur tripod in [(L3)LaLu]6+ (Table 2, entry 2) or to a non-covalent [ZnN6] podand in the HHH-[(L43Zn)(LnA)(2−n)(LnB)n]8+ helicates (Table 2, entries 8 and 9), both the specific binding site affinities (via , eqn (7)) and the intermetallic mixing energies (via
, eqn (7)) and the intermetallic mixing energies (via , eqn (8)) can be exploited for boosting the formation of one targeted heterolanthanide isomer in solution. The systematic preference of the central N9 site for binding the largest lanthanide of the LnA
, eqn (8)) can be exploited for boosting the formation of one targeted heterolanthanide isomer in solution. The systematic preference of the central N9 site for binding the largest lanthanide of the LnA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LnB pair favors the formation of the heterolanthanide HHH-[(L43Zn)LnALnB]8+ isomer when RLnA > RLnB
LnB pair favors the formation of the heterolanthanide HHH-[(L43Zn)LnALnB]8+ isomer when RLnA > RLnB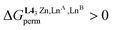 . However, the unfavorable mixing energy
. However, the unfavorable mixing energy  accompanying the distribution of the two lanthanides within the two sites as soon as one is smaller than Gd3+ limits this drift with the formation of only 51% of the heterolanthanide complexes for the La
accompanying the distribution of the two lanthanides within the two sites as soon as one is smaller than Gd3+ limits this drift with the formation of only 51% of the heterolanthanide complexes for the La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lu pair and 35% for the Eu
Lu pair and 35% for the Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lu pair (Table 2, entry 8). The latter restriction is removed when the two lanthanides belong to the first half of the series as demonstrated for the challenging La3+
Lu pair (Table 2, entry 8). The latter restriction is removed when the two lanthanides belong to the first half of the series as demonstrated for the challenging La3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eu3+ ionic pair in HHH-[(L43Zn)LaEu]8+ (Table 2, entry 9; the sizes of the two cations differ by only 8%), where the latter isomer accounts for 63% of the speciation in solution under stoichiometric conditions (|L43Zn|tot = |La|tot = |Eu|tot). This largely exceeds the 25% predicted by the statistical distribution. The road to the selective formation of f–f′ heterometallic complexes under thermodynamic control is still a long one, but the use of non-covalent tripods for programming specific sequences of binding sites, as demonstrated here for HHH-[(L43Zn)LnALnB]8+ helicates, corresponds to a major step forward in the rational design of heterolanthanide complexes obtained under thermodynamic control.
Eu3+ ionic pair in HHH-[(L43Zn)LaEu]8+ (Table 2, entry 9; the sizes of the two cations differ by only 8%), where the latter isomer accounts for 63% of the speciation in solution under stoichiometric conditions (|L43Zn|tot = |La|tot = |Eu|tot). This largely exceeds the 25% predicted by the statistical distribution. The road to the selective formation of f–f′ heterometallic complexes under thermodynamic control is still a long one, but the use of non-covalent tripods for programming specific sequences of binding sites, as demonstrated here for HHH-[(L43Zn)LnALnB]8+ helicates, corresponds to a major step forward in the rational design of heterolanthanide complexes obtained under thermodynamic control.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Swiss National Science Foundation is gratefully acknowledged (grant 200020_207313).References
- J. K. McCusker, Science, 2019, 363, 484–488 CrossRef CAS PubMed.
- P. F. Lang and B. C. Smith, J. Chem. Educ., 2010, 87, 875–881 CrossRef CAS.
- A. J. Freeman and R. E. Watson, Phys. Rev., 1962, 127, 2058–2076 CrossRef CAS.
- M. G. Brik and C.-G. Ma, Theoretical Spectroscopy of Transition Metal and Rare Earth Ions, Jenny Stanford Publishing, Singapore, 2020, ch. 6, pp. 145–244 Search PubMed.
- R. Saez and P. Caro, Rare Earths, Editorial Complutense S.A., Madrid, 1998 Search PubMed.
- S. Cotton, Lanthanide and Actinide Chemistry, John Wiley & Sons, Ltd, 2006 Search PubMed.
- E. N. Rizkalla and G. R. Choppin, Hydration and Hydrolysis of Lanthanides, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, Jr and L. Eyring, Elsevier Science Publishers, 1991, vol. 15, pp. 393–442 Search PubMed.
- G. R. Choppin and E. N. Rizkalla, Solution Chemistry of Actinides and Lanthanides, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, Jr, L. Eyring, G. R. Choppin and G. H. Lander, Elsevier Science B.V., 1994, vol. 18, pp. 559–589 Search PubMed.
- V. S. Sastri, J.-C. Bünzli, V. R. Rao, G. V. S. Rayudu and J. R. Perumareddi, Modern Aspects of Rare Earths and their Complexes, Elsevier B. V., Amsterdam, 2003, ch. 3–4, pp. 127–374 Search PubMed.
- N. André, T. B. Jensen, R. Scopelliti, D. Imbert, M. Elhabiri, G. Hopfgartner, C. Piguet and J.-C. G. Bünzli, Inorg. Chem., 2004, 43, 515–529 CrossRef PubMed.
- S. Floquet, M. Borkovec, G. Bernardinelli, A. Pinto, L.-A. Leuthold, G. Hopfgartner, D. Imbert, J.-C. G. Bünzli and C. Piguet, Chem. – Eur. J., 2004, 10, 1091–1105 CrossRef CAS PubMed.
- N. Dalla-Favera, J. Hamacek, M. Borkovec, D. Jeannerat, G. Ercolani and C. Piguet, Inorg. Chem., 2007, 46, 9312–9322 CrossRef CAS PubMed.
- A. M. Johnson, M. C. Young, X. Zhang, R. R. Julian and R. J. Hooley, J. Am. Chem. Soc., 2013, 135, 17723–17726 CrossRef CAS PubMed.
- L. Bellucci, L. Fioravanti, L. Armelao, G. Bottaro, F. Marchetti, F. Pineider, G. Poneti, S. Samaritani and L. Labella, Chem. – Eur. J., 2022, 29, e202202823 CrossRef PubMed.
- J. Wahsner and M. Seitz, Inorg. Chem., 2015, 54, 9681–9683 CrossRef CAS PubMed.
- J. W. Buchler, A. De Cian, J. Fischer, M. Kihn-Botulinski, H. Paulus and R. Weiss, J. Am. Chem. Soc., 1986, 108, 3652–3659 CrossRef CAS.
- N. Ishikawa, T. Iino and Y. Kaizu, J. Am. Chem. Soc., 2002, 124, 11440–11447 CrossRef CAS PubMed.
- S. Faulkner and S. J. Pope, J. Am. Chem. Soc., 2003, 125, 10526–10527 CrossRef CAS PubMed.
- T. J. Sorensen, M. Tropiano, O. A. Blackburn, J. A. Tilney, A. M. Kenwright and S. Faulkner, Chem. Commun., 2013, 49, 783–785 RSC.
- T. J. Sorensen and S. Faulkner, Acc. Chem. Res., 2018, 51, 2493–2501 CrossRef PubMed.
- M. S. Tremblay and D. Sames, Chem. Commun., 2006, 4116–4118 RSC.
- L. S. Natrajan, A. J. Villaraza, A. M. Kenwright and S. Faulkner, Chem. Commun., 2009, 6020–6022 RSC.
- M. P. Placidi, A. J. Villaraza, L. S. Natrajan, D. Sykes, A. M. Kenwright and S. Faulkner, J. Am. Chem. Soc., 2009, 131, 9916–9917 CrossRef CAS PubMed.
- L. Tei, G. Gugliotta, S. Avedano, G. B. Giovenzana and M. Botta, Org. Biomol. Chem., 2009, 7, 4406–4414 RSC.
- D. J. Lewis, P. B. Glover, M. C. Solomons and Z. Pikramenou, J. Am. Chem. Soc., 2011, 133, 1033–1043 CrossRef CAS PubMed.
- J. J. Le Roy, J. Cremers, I. A. Thomlinson, M. Slota, W. K. Myers, P. H. Horton, S. J. Coles, H. L. Anderson and L. Bogani, Chem. Sci., 2018, 9, 8474–8481 RSC.
- J. D. Dunitz and A. Gavezzotti, Acc. Chem. Res., 1999, 32, 677–684 CrossRef CAS.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201 RSC.
- H. Takezawa and M. Fujita, Bull. Chem. Soc. Jpn., 2021, 94, 2351–2369 CrossRef CAS.
- O. Guillou, C. Daiguebonne, G. Calvez and K. Bernot, Acc. Chem. Res., 2016, 49, 844–856 CrossRef CAS PubMed.
- H. Q. Yin and X. B. Yin, Acc. Chem. Res., 2020, 53, 485–495 CrossRef CAS PubMed.
- J. P. Costes, F. Dahan, A. Dupuis, S. Lagrave and J. P. Laurent, Inorg. Chem., 1998, 37, 153–155 CrossRef CAS PubMed.
- S. Tamburini, S. Sitran, V. Peruzzo and P. A. Vigato, Eur. J. Inorg. Chem., 2009, 155–167 CrossRef CAS.
- X. Y. Chen, Y. Bretonniere, J. Pecaut, D. Imbert, J. C. Bunzli and M. Mazzanti, Inorg. Chem., 2007, 46, 625–637 CrossRef CAS PubMed.
- D. Aguila, L. A. Barrios, V. Velaso, O. Roubeau, A. Repollès, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromi, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef CAS PubMed.
- J. Gonzalez-Fabra, N. A. G. Bandeira, V. Velasco, L. A. Barrios, D. Aguila, S. J. Teat, O. Roubeau, C. Bo and G. Aromi, Chem. – Eur. J., 2017, 23, 5117–5125 CrossRef CAS PubMed.
- D. Aguila, V. Velasco, L. A. Barrios, J. Gonzalez-Fabra, C. Bo, S. J. Teat, O. Roubeau and G. Aromi, Inorg. Chem., 2018, 57, 8429–8439 CrossRef CAS PubMed.
- E. Macaluso, M. Rubin, D. Aguila, A. Chiesa, L. A. Barrios, J. I. Martinez, P. J. Alonso, O. Roubeau, F. Luis, G. Aromi and S. Carretta, Chem. Sci., 2020, 11, 10337–10343 RSC.
- D. Maniaki, D. Garay-Ruiz, L. A. Barrios, D. O. T. A. Martins, D. Aguila, F. Tuna, D. Reta, O. Roubeau, C. Bo and G. Aromi, Chem. Sci., 2022, 13, 5574–5581 RSC.
- D. Maniaki, A. Sickinger, L. A. B. Moreno, D. Aguila, O. Roubeau, N. S. Settineri, Y. Guyot, F. Riobe, O. Maury, L. A. Galan and G. Aromi, Inorg. Chem., 2023, 62, 3106–3115 CrossRef CAS PubMed.
- Spectroscopic Properties of Rare Earths in Optical Materials, ed. R. Hull, J. Parisi, R. M. O. Osgood, H. Warlimont, G. Liu and B. Jacquier, Springer Series in Materials Science, Springer Berlin, Heidelberg, 2005 Search PubMed.
- G. Chem, H. Qiu, P. N. Prasad and X. Chen, Chem. Rev., 2014, 114, 5161–5214 CrossRef PubMed.
- B. Z. Zheng, J. Y. Fan, B. Chen, X. Qin, J. Wang, F. Wang, R. R. Deng and X. G. Liu, Chem. Rev., 2022, 122, 5519–5603 CrossRef CAS PubMed.
- K. A. White, D. A. Chengelis, K. A. Gogik, J. Stehman, N. L. Rosi and S. Petoud, J. Am. Chem. Soc., 2009, 131, 18069–18071 CrossRef CAS PubMed.
- H. Q. Yin and X. B. Yin, Acc. Chem. Res., 2020, 53, 485–495 CrossRef CAS PubMed.
- S. Comby, R. Scopelliti, D. Imbert, L. J. Charbonnière, R. Ziessel and J.-C. G. Bünzli, Inorg. Chem., 2006, 45, 3158–3160 CrossRef CAS PubMed.
- D. A. Galico, A. A. Kitos, J. S. Ovens, F. A. Sigoli and M. Murugesu, Angew. Chem., Int. Ed., 2021, 60, 6130–6136 CrossRef CAS PubMed.
- R. C. Knighton, L. K. Soro, L. Frances-Soriano, A. Rodriguez-Rodriguez, G. Pilet, M. Lenertz, C. Platas-Iglesias, N. Hildebrandt and L. J. Charbonniere, Angew. Chem., Int. Ed., 2022, 61, e202113114 CrossRef CAS PubMed.
- D. A. Galico, C. M. S. Calado and M. Murugesu, Chem. Sci., 2023, 14, 5827–5841 RSC.
- T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O'Brien, Nature, 2010, 464, 45–53 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- P. E. Ryan, G. Canard, S. Koeller, B. Bocquet and C. Piguet, Inorg. Chem., 2012, 51, 10012–10024 CrossRef CAS PubMed.
- S. Koeller, G. Bernardinelli, B. Bocquet and C. Piguet, Chem. – Eur. J., 2003, 9, 1062–1074 CrossRef CAS PubMed.
- S. Koeller, G. Bernardinelli and C. Piguet, Dalton Trans., 2003, 2395–2404 RSC.
- G. Canard, S. Koeller, G. Bernardinelli and C. Piguet, J. Am. Chem. Soc., 2008, 130, 1025–1040 CrossRef CAS PubMed.
- M. Borkovec, J. Hamacek and C. Piguet, Dalton Trans., 2004, 4096–4105 RSC.
- T. Riis-Johannessen, G. Bernardinelli, Y. Filinchuk, S. Clifford, N. Dalla-Favera and C. Piguet, Inorg. Chem., 2009, 48, 5512–5525 CrossRef CAS PubMed.
- C. Piguet, G. Bernardinelli, B. Bocquet, A. Quattropani and A. F. Williams, J. Am. Chem. Soc., 1992, 114, 7440–7451 CrossRef CAS.
- C. Piguet, J.-C. G. Bünzli, G. Bernardinelli, G. Hopfgartner, S. Petoud and O. Schaad, J. Am. Chem. Soc., 1996, 118, 6681–6697 CrossRef CAS.
- J.-M. Bénech, C. Piguet, G. Bernardinelli, J.-C. G. Bünzli and G. Hopfgartner, J. Chem. Soc., Dalton Trans., 2001, 684–689 RSC.
- L. Aboshyan-Sorgho, T. Lathion, L. Guenee, C. Besnard and C. Piguet, Inorg. Chem., 2014, 53, 13093–13104 CrossRef CAS PubMed.
- J. Hamacek, Metallofoldamers, Supramolecular Architectures from Helicates to Biomimetics, ed. G. Maayan and M. Albrecht, John Wiley Sons, Ltd, Chichester, 2013, ch. 3, pp. 91–123 Search PubMed.
- J. Hamacek, S. Blanc, M. Elhabiri, E. Leize, A. van Dorsselaer, C. Piguet and A. M. Albrecht-Gary, J. Am. Chem. Soc., 2003, 125, 1541–1550 CrossRef CAS PubMed.
- M. L. Connolly, J. Am. Chem. Soc., 1985, 107, 1118–1124 CrossRef CAS.
- C. Piguet, J.-C. G. Bünzli, G. Bernardinelli, G. Hopfgartner and A. F. Williams, J. Am. Chem. Soc., 1993, 115, 8197–8206 CrossRef CAS.
- N. Martin, J.-C. G. Bünzli, V. McKee, C. Piguet and G. Hopfgartner, Inorg. Chem., 1998, 37, 577–589 CrossRef CAS PubMed.
- S. Floquet, N. Ouali, B. Bocquet, G. Bernardinelli, D. Imbert, J.-C. G. Bünzli, G. Hopfgartner and C. Piguet, Chem. – Eur. J., 2003, 9, 1860–1875 CrossRef CAS PubMed.
- K. Zeckert, J. Hamacek, J.-M. Senegas, N. Dalla Favera, S. Floquet, G. Bernardinelli and C. Piguet, Angew. Chem., Int. Ed., 2005, 44, 7954–7958 CrossRef CAS PubMed.
- D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763 CrossRef CAS PubMed.
- S. Alvarez, Dalton Trans., 2005, 2209–2233 RSC.
- E. Cremades, J. Echeverria and S. Alvarez, Chem. – Eur. J., 2010, 16, 10380–10396 CrossRef CAS PubMed.
- A. Ruiz-Martinez, D. Casanova and S. Alvarez, Dalton Trans., 2008, 2583–2591 RSC.
- A. Ruiz-Martinez, D. Casanova and S. Alvarez, Chem. – Eur. J., 2008, 14, 1291–1303 CrossRef CAS PubMed.
- M. Seitz, A. G. Oliver and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 11153–11160 CrossRef CAS PubMed.
- R. B. Jordan, Inorg. Chem., 2023, 62, 3715–3721 CrossRef CAS PubMed.
- A. Trzesowska, R. Kruszynski and T. J. Bartczak, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 174–178 CrossRef PubMed.
- A. Trzesowska, R. Kruszynski and T. J. Bartczak, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 429–434 CrossRef PubMed.
- A. Trzesowska, R. Kruszynski and T. J. Bartczak, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 745–753 CrossRef PubMed.
- I. D. Brown, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS PubMed.
- C. Piguet and J.-C. G. Bünzli, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2010, vol. 40, pp. 301–553 Search PubMed.
- G. Koper and M. Borkovec, J. Phys. Chem. B, 2001, 105, 6666–6674 CrossRef CAS.
- J. Hamacek, M. Borkovec and C. Piguet, Dalton Trans., 2006, 1473–1490 RSC.
- K. Zeckert, J. Hamacek, J.-P. Rivera, S. Floquet, A. Pinto, M. Borkovec and C. Piguet, J. Am. Chem. Soc., 2004, 126, 11589–11601 CrossRef CAS PubMed.
- S. Petoud, J.-C. G. Bünzli, F. Renaud, C. Piguet, K. J. Schenk and G. Hopfgartner, Inorg. Chem., 1997, 36, 5750–5760 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2320733–2320735. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00610k |
| This journal is © The Royal Society of Chemistry 2024 |