Computational design of cooperatively acting molecular catalyst systems: carbene based tungsten- or molybdenum-catalysts with rhodium- or iridium-complexes for the ionic hydrogenation of N₂ to NH₃

Abstract

This density functional theory (DFT) study explores the efficacy of cooperative catalytic systems in enabling the ionic hydrogenation of N₂ with H₂, leading to NH₃ formation. A set of N-heterocyclic carbene-based pincer tungsten/molybdenum metal complexes of the form [(PCP)M¹(H)₂] (M¹ = W/Mo) were chosen to bind N₂ at the respective metal centres. Simultaneously, cationic rhodium/iridium complexes of type [Cp*M²{2-(2-pyridyl)phenyl}(CH₃CN)]⁺ (Cp* = C₅(CH₃)₅ and M² = Rh/Ir), are employed as cooperative coordination partners for heterolytic H₂ splitting. The stepwise transfer of protons and hydrides to the bound N₂ and intermediate N_xH_y units results in the formation of NH₃. Interestingly, the calculated results reveal an encouraging low range of energy spans ranging from ∼30 to 42 kcal mol⁻¹ depending on different combinations of ligands and metal complexes. The optimal combination of pincer ligand and metal center allowed for an energy span of unprecedented 29.7 kcal mol⁻¹ demonstrating significant potential for molecular catalysts for the N₂/H₂ reaction system. While exploring obvious potential off-cycle reactions leading to catalyst deactivation, the computed results indicate that no increase in energy span would need to be expected.

---

Introduction

Ammonia stands as a cornerstone in numerous global industries, serving as a fundamental component in a wide variety of fertilizers and chemicals used in the agricultural, industrial, and domestic sectors.^1,2 Additionally, it is integral in the production of many nitrogen based pharmaceutical products and shows promise as an alternative fuel and hydrogen storage molecule.^3,4 As a result, the annual synthesis of ammonia exceeds 150 million tons, making it a staple of contemporary existence.^5,6 The effort to develop artificial catalysts that are capable of imitating the naturally occurring production of NH₃ at the FeMo-cofactor of nitrogenases in the N₂/H⁺/e⁻ reaction system has made significant progress over the course of the past few decades.^7–11

Attempting to develop artificial catalysts capable of mimicking naturally occurring NH₃ synthesis has been a long-standing research goal. To date, the only acknowledged method for NH₃ production in the N₂/H₂ reaction system is the heterogeneously catalyzed Haber–Bosch process. However, this industrial process operates under severe conditions that requires a significant amount of energy input, resulting in significant emissions of greenhouse gases, primarily in the form of carbon dioxide (CO₂), stemming from H₂ production (steam reforming).¹² The high stability of the nitrogen-nitrogen triple bond necessitates harsh reaction conditions, amplifying the energy span and exacerbating the environmental impact of ammonia synthesis. Therefore, despite a century-long endeavor, the synthesis of ammonia from dinitrogen under modest reaction conditions remains an elusive feat and continues to captivate chemist's attention. Thus, developing a molecular catalyst aiming to operate in the N₂/H₂ system under mild conditions is an extremely intriguing endeavor. In this work we use computationally guided catalyst design for the identification of suitable catalyst systems which bases on DFT computations following an approach which has been used earlier by us and was successfully transferred to experimental chemistry.^13–16

The seminal work^17a of Allen and Senoff in isolating the dinitrogen compound, [Ru(NH₃)₅(N₂)]²⁺, prompted extensive research toward achieving catalytic conversion of dinitrogen into ammonia with molecular catalysts. In the late 1960s, Chatt^17b and Hidai^18,19 identified the precursors for converting N₂ to NH₃ at W(0) or Mo(0) centers. Subsequent efforts by Shilov and co-workers^20,21 successfully showcased the transformation of nitrogen gas (N₂) into hydrazine, accompanied by a small quantity of ammonia (NH₃), using a catalyst consisting of a molybdenum complex. The persistent objective of converting nitrogen into ammonia in the reaction system N₂/H⁺/e⁻via well-defined intermediates at experimental ambient circumstances was initially outlined by Yandulov and Schrock.^22–25 The most recent and impressive developments in catalytic ammonia formation using N₂/H⁺/e⁻ were achieved mainly by the groups of Nishibayashi, Nishibayashi/Yoshizawa and Peters.^26–30

With regard to the N₂/H₂ reaction system, Schneider, Holthausen, and co-workers³¹ have observed that the nitrogen center of molecular ruthenium pincer nitrides, which are potentially engaged in an N₂/H₂ catalytic cycle, can undergo conversion into NH₃ upon exposure to H₂. Notably, Hou et al.³² revealed the potential of trinuclear titanium hydrides in breaking the N≡N triple bond in the presence of H₂.

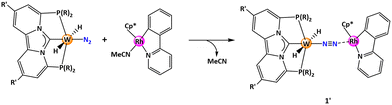
Our research group has a general scientific interest in the development of efficient homogeneous catalysts through computational and experimental studies advancing computational chemistry from an analytic to a predictive tool,^{14,15,33–35} and a description of the overall underlying computational approach is given in the section Computational Details and General Approach. As part of this program, we have been following strategies for in silico exploration of molecular catalysts facilitating N₂ hydrogenation to NH₃ in N₂/H₂ reactions.³⁶ Employing computational modeling, we investigated a catalyst system utilizing cationic ruthenium pincer complexes for the end-on-binding of N₂ binding together and in analogy to the frustrated Lewis-acid-Lewis-base-approach with bulky P(^tBu)₃ as a reaction partner to enable heterolytic cleavage of H₂.^37,38 In this approach high single energy barriers were computed which limit the viability within the typical temperature range useable for molecular catalysts (see also Computational Details and General Approach). Subsequently, we examined the possibility of using a tungsten pincer complex [N₂-W⁰] to bind N₂ and the cationic rhodium complex [Cp*Rh{2-(2-pyridyl)phenyl}(CH₃CN)]⁺ as a cooperative partner for heterolytic H₂ cleavage.³⁹ Both these complexes are easily synthesized and have been previously documented in the literature.^40–44 Optimization of the pincer ligands of the tungsten complex could lower the energy span to approximately 40 kcal mol⁻¹. While this value is the lowest computed for N₂ reduction with H₂ it is still too high to expect catalytic turnover under practical conditions. Therefore, there is still a need to improve the catalyst framework for reducing the energy span.

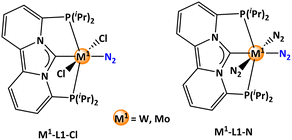
This study aims to conduct a computational screening of potential catalyst candidates based on the N-heterocyclic carbene-phosphorus based pincer frameworks connected with tungsten/molybdenum as the metal component for end-on N₂ activation (Scheme 1a).

Scheme 1 (a) Cooperative catalyst system, consisting of a neutral tungsten/molybdenum pincer complex and a cationic rhodium complex (Cp* = C₅(CH₃)₅). (b) General reaction scheme for the synthesis of NH₃ from N₂/H₂ using the cooperative catalyst system considered in this work.

The experimental synthetic route to arrive at the selected carbene pincer scaffold has recently been introduced in the literature.⁴⁵ The cationic rhodium complex [Cp*Rh{2-(2-pyridyl)phenyl}(CH₃CN)]⁺ is chosen as a cooperative reaction partner for heterolytic H₂ splitting. Initially, a proton is transferred to the terminal N atom of the N₂ molecule at the tungsten/molybdenum complex, establishing a trans configuration with the pincer backbone. Concurrently, the rhodium complex facilitates the reception of the hydride center (Scheme 1b).

In the next step of the reaction, the hydrogen center is transferred as a hydride from the rhodium complex to the [M–N=NH]⁺ unit of the tungsten/molybdenum complex, resulting in the formation of a neutral [M=N–NH₂] unit and the recovery of the cationic rhodium complex. Iterating this reaction sequence with two additional H₂ molecules yields two molecules of NH₃. Ultimately, the catalytic cycle concludes with the coordination of the succeeding N₂ molecule at the pincer complex, closing the cycle.

We aimed to elucidate the complete mechanistic picture in order to comprehend the critical intermediates and transition states involved in the catalytic cycle, as well as the overall energy requirements for the successful operation of the cycle (Scheme 2). A more general introduction to the approach is given in the section Computational details and general approach. Moreover, we intended to modify the electronic and steric characteristics of the ligands by incorporating different substituents on the phosphorus component to understand the fate on the overall energy spans (Scheme 3). Eventually, we concluded the investigation by examining the possible off-cycle reactions that could influence the efficiency of the constructed catalysts or reaction cycle.

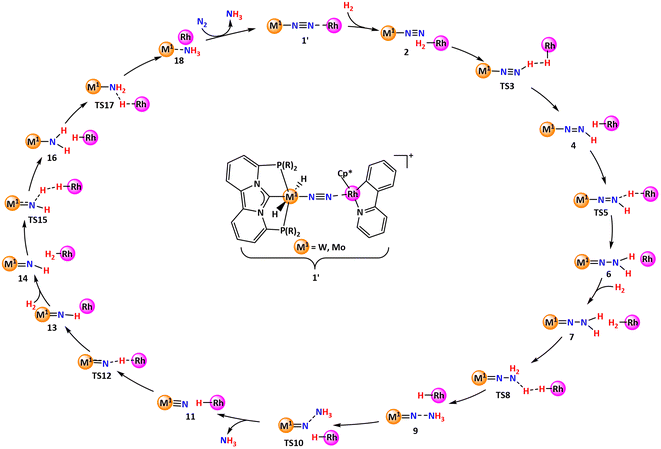Scheme 2 Generalized catalytic cycle proposed for hydrogenation of nitrogen to ammonia from the end-on coordinated complex 1′.

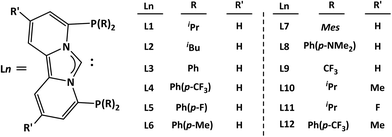Scheme 3 Different carbene-phosphorus pincer frameworks proposed to be used for the computational screening.

Computational details and general approach

The computations for this study were conducted utilizing dispersion-corrected DFT methods (B97D3-BJ),^46–49 coupled with the triple-zeta basis set def2-TZVP^50–52 and the implicit solvent model (IEF-PCM, SMD).⁵³ All the geometries were fully optimized in the polar acetonitrile solvent environment utilizing the Gaussian 16 (Revision B.01)⁵⁴ software package. Subsequently, vibrational frequency calculations were performed on the converged geometries to characterize the minima and saddle points and determine thermodynamic energy corrections. The choice of B97D3-BJ functional stemmed from its computational efficiency and its consistency with our prior research on metal–ligand complexes, aligning well with experimental findings.^13,55,56 However, we also conducted a comparative study involving other DFT functionals for the critical intermediates (TDI) and transition states (TDTS), which are mentioned in detail in the ESI (Fig. S1†). In the main text all free energies (ΔG) are reported in kcal mol⁻¹ for the B97D3-BJ/def2-TZVP/IEFPCM/SMD (acetonitrile) level of theory.

The scientific approach of this study follows the general strategy to evaluate if a given catalyst system is able to catalyze a certain reaction because the Gibbs free activation barrier is low enough. If each and every local minimum and transition state of an energy landscape could be calculated with sufficiently accurate Gibbs free energies then it would be possible to obtain a precise answer to that question. However, a truly comprehensive scanning of the complete energy hyper surface is simply not possible as the computational effort would exceed any practical time frame. Therefore, a generally acknowledged alternative is the computation of selected local minima and transition states, which due to their amount and chemical nature give a representative overview of the energy landscape. In this particular case an energy landscape has already been calculated in significant detail in earlier works for a very similar catalyst system.³⁹ This justifies for a very initial screening to restrict the computations only to the most important points, i.e. the reference point, the lowest local minimum (the turn over determining intermediate, TDI) and the highest transition state (the turn over determining transition state, TDTS).^57,58 Such computations give an initial insight about the energy span (ES; the effective Gibbs free activation barrier of the reaction) and in this way a significant amount of computer time is saved. Once a suitable catalyst system can be identified the next step is to compute an energy profile as complete as possible. In a final step it is necessary to compute the structures and energies of all stationary points which might evolve from potentially available side reactions that could contribute unfavorably to the energy span (i.e. stable “off loop” minima which can be reached via low lying transition states). One must note, however, that it cannot be excluded completely, that unexpected side reactions may be accessible in an experimental system which might not have been envisioned or possibly overlooked in the prior computational work. Computational studies of this kind have demonstrated their potential to narrow down significantly the plethora of choices an experimentalist could make with the potential of predictive catalyst design for example for olefin hydrogenation,¹⁶ decarboxylative Heck-type coupling¹³ and direct insertion of CO₂^14,15 into arenes.

The energy span deduced from the computational approach can be associated with an intrinsic catalytic activity of the system under scrutiny correlating the Eyring equation and the turn over frequency (TOF). In a simple approach, which we⁵⁹ and others⁶⁰ have outlined in significant detail before, a minimum TOF of 1 h⁻¹ is equivalent to an upper threshold for the energy span of 31 kcal mol⁻¹ at a temperature of 140 °C. In other words: If the catalyst system is thermally stable at this temperature it could be expected to affect measurable turn over for the reaction under investigation. In turn if the desired reaction temperature is set to room temperature the maximum threshold for the ES would be ca. 20 kcal mol⁻¹. As a practical rule of thumb, the maximum acceptable energy span typically assumed as 30 kcal mol⁻¹, depending, however, to a large extent on the thermal stability of the concrete catalyst system.

Results and discussion

In commencing our computations, our initial focus as outlined above was on evaluating several key energetics that are crucial to shaping the overall energy landscape of the considered catalytic cycle.

Inspired by our prior investigations, we initially explored tungsten as a metal for diverse carbene pincer complexes, paired with the cationic rhodium complex as a collaborative reaction partner. In our initial calculations, we optimized all tungsten pincer complexes, examining nitrogen's potential to bind in two distinct configurations namely, end-on (Ln-1^E) and side-on (Ln-1^S) fashion, allowing for a comparative assessment of their energies (Fig. S2†). However, the calculated energetics unequivocally indicate that the end-on coordination of nitrogen exhibits notably higher stability compared to the side-on binding mode.

We subsequently examined the feasibility for the acetonitrile replacement reaction from the rhodium complex to form a loosely coordinated W-N₂^Rh complex, 1′ (Table 1). The calculated results consistently demonstrate the thermodynamic favorability of this reaction across various ligands, exhibiting energy levels spanning from 5 to 20 kcal mol⁻¹. It is worth noting that while the feasibility of this reaction advances the catalytic cycle, the over-stability also introduces undesired challenges by increasing overall energy span of the reaction. Thus, alkyl substituents like L1 seem more advantageous for the pincer-ligand complexes than the aryl substituents at the phosphorus centers.

Table 1 Relative Gibbs free energies ΔG_r (kcal mol⁻¹) for the acetonitrile replacement reaction from the rhodium complex for various pincer-ligand complexes

Ln	R	R′	ΔGr
L1	^iPr	H	−6.7
L2	^tBu	H	−9.2
L3	Ph	H	−18.9
L4	Ph(p-CF3)	H	−16.9
L5	Ph(p-F)	H	−18.0
L6	Ph(p-Me)	H	−16.5
L7	Mes	H	−16.0
L8	Ph(p-NMe2)	H	−20.0
L9	CF3	H	−5.5
L10	^iPr	Me	−8.7
L11	^iPr	F	−7.7
L12	Ph(p-CF3)	Me	−17.0

---

Thereafter, our attention turned towards locating the transition state (TS8, in Table 2) that governs the protonation of the [W=N–NH₂] moiety—a crucial step in generating the NH₃ molecule. This step presented the highest energy barrier among similar systems studied previously.³⁹ Interestingly, the computed barrier heights for the ligand systems (L1–L12) examined here fall between 29–37 kcal mol⁻¹, notably lower than those observed in prior studies.³⁹

Table 2 Relative Gibbs free energies of activation ΔG^‡ (kcal mol⁻¹)

Ln	R	R′	ΔG^‡
L1	^iPr	H	29.1
L2	^tBu	H	30.2
L3	Ph	H	33.9
L4	Ph(p-CF3)	H	33.7
L5	Ph(p-F)	H	33.1
L6	Ph(p-Me)	H	33.6
L7	Mes	H	37.0
L8	Ph(p-NMe2)	H	34.2
L9	CF3	H	28.5
L10	^iPr	Me	30.8
L11	^iPr	F	31.0
L12	Ph(p-CF3)	Me	34.0

---

Therefore, the energy barrier of 29.1 kcal mol⁻¹, combined with the practical accessibility of the ⁱPr-substituted pincer-ligand complex, spurred us to compute the entire catalytic cycle for the ligand L1. For the sake of clarity, the catalyst system is abbreviated as W-L1^Rh.

Fig. 1 illustrates the free energy reaction profile for the hydrogenation of nitrogen to ammonia catalyzed by W-L1^Rh. Contrary to initial assumptions, a comprehensive exploration of the reaction trajectory revealed that TS8 did not emerge as the transition state with the highest energy. Instead, TS10, governing NH₃ dissociation from the catalyst core, surfaced as the TDTS (turnover-determining transition state). TS10 needs to surmount an overall energy barrier of 31.6 kcal mol⁻¹, which is 2.5 kcal mol⁻¹ higher than the TS8. Notably, the energies associated with other transition states in the catalytic cycle remain low, ranging between 8–14 kcal mol⁻¹. This characteristic renders the steps straightforward in terms of energy requirements.

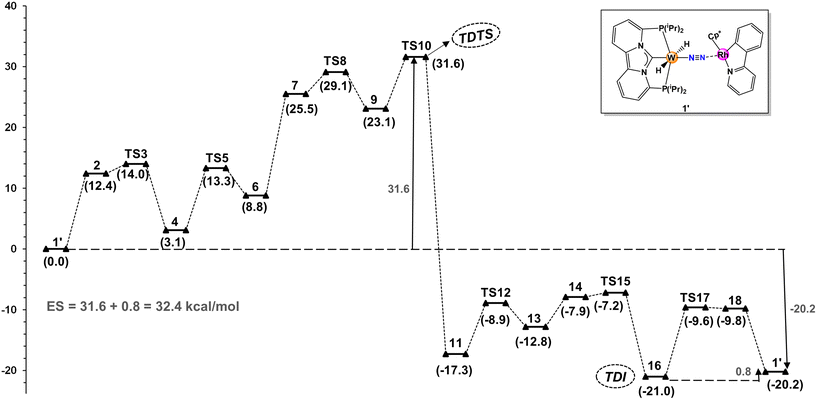Fig. 1 Minimum energy pathway and Gibbs free energies (ΔG, kcal mol⁻¹) for the direct hydrogenation of N₂ to NH₃ with catalyst W-L1^Rh.

Likewise, concerning the intermediate stability, it turns out that tungsten amide 16 is the most stable intermediate (TDI; turn over determining intermediate) involved in the active cycle, which is slightly (0.8 kcal mol⁻¹) more stable than the end point of the first cycle, thus contributes to the overall energy span. Consequently, the overall energy span (ES) is calculated to be 32.4 kcal mol⁻¹. This energy span is low enough to justify further computational screening.

In the next step, we checked how the diverse electronic and steric characteristics of ligands L2–L12 influence the energy span. The energy profiles derived from catalyst system W-L1^Rh reveal that, apart from the reference point, only the transition state TS10 and minimum 16 of the catalytic cycle necessitate re-optimization for obtaining information on the energy span. However, we took TS8 into account as well, as it is only 2.5 kcal mol⁻¹ less stable than TS10, which was initially presumed to be the highest energy state.

As anticipated, the catalyst systems featuring aliphatic substituted ligands L2, L9, and L10 yield comparable ES values, mirroring those of the original system, L1 (Table 3). On the contrary, aromatic group-substituted ligands such as L3–L6 generate notably higher ES values. For these ligands, both transition states TS8 and TS10 exhibit notably elevated energy levels. Interestingly, for L7, the energy levels switch between the two transition states, with TS8 being the highest energy state, unlike others. Similarly, the tungsten amide intermediate 16 displays notably lower stability compared to the others in the series. It is reasonable to assume that the bulky mesityl substitution on the phosphorus facilitates the de-coordination of the NH₃ from the catalyst center and prevents the over-stability of the amide complex formed.

Table 3 Relative Gibbs free energies (in kcal mol⁻¹) of selected stationary points of the catalytic cycle shown in Scheme 2 with tungsten complexes containing ligands L2–L12 in solvent phase

W-Ln^Rh	TS8	TS10	16	ES^a
a ES = energy span; ΔGr = −20.2 kcal mol^−1.
L2	30.2	32.8	−19.7	32.8
L3	33.9	41.4	−16.1	41.4
L4	33.7	41.2	−16.7	41.2
L5	33.1	41.9	−17.0	41.9
L6	33.6	40.0	−18.7	40.0
L7	37.0	34.8	−9.9	37.0
L8	34.2	40.2	−17.8	40.2
L9	28.5	41.5	−17.0	41.5
L10	30.8	32.4	−20.8	33.0
L11	31.0	32.7	−19.7	32.7
L12	34.0	39.7	−18.0	39.7

---

Furthermore, we extended our investigation to include L4 and L7 in studying the entire catalytic cycle to eliminate any potential unwanted switching of other stationary points (refer to Fig. S3†). However, the computations revealed no significant alterations in energy levels, including the anticipated turnover-determining transition state (TDTS) and turnover-determining intermediate (TDI) points. This outcome further solidifies our decision to concentrate on these specific stationary points for computing the overall energy spans.

Next, we investigated the influence of the metal center in the pincer ligand framework. For this purpose, we chose molybdenum pincer complexes for N₂ binding (Scheme 4), while also including the previously examined rhodium complex as a collaborative reaction partner. Unsurprisingly, the calculations echo the trend observed in tungsten complexes, showcasing that molybdenum pincer complexes binding nitrogen in the end-on configuration display a stability advantage of approximately 10–18 kcal mol⁻¹ over those adopting the side-on binding mode (Fig. S4†). In a similar line of reasoning, we calculated the full energy landscape for the Mo-L1^Rh system to reconfirm our assumption for the energy span calculations, which obviously emerged as expected (Fig. S5†). Following that, we pinpointed two pivotal transition states, TS8 and TS10, along with reference points 1′ and minimum 16 for the chosen molybdenum pincer complexes, necessary for conducting the energy span calculations. The calculations revealed relatively higher energy span values for the molybdenum pincer complexes compared to analogous tungsten complexes (Table 4). Specifically, the Mo-L10^Rh complex is anticipated to possess a minimum energy span of 33.2 kcal mol⁻¹, merely 0.8 kcal mol⁻¹ higher than the most favorable tungsten pincer complex, W-L1^Rh.

Scheme 4 Different molybdenum pincer complexes selected for the calculation of relevant stationary points.

Table 4 Relative Gibbs free energies (in kcal mol⁻¹) of selected stationary points of the catalytic cycle shown in Scheme 2 with molybdenum complexes containing ligands L1, L2, L10 and L11 in solvent phase

Ln	TS8	TS10	16	ES^a
a ES = energy span; ΔGr = −20.2 kcal mol^−1.
L1	32.4	35.2	−17.2	35.2
L2	34.3	36.3	−15.7	36.3
L10	31.1	33.2	−18.3	33.2
L11	31.4	34.1	−18.1	34.1

---

Afterward, we shifted our focus to the cationic rhodium complex [Cp*Rh{2-(2-pyridyl)phenyl}(CH₃CN)]⁺. Our objective was to substitute the rhodium center with iridium to gain insights into the dynamics of the reaction energetics. To accomplish this, we examined both tungsten and molybdenum pincer complexes featuring ligands L1, L10, and L11. These complexes demonstrated promising energy spans with the rhodium counterparts, emphasizing their potential relevance in the study. Subsequently, the critical stationary points were re-optimized. Interestingly, the energy span of the tungsten pincer complexes showcased a reduction of the ES by approximately 2 kcal mol⁻¹ (e.g., W-L10^Rh = 33.0 kcal mol⁻¹vs.W-L10^Ir = 30.9 kcal mol⁻¹), while the molybdenum pincer complexes displayed an even more noteworthy reduction of about 3–4 kcal mol⁻¹ (e.g., Mo-L1^Rh = 35.2 kcal mol⁻¹vs.Mo-L1^Ir = 31.0 kcal mol⁻¹), as shown in Table 5. Notably, the most favorable energy span of 29.7 kcal mol⁻¹ was achieved with the molybdenum complex, Mo-L10^Ir. This outcome presents a highly promising outlook for the direct hydrogenation route, suggesting potential avenues for experimental advancements.

Table 5 Relative Gibbs free energies (in kcal mol⁻¹) of selected stationary points of the catalytic cycle shown in Scheme 2 with tungsten/molybdenum complexes containing ligands L1, L10, L11 and cationic iridium as a reaction partner in solvent phase

M-Ln^Ir	TS8	TS10	16	ES^a
a ES = energy span; ΔGr = −20.2 kcal mol^−1.
W-L1^Ir	21.7	26.8	−26.1	32.7
W-L10^Ir	22.6	25.2	−25.9	30.9
W-L11^Ir	23.1	25.1	−25.7	30.6
Mo-L1^Ir	26.0	28.5	−22.7	31.0
Mo-L10^Ir	25.7	27.4	−22.5	29.7
Mo-L11^Ir	25.6	27.9	−22.9	30.6

---

Moreover, we investigated the potential influence of triplet or quintet spin states in the tungsten/molybdenum pincer complexes, considering the L1 ligand. However, after conducting comparative optimizations of twelve different minima using the unrestricted Kohn–Sham mode, it became evident that both the triplet and quintet spin states consistently yielded significantly higher energies compared to the singlet states, effectively ruling out their involvement (Fig. S6†).

Furthermore, we delved into the impact of the solvent by considering an even more polar solvent, dimethylsulfoxide, to discern whether a further increase in solvent polarity would lead to a reduction in the energy span (Table S1†). We re-optimized critical stationary points directly associated with the energy spans in the implicit dimethylsulfoxide (DMSO) solvent environment. However, contrary to expectations, the energy span exhibited an insignificant increase. For the tungsten complex W-L1^Rh, it shifted from 32.4 kcal mol⁻¹ (in CH₃CN) to 33.3 kcal mol⁻¹ (in DMSO), and for the molybdenum complex Mo-L1^Rh, it changed from 35.2 kcal mol⁻¹ (in CH₃CN) to 35.6 kcal mol⁻¹ (in DMSO). As a general remark it should be noted that in principal different solvents might, beyond to what is studied here, open other reaction pathways. However, a detailed investigation of other solvents is beyond the scope of this study.

Eventually, the exploration of potentially occurring off-cycle reactions that may emerge from the active species participating in the catalytic cycle is important. The most obvious side reaction one can assume is the dimerization of the catalyst. We examined two distinct dimeric forms of the catalyst. One involves the direct dimerization from monomer 1 to form 1^di, while the other, 2^di, is formed subsequent to the de-coordination of an N₂ molecule (Scheme 5). Structures like 1^di (two bridging N₂ moieties) have as yet not been observed experimentally in conjunction with these types of complexes, but could in principle be possible as analogues having boron centres as the bridge heads are known.⁶¹ Structures like 2^di (one bridging N₂ moiety) are well known for example from the many Mo–NN–Mo complexes introduced by the Nishibayashi group.^29,30 Assessing the feasibility of dimerization, we studied both tungsten and molybdenum pincer complexes, featuring ligands L1, L10, and L11. Gratifyingly, the formation of 1^di proved to be highly unlikely for all tungsten/molybdenum pincer complexes, with energy ranging from 44.5 to 56.7 kcal mol⁻¹ (Fig. S7†). On the contrary, the formation of 2^di is exergonic, indicating its potential existence. Interestingly, the stability of the tungsten complexes ranges from 12.9 to 13.8 kcal mol⁻¹, whereas the molybdenum complexes displayed significantly lower stabilities, ranging between 4.7 and 6.1 kcal mol⁻¹ (Fig. S8†). As a consequence, in an experimental system the ligand of the W/Mo complex would need to be enlarged at the ligand periphery to suppress the dimerization by steric hindrance, to avoid an increase of the energy span.

Scheme 5 Possible dimeric structures of the tungsten/molybdenum (M¹ = W/Mo) pincer complexes.

Furthermore, we explored the potential for additional H₂ coordination in tungsten/molybdenum pincer complexes, coupled with subsequent proton and hydride transfers from the corresponding reaction partner (Fig. S9†). Nevertheless, the calculation of transition state energies for TS3 showed higher barriers making pathways of this kind less attractive energetically.

In the concluding phase, ligand screening was carried out by substituting the hydride ligand with both an anionic chloride and a neutral nitrogen ligand within the metal-pincer ligand framework (Scheme 6). The original rhodium complex was chosen as the cooperative reaction partner. The influence of these ligand substitutions was evaluated by identifying the relevant stationary points associated with the energy span. The computed energy spans for the neutral nitrogen ligand were excessively high, surpassing 50 kcal mol⁻¹ for both tungsten and molybdenum pincer complexes (Table 6), indicating the use of such complexes for experimental work not to be favorable. The tungsten pincer complex substituted with chloride, however, exhibited a comparable energy span of 34.2 kcal mol⁻¹, only 1.8 kcal mol⁻¹ higher than the parent system (ligand L1 with hydride). Intriguingly, the chloride substitution in the molybdenum pincer complex yielded an energy span of 32.8 kcal mol⁻¹, which is 2.4 kcal mol⁻¹ lower than the parent system, indicating its potential efficacy in the hydrogenation reaction for ammonia formation.

Scheme 6 Different tungsten/molybdenum pincer complexes.

Table 6 Relative Gibbs free energies (in kcal mol⁻¹) of selected stationary points for the tungsten/molybdenum complexes, incorporating ligands L1-Cl and L1-N (as illustrated in Scheme 6), alongside a cationic rhodium complex serving as a reaction partner in the solvent phase

	TS8	TS10	16	ES^a
a ES = energy span; ΔGr = −20.2 kcal mol^−1.
W-L1^Rh
W-L1^Rh-Cl	22.6	30.3	−24.1	34.2
W-L1^Rh-N	52.5	46.3	−17.3	52.5
Mo-L1^Rh
Mo-L1^Rh-Cl	21.5	31.8	−21.2	32.8
Mo-L1^Rh-N	54.9	48.0	−12.0	54.9

---

Conclusions

In summary, we conducted a systematic computational study to unravel mechanistic insights of how N-heterocyclic carbene-phosphine-based tungsten/molybdenum pincer complexes serve as catalysts in the ionic hydrogenation of nitrogen to ammonia. The cationic rhodium complex, [Cp*Rh{2-(2-pyridyl)phenyl}(CH₃CN)]⁺, serves as a cooperative reaction partner for heterolytic H₂ splitting. The calculated results indicate that, among the various carbene-phosphine ligand frameworks (Ln; n = 1–12), the ⁱPr substitution at phosphorus yields relatively low and therefore promising energy spans for both tungsten and molybdenum complexes. Specifically, the calculated energy spans for the M¹-L1^Rh catalysts are 32.4 kcal mol⁻¹ (W-L1^Rh) and 35.2 kcal mol⁻¹ (Mo-L1^Rh), respectively. While the introduction of electron-donating (L10) or electron-withdrawing (L11) substituents at the ligand structure exhibited marginal influence on the energy span for tungsten complexes, it led to a reduction of 1.1–2.0 kcal mol⁻¹ in the energy span for molybdenum complexes (Mo-L10^Rh = 33.2 kcal mol⁻¹ and Mo-L11^Rh = 34.1 kcal mol⁻¹). Interestingly, substituting rhodium with iridium as the cooperative reaction partner leads to a significant decrease in energy spans. The calculated lowest energy span for the tungsten complex, W-L11^Ir, is 30.6 kcal mol⁻¹, while the molybdenum complex, Mo-L10^Ir, exhibits the lowest energy span in this study of 29.7 kcal mol⁻¹. These values are unprecedented for the N₂/H₂ reaction system. Moreover, calculations on potential dimeric structures lead to the conclusion that molybdenum complexes are less prone to dimerization reactions compared to tungsten complexes. In any case, however, for an experimentally successful system the periphery of the ligands would need to be enlarged to avoid dimerizations completely.

To the best of our knowledge, this study is the first to highlight reaction pathways in the N₂/H₂ system with remarkably low energy spans for the reduction of N₂ to NH₃, employing unique carbene-phosphine-based pincer ligands with tungsten/molybdenum complexes. Acknowledging the limitations of solely predictive computational studies in capturing all real-world complexities, they nonetheless deliver a precise assessment of the energy balance linked to proposed pathways. Therefore, the encouraging outcomes of this study emphasize that the aspiration to derive a molecular catalytic system for NH₃ production in the N₂/H₂ system may be potentially achieved by combination of well-designed transition metal complexes with carefully chosen combination of metal centres supplying dedicated properties for integrated N₂ and H₂ activation, respectively.

Author contributions

Conceptualization: M. H. and T. M. Investigation and Visualization: T. M. Funding acquisition: W. L. Project administration: M. H. Supervision: M. H. Writing – original draft: T. M. Writing – review and editing: all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the computing time granted by the NHR4CES Resource Allocation Board and provided on the supercomputer CLAIX at RWTH Aachen University as part of the NHR4CES infrastructure. The calculations for this research were conducted with computing resources under the project p0020327. This study was performed as part of our activities in the framework of the “Fuel Science Center” funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – Exzellenzcluster 2186, The Fuel Science Center “ID 390919832”.

References

1. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500.
2. M. J. Chalkley, M. W. Drover and J. C. Peters, Chem. Rev., 2020, 120, 5582–5636.
3. J. Guo and P. Chen, Chem, 2017, 3, 709–712.
4. M. Appl, Ammonia: Principles and Industrial Practice, Wiley-VCH, Weinheim, 1999.
5. J. G. Chen, R. M. Crooks, L. C. Seefeldt, K. L. Bren, R. M. Bullock, M. Y. Darensbourg, P. L. Holland, B. Hoffman, M. J. Janik, A. K. Jones, M. G. Kanatzidis, P. King, K. M. Lancaster, S. V. Lymar, P. Pfromm, W. F. Schneider and R. R. Schrock, Science, 2018, 360, eaar6611.
6. Mineral Commodity Summaries 2023, U.S. Geological Survey, 2023, https://pubs.usgs.gov/periodicals/mcs2023/mcs2023.pdf.
7. F. Neese, Angew. Chem., Int. Ed., 2006, 45, 196–199.
8. B. E. Smith, R. L. Richards and W. E. Newton, Catalysts for nitrogen fixation: nitrogenases, relevant chemical models and commercial processes, Springer Science & Business Media, 2004, vol. 1.
9. B. M. Hoffman, D. R. Dean and L. C. Seefeldt, Acc. Chem. Res., 2009, 42, 609–619.
10. G. Schwarz, R. R. Mendel and M. W. Ribbe, Nature, 2009, 460, 839–847.
11. K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, Science, 2011, 334, 974–977.
12. L. K. Boerner, Chem. Eng. News, 2019, 97, 1–9.
13. S. Jenthra, T. Mondal, G. Kemper, M. Lantzius-Beninga, M. Hölscher and W. Leitner, ACS Catal., 2023, 13, 10085–10093.
14. G. Kemper, M. Hölscher and W. Leitner, Sci. Adv., 2023, 9, eadf2966.
15. M. Hölscher, G. Kemper, S. Jenthra, C. Bolm and W. Leitner, Chem. – Eur. J., 2022, 28, e202104375.
16. K. Rohmann, M. Hölscher and W. Leitner, J. Am. Chem. Soc., 2016, 138, 433–443.
17. (a) A. D. Allen and C. V. Senoff, Chem. Commun., 1965, 621–622; (b) J. Chatt, J. R. Dilworth and R. L. Richards, Chem. Rev., 1978, 78, 589–625.
18. M. Hidai, Coord. Chem. Rev., 1999, 185, 99–108.
19. M. Hidai and Y. Mizobe, Chem. Rev., 1995, 95, 1115–1133.
20. T. A. Bazhenova and A. E. Shilov, Coord. Chem. Rev., 1995, 144, 69–145.
21. A. E. Shilov, Russ. Chem. Bull., 2003, 52, 2555–2562.
22. D. V. Yandulov and R. R. Schrock, Science, 2003, 301, 76–78.
23. V. Ritleng, D. V. Yandulov, W. W. Weare, R. R. Schrock, A. S. Hock and W. M. Davis, J. Am. Chem. Soc., 2004, 126, 6150–6163.
24. D. V. Yandulov and R. R. Schrock, Inorg. Chem., 2005, 44, 1103–1117.
25. R. R. Schrock, Acc. Chem. Res., 2005, 38, 955–962.
26. K. Arashiba, Y. Miyake and Y. Nishibayashi, Nat. Chem., 2011, 3, 120–125.
27. J. S. Anderson, J. Rittle and J. C. Peters, Nature, 2013, 501, 84–87.
28. J. Fajardo Jr. and J. C. Peters, J. Am. Chem. Soc., 2017, 139, 16105–16108.
29. Y. Ashida, K. Arashiba, K. Nakajima and Y. Nishibayashi, Nature, 2019, 568, 536–540.
30. T. Mitsumoto, Y. Ashida, K. Arashiba, S. Kuriyama, A. Egi, H. Tanaka, K. Yoshizawa and Y. Nishibayashi, Angew. Chem., 2023, 135, e202306631.
31. B. Askevold, J. T. Nieto, S. Tussupbayev, M. Diefenbach, E. Herdtweck, M. C. Holthausen and S. Schneider, Nat. Chem., 2011, 3, 532–537.
32. T. Shima, S. Hu, G. Luo, X. Kang, Y. Luo and Z. Hou, Science, 2013, 340, 1549–1552.
33. S. Wesselbaum, V. Moha, M. Meuresch, S. Brosinski, K. M. Thenert, J. Kothe, T. vom Stein, U. Englert, M. Hölscher and J. Klankermayer, Chem. Sci., 2015, 6, 693–704.
34. C. Erken, A. Kaithal, S. Sen, T. Weyhermüller, M. Hölscher, C. Werlé and W. Leitner, Nat. Commun., 2018, 9, 4521.
35. A. Kaithal, P. van Bonn, M. Hölscher and W. Leitner, Angew. Chem., Int. Ed., 2020, 59, 215–220.
36. M. Hölscher, M. H. G. Prechtl and W. Leitner, Chem. – Eur. J., 2007, 13, 6636–6643.
37. M. Hölscher and W. Leitner, Angew. Chem., Int. Ed., 2012, 51, 8225–8229.
38. M. Hölscher and W. Leitner, Z. Anorg. Allg. Chem., 2015, 641, 72–77.
39. V. Moha, W. Leitner and M. Hölscher, Chem. – Eur. J., 2016, 22, 2624–2628.
40. O. öztopcu, C. Holzhacker, M. Puchberger, M. Weil, K. Mereiter, L. F. Veiros and K. Kirchner, Organometallics, 2013, 32, 3042–3052.
41. L. A. Wingard, P. S. White and J. L. Templeton, Dalton Trans., 2012, 41, 11438–11448.
42. K. Arashiba, K. Sasaki, S. Kuriyama, Y. Miyake, H. Nakanishi and Y. Nishibayashi, Organometallics, 2012, 31, 2035–2041.
43. Y. Nishibayashi, S. Iwai and M. Hidai, Science, 1998, 279, 540–542.
44. M. Hidai, Y. Mizobe, M. Sato, T. Kodama and Y. Uchida, J. Am. Chem. Soc., 1978, 100, 5740–5748.
45. G. De Ruiter, S. Garhwal, A. Kaushansky, N. Fridman and L. J. W. Shimon, J. Am. Chem. Soc., 2020, 142, 17131–17139.
46. A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560.
47. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
49. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
50. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
51. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
52. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
53. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Wallingford CT, 2016.
55. D. A. Kuß, M. Hölscher and W. Leitner, ACS Catal., 2022, 12, 15310–15322.
56. I. Dutta, S. Yadav, A. Sarbajna, S. De, M. Hölscher, W. Leitner and J. K. Bera, J. Am. Chem. Soc., 2018, 140, 8662–8666.
57. S. Kozuch, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 795–815.
58. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
59. A. Uhe, M. Hölscher and W. Leitner, Chem. – Eur. J., 2013, 19, 1020–1027.
60. H. Ryu, J. Park, H. K. Kim, J. Y. Park, S. T. Kim and M. H. Baik, Organometallics, 2018, 37, 3228–3239.
61. M. A. Légaré, M. Rang, G. Bélanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, Science, 2019, 363, 1329–1332.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt00563e

---