Metal- and ligand-substitution-induced changes in the kinetics and thermodynamics of hydrogen activation and hydricity in a dinuclear metal complex

Abstract

Catalytic function in organometallic complexes is achieved by carefully selecting their central metals and ligands. In this study, the effects of a metal and a ligand on the kinetics and thermodynamics of hydrogen activation, hydricity degree of the hydride complex, and susceptibility to electronic oxidation in bioinspired NiFe complexes, [Ni^IIX Fe^II(Cl)(CO)Y]⁺ ([NiFe(Cl)(CO)]⁺; X = N,N′-diethyl-3,7-diazanonane-1,9-dithiolato and Y = 1,2-bis(diphenylphosphino)ethane), were investigated. The density functional theory calculations revealed that the following order thermodynamically favored hydrogen activation: [NiFe(CO)]²⁺ > [NiRu(CO)]²⁺ > [NiFe(CNMe)]²⁺ ∼ [PdRu(CO)]²⁺ ∼ [PdFe(CO)]²⁺ ≫ [NiFe(NCS)]⁺. Moreover, the reverse order thermodynamically favored the hydricity degree.

---

1. Introduction

Hydrogen represents a clean energy resource, which does not emit carbon dioxide. Thus, catalytic systems that efficiently activate/produce hydrogen are desirable. Hydrogen can be produced by hydrogenase, a biological enzyme. There are three types of hydrogenases based on their metal compositions: [NiFe], [FeFe], and [Fe]. Among them, [NiFe]-hydrogenase favors hydrogen activation. In the active site of [NiFe], a nickel ion is bound to the protein by four cysteine residues, two of which are also coordinated to an iron ion. Further, two cyanos (CN) and one carbonyl (CO) ligands are coordinated to the iron. However, the construction of artificial systems with similar functions to those of enzymes is challenging because enzyme functions are not solely expressed by the active center; they are expressed by the active center in coordination with the surrounding amino acid residues and neighboring metal clusters.^1,2 To elucidate the highly complex catalysis of hydrogenases, numerous attempts have been made to mimic their catalytic centers, particularly their compositions and functions, thereby constructing highly catalytic organometallic complexes.³

Although precious metals are generally known to be highly active in various catalytic reactions, including hydrogen activation/production, the generation of highly efficient catalysts with 3d transition metals, which are abundant on earth, without incorporating precious metals represents a crucial issue from the sustainability and industrial application viewpoints.⁴ Several hydrogen activation catalysts comprising Ni and Fe, as well as noble metals, have been reported as model complexes for the active site of [NiFe]-hydrogenases.^5,6 However, only a few studies have investigated the effect of metal substitution on hydrogen activation by hydrogenase model complexes.⁷

One approach to understanding the origin of the catalytic activity of metal complexes is to investigate the quantitative changes in kinetics and thermodynamics of replacing noble metals with 3d transition metals, and vice versa, in existing model complexes. If replacing noble metals with 3d transition metals and vice versa does not result in significant differences in reaction kinetics and thermodynamics, then it is likely that 3d transition metal-based catalysts can be obtained from the noble metal-containing catalysts that have been synthesized. The accumulation of such data is also important for the recently active derivation of superior catalysts by machine learning models.⁸

Previous studies demonstrated that non-native metal-based mimics of the active sites of hydrogenases are catalytically active. Hu and coworkers⁹ reported the design and development of manganese(I) complexes that mimic [Fe]-hydrogenases. They reported that the synthesized complexes exhibited very high hydrogenation activity. Shima and coworkers^10,11 reported the development of a biomimetic model complex of [Fe]-hydrogenase comprising manganese as the metal center rather than iron. They demonstrated that this manganese complex heterolytically cleaved dihydrogen and catalyzed hydrogenation reactions. Furthermore, they demonstrated that the incorporation of this model into the apoenzyme of an [Fe]-hydrogenase would yield an [Mn]-hydrogenase with higher activity than a similar semisynthetic [Fe]-hydrogenase. These studies indicate the possibility of improving catalytic activity via the substitution of various metals. Additionally, several NiRu complexes have been developed as mimics of [NiFe]-hydrogenase exhibiting hydrogen activation/evolution activity,^12–16 and these metal substitutes may also be active.

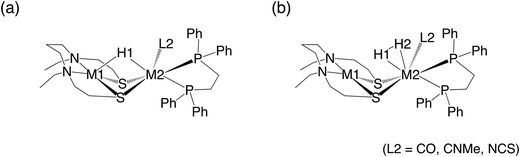
A dinuclear transition-metal complex, [Ni^IIXFe^II(Cl)(CO)Y]⁺ ([NiFe(Cl)(CO)]⁺, where X = N,N′-diethyl-3,7-diazanonane-1,9-dithiolato and Y = 1,2-bis(diphenylphosphino)ethane) (Fig. 1a), was recently synthesized.¹⁷ Similar to the [NiFe]-hydrogenase, this transition-metal complex is composed of Ni and Fe, with the CO ligand being coordinated to Fe. In this catalytic system, hydride complexes (μ-hydride) are formed by heterolytic hydrogen activation in aqueous solutions. Experiments have demonstrated that these μ-hydrides undergo electron and hydride transfer (Fig. 1a–c).

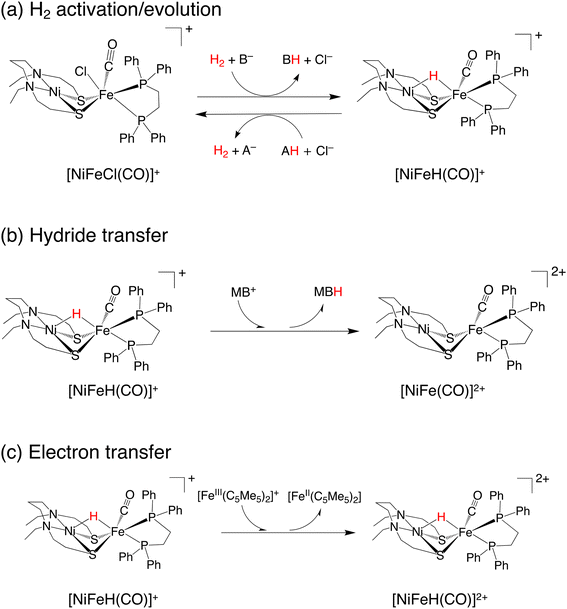Fig. 1 Three reactions performed by NiFe complexes: (a) hydrogen activation/evolution, (b) hydride transfer reaction, and (c) electron transfer reaction.

Employing density functional theory (DFT) calculations, I previously elucidated the mechanism of hydrogen activation by the NiFe complex, confirming that the NiFe metal complex and added base acted as a frustrated Lewis pair and facilitated the reaction.¹⁸ Following mechanistic studies, it is crucial to investigate the effect of substitution by other metals or ligands on the kinetics and thermodynamics of hydrogen activation and on the change in the degree of hydrogenation of the μ-hydrides produced. Such structure-conserving local modifications may not only provide guidance for tuning the kinetics and thermodynamics of hydrogen activation/production of hydrogenase model complexes, but may also provide clues for the activation of experimentally synthesized catalytically inactive model complexes.

In this study, the effects of metal and ligand substitutions (Fig. 2) on the reaction kinetics and thermodynamics of the recently developed [NiFe]-hydrogenase model complex were investigated. Specifically, regarding the metal substitutions, Ni and Fe were substituted with homologous elements in the periodic table, namely Pd and Ru, respectively. Regarding the ligands, the CO ligands were substituted with CN and NCS ligands. Further, the effects of these substitutions on the kinetics and thermodynamics of hydrogen activation, as well as hydride- and electron-transfer reactions of µ-hydrides, which are the products of hydrogen activation, were discussed.

Fig. 2 Metal- and ligand-substituted dinuclear complexes.

2. Computational details

The calculations in this study were performed by the Gaussian 09 software.¹⁹ The structures were fully optimized without constraints using the BP86 functional,^20,21 as well as Grrimme's empirical dispersion corrections.²² The BP86 functional is known to correctly predict the ground-state spin state of similar [NiFe] complexes^17,23,24 and also has been applied to the active center of hydrogenases.^25,26 The Stuttgart/Dresden (SDD) basis sets²⁷ and associated effective-core potentials were used for Fe, Ni, Ru, and Pd, and the def2-SVP basis sets²⁸ were used for the other atoms. To account for the water-solvation effects, an SMD implicit model²⁹ was employed (ε = 78.4).

To confirm the minima and obtain the zero-point vibrational energy correction, the vibrational frequency was calculated at the same level of theory. Further, thermal corrections were performed at 298.15 K and 1 atm. The potential energies of the optimized stationary points were calculated using the SDD basis set²⁷ and associated effective-core potentials (for Fe, Ni, Ru, and Pd) and def2-TZVP (for the other atoms) using the SMD model.²⁹

The integrations were evaluated using a pruning grid comprising 99 radius shells and 590 angle points per shell. The stabilities of the wavefunction of all the metal complexes were confirmed.

Regarding the labels of the complexes, for example, ¹[NiFeH(CO)]⁺ indicates that NiFe comprised a hydride ligand and a CO one in addition to X and Y (X = N,N′-diethyl-3,7-diazanonane-1,9-dithiolato and Y = 1,2-bis(diphenylphosphino)ethane). The “1” on the left shoulder indicates the singlet spin state, and the “+” on the right shoulder indicates the charge of the complex.

3. Results and discussion

Analysis of the complexes involved in hydrogen activation

Our previous computational studies confirmed that the NiFe complex-catalyzed hydrogen activation involved two elementary reactions: the binding of molecular hydrogen to the metal site and proton transfer.

¹[NiFe(CO)]²⁺ + H₂ → ¹[NiFe(H₂)(CO)]²⁺ (1)

¹[NiFe(CO)(H₂)]²⁺ + A⁻ → ¹[NiFeH(CO)]⁺ + AH, (2)

where A⁻ is the Lewis base, which was added to abstract the proton. Starting from the complex with vacant coordination (¹[NiFe(CO)]²⁺), a dihydrogen complex (¹[NiFe(H₂)(CO)]²⁺) was formed as an intermediate, after which µ-hydride (¹[NiFeH(CO)]⁺) was obtained as a product.

Regarding the structure, a bridging state was experimentally detected in a previous study, as in [NiFe]-hydrogenase.³⁰ Additionally, our previous computational study¹⁸ confirmed that Fe and Ni in the NiFe complex represent the active and inactive sites for hydrogen-activation reactions, respectively. This is because all the Ni d-orbitals in the axial position of the Ni site are occupied. Moreover, it is the electron-unoccupied orbitals of Fe that allow hydrogen to donate electrons.

In the ¹[NiFe(CO)]²⁺-catalyzed H₂ activation, the ground states of the starting complex, intermediates, and products were all singlet.¹⁷ However, the spin states could change with the metal or ligand substitution. Therefore, the structural optimizations of four spin multiplicities (S = 0–3) were performed to determine the spin multiplicity of the ground state of each complex by comparing the relative free energies.

Table 1 summarizes the relative energies of the four spin states (S = 0, 1, 2, 3) of the three complexes: the complex with vacant coordination, [M1M2(L2)]²⁺; the dihydrogen complex, [M1M2(H₂)(L2)]²⁺; and the hydride complex, [M1M2H(L2)]⁺. Regarding [M1M2(L2)]²⁺, it was predicted that the coordination of water in an aqueous solution, i.e., the complex formation of [M1M2(H₂O)(L2)]²⁺, was thermodynamically unfavorable (Table S1†), thus not coordinating.

Table 1 Relative free energies (kcal mol⁻¹) of the four spin states (S = 1, 2, and 3) of the ligand-free complex, dihydrogen complexes, and hydride complexes

	[NiFe(CO)]^2+	[NiFe(H2)(CO)]^2+	[NiFeH(CO)]^+	[NiRu(CO)]^2+	[NiRu(H2)(CO)]^2+	[NiRuH(CO)]^+
S = 0	0.0	0.0	0.0	0.0	0.0	0.0
S = 1	11.1	13.7	3.3	15.7	13.2	3.4
S = 2	26.0	31.8^a	34.8	51.5	64.6	56.7
S = 3	54.2	50.7^a	61.9	108.7	95.6^a	115.1

---

	[PdFe(CO)]^2+	[PdFe(H2)(CO)]^2+	[PdFeH(CO)]^+	[PdRu(CO)]^2+	[PdRu(H2)(CO)]^2+	[PdRuH(CO)]^+
S = 0	0.0	0.0	0.0	0.0	0.0	0.0
S = 1	8.6	27.8	18.5	35.6	31.7	21.0
S = 2	34.0	26.3^a	43.6	76.4	72.1	70.7
S = 3	72.4	61.4^a	75.9	127.9	123.9^a	129.8

---

	[NiFe(CNMe)]^2+	[NiFe(H2)(CNMe)]^2+	[NiFeH(CNMe)]^+	[NiFe(NCS)]^+	[NiFe(H2)(NCS)]^+	[NiFeH(NCS)]^0
a H2 dissociates.
S = 0	0.0	0.0	0.0	0.0	0.0	1.0
S = 1	9.2	11.0	1.6	2.8	15.6	0.0
S = 2	23.7	29.8	29.6	11.2	36.5	11.4
S = 3	41.7	41.7	51.7	23.8	28.8^a	31.0

---

Regarding the complexes with CO ligands, their ground states exhibited low spins (S = 0). Regarding metal substitution and replacement of the CO ligand with a CNMe ligand, the order of the spin-state stability remained unchanged, whereas substituting the CO ligand with an NCS ligand stabilized the triplet state. The triplet state corresponded to the ground states of µ-hydride. This result is consistent with the findings for hydrogenases, where the low-spin states were stabilized by the CO ligands.³¹

In the complexes where the CO ligand was replaced by an NCS ligand, the energy splitting between the ground-state spin and second-lowest energy spin was small (∼1 kcal mol⁻¹), allowing spin conversion retaining the spin crossover properties.

Overall, the ligand substitution (CO → NCS) at the active site (M2, Fig. 1) exerted the highest influence on the spin state of the complex. The calculations of the relative energies between the different spins indicated that the low spins dominated H₂ activation by the CO-containing complexes, whereas the low and medium spins (S = 0, 1) in the [NiFe(L1)(NCS)] complexes containing NCS ligands contributed.

Hydrogen activation

Table 2 summarizes the reaction energies of the two elementary reactions (eqn (1) and (2)) of the [M1M2(L2)]²⁺-catalyzed H₂-activation reaction. Fig. 3 shows the free-energy profile of H₂ activation.

Fig. 3 Free energy profile of H₂ activation by the dinuclear complex, [M1M2(L2)]²⁺, with (a) CH₃COO⁻ and (b) HPO₄⁻ as Brønsted base, consisting of two elementary processes, H₂ binding and proton abstraction. The proton abstraction step has no or low reaction barrier (Fig. S1 and S2†).

Table 2 Reaction energies (kcal mol⁻¹) of the elementary reactions of H₂ activation catalyzed by the [M1M2(L2)] complex; (1) H₂ binding and (2) H–H bond cleavage

	Spin state		ΔG	ΔG^‡	ΔGtotal
a Overall energy of H2 activation.
(M1,M2,L2)	(1) [M1M2(L2)] + H2 → [M1M2(H2)(L2)]
	[M1M2(L2)]^2+	[M1M2(H2)(L2)]^2+
(Ni,Fe,CO)	S = 0	S = 0	8.5	11.3
(Ni,Ru,CO)	S = 0	S = 0	9.9	9.3
(Pd,Fe,CO)	S = 0	S = 0	14.3	13.9
(Pd,Ru,CO)	S = 0	S = 0	12.6	11.6
(Ni,Fe,CNMe)	S = 0	S = 0	7.0	8.6
	[M1M2(L2)]^+	[M1M2(H2)(L2)]^+
(Ni,Fe,NCS)	S = 0	S = 0	12.3	13.3
	(2) [M1M2(H2)(L2)] + CH3COO^− → [M1M2H(L2)] + CH3COOH
	[M1M2(H2)(L2)]^2+	[M1M2H(L2)]^+			(1) + (2)^a
(Ni,Fe,CO)	S = 0	S = 0	−14.6		−6.0
(Ni,Ru,CO)	S = 0	S = 0	−13.1		−3.3
(Pd,Fe,CO)	S = 0	S = 0	−13		1.3
(Pd,Ru,CO)	S = 0	S = 0	−11.9		0.6
(Ni,Fe,CNMe)	S = 0	S = 0	−5.7		−0.3
	[M1M2(H2)(L2)]^+	[M1M2H(L2)]^0
(Ni,Fe,NCS)	S = 0	S = 1	0.0		12.3

---

Regarding the binding of dihydrogen to the metal, replacing Fe with Ru did not yield a noticeable difference; the binding energy of the hydrogen molecule is smaller than that of Fe, but the difference is ∼1 kcal mol⁻¹. The similarity of the H₂-binding energies of homologous elements has also been observed in complexes composed of group 6 elements (Cr, Mo, W, etc.).³²

When Ni is replaced by Pd, the H₂-binding energy becomes smaller probably because Pd, which is softer (and more easily polarized) than Ni,³³ exerts an increasing effect on the electron density of Fe (Table 3, q(Fe) = −1.16 for ¹[NiFe(CO)]²⁺ and −1.35 for ¹[PdFe(CO)]²⁺), making H₂ less favorable for nucleophilic binding to Fe. Conversely, replacing the more electron-donating CO ligand with the less electron-donating NCS ligand reduced the electron density of Fe (Table 3; q(Fe) = −1.16 and −0.77 for ¹[NiFe(CO)]²⁺ and ¹[NiFe(NCS)]⁺); however, unexpectedly, the H₂ binding energy is not enhanced.

Table 3 Mulliken charge of the (a) ligand-free complex, (b) dihydrogen complex, and (c) hydride complexes

	^1[NiFe(CO)]^2+	^1[NiRu(CO)]^2+	^1[PdFe(CO)]^2+	^1[PdRu(CO)]^2+		^1[NiFe(CNMe)]^2+		^1[NiFe(NCS)]^+
	(a) Ligand-free complex
M1^a	−0.28	−0.40	0.00	−0.21		−0.33		−0.55
M2	−1.16	−0.04	−1.35	−0.23		−1.06		−0.77
C	0.60	0.22	0.60	0.22
O	−0.10	−0.11	−0.10	−0.11
					C	0.36	N	0.07
					N	−0.05	C	−0.17
					Me	0.37	S	−0.33

---

	^1[NiFe(H2)(CO)]^2+	^1[NiRu(H2)(CO)]^2+	^1[PdFe(H2)(CO)]^2+	^1[PdRu(H2)(CO)]^2+		^1[NiFe(H2)(CNMe)]^2+		^1[NiFe(H2)(NCS)]^+
	(b) Dihydrogen complex
M1	−0.66	−0.69	−0.34	−0.49		−0.66		−0.36
M2	−1.92	−0.63	−2.00	−0.62		−1.83		−1.47
C	0.63	0.26	0.66	0.26
O	−0.08	−0.08	−0.08	−0.08
					C	0.38	N	0.09
					N	−0.04	C	−0.20
					Me	0.36	S	−0.36
H1	0.53	0.38	0.55	0.35		0.25		0.29
H2	0.26	0.14	0.23	0.13		0.51		0.35

---

	^1[NiFeH(CO)]^+	^1[NiRuH(CO)]^+	^1[PdFeH(CO)]^+	^1[PdRuH(CO)]^+		^1[NiFeH(CNMe)]^+		^3[NiFeH(NCS)]^0
a The label of atom is shown in Fig. 4.
	(c) Hydride complex
M1	−0.62	−0.73	−0.34	−0.56		−0.66		−0.49
M2	−1.83	−0.66	−1.91	−0.66		−1.85		−1.47
C	0.53	0.22	0.57	0.23
O	−0.16	−0.15	−0.16	−0.15
					C	0.36	N	0.11
					N	−0.15	C	−0.19
					Me	0.29	S	−0.38
H1	0.54	0.24	0.46	0.18		0.57		0.51

---

The CO ligand is known to be crucial to the oxidative addition of H₂ as it relaxes the excess electron density of the metal center via π-backdonation.³² However, the CO-donating potential, as predicted from the charge of Fe, was significantly greater than that of the NCS ligand, even with the π-backdonation (Table 3).

Fig. 4 Labelling of the atoms of µ-hydride (a) [M1M2(H)L2] and (b) dihydrogen complex [M1M2(H₂)L2].

The backdonation degree in iron carbonyl complexes can be predicted from the M–CO and C–O distances of the carbonyl complex.^34,35 Namely, when the dπ-electrons of iron are back-donated to the CO π*-orbital, the Fe–C(O) bond strength and length become higher and lower, respectively, whereas the C–O bond strength and length become lower and higher, respectively. A comparison of [NiFeH(CO)]⁺ and [PdFeH(CO)]⁺ reveals that Fe–C(O) and C–O exhibited the same bond lengths (Table 4); thus, their π-backdonation degrees are assumed to be comparable.

Table 4 Geometrical parameters of the (a) dihydrogen complex and (b) hydride complexes (Å)

	^1[NiFe(H2)(CO)]^2+	^1[NiRu(H2)(CO)]^2+	^1[PdFe(H2)(CO)]^2+	^1[PdRu(H2)(CO)]^2+	^1[NiFe(H2)(CNMe)]^2+	^1[NiFe(H2)(NCS)]^+
	(a) Dihydogen complex
M1–M2^a	2.71	2.85	2.90	2.98	2.72	3.24
M1–H1	1.77	1.87	1.96	2.08	2.60	3.53
M2–H2	1.67	1.80	1.68	1.79	1.67	1.65
M1–H1	2.58	2.71	2.79	2.89	2.60	3.53
M2–H2	1.58	1.73	1.60	1.73	1.67	1.65
H1–H2	0.93	0.93	0.91	0.91	0.92	0.86
M2–C	1.74	1.86	1.74	1.85
C–O	1.17	1.17	1.17	1.17

---

	^1[NiFeH(CO)]^+	^1[NiRuH(CO)]^+	^1[PdFeH(CO)]^+	^1[PdRuH(CO)]^+	^1[NiFeH(CNMe)]^+	^3[NiFeH(NCS)]^0
a The label of atom is shown in Fig. 3.
	(b) Hydride complex
M1–M2	2.61	2.74	2.77	2.88	2.62	2.50
M1–H1	1.78	1.88	2.02	2.17	1.78	1.68
M2–H1	1.56	1.67	1.54	1.66	1.57	1.60
M2–C	1.71	1.83	1.71	1.83
C–O	1.18	1.18	1.18	1.18

---

Regarding the H–H bond length of the dihydrogen that is bound to the metal, those of ¹[NiFe(H₂)(CO)]²⁺ and ¹[NiRu(H₂) (CO)]²⁺ were the highest, indicating that they might be the most activated. However, no correlation was observed between the H–H bond distance, as well as the binding energy of H₂. Moreover, the binding strength of H₂ could not be predicted from the H–H distance. One reason for the lack of a simple correlation between the structure and energy might be that hydrogen does not interact with one metal, although it does with the other, making it more complicated.

The H₂ bond exhibited an endergonic character that was consistent for all the complexes; this character was revealed in previous studies and attributed to the entropy effects estimated by dielectric models. Thus, it is not as endergonic as the model calculations indicate.^23,36 The difference between the H₂ binding barrier and the H₂ binding energy is at most 2.8 kcal mol⁻¹, which is not a large gap for any complex (Table 1). This is also the case for the NiFe and NiIr complexes that I have studied previously.^23,24 For [NiRu(CO)]²⁺, [PdFe(CO)]²⁺, and [PdRu(CO)]²⁺, the H₂-bound state has a higher energy than the transition state. This is either due to thermodynamic corrections or because different basis functions are used in the electronic energy calculations and the structural optimization.

When using computational chemistry methods to develop metal complexes for H₂ activation, it is valuable to predict the H₂ binding energy from the charge of the H₂-binding site of the complex. Comparing the Mulliken charges in the complexes with Fe as a constituent, the electron densities of Fe were in the following order: [PdFe(CO)]²⁺ > [NiFe(CO)]²⁺ > [NiFe(CNMe)]²⁺ > [NiFe(NCS)]⁺. Here, the H₂ binding energy decreases in this order except for [NiFe(NCS)]⁺, whose total charge is 1+. This result suggests that both partial and total charges of the complexes are important as descriptors in machine learning for predicting H₂ binding energies. Notably, such a comparison cannot be made for dissimilar metals, such as Fe and Ru.

Next, the proton-abstraction step was considered. As CH₃COO⁻ was used consistently in all the complexes as the proton acceptor, the reaction energies of this elementary process indicated the stability of the product (µ-hydride) with respect to the dihydrogen complexes. During the cleavage of the H–H bonds, the substitution of the CO ligands for the NCS ligands made the reaction significantly endergonic and thermodynamically unfavorable (Table 2).

The transition state structure of the proton abstraction process by CH₃COO⁻ could not be determined in the metal- and ligand-substituted forms of [NiFe(CO)]²⁺, despite numerous attempt. For [NiFe(CO)]²⁺, which has been optimized in previous studies, the reaction barrier is very small at 0.7 kcal mol⁻¹.¹⁸ Therefore, relax energy scan was performed for the distance between the oxygen of the base CH₃COO⁻ and the proton of the dihydrogen complex (Fig. S1†). As a result, [PdFe(H₂)(CO)]²⁺, [PdRu(H₂)(CO)]²⁺, and [PdRu(H₂)(CO)]²⁺ were found to be barrier-free processes. In addition, [NiFe(H₂)(CNMe)]²⁺ and [NiFe(H₂)(NCS)]⁺ are broad with low barriers, which may have prevented locating the transition state. For the same reason, the transition state of proton desorption by HPO₄²⁻ could not be captured (Fig. S2†).

Because implicit solvation models do not accurately describe local interactions such as hydrogen bonding, explicit water is often placed as an improvement. In this study, one explicit water molecule was coordinated to oxygen of CH₃COO⁻. Our previous work suggests that it is difficult to verify whether increasing the number of water molecules increases accuracy.²³ When 1–5 water molecules were added, the reaction barrier did not converge as the number of water molecules increased. To obtain more accurate reaction barriers, the application of a hybrid QM/MM method³⁷ would be more appropriate instead of such localized water arrangements.

To describe the kinetics and thermodynamics of H₂ activation more accurately, counterion effects may also need to be considered. Previous studies have reported that counterion considerations are particularly important for highly charged complexes.³⁸ In the present model system, sodium derived from acetate and phosphate buffers was not considered. The verification of the effects of these ions should not be simple. Statistical considerations are necessary because of the various possible arrangements of the ions with respect to the complexes and bases.

Compared to the structures of [NiFeH(CO)]⁺ and [NiFeH(NCS)]⁰, the Ni–H bond distance of [NiFeH(NCS)]⁰ is shorter than that of [NiFeH(CO)]⁺ and the Fe–H bond distance is longer, making them more nearly equidistant (R(Ni–H) = 1.68, R(Fe–H) = 1.60 Å, Table 4), resulting in more contrasting cross-linked structures.

The M1–M2 bond distance was shorter (R(Ni–Fe) = 2.50 Å, Table 4) in [NiFeH(NCS)]⁰ than in [NiFeH(CO)]⁺ (R(Ni–Fe) = 2.61 Å, Table 4), indicating the formation of a metal–metal bond in [NiFeH(H₂O)]⁺. In [NiFe]-hydrogenase, the metal–metal bond acts as a base and oxidatively facilitates proton addition.^39,40 This is consistent with the fact that [NiFeH(NCS)]⁺ is thermodynamically more favorable than [NiFeH(CO)]⁺ for proton addition to form the dihydrogen complex.

The free-energy profile of H₂ activation with CH₃COO⁻ as a base revealed that all the reactions, except [NiFe(CO)]²⁺ and [NiRu(CO)]²⁺, were endergonic and possibly failed to proceed (Fig. 3a). Conversely, when a stronger base, HPO₄²⁻, was used, all the reactions except [NiFe(NCS)]⁺ were exergonic, and the H₂-activation reactions proceeded (Fig. 3b). This indicates that exogenous bases significantly impact the thermodynamics of H₂-activation reactions. Also for [NiFe(NCS)]⁺, the use of stronger CH₃O⁻ that was previously used for H₂ activation^24,41 would be exergonic. Even for complexes mimicking the active centers of hydrogenases whose activities toward H₂ activation have not been confirmed, such activities may emerge simply by changing the base.

Overall, regarding the dinuclear transition-metal complexes, H₂ binding to the metal site was demonstrated as a more thermodynamically challenging process than the proton-abstraction process to form µ-hydride. This is because the second step, namely the proton-abstraction step, can be tuned outside the catalyst, whereas the first step, i.e., H₂ binding, is solely determined by the catalyst. Thus the catalyst design for H₂ activation must consider H₂ binding to the metal site.

Hydricity

Hydricity is a crucial thermodynamic parameter in reactions, such as H₂ oxidation and formation, as well as CO₂ reduction.^42–44 Thermodynamic hydricity is synonymous with the hydride-donating ability of a reaction. For example, in a CO₂-reduction reaction, the greater the hydricity degree, the more thermodynamically favorable the reaction would be for the formation of formic acid.^39,44–46

The hydricity degrees of six µ-hydrides containing substituted metals and ligands were investigated. Hydricity is calculated as the free energy of the dissociation reaction of the metal hydride into the metal cation and hydride anion (eqn (3)). However, the isolated free state of the hydride anion has not been experimentally detected. Therefore, determining hydricity is experimentally challenging and requires the use of complex schemes to obtain it from experimental values.^43,47,48 Conversely, theoretical calculations allow for the estimation of the hydricity degree according to eqn (3). The possibility of hydride transfer to a particular hydride receptor can also be predicted by eqn (4).

[M1M2H(L2)]⁺ → [M1M2(L2)]²⁺ + H⁻ (3)

[M1M2H(L2)]⁺ + MB⁺ → [M1M2(L2)]²⁺ + MBH. (4)

In eqn (4), “MB” represents methylene blue, which receives the hydride, and nitrogen is the atomic site that accepts the hydride. In the experimental measurement of hydricity degrees, if a ligand other than the solvent binds to the metal center after hydride transfer, the metal–ligand binding energy is included in the measured thermodynamic value. However, regarding the complexes in this study, the binding of the solvent destabilized the complex (Table S1†); thus, the hydrogen-donating nature corresponds to the energy of simple hydride transfer.

The calculated hydricity degrees are summarized in Table 5. The largest change in the hydricity, from [NiFeH(CO)]⁺, was observed in [NiFeH(NCS)]⁺, where the hydricity degree increased by ∼18 kcal mol⁻¹. This might be so because the absence of a CO ligand with high electron-donating ability resulted in a smaller electron density of Fe, which facilitated lowered electron donation to H and produced a weak metal–hydride bond. The largest change observed with metal replacement was in [PdFeH(CO)]⁺, where Ni was replaced by Pd. This change might be due to Pd, which is more polarizing than Ni, increasing the electron density of Fe even though the electron density of Pd is low (Table 3); this reduced the strength of the Pd–H bonds in the bridging coordination structure. Moreover, the lowest substitution effect was observed when Fe was replaced by Ru.

Table 5 Reaction energies (kcal mol⁻¹) of hydride transfer from [M1M2H(L2)] to MB⁺ (R1), [M1M2H(L2)] + MB^+a → [M1M2(L2)] + MBH^b, and hydricity (R2), [M1M2H(L2)] → [M1M2(L2)] + H⁻

(M1,M2,L2)	Spin state		ΔG (R1)	ΔG (R2)
a MB^+: methylene blue. b MBH: protonated methylene blue.
	[M1M2H(L2)]^+	[M1M2(L2)]^2+
(Ni,Fe,CO)	S = 0	S = 0	42.9	−5.6
(Ni,Ru,CO)	S = 0	S = 0	40.1	−8.4
(Pd,Fe,CO)	S = 0	S = 0	35.6	−12.9
(Pd,Ru,CO)	S = 0	S = 0	36.2	−12.3
(Ni,Fe,CNMe)	S = 2	S = 1	37.1	−11.4
	[M1M2H(L2)]^0	[M1M2(L2)]^+
(Ni,Fe,NCS)	S = 1	S = 1	24.5	−24.0

---

Regarding the complexes in which M2 was Fe, the [NiFeH(NCS)]⁰ with the largest hydrogen-donating capacity exhibited the longest Fe–H distance (Table 4), although no clear correlation could facilitate the prediction of hydrogen-donating properties from the Fe–H distance. This is probably because of the complicated interaction due to the presence of another metal.

In our previous study, the reaction energies of hydride transfer to MB were compared for three isomers of µ-hydride, [NiFeH(CO)]⁺.⁴⁹ The hydricity (eqn (4)) ranged from −5.8 to −13.8 kcal mol⁻¹. The range of the variation in the hydricity of µ-hydrides in this study involving metal and ligand substitutions was −5.6 to −24.0 kcal mol⁻¹, which is wider than the reactivity difference due to isomerization.

Regarding the solvent dependence of hydricity, Matsubara et al.⁴⁷ reported that the hydricity of Ru complexes was ∼20 kcal mol⁻¹ higher than that of acetonitrile in water. Contrarily, in this study, the calculated hydride-donating potentials of [NiFeH(CO)]⁺ were −5.6 and −5.8 kcal mol⁻¹ in an aqueous solution (Table 5) and acetonitrile, respectively, and these values were almost the same.⁴⁹ Although the solvent dependence of hydricity may be unique to metal complexes, careful verification of these discrepancies requires the application of more accurate solvation models such as the hybrid QM/MM.

The criticality of the solvent dependence of the hydricity degrees of complexes has been highlighted in product selectivity, e.g., in photocatalytic CO₂ reduction catalyzed by an RuRe supramolecular complex to produce formic acid or CO in water⁵⁰ or organic solvents (acetonitrile), respectively.^51,52 Thus, subsequent studies must consider the quantitative examination of the contribution of the solvent-dependent hydricity degree to product selectivity.

Fig. 5 shows the plots of the overall reaction energy of H₂ activation versus the hydricity degrees of the six dinuclear complexes. A simple linear relationship existed between the hydricity degree and overall reaction energy for H₂ activation. The more hydride-donating complexes were less suitable for H₂ activation. ¹[NiFeH(CO)]⁺ was the most suitable complex for hydrogen activation, whereas ³[NiFeH(NCS)]⁰ was the most suitable hydride donor. Overall, it was demonstrated that the range of the reaction energies for H₂ activation and hydricity can be tuned to ∼20 kcal mol⁻¹ by the metal and ligand substitutions performed in this study.

Fig. 5 Plots of the overall energy of H₂ activation against the thermodynamic hydricity.

The reported hydricity of [FeFe]-hydrogenase was 25.7–28.7 kcal mol⁻¹,⁵³ whereas the maximum hydricity for the complexes produced by the substitutions of metals and ligands in this study was 24.5 kcal mol⁻¹, corresponding to the approximate upper end of the hydricity degree of [FeFe]-hydrogenase. In this study, only the bridging hydride complexes were investigated. However, in previous studies,^17,54 terminal hydride complexes were detected as isomers of bridging hydride complex for the [NiFeH(CO)]⁺ (Fig. S3†), which shows a higher degree of hydricity than bridging hydride complex. Therefore, a possible approach to further increase hydricity is to target the terminal hydride in addition to metal and ligand substitutions in the synthesis.

Electron transfer

In hydrogenase, a large subunit comprising an [NiFe] active site and a small subunit comprising iron–sulfur clusters that form an electron-transfer relay account for the reversible conversion of molecular hydrogen into protons and electrons, with the small subunit comprising the iron–sulfur clusters being particularly responsible for electron transfer.^55,56

In an artificial catalytic system, the redox state of the catalyst is generally controlled by the added oxidant or reductant. The ease of forming the oxidized form of µ-hydrides, which is an intermediate in the H₂-activation reaction, is crucial as it affects the catalytic efficiency.^57,58 For some catalytic systems, proton-coupled electron transfer in which proton transfer proceeds in conjunction with electron transfer, would also be possible.^59–61

Previous experimental studies revealed that [NiFeH(CO)]⁺ is oxidized by ferrocene:¹⁷

[NiFeH(L)]⁺ + [Fe^III(C₅Me₅)₂]²⁺ → [NiFeH(L)]²⁺ + [Fe^II(C₅Me₅)₂]⁺ (5)

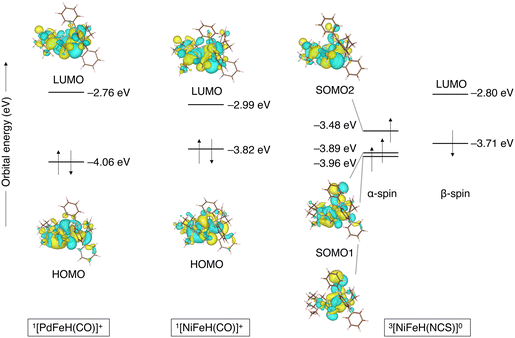
Table 6 presents the electron-transfer energies to ferrocene for metal- and ligand-substituted µ-hydrides. In [NiFeH(NCS)]⁰, which has an NCS ligand with smaller electron-donating potential than the CO ligand, the thermodynamic advantage is more than 10 kcal mol⁻¹ higher than [NiFeH(CO)]⁺, making it susceptible to electron oxidation. This can be seen from the molecular orbital energy levels: the single occupied molecular orbital level of [NiFeH(NCS)]⁺ (ε(SOMO2) = −3.48 eV) and the highest occupied molecular orbital energy level of [NiFeH(CO)]⁺ (ε(HOMO) = −3.82 eV). Thus, the highest occupied molecular orbital increases when the NCS ligand is coordinated instead of the CO ligand. Here, HOMO of [NiFeH(CO)]⁺ is distributed over the metal rather than over the ligand; thus, it is assumed that the two metals were mainly oxidized. Conversely, replacing Ni in [NiFeH(CO)]⁺ with Pd lowers the highest occupied molecular orbital energy level (ε(HOMO) = −3.82 eV for [NiFeH(CO)]⁺ and ε(SOMO) = −4.06 eV for [PdFeH(CO)]⁺, Fig. 6), indicating it more challenging to oxidize [PdFeH(CO)]⁺ than [NiFeH(CO)]⁺ (Fig. 6). Overall, the electron-transfer reaction energy ranged from −5.2 to −25.6 kcal mol⁻¹ depending on the metal or ligand substitution.

Fig. 6 Energies of the molecular orbitals of the three Fe containing dinuclear complexes.

Table 6 Electron transfer energy (kcal mol⁻¹) [M1M2H(L2)] + [Fe^III(C₅Me₅)₂]⁺ → [M1M2H(L2)] + [Fe^II(C₅Me₅)₂]⁰

(M1,M2,L2)			ΔG
	[M1M2H(L2)]^+	[M1M2H(L2)]^2+
(Ni,Fe,CO)	S = 0	S = 1/2	−10.8
(Ni,Ru,CO)	S = 0	S = 1/2	−8.6
(Pd,Fe,CO)	S = 0	S = 1/2	−9.8
(Pd,Ru,CO)	S = 0	S = 1/2	−5.2
(Ni,Fe,CNMe)	S = 0	S = 1/2	−18.5
	[M1M2H(L2)]^0	[M1M2H(L2)]^+
(Ni,Fe,NCS)	S = 1	S = 1/2	−25.6

---

4. Conclusions

In this study, the effects of metal and ligand substitutions on the H₂ activation, hydride transfer, and electron oxidation of µ-hydrides in the [NiFe]-hydrogenase model complex were investigated by DFT calculations. For H₂ activation, the thermodynamically suitable catalysts were in the following order: [NiFe(CO)]²⁺ > [NiRu(CO)]²⁺ > [NiFe(CNMe)]²⁺ ∼ [PdRu(CO)]²⁺ ∼ [PdFe(CO)]²⁺ ≫ [NiFe(NCS)]⁺.

The metal and ligand substitutions caused a reaction-energy differences of up to 18 kcal mol⁻¹ in the H₂-activation reaction. Thermodynamic H₂ activation did not proceed in [PdRu(CO)]²⁺, [PdFe(CO)]²⁺, and [NiFe(CNMe)]²⁺ when CH₃COO⁻ was used as a base, although the reaction proceeded when a stronger base, H₂PO₄⁻, was used. It was also suggested that [NiFe(NCS)]⁺ requires an even stronger base, CH₃O⁻. From this base dependence, it is possible to induce catalytic activity by simply changing the base in complexes that mimic the active center of hydrogenases with unknown H₂-activation performances.

The hydricity degree correlated inversely with the reaction energy of H₂ activation, and the introduction of a noble metal exhibiting higher polarizability than the 3d-transition metal into the other metal, which is not the catalytic center, increased the hydricity degree. Furthermore, when the CO ligand was replaced by a less electron donating NCS ligand, the degree of hydricity was higher than when the noble metal was introduced.

Although it is generally known that noble metals are very catalytically active, it was quantitatively demonstrated that the replacement of noble metals with transition metals did not necessarily improve the catalytic reaction thermodynamically. However, the combination of the transition metal with a ligand in the dinuclear complex significantly increased the thermodynamics of the catalytic reaction. The findings offer guidelines for developing catalysts that mimic the active centers of hydrogenases.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was in supported by the Grants-in-Aid for Scientific Research (KAKENHI 18K05297 and 22K05298). Computer resources at the Academic Center for Computing and Media Studies at Kyoto University, Research Center of Computer Science at the Institute for Molecular Science are also acknowledged.

References

1. J. W. Slater, S. C. Marguet, M. E. Gray, H. A. Monaco, M. Sotomayor and H. S. Shafaat, Power of the Secondary Sphere: Modulating Hydrogenase Activity in Nickel-Substituted Rubredoxin, ACS Catal., 2019, 9, 8928–8942.
2. S. T. Stripp, B. R. Duffus, V. Fourmond, C. Léger, S. Leimkühler, S. Hirota, Y. Hu, A. Jasniewski, H. Ogata and M. W. Ribbe, Second and Outer Coordination Sphere Effects in Nitrogenase, Hydrogenase, Formate Dehydrogenase, and CO Dehydrogenase, Chem. Rev., 2022, 122, 11900–11973.
3. M. E. Ahmed and A. Dey, Recent developments in bioinspired modelling of [NiFe]- and [FeFe]-hydrogenases, Curr. Opin. Electrochem., 2019, 15, 155–164.
4. J. Liu, H. Zhang, M. Qiu, Z. H. Peng, M. K. H. Leung, W. F. Lin and J. Xuan, A review of non-precious metal single atom confined nanomaterials in different structural dimensions (1D-3D) as highly active oxygen redox reaction electrocatalysts, J. Mater. Chem. A, 2020, 8, 2222–2245.
5. D. Schilter, J. M. Camara, M. T. Huynh, S. Hammes-Schiffer and T. B. Rauchfuss, Hydrogenase Enzymes and Their Synthetic Models: The Role of Metal Hydrides, Chem. Rev., 2016, 116, 8693–8749.
6. J. T. Kleinhaus, F. Wittkamp, S. Yadav, D. Siegmund and U. P. Apfel, [FeFe]-Hydrogenases: maturation and reactivity of enzymatic systems and overview of biomimetic models, Chem. Soc. Rev., 2021, 50, 1668–1784.
7. D. Brazzolotto, L. Wang, H. Tang, M. Gennari, N. Queyriaux, C. Philouze, S. Demeshko, F. Meyer, M. Orio, V. Artero, M. B. Hall and C. Duboc, Tuning Reactivity of Bioinspired [NiFe]-Hydrogenase Models by Ligand Design and Modeling the CO Inhibition Process, ACS Catal., 2018, 8, 10658–10667.
8. W. Yang, T. T. Fidelis and W.-H. Sun, Machine Learning in Catalysis, From Proposal to Practicing, ACS Omega, 2020, 5, 83–88.
9. H. J. Pan and X. Hu, Biomimetic Hydrogenation Catalyzed by a Manganese Model of [Fe]-Hydrogenase, Angew. Chem., Int. Ed., 2020, 59, 4942–4946.
10. H. J. Pan, G. Huang, M. D. Wodrich, F. F. Tirani, K. Ataka, S. Shima and X. Hu, A catalytically active [Mn]-hydrogenase incorporating a non-native metal cofactor, Nat. Chem., 2019, 11, 669–675.
11. H. J. Pan, G. Huang, M. D. Wodrich, F. F. Tirani, K. Ataka, S. Shima and X. Hu, Diversifying Metal-Ligand Cooperative Catalysis in Semi-Synthetic [Mn]-Hydrogenases, Angew. Chem., Int. Ed., 2021, 60, 13350–13357.
12. Y. Oudart, V. Artero, J. Pecaut and M. Fontecave, Ni(xbsms)Ru(CO)(2)Cl-2]: A bioinspired nickel-ruthenium functional model of [NiFe] hydrogenase, Inorg. Chem., 2006, 45, 4334–4336.
13. S. Canaguier, V. Fourmond, C. U. Perotto, J. Fize, J. Pecaut, M. Fontecave, M. J. Field and V. Artero, Catalytic hydrogen production by a Ni-Ru mimic of NiFe hydrogenases involves a proton-coupled electron transfer step, Chem. Commun., 2013, 49, 5004–5006.
14. L. Vaccaro, V. Artero, S. Canaguier, M. Fontecave and M. J. Field, Mechanism of hydrogen evolution catalyzed by NiFe hydrogenases: insights from a Ni-Ru model compound, Dalton Trans., 2010, 39, 3043–3049.
15. Y. Oudart, V. Artero, L. Norel, C. Train, J. Pecaut and M. Fontecave, Synthesis, crystal structure, magnetic properties and reactivity of a Ni-Ru model of NiFe hydrogenases with a pentacoordinated triplet (S=1) Ni-II center, J. Organomet. Chem., 2009, 694, 2866–2869.
16. S. Ogo, R. Kabe, K. Uehara, B. Kure, T. Nishimura, S. C. Menon, R. Harada, S. Fukuzumi, Y. Higuchi, T. Ohhara, T. Tamada and R. Kuroki, A dinuclear Ni(mu-H)Ru complex derived from H-2, Science, 2007, 316, 585–587.
17. S. Ogo, T. Kishima, T. Yatabe, K. Miyazawa, R. Yamasaki, T. Matsumoto, T. Ando, M. Kikkawa, M. Isegawa, K. S. Yoon and S. Hayami, [NiFe], [FeFe], and [Fe] hydrogenase models from isomers, Sci. Adv., 2020, 6, eaaz8181.
18. M. Isegawa, T. Matsumoto and S. Ogo, H₂ activation by hydrogenase-inspired NiFe catalyst using frustrated Lewis pair: effect of buffer and halide ion in the heterolytic H–H bond cleavage, RSC Adv., 2021, 11, 28420–28432.
19. M. J. T. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, 2009.
20. A. D. Becke, Density Functional Calculations of Molecular Bond Energies, J. Chem. Phys., 1986, 84, 4524–4529.
21. J. P. Perdew, Density-Functional Approximation for the Correlation-Energy of the Inhomogeneous Electron-Gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
22. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
23. M. Isegawa, T. Matsumoto and S. Ogo, Selective Oxidation of H₂ and CO by NiIr Catalyst in Aqueous Solution: A DFT Mechanistic Study, Inorg. Chem., 2020, 59, 1014–1028.
24. M. Isegawa, A. K. Sharma, S. Ogo and K. Morokuma, Electron and Hydride Transfer in a Redox-Active NiFe Hydride Complex: A DFT Study, ACS Catal., 2018, 8, 10419–10429.
25. M. G. Delcey, K. Pierloot, Q. M. Phung, S. Vancoillie, R. Lindh and U. Ryde, Accurate calculations of geometries and singlet–triplet energy differences for active-site models of [NiFe] hydrogenase, Phys. Chem. Chem. Phys., 2014, 16, 7927–7938.
26. S. Qiu, Q. Li, Y. Xu, S. Shen and C. Sun, Learning from nature: Understanding hydrogenase enzyme using computational approach, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1422.
27. M. Dolg, U. Wedig, H. Stoll and H. Preuss, Ab initio pseudopotential study of the 1st row transition-metal monoxides and Iron monohydride, J. Chem. Phys., 1987, 86, 2123–2131.
28. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on the generalized Born approximation with asymmetric descreening, J. Chem. Theor. Comput., 2009, 5, 2447–2464.
30. H. Ogata, T. Kramär, H. Wang, D. Schilter, V. Pelmenschikov, M. Van Gastel, F. Neese, T. B. Rauchfuss, L. B. Gee, A. D. Scott, Y. Yoda, Y. Tanaka, W. Lubitz and S. P. Cramer, Hydride Bridge in [NiFe]-Hydrogenase Observed by Nuclear Resonance Vibrational Spectroscopy, Nat. Commun., 2015, 6, 7890.
31. D. J. Evans and C. J. Pickett, Chemistry and the hydrogenases, Chem. Soc. Rev., 2003, 32, 268–275.
32. G. J. Kubas, Activation of dihydrogen and coordination of molecular H2 on transition metals, J. Organomet. Chem., 2014, 751, 33–49.
33. R. G. Pearson, Hard and Soft Acids and Bases, J. Am. Chem. Soc., 1963, 85, 3533–3539.
34. G. Bistoni, S. Rampino, N. Scafuri, G. Ciancaleoni, D. Zuccaccia, L. Belpassi and F. Tarantelli, How π back-donation quantitatively controls the CO stretching response in classical and non-classical metal carbonyl complexes, Chem. Sci., 2016, 7, 1174–1184.
35. K. M. Vogel, P. M. Kozlowski, M. Z. Zgierski and T. G. Spiro, Role of the axial ligand in heme-CO backbonding; DFT analysis of vibrational data, Inorg. Chim. Acta, 2000, 297, 11–17.
36. P. E. M. Siegbahn and R. Z. Liao, The Energetics of Hydrogen Molecule Oxidation in NiFe-hydrogenase, ACS Catal., 2020, 10, 5603–5613.
37. J. Gao, Hybrid quantum and molecular mechanical simulations: an alternative avenue to solvent effects in organic chemistry, Acc. Chem. Res., 1996, 29, 298–305.
38. P. A. Dub and R. Poli, A computational study of solution equilibria of platinum-based ethylene hydroamination catalytic species including solvation and counterion effects: Proper treatment of the free energy of solvation, J. Mol. Catal. A: Chem., 2010, 324, 89–96.
39. G. J. Kubas, Fundamentals of H₂ Binding and Reactivity on Transition Metals Underlying Hydrogenase Function and H₂ Production and Storage, Chem. Rev., 2007, 107, 4152–4205.
40. P. A. Lindahl, Metal–metal bonds in biology, J. Inorg. Biochem., 2012, 106, 172–178.
41. S. Ogo, K. Ichikawa, T. Kishima, T. Matsumoto, H. Nakai, K. Kusaka and T. Ohhara, A Functional [NiFe]Hydrogenase Mimic That Catalyzes Electron and Hydride Transfer from H₂, Science, 2013, 339, 682–684.
42. D. L. Dubois and D. E. Berning, Hydricity of Transition-Metal Hydrides and Its Role in CO₂ Reduction, Appl. Organomet. Chem., 2000, 14, 860–862.
43. E. S. Wiedner, M. B. Chambers, C. L. Pitman, R. M. Bullock, A. J. Miller and A. M. Appel, Thermodynamic Hydricity of Transition Metal Hydrides, Chem. Rev., 2016, 116, 8655–8692.
44. K. M. Waldie, A. L. Ostericher, M. H. Reineke, A. F. Sasayama and C. P. Kubiak, Hydricity of Transition-Metal Hydrides: Thermodynamic Considerations for CO2 Reduction, ACS Catal., 2018, 8, 1313–1324.
45. M. Bhattacharya, S. Sebghati, R. T. Vanderlinden and C. T. Saouma, Toward Combined Carbon Capture and Recycling: Addition of an Amine Alters Product Selectivity from CO to Formic Acid in Manganese Catalyzed Reduction of CO2, J. Am. Chem. Soc., 2020, 142, 17589–17597.
46. A. Kumar, S. Semwal and J. Choudhury, Emerging Implications of the Concept of Hydricity in Energy-Relevant Catalytic Processes, Chem. – Eur. J., 2021, 27, 5842–5857.
47. Y. Matsubara, E. Fujita, M. D. Doherty, J. T. Muckerman and C. Creutz, Thermodynamic and kinetic hydricity of ruthenium(II) hydride complexes, J. Am. Chem. Soc., 2012, 134, 15743–15757.
48. K. R. Brereton, N. E. Smith, N. Hazari and A. J. M. Miller, Thermodynamic and kinetic hydricity of transition metal hydrides, Chem. Soc. Rev., 2020, 49, 7929–7948.
49. M. Isegawa, T. Matsumoto and S. Ogo, Hydrogen evolution, electron-transfer, and hydride-transfer reactions in a nickel-iron hydrogenase model complex: a theoretical study of the distinctive reactivities for the conformational isomers of nickel-iron hydride, Dalton Trans., 2021, 51, 312–323.
50. A. Nakada, K. Koike, T. Nakashima, T. Morimoto and O. Ishitani, Photocatalytic CO2 reduction to formic acid using a Ru(II)-Re(I) supramolecular complex in an aqueous solution, Inorg. Chem., 2015, 54, 1800–1807.
51. G. Sahara, R. Abe, M. Higashi, T. Morikawa, K. Maeda, Y. Ueda and O. Ishitani, Photoelectrochemical CO2 reduction using a Ru(II)-Re(I) multinuclear metal complex on a p-type semiconducting NiO electrode, Chem. Commun., 2015, 51, 10722–10725.
52. Y. Yamazaki, H. Takeda and O. Ishitani, Photocatalytic reduction of CO₂ using metal complexes, J. Photochem. Photobiol., C, 2015, 25, 106–137.
53. E. S. Wiedner, Thermodynamic Hydricity of [FeFe]-Hydrogenases, J. Am. Chem. Soc., 2019, 141, 7212–7222.
54. M. Isegawa, T. Matsumoto and S. Ogo, Hydrogen evolution, electron-transfer, and hydride-transfer reactions in a nickel–iron hydrogenase model complex: a theoretical study of the distinctive reactivities for the conformational isomers of nickel–iron hydride, Dalton Trans., 2022, 51, 312–323.
55. H. Tai and S. Hirota, Mechanism and Application of the Catalytic Reaction of [NiFe] Hydrogenase: Recent Developments, ChemBioChem, 2020, 21, 1573–1581.
56. X. Feng, G. J. Schut, D. K. Haja, M. W. W. Adams and H. Li, Structure and electron transfer pathways of an electron-bifurcating NiFe-hydrogenase, Sci. Adv., 2022, 8, eabm7546.
57. M. L. K. Sanchez, C.-H. Wu, M. W. W. Adams and R. B. Dyer, Optimizing electron transfer from CdSe QDs to hydrogenase for photocatalytic H2 production, Chem. Commun., 2019, 55, 5579–5582.
58. A. Schleusener, M. Micheel, S. Benndorf, M. Rettenmayr, W. Weigand and M. Wächtler, Ultrafast Electron Transfer from CdSe Quantum Dots to an [FeFe]-Hydrogenase Mimic, J. Phys. Chem. Lett., 2021, 12, 4385–4391.
59. D. W. Mulder, M. W. Ratzloff, M. Bruschi, C. Greco, E. Koonce, J. W. Peters and P. W. King, Investigations on the Role of Proton-Coupled Electron Transfer in Hydrogen Activation by [FeFe]-Hydrogenase, J. Am. Chem. Soc., 2014, 136, 15394–15402.
60. B. L. Greene, C.-H. Wu, P. M. Mcternan, M. W. W. Adams and R. B. Dyer, Proton-Coupled Electron Transfer Dynamics in the Catalytic Mechanism of a [NiFe]-Hydrogenase, J. Am. Chem. Soc., 2015, 137, 4558–4566.
61. B. L. Greene, G. E. Vansuch, C.-H. Wu, M. W. W. Adams and R. B. Dyer, Glutamate Gated Proton-Coupled Electron Transfer Activity of a [NiFe]-Hydrogenase, J. Am. Chem. Soc., 2016, 138, 13013–13021.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt00361f

---