Contrasting impact of coordination polyhedra and site symmetry on the electronic energy levels in nine-coordinated Eu(III) and Sm(III) crystals structures determined from single crystal luminescence spectra†
Sabina Svava
Mortensen
 ,
Villads R. M.
Nielsen
and
Thomas Just
Sørensen
,
Villads R. M.
Nielsen
and
Thomas Just
Sørensen
 *
*
Department of Chemistry & Nano-Science Center, University of Copenhagen, Universitetsparken 5, 2100 København Ø, Denmark. E-mail: TJS@chem.ku.dk
First published on 29th April 2024
Abstract
Lanthanide luminescence is characterised by “forbidden” 4f–4f transitions and a complicated electronic structure. Our understanding of trivalent lanthanide(III) ion luminescence is centered on Eu3+ because absorbing and emitting transitions in Eu3+ occur from a single electronic energy level. In Sm3+ both absorbing and emitting multiplets have a larger multiplicity. A band arising in transitions from the first emitting state multiplet to the ground state multiplet will have nine lines for a Sm3+ complex. In this study, high-resolution emission and excitation spectra were used to determine the electronic energy levels for the lowest multiplet and first emitting multiplet in four Sm3+ compounds with either tricapped trigonal prismatic TTP or capped square antiprismatic cSAP coordination polyhedra but different site symmetry. This was achieved by the use of Boltzmann distribution population analysis and experimentally determined transition probabilities from emission and excitation spectra. Using this analysis it was possible to show the effect of changing three oxygen atoms with three nitrogen atoms in the donor set for two compounds with the same coordination polyhedra and site symmetry. This work celebrates the 40th anniversary of Kirby and Richardson's first report of [Eu(ODA)3]3− luminescence.
Introduction
Lanthanide luminescence fascinates as it is characterised by sharp bands in the luminescence spectra and forbidden transitions with long luminescent lifetimes.2–9 Similar properties are explained by the similar electron configuration of the lanthanide(III) ions,2,3 and these are exploited in applications including bioassay, bioimaging, and anti-counterfeiting technologies.5,6,10–16 The applications rely on our ability to understand the complicated molecular and electronic structure of the lanthanide(III) ions.4,13,17–22 While the electronic splitting caused by the strong spin–orbit coupling, observed as bands in the luminescence spectra, has been extensively studied for the lanthanide(III) ions,5,6,23,24 the spectral fine structure arising from the crystal field splitting remains a puzzle. The fine structure occurs when individual lines are resolved. Each line is from the transition between the electronic states (mJ levels for integer J, and double degenerate Kramers levels for half-integer J) of the spin–orbit multiplets (SLJ terms).8,9,25 The energy of each electronic state is defined by how the crystal field splits the spin–orbit multiplet.The crystal field is defined by the coordination polyhedra modulated by differences in the type and position of donor atoms and actual positioning—potentially simplified by molecular symmetry. The crystal field defining the symmetry of a lanthanide(III) we determine as the site symmetry. The crystal field splitting we observe is defined by the site symmetry and the nature of the donor atoms.26 In lanthanide luminescence we consider the site symmetry as low, when all states are be non-degenerate. Historically, we have observed this when more lines are resolved in the luminescence spectra. In lanthanide(III) ions, higher site symmetry does not lift the degeneracy of the spin–orbit multiplet, and fewer lines are observed, see below.27–30
The knowledge of trivalent lanthanide(III) ion photophysics is centered around Eu3+.13,23,27,31–33 For Eu3+ the transition from the ground state (7F0) to the first emitting state (5D0) can be observed as a single line, as both states—indeed both spin–orbit multiplets—are non-degenerate.34,35 This makes the interpretation of europium luminescence spectra simpler than for other lanthanide(III) ions.27,36 The non-degenerate ground and emitting states combined with the fact that the Eu3+ ion has been comprehensively studied, is the starting point for a broader understanding of other trivalent lanthanide(III) ions.13,23,27,31–33
In contrast to Eu3+, Sm3+ has 6H5/2 as the low energy spin–orbit multiplet and 4G5/2 as the emitting spin–orbit multiplet.5,28–30,36–38 Both multiplets contain three Kramers levels. For Eu3+ the site symmetry has been evaluated by counting the number of observed lines in the emission spectrum.23,27,31,39,40 For Sm3+—and all lanthanide(III) ions with an uneven number of electrons—the maximum splitting of each spin–orbit multiplet is expected. That is (2J + 1)/2 Kramers levels for each spin–orbit multiplet in the half-integer J Kramers lanthanide(III) ions.9,37 For the high energy band in the Sm3+ emission spectrum e.g.4G5/2 → 6H5/2, nine lines should be expected.38 Resolving high numbers of spectral fine structure can be difficult, and Sm3+ luminescence remains less explored.37,38,41–44 The other bands in the Sm3+ luminescence spectrum have twelve, fifteen, and eighteen lines for 4G5/2 → 6H7/2, 4G5/2 → 6H9/2, and 4G5/2 → 6H11/2 respectively.
As the multiplets of Sm3+ contain more than one level, there will be a difference in the population between these states. The population of each state is given by the Boltzmann distribution,49 which depends on the energy between the states and the temperature. The spectra can be simplified using cryogenic temperatures as fewer states in 4G5/2 and 6H5/2 will be populated. In this case, the number of resolved lines can be counted, but we show that a more robust analysis relying on the Boltzmann distribution can be used to resolve the electronic structure.9,37,38,45–48
To investigate the electronic structure of Sm3+, four compounds were prepared and crystallised, see Fig. 1. To be able to contrast and compare, the corresponding Eu3+ compounds were also crystallised. By using what is known for Eu3+ as a symmetry probe,23,27,31,39,40 the Eu3+ model system allows us to expand the knowledge on Sm3+.
 | ||
| Fig. 1 Polyhedra depicting coordination around the Sm3+ ion and molecular structure of the compounds: Na3[Sm(ODA)3]·7H2O, Cs3[Sm(DPA)3]·9H2O, Na[Sm(DOTA)H2O]·4H2O, and Na[Sm(EDTA)(H2O)3]·5H2O. | ||
The series is composed of two compounds that have been assigned a Trigonal Tricapped Prismatic TTP coordination polyhedra, Na3[Ln(ODA)3]·7H2O and Cs3[Ln(DPA)3]·9H2O, but with different donor sets. (H2ODA = 2,2′-oxydiacetic acid/diglycolic acid, H2DPA = 2,6,dipicolinic acid or pyridine-2,6-dicarboxylic acid). The Na3[Ln(ODA)3]·7H2O compound has a donor set consisting of nine oxygen atoms. The Cs3[Ln(DPA)3]·9H2O compound has a donor set with three nitrogen atoms in the capping layer and six oxygen atoms in the two trigonal layers.17,18,49,50
The other half of the series is two compounds which have been assigned a capped square-antiprismatic cSAP geometry polyhedra with different donor sets: Na[Ln(DOTA)H2O]·4H2O and Na[Ln(EDTA)(H2O)3]·5H2O (H4DOTA = 1,4,7,10-tetraazacyclododecane-N,N′,N′′,N′′′-tetraacetate, H4EDTA = (2,2′,2′′,2′′′-(ethane-1,2-diyldinitrilo))tetraacetic acid). The Na[Ln(DOTA)H2O]·4H2O compound has a donor set consisting of four nitrogen atoms, four oxygen atoms, and a capping oxygen, and Na[Ln(EDTA)(H2O)3]·5H2O compound has a mixed oxygen/nitrogen donor set without any apparent symmetry. The crystal structures were determined, and luminescence spectra were recorded from single crystals and microcrystalline powders. To quantify the site symmetry of each compound, deviations from ideal coordination polyhedra and site symmetry were computed.51 While the compounds have geometries close to the idealised coordination polyhedra they have previously been assigned, we show that the site symmetry is lower than expected. None of the four compounds were found to have the previously empirically predicted number of lines in the luminescence spectra.36
Experimental section
Synthesis
All chemicals were used as received without further purification.0.2 M Eu(CF3SO3)3 stock solution
Eu(CF3SO3)3 (2.40 g, 4.00 mmol) (98% from STREM Chemicals) was used to make a 0.20 M stock solution by dissolving the salt in water making a solution with a volume of 20.0 ± 0.04 ml.Na3[Eu(ODA)3]·8H2O crystallisation
H2ODA (0.538 g, 4.01 mmol) (H2ODA 98% from Sigma Aldrich), H2ODA = 2,2′-oxydiacetic acid/diglycolic acid was used to make a 0.20 M stock solution by dissolving the acid in water to make a solution with a volume of 20 ± 0.04 ml with pH = 5 using NaOH (1.0 M). Na3[Eu(ODA)3]·9H2O was made by adding 0.5 ml of the 0.20 M Eu(CF3SO3)3 to a sample vial with 1.5 ml of the 0.20 M H2ODA stock. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 3 days crystals had formed. The procedure was repeated 3 times to ensure reproducibility of the crystal growth.Cs3[Eu(DPA)3]·9H2O crystallisation
H2DPA (0.669 g, 4.01 mmol) (H2DPA from Riedel-De Haën Seelze-Hannover), H2DPA = pyridine-2,6-dicarboxylate was used to make a 0.20 M stock solution by dissolving the acid in water to make a solution with a with a volume of 20 ± 0.04 ml with pH = 7 using NaOH (1.0 M).Cs2CO3 (0.326 g, 1.00 mmol) (Cs2CO3 99% from Sigma Aldrich) was used to make a 0.10 M stock solution by dissolving the salt in the water to make a solution with a volume of 10 ± 0.06 ml.
Cs3[Eu(DPA)3]·9H2O was made by adding 0.5 ml of the 0.20 M Eu(CF3SO3)3 stock to a sample vial with 1.5 ml of the 0.20 M H2DPA stock and 2.0 ml of the 0.20 M Cs2CO3 stock. The sample was filtered through a Q-Max RR syringe filter from Frisinette and transferred to a sample vial. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 3 days crystals had formed. The procedure was repeated 3 times to ensure reproducibility of the crystal growth.
Na[Eu(DOTA)H2O]·4H2O crystallisation
H4DOTA (0.80918 g, 2.001 mmol), (H4DOTA from CheMatech) H4DOTA = 1,4,7,10-tetraazacyclododecane-N,N′,N′′,N′′′-tetraacetate was used to make a 0.10 M stock solution by dissolving the acid in water to make a solution with a with a volume of 20 ± 0.04 ml with pH = 8 using NaOH (1.0 M). Na[Eu(DOTA)H2O]·9H2O was made by adding 1.0 ml of the 0.20 M Eu(CF3SO3)3 stock to a sample vial with 2.0 ml of the 0.1 M H4DOTA stock. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 1 day crystals had formed. The procedure was followed 3 times to ensure reproducibility of the crystal growth.Na[Eu(EDTA)(H2O)3]·5H2O crystallisation
H4EDTA (0.26888 g, 0.8045 mmol) (H4EDTA 98% from STREM Chemicals), H4EDTA = (2,2′,2′′,2′′′-(ethane-1,2-diyldinitrilo))tetraacetic acid was used to make a 0.20 M stock solution by dissolving the acid in water to make a solution with a with a volume of 20 ± 0.04 ml with pH = 8 using NaOH (1.0 M). Na[Eu(EDTA)(H2O)3]·5H2O was made by adding 1.0 ml of the 0.2 M Eu(CF3SO3)3 stock to a sample vial with 1.0 ml of the 0.20 M H4EDTA stock. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 1 day crystals had formed. The procedure was repeated 3 times to ensure reproducibility of the crystal growth.0.2 M Sm(CF3SO3)3 stock solution
Sm(CF3SO3)3 (2.39 g, 4.00 mmol) (98% from ABCR) was used to make a 0.20 M stock solution by dissolving the salt in water making a solution with a volume of 20.0 ± 0.04 ml.Na3[Sm(ODA)3]·7H2O crystallisation
H2ODA (0.538 g, 4.01 mmol) (H2ODA 98% from Sigma Aldrich), H2DPA = 2,2′-dioxyacetic acid was used to make a 0.20 M stock solution by dissolving the acid in water to make a solution with a with a volume of 20 ± 0.04 ml with pH = 5 using NaOH (1.0 M). Na3[Sm(ODA)3]·7H2O was made by adding 0.5 ml of the 0.20 M Sm(CF3SO3)3 to a sample vial with 1.5 ml of the 0.20 M H2ODA stock. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 3 days crystals had formed. The procedure was repeated 3 times to ensure reproducibility of the crystal growth.Cs3[Sm(DPA)3]·9H2O crystallisation
H2DPA (0.669 g, 4.01 mmol) (H2DPA from Riedel-De Haën Seelze-Hannover), H2DPA = pyridine-2,6-dicarboxylate was used to make a 0.20 M stock solution by dissolving the acid in water to make a solution with a with a volume of 20 ± 0.04 ml with pH = 7 using NaOH (1.0 M).Cs2CO3 (0.326 g, 1.00 mmol) (Cs2CO3 99% from Sigma Aldrich) was used to make a 0.10 M stock solution by dissolving the salt in the water to make a solution with a volume of 10 ± 0.06 ml.
Cs3[Sm(DPA)3]·9H2O was made by adding 0.5 ml of the 0.20 M Sm(CF3SO3)3 stock to a sample vial with 1.5 ml of the 0.20 M H2DPA stock and 2.0 ml of the 0.20 M Cs2CO3 stock. The sample was filtered through a Q-Max RR syringe filter from Frisinette and transferred to a sample vial. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 3 days crystals had formed. The procedure was repeated 3 times to ensure reproducibility of the crystal growth.
Na[Sm(DOTA)H2O]·4H2O crystallisation
H4DOTA (0.80918 g, 2.001 mmol), (H4DOTA from CheMatech) H4DOTA = 1,4,7,10-tetraazacyclododecane-N,N′,N′′,N′′′-tetraacetate was used to make a 0.10 M stock solution by dissolving the acid in water to make a solution with a with a volume of 20 ± 0.04 ml with pH = 8 using NaOH (1.0 M). Na[Sm(DOTA)H2O]·4H2O was made by adding 1.0 ml of the 0.20 M Sm(CF3SO3)3 stock to a sample vial with 2.0 ml of the 0.1 M H4DOTA stock. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 1 day crystals had formed. The procedure was repeated 3 times to ensure reproducibility of the crystal growth.Na[Sm(EDTA)(H2O)3]·5H2O crystallisation
H4EDTA (0.26888 g, 0.8045 mmol) (H4EDTA 98% from STREM Chemicals), H4EDTA = (2,2′,2′′,2′′′-(ethane-1,2-diyldinitrilo))tetraacetic acid was used to make a 0.20 M stock solution by dissolving the acid in water to make a solution with a with a volume of 20 ± 0.04 ml with pH = 8 using NaOH (1.0 M). Na[Sm(EDTA)(H2O)3]·5H2O was made by adding 1.0 ml of the 0.2 M Sm(CF3SO3)3 stock to a sample vial with 1.0 ml of the 0.20 M H4EDTA stock. The sample was heated at 80 °C for 1 h. The sample vial was placed in a container with acetone placing a lid on top and left for acetone diffusion. After 1 day crystals had formed. The procedure was repeated 3 times to ensure reproducibility of the crystal growth.Single crystal X-ray diffraction
Single-crystal X-ray diffraction data was collected using a Bruker D8 Venture diffractometer with a PHOTON 100 CMOS detector, a Mo Kα high brilliance IμS X-ray tube (λ = 0.71073 Å), a multilayer X-ray mirror, and the temperature kept at 100 K using an Oxford Cryo system.The structures were solved using Olex252 with the ShelXT program53 using intrinsic phasing. Refinement was done using the ShelXL refinement package with least square minimisation. Aromatic hydrogens were added automatically using a riding model all other hydrogens were added manually to residual peaks. All other atoms were refined anisotropically.
Deviation between coordination polyhedra and ideal polyhedra
The deviation between coordination polyhedra and ideal reference polyhedra was calculated using AlingIt51 after manual rotational optimisation in Mercury.54 The geometry in lanthanide(III) complexes was compared to the ideal polyhedra and the values were scaled with the average bond length in the coordinating lanthanide(III) polyhedral. The coordination number (in this case N = 9 for all lanthanide(III) complexes) were used to normalise the results. AlignIt implements eqn (1), after manual rotational optimisation in Mercury, to calculate a deviation value, σideal:51 | (1) |
Point group symmetry analysis1
In addition to the geometrical deviation analysis, the fit and structural deviations to symmetry point groups were evaluated.1 The deviation from ideal point group symmetry was evaluated with eqn (2). | (2) |
Crystal powders
For both PXRD and Optical spectroscopy the crystals that precipitated in each sample, were collected by vacuum filtration. The crystals were removed from the filter and crushed to a powder.Powder X-ray diffraction
The samples for PXRD were filtered crystals crushed to a powder. Data was collected using a Bruker D8 Advance diffractometer using a Cu Kα source (λ = 1.5406 Å) at 293 K with an integration time of 1 s and a resolution of 1500. Samples were measured using a low background silica sample holder.Spectroscopy for crystals crushed to a powder
After recording PXRD diffractograms, the crystal powders were added to a 5.0 mm diameter NMR quartz tube from Bruker loaded with 2-methyltetrahydrofuran. The resulting suspensions were cooled using liquid nitrogen and measured in a quartz dewar.Solid-state single crystal spectroscopy
Solid-state single crystal spectroscopy was measured for Eu3+ complexes at 293 K. The spectroscopy settings described before were used to measure emission and excitation, respectively. A single crystal was mounted on a crystal mounting loop. The crystal mounting loop was then placed inside the spectrometer. The setup is the same as in our Eu(DPA) paper.55Optical spectroscopy for Eu3+ samples
Emission and excitation spectra were measured with a xenon arc lamp as the excitation source on a PTI QuantaMaster8075 from Horiba Scientific. For emission spectroscopy, an excitation wavelength at 394 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1) was used. Emission was detected from 575 nm (17
400 cm−1) was used. Emission was detected from 575 nm (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1) to 765 nm (14
400 cm−1) to 765 nm (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). The emission slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit for all samples. The excitation slits were all kept at 4.0 nm for the powder in a glass setup, and 8.0 nm when using single crystals. The voltage bias was kept at 3.200 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm. For excitation spectroscopy, an emission wavelength at 614 nm (16
000 cm−1). The emission slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit for all samples. The excitation slits were all kept at 4.0 nm for the powder in a glass setup, and 8.0 nm when using single crystals. The voltage bias was kept at 3.200 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm. For excitation spectroscopy, an emission wavelength at 614 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1) was used. Excitation was detected from 310 nm (32
900 cm−1) was used. Excitation was detected from 310 nm (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) to 585 nm (17
300 cm−1) to 585 nm (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1). Emission slits were all kept at 3.0 nm and excitation slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit. These settings were used for both the powder in a glass setup and single crystals. The voltage bias was kept at 6.800 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm.
100 cm−1). Emission slits were all kept at 3.0 nm and excitation slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit. These settings were used for both the powder in a glass setup and single crystals. The voltage bias was kept at 6.800 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm.
Optical spectroscopy for Sm3+ samples
For all samples used for optical spectroscopy and luminescence lifetimes, crystals were crushed to a powder and added to a 5.0 mm diameter NMR quartz cylinders from Bruker with 2-methyl tetrahydrofuran glass.Emission and excitation on a PTI QuantaMaster8075 from Horiba scientific
Emission and excitation spectra were measured with a xenon arc lamp as the excitation source on a PTI QuantaMaster8075 from Horiba Scientific. For this set-up spectra were recorded at 77 K using liquid nitrogen to cool the samples and measured using a quartz dewar. For emission spectroscopy, an excitation wavelength at 401 nm (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1) was used. Emission was detected from 550 nm (18
900 cm−1) was used. Emission was detected from 550 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1) to 760 nm (13
200 cm−1) to 760 nm (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1). The emission slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit for all samples. The excitation slits were all kept at 8.0 nm. The voltage bias was kept at 3.200 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm. For excitation spectroscopy, an emission wavelength at 598 nm (16
200 cm−1). The emission slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit for all samples. The excitation slits were all kept at 8.0 nm. The voltage bias was kept at 3.200 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm. For excitation spectroscopy, an emission wavelength at 598 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1) was used. Excitation was detected from 250 nm (40
700 cm−1) was used. Excitation was detected from 250 nm (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) to 590 nm (16
000 cm−1) to 590 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1). Emission slits were all kept at 8.0 nm and excitation slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit. The voltage bias was kept at 6.800 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm. Emission and excitation spectra measured using this setup can be found in ESI.†
900 cm−1). Emission slits were all kept at 8.0 nm and excitation slits were kept at 1.0 nm for the two outermost slits and 5.0 nm for the middle slit. The voltage bias was kept at 6.800 V for the reference detector. The integration time was kept at 1 s with a step size of 0.1 nm. Emission and excitation spectra measured using this setup can be found in ESI.†
Emission and excitation on a custom build spectrometer with a supercontinuum laser
Emission and excitation spectra were measured using a custom build spectrometer,56 equipped with a supercontinuum laser (NKT SuperK Fianium FIU-15) coupled to a tunable band pass filter (NKT LLTF Contrast VIS/SWIR HP8). Samples were measured both at 298 K and cooled to 77 K using liquid nitrogen to cool the samples and measured in a quartz dewar. For emission spectroscopy, an excitation wavelength at 463 nm (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1) was used with 90% laser power and a maximum repetition rate (78 MHz). A 500 nm (20
600 cm−1) was used with 90% laser power and a maximum repetition rate (78 MHz). A 500 nm (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) long pass filter was used. The center wavelength was set to 640 nm (15
000 cm−1) long pass filter was used. The center wavelength was set to 640 nm (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1). The integration time was kept at 1 s, with 10 exposures per frame and a 0.54 nm resolution. The slit was kept at 5 μm. The intensity was calibrated using the procedure described in ref. 56 Excitation spectra were measured by scanning the excitation source at 100% laser power from 520 nm (19
600 cm−1). The integration time was kept at 1 s, with 10 exposures per frame and a 0.54 nm resolution. The slit was kept at 5 μm. The intensity was calibrated using the procedure described in ref. 56 Excitation spectra were measured by scanning the excitation source at 100% laser power from 520 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1) to 580 nm (17
200 cm−1) to 580 nm (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1) through a Python code that connects to the tuneable band pass filter (NKT LLTF Contrast VIS/SWIR HP8) with an 880 nm (11
200 cm−1) through a Python code that connects to the tuneable band pass filter (NKT LLTF Contrast VIS/SWIR HP8) with an 880 nm (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1) centre wavelength. A 750 nm (13
400 cm−1) centre wavelength. A 750 nm (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) long pass filter was used.
300 cm−1) long pass filter was used.
The exposure time per data point was 2 s with 1 exposure per frame, and the step size was set to 0.25 nm. The slit was kept at 15 μm. The setup is described in more detail in ref. 48 and 56.
Luminescence lifetimes for Eu3+ samples
The luminescence lifetimes were determined using a PTI QuantaMaster8075 from Horiba Scientific. The excitation wavelength was 394 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1), and the emission wavelength was 598 nm (17
400 cm−1), and the emission wavelength was 598 nm (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1). The slits were all kept at 5 nm for both emission and excitation. The time window was from 200 μs to 3000 μs with an integration time of 28 μs. The luminescence lifetimes were fitted using a mono-exponential decay function using the software Origin Lab Pro's ExpDec1 function. These settings were used for both the powder in a glass setup and single crystals.
100 cm−1). The slits were all kept at 5 nm for both emission and excitation. The time window was from 200 μs to 3000 μs with an integration time of 28 μs. The luminescence lifetimes were fitted using a mono-exponential decay function using the software Origin Lab Pro's ExpDec1 function. These settings were used for both the powder in a glass setup and single crystals.
Luminescence lifetimes for Sm3+ samples
The luminescence lifetimes were determined using a TCSPC FluoTime300 from PicoQuant. The excitation wavelength was 405 nm (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1), and the emission wavelength was 600 nm (16
700 cm−1), and the emission wavelength was 600 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1). The luminescence lifetimes were fitted using a mono-exponential decay function using the PicoQuant EasyTau 2 software.
700 cm−1). The luminescence lifetimes were fitted using a mono-exponential decay function using the PicoQuant EasyTau 2 software.
Deconvoluting the electronic energy levels in the Sm3+ compounds using Boltzmann population analysis
To determine which transitions originated from which electronic energy levels (mJ) in the ground state multiplet (6H5/2) and the first emitting state multiplet (4G5/2) in samarium(III), we used our Boltzmann analysis procedure.48 Briefly summarised: the calculated populations from the Boltzmann distribution were compared to the observed difference in emission and excitation intensity of each line. The observed relative transition intensities for emission and excitation were extracted from the area of Voigt functions that were fitted to the data using a least square minimiser. The relative emission intensity for a transition from j to i is assumed to be proportional to the population of the state, j, at a given temperature and the relative emission transition probability. The same is assumed for the excitation intensity. Ai→j is the absorption transition probability for from i to j, and Bi←j is the emission transition probability for a from j to i. It is assumed that the ratio of transition probability between two levels i and j is the same for both emission and excitation. For Sm3+ specifically, the observed thermal population for the ground state multiplet, 6H5/2, and the emitting state multiplet, 4G5/2, can be expressed as (eqn (3) and (4)):48 | (3) |
and
 | (4) |
This observed thermal population is compared to the calculated Boltzmann distribution (eqn (5)):48
 | (5) |
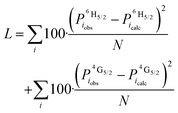 | (6) |
This was used to resolve ambiguities in the interpretation of the splitting of the energy levels determined from the spectra. Here the loss function is used to determine which of the different calculated populations agree with the observed population the best.
Results and discussion
To ensure reproducible results, all compounds were prepared in triplicates. For all crystals used in luminescence experiments the unit cell was determined, see the ESI for details.†Crystal structure and coordination geometry
For all eight Eu3+ and Sm3+ compounds the single crystal structure was determined. Crystallographic information can be found in the ESI.†Na3[Eu(ODA)3]·9H2O crystallises in the monoclinic C2/c space group (CCDC deposition number 2291817†) and was found to be isostructural to previously reported compound (CCDC entries DOFXIF 1143446 and DOFIX01 209363).57,58 The Na3[Sm(ODA)3]·7H2O compound crystallises in the monoclinic Cc space group. Na3[Sm(ODA)3]·7H2O (CCDC deposition number 2291821†) was found to be isostructural to the Na3[Ln(ODA)3]·7H2O compounds, which has previously been reported for Eu3+ and Gd3+ (CCDC entries DOFXIF 1143446, DOFIX01 209363, and QUMYON 721017).57–59Fig. 2a illustrates the nine-coordinated oxygen-only [ODA]2− donor set reported with TTP coordination polyhedra.57,58Fig. 2b shows that for both Na3[Eu(ODA)3]·8H2O and Na3[Sm(ODA)3]·7H2O three [ODA]2− ligands coordinate to the central lanthanide(III) ion, and Fig. 2c illustrates the four Na3[Sm(ODA)3]·7H2O complexes placed within the unit cell.
The Cs3[Eu(DPA)3]·9H2O crystallises in the orthorhombic C2221 space group. The crystal grown following the procedure outlined in the Experimental section was found to be twinned, and the structure could not be determined. The Bravais lattice and unit cell agreed with the previously reported structure,50 and this crystal was used for single crystal luminescence measurements. However, the structure analysis was done using the crystal structure by Brayshaw et al. in 1995 (CCDC entry YOZRUA 1306070).50 The Cs3[Sm(DPA)3]·9H2O crystallises in the orthorhombic C2221 space group (CCDC deposition number 2291822†). Cs3[Sm(DPA)3]·9H2O was found to be isostructural to the Cs3[Ln(DPA)3]·9H2O compounds, which has previously been reported for Ce3+, Eu3+, Tb3+, and Yb3+ (CCDC entries FEMPUL, YOZRUA 1306070 1497223, HOYTEV 622323, and HOYTIZ 623104).49,50,60Fig. 2d illustrates the [DPA]2− donor set that consists of three nitrogen atoms placed in the capping layer, and six oxygen atoms in the two trigonal layers in the assumed nine coordinated TTP coordination polyhedra. Fig. 2e shows three [DPA]2− ligands coordinate to the central lanthanide(III) ion.34,50,61–64Fig. 2f illustrates the four Cs3[Sm(DPA)3]·9H2O complexes placed within the unit cell.
The Na[Eu(DOTA)H2O]·4H2O (CCDC deposition number 2291807†) and Na[Sm(DOTA)H2O]·4H2O (CCDC deposition number 2291819†) compounds were found to be isostructural. They crystallise in the trigonal P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group as previously reported.65,66 The compounds are reported to have the cSAP coordination polyhedra.65–67 In the DOTA compounds, the donor set consists of four nitrogen atoms in the lower square antiprism plane, and five oxygen atoms, with four originating from the [DOTA]4− in the upper square antiprism layer and a single water molecule in the capping position.
space group as previously reported.65,66 The compounds are reported to have the cSAP coordination polyhedra.65–67 In the DOTA compounds, the donor set consists of four nitrogen atoms in the lower square antiprism plane, and five oxygen atoms, with four originating from the [DOTA]4− in the upper square antiprism layer and a single water molecule in the capping position.
Na[Eu(EDTA)(H2O)3]·5H2O (CCDC deposition number 2291811†) and Na[Sm(EDTA)(H2O)3]·5H2O (CCDC deposition number 2291820†) were found to be isostructural and crystallises in the orthorhombic Fdd2 space group. They are isostructural to previously reported compounds with cSAP coordination polyhedra.68–73 The lanthanide(III) donor set consists of two nitrogen atoms, with one occupying the capping position and the other being placed in the first square antiprism layer, and seven oxygen atoms, with four originating from [EDTA]4− and three from water molecules. As the structures of the eight compounds were determined, the coordination polyhedra, site symmetry, and molecular symmetry of all eight nine-coordinated Ln3+ compounds could then be examined.
Evaluation of coordination polyhedra and site symmetry
The site symmetry and donor atoms determine the crystal field splitting of a lanthanide complex. We first consider the coordination polyhedral of the eight compounds using σideal from the AlignIt methodology.51 The method does not distinguish between atoms, and we thus move on to determine the site symmetry and molecular symmetry using σsym.Table 1 compares experimental coordination polyhedral to the relevant ideal TTP and cSAP polyhedra.74,75 Additional ideal polyhedra can be found in ESI.† A cursory inspection of Table 1 shows that Na3[Eu(ODA)3]·8H2O and, Cs3[Eu(DPA)3]·9H2O are best described by the TTP structure.34,50,61–64 The ODA σideal values are lower than that of the DPA complexes. As the Ln–N and Ln–O bond distances differ by 0.3 Å this is in good agreement with the more symmetric all oxygen donor set.50,64 The DOTA and EDTA complexes are best described by the cSAP polyhedral, with DOTA closer to an ideal cSAP structure than EDTA.67,73
To analyse the site symmetry of the lanthanide ions, the point group symmetry deviation value or σsym was used. This method is derived from the continuous symmetry measure and evaluates how well a point group matches to a structure by computing the distance between the structures, before and after it has been operated by all symmetry operations within the point group. This takes both coordination geometry and the difference in donor atoms into account.1 Further, the analysis can be done for the coordination polyhedra alone and for the entire compound. Table 2 shows the σsym-values calculated for the six most relevant point groups, as described in eqn (2) in the Experimental section.
For the two compounds conventionally assigned to a TTP structure, Na3[Ln(ODA)3]·8H2O and Cs3[Ln(DPA)3]·9H2O, the site symmetry is best described by the D3 point group. For D3h, which should be the case for if the compound had an ideal TTP structure, a higher σsym-value was found. This indicates that the compounds do not contain a horizontal mirror plane. Interestingly, Cs3[Ln(DPA)3]·9H2O has a perfect σsym value against D3. If we expand the evaluation to include the ligand backbone, we find that the molecular symmetry of [ODA]2− complex is lower than that of the [DPA]2− complex. The [ODA]2− ligands are disordered, while the rigid [DPA]2− ligand maintains high symmetry even at the molecular structure level.
The site symmetry of Na[Ln(DOTA)H2O]·4H2O was found to be well-described by the C4 point group, and it could be argued that the coordination polyhedra has C4v symmetry. The molecular symmetry is C4 as the molecular structure does not contain the vertical mirror planes as they are not present in the [DOTA]4− ligand backbone. Na[Ln(EDTA)(H2O)3]·5H2O has very little symmetry, and all σsym values in Table 2 are high. A single vertical mirror plane is possible, but the site symmetry of the compound does not have this symmetry element and belongs to the C1 point group. This clearly illustrates the difference in analysing coordination polyhedral and site symmetry.
The analysis shows that the Na3[Ln(ODA)3]·8H2O and, Cs3[Ln(DPA)3]·9H2O compounds have TTP coordination polyhedra with D3 site symmetry. And that Na[Ln(DOTA)H2O]·4H2O has a cSAP coordination polyhedra with C4 site symmetry, while Na[Ln(EDTA)(H2O)3]·5H2O has a cSAP coordination polyhedra with no (C1) site symmetry.
Luminescence spectra
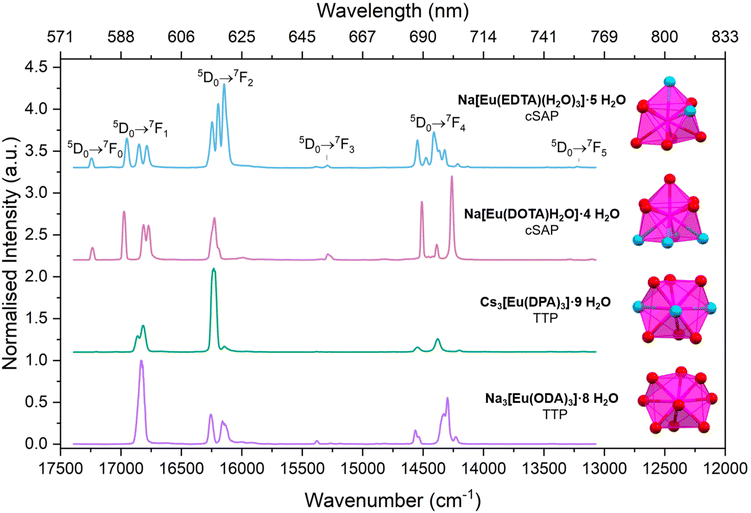
To examine the effect of the crystal field on the electronic structure of the central lanthanide ion, emission and excitation spectra and luminescence lifetimes were recorded for single crystals at 298 K and microcrystalline powders at 77 K.The two Eu compounds with cSAP coordination polyhedra, Na[Eu(DOTA)H2O]·4H2O and Na[Eu(EDTA)(H2O)3]·5H2O, were analysed first. The symmetry analysis revealed C4 and C1 site symmetry for the two compounds, respectively. In the luminescence spectra, shown in Fig. 3, we count one line for the 5D0 → 7F0 band for both of the two cSAP species. This is predicted in Table 3 for these symmetries and also indicates that only one compound is present in the samples.27 For the 5D0 → 7F1 band we count three lines, which is higher than what is predicted for C4. We are investigating crystalline samples at 77 K with modern equipment, which could explain why the empirical predictions fail.23,27,39
For the 5D0 → 7F2 band only three lines were resolved for Na[Eu(DOTA)H2O]·4H2O and Na[Eu(EDTA)(H2O)3]·5H2O. This is a lower than what is expected cf.Table 3, and that coincidental degeneracy also has a role to play. Another issue, if you rely strongly on counting lines, is that you rely on spectral resolution, which is limited by both equipment and temperature.38
Due to low intensity, the 5D0 → 7F3 and 5D0 → 7F5 bands are seldom included in an analysis. Here, we count two lines in the 5D0 → 7F3 band for both cSAP species, and we count two lines in the 5D0 → 7F5 band for Na[Eu(DOTA)H2O]·4H2O and three lines for Na[Eu(EDTA)(H2O)3]·5H2O. The resolution and total splitting of these multiplets make it hard to differentiate between real and coincidental/experimental degeneracy.
Finally, the 5D0 → 7F4 band has five lines in the Na[Eu(DOTA)H2O]·4H2O spectra and seven in the Na[Eu(EDTA)(H2O)3]·5H2O spectra. Also, here the number of lines is lower than what is predicted by Table 3, but we note that fewer high-intensity lines are seen in the more symmetric DOTA complex compared to the less symmetric EDTA complex.
Single crystals of Na[Eu(DOTA)H2O]·4H2O have previously been analysed by Thomsen et al. and Parker et al.77–80 Our spectra are consistent with their spectra. The failure of the empirical model and the predictions in Table 3 have been described previously.27,29,51,77–81 We often find these descriptors only work for some multiplets in a spectrum, and that the symmetry reported by each multiplet in a spectrum can be different.
Both compounds with TTP coordination polyhedra have D3 site symmetry. For both Na3[Eu(ODA)3]·8H2O and Cs3[Eu(DPA)3]·9H2O the 5D0 → 7F0 transition was not observed, see Fig. 3. This line is often barely detectable for compounds with TTP coordination polyhedra. The lack of at 5D0 → 7F0 band is often explained by the horizontal mirror plane in the D3h point group.27 Even though the compounds were found to have D3 symmetry, σsym-values < 2 for the D3h symmetry could explain that no 5D0 → 7F0 transitions were observed.
Continuing the analysis of the TTP compounds, we move to the 5D0 → 7F1 band. Here, we count two lines for Cs3[Eu(DPA)3]·9H2O indicating a splitting of mJ = ±1 and mJ = 0. In contrast, only one (broad) line was observed in the 5D0 → 7F1 band of Na3[Eu(ODA)3]·8H2O.
If we rely only on counting, this indicates that all the electronic energy levels are degenerate, which is not predicted for any symmetries lower than cubic. The splitting of mJ = ±1 and mJ = 0 should occur in compounds with D3 symmetry, but the splitting of these levels is not resolved in the data for Na3[Eu(ODA)3]·8H2O.9,23,27,39,76 An alternative explanation is that transitions from the mJ = 0 level are forbidden, but there is limited precedence for assuming that single mJ-states are pure states.9,23,27,39 With the level of theory used in creating Table 3, the 7F1 and 7F2mJ-states can be pure states in D3 symmetry, and with mJ = 0 forbidden, only degenerate bands for mJ = ±1 and mJ = 2 would be observed. However, the 7F3, 7F4, and 7F5 bands cannot contain a pure mJ = 0 state as it must mix with the mJ = ±3 states. That is the theory predicts mJ mixing when ΔmJ ≥ 3.8,66,80,82 In modern computational chemistry mJ mixing is seen in all multiplets.
For Cs3[Eu(DPA)3]·9H2O two and three lines were counted for the 5D0 → 7F2 and 5D0 → 7F4 band, respectively. This indicates a lower splitting than what is predicted in Table 3 for D3 point group symmetry.9,23,27,39 Even though the two compounds, Na3[Eu(ODA)3]·8H2O and Cs3[Eu(DPA)3]·9H2O, are both best described by a TTP coordination polyhedra and both have D3 site symmetry, the observed splitting in the emission spectra are different. A possible explanation for a larger number of lines in the 5D0 → 7F2 and 5D0 → 7F4 bands in Na3[Eu(ODA)3]·8H2O compared to Cs3[Eu(DPA)3]·9H2O might be ascribed to the lower molecular symmetry for Na3[Eu(ODA)3]·8H2O (C2).
Overall, we cannot reproduce the prediction in Table 3 for the number of lines we should be able to count in the Eu3+ model compounds. To do so we must fit all bands in the spectra and compare them to computational data that remains exceedingly difficult to obtain for Eu3+ complexes. Instead we determine the electronic structure of the Sm3+ compounds and compare the properties of the two ions.
For Sm3+ we do not expect to see any simplifications due to set symmetry. The predictions shown for Eu3+ in Table 3 only predict degenerate electronic energy levels for Sm3+ in cubic symmetry.38 Even so, we start by considering the number of lines we can count in Fig. 4 before we move to a more robust method of determining the electronic structure of the 4G5/2 and 6H5/2 states in the four samarium(III) compounds.
A cursory inspection of the spectra in Fig. 4 shows that the two Sm3+ compounds with cSAP coordination polyhedra contain fewer lines than the two compounds with TTP coordination polyhedra. A more detailed analysis of the Sm3+ compounds with cSAP coordination polyhedra, Na[Sm(DOTA)H2O]·4H2O and Na[Sm(EDTA)(H2O)3]·5H2O, shows that this may be due to a larger splitting of the emitting multiplet in these two compounds. For Na[Sm(DOTA)H2O]·4H2O we count three lines in the 4G5/2 → 6H5/2 band at 77 K. We see the three Kramers levels of 6H5/2 and only one of the levels in 4G5/2, which indicates a large crystal field splitting in 4G5/2. Counting the number of lines in the 4G5/2 → 6H7/2, 4G5/2 → 6H9/2, and 4G5/2 → 6H11/2 bands become increasingly difficult, but the number of lines is lower than what we would see with more than one emittinglevel in 4G5/2.38 This supports the assumption of a large crystal field splitting in 4G5/2.
For Na[Sm(EDTA)(H2O)3]·5H2O we count four lines in the 4G5/2 → 6H5/2 band. And we count more lines in the 4G5/2 → 6H7/2, 4G5/2 → 6H9/2, and 4G5/2 → 6H11/2 bands than we did for the DOTA complex. This indicates that more levels in 4G5/2 are populated at 77 K, which suggests a smaller crystal field splitting in the 4G5/2 multiplet. As site symmetry should not influence the number of observed lines, we cannot use the difference between C1 and C4 to rationalise the observations.
For the two Sm3+ compounds with TTP coordination polyhedra, Na3[Sm(ODA)3]·7H2O and Cs3[Sm(DPA)3]·9H2O, have the same problem as we did for Eu3+. When we consider Fig. 4 we arrive at different numbers of lines when each author counts the number of lines. We all count three lines in the 4G5/2 → 6H5/2 band of Cs3[Sm(DPA)3]·9H2O, while we can count both two and three lines in the 4G5/2 → 6H5/2 band of Na3[Sm(ODA)3]·7H2O. We leave it to the reader to decide how many lines they can resolve in Fig. 4.
For both compounds, we count more lines in the 4G5/2 → 6H7/2 and 4G5/2 → 6H9/2 bands than can be explained with the maximum splitting of 6H7/2 and 6H9/2 alene. The maximum number of levels in the two states are four and five respectively. This indicates that two or more of the states in 4G5/2 are thermally populated to a degree where we easily observe transitions from both levels.37,38,47 While the spectra at 298 K show how the thermal population of the states changes as well as a thermal broadening of the peaks, see Fig. 4, the complexity of the spectra does not allow us to extract more information without fitting. Nevertheless, the Na3[Sm(ODA)3]·7H2O and Cs3[Sm(DPA)3]·9H2O spectra suggest degeneracy in both the 6H5/2 and 4G5/2 multiplet. For a Kramers ion such as Sm3+ the crystal field splitting in these multiplets should result in three Kramers levels in all symmetries lower than cubic.9,37,45–47 This is not what we see.
Deconvoluting the electronic energy levels of Sm3+
As counting is not enough, see above, a robust method to deconvolute the spectra and determine electronic energy levels must be used.8,9,24,37,38,41–43,45,47,83–85 We can determine the electronic energy levels through a Boltzmann distribution analysis. This requires excitation and emission spectra, see Fig. 5, and can be supported by all the bands in the emission spectra. Further, the method relies on good spectral resolution. The analysis can be made simpler by having the spectra at different temperatures, as the population of the electronic energy levels change with temperature. Here, we record the spectra at 77 K and 298 K, see Fig. 4.The analysis uses that the lines in the 4G5/2 → 6H5/2 band are recovered from emission spectra, while the lines in the 4G5/2 ← 6H5/2 band are recovered from the excitation spectra, see Fig. 5. Each band was fitted to a sum of Voigt functions (see ESI for details†), where each non-degenerate line is described by a single Voigt function. In the fit, the Gaussian width applied accounts for the instrumental broadening plus structural fluctuations, and the Lorentzian broadening is associated with the electronic transition. Fixing the Gaussian width was assumed to be a valid assumption for these samples.48 These fits are used in a Boltzmann population analysis for Na3[Sm(ODA)3]·7H2O and Cs3[Sm(DPA)3]·9H2O from which the electronic energy levels in the two Sm3+ compounds were obtained. The fit alone was enough to resolve the electronic structure of Na[Sm(DOTA)H2O]·4H2O and Na[Sm(EDTA)(H2O)3]·5H2O.
In the Boltzmann analysis, the best solution was found using a Loss function. This method relies on the intensities being representative of the transition probability, which could be an issue in the case of different emitting species. As the powders were monophasic, and as only one species was seen in the Eu3+ compounds, we assume that only one emitting species is present in the samples. Further, in the case of Na3[Sm(ODA)3]·7H2O, the spectra were identical when measured on a single crystal and a single crystal crushed to a powder, see ESI.†
The deconvolution process for Na3[Sm(ODA)3]·7H2O is shown in Fig. 6. Briefly, two lines are observed in the emission spectrum. Thus, we assume that only one of the three levels in 4G5/2 is significantly populated. The observed lines are to the three levels in 6H5/2. Since only two lines are observed, three different electronic structures of the 6H5/2 multiplet are possible: (i) only two energy levels exist in 6H5/2 (0,1). (ii) The two lowest energy levels in 6H5/2 are degenerate 6H5/2 (0,0,1). And (iii) The two highest energy levels in 6H5/2 are degenerate 6H5/2 (0,1,1). To select the correct electronic structure a Loss number is calculated, see Fig. 6. For more details, we refer the reader to the detailed description of the method in ref. 49.
This analysis computes state populations, compares models, and clearly shows that model (iii) is the correct electronic structure for Na3[Sm(ODA)3]·7H2O. Based on this model all transitions in the excitation spectra can now also be rationalised. Fitting the spectrum with three sets of two Voigt functions reveals the electronic splitting of the 4G5/2 term. The fitting is done with the splitting in 6H5/2 optimised as a global parameter.
The resulting electronic energy levels are shown in Fig. 7. The determined crystal field splitting for Sm3+ in the four compounds, confirms the initial qualitative assignments done based on the spectra alone, but we now have a figure of merit and can trust the assignments.
 | ||
| Fig. 7 Dieke diagram for the energy levels from the ground state multiplet (6H5/2) and first emitting state multiplet (4G5/2) for the Sm3+ compounds resolved at 77 K. Symmetry deviation values (σsym)1 are shown above. σsym-inner indicates the symmetry deviation value for the inner sphere coordination polyhedral and σsym-mol indicates the symmetry deviation value for the molecular symmetry. | ||
Fig. 7 shows that a larger total splitting occurs in the two compounds with cSAP coordination polyhedra, Na[Sm(DOTA)H2O]·4H2O and Na[Sm(EDTA)(H2O)3]·5H2O, compared to the two compounds with TTP coordination polyhedra and D3 site symmetry, Na3[Sm(ODA)3]·7H2O and Cs3[Sm(DPA)3]·9H2O. The splitting pattern of 6H5/2 Na3[Sm(ODA)3]·7H2O and Cs3[Sm(DPA)3]·9H2O are similar, but in 4G5/2 it is reversed.
If 6H5/2 does not have the maximum splitting e.g. show three Kramers level, this would indicate higher symmetry than D3. The data reported here show that D3 site symmetry does not lift the degeneracy in the 6H5/2 multiplet. This is in agreement with the observations done for the Eu3+ model compounds. We cannot say why the crystal field symmetry has these effects on the Sm3+ electronic energy levels, yet.
Conclusions
In this study, four Sm3+ compounds were made and compared to four isostructural Eu3+ model compounds. Two new compounds were reported: Na3[Sm(ODA)3]·7H2O and Cs3[Sm(DPA)3]·9H2O. They were both found to have TTP coordination polyhedra, quantified with the AlignIt method, and they were shown to have D3 site symmetry by calculating the σsym-values. The shape and symmetry were evaluated for all eight compounds, and while the coordination polyhedra alone does not rationalise the data, the site symmetry is determining for the observed electronic structure of Eu3+ and Sm3+.To evaluate the electronics structure, the luminescent properties of the compounds were characterised at 77 K and 298 K. By using a Boltzmann population analysis, the electronic energy levels in the Sm3+ compounds were determined. Generally, a smaller splitting was observed in the 6H5/2 low energy spin–orbit multiplet for the two compounds with D3 site symmetry compounds, Na3[Sm(ODA)3]·7H2O and Cs3[Sm(DPA)3]·9H2O, compared to the two compounds with just a single rotational axis, Na[Sm(DOTA)H2O]·4H2O and Na[Sm(EDTA)(H2O)3] ·5H2O. We note that the splitting of the 6H5/2 spin–orbit multiplet is largest for Na[Sm(DOTA)H2O]·4H2O (C4), while the splitting of the 4G5/2 emitting spin–orbit multiplet is similar for all four compounds. This takes the first steps towards understanding the crystal field splitting in Sm3+ compounds.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Villum Foundation, the Carlsberg Foundation, and the University of Copenhagen for financial support.References
- V. R. M. Nielsen, B. Le Guennic and T. J. Sørensen, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-qf84c.
- V. Balaram, Geosci. Front., 2019, 10, 1285–1303 CrossRef CAS.
- S. Cotton, Lanthanide and actinide chemistry, John Wiley & Sons, 2013 Search PubMed.
- J.-C. G. Bünzli and S. V. Eliseeva, Chem. Sci., 2013, 4, 1939–1949 RSC.
- W. Carnall, P. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4424–4442 CrossRef CAS.
- W. T. Carnall, P. Fields and B. Wybourne, J. Chem. Phys., 1965, 42, 3797–3806 CrossRef CAS.
- F. A. Cotton, G. Wilkinson and P. L. Gaus, Basic inorganic chemistry, John Wiley & Sons, 1995 Search PubMed.
- A. de Bettencourt-Dias, Luminescence of lanthanide ions in coordination compounds and nanomaterials, John Wiley & Sons, 2014 Search PubMed.
- S. V. Eliseeva and J.-C. G. Bünzli, Chem. Soc. Rev., 2010, 39, 189–227 RSC.
- C. N. Dansholm, A. K. R. Junker, L. G. Nielsen, N. Kofod, R. Pal and T. J. Sørensen, ChemPlusChem, 2019, 84, 1778–1788 CrossRef CAS PubMed.
- I. Hemmilä, S. Dakubu, V.-M. Mukkala, H. Siitari and T. Lövgren, Anal. Biochem., 1984, 137, 335–343 CrossRef.
- G. Vereb, E. Jares-Erijman, P. R. Selvin and T. M. Jovin, Biophys. J., 1998, 74, 2210–2222 CrossRef CAS PubMed.
- W. D. Horrocks Jr and D. R. Sudnick, Acc. Chem. Res., 1981, 14, 384–392 CrossRef.
- X. Zhu, X. Wang, H. Zhang and F. Zhang, Angew. Chem., 2022, 134, e202209378 CrossRef.
- M. Wang, C. Hu and Q. Su, Biosensors, 2022, 12, 131 CrossRef CAS PubMed.
- R. Arppe and T. J. Sørensen, Nat. Rev. Chem., 2017, 1, 1–13 CrossRef.
- S. J. Butler, M. Delbianco, L. Lamarque, B. K. McMahon, E. R. Neil, R. Pal, D. Parker, J. W. Walton and J. M. Zwier, Dalton Trans., 2015, 44, 4791–4803 RSC.
- S. J. Butler, L. Lamarque, R. Pal and D. Parker, Chem. Sci., 2014, 5, 1750–1756 RSC.
- P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Chem. Rev., 1999, 99, 2293–2352 CrossRef CAS PubMed.
- J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556–13567 RSC.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS.
- D. Parker, Coord. Chem. Rev., 2000, 205, 109–130 CrossRef CAS.
- K. Binnemans, Coord. Chem. Rev., 2015, 295, 1–45 CrossRef CAS.
- G. H. Dieke, Spectra and Energy Levels of Rare Earth Ions in Crystals, John Wiley and Sons, New York, USA, 1968 Search PubMed.
- J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Lanthanides Actinides Mol. Magn., 2015, 12, 27–59 Search PubMed.
- P. R. Nawrocki and T. J. Sørensen, Phys. Chem. Chem. Phys., 2023, 25, 19300–19336 RSC.
- P. A. Tanner, Chem. Soc. Rev., 2013, 42, 5090–5101 RSC.
- T. Cheisson and E. J. Schelter, Science, 2019, 363, 489–493 CrossRef CAS.
- D. Parker, in Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 2016, vol. 50, pp. 269–299 Search PubMed.
- B. G. Wybourne, J. Alloys Compd., 2004, 380, 96–100 CrossRef CAS.
- J. C. G. Bünzli and G. O. Pradervand, J. Chem. Phys., 1986, 85, 2489–2497 CrossRef.
- W. D. Horrocks Jr and D. R. Sudnick, Science, 1979, 206, 1194–1196 CrossRef CAS PubMed.
- G. B. Jean-claude, Inorg. Chim. Acta, 1987, 139, 219–222 CrossRef.
- P. R. Nawrocki, N. Kofod, M. Juelsholt, K. M. Jensen and T. J. Sørensen, Phys. Chem. Chem. Phys., 2020, 22, 12794–12805 RSC.
- N. Kofod, P. Nawrocki, M. Juelsholt, T. L. Christiansen, K. M. Jensen and T. J. Sørensen, Inorg. Chem., 2020, 59, 10409–10421 CrossRef CAS PubMed.
- C. Görller-Walrand and K. Binnemans, Handb. Phys. Chem. Rare Earths, 1996, 23, 121–283 Search PubMed.
- X. Chen, M. Jensen and G. Liu, J. Phys. Chem. B, 2005, 109, 13991–13999 CrossRef CAS PubMed.
- S. S. Mortensen, M. A. Marciniak Nielsen, P. Nawrocki and T. J. Sørensen, J. Phys. Chem. A, 2022, 126, 8596–8605 CrossRef CAS PubMed.
- K. Binnemans and C. Görller-Walrand, Chem. Phys. Lett., 1995, 245, 75–78 CrossRef CAS.
- W. Carnall, P. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4450–4455 CrossRef CAS.
- B.-L. An, M.-L. Gong, M.-X. Li and J.-M. Zhang, J. Mol. Struct., 2004, 687, 1–6 CrossRef CAS.
- S. Mohan, S. Kaur, D. Singh and P. Kaur, Opt. Mater., 2017, 73, 223–233 CrossRef CAS.
- O. Chukova, S. Nedilko, Z. Moroz and M. Pashkovskyi, J. Lumin., 2003, 102, 498–503 CrossRef.
- I. Kebaïli and M. Dammak, J. Lumin., 2012, 132, 2092–2097 CrossRef.
- A. Lupei, C. Tiseanu, C. Gheorghe and F. Voicu, Appl. Phys. B: Lasers Opt., 2012, 108, 909–918 CrossRef CAS.
- R. Skaudzius, S. Sakirzanovas and A. Kareiva, J. Electron. Mater., 2018, 47, 3951–3956 CrossRef CAS.
- S. Sakirzanovas, A. Katelnikovas, H. Bettentrup, A. Kareiva and T. Jüstel, J. Lumin., 2011, 131, 1525–1529 CrossRef CAS.
- V. R. M. Nielsen, P. R. Nawrocki and T. J. Sørensen, J. Phys. Chem. A, 2023, 127(16), 3577–3590 CrossRef CAS PubMed.
- G. Kervern, A. d'Aléo, L. Toupet, O. Maury, L. Emsley and G. Pintacuda, Angew. Chem., Int. Ed., 2009, 48, 3082–3086 CrossRef CAS PubMed.
- P. A. Brayshaw, J.-C. G. Buenzli, P. Froidevaux, J. M. Harrowfield, Y. Kim and A. N. Sobolev, Inorg. Chem., 1995, 34, 2068–2076 CrossRef CAS.
- M. S. Thomsen, A. S. Anker, L. Kacenauskaite and T. J. Sørensen, Dalton Trans., 2022, 51, 8960–8963 RSC.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens and M. Towler, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- S. S. Mortensen and T. J. Sørensen, Eur. J. Inorg. Chem., 2023, e202300159 CrossRef CAS.
- P. R. Nawrocki, V. R. Nielsen and T. J. Sørensen, Methods Appl. Fluoresc., 2022, 10, 045007 CrossRef CAS PubMed.
- M. Albin, R. R. Whittle and W. D. Horrocks Jr, Inorg. Chem., 1985, 24, 4591–4594 CrossRef CAS.
- F. A. Cotton and P. Huang, Inorg. Chim. Acta, 2003, 346, 223–226 CrossRef CAS.
- A. Lennartson and M. Håkansson, CrystEngComm, 2009, 11, 1979–1986 RSC.
- S. M. Elahi and M. V. Rajasekharan, ChemistrySelect, 2016, 1, 6515–6522 CrossRef.
- D. Zhou, C. Huang, K. Wang and G. Xu, Polyhedron, 1994, 13, 987–991 CrossRef CAS.
- J.-G. Kim, S.-K. Yoon, Y. Sohn and J.-G. Kang, J. Alloys Compd., 1998, 274, 1–9 CrossRef CAS.
- M. Autillo, M. A. Islam, J. Jung, J. Pilmé, N. Galland, L. Guerin, P. Moisy, C. Berthon, C. Tamain and H. Bolvin, Phys. Chem. Chem. Phys., 2020, 22, 14293–14308 RSC.
- J. Salaam, I. N’Dala-Louika, C. Balogh, I. Suleimanov, G. Pilet, L. Veyre, C. Camp, C. Thieuleux, F. Riobé and O. Maury, Eur. J. Inorg. Chem., 2022, 2022, e202200412 CrossRef CAS.
- F. Benetollo, G. Bombieri, S. Aime and M. Botta, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 353–356 CrossRef.
- M. Briganti, E. Lucaccini, L. Chelazzi, S. Ciattini, L. Sorace, R. Sessoli, F. Totti and M. Perfetti, J. Am. Chem. Soc., 2021, 143, 8108–8115 CrossRef CAS PubMed.
- S. Aime, A. Barge, F. Benetollo, G. Bombieri, M. Botta and F. Uggeri, Inorg. Chem., 1997, 36, 4287–4289 CrossRef CAS.
- D. W. Engel, F. Takusagawa and T. F. Koetzle, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 1687–1693 CrossRef.
- R. J. Holmberg, I. Korobkov and M. Murugesu, RSC Adv., 2016, 6, 72510–72518 RSC.
- K. Nakamura, T. Kurisaki, H. Wakita and T. Yamaguchi, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1995, 51, 1559–1563 CrossRef.
- L. Templeton, D. Templeton, A. Zalkin and H. Ruben, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 2155–2159 CrossRef.
- J. Wang, P. Hu, B. Liu, L. Q. Zhang, G. X. Han, R. Xu and X. D. Zhang, Russ. J. Inorg. Chem., 2010, 55, 1567–1573 CrossRef CAS.
- R. Ragul and B. Sivasankar, Synth. React. Inorg., Met.-Org., Nano-Met. Chem., 2013, 43, 382–389 CrossRef CAS.
- J. J. Thomson, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1904, vol. 7, pp. 237–265 Search PubMed.
- M. G. Drew, Coord. Chem. Rev., 1977, 24, 179–275 CrossRef CAS.
- A. F. Kirby and F. S. Richardson, J. Phys. Chem., 1983, 87, 2557–2563 CrossRef CAS.
- M. S. Thomsen, H. O. B. Andersen and T. J. Sørensen, Dalton Trans., 2022, 51, 14118–14124 RSC.
- M. S. Thomsen, A. O. Madsen and T. J. Sorensen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2021, 77, 354–364 CrossRef CAS PubMed.
- M. Woods, S. Aime, M. Botta, J. A. K. Howard, J. M. Moloney, M. Navet, D. Parker, M. Port and O. Rousseaux, J. Am. Chem. Soc., 2000, 122, 9781–9792 CrossRef CAS.
- D. Parker, E. A. Suturina, I. Kuprov and N. F. Chilton, Acc. Chem. Res., 2020, 53, 1520–1534 CrossRef CAS PubMed.
- R. S. Dickins, D. Parker, J. I. Bruce and D. J. Tozer, Dalton Trans., 2003, 1264–1271 RSC.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- W. Carnall, G. Goodman, K. Rajnak and R. Rana, J. Chem. Phys., 1989, 90, 3443–3457 CrossRef CAS.
- S. K. Gupta, P. S. Ghosh, N. Pathak, A. Arya and V. Natarajan, RSC Adv., 2014, 4, 29202–29215 RSC.
- S. K. Gupta, N. Pathak, S. K. Thulasidas and V. Natarajan, J. Lumin., 2016, 169, 669–673 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The following files are available free of charge. Emission and excitation spectra, time-resolved emission decay profiles, PXRD, and crystallographic information (PDF-file and CIF-files). CCDC 2291807, 2291811, 2291817 and 2291819–2291822. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00157e |
| This journal is © The Royal Society of Chemistry 2024 |