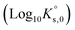Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics of the Eu(III)–Mg–SO4–H2O and Eu(III)–Na–SO4–H2O systems. Part II: spectroscopy experiments, complexation and Pitzer/SIT models†
P. F.
dos Santos
 *a,
X.
Gaona
*a,
X.
Gaona
 *a,
A.
Lassin
*a,
A.
Lassin
 b,
A.
Skerencak-Frech
a,
D.
Fellhauer
a,
M.
Altmaier
a and
B.
Madé
c
b,
A.
Skerencak-Frech
a,
D.
Fellhauer
a,
M.
Altmaier
a and
B.
Madé
c
aInstitute for Nuclear Waste Disposal, Karlsruhe Institute of Technology, Karlsruhe, Germany. E-mail: pedro.santos@kit.edu; xavier.gaona@kit.edu
bWater, Environment, Process Development and Analysis Division, BRGM, Orléans, France
cResearch and Development Division, ANDRA, Châtenay-Malabry, France
First published on 15th March 2024
Abstract
A time-resolved laser fluorescence spectroscopy (TRLFS) study was carried out to investigate the Eu(III)–SO4 complexation at room temperature over a wide range of Na2SO4 concentrations (0–2 mol kg−1). Spectroscopic observations confirm the step-wise formation of the aqueous complexes Eu(SO4)+, Eu(SO4)2− and Eu(SO4)33− over the investigated Na2SO4 concentrations. Combining TRLFS data obtained in this study and solubility data reported in Part I of this work for the Eu2(SO4)3–Na2SO4–H2O and Eu2(SO4)3–MgSO4–H2O systems, thermodynamic and activity models were derived based on the SIT and Pitzer formalisms. A combination of the geochemical calculation codes PhreeqC (SIT), PhreeSCALE (Pitzer) and the parameter estimation code PEST was used to determine the solubility products  of Eu2(SO4)3·8H2O(cr) and Na2Eu2(SO4)4·2H2O(cr), stability constants of the Eu(III)–SO4 complexes (β0i), and the specific binary and ternary interaction parameters (εij, β(0)ij, β(1)ij, Cϕij, θik, Ψijk) for both activity models. The thermodynamic constants determined in this work are discussed with reference to values available in the literature.
of Eu2(SO4)3·8H2O(cr) and Na2Eu2(SO4)4·2H2O(cr), stability constants of the Eu(III)–SO4 complexes (β0i), and the specific binary and ternary interaction parameters (εij, β(0)ij, β(1)ij, Cϕij, θik, Ψijk) for both activity models. The thermodynamic constants determined in this work are discussed with reference to values available in the literature.
1. Introduction
The sulfate ion behaves as a ligand of moderate strength in the presence of hard Lewis acids such as lanthanides, Ln(III), and actinides, An(III).1 The aqueous complexes resulting from these interactions have been extensively studied in the case of Ln(III), Am(III) and Cm(III).2–10 The systems Eu(III)–Mg–SO4–H2O and Eu(III)–Na–SO4–H2O were approached in Part I of this work11 with new solubility data and solid phase characterization using the Pitzer equations to derive the corresponding thermodynamic and activity models. As often considered with the Pitzer formalism, full dissociation was assumed and only binary and ternary Pitzer interaction parameters for Eu3+ with SO42−, Na+ and Mg2+ were accounted for, i.e., the explicit formation of Eu(III) complexes with sulfate was disregarded. This approach accurately describes the solubility of Eu(III) in acidic, dilute to concentrated Na2SO4 and MgSO4 aqueous systems, but ignores the ample spectroscopic evidence on the formation of complexes between Eu3+ and SO42−, i.e., Eu(SO4)+, Eu(SO4)2− and Eu(SO4)33−. Such complexes with Ln(III) and An(III) are considered in most thermodynamic databases developed in the context of radioactive waste disposal applications, e.g., NEA-TDB,2 ThermoChimie,12 PSI-Nagra13 or THEREDA,14 using either SIT or Pitzer models for activity corrections. However, these databases do not consider the double-salt identified in Part I of this work (Na2Eu2(SO4)4·2H2O(cr)) and have the focus on lower sulfate concentrations (<0.1 M), thus neglecting the formation of Eu(SO4)33− and disregarding ion interaction coefficients with SO42−.The most relevant complexation studies dealing with the system Eu(III)–SO4 are briefly summarized in the following. Equilibrium constants for aqueous complex formation in the reference state (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0i) reported in these studies are listed in Table 1 and are used in the discussion of the results obtained in this work. Barnes15 studied the complexation of Eu(III) with sulfate by spectrophotometry at 25 °C. The concentration of Eu(III) was 5.01 × 10−3 mol kg−1, with Na2SO4 concentration ranging from 3.00 × 10−3 to 1.213 × 10−2 mol kg−1. NaClO4 was used to adjust the ionic strength to ca. 0.05 mol kg−1. Within these boundary conditions, the author reported the presence of Eu(SO4)+ only. Izatt et al.6 determined calorimetrically the values log10
β0i) reported in these studies are listed in Table 1 and are used in the discussion of the results obtained in this work. Barnes15 studied the complexation of Eu(III) with sulfate by spectrophotometry at 25 °C. The concentration of Eu(III) was 5.01 × 10−3 mol kg−1, with Na2SO4 concentration ranging from 3.00 × 10−3 to 1.213 × 10−2 mol kg−1. NaClO4 was used to adjust the ionic strength to ca. 0.05 mol kg−1. Within these boundary conditions, the author reported the presence of Eu(SO4)+ only. Izatt et al.6 determined calorimetrically the values log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, Δ°H and Δ°S for the complexation of Eu(III) with sulfate. Calorimetric titrations were performed at 25 °C with 0.02 mol kg−1 Eu(III) perchlorate solutions and tetramethylammonium sulfate. Thermometric titration curves were best described considering the formation of both Eu(SO4)+ and Eu(SO4)2−. McDowell and Coleman16 investigated the complexation of trivalent transplutonium actinides (Am, Cm, Bk, Cf and Es) and europium with sulfate by means of solvent extraction (1-nonyldecylamine sulfate in benzene) at T = 25 °C. Stability constants of the An(III)/Eu(III)–sulfate complexes were determined in H2SO4/Na2SO4 mixtures with 0.01 mol kg−1 ≤ [SO4]tot ≤ 0.5 mol kg−1 and varying ionic strength. The authors reported the formation of the complexes An/Eu(SO4)+, An/Eu(SO4)2− and (for the first time) An/Eu(SO4)33−. Skerencak and co-workers4 investigated the complexation of Cm(III) with sulfate by means of Time Resolved Laser Fluorescence Spectroscopy (TRLFS). Spectroscopic measurements were conducted at T = 25–200 °C, with 0.006 mol kg−1 ≤ [SO4]tot ≤ 0.365 mol kg−1 and ionic strength adjusted to 1.0 mol kg−1 ≤ Im ≤ 4.0 mol kg−1 with NaClO4. The formation of the complexes Cm(SO4)+ and Cm(SO4)2− was observed at T = 25 °C, whereas the complex Cm(SO4)33− only formed in aqueous solutions with [Na2SO4] ≥ 0.1 M and T ≥ 100 °C. Vercouter et al.8 studied the complexation of Eu(III) with sulfate at T = 23 ± 1 °C using TRLFS. Experiments were performed in H2SO4/HClO4 and Na2SO4/NaClO4 solutions with 10−4 mol kg−1 Eu(III). Within the investigated boundary conditions, the authors observed only the formation of the complexes Eu(SO4)+ and Eu(SO4)2−, whereas the formation of Eu(SO4)33− was considered negligible. In addition to the complexation constants for the (1,1) and (1,2) complexes, Vercouter et al.8 reported also SIT ion interaction parameters (εij) for the ionic pairs Eu3+/SO42−, Eu(SO4)+/SO42− and Eu(SO4)2−/Na+. We note that this is the only experimental study available to date that reports SIT parameters for these species. Recently, Jordan et al.17 conducted a comprehensive critical review of the literature available for the Eu(III)–sulfate system. Following a similar approach as NEA-TDB, the authors provided selected thermodynamic values for the evaluated Eu(III) systems. Equilibrium constants selected by Jordan et al.17 are also included in Table 1.
K, Δ°H and Δ°S for the complexation of Eu(III) with sulfate. Calorimetric titrations were performed at 25 °C with 0.02 mol kg−1 Eu(III) perchlorate solutions and tetramethylammonium sulfate. Thermometric titration curves were best described considering the formation of both Eu(SO4)+ and Eu(SO4)2−. McDowell and Coleman16 investigated the complexation of trivalent transplutonium actinides (Am, Cm, Bk, Cf and Es) and europium with sulfate by means of solvent extraction (1-nonyldecylamine sulfate in benzene) at T = 25 °C. Stability constants of the An(III)/Eu(III)–sulfate complexes were determined in H2SO4/Na2SO4 mixtures with 0.01 mol kg−1 ≤ [SO4]tot ≤ 0.5 mol kg−1 and varying ionic strength. The authors reported the formation of the complexes An/Eu(SO4)+, An/Eu(SO4)2− and (for the first time) An/Eu(SO4)33−. Skerencak and co-workers4 investigated the complexation of Cm(III) with sulfate by means of Time Resolved Laser Fluorescence Spectroscopy (TRLFS). Spectroscopic measurements were conducted at T = 25–200 °C, with 0.006 mol kg−1 ≤ [SO4]tot ≤ 0.365 mol kg−1 and ionic strength adjusted to 1.0 mol kg−1 ≤ Im ≤ 4.0 mol kg−1 with NaClO4. The formation of the complexes Cm(SO4)+ and Cm(SO4)2− was observed at T = 25 °C, whereas the complex Cm(SO4)33− only formed in aqueous solutions with [Na2SO4] ≥ 0.1 M and T ≥ 100 °C. Vercouter et al.8 studied the complexation of Eu(III) with sulfate at T = 23 ± 1 °C using TRLFS. Experiments were performed in H2SO4/HClO4 and Na2SO4/NaClO4 solutions with 10−4 mol kg−1 Eu(III). Within the investigated boundary conditions, the authors observed only the formation of the complexes Eu(SO4)+ and Eu(SO4)2−, whereas the formation of Eu(SO4)33− was considered negligible. In addition to the complexation constants for the (1,1) and (1,2) complexes, Vercouter et al.8 reported also SIT ion interaction parameters (εij) for the ionic pairs Eu3+/SO42−, Eu(SO4)+/SO42− and Eu(SO4)2−/Na+. We note that this is the only experimental study available to date that reports SIT parameters for these species. Recently, Jordan et al.17 conducted a comprehensive critical review of the literature available for the Eu(III)–sulfate system. Following a similar approach as NEA-TDB, the authors provided selected thermodynamic values for the evaluated Eu(III) systems. Equilibrium constants selected by Jordan et al.17 are also included in Table 1.
| Solubility reactions | ||
|---|---|---|
| Reactions | References | |
| Eu2(SO4)3·8H2O(cr) ↔ 2Eu3+(aq) + 3SO42−(aq) + 8H2O(l) | −12.71 ± 0.10f | This work/SIT |
| −12.80 ± 0.10f | This work/Pitzer | |
| −11.911a,d | Das et al.28 | |
| −11.232 ± 0.02c,d | F. dos Santos et al.11 | |
| −9.11 ± 0.10b,d | Jordan et al.17 | |
| −10.20 ± 0.70d | ThermoChimie12 | |
| Na2Eu2(SO4)4·2H2O(cr) ↔ 2Na+(aq) + 2Eu3+(aq) + 4SO42−(aq) + 2H2O(l) | −19.23 ± 0.03c | This work |
| −17.518d | Das et al.28 | |
| −17.056 ± 0.03c,d | F. dos Santos et al.11 | |
| Complexation reactions | ||
|---|---|---|
| Reactions | References | |
| a Value calculated from the Gibbs energies of formation proposed by the author together with the Gibbs energies of formation of each species from the ThermoChime database.12 b Calculated from the Rard29 solubility data and using the Davies equation30 for ionic strength corrections. c Uncertainty = 2σ. d Calculated without considering aqueous complexation. e As recalculated by Jordan et al.17 f Uncertainty increased as compared to the value of 2σ, i.e., ±0.03. | ||
| Eu3+ + SO42− ↔ Eu(SO4)+ | 3.41 ± 0.12c | This work |
| 3.50 ± 0.30 | ThermoChimie12 | |
| 3.35 ± 0.02 | Barnes15 | |
| 3.54 ± 0.02 | Izatt et al.6 | |
| 3.78 ± 0.10 | Vercouter et al.8 | |
| 3.87 ± 0.13e | McDowell and Coleman16 | |
| Eu3+ + 2SO42− ↔ Eu(SO4)2− | 5.84 ± 0.15c | This work |
| 5.77 ± 0.02 | Jordan et al.17 | |
| 5.20 ± 0.30 | ThermoChimie12 | |
| 5.38 ± 0.30 | Vercouter et al.8 | |
| 5.32 ± 0.12 | Izatt et al.6 | |
| 5.74e | McDowell and Coleman16 | |
| Eu3+ + 3SO42− ↔ Eu(SO4)33− | 5.15 ± 0.12c | This work |
| 5.09e | McDowell and Coleman16 | |
| Mg2+ + SO42− ↔ Mg(SO4)(aq) | 2.39 ± 0.03c | This work/SIT |
| 2.23 ± 0.03 | ThermoChimie12 | |
| Na+ + SO42− ↔ NaSO4− | 0.94 ± 0.20 | ThermoChimie12 |
On the basis of the existing literature and considering the solubility data presented in Part I of this work,11 a TRLFS study was conducted at room temperature over a wide range of Na2SO4 concentrations (0–2 mol kg−1). By combining the independent evidences obtained by TRLFS with our solubility data in the Eu2(SO4)3–Na2SO4–H2O and Eu2(SO4)3–MgSO4–H2O systems,11 thermodynamic properties and activity models (SIT and Pitzer) were derived accounting for the formation of Eu(III)–SO4 aqueous complexes.
2. Experimental
2.1. Chemicals
Europium(III) sulfate octahydrate (Eu2(SO4)3·8H2O(cr), p.a., 99.9 wt%) and magnesium sulfate heptahydrate (MgSO4·7H2O, p.a., 99.5 wt%) were obtained from ThermoFisher Scientific. Anhydrous sodium sulfate (Na2SO4, p.a., >99 wt%) was purchased from Merck. All solutions were prepared with ultrapure water purified with a Milli-Q academic apparatus (Merck Millipore, 18.2 M Ω cm, 22 ± 2 °C, pore size 0.22 μm).2.2. TRLFS experiments
The Eu(III)–Na–SO4–H2O system was investigated with 26 independent samples containing 10−6 mol kg−1 Eu(III) and 0–2 mol kg−1 Na2SO4 (see ESI†). The pH was measured with combined pH–electrodes (type Orion Ross, Thermo Scientific) to confirm the weakly acidic conditions preventing Eu3+ hydrolysis and the formation of HSO4− (<1%) (see ESI†). The excitation laser beam was generated by a Nd:YAG (Surelite II Laser, Continuum) pumping a dye laser (Narrowscan Dye Laser, Radiant Dyes) as described in Skerencak et al.4,5 The wavelength (λex) was tuned to 394 nm, with a maximum laser energy of 2 mJ with a repetition rate of 10 Hz. Emission spectra were recorded over a range of 575–635 nm with a delay of 1 μs and a time window of 1 ms. The emission spectra of each sample were integrated into 1000 accumulations. The obtained spectra can be qualitatively interpreted by the position of the intensity of the 5D0 → 7F2 transition peak (see also section 5.1.).3. Thermodynamic modelling
Thermodynamic and (SIT, Pitzer) activity models derived in this work rely on the solubility experiments with Eu2(SO4)3·8H2O(cr) and Na2Eu2(SO4)4·2H2O(cr) described in Part I of this study11 in combination with new TRLFS data presented here. The formation of Eu(III)–SO4 complexes is explicitly considered in the thermodynamic modelling, as evidenced by spectroscopic means. The following step-wise complexation reactions are expected to take place with increasing sulfate concentration in solution:| Eu3+ + iSO42− ↔ Eu(SO4)i3−2i; i = 1, 2, 3 | (1) |
At the thermodynamic equilibrium, the stability constants in the reference state (β0i) can be expressed according to the law of mass action (2) – where ai is the chemical activity of a given ion (unitless), with  . mj and γj are the molality (mol kg−1) and the activity coefficient (unitless) of the ion j, respectively, at a given background electrolyte concentration and temperature, and m0 = 1 mol kg−1 is the reference concentration. The term βi refers to the conditional stability constant determined at a given ionic strength.
. mj and γj are the molality (mol kg−1) and the activity coefficient (unitless) of the ion j, respectively, at a given background electrolyte concentration and temperature, and m0 = 1 mol kg−1 is the reference concentration. The term βi refers to the conditional stability constant determined at a given ionic strength.
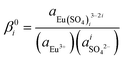 | (2) |
 | (3) |
In the present work, the activity coefficient (γi) is calculated using both the Pitzer equations as described in Part I of this study11 and the Specific Ion Interaction Theory (SIT).2,3,18 According to the SIT approach, the activity coefficient and the stability constant at infinite dilution (β0i) of an aqueous species i can be calculated according to:
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi = −zi2D + Δi(εm)i,j γi = −zi2D + Δi(εm)i,j | (4) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0i = log10 β0i = log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi − Δz2D + Δi(εm)i,j βi − Δz2D + Δi(εm)i,j | (5) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β01 = log10 β01 = log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1 − 12D + Δ1(εm) β1 − 12D + Δ1(εm) | (6) |
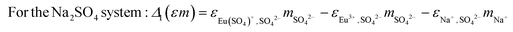 | (7) |
 | (8) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β02 = log10 β02 = log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2 − 16D + Δ2(εm) β2 − 16D + Δ2(εm) | (9) |
 | (10) |
 | (11) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β03 = log10 β03 = log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β3 − 12D + Δ3(εm) β3 − 12D + Δ3(εm) | (12) |
 | (13) |
 | (14) |
Chemical and thermodynamic models considered in this work include two solid phases, Eu2(SO4)3·8H2O(cr) and Na2Eu2(SO4)4·2H2O(cr), and four europium aqueous species, Eu3+, Eu(SO4)+, Eu(SO4)2− and Eu(SO4)33−, as well as the interaction parameters of the later ionic species with Na+, Mg2+ and SO42− when oppositely charged. This allows a more realistic description of the aquatic chemistry of the investigated systems, at the cost of significantly increasing the number of parameters needed for accurate model calculations using Pitzer and SIT formalisms.
4. Parametrization procedure
The parameters required to reproduce the solubility and complexation of europium in the Eu2(SO4)3–Na2SO4–H2O and Eu2(SO4)3–MgSO4–H2O systems are:- Solubility products of the solid phases at I = 0,  and
and 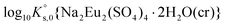 .
.
- Equilibrium constants of the Eu(III)–SO4 aqueous complexes at I = 0, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0{Eu(SO4)+}, log10
β0{Eu(SO4)+}, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0{Eu(SO4)2−} and log10
β0{Eu(SO4)2−} and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0{Eu(SO4)33−}.
β0{Eu(SO4)33−}.
- Ion interaction parameters according to the SIT (εij) and Pitzer (β(0)ij, β(1)ij, Cϕij, θik) approaches.
The development of the Pitzer activity model for the investigated systems requires a total of 75 interaction parameters when considering all possible combinations of binary and ternary interactions. This includes 12 triplets of binary β(0)ij, β(1)ij, Cϕij, parameters (for two oppositely charged ions), 9 ternary θik parameters (for two same-sign charged ions), and 30 ternary Ψijk parameters (for cation/cation/anion or anion/anion/cation triplets). Most of them are neglected to avoid over-parameterization, in particular those involving interactions between two Eu(III) species and/or one ion of the background electrolyte. In the end, 18 parameters were considered most significant and thus included in the optimization process (see Table 2). Note that only 7 interaction parameters were required in Part I of this work to accurately describe the solubility datasets determined for the Eu2(SO4)3–Na2SO4–H2O and Eu2(SO4)3–MgSO4–H2O systems, at the cost of disregarding Eu(III)–SO4 aqueous complexes, i.e. assuming the only presence of Eu3+ in the aqueous phase.
| SIT binary parameters | |||||||
|---|---|---|---|---|---|---|---|
| Species, i | Species, j | ε ij (mol kg−1) | References | Species, i | Species, j | ε ij (mol kg−1) | References |
| Eu3+ | SO42− | 0.86 ± 0.50 | Vercouter et al.8 | Mg2+ | Eu(SO4)33− | 0.39 ± 0.30a | This work |
| Eu(SO4)+ | SO42− | −0.20 ± 0.12a | This work | Mg2+ | SO42− | −0.27 ± 0.03a | This work |
| Na+ | Eu(SO4)2− | −0.10 ± 0.04a | This work | Na+ | SO42− | −0.12 ± 0.06 | ThermoChimie12 |
| Na+ | Eu(SO4)33− | −0.16 ± 0.04a | This work | Na+ | NaSO4− | 0 | This work |
| Mg2+ | Eu(SO4)2− | 0.48 ± 0.27a | This work | MgSO4(aq) | Mg2+, SO42− | 0 | By definition in SIT |
| Pitzer parameters | |||||||
|---|---|---|---|---|---|---|---|
| Species, i | Species, j | β (0) ij | References | Species, i | Species, j | β (1) ij | References |
| Eu3+ | SO42− | 1.792 | Fanghänel and Kim9 | Eu3+ | SO42− | 15.040 | Fanghänel and Kim9 |
| Eu(SO4)+ | SO42− | −0.281 | This work | Eu(SO4)+ | SO42− | 1.560 | NEA-TDB3 |
| Na+ | Eu(SO4)2− | −0.056 | This work | Na+ | Eu(SO4)2− | 0.340 | NEA-TDB3 |
| Na+ | Eu(SO4)33− | 0.137 | This work | Na+ | Eu(SO4)33− | 5.788 | This work |
| Mg2+− | Eu(SO4)2− | 0.990 | This work | Mg2+ | Eu(SO4)2− | 1.843 | This work |
| Mg2+ | Eu(SO4)33− | 1.755 | This work | Mg2+ | Eu(SO4)33− | 8.744 | This work |
| Species, i | Species, j | Cϕij | References | Species, i | Species, j | Cϕij | References |
|---|---|---|---|---|---|---|---|
| Eu3+ | SO42− | 0.600 | Fanghänel and Kim9 | Eu(SO4)+ | SO42− | 0 | This work |
| Na+ | Eu(SO4)2− | 0 | This work | Mg2+ | Eu(SO4)2− | 0.921 | This work |
| Na+ | Eu(SO4)33− | 0 | This work | Mg2+ | Eu(SO4)33− | −0.144 | This work |
| Species, i | Species, k | θ ik | References | Species, i | Species, k | θ ik | References |
|---|---|---|---|---|---|---|---|
| a Uncertainty calculated as 2σ. | |||||||
| Na+ | Eu(SO4)+ | 0 | This work | Mg2+ | Eu(SO4)+ | 0.577 | This work |
The procedure of parameterization and development of the model is divided into three main stages:
(1) Verification of the databases used in the present work – ThermoChimie12 and PhreeScale.19 Using experimental osmotic coefficient data available in the literature20–23 for the binary systems Na2SO4–H2O and MgSO4–H2O, both databases are tested to verify the applicability limits within the salt concentrations considered in this study. If required, the available models are improved to extend their range of validity.
(2) Implementation of the SIT model. On the basis of the TRLFS results presented in this study and of solubility data reported in Part I of this work,11 the parameters  , log10
, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0i and εij are simultaneously determined for the system Eu2(SO4)3–Na2SO4–H2O. Built on this model and in combination with solubility data reported for the Eu2(SO4)3–MgSO4–H2O system, ionic interaction parameters for the MgSO4 system are derived.
β0i and εij are simultaneously determined for the system Eu2(SO4)3–Na2SO4–H2O. Built on this model and in combination with solubility data reported for the Eu2(SO4)3–MgSO4–H2O system, ionic interaction parameters for the MgSO4 system are derived.
(3) Implementation of the Pitzer model. The values of  and log10
and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0i obtained with the SIT model are adopted to ensure consistency among both activity models. On this basis, ion interaction parameters for the europium species are determined following a step-wise approach: (1) Eu2(SO4)3–Na2SO4–H2O system considering both solubility and TRLFS data; (2) Eu2(SO4)3–MgSO4–H2O system based on solubility data.
β0i obtained with the SIT model are adopted to ensure consistency among both activity models. On this basis, ion interaction parameters for the europium species are determined following a step-wise approach: (1) Eu2(SO4)3–Na2SO4–H2O system considering both solubility and TRLFS data; (2) Eu2(SO4)3–MgSO4–H2O system based on solubility data.
The same approach as described in Part I of this work is considered for the optimization of the equilibrium constants and the ion interaction coefficients.11 The PEST optimization software24 is used in combination with the PhreeSCALE19 (Pitzer formalism) or the Phreeqc325 (SIT model) codes and the databases described above. In addition to the calculation of the saturation ratio from solubility data, the independent normalized intensities of the TRLFS data (see section 5.1.) are used to fit the thermodynamic parameters of interest (solubility products, stability constants, ionic interaction parameters). The results of the calculations – solubility and normalized intensity – are compared to the corresponding experimental values by calculating the objective function that characterizes the deviation from the experimental data. In total, 45 solubility data and 26 TRLFS data with normalized intensity were used to derive SIT and Pitzer model parameters.
5. Results and discussion
5.1. TRLFS measurements
TRLFS spectra collected for Eu(III) (10−6 mol kg−1) at increasing Na2SO4 concentrations (0–2 mol kg−1) are shown in Fig. 1 (only 7F1 and 7F2 transition peaks shown). The spectra are normalized to equal total emission intesity for a better visualization of the change of the ratio of the 7F1 to 7F2 band with increasing ligand concentration. The 7F1 (magnetic dipole) and 7F2 (electric dipole) transition peaks are centered at 592 and 617 nm, respectively, and exhibit high sensitivity with increasing sulfate concentrations. The intensity of the 5D0 → 7F2 peak transition (so-called “hypersensitive transition”) is significantly more influenced by the local symmetry of the Eu3+ ion and the nature of the ligands than by the intensities of the other electric dipole transitions.8,26 A similar approach has been previously considered to evaluate the Eu(III)–SO4 complexation in NaClO4–Na2SO4 mixtures, although at lower total sulfate concentrations as those considered in the current study.8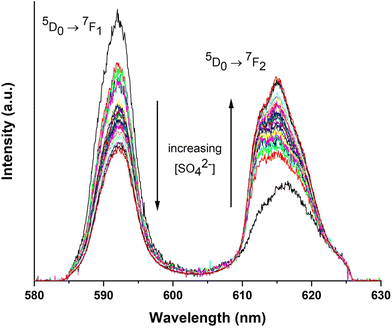 | ||
| Fig. 1 TRLFS spectra of Eu(III) (10−6 mol kg−1) with 0 mol kg−1 < [Na2SO4] < 2 mol kg−1, in Na2SO4 aqueous solutions at room temperature. The spectra are normalized to equal emission intensity. | ||
With increasing sulfate concentration in the system, the hypersensitive peak increases by more than 360%. The changes in the intensity of the 5D0 → 7F2 transition peak (at ∼617 nm) are attributed to the formation of Eu(III)–sulfato complexes.8,26 The quantitative analysis of the TRLFS spectra is thus based on these changes, as previously described by Vercouter et al.8 The measured intensity (Imes) is normalized (IRnorm) with respect to the total concentration of Europium ([Eu(III)T]), without a normalization to the total emission intensity, and the evolution of the Eu(III) fluorescence intensity is described according to:
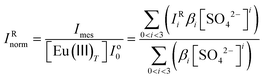 | (15) |
With IRi = Ioi/Io0, where Ioi is the molar fluorescence intensity of the Eu(SO4)i3−2i species and Io0 is the molar fluorescence intensity in the absence of ligand (which means Eu3+ species). The βi are the conditional stability constants defined in section 3. Therefore, in addition to the specific ion interaction coefficients (for the SIT and Pitzer models), the IRi intensities were also adjusted to obtain the complete model. Fig. 2 shows the experimental values of IRnorm as a function of sulfate concentration, together with the calculations using the SIT and Pitzer models derived in this work. All experimental values are also provided in the ESI.†
5.2. Thermodynamic modelling
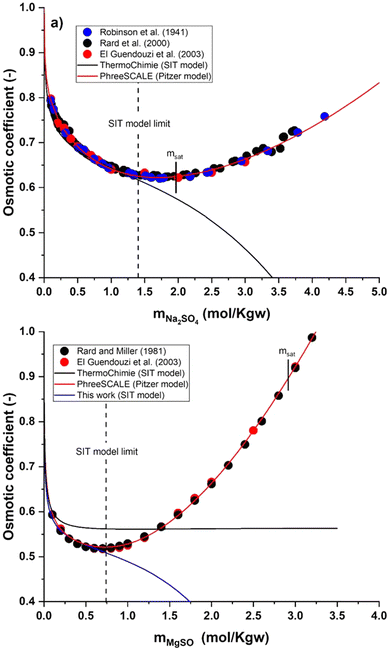 | ||
| Fig. 3 (a) Osmotic coefficient of the Na2SO4–H2O system at 25 °C as a function of Na2SO4 molality. (b) Osmotic coefficient of the MgSO4–H2O system at 25 °C as a function of MgSO4 molality. Symbols are experimental or recommended values from the literature.20–23 Lines are calculated values. Saturated solutions are indicated with the bars labelled msat. | ||
Fig. 3a shows that the ThermoChimie database (TDB) is able to correctly describe experimental osmotic coefficient data for the Na2SO4 system up to salt concentrations of ∼1.45 mol kg−1. Note that ThermoChimie considers the formation of the aqueous complex NaSO4− with a  , but no value is provided for the SIT coefficient
, but no value is provided for the SIT coefficient  . The reevaluation of the
. The reevaluation of the  and
and  parameters was attempted to improve the performance of the model. This exercise proved unsuccessful, and thus the
parameters was attempted to improve the performance of the model. This exercise proved unsuccessful, and thus the  value selected in ThermoChimie was retained, together with
value selected in ThermoChimie was retained, together with  .
.
ThermoChimie also includes the neutral complex Mg(SO4)(aq) with 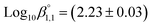 . In contrast to the NaSO4 system, Fig. 3b shows that this set of parameters only able to describe experimental values of the osmotic coefficients up to MgSO4 concentrations of ∼0.1 mol kg−1 (blue full line). To improve the performance of the available model, the values of
. In contrast to the NaSO4 system, Fig. 3b shows that this set of parameters only able to describe experimental values of the osmotic coefficients up to MgSO4 concentrations of ∼0.1 mol kg−1 (blue full line). To improve the performance of the available model, the values of  and
and 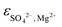 were fitted after the experimental osmotic coefficients. As a result, the revised values of
were fitted after the experimental osmotic coefficients. As a result, the revised values of 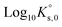 and
and 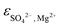 reported in Table 1 are able to accurately reproduce experimental data up to MgSO4 concentration extended to 0.75 mol kg−1 (see Fig. 3b, black full line).
reported in Table 1 are able to accurately reproduce experimental data up to MgSO4 concentration extended to 0.75 mol kg−1 (see Fig. 3b, black full line).
5.2.2.1. Ternary system Eu2(SO4)3–Na2SO4–H2O. The experimental data available for the Eu2(SO4)3–Na2SO4–H2O system – solubility and fluorescence intensities – were used to derive the values of
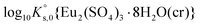 ,
,  , log10
, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β01, log10
β01, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β02, log10
β02, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β03,
β03,  ,
,  ,
,  , IR1, IR2 and IR2. Vercouter et al.8 proposed a value for the
, IR1, IR2 and IR2. Vercouter et al.8 proposed a value for the  parameter, which we selected and therefore was not optimized in the present work. Jordan et al.17 highlighted that the lack of experimental solubility data on the Eu2(SO4)3–Na2SO4–H2O system makes the evaluation of
parameter, which we selected and therefore was not optimized in the present work. Jordan et al.17 highlighted that the lack of experimental solubility data on the Eu2(SO4)3–Na2SO4–H2O system makes the evaluation of 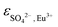 difficult, and suggested the use of isopiestic measurements for a more accurate determination of
difficult, and suggested the use of isopiestic measurements for a more accurate determination of  . This is however not feasible due to the predominance of the Eu(III)–SO4 complexes at [SO42−] > 0.001 mol kg−1 and the relatively low solubility imposed by the sulfate salts of Eu(III). The fit of the available experimental data resulted in the thermodynamic parameters summarized in Tables 1 and 2, together with the values of IR1 = 1.081, IR2 = 2.282 and IR3 = 4.413.
. This is however not feasible due to the predominance of the Eu(III)–SO4 complexes at [SO42−] > 0.001 mol kg−1 and the relatively low solubility imposed by the sulfate salts of Eu(III). The fit of the available experimental data resulted in the thermodynamic parameters summarized in Tables 1 and 2, together with the values of IR1 = 1.081, IR2 = 2.282 and IR3 = 4.413.
Experimental data and model calculations performed using the SIT model derived in this work are plotted (as black lines) in Fig. 2 for the normalized relative intensity and in Fig. 4 for the Eu(III) solubility in the Eu2(SO4)3–Na2SO4–H2O ternary system. Note that in spite of the limitations identified for the SIT model (m(Na2SO4) < 1.45 mol kg−1, see section 5.2.1), the new set of parameters is able to reproduce satisfactorily all experimental observations. Additional details on the normalized intensity calculated with the SIT model (IR,SITnorm) are provided in the ESI.†
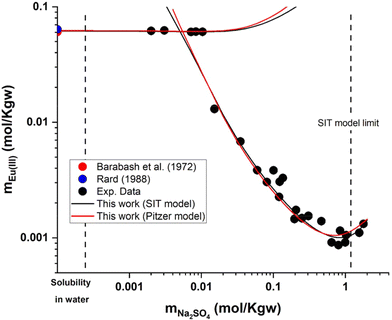 | ||
| Fig. 4 Solubility in the system Eu2(SO4)3–Na2SO4–H2O at room temperature in logarithmic scale, according to SIT (black lines) and Pitzer (red lines) models. Symbols: experimental data reported in Part I of this work or in the literature.11 | ||
Table 2 summarizes the SIT ion interaction parameters  ,
,  and
and 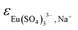 determined in this work. These values are consistent with those determined by Vercouter et al.8 for the (1
determined in this work. These values are consistent with those determined by Vercouter et al.8 for the (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and (1
1) and (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) complexes
2) complexes  , as well as those estimated by Hummel18 for the (1,2) and (1,3) based on charge analogies
, as well as those estimated by Hummel18 for the (1,2) and (1,3) based on charge analogies 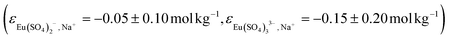 .
.
Fig. 5 shows the aqueous speciation Eu(III)-as a function of Na2SO4 concentration, calculated using the SIT model derived in this work (solid lines in the figure). As expected, europium is primarily found as complexed species (Eu(SO4)+) as soon as the Na2SO4 molality exceeds 0.0008 mol kg−1. The complex Eu(SO4)2− dominates for ∼0.07 < [Na2SO4] < ∼1 mol kg−1, whereas the (1,3) complex Eu(SO4)33− becomes predominant only above the later concentration.
 | ||
| Fig. 5 Aqueous speciation of Eu(III) with increasing Na2SO4 concentrations at 25 °C, as calculated using the SIT (solid lines) and Pitzer (dashed lines) activity models derived in this work. | ||
This study represents the most comprehensive work on the solubility and aqueous complexation of Eu(III) in sulfate media, providing a consistent set of solubility and complexation constants ( ,
,  , log10
, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β01, log10
β01, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β02 and log10
β02 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β03) on the basis of new and previously reported experimental data. Table 1 shows that solubility constants derived in this work are in disagreement with
β03) on the basis of new and previously reported experimental data. Table 1 shows that solubility constants derived in this work are in disagreement with 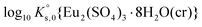 and
and  values reported in previous studies. This is explained by the fact that previous
values reported in previous studies. This is explained by the fact that previous  values were determined disregarding the formation of aqueous Eu(III)-sulfate complexes,11,12,28 despite they form at very low sulfate concentration values like those resulting from the dissolution of Eu2(SO4)3·8H2O(cr) in water. The only value provided in the literature for
values were determined disregarding the formation of aqueous Eu(III)-sulfate complexes,11,12,28 despite they form at very low sulfate concentration values like those resulting from the dissolution of Eu2(SO4)3·8H2O(cr) in water. The only value provided in the literature for 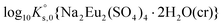 was estimated by Das et al.28 The present work thus provides the first evidence for the experimental determination of this solubility product. The values of log10
was estimated by Das et al.28 The present work thus provides the first evidence for the experimental determination of this solubility product. The values of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β01 and log10
β01 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β02 determined in this work agree well with literature data when considering the corresponding uncertainties. Note that most of the previous studies were performed in the presence of mixed background electrolytes (NaClO4–Na2SO4), with lower sulfate concentrations, and using the Debye–Hückel approach for ionic strength corrections in most cases.
β02 determined in this work agree well with literature data when considering the corresponding uncertainties. Note that most of the previous studies were performed in the presence of mixed background electrolytes (NaClO4–Na2SO4), with lower sulfate concentrations, and using the Debye–Hückel approach for ionic strength corrections in most cases.
The value of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β03 determined in this work based on solubility and spectroscopic data agrees within the corresponding uncertainties with the value determined by means of solvent extraction by McDowell and Coleman.16 The original conditional equilibrium constant reported by the authors was recently extrapolated to I = 0 by Jordan et al.17 using the Debye–Hückel equation. Note that ionic strength corrections with this method are less accurate at the high salt/acid concentrations considered in the original solvent extraction study.
β03 determined in this work based on solubility and spectroscopic data agrees within the corresponding uncertainties with the value determined by means of solvent extraction by McDowell and Coleman.16 The original conditional equilibrium constant reported by the authors was recently extrapolated to I = 0 by Jordan et al.17 using the Debye–Hückel equation. Note that ionic strength corrections with this method are less accurate at the high salt/acid concentrations considered in the original solvent extraction study.
5.2.2.2. Ternary system Eu2(SO4)3–MgSO4–H2O. Solubility and complexation constants, as well as SIT coefficients for cationic species with SO42− determined from solubility and spectroscopic data in the Na2SO4 system were kept constant for the modelling of the MgSO4 system. Thus, only the parameters
 and
and 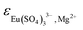 were fitted on the basis of Eu(III) solubility data reported in Part I of this work for MgSO4 solutions (19 independent data points). The resulting parameters summarized in Table 2 are able to successfully reproduce the experimental solubility data (see black line in Fig. 6), in spite of the limitations identified in section 5.2.1 for the application of the SIT model to MgSO4 solutions above 0.75 mol kg−1. Fig. 7 shows the speciation diagram of Eu(III) calculated for the Eu2(SO4)3–MgSO4–H2O system up to a MgSO4 concentration of 2 mol kg−1. As expected, the speciation diagram calculated for the MgSO4 system presents close similarities with respect to the Eu(III) species distribution in Na2SO4 solutions (see Fig. 5). However, the calculated concentration of the Eu(SO4)+ complex unexpectedly increases above 1 M MgSO4. This artifact of the model is partially attributed to the limited performance of the SIT model for the binary system MgSO4–H2O. Note that the formation of a ternary solid phase with Mg (analogous to Na2Eu2(SO4)4·2H2O(cr) controlling the solubility in the Na2SO4 system) was not confirmed experimentally by XRD analysis. The formation of such a phase could be also responsible of the decrease in solubility observed above 1 M MgSO4.
were fitted on the basis of Eu(III) solubility data reported in Part I of this work for MgSO4 solutions (19 independent data points). The resulting parameters summarized in Table 2 are able to successfully reproduce the experimental solubility data (see black line in Fig. 6), in spite of the limitations identified in section 5.2.1 for the application of the SIT model to MgSO4 solutions above 0.75 mol kg−1. Fig. 7 shows the speciation diagram of Eu(III) calculated for the Eu2(SO4)3–MgSO4–H2O system up to a MgSO4 concentration of 2 mol kg−1. As expected, the speciation diagram calculated for the MgSO4 system presents close similarities with respect to the Eu(III) species distribution in Na2SO4 solutions (see Fig. 5). However, the calculated concentration of the Eu(SO4)+ complex unexpectedly increases above 1 M MgSO4. This artifact of the model is partially attributed to the limited performance of the SIT model for the binary system MgSO4–H2O. Note that the formation of a ternary solid phase with Mg (analogous to Na2Eu2(SO4)4·2H2O(cr) controlling the solubility in the Na2SO4 system) was not confirmed experimentally by XRD analysis. The formation of such a phase could be also responsible of the decrease in solubility observed above 1 M MgSO4.
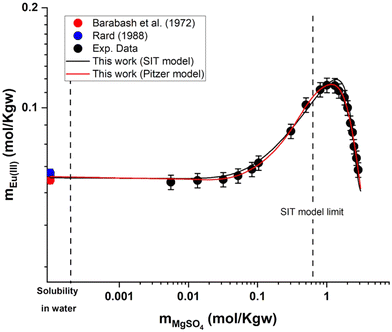 | ||
| Fig. 6 Solubility in the system Eu2(SO4)3–MgSO4–H2O at room temperature in logarithmic scale, according to SIT (black line) and Pitzer (red line) models. Symbols: experimental data as reported in Part I of this work or in the literature.11 | ||
 ,
,  , log10
, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β01, log10
β01, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β02, log10
β02, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β03, IR1, IR2 and IR2 were taken from the SIT model to maintain internal consistency between the models. To further minimize the number of fitting parameters and avoid over-parameterization, a number of Pitzer parameters were adopted from the literature. Fanghänel and Kim9 determined
β03, IR1, IR2 and IR2 were taken from the SIT model to maintain internal consistency between the models. To further minimize the number of fitting parameters and avoid over-parameterization, a number of Pitzer parameters were adopted from the literature. Fanghänel and Kim9 determined  ,
,  and
and 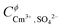 based on Cm(III) TRLFS measurements. Considering the analogy between An(III) and Ln(III), Xiong et al.31 adopted the same parameters for the description of the Nd2(SO4)32−–H2O system. These values have been also taken as fixed parameters,
based on Cm(III) TRLFS measurements. Considering the analogy between An(III) and Ln(III), Xiong et al.31 adopted the same parameters for the description of the Nd2(SO4)32−–H2O system. These values have been also taken as fixed parameters,  ,
,  and
and 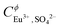 , in the present work, in addition to the standard values of
, in the present work, in addition to the standard values of  and
and 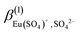 proposed in the NEA publication “Modelling in Aquatic Chemistry”3 for (1
proposed in the NEA publication “Modelling in Aquatic Chemistry”3 for (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and (1
1) and (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) interactions.
2) interactions.
Taking into account these assumptions and a slight modification in 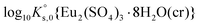 (from −12.71 to −12.80), we obtained binary Pitzer interaction parameters (see Table 2) that are able to satisfactorily reproduce both experimental solubility data and normalized intensity for the Eu2(SO4)3–Na2SO4–H2O system (red lines in Fig. 2 and 4). Moreover, Fig. 5 shows that this set of parameters results in a similar distribution of species as calculated with the SIT model. This underpins that both activity models provide a consistent description of the solubility and speciation in the Eu2(SO4)3–Na2SO4–H2O system.
(from −12.71 to −12.80), we obtained binary Pitzer interaction parameters (see Table 2) that are able to satisfactorily reproduce both experimental solubility data and normalized intensity for the Eu2(SO4)3–Na2SO4–H2O system (red lines in Fig. 2 and 4). Moreover, Fig. 5 shows that this set of parameters results in a similar distribution of species as calculated with the SIT model. This underpins that both activity models provide a consistent description of the solubility and speciation in the Eu2(SO4)3–Na2SO4–H2O system.
In addition to  ,
,  ,
,  and
and 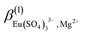 , the incorporation of the parameters
, the incorporation of the parameters  ,
, 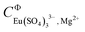 . and
. and  was required to properly explain the solubility data in the Eu2(SO4)3–MgSO4–H2O system (see Fig. 6, and Fig. SI-1 in the ESI†). The speciation diagram calculated with this model is shown in Fig. 7 (dashed lines corresponding to the Pitzer model). The figure underpins a good agreement between the SIT and Pitzer speciation calculations up to a sulfate molality of ∼0.1 mol kg−1. Above this sulfate concentration, the Pitzer model predicts a greater stability of the complex Eu(SO4)33− with increasing MgSO4 concentration. Considering the limitations of SIT at high ionic strength conditions, and in particular those identified for the SIT model of the binary MgSO4–H2O system (see section 5.2.1), a higher reliability is attributed to the Pitzer speciation model at high MgSO4 concentrations. Based on solubility and TRLFS measurements, Herm et al.10 proposed the formation of ternary complexes betwn Mg, Cm(III)/Nd(III) and nitrate at high Mg(NO3)2 concentrations. In line with these observations, the enhanced stability of the Eu(SO4)33− complex predicted by the Pitzer model in the MgSO4 compared to the Na2SO4 system could be attributed to the strong interaction expected between this anionic species with charge −3 and a divalent cation like Mg2+. Attempting to include a ternary complex (e.g. Mg[Eu(SO4)3]−) in the chemical model was unsuccessful, and this option was disregarded as the species is not required to properly explain solubility.
was required to properly explain the solubility data in the Eu2(SO4)3–MgSO4–H2O system (see Fig. 6, and Fig. SI-1 in the ESI†). The speciation diagram calculated with this model is shown in Fig. 7 (dashed lines corresponding to the Pitzer model). The figure underpins a good agreement between the SIT and Pitzer speciation calculations up to a sulfate molality of ∼0.1 mol kg−1. Above this sulfate concentration, the Pitzer model predicts a greater stability of the complex Eu(SO4)33− with increasing MgSO4 concentration. Considering the limitations of SIT at high ionic strength conditions, and in particular those identified for the SIT model of the binary MgSO4–H2O system (see section 5.2.1), a higher reliability is attributed to the Pitzer speciation model at high MgSO4 concentrations. Based on solubility and TRLFS measurements, Herm et al.10 proposed the formation of ternary complexes betwn Mg, Cm(III)/Nd(III) and nitrate at high Mg(NO3)2 concentrations. In line with these observations, the enhanced stability of the Eu(SO4)33− complex predicted by the Pitzer model in the MgSO4 compared to the Na2SO4 system could be attributed to the strong interaction expected between this anionic species with charge −3 and a divalent cation like Mg2+. Attempting to include a ternary complex (e.g. Mg[Eu(SO4)3]−) in the chemical model was unsuccessful, and this option was disregarded as the species is not required to properly explain solubility.
6. Summary and conclusions
The complexation of Eu(III) with sulfate in dilute to concentrated Na2SO4 solutions (0–2 mol kg−1) was studied at room temperature by means of TRLFS. Sulfate has a significant influence on the hypersensitive emission peak 5D0 → 7F2 of the Eu(III) spectra. The evaluation of TRLFS data collected for the Eu2(SO4)3–Na2SO4–H2O system allows the identification of three main aqueous complexes, i.e., Eu(SO4)+, Eu(SO4)2− and Eu(SO4)33−. The combination of these TRLFS results with solubility data determined in Part I of this work for the systems Eu2(SO4)3–Na2SO4–H2O and Eu2(SO4)3–MgSO4–H2O, allows deriving complete chemical, thermodynamic and activity models based on both the SIT and Pitzer formalisms.Both activity models are able to successfully and consistently describe solubility and TRLFS data in the Eu2(SO4)3–Na2SO4–H2O system. Equilibrium constants derived in this work for the complexes Eu(SO4)+, Eu(SO4)2− and Eu(SO4)33− agree well with those previously reported in the literature. Discrepancies with  in the literature are harmonized when considering the formation of Eu(III)–SO4 complexes, which become predominant already at the sulfate concentrations defined by the solubility of this solid phase in water. The value of
in the literature are harmonized when considering the formation of Eu(III)–SO4 complexes, which become predominant already at the sulfate concentrations defined by the solubility of this solid phase in water. The value of  determined in this work is based on the first experimental evidence available to date.
determined in this work is based on the first experimental evidence available to date.
SIT and Pitzer activity models derived in this work describe well the solubility data available for the Eu2(SO4)3–MgSO4–H2O system. However, both models provide discrepant speciation schemes at high MgSO4 concentrations, which can be due to: (i) limitations of the thermodynamic data available for the binary system MgSO4–H2O, (ii) the possible formation of a ternary complex Mg–Eu(III)–SO4 at high MgSO4 concentrations, currently not included in the model, (iii) the possible formation of a ternary solid phase Mg–Eu(III)–SO4 (analogous to the Na2Eu2(SO4)4·2H2O(cr) observed in the Na2SO4 system) that would explain the decrease in solubility observed at high MgSO4 concentrations, or (iv) a combination of (i)–(iii).
This work is the second of a series targeting the thermodynamic description of complex Ln(III)/An(III)–SO4–NO3 systems of relevance in the context of radioactive waste disposal.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The present work was realized in the collaborative project co-funded by KIT–INE, BRGM and ANDRA (contracts numbers KIT-35048079 and COX-20086445).References
- M. Altmaier, X. Gaona and T. Fanghänel, Chem. Rev., 2013, 113, 901–943 CrossRef CAS PubMed.
- NEA, Second update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium And Technetium, OECD, 2021, vol. 14 Search PubMed.
- NEA, Modelling in Aquatic Chemistry, OECD Publishing, Paris, 2020 Search PubMed.
- A. Skerencak, P. J. Panak and T. Fanghänel, Dalton Trans., 2013, 42, 542–549 RSC.
- A. Skerencak, P. J. Panak, W. Hauser, V. Neck, R. Klenze, P. Lindqvist-Reis and T. Fanghänel, Radiochim. Acta, 2009, 97(8), 385–393 CAS.
- R. M. Izatt, D. Eatough, J. J. Christensen and C. H. Bartholomew, J. Chem. Soc. A, 1969, 47–53 RSC.
- I. L. Jenkins and C. B. Monk, J. Am. Chem. Soc., 1950, 72, 2695–2698 CrossRef CAS.
- T. Vercouter, B. Amekraz, C. Moulin, E. Giffaut and P. Vitorge, Inorg. Chem., 2005, 44, 7570–7581 CrossRef CAS PubMed.
- T. Fanghänel and J.-I. Kim, J. Alloys Compd., 1998, 271–273, 728–737 CrossRef.
- M. Herm, X. Gaona, T. Rabung, D. Fellhauer, C. Crepin, K. Dardenne, M. Altmaier and H. Geckeis, Pure Appl. Chem., 2015, 87, 487–502 CrossRef CAS.
- P. F. dos Santos, A. Lassin, X. Gaona, K. Garbev, M. Altmaier and B. Madé, Dalton Trans., 2024 10.1039/d3dt04322c.
- E. Giffaut, M. Grivé, P. Blanc, P. Vieillard, E. Colàs, H. Gailhanou, S. Gaboreau, N. Marty, B. Madé and L. Duro, Appl. Geochem., 2014, 49, 225–236 CrossRef CAS.
- W. Hummel and T. Thoenen, The PSI Chemical Thermodynamic Database 2020, 2023 Search PubMed.
- H. C. Moog, F. Bok, C. M. Marquardt and V. Brendler, Appl. Geochem., 2015, 55, 72–84 CrossRef CAS.
- J. C. Barnes, J. Chem. Soc., 1964, 3880 RSC.
- W. J. McDowell and C. F. Coleman, J. Inorg. Nucl. Chem., 1972, 34, 2837–2850 CrossRef CAS.
- N. Jordan, T. Thoenen, S. Starke, K. Spahiu and V. Brendler, Coord. Chem. Rev., 2022, 473, 214608 CrossRef CAS.
- W. Hummel, Ionic strength corrections and estimation of SIT ion interaction coefficients, Villigen, Switzerland, 2009 Search PubMed.
- A. Lach, F. Boulahya, L. André, A. Lassin, M. Azaroual, J.-P. Serin and P. Cézac, Comput. Geosci., 2016, 92, 58–69 CrossRef CAS.
- C. K. Chan, Z. Liang, J. Zheng, S. L. Clegg and P. Brimblecombe, Aerosol Sci. Technol., 1997, 27, 324–344 CrossRef CAS.
- R. A. Robinson, J. M. Wilson and R. H. Stokes, J. Am. Chem. Soc., 1941, 63, 1011–1013 CrossRef CAS.
- M. E. Guendouzi, A. Mounir and A. Dinane, J. Chem. Thermodyn., 2003, 35, 209–220 CrossRef.
- J. A. Rard and D. G. Miller, J. Chem. Eng. Data, 1981, 26, 33–38 CrossRef CAS.
- J. Doherty, PEST: Model-Independent Parameter Estimation, 5th edn, 2004 Search PubMed.
- C. A. J. Appelo, Appl. Geochem., 2015, 55, 62–71 CrossRef CAS.
- K. Binnemans, Coord. Chem. Rev., 2015, 295, 1–45 CrossRef CAS.
- A. Lach, L. André and A. Lassin, Appl. Geochem., 2017, 78, 311–320 CrossRef CAS.
- G. Das, M. M. Lencka, A. Eslamimanesh, P. Wang, A. Anderko, R. E. Riman and A. Navrotsky, J. Chem. Thermodyn., 2019, 131, 49–79 CrossRef CAS.
- J. A. Rard, J. Solution Chem., 1988, 17, 499–517 CrossRef CAS.
- C. W. Davies, Ion association, Butterworths, London, 1962 Search PubMed.
- Y. Xiong, G. Xu and Y. Wang, J. Solution Chem., 2023, 52, 447–466 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt04323a |
| This journal is © The Royal Society of Chemistry 2024 |