Revisiting ion-pair interactions in phase transfer catalysis: from ionic compounds to real catalyst systems

Abstract

Ion-pairing is a fundamental phenomenon that significantly influences phase-transfer catalysis. In this study, we conduct a comprehensive investigation of ion-pair interactions, aiming to establish a comprehensive understanding of their nature and implications. The study begins with the examination of polar ionic compounds to define the concept of an ion-pair in the context of phase-transfer catalysis. Subsequently, a diverse range of ion-pair catalyst models were explored to gain insight into the factors governing their interactions. Finally, the focus shifts towards the characterisation of real phase-transfer catalysts, bridging the gap between theoretical models and practical applications. Through a combination of computational approaches and theoretical analysis, this work provides valuable insight into the nature of ion-pair interactions within phase-transfer catalysis fields.

---

1 Introduction

Asymmetric ion pairing catalysis, a prominent form of noncovalent organocatalysis, takes advantage of specifically charged intermediates or reagents. By forming ion pairs between the catalyst and the substrate, reactivity and selectivity can be significantly enhanced.^1,2 The emergence of chiral ion pairs has played a pivotal role in the development of asymmetric catalysis, enabling precise control and improving reactivity across a diverse range of chemical reactions. However, the pursuit of a general approach to achieving exceptional enantioselectivity in asymmetric ion pairing catalysis faces notable challenges stemming from the inherent directionless nature associated with ion pairing interactions, in contrast to the discernible behaviour exhibited by hydrogen bonding and covalent interactions.^1,3–11 Enantioselective ion pairing catalysis encompasses a diverse array of small organic molecules, among which quaternary ammonium salts have emerged as the most extensively studied class of chiral phase-transfer catalysts (PTCs).

These catalysts feature a nitrogen atom positioned at the centre of a tetrahedron formed by carbon atoms, with three sterically hindered faces, resulting in a single accessible face for anion interaction, thereby facilitating the establishment of ion pairs (Fig. 1a). The successful use of electrostatic interactions between the ammonium cation and the counterion holds significant promise in the induction of chiral information, thus enabling asymmetric induction (Fig. 1b).⁴

Fig. 1 (a) General structure of quaternary ammonium salts (b) concept of asymmetric ammonium ion pairing catalysis.

The introduction of a second interaction point, such as a hydrogen bond (HB) donor, has been reported to influence the ion pairing process in PTCs and competes with the establishment of a HB interaction. As a result, two distinct modes of activation for these bifunctional PTCs have been proposed, wherein the catalyst can act either through ion-pair formation or hydrogen bonding.

In this context, our group conducted a comprehensive theoretical investigation aimed at elucidating the preferred binding mode and its impact on enantioselectivity. Contrary to the conventional notion of a “strict ion pair” in bifunctional catalysis, our study revealed that a definitive binding mode through a HB is energetically more favourable. This highly stabilising and directional interaction was found to exert a profound influence on the control of enantioselectivity in reactions. Intriguingly, our computational analysis did not provide conclusive evidence supporting the sole existence of a discernible strict ion-pair interaction, underscoring the significance of hydrogen bonding in these systems.¹² Consequently, these findings prompt the need for an updated definition of ion pairing within the field of phase-transfer catalysis.

The definition of ion pairing has evolved over time, driven by advances in our understanding of electrostatic interactions and molecular behaviour. Historically, ion pairing started with Bjerrum's pioneering work in 1926,¹³ where he proposed a definition based on the electrostatic work required to separate two ions. Subsequently, Anslyn and Dougherty introduced a physical-organic definition in 2006,¹⁴ emphasising the spatial proximity and the energetic strength of the electrostatic attraction between ions. Their definition considers the comparison between the electrostatic energy and the thermal energy available for ion separation.

In addition, the influence of Coulomb's law on ion pairing interactions emphasises the role of distance and the dielectric constant in determining the strength of these interactions. Coulomb's law (eqn (1)) describes the attractive potential energy between two ions (q₁ and q₂). The magnitude of the electrostatic interaction is inversely related to the distance between the ions (r) and the dielectric constant of the medium (ε₀). Thus, strong ion-pairing interactions are preferred at short distances and in nonpolar solvents.^1,15

Given the influence of this interaction in the structural stabilisation of ionic complexes, especially at short distances, the concept of ion-pairing is ubiquitously used in literature as the key factor governing catalytic activity and selectivity in ionic complexes, with little emphasis on other major potential sources of stabilisation. This is especially significant in experimental works where theoretical insights are unavailable. Thus, unravelling the true nature of relevant ion pairs found in literature is key to understanding where and how ion-pairing interactions are key players in the formation of these complexes or whether they are mere spectators in a network of equally stronger types of interactions. This will provide a new framework of reference for the use of the concept of ion-pairing in the emerging field of asymmetric organocatalysis. To achieve this, we have investigated and thoroughly characterised the nature of relevant ion-pair interactions, challenging different systems in which, in theory, only strict ion-pair or HB-assisted ion-pairing interactions can be established within PTCs (Fig. 2) and comparing them with their neutral counterparts.

Fig. 2 Different types of ion-pairing interactions often defined in current literature.

2 Computational methods

The structures of the salts and the different models of the catalysts under study were optimised at the wB97x-D/def2-tzvp^16–18 computational level and the real catalysts were optimised at wB97x-D/def2-svp. Harmonic frequencies were computed at the optimisation level to confirm that the relaxed structures correspond to local minima. In some structures, marked with *, the distance N–H was fixed to avoid H transfer and to keep all complexes consistent for analysis. Single-point calculations were performed to improve the energy description at the computational level of wB97x-D/def2-qzvp^16–18 for salts and models and wB97x-D/def2-tzvp computational level for the real catalysts under study. Structure optimisations and energy calculations were performed using the Gaussian16 software.¹⁹ All the calculations were performed in the gas phase. The optimised structures can be found in Table S1.†

The binding energies (ΔE) were calculated as the difference between the free energy of the optimised complexes (E_complex) and the energy of each optimised monomer (E_monomer) as shown in eqn (2) and the results can be found in Table S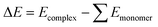2.†

An energy decomposition analysis was performed based on the localised molecular orbital energy decomposition analysis (LMO-EDA)²⁰ scheme at the M06-2X/KTZVP computational level. The interaction energy was obtained as the sum of different energetic terms, as shown in eqn (3)

E^LMO-EDA_int = E_elec + E_exc + E_rep + E_pol + E_disp (3)

where E_elec is the electrostatic term that describes the classical coulombic interaction of the occupied orbitals of one monomer with those of the other. The term E_exc is attractive and denotes the contribution of the exact exchange energy between the orbitals of one monomer and the orbitals of the others, E_rep is repulsive and is associated with the Pauli exclusion principle, and the terms LP(X⁻) → BD*(N–C) and E_disp correspond to the terms of polarisation and dispersion, respectively. These calculations were carried out using GAMESS software (version 2018-R2).²¹ Numerical LMO-EDA values are collected in Table S3.†

Due to some technical problems when running GKS-EDA calculations, the energy decomposition analysis in for the systems in solution was calculated using the electron-density based energy partitioning scheme EDA-NCI^22,23 at the wB97x-D/def2-tzvp level of theory. Solvent effects were included in the optimisation by means of a continuum method, the Solvation Model based on Density (SMD) approach²⁴ in Gaussian16. The use of an implicit solvent model allows us to consider the electrostatic and non-electrostatic cavitation, solvation, and structural effects of the solvent while, at the same time, allowing for an undisturbed and in-detail analysis of any inter- and intramolecular interactions governing structural stabilisation of our PTCs. The interaction energies are obtained as the sum of the energy terms expressed in eqn (4)

E^EDA-NCI_int = E_elec + E_exc + E_rep + E_pol (4)

where E_elec, E_exc, and E_rep represent the same magnitudes as in LMO-EDA and the term E_pol correspond to the term of polarisation and it is calculated using eqn (5)

E_pol = E_def + E_{exc\_def} (5)

where E_def is the electron density deformation energy, E_{exc_def} is the deformation energy associated with the exchange–correlation density.

The Natural Bond Orbital (NBO7)²⁵ methodology was used to evaluate atomic charges in the different systems, to evaluate the strength of individual interactions by measuring the charge transfer between occupied and unoccupied orbitals within different fragments. The calculations were performed at the same level of theory as the geometry optimisations: wB97x-D/def2tzvp for the salts and small models and wB97x-D/def2svp for the real catalysts. Intermolecular NBO charge transfer values can be found in Table S4† and NBO charges in Table S6.† The NBO calculations yield the E(2) value, which will be thoroughly discussed in this manuscript. E(2) is defined as second-order perturbative energy, determined by the analysis of all possible interactions between donor Lewis-type NBOs and acceptor non-Lewis-type NBOs, with their energetic importance estimated through second-order perturbation theory. “For each donor NBO (i) and acceptor NBO (j), the donor–acceptor stabilisation energy E(2) associated with i → j delocalisation is calculated as, where q_irepresents the donor orbital occupancy (2 for closed shell, 1 for open shell), ε_iand ε_jdenote the diagonal elements (orbital energies), and F(i, j) stands for the off-diagonal NBO Fock matrix element”.²⁶

The quantum theory of atoms in molecules (QTAIM) methodology^27,28 was used to analyse the electron density of the systems within the AIMAll software, and the electron density at the bond critical points (BCPs) between the systems and the different anions upon complexation was extracted. The calculations were performed at the same level of theory as the geometry optimisations: wB97x-D/def2tzvp for the salts and small models and wB97x-D/def2svp for the real catalysts. Densities at the bond critical points and bond distances can be found in Table S5† and 3D molecular graphs of all the systems in Fig. S4.†

3 Results and discussion

To establish a comprehensive understanding of ion-pair interactions, this study investigates various scenarios, starting with a discussion of ionic compounds to define the concept of an ion pair. Subsequently, a wide range of ion-pair catalyst models is examined, as well as their neutral forms for comparison, followed by the characterisation of real PTCs. To ensure homogeneity and comparability, all calculations are performed in the gas phase.

By examining these systems, we aimed to unravel the intricate interplay between hydrogen-bonding and ion-pair interactions by discerning the subtle differences that influence the nature and strength of hydrogen-bonding and its role in facilitating ion-pair formation, shedding light on their impact on the overall catalytic activity and selectivity.

3.1 Ion-pair

In this part of the study, our primary objective is to explore notable instances of ionic salts characterised by polar bonding²⁹ between atoms (i.e. between Na⁺ and Cl⁻, CN⁻—through both terminations—and PO₄(CH₃)₂⁻ through O atoms). Furthermore, an additional cation, namely [N(CF₃)₄]⁺, has been introduced to encompass a structural motif comparable to the predominant PTC scaffold died (Fig. 3). By studying these systems, we aim to obtain an accurate definition of a strict ion-pair and therefore shed light on the nature of the interactions of the following systems studied by comparison.

Fig. 3 Representation of the ionic salt models used to investigate strict ion-pairing interactions.

The interaction energies of the studied complexes are presented in Table 1. The values obtained fall within the expected range for polar ionic interactions, providing evidence of the electrostatic attraction between the cation and the negatively charged anion. Additionally, the calculated distances between the ions are in excellent agreement with the reports found in the literature, further validating the accuracy of the computational approach.³⁰ In the case of complexes including the [N(CF₃)₄]⁺ cation, the interaction energies are comparatively lower and present cation–anion distances around ca. 4 Å, primarily attributable to the steric hindrance arising from its larger molecular structure, thereby highlighting the establishment of a longer-range ion-pair interaction.

Table 1 Ionic salts and [N(CF₃)₄]–X DFT interaction energies, ΔE in kJ mol⁻¹. Distances in Å

Ionic complex	ΔE	d(Na^+X^−)
Na–Cl	−546.4	2.39
Na–CN	−521.0	2.27
Na–NC	−539.1	2.14
Na–PO4Me2	−586.1	2.26

---

Ionic complex	ΔE	d(N^+X^−)
N(CF3)4–Cl	−316.5	4.20
N(CF3)4–CN	−315.3	4.25
N(CF3)4–NC	−320.7	4.11
N(CF3)4–PO4Me2	−313.3	3.92

---

3.1.1 Characterisation of the ionic interactions. To characterise and define what can be considered an ion-pair from a theoretical perspective, an exhaustive analysis of the interactions established within the different systems under study has been carried out. First, to investigate the physical origins of the interactions involved, an analysis of localised molecular orbital energy decomposition (LMO-EDA) was performed, which allows the determination of the contribution of the different energy components to the global stability of the systems (Fig. 4). This approach has been extensively used in the literature to describe non-covalent interactions, such as those reported in this paper.³¹ These contributions will provide insight into the nature and magnitude of interactions within the systems under study.

Fig. 4 (Top) LMO-EDA energy partition terms for the different salts under study. (Bottom) LMO-EDA energy partition terms for the [N(CF₃)₄]⁺ system.

From the analysis of the various contributions to the total energy, it is evident that the electrostatic term corresponding to a quasiclassical coulombic interaction between monomers constitutes the major component of the overall energy in these systems. This observation further reinforces the fundamental nature of the electrostatic interactions in governing the stability and behaviour of ionic compounds. A similar trend was observed across both types of systems, encompassing both ionic and N(CF₃)₄–X complexes. However, it is noteworthy that the total energy and the electrostatic term associated with the N(CF₃)₄–X systems are approximately half the corresponding values observed for the proper ionic compounds in the ion-pair configuration, emphasising that although both cases involve electrostatic interactions, the latter exhibits remarkably weaker interactions in comparison, being the distances between anion and cation increased accordingly. More importantly, the dispersion term becomes more negative in the case of N(CF₃)₄–X salts, being almost negligible in the case of ionic compounds, but the repulsion term is lower since the distance between the anion and the cation increases sensibly.

Next, an NBO analysis was performed, along with a comprehensive study of the charges, both isolated and upon complexation (Fig. 5). Since ionic bonds do not involve electron sharing, low values for E(2) were found.

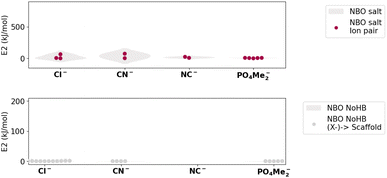Fig. 5 (Top) NBO E(2) values corresponding to the different ionic salts studied (Bottom) NBO E(2) values corresponding to the different [N(CF₃)₄]–X systems studied.

In the scenario of a polar ionic pair, all possible interactions between the lone pair of the anion and the lone vacancy LV (unoccupied borane-like valence orbital) of the cation and their contributed energy were considered (Fig. 5 (top)). We observed extremely low charge transfer processes for almost all of the studied N(CF₃)₄–X salts originating from the lone pair of the anion (LP(X⁻)) to the C–F anti-bonding sigma orbital (BD*(C–F)) of the scaffold (Fig. 5 (bottom)).

Upon analysing the charge of the monomer and its variation upon complexation (Fig. S1.1†), we found that the N atom's charge remains unchanged upon interaction with the anions, while C3 becomes slightly more negatively charged, in agreement with the charge transfer process described by the NBO analysis. Through analysis of the monomer, it becomes evident that the positive charge is not confined to the N atom but delocalised within the C atoms of the scaffold.

Finally, we turned our attention to investigating the electronic behaviour of the intermolecular interactions studied. In this regard, QTAIM has been widely shown to be an excellent tool for analysing various properties of the electron density and the nature of chemical bonding within a molecule, including bond strengths, and understanding the presence of charge transfer or electronic delocalisation within the molecule.³²

First, the electron density at the BCPs of the relevant bond was studied, as well as their corresponding Laplacian values (∇²ρ(r), Table 2). In the topological analysis, (∇²ρ(r)) plays a very important role in the characterisation of chemical bonding, providing the physical basis for the well-known electron-pair model of Lewis.^27,33 A positive ∇²ρ(r) indicates the dominance of excess kinetic energy, corresponding to local depletions, and is associated with non-covalent interactions (lower positive values) and ionic bonds (higher positive values).

Table 2 Electron density (ρ_BCP) and Laplacian (∇²ρ(r)) at the bond critical point for the ionic systems studied

Anion	Cation	ρ BCP (a.u.)	∇ ^2 ρ(r)
Cl^−	Na^+	0.0356	0.1899
NC^−	Na^+	0.0343	0.2424
CN^−	Na^+	0.0383	0.1764
PO4 Me2^−	Na^+	0.0264	0.1769
PO4 Me2^−	Na^+	0.0257	0.1718

---

The values obtained for the electron density and ∇²ρ(r) in Table 2 reinforce our previous analysis of the ionic nature of the salts studied and will be used as a reference for analysing the nature of the remaining systems.

The QTAIM analysis was performed for the N(CF₃)₄–X systems under study, and the corresponding values are provided in the ESI (Table S5.2†) for clarity. Of these, a representative example has been chosen to highlight the presence and values of BCPs, as shown in Fig. 6. When the density values are analysed at the various BCPs, it becomes apparent that the interactions within the ammonium salts are comparatively weaker. Furthermore, the Laplacian values indicate the presence of non-covalent interactions; however, they do not reach the magnitude observed in the ionic salts (∇²ρ(r) ranges between 0.1 and 0.2 a.u.).

Fig. 6 QTAIM molecular graph corresponding to N(CF₃)₄–Cl.

3.2 Imine- and iminium-based models

As noted above, a previous study conducted by our group considered an alternative interaction, a HB interaction, contrasting it with what was known or proposed in the literature as strict ion-pair.¹² However, the latter interaction was found to be energetically less favourable, as demonstrated by its lower energy interaction. As a result, for the current investigation, we focus solely on the interaction between the anions involved and the HB donor, if feasible.

To continue our investigation, we explored systems in which the tetra-bonded N atom within the scaffold corresponds to a strong hydrogen-bond donor and, therefore, facilitates the formation of a traditional hydrogen-bonding interaction. This encompassed the study of both neutral and positively charged catalyst-based systems, aiming to discern and characterize the variations between the neutral cases, and the interactions encountered in charged systems. Furthermore, various substituents, including CF₃, CH₃, and ^tBu, were considered to account for multiple electronic and steric scenarios (Fig. 7).

Fig. 7 Different imine- and iminimum-based derivatives under study.

The calculated interaction energies and anion–cation distances, for positively charged and neutral species, are summarised in Table 3. As expected, the interaction energies obtained are all negative, indicating favourable intermolecular interactions. Notably, when comparing the neutral species (imine derivatives) to their positively charged counterparts (iminium derivatives), a significant increase in interaction energies is observed. In terms of the different substituents studied, it is evident that CF₃ exhibits the most negative values, indicating the strongest interactions within the formed complexes. Conversely, ^tBu demonstrates the weakest interaction energies. In general, the intermolecular interactions studied are more favourable when Cl⁻ is involved as the counteranion.

Table 3 Iminium charged and imine complexes DFT interaction energies, ΔE in kJ mol⁻¹. Distances in Å. Distances between brackets () refer to the second shortest N–O distance in those systems where two O atoms of the PO₄Me₂ anion are interacting with the other monomer. Those systems marked with * were optimised with fixed X–H distance because a H transfer was produced otherwise

Complex	ΔE	d(N^+X^−)
Iminium_CF3–Cl	−535.3	2.68
Iminium_CF3–CN	−527.5	2.52
Iminium_CF3–NC	−527.3	2.41
Iminium_CF3–PO4Me2	−518.6	2.34
Iminium_CH3–Cl*	−456.3	2.86
Iminium_CH3–CN*	−445.5	2.69
Iminium_CH3–NC*	−449.0	2.57
Iminium_CH3–PO4Me2*	−456.9	2.55
Iminium_^tBu-Cl	−397.7	3.04
Iminium_^tBu-CN	−387.1	2.79
Iminium_^tBu-NC	−393.8	2.68
Iminium_^tBu-PO4Me2	−399.2	2.62
Imine_CF3–Cl	−97.4	3.07
Imine_CF3–CN	−90.0	2.90
Imine_CF3–NC	−91.9	2.77
Imine_CF3–PO4Me2	-84.7	2.74 (3.81)
Imine_CH3–Cl	−61.2	3.42
Imine_CH3–CN	−49.3	3.27
Imine_CH3–NC	−52.9	3.11
Imine_CH3–PO4Me2	−52.3	3.01 (4.41)
Imine_^tBu-Cl	−65.1	3.40
Imine_^tBu-CN	−50.7	3.26
Imine_^tBu-NC	−55.5	3.09
Imine_^tBu-PO4Me2	−56.5	3.06 (4.99)

---

Changing our focus to the distance between the N⁺ (or N for neutral compounds) and X⁻ ions, it is notable that the distances in all neutral complexes surpass those observed in their charged counterparts. Additionally, by comparing the distances of the cation–anion in the iminium complexes with the previously studied [N(CF₃)₄]–Xm systems, we find that all distances are consistently shorter than the latter.

An analysis of the different anions reveals that systems containing Cl⁻ exhibit the longest intermolecular distances for both neutral and cationic complexes. Considering the influence of the various substituents within the main scaffold, the distances follow the trend of ^tBu > CH₃ > CF₃. Remarkably, the presence of a bulky electron-donating substituent, such as ^tBu, leads to the highest distance between the ions. On the contrary, when the CF₃ substituent is involved, the shortest distance is observed, as a consequence of its electron-withdrawing nature, which strengthens the existing HB.

3.2.1 Characterisation of the non-covalent interactions. Building upon the preceding section, this section focusses on the characterisation of interactions using LMO-EDA, NBO, and QTAIM analyses. Regarding the results obtained from the LMO-EDA analysis, it is evident that in the charged system scenario, the electrostatic term makes the most significant contribution to the total energy (Fig. 8), which aligns with the expected dominance of coulombic interactions in charged systems. However, even though the distances are not much larger, in most of the systems studied, the electrostatic term is lower compared to that found for ionic salts, similar to that found within the quaternary ammonium salts, N(CF₃)₄–X. However, it becomes apparent that iminium/imine systems, attractive terms, polarisation, exchange and dispersion have increased significantly as a result of the establishment of HBs upon complexation (almost −200 kcal mol⁻¹). It is noteworthy that in the preceding section, these terms were found to be extremely low in N(CF₃)₄–X complexes and almost negligible in the ion-pair systems examined.

Fig. 8 LMO-EDA energy partition terms for the different iminium-based complexes under study.

Additionally, it should be highlighted that the electron–electron repulsion term has also increased notably, surpassing its contribution in the previous case. On the contrary, in the case of the neutral counterpart, the repulsion term emerges as the primary contributor to the total energy (Fig. S2.3 and S2.4†). This significant Pauli repulsion effect leads to an increased distance between the interacting species, resulting in a weaker interaction.

The NBO analysis, as depicted in Fig. 9, S3.3 and S3.4,† reveals that the highest values correspond to the presence of charge transfer interactions specifically associated with hydrogen bond formation for both cases, for charged and neutral systems, respectively. These interactions involve the donation of electron density from the lone pair (LP(X⁻)) of the anion to any sigma antibonding orbital involving the theoretically positively charged nitrogen atom (BD*(N)). The obtained values of E(2), which represent the stabilisation energy due to charge transfer between the aforementioned orbitals, follow a trend similar to that of the interaction energy with respect to different substituents, i.e. CF₃ > CH₃ > ^tBu. Furthermore, considering the charged systems, we find that the E(2) values are higher than their neutral counterparts because of the positive charge distribution within the molecule. Nevertheless, the nature of the charge transfer interaction remains unchanged.

Fig. 9 NBO E(2) values corresponding to the different iminium-based complexes under study.

The obtained results from the QTAIM analysis provide compelling support for the findings obtained from the previous analyses (Fig. S4.3 and S4.4 and Tables S5.3 and S5.4†). Examination of the electron density at various BCPs within the studied complexes reaffirms the nature of the non-covalent interactions established upon complexation. In addition, the positive ∇²ρ(r) values derived from the QTAIM analysis further validate the non-covalent nature of the interactions observed in all the cases under study. Interestingly, the values obtained for ∇²ρ(r) are consistently similar for both neutral and charged compounds; however, these values are consistently an order of magnitude lower than those observed in polar ionic compounds (Fig. 10). This observation suggests that the presence of HBs is influenced by the surrounding charges, and consequently the systems present a clear HB-assisted ion-pair rather than a strict-ion-pair interaction.

Fig. 10 QTAIM molecular graphs for imine_CH₃–CN (left) and iminium_CH₃–CN (right).

It has been established that the charge carried within the PTCs’ structure is vital, and therefore it becomes crucial to conduct an in-depth investigation of the charges associated with the monomer in its isolated state and upon complexation. Firstly, a comparative analysis of the charges between the charged monomers (Fig. 11) and their neutral counterparts (Table S6.4†) was conducted. In the isolated monomers, the C1 atom, which is directly attached to nitrogen, was revealed to exhibit a significant increase in positive charge in all the cases studied, from neutral to charged monomers. In contrast, the nitrogen remains relatively unchanged in the CF₃ case and slightly more negative in the presence of CH₃ and ^tBu substituents, in agreement with the electrodonating nature of those substituents. Upon complexation with the anion, visible modification is observed in the C1 atom's charge for most cases, indicating a charge transfer from the anion to C1. Consequently, the C1 atom becomes less positively charged in all cases, with a more pronounced effect observed in the scenario involving the CF₃ substituents. A similar behaviour is observed for the neutral case (Fig. S1.3†), in which C1 presents the highest charge difference between the monomer and the complex. The aforementioned variation in the charge distribution within the C1 atom can also be seen in the NBO calculations. Specifically, the charge transfer from the lone pair (LP(X⁻)) of the anion to the antibonding orbital of the N–C bond (BD*(NC)) highlights this distinction (Table S4†). Nevertheless, it is important to emphasise that the magnitude of this charge transfer is significantly low when compared to the corresponding value associated with the HB, (Fig. 9, light grey, Table S4†). Specifically, the highest value obtained for E(2) BD*(N–C) is 27.0 kJ mol⁻¹, while E(2) involving BD(N–H) ranges from 292.1 to 768.1 kJ mol⁻¹.

Fig. 11 NBO charges of the monomers and different iminium-based complexes under study. Legend: charge difference between the complexes and the monomers is depicted.

Finally, it is important to note that the positive charge in these systems is not localised in a single atom but is shared among multiple atoms. This shared positive charge results in an increased positive character (+0.1 e higher) of the hydrogen atom (NH) when the NH transitions from neutral to cationic structure. Consequently, the establishment of hydrogen bonds with the different anions studied is arguably strengthened and favoured because of the increased positive charge exhibited by the hydrogen (H) atom involved.

The outcome regarding the nature of the different interactions upon complexation studied within the iminium-based complexes is far from surprising since it has been previously theoretically described in the literature as “charge-assisted hydrogen bonds”.^34,35

3.2.2 Solvent effects. The present investigation was primarily conducted in the gas phase to focus on the characterisation of the nature of the diverse interactions inherent within ionic compounds. Nonetheless, for the purpose of achieving a comprehensive evaluation, a supplementary investigation involving solvents was undertaken, as illustrated in Table 4. As anticipated, the calculated interaction energies exhibited a substantial reduction across all the solvents examined, with particularly pronounced effects observed in the case of dimethyl sulfoxide (DMSO) and water, across all complexes studied. When the changes in intermolecular distances between both charged atoms, Na⁺ and X⁻ atoms, caused by solvation were examined, it was observed that the separation between cations and anions augmented uniformly in all cases, aligning with theoretical expectations. Furthermore, as the distance increased, the interaction energy presented upon complexation weakened.

Table 4 DFT interaction energies in three different solvents and gas phase, for ionic salts and iminium charged complexes, ΔE in kJ mol⁻¹. Distances in Å

Cation	Anion	Solvent	ΔE	d(Na^+X^−)
Na	Cl	H2O	−61.4	2.52
Na	Cl	DMSO	−64.9	2.52
Na	Cl	Toluene	−250.6	2.44
Na	Cl	Gas	−546.4	2.39
Iminium_CF3	Cl	H2O	−69.6	2.87
		DMSO	−72.2	2.86
		Toluene	−268.0	2.75
		Gas	−535.3	2.68
Iminium_CH3	Cl	H2O	−40.2	3.08
		DMSO	−42.3	3.08
		Toluene	−209.3	2.94
		Gas	−456.3	2.86
Iminium_^tBu	Cl	H2O	−19.5	3.72
		DMSO	−19.1	3.69
		Toluene	−167.7	3.22
		Gas	−397.7	3.04

---

A partition energy analysis was conducted for the complexes studied under solvation conditions (Fig. S5†). The EDA-NCI calculation reveals that both repulsion energy and polarisation are the most affected terms, while the corresponding electrostatic term experiences only a slight decrease. This decrease in electrostatics arises from the longer distance between the ions, as evident from the EDA-NCI calculated for the gas-phase optimised geometry in solvent (left side of Fig. S5†).

More importantly, when implicit solvent molecules are included, the repulsion term decreases; however, the polarisation term becomes positive and repulsive, particularly in the cases of DMSO and water. This alignment with the obtained low interaction energy is notable. Consequently, the sharp decrease in interaction energy can primarily be attributed to the repulsive polarisation force.³⁶

3.3 Guanidine- and guanidinium-based models

Guanidinium-based scaffolds have long been recognised for their ability to function as general-acid catalysts, and therefore we decided to conduct an extensive computational investigation to gain a deeper understanding of the interactions that occur upon complexation. To ensure clarity and avoid clutter, we present the key findings from our analysis of both neutral (guanide-based) and charged (guanidinium-based, Fig. 12) complexes in the ESI (Fig. S1–S4 and Tables S2–S6†), utilising the same methodologies as before, i.e. LMO-EDA, QTAIM and NBO.

Fig. 12 Guanidine- and guanidinium-based systems under study.

The calculated interaction energies for both the neutral and charged complexes were found to be negative, as anticipated. Furthermore, the interaction energies for the neutral complexes were consistently lower than those for the charged complexes. In particular, an unexpected case that warrants attention concerns the guanidininium ^tBu complexes, which exhibited interaction energies that were one order of magnitude lower than the rest of the charged complexes under investigation. When the monomer and the complexes were carefully examined, it became evident that accommodating the anion within such a bulky species requires substantial deformation energy. However, looking at the LMOEDA total energies the results are consistent among the three substituents and present the expected stability trend. The distance between positively charged N⁺ and negatively charged X⁻ ranged from 2.65 to 3.43 Å, higher than in the cases previously analysed.

Furthermore, our analysis of the interactions established upon complexation revealed HBs, which are notably stronger in the charged species. Most cases exhibited Laplacian values consistent with a non-covalent interaction nature. However, some particular cases (five among all the different complexes under study) showed a larger positive Laplacian value at the BCP corresponding to the X⁻⋯HN hydrogen bond, as indicated in Table S5.5.† In these particular cases, the H atom was in close proximity to the anion, resulting in a highly positive charge and the emergence of a slight ionic character between the H and the involved anion. By analysing the NBO calculations performed in all systems, it can be corroborated that the established HBs correspond to the main charge transfers process (LP(X⁻)) to the antibonding orbital of the N–H bond (BD*(NH)) and the weak ones can be found from the LP of the anion to the N of the scaffolds (LP(X⁻) → BD*(N–C)) (Tables S4.5 and S4.6 and Fig. S3.5 and S3.6†).

Finally, the distribution of the different charges was analysed. As we transitioned from neutral monomers to charged complexes, for the CF₃ case, the C-centred atom becomes more positive due to the electron-withdrawing nature of the substituents. Conversely, in the CH₃ and ^tBu cases, the positive charge was delocalised among the carbon and nitrogen atoms within the scaffold. Remarkably, in all cases, the hydrogen atom of the NH moiety experiences an increase in positive charge, which facilitates and reinforces the HB interaction. Upon complexation, a charge distribution analysis revealed that for neutral compounds, the only significant change was observed in the carbon atom for CF₃ systems, which becomes less positive. However, for the charged counterparts, a more heterogeneous picture emerges, with the carbon (C) and N1 atoms being the most affected. In the case of CF₃ and CH₃ systems, the central carbon atom generally becomes slightly more positive, while N1 becomes more negative. Conversely, for the ^tBu substituent systems, both the carbon (C) and nitrogen (N1) atoms present an increase in negative charge and therefore become less positive. The variations in charge exhibited by the diverse atoms during complexation align remarkably well with the NBO model, as depicted in Fig. S1.4 and S1.5.† Our findings indicate a discernible but not substantial charge transfer from the examined anions to the N1 and C atoms (LP(X⁻) → BD*(NC)). It is important to note that the magnitude of this charge transfer is consistently lower compared to the corresponding transfer observed in the HB interaction (LP(X⁻) → BD*(NC)).

3.4 Ammonia- and ammonium-based models

In the subsequent phase of our study, we examined more realistic systems in which the theoretical establishment of HBs is hindered due to the presence of four substituents bonded to the nitrogen atom and the absence of any strong HB-donor (Fig. 13). These quaternary ammonium salts and their neutral counterparts serve as representative examples for exploring alternative modes of interaction in the absence of direct strong hydrogen bonding.

Fig. 13 Ammonia- and ammonium-based models under study.

The interaction energy values for both the cationic and neutral scenarios are compiled in Tables S7 and S8.† Consistent with expected behaviour, charged species exhibit significantly higher values ΔE compared to their neutral counterparts, highlighting that the introduction of positive charges enhances the strength of interactions within these systems. Furthermore, charged systems consistently exhibit interaction energies lower than those of ionic compounds, and the separation distance between the positively charged ion N⁺ and the negatively charged ion X⁻ varied between 3.35 and 4.50 Å, exhibiting the greatest distances observed among the various complexes investigated in this study.

3.4.1 Characterisation of the non-covalent interactions. When an LMO-EDA analysis is performed, in Fig. 14 and Fig. S2.7 and S2.8,† the predominance of the electrostatic term for charged complexes is clear. A comparison of these values with those obtained in the previous section (iminium complexes) reveals a lower interaction energy than that observed for the strict ion-pair systems discussed in the first section. However, compared to the N(CF₃)₄–X systems, the values are found to be higher.

Fig. 14 LMO-EDA energy partition terms for the different ammonium-based complexes under study.

Furthermore, we find that the terms associated with polarisation, exchange, and dispersion, although lower than those observed for the iminium/imine systems, are higher than those observed for the ionic systems, indicating their non-negligible contribution. Additionally, the repulsion term is lower than that of the iminium-charged systems but higher than the N(CF₃)₄–X systems. Thus, it appears that the ammonium salts studied herein exhibit a behaviour that lies between the HB-assisted ion pairs and the longer-range ion pairs.

The NBO analysis reported the presence of two primary types of charge transfers in the system under investigation. The first type is commonly associated with hydrogen bonding and involves the donation from the lone pair (LP(X⁻)) of the anion to the antibonding orbital of the H–C bond (BD*(CH)). The second type involves the donation from the anion to the centrally positioned nitrogen atom within the tetrahedral structure, which is assumed to carry a positive charge in ammonium-based models. The NBO results clearly indicate the establishment of weak to moderate hydrogen bond interactions upon complexation, as well as a weak charge transfer from the LP of the anion to the orbital involving the central nitrogen atom (LP(X⁻) → BD*(NC)) (Fig. 15 and S3.8†).

Fig. 15 NBO E(2) values corresponding to the different ammonia_based complexes under study.

The QTAIM analysis presented in Table S2† provides additional support for the aforementioned findings. Overall, the charged complex exhibits higher density and Laplacian values compared to the neutral ones, albeit falling within the expected range for such interactions. Fig. 16 represents the molecular graphs specifically associated with ammonia_based_CH₃–Cl and ammonium-based_CH₃–Cl. These graphs visually depict the distinct hydrogen bond interactions formed between the Cl⁻ ion and the hydrogen atoms of the CH₃ groups. The figures illustrate the electron density at various BCPs and also display the corresponding Laplacian values. The densities identified at the BCPs are comparatively lower than those observed within the iminium complexes because of the weaker HB donor. Additionally, the Laplacian values exhibit a similar range, yet consistently remain one order of magnitude lower when compared to the tight ion-pair formations detected in the salts.

Fig. 16 QTAIM molecular graph for ammonia_based_CH₃–Cl and ammonium_CH₃–Cl.

To finish this section, the charge difference within the monomers and upon complexation for both, neutral and charged complexes will be discussed (Fig. 17 and S1.6 and S1.7†).

Fig. 17 NBO E(2) charges to the different ammonium-based complexes under study.

The charge distribution of the monomers varies as they transition from neutral to charged states. Both the N and H atoms in the methyl group exhibit an increase in positive charge. Upon complexation, a similar trend is observed for both neutral and charged compounds. However, this trend is more pronounced in complexes based on ammonium. The charge on the central N atom remains constant, whereas the charge on the C1 atom experiences a significant decrease, becoming more negative in all cases, due to the interaction with the anion. In the case of the R=CH₃ substituent, C1, C2, and C3 are interacting with the anion and so their charges become slightly more negative.

The findings of our study are in perfect alignment with the literature. Specifically, in a seminal work published in 2002, Cannizzaro and Houk conducted a comprehensive evaluation of the interactions present in the Me₃NH–CH₂COOMe complex.³⁷ This complex, which served as an ion-pair model, was examined using the MP2 level of theory. The study identified the presence of an ion-pair arrangement stabilised by HBs (Fig. 18) but also placed the positive charge shared among the different C atoms. The work by Cannizzaro and Houk provided significant insights into the nature and stability of ion-pair complexes involving HB interactions, but it falls short of describing the nature of the interactions of the broad range of possible ion-pair interactions. As discussed, our current investigation builds upon the work of the authors by focusing on expanding the scope and applicability of the concept of ion-pair interactions in a broader context of phase-transfer catalysis.

Fig. 18 Non-covalent interactions established within the model Me₃NH–CH₂COOMe studied by Houk et al.³⁷

3.5 Phase transfer catalysts

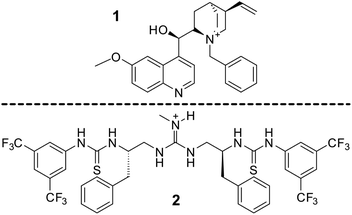
As a final investigation, two real phase transfer catalysts have been studied, 1 and 2, Fig. 19.

Fig. 19 PTCs under study, 1 and 2.

In this investigation, our focus was directed solely towards analysing the possible ion-pair interactions established in both systems. The primary objective of this scrutiny was to ensure an equitable comparison with the previously elucidated models.

The interaction energies obtained for both 1 and 2 are smaller than the models used in the previous sections based on ammonium and guanidinium (Table 5). Furthermore, the distances between the anion and the theoretically positively charged atom, N⁺, are smaller than those observed in the corresponding similar models examined earlier, both models based on ammonium and guanidinium. These distances range between 3.39 and 3.60 Å for 1 and, 2.54 and 2.97 Å for 2, respectively.

Table 5 Cinchona-based catalyst (1) and guanidinium-based catalyst (2) DFT Interaction energies, ΔE in kJ mol⁻¹. Distances in Å

Complex	ΔE	N^+X^−
1-Cl	−304.2	3.55
1-CN	−308.9	3.60
1-NC	−312.7	3.39
1-PO4Me2	−225.5	3.47 (3.90)
2-Cl	−326.2	2.97
2-CN	−347.7	2.69
2-NC	−331.0	2.64
2-PO4Me2	−188.4	2.54

---

We performed the same analysis of the interactions upon complexation, i.e. LMO-EDA, NBO, and QTAIM (Fig. S2.9–S2.10, S3.9–S3.10 and Tables S3.9–S3.10, S4.9–S4.10, S5.9–S5.10, S6.9–S6.10†).

All LMO-EDA values related to the nature of the interaction are found to be close to those found for the models studied previously, models based on guanidinium and ammonium, presenting a behaviour between the HB-assisted ion pairs and the longer-range ionpair, as expected (Fig. S2.9 and S2.10†).

In both cases, complexation leads to the formation of a web of weak hydrogen bonds, which is closely aligned with the observed NBO interactions. For catalyst 1, a network of hydrogen bonds forms between the anion and the C–H groups of the quinuclidine ring. The E(2) values in this arrangement are quite comparable to the range observed in the ammonium-based (R=CH₃) system, approximately 10 kJ mol⁻¹. On the other hand, 2 exhibits two distinct HB-donors, resulting in two types of hydrogen bonds, much like the small guanidinium-based model. The E(2) values for this system are approximately −50 kJ mol⁻¹ for NH as an HB donor, while those that involve the CH group are weaker, around −10 kJ mol⁻¹.

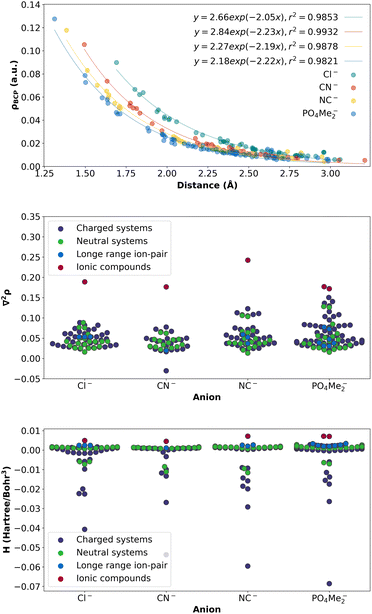
Finally, to obtain a complete picture of the density values at the BCPs involving the anion interaction for all the complexes studied, a graph was generated by plotting the density at the BCPs against the distance between the atoms involved in the interaction. For this particular correlation, all complexes were taken into account, including previous sections and current (Fig. 20 (top)). Only the BCPs corresponding to the same pair of atoms involved were depicted for comparison. The results clearly demonstrate a nearly perfect exponential correlation, indicating a consistent pattern of non-covalent interactions across all complexes. Regarding the different anions under study, PO₄Me₂-X systems present the highest density values, corresponding, therefore, to the strongest HB interaction. The strength of the interaction decays with distance.

Fig. 20 (Top) QTAIM exponential correlation of the different models under study. Bigger dots correspond to the salts and N(CF₃)₄–X systems. (Middle) Laplacian values for all the different compounds under study. (Bottom) Energy density values for all the different compounds under study.

More interestingly, the Laplacian values in all systems were investigated (refer to Fig. 20 (middle)). Notably, the values obtained for all the systems analysed were found to be lower compared to those corresponding to the ionic complexes.

Finally, and in order to obtain a complete picture of the nature of the interactions upon complexation, the value for the energy density³⁸ was analysed for all the complexes under study (Fig. 20 (bottom)). It is clear that the outcome is in excellent agreement with the Laplacian values, showing an H positive value for the polar compounds, while it is becoming slightly negative for the hydrogen bonds, and a few more negative values corresponding to a very strong HB slightly covalent nature for the cases in which the phosphate is involved.

The general results from these analyses are in perfect agreement with the findings obtained from both previously studied models, guanidinium-based and ammonium-based. They demonstrate an intermediate behaviour between HB-assisted ion-pair and longer-range ion-pair interactions, underscoring the consistency and validity of the conclusions drawn from this analysis.

4 Conclusions

In this work, we have conducted a comprehensive investigation of ion-pair interactions in the context of phase-transfer catalysis. Our study firstly focused on the examination of polar ionic compounds to define the concept of an ion-pair in phase-transfer catalysis. This was then followed by the analysis of a diverse range of ion-pair catalyst models to gain insight into the factors governing their interactions. Finally, we focused on the characterisation of real PTCs, providing crucial insights into the behaviour of these systems in real applications.

Our examination of these systems aimed to unravel the intricate interplay between hydrogen bonding and ion-pair interactions, discerning the subtle differences that influence the nature and strength of hydrogen bonding and its role in facilitating ion-pair formation.

In particular, our thorough investigation of a wide range of PTC-based systems has revealed distinct interaction characteristics: a strict ion-pair nature exhibited by salts, longer ion-pair interactions, HB-assisted ion pairs, and finally, charged-assisted HBs (Fig. 21). We have demonstrated that the presence of HB donors, either weak or strong, facilitates the formation of ion pairs through one or an intricate network of HBs and also provides directionality and structural stability to an interaction that, by definition, lacks such features. On the other hand, in the absence of these donors, longer-range ion pairs spanning approximately 4 Å are established, whose electronic nature and distance-dependent behaviour we have characterised and discussed in depth.

Fig. 21 Different types of intermolecular non-covalent interactions under study in the work, within the phase transfer catalysis field.

In conclusion, our thorough investigation, employing state-of-the-art charge density-based theoretical methods, has revealed that the true interactions governing ion-pair systems undoubtedly depend on the existence of moieties capable of forming HBs. In the presence of such structural motifs, the structural stability and catalytic selectivity in PTCs are governed by one or several of these highly directional and charge-independent NCIs. In their absence, we have demonstrated the formation of classical ion-pairing interactions.

Therefore, a preliminary discussion of the baseline structure and potential intermolecular interactions of PTCs under study is imperative to unravel the nature of these systems. Understanding the true interactions within PTCs and how they extend beyond the classic interpretation of ion-pairs is key to rationalising experimental observations and unlocking the full potential that these systems hold.

To assist synthetic chemists in understanding ion-pair interactions, we suggest examining not only the system structure, where the presence of different interactions, such as HBs is evident, but also considering the relative importance between coulombic interaction and other energy contributions. This involves naming the interaction under study based on their relative importance, as indicated by the scale proposed in Fig. 21. This straightforward guideline provides a practical means to discern whether newly designed synthetic systems predominantly involve coulombic interactions or if other NCIs play a significant role.

Finally, we encourage computational calculations to unequivocally determine the nature of these interactions. This computational approach improves the precision in identifying and understanding the interaction between coulombic forces and other contributing factors in ion-pair systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication has emanated from research supported by the Science Foundation Ireland (SFI 18/SIRG/5517). For the purpose of Open Access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. The authors acknowledge the assistance provided by Research IT and the use of the Computational Shared Facility at The University of Manchester. The authors thank the Irish Centre for High-End Computing (ICHEC) for their continued computational support. We are deeply grateful for Professor Alkorta's willingness to share his expertise and make NBO.7 accessible to us. And finally, we thank Dr Goar Sánchez and Maxime Ferrer for their invaluable input, insights, and expertise, which were instrumental in shaping this project.

References

1. K. Brak and E. N. Jacobsen, Angew. Chem., Int. Ed., 2013, 52, 534–561.
2. C. C. Sorensen, C. T. Kozuszek, M. A. Borden and F. A. Leibfarth, ACS Catal., 2023, 13, 3272–3284.
3. M. Mahlau and B. List, Angew. Chem., Int. Ed., 2013, 52, 518–533.
4. D. Qian and J. Sun, Chem. – Eur. J., 2019, 25, 3740–3751.
5. J. E. Gillespie, A. Fanourakis and R. J. Phipps, J. Am. Chem. Soc., 2022, 144, 18195–18211.
6. T. E. Schirmer and B. König, J. Am. Chem. Soc., 2022, 144, 19207–19218.
7. L. Zong and C.-H. Tan, Acc. Chem. Res., 2017, 50, 842–856.
8. D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2017, 117, 10608–10620.
9. R. J. Phipps, G. L. Hamilton and F. D. Toste, Nat. Chem., 2012, 4, 603–614.
10. J.-F. Brière, S. Oudeyer, V. Dalla and V. Levacher, Chem. Soc. Rev., 2012, 41, 1696–1707.
11. A. M. Piatek, M. Gray and E. V. Anslyn, J. Am. Chem. Soc., 2004, 126, 9878–9879.
12. I. Iribarren and C. Trujillo, Phys. Chem. Chem. Phys., 2020, 22, 21015–21021.
13. N. K. Bjerrum, Dan. Vidensk. Selsk., Mat.-Fys. Medd., 1926, 9, 7; Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621.
14. D. A. Dougherty and E. V. Anslyn, Modern Physical Organic Chemistry, University Science Books, CA, Sausalito, 2006.
15. K. Dong, S. Zhang and J. Wang, Chem. Commun., 2016, 52, 6744–6764.
16. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
17. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
18. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian ∼ 16 Revision C.01, Gaussian Inc., Wallingford, CT, 2016.
20. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
21. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr., J. Comput. Chem., 1993, 14, 1347–1363.
22. M. Mandado and J. M. Hermida-Ramon, J. Chem. Theory Comput., 2011, 7, 633–641.
23. N. Ramos-Berdullas, I. Pérez-Juste, C. Van Alsenoy and M. Mandado, Phys. Chem. Chem. Phys., 2015, 17, 575–587.
24. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
25. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241.
26. F. Weinhold, Discovering chemistry with natural bond orbitals, John Wiley & Sons, 2012.
27. X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304–314.
28. P. S. V. Kumar, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527–1536.
29. L. Zhao, S. Pan and G. Frenking, J. Chem. Phys., 2022, 157, 034105.
30. P. D. McCaffrey, R. J. Mawhorter, A. R. Turner, P. T. Brain and D. W. H. Rankin, J. Phys. Chem. A, 2007, 111, 6103–6114.
31. P. Su, Z. Tang and W. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1460.
32. P. L. A. Popelier, in The QTAIM Perspective of Chemical Bonding, John Wiley & Sons, Ltd, 2014, ch. 8, pp. 271–308.
33. R. F. W. Bader, S. Johnson, T.-H. Tang and P. L. A. Popelier, J. Phys. Chem., 1996, 100, 15398–15415.
34. C. Heering, B. Nateghi and C. Janiak, Crystals, 2016, 6(3), 22.
35. J. Ni and J. J. Pignatello, Environ. Sci.: Processes Impacts, 2018, 20, 1225–1233.
36. D. Hait and M. Head-Gordon, Angew. Chem., Int. Ed., 2023, 62, e202312078.
37. C. E. Cannizzaro and K. N. Houk, J. Am. Chem. Soc., 2002, 124, 7163–7169.
38. D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628.

---

Footnotes

† Supplementary information (ESI) is available from https://zenodo.org/records/10001071

‡ Present address: Department de Química, Universitat Autònoma de Barcelona, 08193, Bellaterra, Catalonia, Spain.

§ Present address: Department of Chemistry, The University of Manchester, Oxford Road, M13 9PL Manchester, UK. E-mail: cristina.trujillodelvalle@manchester.ac.uk.

---