Single-molecule magnet behavior in heterometallic decanuclear [Ln₂Fe₈] (Ln = Y, Dy, Ho, Tb, Gd) coordination clusters

Abstract

Five decanuclear lanthanide–iron clusters, formulated as [Ln₂Fe₈(hmp)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]·6ClO₄·xH₂O (x ≈ 8, Ln = Y for 1; x ≈ 6, Ln = Dy for 2; x ≈ 6, Ln = Ho for 3; x ≈ 7, Ln = Tb for 4; x ≈ 7, Ln = Gd for 5, Hhmp = 2-(hydroxymethyl)pyridine), have been synthesized and structurally characterized. Single-crystal structural analysis reveals that the cluster consists of six face-sharing defective cubane units. Dynamic magnetic investigations indicated that cluster 2 exhibits single-molecule magnet behavior under a zero dc field eliciting an effective energy barrier of U_eff = 17.76 K and a pre-exponential factor of τ₀ = 7.93 × 10⁻⁸ s. Investigation of the performance of a series of Fe^III–Dy^III SMMs indicates that the relatively low energy barrier in 2 is associated with the weak ferromagnetic coupling between Fe^III and Dy^III ions, while the strength of ferromagnetic interaction in these clusters is mainly related to the bond distances between Dy^III and O atoms coordinated to Fe^III ions. Clusters 3 and 4 exhibit similar dual relaxation pathways under their respective optimal external applied dc field, where the direct relaxation process occurs in the low-frequency area, which impedes the extraction of the U_eff, while the secondary relaxation process appears at a higher frequency, which is probably a connection with intermolecularly driven relaxation. Our findings offer a magneto-structural correlation model for further investigating the single-molecule magnet behavior in lanthanide–iron systems.

---

Introduction

A single-molecule magnet (SMM) is a nanomagnet of molecular size, characterized by potential energy barriers (U_eff) that facilitate the reversal of magnetic moments. It is distinguished by its slow magnetization relaxation, which stems from the high-spin ground state (S) and significant magnetic anisotropy (D) of an individual molecule.¹ Since the discovery of the first Mn₁₂-SMM, which exhibits slow paramagnetic relaxation within two bistable magnetic states by rendering the U_eff for the reversal of magnetization,² SMMs have attracted considerable attention due to their potential applications in quantum computing,³ high-density data storage⁴ and molecular spintronics.⁵ To reveal the factors that affect the performance of SMMs, it was found that large magnetic anisotropy and large ground-state spin are of key importance in enhancing the performance of SMMs.⁶ The dysprosium (Dy^III) ion, having a Kramers’ spin ground state doublet of ⁶H_15/2, is expected to generate large magnetic anisotropy and is regarded as a promising candidate for obtaining SMMs with high U_eff values.⁷ The Fe^III ion, on the other hand, has the largest single-site spin and is expected to attain large ground-state spin in 3d metals, in addition to contributing to the enhancement of magnetic exchange–coupling interactions.⁸ Therefore, the combination of Dy^III ions and Fe^III ions is expected to improve the performance of SMMs. However, although the first binuclear Fe^III–Dy^III SMM was reported in 2006,⁹ the highest U_eff value reported so far in any Fe^III–Dy^III cluster is only 65.1 K in the nonanuclear {Fe^III₆Dy^III₃} cluster.¹⁰ One of the reasons might be attributed to the stray magnetic fields generated by the Fe^III spin center, which significantly increases the possibility of relaxation through the quantum tunneling mechanism. In addition, the weak or very weak magnetic coupling between Fe^III and Dy^III ions leads to low-energy relaxation pathways between the low-lying split sublevels, resulting in a low U_eff value.¹¹ Here we report the syntheses, structures, and magnetic properties of five decanuclear 3d–4f clusters, formulated as [Ln₂Fe₈(hmp)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]·6(ClO₄)·x(H₂O) (x ≈ 8, Ln = Y for 1; x ≈ 6, Ln = Dy for 2; x ≈ 6, Ln = Ho for 3; x ≈ 7, Ln = Tb for 4; x ≈ 7, Ln = Gd for 5; Hhmp = 2-(hydroxymethyl)pyridine).

Experimental

Materials and methods

The raw materials and reagents were all commercially purchased and used directly without further purification. Elemental analyses were carried out using a Flash Smart elemental analyzer. Powder X-ray diffraction (XRD) data were collected using a Rigaku Ultima IV powder X-ray diffractometer (Cu Kα, λ = 1.54184 Å). Thermogravimetric analysis (TGA) curves were obtained using an STA-449F5 thermal analyzer. The measurement of magnetic susceptibilities was conducted using a Quantum Design MPMS-XL5 superconducting quantum interference device (SQUID) and a physical property measurement system (PPMS-9T).

Preparation of [Y₂Fe₈(C₆H₆NO)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]·6(ClO₄)·8H₂O (1)

2-Hydromethyl pyridine (1 mmol, 109.1 mg) and Fe(ClO₄)₃ (1 mmol, 372.2 mg) were mixed with a 1 mmol aqueous solution of Y(ClO₄)₃ (1.0 M) in methanol (8 mL) and 300 μL Et₃N was added. The resulting solution was then heated and stirred at approximately 80 °C for 2 hours, and then the filtrate was volatilized in the air for about 1 day to obtain yellow block crystals. Yield: ca. 40% (based on Y³⁺). Anal. calcd (%) for C₆₀H₉₄N₁₀Cl₆Fe₈Y₂O₅₈ (FW = 2720.7, based on 6 ClO₄⁻ and 8 guest water molecules): C, 26.49; N, 5.15; H, 3.48. Found (%): C, 26.72; N, 5.27; H, 3.39.

Preparation of [Dy₂Fe₈(C₆H₆NO)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]·6(ClO₄)·6H₂O (2)

The synthesis scheme of 2 was similar to that of 1, only replacing Y(ClO₄)₃ with Dy(ClO₄)₃. Yield: ca. 40% (based on Dy³⁺). Anal. calcd (%) for C₆₀H₉₀N₁₀Cl₆Fe₈Dy₂O₅₆ (FW = 2831.9, based on 6 ClO₄⁻ and 6 guest water molecules): C, 25.45; N, 4.95; H, 3.20. Found (%): C, 25.72; N, 5.08; H, 3.16.

Preparation of [Ho₂Fe₈(C₆H₆NO)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]·6(ClO₄)·6H₂O (3)

The synthesis scheme of 3 was similar to that of 1, only replacing Y(ClO₄)₃ with Ho(ClO₄)₃. Yield: ca. 40% (based on Ho³⁺). Anal. calcd (%) for C₆₀H₉₀N₁₀Cl₆Fe₈Ho₂O₅₆ (FW = 2836.7, based on 6 ClO₄⁻ and 6 guest water molecules): C, 25.40; N, 4.94; H, 3.20. Found (%): C, 25.77; N, 4.84; H, 3.19.

Preparation of [Tb₂Fe₈(C₆H₆NO)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]·6(ClO₄)·7H₂O (4)

The synthesis scheme of 4 was similar to that of 1, only replacing Y(ClO₄)₃ with Tb(ClO₄)₃. Yield: ca. 40% (based on Tb³⁺). Anal. calcd (%) for C₆₀H₉₂N₁₀Cl₆Fe₈Tb₂O₅₇ (FW = 2842.7, based on 6 ClO₄⁻ and 7 guest water molecules): C, 25.35; N, 4.93; H, 3.26. Found (%): C, 25.83; N, 4.81; H, 3.16.

Preparation of [Gd₂Fe₈(C₆H₆NO)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]·6(ClO₄)·7H₂O (5)

The synthesis scheme of 5 was similar to that of 1, only replacing Y(ClO₄)₃ with Gd(ClO₄)₃. Yield: ca. 40% (based on Gd³⁺). Anal. calcd (%) for C₆₀H₉₂N₁₀Cl₆Fe₈Gd₂O₅₇ (FW = 2839.4, based on 6 ClO₄⁻ and 7 guest water molecules): C, 25.38; N, 4.93; H, 3.27. Found (%): C, 25.42; N, 4.86; H, 3.15.

X-ray crystallography

The X-ray diffraction data of clusters 1–4 were collected using a Rigaku Oxford Diffraction single-crystal X-ray diffractometer with Cu K_α radiation (λ = 1.54184 Å) at 100 K. Data for cluster 5 was collected using an Agilent SuperNova four-circle X-ray single-crystal diffractometer using Cu K_α radiation (λ = 1.54184 Å) at 100 K. The structures were solved and refined with full-matrix least-squares based on F² using ShelXT and ShelXL programs on Olex2.^12,13 Due to the high disorder of the guest H₂O molecules, they were removed using SQUEEZE during structural refinement.¹⁴ Crystallographic data and structural refinements for 1–5 are summarized in Table S1.† CCDC 2195974 and 2195975 for 1 and 2, and 2314827–2314829 for 3–5, respectively.†

Results and discussion

Crystal structures

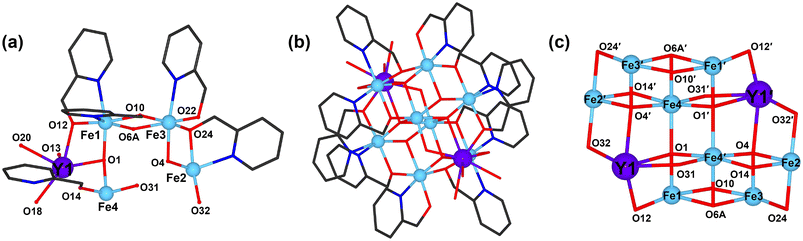
The experimental XRD patterns of clusters 1–5 were very similar to the simulated ones, confirming the phase purity of 1–5 (Fig. S1†). Single-crystal structural analysis reveals that clusters 1–5 are isostructural and crystallize in the monoclinic space group P2₁/n (Table S1†). Therefore, cluster 1 was used as a representative example to describe the configurational characteristics. From the chemical composition aspect, cluster 1 is composed of a cationic cluster of [Y₂Fe₈(hmp)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]⁶⁺, 6 ClO₄⁻ anions, and 8 H₂O molecules. The number of guest water molecules was determined by elemental analysis, which is consistent with the thermogravimetric analysis result of 1. As shown in Fig. S2a,† the weight loss of 1 is approximately 5.19% at 140 °C, which corresponds to the calculated value of 5.29% for the removal of 8 guest water molecules. The XRD pattern confirmed that the final thermal decomposition product of 1 was a mixed phase, mainly including YFeO₃ and Fe₂O₃ (Fig. S2b†).

The asymmetric unit in the cationic cluster contains 5 hmp⁻ ligands, 1 Y³⁺ ion, 4 Fe³⁺ ions, and 3 coordinated H₂O molecules (O13, O18 and O20) (Fig. 1a). The eight hmp⁻ ligands allow the alkoxide O atoms to bridge Fe2–Fe3(O24), Fe2–Fe4′(O14), Fe3–Fe1(O10), and Fe1–Y1(O12) atoms in μ₂-η¹:η² coordination modes (Fig. S3a and S3b†), the remaining two hmp⁻ ligands only coordinate with Fe3 atoms in a μ₁-η¹:η¹ pattern (Fig. S3c†). The connection of two asymmetric units through O1 and O4 atoms from one asymmetric unit coordinated with the Fe4′ and Y1′ atoms from another asymmetric unit, respectively, generates a cationic cluster of [Y₂Fe₈(hmp)₁₀(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄(H₂O)₆]⁶⁺ (Fig. 1b). Therefore, the cationic cluster core in 1 (Fig. 1c) can be viewed as six face-sharing defective cubane units of two Fe₃(μ₂-OR)₂(μ₃-OH)(μ₄-O) units, two Fe₃(μ₂-OR)(μ₃-OH)(μ₄-O)₂ units, and two YFe₂(μ₂-OR)(μ₂-OH)(μ₃-OH)(μ₄-O) units linked together by two μ₂-OH⁻ groups and four μ₄-O²⁻ groups (where the O atoms are from hmp⁻ ligands in the OR group). Such a face-sharing defective cubane unit is very similar to that observed in Mn clusters.¹⁵

Fig. 1 (a) The asymmetric unit of cluster 1. (b) Molecular structure of 1 along the a-axis. (c) Metal-oxo cluster core of [Y₂Fe₈(μ₂-OR)₈(μ₂-OH)₄(μ₃-OH)₂(μ₄-O)₄]⁸⁺. Purple Y; sky blue Fe; red O; dark blue N; and dark gray C. H atoms are omitted for clarity.

The Y1³⁺ ion in 1 is octa-coordinated with a triangular dodecahedron configuration from one O atom from the hmp⁻ ligand, two μ₂-OH⁻ groups, two μ₄-O²⁻ groups, and three coordination water molecules (Fig. S4a†). All Fe atoms are hexa-coordinated in a distorted octahedral coordination sphere: Fe1 and Fe2 are surrounded by two N and two O atoms from two hmp⁻ ligands and one μ₄-O²⁻ group, respectively. The coordination environment of Fe1 is slightly different from that of Fe2, that is, one μ₃-OH⁻ group in Fe1 is replaced by one μ₂-OH⁻ group in Fe2 (Fig. S4b and S4c†). Fe3 is coordinated with one N and three O atoms, respectively, from three hmp⁻ ligands, one μ₃-OH⁻ group, and one μ₄-O²⁻ group (Fig. S4d†), while the Fe4 atom is coordinated with one O atom from the hmp⁻ ligand, one μ₂-OH⁻ group, one μ₃-OH⁻ group, and three μ₄-O²⁻ groups (Fig. S4e†). According to bond valence sum (BVS) calculations and the charge balance principle, all iron ions are trivalent (Table S2†). The Y⋯Fe distances are between 3.387(15) Å (Y1⋯Fe2′) and 3.498(6) Å (Y1⋯Fe4). The bond lengths of Fe–O and Fe–N are in the range of 1.887(6)–2.231(9) Å and 1.934(9)–2.184(7) Å, respectively. The Fe–O bond lengths in 1 are comparable to the YFe₆ cluster of Fe–O bond lengths of 1.936(2)–2.243(2) Ź⁶ and the Fe–N bond distances correspond to the Y₂Fe₈ cluster of 2.091(5)–2.216(6) Å.¹⁷ The Y–O bond length falls in the range of 2.279(5)–2.493(4) Å and the O–Y–O bond angles vary from 65.99(16)–152.63(18)°, respectively, in agreement with the bond lengths of 2.245 (9)–2.468 (9) Å and bond angles of 66.1 (3)–159.2 (4)° reported for the Y₄Fe₄ cluster.¹⁸

The structure of cluster 2 is very similar to that of cluster 1. The bond distances of Dy⋯Fe are in the range of 3.396(14)–3.412(11) Å, while the Fe–O and Fe–N bond lengths are in the range of 1.890(6)–2.180(2) Å and 1.938(9)–2.188(7) Å, respectively. The bond distance values of Fe–O and Fe–N in 2 are comparable to those of 1.880(7)–2.143(7) Å and 1.971(9)–2.240(10) Å, respectively, in the Dy₃Fe₇ cluster reported previously.¹⁹ The distances of Dy–O are in the range of 2.297 (5)–2.504 (4) Å and the O–Dy–O bond angles vary from 66.32(16)–152.65(18)°, which agree well with the Dy–O bond distances of 2.268(7)–2.523(7) Å and O–Dy–O bond angles of 55.4(3)°–157.8(3)° reported for the Dy₈Fe₄ cluster.²⁰

Magnetic properties

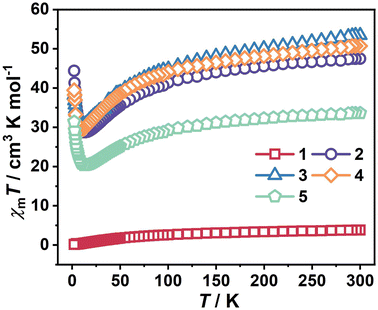
Temperature-dependent magnetic susceptibility of clusters 1–5 was measured between 2 and 300 K by applying a direct-current (dc) field of 1000 Oe. As shown in Fig. 2, upon cooling, the χ_mT value of 1 continuously decreases and reaches 0.11 cm³ K mol⁻¹ at 2 K. The χ_mT value of 3.78 cm³ K mol⁻¹ at room temperature is much smaller than the expected value of 35 cm³ K mol⁻¹ based on 8 noninteracting Fe^III ions (S = 5/2; g = 2). The significant discrepancy between experimental and theoretical χ_mT values at room temperature is attributed to the antiferromagnetic interaction between Fe^III ions.²¹ The magnetic susceptibility data above 100 K were fitted using the Curie–Weiss law, generating the Curie constant C = 4.93 cm³ mol⁻¹ and the Weiss constant θ = −92.07 K (Fig. S5a†). The negative θ value indicates that antiferromagnetic interactions exist in 1.²² The χ_mT value for 2 slowly decreases from 47.48 cm³ K mol⁻¹ at 300 K to a minimum value of 28.74 cm³ K mol⁻¹ at 14 K and then steeply increases to 44.36 cm³ K mol⁻¹ at 2 K on lowering the temperature. The decrease of the χ_mT value in the range of 14–300 K could be attributed to the depopulation of the Stark sublevels of the Dy^III ions²³ and the existence of weak antiferromagnetic interactions between spin carriers, and the increase of the χ_mT value below 14 K observed in 2 shows the presence of ferromagnetic interactions. It is worth noting that the ferro- or antiferromagnetic interaction may be induced by weak Dy^III–Fe^III coupling.²⁴ At 300 K, the χ_mT product is 47.48 cm³ K mol⁻¹, which is lower than the expected value of 63.33 cm³ K mol⁻¹ for 2 uncoupled Dy^III (J = 15/2; g = 4/3) and 8 Fe^III (S = 5/2; g = 2) ions, indicating antiferromagnetic interaction between spin carriers in 2.²⁵ The plot of 1/χ_mT vs. T obeys the Curie–Weiss law above 100 K, leading to the values of C = 51.28 cm³ mol⁻¹ and θ = −24.77 K for 2 (Fig. S5b†). It has been mentioned that the θ value in 1 is more negative than that in 2, suggesting that the antiferromagnetic coupling in 1 is stronger than that in 2. This fact indicates the presence of ferromagnetic interactions between Dy^III–Fe^III ions.

Fig. 2 Temperature dependence of χ_mT in the range of 2–300 K for clusters 1–5.

The magnetic behavior of clusters 3–5 reflected by their χ_mT values is rather similar to that in cluster 2. The magnetic data are summarized in Table 1. Cluster 5 contains two isotropic Gd^III ions without orbital contributions to the ground state. The subtraction of the χ_mT value of cluster 1, containing the diamagnetic Y^III ions and thus revealing the Fe^III interactions, could provide insights into magnetic interactions. The shape of the subtracted Δχ_mT curves is shown in Fig. S6,† where the Δχ_mT value of χ_mT (5)–χ_mT (1) gradually decreases to reach the minimum value of 19.81 cm³ K mol⁻¹ from 300 to 14 K due to the antiferromagnetic interactions between Gd^III–Fe^III ions and/or Gd^III–Gd^III ions, and then increases significantly in the range of 14–2 K indicating a ferromagnetic arrangement in cluster 5, which may be attributed to the interactions of Gd^III–Fe^III ions and/or Gd^III–Gd^III ions.¹⁷ For clusters 2–4, the thermal behavior of Δχ_mT will become more complicated due to the depopulation of Stark sublevels of the anisotropic Dy^III, Ho^III and Tb^III ions, which can also contribute to the decrease of Δχ_mT.²³

Table 1 Comparison of dc magnetic data for clusters 1–5

	1 (Y)	2 (Dy)	3 (Ho)	4 (Tb)	5 (Gd)
Ground-state term of Ln^III ion	^1S0	^6H15/2	^5I8	^7F6	^8S7/2
g for Ln^III ion	0	4/3	5/4	3/2	2
X m T (cm^3 K mol^−1) expected value at 300 K	35	63.33	63.13	58.63	50.75
X m T (cm^3 K mol^−1) experimental value at 300 K	3.78	47.48	53.44	50.71	33.62
X m T (cm^3 K mol^−1) experimental value at 2 K	0.11	44.36	38.14	39.45	31.40
Magnetization (NμB) observed at 7 T and 2 K	2.62	46.03	18.23	16.20	15.30
Curie constant (cm^3 K mol^−1) above 100 K	4.93	51.28	59.14	55.22	36.34
Weiss constant, θ (K), above 100 K	−92.07	−24.77	−34.41	−27.65	−24.88

---

The field dependence of the magnetization for 1–5 was measured at 2 K in the field range of 0–7 T (Fig. S7†). For 1, the observed value of 2.62Nμ_B at 7 T was much lower than the calculated saturation value of 40Nμ_B based on the 8 uncorrelated Fe^III ions, which might be ascribed to the low-lying excited states resulting from weak intra-cluster magnetic coupling in magnetic centers.²⁶ The magnetization for 2–5 occurred at 7 T with no real sense of saturation, and for all of them saturation values are lower than the theoretical values if all the spins are ferromagnetically aligned. The lack of saturation indicates the existence of low-lying excited states and/or intrinsic magnetic anisotropy.^8b,27

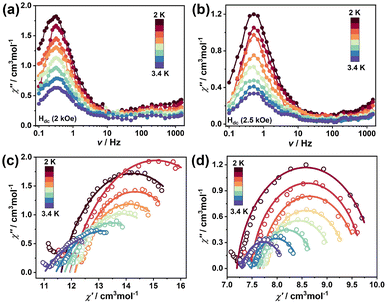
To gain insights into the magnetization dynamics in 2, ac susceptibilities were measured under zero external field. The temperature dependence plots of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibility signals under the zero dc field vary with frequencies (Fig. S8a and S8b†) and the frequency dependence plots of χ′ and χ′′ are shown in Fig. 3a and b. A series of continuous peaks was observed within a temperature range of 2–3.4 K, indicating the presence of slow relaxation of the magnetization and the SMM response. Cole–Cole plots at fixed temperatures in the range of 2–3.4 K exhibit typical semicircular profiles, which are well fitted by the generalized Debye model²⁸ (Fig. 3c) and give the α parameters of 0.15–0.29 (Table S3†), suggesting the narrow distribution in the relaxation times of the system. The plot of the natural logarithm of relaxation time ln(τ) versus 1/T for 2 remains linear (Fig. 3d), indicating that an Orbach process is dominant for slow magnetic relaxation. Fitting of the plot of ln(τ) versus 1/T with the Arrhenius law afforded a characteristic U_eff value of 17.76 K with a pre-exponential factor τ₀ value of 7.93 × 10⁻⁸ s for 2. Cluster 1 reveals antiferromagnetic coupling containing two diamagnetic Y^III ions and does not exhibit SMM behavior, whereas cluster 2 displays χ′′ ac susceptibility signals, which is typical of SMMs due to the introduction of anisotropic Dy^III ions, the relatively low U_eff value likely being due to the weak magnetic coupling between Fe^III−Dy^III ions.²⁹

Fig. 3 (a) Frequency dependence of the in-phase (χ′) and (b) out-of-phase (χ′′) ac susceptibility for cluster 2. (c) Cole–Cole plots for 2 under a zero dc field. The solid lines are the best fit for the generalized Debye model. (d) Natural logarithm of the relaxation time ln τ vs. T⁻¹ plots for 2. The solid line corresponds to the fit for the Orbach process.

Table 2 lists the SMM performances of Fe^III–Dy^III SMMs reported previously. The U_eff of 2 is lower than that of {Fe^III₆Dy^III₃},¹⁰ {Fe^III₄Dy^III₂},^30,33 {Fe^III₂Dy^III₄},³¹ {Fe^III₇Dy^III₃},³² and {Fe^III₄Dy^III₄},³⁴ but higher than that of some clusters, such as {Fe^III₇Dy^III₄},³⁵ {Fe^III₁₈Dy^III₆},³⁶ {Fe^III₆Dy^III₃},³⁷ {Fe^IIIDy^III},²³ {Fe^III₂Dy^III₃},³⁸ {Fe^III₈Dy^III₂},¹⁷ and {Fe^III₄Dy^III₂}.³⁹ Based on Table 2, it is difficult to judge the SMM performance of these clusters according to the macroscopic magnetic properties of these clusters. To further reveal the factors that affect the performance of SMMs in this system, the performance of SMMs in {Fe^III₄Dy^III₂},^30,33 {Fe^III₄Dy^III₂}³⁹ and cluster 2 was compared, not only because they all contain two discrete Dy^III ions that are symmetrically related, but also because the iron clusters themselves within them do not show SMM behavior. Based on the performance of these SMMs, it is clear that the performance of SMMs in these clusters is in the order of {Fe^III₄Dy^III₂}³⁰ > {Fe^III₄Dy^III₂}³³ > 2 > {Fe^III₄Dy^III₂}.³⁹ This result indicates that the strength of ferromagnetic interaction is conducive to obtaining excellent SMMs, because the strength of the ferromagnetic interaction in these clusters in the temperature range of 2–10 K is in the order of {Fe^III₄Dy^III₂}³⁰ > {Fe^III₄Dy^III₂}³³ > 2 > {Fe^III₄Dy^III₂}.³⁹ To reveal the key factor that influences the ferromagnetic interaction in these clusters, their bond distances between Dy^III and O atoms coordinated to Fe^III ions and bond angles of Dy–O–Fe are investigated. The bond distances between Dy^III and O atoms coordinated to FeIII ions and bond angles of Dy–O–Fe are respectively 2.288(4)–2.307(5) Å and 105.42(18)–105.92(19)° for {Fe^III₄Dy^III₂},³⁰ 2.248(3)−2.353(3) Å and 100.79(13)–128.89(16)° for {Fe^III₄Dy^III₂},³³ 2.297(5)–2.504(4) Å and 100.43(18)−110.3(2)° for 2, and 2.405(6)−2.508(5) Å and 100.49(18)−127.7(2)° for {Fe^III₄Dy^III₂}.³⁹ These results indicate that the strength of the ferromagnetic interaction in these clusters is mainly related to the bond distances between Dy^III and O atoms coordinated to Fe^III ions.

Table 2 Representative Fe^III–Dy^III SMM clusters

Fe^III–Dy^III SMM	U eff/K [Hdc ≠ 0, Oe]	τ 0/s	Ref.
Fe6^IIIDy3^III	65.1	1.64 × 10^−12	10
Fe4^IIIDy2^III	36.9	6.8 × 10^−10	30
Fe2^IIIDy4^III	34	2.0 × 10^−11	31
Fe7^IIIDy3^III	30.9	1.3 × 10^−7	32
Fe4^IIIDy2^III	30.85 (1200)	3.70 × 10^−8	33
Fe4^IIIDy4^III	30.5	2.0 × 10^−9	34
Fe7^IIIDy4^III	16.9	4.6 × 10^−7	35
Fe18^IIIDy6^III	14.7	2.98 × 10^−7	36
Fe6^IIIDy3^III	12.4 (2000)	8.0 × 10^−5	37
Fe^IIIDy^III	9.72 (1000)	3.69 × 10^−6	23
Fe2^IIIDy3^III	6.78 (1200)	2.01 × 10^−5	38
Fe8^IIIDy2^III	4.1 (600)	4.90 × 10^−5	17
Fe4^IIIDy2^III	0.44	1.60 × 10^−6	39
2	17.76	7.93 × 10^−8	This work

---

The dynamic magnetic behavior of clusters 3 and 4 was further investigated by conducting ac susceptibility measurements within the temperature range of 2–10 K. In the absence of an external magnetic field, frequency-dependent χ′′ signals were observed below 4 K (Fig. S9†), indicating the onset of the slow magnetization relaxation. However, no expected maximum peaks in χ′′ signals are indicative of a quantum tunneling relaxation of the magnetization (QTM) driven by inter-cluster dipolar interactions.⁴⁰ The frequency dependence of χ′′ ac susceptibility for clusters 3 and 4 have been recorded in an external applied dc field from 1 to 4 kOe at 2 K (Fig. S10†), where the optimal field is observed at 2 kOe for 3 and 2.5 kOe for 4 (Fig. S11†). The temperature dependence of χ′ and χ′′ ac susceptibilities of 3 and 4 were measured under optimal 2 kOe and 2.5 kOe dc fields, respectively. Both the χ′ and χ′′ signals are frequency dependent, indicating the slow magnetic relaxation (Fig. S12†). As shown in Fig. 4a and b, the intensity of the χ′′ signals increased with decreasing temperature, but frequency-independent peaks almost appeared in the low-frequency range of 0.1–10 Hz for 3 and 4, which were probably induced by low-lying excited exchange states promoting the QTM,⁴¹ causing a direct relaxation process rather than thermal activation relaxation.⁴² Moreover, a small tail of peaks was observed in the high-frequency region of 100–1500 Hz revealing that secondary relaxation occurs.⁴³ The Cole–Cole plots were fitted using the generalized Debye model²⁸ and show pronounced asymmetric semicircle shapes (Fig. 4c and d). The distribution coefficient α values range from 0.26 to 0.60 for 3, indicating a broader distribution of relaxation times, while the smaller α values of 0.08–0.22 for 4 show a narrow relaxation time distribution. A minor second tail of peaks could also be observed in the Cole–Cole plots,⁴⁴ thus supporting the presence of secondary relaxation pathways in the high-frequency region.⁴² This phenomenon is commonly found in lanthanide-based molecular magnets, which presumably originates from intermolecular interactions.⁴⁵

Fig. 4 The frequency dependence of the χ′′ signals for (a) cluster 3 under 2 kOe, (b) cluster 4 under 2.5 kOe optimum external magnetic field. The corresponding Cole–Cole plots for (c) 3 and (d) 4. The solid lines are the best fit for the generalized Debye model.

Conclusions

In conclusion, we have synthesized and characterized five decanuclear 3d–4f clusters [Ln₂Fe₈] {Ln = Y (1)/Dy (2)/Ho (3)/Tb (4)/Gd (5)} featuring six face-sharing defective cubane cores. Cluster 2 exhibits SMM behavior under a zero dc field, giving an energy barrier of 17.76 K. Investigation of the performance of a series of Fe^III–Dy^III SMMs indicates that the energy barrier in these clusters is associated with the strength of the ferromagnetic interaction between Fe^III and Dy^III ions, while the strength of the ferromagnetic interaction in these clusters is mainly related to the bond distances between Dy³⁺ and O atoms coordinated to Fe³⁺ ions. Clusters 3 and 4 exhibit two similar relaxation processes under optimal 2 kOe and 2.5 kOe dc fields, respectively. Frequency-independent behavior was almost observed in the low-frequency region, implying that direct relaxation dominates, while the weak tail signal at higher frequencies may be ascribed to the presence of secondary relaxation pathways, which may be related to the intermolecularly driven relaxation process. The current work unravels the magneto-structural correlations in heterometallic lanthanide–iron coordination clusters and provides the opportunity to identify SMM behavior under a magnetic field.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (grants 21971214 and 92161203).

References

1. (a) S. M. J. Aubin, N. R. Dilley, L. Pardi, J. Krzystek, M. W. Wemple, L.-C. Brunel, M. B. Maple, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1998, 120, 4991–5004; (b) F. R. Renani and G. Kirczenow, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 121403.
2. R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816.
3. (a) M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793; (b) N. Roch, S. Florens, V. Bouchiat, W. Wernsdorfer and F. Balestro, Nature, 2008, 453, 633–637.
4. (a) S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138; (b) R. Sessoli, Nature, 2017, 543, 189–190.
5. (a) L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186; (b) M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197.
6. (a) D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297; (b) T. Gupta, M. F. Beg and G. Rajaraman, Inorg. Chem., 2016, 55, 11201–11215.
7. (a) S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, Angew. Chem., 2010, 122, 7610–7613; (b) J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310; (c) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148; (d) Y. Huo, Y.-C. Chen, J.-L. Liu, J.-H. Jia, W.-B. Chen, S.-G. Wu and M.-L. Tong, Dalton Trans., 2017, 46, 16796–16801; (e) J.-H. Jia, Q.-W. Li, Y.-C. Chen, J.-L. Liu and M.-L. Tong, Coord. Chem. Rev., 2019, 378, 365–381.
8. (a) M. K. Singh and G. Rajaraman, Inorg. Chem., 2019, 58, 3175–3188; (b) H.-L. Zhang, Y.-Q. Zhai, L. Qin, L. Ungur, H. Nojiri and Y.-Z. Zheng, Matter, 2020, 2, 1481–1493.
9. M. Ferbinteanu, T. Kajiwara, K.-Y. Choi, H. Nojiri, A. Nakamoto, N. Kojima, F. Cimpoesu, Y. Fujimura, S. Takaishi and M. Yamashita, J. Am. Chem. Soc., 2006, 128, 9008–9009.
10. S. Schmidt, D. Prodius, V. Mereacre, G. E. Kostakis and A. K. Powell, Chem. Commun., 2013, 49, 1696–1698.
11. (a) L. R. Piquer and E. C. Sañudo, Dalton Trans., 2015, 44, 8771–8780; (b) H.-S. Wang, Q.-Q. Long, Z.-B. Hu, L. Yue, F.-J. Yang, C.-L. Yin, Z.-Q. Pan, Y.-Q. Zhang and Y. Song, Dalton Trans., 2019, 48, 13472–13482; (c) A. Dey, J. Acharya and V. Chandrasekhar, Chem. – Asian J., 2019, 14, 4433–4453; (d) S. G. Baca, J. van Leusen, M. Speldrich and P. Kögerler, Inorg. Chem. Front., 2016, 3, 1071–1075.
12. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. a. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
13. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
14. (a) A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13; (b) A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18.
15. (a) N. C. Harden, M. A. Bolcar, W. Wernsdorfer, K. A. Abboud, W. E. Streib and G. Christou, Inorg. Chem., 2003, 42, 7067–7076; (b) J. Liu, C. Ma, H. Chen, M. Hu, H. Wen, H. Cui, X. Song and C. Chen, Dalton Trans., 2013, 42, 2423–2430; (c) L. Sun, H. Chen, C. Ma and C. Chen, Inorg. Chem. Commun., 2017, 77, 77–79.
16. M. N. Akhtar, M. A. AlDamen, M. Fitta, M. Shahid and A. M. Kirillov, Cryst. Growth Des., 2022, 22, 608–614.
17. X. Zhao, Y. Wang, D. Bao, F. Zhang, W. Wu, F. Xu, Q. Zhang and Y. Li, Appl. Organomet. Chem., 2019, 33, e5222.
18. A. Mondal, M. Raizada, P. K. Sahu and S. Konar, Inorg. Chem. Front., 2021, 8, 4625–4633.
19. G. Abbas, Y. Lan, V. Mereacre, W. Wernsdorfer, R. Clérac, G. Buth, M. T. Sougrati, F. Grandjean, G. J. Long, C. E. Anson and A. K. Powell, Inorg. Chem., 2009, 48, 9345–9355.
20. X. He, W. Cheng, Q. Lin, Y. Dong and Y. Xu, Cryst. Growth Des., 2017, 17, 347–354.
21. M. N. Akhtar, M. A. AlDamen, C. D. McMillen, A. Escuer and J. Mayans, Inorg. Chem., 2021, 60, 9302–9308.
22. A. Baniodeh, Y. Lan, G. Novitchi, V. Mereacre, A. Sukhanov, M. Ferbinteanu, V. Voronkova, C. E. Anson and A. K. Powell, Dalton Trans., 2013, 42, 8926–8938.
23. A. Topor, D. Liu, C. Maxim, G. Novitchi, C. Train, Z. A. AlOthman, A. A. S. Al-Kahtani, L. Ungur, L. T. A. Ho, L. F. Chibotaru and M. Andruh, J. Mater. Chem. C, 2021, 9, 10912–10926.
24. D. Prodius, V. Mereacre, P. Singh, Y. Lan, S. Mameri, D. D. Johnson, W. Wernsdorfer, C. E. Anson and A. K. Powell, J. Mater. Chem. C, 2018, 6, 2862–2872.
25. S. Chen, V. Mereacre, D. Prodius, G. E. Kostakis and A. K. Powell, Inorg. Chem., 2015, 54, 3218–3227.
26. A. M. Ako, V. Mereacre, R. Clérac, I. J. Hewitt, Y. Lan, C. E. Anson and A. K. Powell, Dalton Trans., 2007, 45, 5245–5247.
27. Y.-Z. Zheng, Y. Lan, C. E. Anson and A. K. Powell, Inorg. Chem., 2008, 47, 10813–10815.
28. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
29. K.-Q. Hu, X. Jiang, S.-Q. Wu, C.-M. Liu, A.-L. Cui and H.-Z. Kou, Inorg. Chem., 2015, 54, 1206–1208.
30. S. F. M. Schmidt, C. Koo, V. Mereacre, J. Park, D. W. Heermann, V. Kataev, C. E. Anson, D. Prodius, G. Novitchi, R. Klingeler and A. K. Powell, Inorg. Chem., 2017, 56, 4796–4806.
31. C. D. Polyzou, A. Baniodeh, N. Magnani, V. Mereacre, N. Zill, C. E. Anson, S. P. Perlepes and A. K. Powell, RSC Adv., 2015, 5, 10763–10767.
32. G. Abbas, Y. Lan, V. Mereacre, W. Wernsdorfer, R. Clérac, G. Buth, M. T. Sougrati, F. Grandjean, G. J. Long, C. E. Anson and A. K. Powell, Inorg. Chem., 2009, 48, 9345–9355.
33. M. N. Akhtar, V. Mereacre, G. Novitchi, J.-P. Tuchagues, C. E. Anson and A. K. Powell, Chem. – Eur. J., 2009, 15, 7278–7282.
34. D. Schray, G. Abbas, Y. Lan, V. Mereacre, A. Sundt, J. Dreiser, O. Waldmann, G. E. Kostakis, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 5185–5188.
35. D. Prodius, V. Mereacre, P. Singh, Y. Lan, S. Mameri, D. D. Johnson, W. Wernsdorfer, C. E. Anson and A. K. Powell, J. Mater. Chem. C, 2018, 6, 2862–2872.
36. H. Kaemmerer, A. Baniodeh, Y. Peng, E. Moreno-Pineda, M. Schulze, C. E. Anson, W. Wernsdorfer, J. Schnack and A. K. Powell, J. Am. Chem. Soc., 2020, 142, 14838–14842.
37. I. A. Kühne, V. Mereacre, C. E. Anson and A. K. Powell, Chem. Commun., 2016, 52, 1021–1024.
38. H. Li, W. Shi, Z. Niu, J.-M. Zhou, G. Xiong, L.-L. Li and P. Cheng, Dalton Trans., 2015, 44, 468–471.
39. F.-W. Zheng, H.-T. Chen, D.-J. Li, F.-J. Han and L. Yang, J. Cluster Sci., 2021, 32, 461–467.
40. (a) D. Grebenyuk, M. Zobel, M. Polentarutti, L. Ungur, M. Kendin, K. Zakharov, P. Degtyarenko, A. Vasiliev and D. Tsymbarenko, Inorg. Chem., 2021, 60, 8049–8061; (b) G. Brunet, F. Habib, I. Korobkov and M. Murugesu, Inorg. Chem., 2015, 54, 6195–6202.
41. (a) K. L. M. Harriman, J. J. Le Roy, L. Ungur, R. J. Holmberg, I. Korobkov and M. Murugesu, Chem. Sci., 2017, 8, 231–240; (b) J. D. Rinehart, K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7572–7573.
42. M. Li, H. Wu, Q. Wei, H. Ke, B. Yin, S. Zhang, X. Lv, G. Xie and S. Chen, Dalton Trans., 2018, 47, 9482–9491.
43. Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538–8539.
44. (a) X.-L. Li, H. Li, D.-M. Chen, C. Wang, J. Wu, J. Tang, W. Shi and P. Cheng, Dalton Trans., 2015, 44, 20316–20320; (b) H.-J. Lun, X.-J. Kong, L.-S. Long and L.-S. Zheng, Dalton Trans., 2020, 49, 2421–2425.
45. (a) G. Cosquer, F. Pointillart, S. Golhen, O. Cador and L. Ouahab, Chem. – Eur. J., 2013, 19, 7895–7903; (b) M. Dolai, M. Ali, J. Titiš and R. Boča, Dalton Trans., 2015, 44, 13242–13249; (c) K. R. Meihaus, J. D. Rinehart and J. R. Long, Inorg. Chem., 2011, 50, 8484–8489; (d) F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278–3288.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental section, tables and additional figures. CCDC 2195974, 2195975 and 2314827–2314829. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt03832g

---