Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comprehensive understanding of the crystal structure of perovskite-type Ba3Y4O9 with Zr substitution: a theoretical and experimental study†
Katsuhiro
Ueno
 *a,
Atsunori
Hashimoto
a,
Kazuaki
Toyoura
*a,
Atsunori
Hashimoto
a,
Kazuaki
Toyoura
 *a,
Naoyuki
Hatada
*a,
Naoyuki
Hatada
 a,
Shigeo
Sato
a,
Shigeo
Sato
 b and
Tetsuya
Uda
b and
Tetsuya
Uda
 a
a
aDepartment of Materials Science and Engineering, Kyoto University, Yoshida Honmachi, Sakyo-ku, Kyoto, 606-8501, Japan. E-mail: ueno.katsuhiro.5z@kyoto-u.ac.jp; toyoura.kazuaki.5r@kyoto-u.ac.jp; Fax: +81-75-753-5284; Tel: +81-75-753-5445
bGraduate School of Science and Engineering, Ibaraki University, 4-12-1 Nakanarusawa, Hitachi, Ibaraki 316-8511, Japan
First published on 28th February 2024
Abstract
We previously reported that Zr substitution improves the chemical stability of Ba3Y4O9 and nominally 20 mol% Zr-substituted Ba3Y4O9 is an oxide-ion conductor at intermediate temperatures (500–700 °C). However, the influence of Zr substitution on the structural properties of Ba3Y4O9 was poorly understood. This paper aims to comprehensively understand the crystal structure of Ba3Y4O9 with Zr substitution by powder X-ray diffraction (XRD), extended X-ray absorption fine structure (EXAFS) measurements, and first-principles calculations. From the results, firstly we found that the hexagonal unit cell of Ba3Y4O9 reported in the database should be revised as doubled along the c-axis in terms of the periodicity of oxide-ion positions. The revised unit cell of Ba3Y4O9 consists of 18 layers of BaO3 and 24 layers of Y which periodically stack along the c-axis. In this work, we focused on the cationic lattice and noticed that the periodical stacking of Ba and Y layers comprises a similar sequence to that in the body-centered cubic (BCC) structure. There are two regions in the Ba3Y4O9 structure: one is a hetero-stacking region of Ba and Y layers (Ba–Y–Ba–Y–Ba) and the other is a homo-stacking region (Ba–Y–Y–Ba). It is noteworthy that the former region is similar to a cubic perovskite. In Zr-substituted Ba3Y4O9, Zr ions preferentially substitute for Y ions in the hetero-stacking region, and therefore the local environment of Zr ions in Ba3Y4O9 is quite similar to that in BaZrO3. Besides, the Zr substitution for Y in Ba3Y4O9 increases the fraction of the cubic-perovskite-like region in the stacking sequences. The structural change in the long-range order strongly affects the other material properties such as chemical stability and the ionic-conduction mechanism. Our adopted description of perovskite-related compounds based on the stacking sequence of the BCC structure should help in understanding the complex structure and developing new perovskite-related materials.
1 Introduction
Ba3Y4O9 is a potential host compound for ionic, optic, and catalytic applications.1–10 As for the ionic conductor, in the 1990s, Ba3Y4O9 was reported to be an oxide-ion conductor with conductivity beyond 10−2 S cm−1 at 500 °C.11,12 However, the high conductivity was found to be caused by liquid phases formed in the reaction between Ba3Y4O9 and CO2 and/or H2O.13 Recently, we have found that Zr substitution on Y sites enhances the chemical stability of Ba3Y4O9, and nominally 20 mol% Zr-substituted Ba3Y4O9 exhibits oxide-ion conductivity at intermediate temperatures (500–700 °C).14 The solubility limit of Zr ions on Y sites is as much as ∼47 mol%, and Ba deficiency is often seen in sintered samples at 1600 °C.15 The excess charge due to the Zr substitution is possibly compensated by the following: (i) the generation of interstitial oxide ions. | (1) |
(ii) The consumption of oxide-ion vacancies derived from the generation of Ba vacancies.
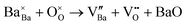 | (2) |
 | (3) |
Therefore, information about the structural properties and the chemical composition is important for understanding the mechanism of oxide-ion conduction. However, in our previous work, the powder X-ray diffraction (XRD) patterns of Zr-substituted Ba3Y4O9 could not be explained only by the change in the lattice parameters of the unit cell from pristine Ba3Y4O9. This suggests the need for the reconsideration of powder pattern indexing for Zr-substituted Ba3Y4O9.
The crystal structure of unsubstituted Ba3Y4O9 has a rhombohedral symmetry with the space group R3 as shown in Fig. 1(a).16,17 Darriet et al. focused on the stacking sequence of BaO3 layers in the Ba3M4O9 (M = Sc, Y and Ln3+ = Gd to Lu) structure, and pointed out the relationship with hexagonal perovskite BaRuO3 (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) in terms of the nine-layer stacking sequence.18
m) in terms of the nine-layer stacking sequence.18
 | ||
| Fig. 1 Crystal structure of Ba3Y4O9 reported in the ICDD database (PDF #04-012-0214, space group R3). Half of the Y ions (Y2 and Y4) occupy the octahedral sites in the hetero-stacking regions, while the others (Y1 and Y3) occupy the trigonal-prismatic sites in the homo-stacking regions. (a) and (b) is an overview and a view from the [100] direction, respectively. For the description of the crystal structure, we used the VESTA software.19 | ||
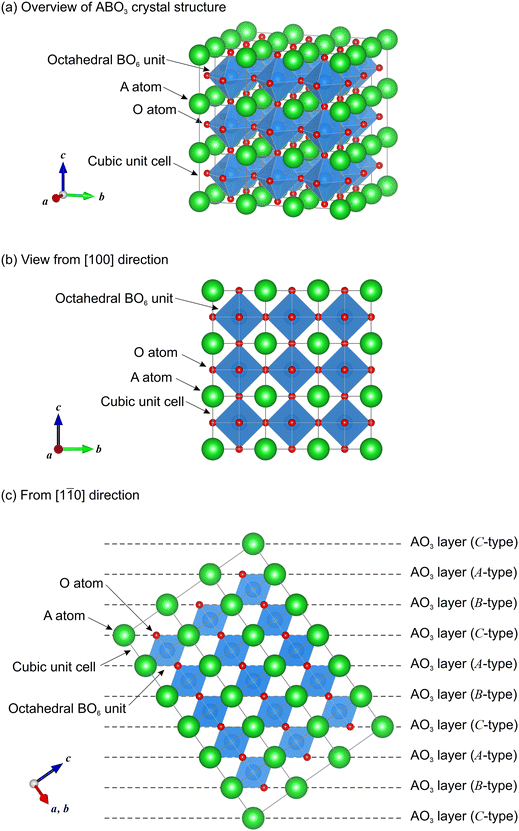
In general, two types of conventional descriptions for perovskite structures are employed, which are shown hereafter taking cubic perovskite ABO3 as a model system. Fig. 2 shows the crystal structure of the cubic perovskite (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), in which A atoms form a cubic lattice, and B and O atoms are located at the body-centered and face-centered positions of the cubic lattice, respectively. Hence, the oxygen-coordinated numbers are 12 for A atoms and 6 for B atoms. The first type of conventional description for perovskite structures is based on the network of octahedral BO6 units. In the cubic phase, all BO6 units are regular octahedra, which are corner-shared to form a three-dimensional (3D) BO6 network. In general, the BO6 units can be distorted and tilted/rotated in the crystal, leading to lower symmetry. In hexagonal perovskite-related structures such as BaRuO3, some of the BO6 units are not corner-shared but face-shared. Hence, this description method clarifies how the 3D BO6 network spreads and visualizes the distortion and tilt of the BO6 units in the structures.
m), in which A atoms form a cubic lattice, and B and O atoms are located at the body-centered and face-centered positions of the cubic lattice, respectively. Hence, the oxygen-coordinated numbers are 12 for A atoms and 6 for B atoms. The first type of conventional description for perovskite structures is based on the network of octahedral BO6 units. In the cubic phase, all BO6 units are regular octahedra, which are corner-shared to form a three-dimensional (3D) BO6 network. In general, the BO6 units can be distorted and tilted/rotated in the crystal, leading to lower symmetry. In hexagonal perovskite-related structures such as BaRuO3, some of the BO6 units are not corner-shared but face-shared. Hence, this description method clarifies how the 3D BO6 network spreads and visualizes the distortion and tilt of the BO6 units in the structures.
The other conventional description is based on the stacking sequences of AO3 layers and was originally proposed by Katz and Ward.20 In the cubic perovskite structure, A atoms and O atoms form an ordered face-centered cubic (FCC) lattice, and B atoms are located at the body-centered positions in the lattice. Consequently, AO3 layers are periodically stacked as –A–B–C– sequences (from top to bottom) along the 〈111〉 directions in the cubic unit cell as shown in Fig. 2(c). Such a type of stacking sequence is often labeled as “c” (derived from cubic) in contrast to the stacking sequence of –A–B– which is labeled as “h” (derived from hexagonal) in the Ramsdell notation.21,22 This method is often used for hexagonal perovskite-related compounds. This is because the stacking sequences of “c” and “h” are periodically mixed in many of the perovskite-related structures.
Fig. 1(b) shows the crystal structure of Ba3Y4O9 (space group R3) viewed from the [100] direction. In the unit cell, there are three types of Ba sites, four types of Y sites, and three types of O sites. Based on the first description, YO6 units are classified into two types: octahedral units (Y2O6 and Y4O6) and triangular-prismatic units (Y1O6 and Y3O6) as shown in Fig. S1.† As seen in Fig. 2(b), an octahedral unit is corner-shared with three octahedral units and face-shared with a prismatic unit. In contrast, a prismatic unit is edge-shared by three prismatic units and face-shared with an octahedral unit. The Ba3Y4O9 structure is more understandable using the second description method based on the BaO3 stacking sequence. Similar to the cubic perovskite structure, nine of the BaO3 layers are stacked in the 〈001〉 direction in the unit cell of Ba3Y4O9. However, unlike BaZrO3, O sites in Ba1O3 and Ba2O3 layers are slightly shifted to Y3 and Y1 sites, respectively. Besides, note that the periodical stacking sequence of Ba3Y4O9 is –C–A–B–B–C–A–A–B–C– from top to bottom, which is not only composed of the –A–B–C– stacking sequence but also includes those of the same type of BaO3 layer as –A–A–. Therefore, the crystal structure cannot be described by the Ramsdell notation using “c” and “h”. Hereafter, the –A–B–C– stacking region is called a hetero-stacking region. On the other hand, the –A–A– stacking region is called a homo-stacking region. Half of the Y ions (Y2 and Y4) occupy the octahedral sites in the hetero-stacking regions, while the others (Y1 and Y3) occupy the trigonal-prismatic sites in the homo-stacking regions.
In this study, the crystal structure of Ba3Y4O9 and the structural change by Zr substitution have been revisited for a comprehensive understanding of the crystal structure of Zr-substituted Ba3Y4O9. For this purpose, we performed first-principles molecular dynamics (FPMD) simulations to determine the stable structure of pristine Ba3Y4O9 and the Zr substitution site. The local environment of Zr ions was experimentally evaluated by the extended X-ray absorption fine structure (EXAFS) measurement with synchrotron radiation. In addition, we carried out powder XRD analysis with laboratory CuKα1 radiation for consistent indexing of Zr-substituted Ba3Y4O9, and we propose another description for the Ba3Y4O9 crystal structure based on the cationic stacking sequence of the body-centered cubic (BCC) structure.
2 Experiments and calculations
2.1 Experimental procedure
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Y + Zr) = 2.67
(Y + Zr) = 2.67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 = 4
4 = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) compared to the stoichiometric composition (Ba
6) compared to the stoichiometric composition (Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Y + Zr) = 3
(Y + Zr) = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4).14 In the following, the samples are called “Ba-def Ba3Y4-Zrx” where x means the Zr substitution level.
4).14 In the following, the samples are called “Ba-def Ba3Y4-Zrx” where x means the Zr substitution level.
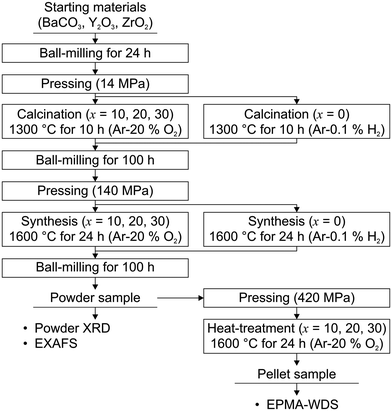 | ||
| Fig. 3 Sample preparation procedure by the solid-state reaction method in this work. All powder samples were synthesized at 1600 °C for 24 hours. | ||
BaCO3 (Wako Pure Chemical Industries, Ltd, Japan, 99.9%), Y2O3 (Shin-Etsu Chemical Industries, Ltd, Japan, 99.9%), and ZrO2 (Tosoh Corporation, Japan, 97.031%) powder were used as starting materials. The reagents mixed at the desired ratios were put into polyvinyl bottles with yttria-stabilized zirconia (YSZ) balls and 2-propanol and ball-milled for 24 h. After the YSZ balls were removed, 2-propanol was evaporated by the vacuum drying method at 75 °C. Notably, we did not use silicone grease to ensure the airtightness of the recovery flask in this drying method because the usage of the grease caused the contamination of Si in the sample powder. Detailed information on the investigation of the cause of the Si contamination is explained in the subsection “Investigation of the cause of the Si contamination” in the ESI.† The obtained powder was pressed into a pellet with a diameter of 19 mm under an uniaxial pressure of 14 MPa and then calcined at 1300 °C for 10 hours under a dry Ar–0.1% H2 atmosphere for x = 0 and dry Ar–20% O2 atmospheres for x = 10, 20, and 30, respectively.‡ Then the pellets were ground, ball-milled for 100 h, and vacuum-dried as per the above procedure. Subsequently, the powder samples were pressed into a pellet with a diameter of 19 mm again under an uniaxial pressure of 140 MPa. The pelletized samples were synthesized at 1600 °C for 24 hours under a dry Ar–0.1% H2 atmosphere for x = 0 and dry Ar–20% O2 atmospheres for x = 10, 20, and 30, respectively.‡ Then, the pellet samples were ground and ball-milled for 100 h again and the powder samples were obtained. For the evaluation of the Zr substitution levels in the Ba3Y4O9 phase in the samples with x = 10, 20, and 30, we prepared pellet samples using the synthesized powder mixed with an organic binder (NCB-166, DIC Corporation, Japan). The synthesized powder was pressed into a pellet with a diameter of 11 mm under an uniaxial pressure of about 400 MPa and then heat-treated at 600 °C for 10 hours to remove the binder. The pellet samples were subsequently heat-treated at 1600 °C for 24 hours under dry Ar–20% O2 atmospheres. It is noted that for the suppression of BaO evaporation at high temperatures, the pellets were embedded in sacrificial powder which had the same composition and heat-treatment history as the sample in all heat-treatment processes in the sample preparation.23
| Sample name | Nominal composition (mol%) | Average composition (WDS) (mol%) | The point analysis result of the main phase (WDS) (mol%) | Subphase coexisting with the Ba3Y4O9 phase | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BaO | ZrO2 | YO1.5 | BaO | ZrO2 | YO1.5 | BaO | ZrO2 | YO1.5 | ||
| Ba-def Ba3Y4-Zr0 | 40.0 | 0.0 | 60.0 | Not measured | Not measured | None (XRD) | ||||
| Ba-def Ba3Y4-Zr10 | 40.0 | 6.0 | 54.0 | 38.6 | 6.0 | 55.4 | Not measured | None (XRD and WDS) | ||
| Ba-def Ba3Y4-Zr20 | 40.0 | 12.0 | 48.0 | 37.4 | 11.9 | 49.0 | Not measured | None (XRD and WDS) | ||
| Ba-def Ba3Y4-Zr30 | 40.0 | 18.0 | 42.0 | 38.9 | 18.0 | 43.0 | 39.2 | 18.7 | 42.2 | Y2O3 (XRD and WDS) |
EXAFS measurements were performed using the BL14B2 beam line at the SPring-8 synchrotron radiation facility (Hyogo, Japan). The measurement was performed on Ba-def B3Y4-Zx (x = 0, 10, 20, and 30), diluted to a suitable concentration using boron nitride (BN) and pressed into pellets with a diameter of 11 mm. EXAFS spectra were collected at the Y K-edge (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045.0 eV) and Zr K-edge (18
045.0 eV) and Zr K-edge (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005.6 eV). A transmission geometry was selected and a Si(311) double-crystal monochromator was used. The samples were cooled down to about 30 K in a vacuum with a cryostat. Data processing and curve fitting were performed using Athena and Artemis, respectively.28 ZrO2 and Y2O3 were used for the determination of the reduced amplitude due to many body effects as well as the absorption energies of the Y K-edge and Zr K-edge, respectively. All the fittings were performed with the Debye–Waller factor and the atomic distance as fitting parameters and the coordination number as a fixed parameter. The curve fittings were performed in the q space which is the reverse Fourier transform of the radial distribution function.
005.6 eV). A transmission geometry was selected and a Si(311) double-crystal monochromator was used. The samples were cooled down to about 30 K in a vacuum with a cryostat. Data processing and curve fitting were performed using Athena and Artemis, respectively.28 ZrO2 and Y2O3 were used for the determination of the reduced amplitude due to many body effects as well as the absorption energies of the Y K-edge and Zr K-edge, respectively. All the fittings were performed with the Debye–Waller factor and the atomic distance as fitting parameters and the coordination number as a fixed parameter. The curve fittings were performed in the q space which is the reverse Fourier transform of the radial distribution function.
2.2 Computational methodology
All computational studies were performed based on the projector augmented wave (PAW) method29,30 as implemented in the VASP code.31–33 The 5s, 5p, and 6s orbitals for Ba atoms, 4s, 4p, 5s, and 4d orbitals for Y and Zr atoms, and 2s and 2p orbitals for O atoms were treated as valence states. The generalized gradient approximation parameterized by Perdew, Burke, and Ernzerhof (PBE_GGA) was used for the exchange–correlation term.34 The plane wave cutoff energy was set to 500 or 400 eV depending on whether optimization of the lattice vectors was required or not. For total energy calculations, the unit cell reported in ICDD (PDF #04-012-0214, space group: R3) was used with a 4 × 4 × 1 mesh for the k-point sampling. The k-point mesh was changed inversely with the cell size when calculating the total energy of a supercell constructed by expanding the R3 ICDD unit cell.For verifying the structural stability of the R3 ICDD crystal structure, the MD simulation was performed using a 2 × 2 × 1 supercell with a single k-point sampling at the Γ point. The NVT ensemble was employed at a constant temperature of 1000 K controlled by the Nose–Hoover thermostat.35 The time step was set to 1 fs and the total simulation time was 50 ps corresponding to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. The pre-simulation was preliminarily carried out for 10 ps (10
000 steps. The pre-simulation was preliminarily carried out for 10 ps (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps) as thermal equilibration steps. Subsequently, structural optimizations were performed using fifty initial structures, which were the time-averaged structures at intervals of 1 ps in the MD simulations, to explore lower-energy structures around the crystal structure reported in ICDD.
000 steps) as thermal equilibration steps. Subsequently, structural optimizations were performed using fifty initial structures, which were the time-averaged structures at intervals of 1 ps in the MD simulations, to explore lower-energy structures around the crystal structure reported in ICDD.
As for Zr substitution, exhaustive structural optimizations were performed for all Y sites in the most stable Ba3Y4O9 structure determined in this study. All structural optimizations in the present study were performed until the residual forces of all atoms became less than 0.01 eV Å−1.
3 Results and discussion
3.1 Phase identification of Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples
Fig. 4(a) shows powder XRD patterns of Ba-def Ba3Y4-Zrx samples heat-treated at 1600 °C for 24 hours. Firstly focusing on subphases, a small amount of Y2O3 existed only in the Ba-def Ba3Y4-Zr30 sample. On the other hand, no Si-contaminated impurities (e.g., Ba2SiO4) were confirmed in the patterns of any samples, unlike our previous work.14 Hence, the modified procedure as described in the subsection “Material preparation” was effective in suppressing the Si contamination. From the WDS elemental mapping analysis as shown in Fig. S2–S4,† the same results of phase identification for subphases were obtained as the powder XRD pattern for Ba-def Ba3Y4-Zrx (x = 10, 20, and 30) samples. | ||
| Fig. 4 (a) The powder XRD patterns of the Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples collected at room temperature under ambient atmospheres. The powder samples were synthesized at 1600 °C for 24 h under a dry Ar–0.1% H2 atmosphere for x = 0 and dry Ar–20% O2 atmospheres for x = 10, 20, and 30, respectively. The starred peaks were used for re-indexing with the Pawley refinement. (b) The magnified view around 2θ = 32–39° on an I0.5 scale. Szymanik et al. mentioned that the diffraction peak with a symbol (◆) was an unindexed line in the structural refinement of Ba3Y4O9.17 However, in this work, the unindexed peak shifted with an increase in the Zr substitution level as well as those attributed to 202 and 205. | ||
In the pattern of the Ba-def Ba3Y4-Zr0 sample, it was possible to index the diffraction peaks except for the one at 2θ = 33.3° based on the crystal structure of Ba3Y4O9 (space group R3) reported in the ICDD database (PDF #04-012-0214). Besides, the peaks, except for those attributed to the Y2O3 phase in the Ba-def Ba3Y4-Zr30 sample, continuously shifted with an increase in the Zr substitution level of the samples. It suggests that the shifted peaks were attributed to Ba3Y4O9 and the Zr substitution caused changes in structural properties of Ba3Y4O9.
3.2 Revisit of the crystal structure of unsubstituted Ba3Y4O9
Fig. 4(b) shows the magnified view of the powder XRD pattern of the samples around 2θ = 32–39°. As mentioned in the preceding subsection, we confirmed the existence of an unindexed diffraction peak at 2θ = 33.3° (d = 2.683 Å) in the Ba-def Ba3Y4-Zr0 sample. Szymanik et al. also reported the unindexed peak with d = 2.6805 Å in the structural study of stoichiometric Ba3Y4O9,17 and the Ba3Y4O9 structures in the database (ICDD PDF #01-089-5891 and #04-012-0214, LPF collection code: 1420451) are based on their study. However, the unindexed peak shifted continuously with an increase in the Zr substitution level of the samples as well as the indexed peaks (e.g., 202 and 205), suggesting that the unindexed peak should be explained with the Ba3Y4O9 structure, not the co-existence of the subphase. In fact, there were no subphases except for the Y2O3 phase in our samples. Therefore, it is necessary to revisit the crystal structure of unsubstituted Ba3Y4O9 before investigating the structural properties of Zr-substituted Ba3Y4O9.Note that Ba and O ions do not exactly form the two-dimensional closely-packed structure in the BaO3 layers. Fig. S6(c, d) and S7† show the two types of O displacements in the BaO3 layers (types I and II). Focusing on the six O ions around a Ba ion, three O ions are displaced from the hexagonal lattice points to the Ba ion, while the other three are displaced away from the Ba ion. The displacement directions of O ions are opposite between the two types of O displacements. In the homo-stacking regions, the two BaO3 layers with different types of O displacements are stacked, leading to the octahedral interstitial space but not the triangular prism.
In terms of the orientation of the BaO3 triangles, the orientations are different by ∼60° between the two types. The alternate orientation of BaO3 triangles along the c-axis is not limited only to the hetero-stacking regions, which are the same also in the hetero-stacking regions. However, the low-energy P1 structure exhibits exceptional stacking concerning the alternate orientation, which originates from the number of BaO3 layers in the unit cell. Since the alternate orientation of BaO3 triangles along the c-axis requires an even number of BaO3 layers in the unit cell, the MD simulation in the employed supercell including nine BaO3 layers found a low-symmetry P1 structure with the violation of the alternate orientation as a low-energy structure.
From the above findings, we here reconstructed the most likely stable structure. Specifically, the unit cell of the R3 structure was doubled along the c-axis, and the BaO3 triangles in the BaO3 layers are alternately oriented along the c-axis. The offsets of the Ba and O positions along the c-axis in each BaO3 layer were set based on those in the R3 structure. After the structural optimization, a R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure (see Fig. 5 and Ba3Y4O9_R
c structure (see Fig. 5 and Ba3Y4O9_R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c_predicted.cif in the ESI†) was obtained, whose calculated total energy is −0.39 eV per f.u. vs. the R3 structure and −0.06 eV per f.u. vs. the P1 structure. This means that the R
c_predicted.cif in the ESI†) was obtained, whose calculated total energy is −0.39 eV per f.u. vs. the R3 structure and −0.06 eV per f.u. vs. the P1 structure. This means that the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure with a relatively high symmetry is energetically reasonable, in which there are two types of Ba ions (Ba1 and Ba2), two types of Y ions (Y1 and Y2), and two types of O ions (O1 and O2). The Y1 and Y2 ions are located in the hetero-stacking and homo-stacking regions, respectively. In the subsequent subsection, we examine the validity of the obtained R
c structure with a relatively high symmetry is energetically reasonable, in which there are two types of Ba ions (Ba1 and Ba2), two types of Y ions (Y1 and Y2), and two types of O ions (O1 and O2). The Y1 and Y2 ions are located in the hetero-stacking and homo-stacking regions, respectively. In the subsequent subsection, we examine the validity of the obtained R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure by Rietveld analysis of the XRD pattern of the Ba-def Ba3Y4-Zr0 sample.
c structure by Rietveld analysis of the XRD pattern of the Ba-def Ba3Y4-Zr0 sample.
 | ||
Fig. 5 Crystal structure of Ba3Y4O9 (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) obtained by first-principles calculations. While 9 layers of BaO3 are stacked along the c-axis in the unit cell of the R3 structure reported in the database (Fig. 1), 18 layers of BaO3 are stacked along the c-axis in the unit cell of the R c) obtained by first-principles calculations. While 9 layers of BaO3 are stacked along the c-axis in the unit cell of the R3 structure reported in the database (Fig. 1), 18 layers of BaO3 are stacked along the c-axis in the unit cell of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure. While there are both triangular-prismatic YO6 and octahedral YO6 in the R3 structure, there is only octahedral YO6 in the R c structure. While there are both triangular-prismatic YO6 and octahedral YO6 in the R3 structure, there is only octahedral YO6 in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure. c structure. | ||
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c). The results of the refinement are shown in Fig. 6, Table 2, and Table S1.†Rwp, Rexp, and GOF are the weighted profile reliability factor (R-factor), the expected R-factor, and goodness of fit value (=Rwp/Rexp), respectively. Although the value of Rwp was relatively high36 in both refinements with the R3 structure and the R3c structure, Rwp and GOF slightly decreased using the R
c). The results of the refinement are shown in Fig. 6, Table 2, and Table S1.†Rwp, Rexp, and GOF are the weighted profile reliability factor (R-factor), the expected R-factor, and goodness of fit value (=Rwp/Rexp), respectively. Although the value of Rwp was relatively high36 in both refinements with the R3 structure and the R3c structure, Rwp and GOF slightly decreased using the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure instead of the R3 structure. Besides, the unindexed diffraction peak at 2θ = 33.3° mentioned in the opening of this subsection could be explained by the reflection of the (119) plane in the R
c structure instead of the R3 structure. Besides, the unindexed diffraction peak at 2θ = 33.3° mentioned in the opening of this subsection could be explained by the reflection of the (119) plane in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure. As shown in Fig. S8,† the (119) plane reflection is considered to be attributed to oxygen atoms in the R
c structure. As shown in Fig. S8,† the (119) plane reflection is considered to be attributed to oxygen atoms in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure. The same reflection attributed to oxygen atoms could not occur in the R3 structure due to the co-existence of a triangular-prismatic YO6 unit and an octahedral YO6 unit. Therefore, the R
c structure. The same reflection attributed to oxygen atoms could not occur in the R3 structure due to the co-existence of a triangular-prismatic YO6 unit and an octahedral YO6 unit. Therefore, the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure consisting of 18 stacking of BaO3 layers is probably more realistic for the unit cell of Ba3Y4O9 than the R3 structure consisting of 9 stacking of BaO3 layers.¶
c structure consisting of 18 stacking of BaO3 layers is probably more realistic for the unit cell of Ba3Y4O9 than the R3 structure consisting of 9 stacking of BaO3 layers.¶
 | ||
Fig. 6 Results of the Rietveld refinement of the Ba-def Ba3Y4-Zr0 sample with (a) the structure reported in the database (Fig. 1, space group R3) and (b) the one obtained in this work (Fig. 5, space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c). The fitting parameters are summarized in Table 2 and Table S1.† c). The fitting parameters are summarized in Table 2 and Table S1.† | ||
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure model (Fig. 5). The measurement was carried out at room temperature. While the atomic positions of Ba1, Y1, Y2, O1, and O2 in addition to the occupancies at Ba1 and Ba2 sites were refined, the isotropic atomic displacement factor was set to 0.01 for all atoms. The chemical composition was assumed to be the same as the nominal composition (Ba2.67Y4.00O8.67). Because the occupancy at the O2 site exceeded 1 when the value was used as a variable, the value was set to be 1 in the refinement. Lattice parameters were refined to be a = 6.11492(19) Å and c = 50.4058(9) Å. Rwp, Rexp, and GOF were 20.36%, 7.72%, and 2.64, respectively
c structure model (Fig. 5). The measurement was carried out at room temperature. While the atomic positions of Ba1, Y1, Y2, O1, and O2 in addition to the occupancies at Ba1 and Ba2 sites were refined, the isotropic atomic displacement factor was set to 0.01 for all atoms. The chemical composition was assumed to be the same as the nominal composition (Ba2.67Y4.00O8.67). Because the occupancy at the O2 site exceeded 1 when the value was used as a variable, the value was set to be 1 in the refinement. Lattice parameters were refined to be a = 6.11492(19) Å and c = 50.4058(9) Å. Rwp, Rexp, and GOF were 20.36%, 7.72%, and 2.64, respectively
| Atom | x | y | z | Occupancy | Wyckoff position |
|---|---|---|---|---|---|
| Ba1 | 0 | 0 | 0.0410(2) | 0.862(11) | 12c |
| Ba2 | 0 | 0 | 0.25 | 0.942(22) | 6a |
| Y1 | 0 | 0 | 0.1093(2) | 1 | 12c |
| Y2 | 0 | 0 | 0.1723(2) | 1 | 12c |
| O1 | −0.018(5) | 0.565(5) | 0.4727(5) | 0.9445 | 36f |
| O2 | 0 | 0.418(7) | 0.75 | 1 | 18e |
From the structural refinement as summarized in Table 2, barium vacancies (V′′Ba) are preferably introduced on Ba1 sites with generating O-ion vacancies  on O1 sites. It suggests that the deficit of BaO according to eqn (2) tends to form on a BaO3 layer sandwiched between the homo-stacking region and the hetero-stacking region.
on O1 sites. It suggests that the deficit of BaO according to eqn (2) tends to form on a BaO3 layer sandwiched between the homo-stacking region and the hetero-stacking region.
3.3 Identification of Zr-substitution sites in Ba3Y4O9
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure of Ba3Y4O9 with a Zr ion at a Y1 or Y2 ion. Zr substitution on the Y1 site is energetically favorable compared to that at the Y2 site, where the difference in the calculated substitution energy is 0.35 eV per site. The site selectivity of Zr ions is reasonable because the local structure around the Y1 site in the hetero-stacking region is similar to that around the Zr sites in BaZrO3 with the cubic perovskite structure.
c structure of Ba3Y4O9 with a Zr ion at a Y1 or Y2 ion. Zr substitution on the Y1 site is energetically favorable compared to that at the Y2 site, where the difference in the calculated substitution energy is 0.35 eV per site. The site selectivity of Zr ions is reasonable because the local structure around the Y1 site in the hetero-stacking region is similar to that around the Zr sites in BaZrO3 with the cubic perovskite structure.
Note that we cannot discuss the trend of Zr substitution sites in the high-concentration case based on the obtained computational results because the Zr substitution energies were calculated under the assumption of diluting Zr ions without Zr–Zr interactions. The EXAFS analyses can reveal the realistic site preference of Zr ions in densely Zr-substituted samples.
The calculation results suggested that the neighboring condition of Zr atoms in the Ba3Y4O9 was expected to be similar to that in the BaZrO3 structure at least in the low Zr concentration. Thereby, we evaluated the local environment of Zr in the Ba-def Ba3Y4-Zrx samples by the curve fitting assuming Zr in BaZrO3 as an absorption site. For the curve fitting of the EXAFS spectra collected at Y K-edge, we assumed that Y which fully substituted for Zr in BaZrO3 is an absorption site. Besides, as shown in Fig. S9 and S10,† we took account of the multiple-scattering paths with relatively high contributions for the EXAFS spectra as well as the single-scattering paths for the curve fittings.
The fitting results and the R-factors are shown in Fig. 7 (more detailed information such as the fitting parameters is summarized in the ESI†). For reference, Fig. S10† shows the simulated EXAFS spectrum of BaZrO3 with the assumption that Zr is an absorption site. The R-factors of the curve fittings for the EXAFS spectra collected at the Zr K-edge are sufficiently small at any Zr-substitution level, while those at the Y K-edge are relatively large and tend to increase with an increase in the substitution level. This indicates that Zr ions predominantly occupy Y ion sites in the hetero-stacking regions even though the substitution level becomes high. In conclusion, it was found that the local environment of Zr ions in Ba3Y4O9 is very close to that in BaZrO3 even when the Zr substitution level is relatively high.
3.4 Crystal structure of Zr-substituted Ba3Y4O9
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) significantly increased with an increase in the Zr substitution level in Ba3Y4O9, whereas the d-spacing of the (1014) plane (d1014) was hardly changed. The d-spacing is written as follows using a and c which are the lattice parameters of the hexagonal unit cell along the a-axis and the c-axis, respectively.
c) significantly increased with an increase in the Zr substitution level in Ba3Y4O9, whereas the d-spacing of the (1014) plane (d1014) was hardly changed. The d-spacing is written as follows using a and c which are the lattice parameters of the hexagonal unit cell along the a-axis and the c-axis, respectively.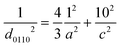 | (4) |
 | (5) |
Combining eqn (4) and (5), the following relationship is obtained.
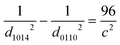 | (6) |
According to eqn (6), the lattice parameter c should decrease with an increase in the Zr substitution level in Ba3Y4O9. On the other hand, the d-spacing of (300) (d300) decreased with an increase in the Zr substitution level, indicating a decrease in the lattice parameter a. Therefore, according to eqn (4), the Zr substitution should cause an increase in the lattice parameter c, which is inconsistent with eqn (6). It suggests that the Zr substitution for Y in Ba3Y4O9 does not only simply change the lattice parameter of the unit cell but also the need for re-indexing the XRD patterns of Zr-substituted Ba3Y4O9.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c). While diffraction peaks with weak intensities could not be explained by the R
c). While diffraction peaks with weak intensities could not be explained by the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure as mentioned in the previous sub-subsection, those with high intensities could be relatively well fitted. It suggests that the strong diffraction peaks were derived from a common lattice among the Zr-substituted Ba3Y4O9 samples. Therefore, in order to obtain the common lattice among Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples, we carried out Pawley refinement and the charge flipping method using the starred diffraction peaks in Fig. 4(a).25,26
c structure as mentioned in the previous sub-subsection, those with high intensities could be relatively well fitted. It suggests that the strong diffraction peaks were derived from a common lattice among the Zr-substituted Ba3Y4O9 samples. Therefore, in order to obtain the common lattice among Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples, we carried out Pawley refinement and the charge flipping method using the starred diffraction peaks in Fig. 4(a).25,26
As a result, we obtained the common lattice (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as shown in Fig. 8(a). Because strong diffraction peaks in oxides are usually attributed to cations, the common lattice is considered to be composed of Ba2+, Y3+, and Zr4+. Using the common lattice and the starred diffraction peaks in Fig. 4(a), we carried out Rietveld refinement of Ba-def Ba3Y4-Zrx samples. For the refinement, the diffraction peaks without stars in Fig. 4(a) were included in the background. The fitting results are shown in the ESI (Fig. S21–S24†) and the lattice parameters (aelm and celm where the subscript “elm” corresponds to a “cationic elementary unit” as described in the following sub-subsection) are summarized in Fig. 8(b) and Table 3. With an increase in the Zr substitution level, aelm significantly decreased while celm slightly increased, resulting in the reduction of the volume of the common lattice. It is in good agreement with the effective ionic radius relationship between Y3+ (6-coordination) (0.90 Å) and Zr4+ (6-coordination) (0.72 Å).34,35
m) as shown in Fig. 8(a). Because strong diffraction peaks in oxides are usually attributed to cations, the common lattice is considered to be composed of Ba2+, Y3+, and Zr4+. Using the common lattice and the starred diffraction peaks in Fig. 4(a), we carried out Rietveld refinement of Ba-def Ba3Y4-Zrx samples. For the refinement, the diffraction peaks without stars in Fig. 4(a) were included in the background. The fitting results are shown in the ESI (Fig. S21–S24†) and the lattice parameters (aelm and celm where the subscript “elm” corresponds to a “cationic elementary unit” as described in the following sub-subsection) are summarized in Fig. 8(b) and Table 3. With an increase in the Zr substitution level, aelm significantly decreased while celm slightly increased, resulting in the reduction of the volume of the common lattice. It is in good agreement with the effective ionic radius relationship between Y3+ (6-coordination) (0.90 Å) and Zr4+ (6-coordination) (0.72 Å).34,35
 | ||
| Fig. 8 (a) A common lattice obtained by the Pawley refinement and the charge flipping method with the starred diffraction peaks in Fig. 4(a). (b) The relationship between the lattice parameters of the common lattices and the Zr substitution levels in the samples. The parameters were obtained by the Rietveld refinement of Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples with the common lattice. Error bars were not clearly visible because of the small values compared to the lattice parameters. | ||
| Sample name | Lattice parameters of the common lattice (i.e., cationic elementary unit) | R wp/% | R exp/% | GOF | Diffraction peak near to the (1010) plane in Ba3Y4O9 (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) which consists of 14 stackings of cationic elementary units c) which consists of 14 stackings of cationic elementary units |
||
|---|---|---|---|---|---|---|---|
| a elm/Å | c elm/Å | d-Spacing/Å | l value in (10l) in the structure of N stackings of cationic elementary units along the c-axis | ||||
| Ba-def Ba3Y4-Zr0 | 6.11426(26) | 3.60020(7) | 22.41 | 7.72 | 2.90 | 3.657 | 4.98 when N = 7 |
| Ba-def Ba3Y4-Zr10 | 6.05875(28) | 3.61697(8) | 19.61 | 7.66 | 2.56 | 3.778 | 1.99 when N = 3 |
| Ba-def Ba3Y4-Zr20 | 6.03593(20) | 3.61888(5) | 17.83 | 7.42 | 2.40 | 3.849 | 7.00 when N = 11 |
| Ba-def Ba3Y4-Zr30 | 6.01455(26) | 3.62109(7) | 19.35 | 7.36 | 2.63 | 3.909 | 7.96 when N = 13 |
For x = 0 in Fig. 8(b), aelm is almost the same as the a-axis lattice parameter of the unit cell of the Ba3Y4O9 structure obtained in this work. On the other hand, celm is almost equal to one-fourteenth of the c-axis of Ba3Y4O9. This relationship between the common lattice (Fig. 8(a)) and the unit cell of Ba3Y4O9 (Fig. 5) is explained in Fig. 9(a). The hexagonal unit cell of Ba3Y4O9 is represented as fourteen stacks of the small unit defined by cationic periodicity, and the stacks correspond to the common lattice. In this work, the common lattice is defined as a “cationic elementary unit”. Because both the cation configurations (Ba and Y) and the lengths along the c-axis are different between the fourteen types of cationic elementary units, the major X-ray diffractions and the lattice parameters (aelm and celm) of the Ba-def Ba3Y4-Zr0 sample are considered to be derived from the average structure of the whole elementary units without a distinction of the cation elements.
 | ||
Fig. 9 Crystal structures of (a) Ba3Y4O9 (space group: R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) and (b) BaZrO3 (space group: Pm c) and (b) BaZrO3 (space group: Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) in hexagonal representation. For simplicity, O ions are abbreviated. In (b), the cationic elementary unit without a distinction between Ba and Zr ions is obtained by the conversion from a body-centered cubic (BCC) lattice to a hexagonal one. For drawing the crystal structures, we used the Blender software.37 m) in hexagonal representation. For simplicity, O ions are abbreviated. In (b), the cationic elementary unit without a distinction between Ba and Zr ions is obtained by the conversion from a body-centered cubic (BCC) lattice to a hexagonal one. For drawing the crystal structures, we used the Blender software.37 | ||
Therefore, regardless of the Zr substitution, the diffraction peaks of Ba3Y4O9 in Fig. 4(a) can be grouped into two families as follows. First, the starred peaks are attributed to the average structure of the cationic elementary units while ignoring the distinction between Ba ions and Y/Zr ions. Second, the other diffraction peaks belong to scattering from O ions and/or the long-range ordered structure from the view of the cationic elementary unit with cation distinction.
As mentioned in the section “Introduction”, BaO3 layers are periodically stacked as –A–B–C– (–α–β–γ– from top to bottom in Fig. 10) sequences. In contrast, Ba and Zr layers are alternately stacked with another sequence as –α–γ–β– from top to bottom, and one sequence is composed of one cationic elementary unit. It indicates that, similarly to BaO3 layers, both Ba and Zr layers are two-dimensional hexagonal (triangular) lattices.|| Therefore, the stacking period of BaZrO3 is written with six types of layers: –Ba layer (α)–Zr layer (γ)–Ba layer (β)–Zr layer (α)–Ba layer (γ)–Zr layer (β)–. Ignoring oxygen atoms in the BaZrO3 structure, such a stacking sequence is considered to be equal to the description of a body-centered cubic (BCC) lattice in which Ba atoms and Zr atoms are ordered.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction. The Ba-ion and Y-ion layers are stacked along the c-axis in the order Ba1–Y1–Ba2–Y1–Ba1–Y2–Y2 forming the stacking sequences as α–γ–β from top to bottom. Considering the periodicity of O ions on BaO3 layers with forming octahedral YO6 units (as discussed in the subsection “Low energy structure found by first-principles calculations”), the number of cation layers in the unit cell of Ba3Y4O9 is (7 × 3) × 2 = 42.
00] direction. The Ba-ion and Y-ion layers are stacked along the c-axis in the order Ba1–Y1–Ba2–Y1–Ba1–Y2–Y2 forming the stacking sequences as α–γ–β from top to bottom. Considering the periodicity of O ions on BaO3 layers with forming octahedral YO6 units (as discussed in the subsection “Low energy structure found by first-principles calculations”), the number of cation layers in the unit cell of Ba3Y4O9 is (7 × 3) × 2 = 42.
There are two kinds of stacking regions in the Ba3Y4O9 structure. One is the alternate stacking of Ba and Y atoms (e.g., Ba1 layer (α)–Y1 layer (γ)–Ba2 layer (β)–Y1 layer (α)–Ba1 layer (γ)) along the c-axis, which corresponds to the hetero-stacking region in Fig. 5. The other is the symmetrical stacking of Ba and Y atoms (e.g., Ba1 layer (α)–Y2 layer (γ)–Y2 layer (β)–Ba1 layer (α)), which corresponds to the homo-stacking region in Fig. 5. The former sequence is also confirmed in the BaZrO3 structure and, thus, is considered a cubic perovskite-like region as pointed out in the subsection “Identification of Zr-substitution sites in Ba3Y4O9”. If we were to describe it by ignoring the charge neutrality, it would be written as BaYO3.
Conventionally, perovskite(-related) oxides are classified according to the stacking sequences of only AO3 layers.22 While Ba3Y4O9 could be regarded as one of the layered perovskites with partial deficits of AO3 layers, such complex oxides are not sufficiently concerned possibly due to the lack of the appropriate representation for the homo-stacking region in the Ramsdell notation. Through the crystallographic investigation of Ba3Y4O9 compared to BaZrO3 in this work, our adopted description using cationic elementary units and stacking sequences based on the BCC structure is very helpful in understanding the complex crystal structure of perovskite-related oxides.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure. Therefore, we first guessed the periodicity number N with the values of l in the indices using the diffraction peak at around 2θ = 23°. The ratio of the l value and the periodic number N is obtained as follows:
c structure. Therefore, we first guessed the periodicity number N with the values of l in the indices using the diffraction peak at around 2θ = 23°. The ratio of the l value and the periodic number N is obtained as follows: | (7) |
Because Zr ions in the substituted Ba3Y4O9 samples are in the hetero-stacking regions according to the subsection “Identification of Zr-substitution sites in Ba3Y4O9”, the Zr substitution possibly decreases the frequency of the homo-stacking region in the stacking sequence. From the N values in Table 3, the stacking frequencies of the homo-stacking region are presumed to be every 7, 9, 11, and 13 cationic layers in Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples, respectively. Hence, the minimum periodicities along the c-axis for Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples are 21, 9, 33, and 39 layers, respectively, which are the lowest common multiples of 3 (the type of periodicity of cationic layers in the cationic elementary unit (–α–γ–β–)) and the stacking frequencies of the homo-stacking region. Considering the alternate coordination of BaO3 triangles as explained in the sub-subsection “Low energy structure found by first-principles calculations”, the number of BaO3 layers in a unit cell must be an even number. Therefore, the number of cationic layers along the c-axis in a unit cell is 42, 9, 66, and 39 for Ba-def Ba3Y4-Zrx (x = 0, 10, 20, and 30) samples, respectively.
For the validation of our proposed mechanism, we prepared the structure models for the substituted Ba3Y4O9 samples for satisfying both the above cationic stacking sequences and the formation of octahedral YO6 units. Fig. 12 shows a comparison between the unsubstituted Ba3Y4O9 structure (Fig. 12(a)) and the model structures for Ba-def Ba3Y4-Zr10 (Fig. 12(b)), Ba-def Ba3Y4-Zr20 (Fig. 12(c)), and Ba-def Ba3Y4-Zr30 (Fig. 12(d)) samples. Note that the charge neutrality is ignored when the three structure models are constructed.
We carried out the Rietveld refinements of the substituted Ba3Y4O9 samples with the model structures. The results are summarized in Table 4 and detailed information such as atomic displacement is shown in the ESI.† Both the weighted R-factors (Rwp) and goodness of fit (GOF) of the substituted samples dramatically decreased when using the model structures instead of the structure of unsubstituted Ba3Y4O9, suggesting that our proposed mechanism of the Zr substitution effect on the Ba3Y4O9 structure is (at least qualitatively) probable.¶ A decrease in a volume fraction of the homo-stacking region in the substituted Ba3Y4O9 structure is equal to an increase in the fraction of the cubic perovskite-like region including locally-formed BaZrO3.** This behavior possibly relates to the improvement of the chemical stability of the substituted Ba3Y4O9 at intermediate temperatures14 because BaZrO3 is relatively stable to H2O and CO2 at those temperatures.38,39
| Sample name | Ba-def Ba3Y4-Zr0 | Ba-def Ba3Y4-Zr10 | Ba-def Ba3Y4-Zr20 | Ba-def Ba3Y4-Zr30 | |
|---|---|---|---|---|---|
| Model structure | Fig. 12(a) | Fig. 12(b) | Fig. 12(c) | Fig. 12(d) | |
| Stacking number N | 14 | 3 | 22 | 13 | |
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
|
| Stoichiometric composition of the structure ignoring the charge neutrality | Ba3Y4O9 (Ba/Y = 0.75) | Ba4Y5O12 (Ba/Y = 0.80) | Ba5Y6O15 (Ba/Y = 0.83) | Ba6Y7O18 (Ba/Y = 0.86) | |
| Chemical composition of the sample | Ba2.67Y4.00O8.67 (nominal composition) (Ba/Y = 0.67) | Ba3.14(Y0.90Zr0.10)5.00O10.89 (WDS analysis) (Ba/(Y + Zr) = 0.63) | Ba3.58(Y0.80Zr0.20)6.00O13.18 (WDS analysis) (Ba/(Y + Zr) = 0.60) | Ba4.51(Y0.69Zr0.31)7.00O16.09 (WDS analysis) (Ba/(Y + Zr) = 0.64) | |
| Frequency of the homo-stacking region along the c-axis | Every 7 cationic layers | Every 9 cationic layers | Every 11 cationic layers | Every 13 cationic layers | |
| R wp of Rietveld refinement | 20.36% | 18.09% (cf., 27.20% when fitted with Fig. 12(a)) | 19.71% (cf., 31.47% when fitted with Fig. 12(a)) | 15.73% (cf., 28.20% when fitted with Fig. 12(a)) | |
| GOF of Rietveld refinement | 2.64 | 2.36 (cf., 3.55 when fitted with Fig. 12(a)) | 2.65 (cf., 4.24 when fitted with Fig. 12(a)) | 2.13 (cf., 3.83 when fitted with Fig. 12(a)) | |
| Lattice parameter | a (Å) | 6.11492(19) | 6.05888(19) | 6.03577(20) | 6.01463(15) |
| c (Å) | 50.4058(9) | 10.85161(22) | 79.6139(14) | 47.0744(8) | |
Focusing on site occupancies in the substituted Ba3Y4O9 structure as shown in Tables S12–S14,† the occupancy of Ba ions in the homo-stacking region tends to be smaller than that in the hetero-stacking region. This indicates that the deficit of Ba ions with O ions in BaO3 layers according to eqn (2) occurred mainly in the homo-stacking regions. Besides, comparing the actual chemical compositions of the substituted Ba3Y4O9 with the stoichiometric ones in the model structure, O ions were deficient, not excess. Therefore, the generation of interstitial O ions according to eqn (1) did not occur in the substituted Ba3Y4O9 samples probably due to the deficit of BaO. Moreover, based on this finding, the oxide-ion conduction in the substituted Ba3Y4O9 is probably mediated by oxide-ion vacancies 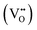 .
.
In conclusion, Ba3Y4O9 with Zr substitution is considered a modular structure consisting of the homo-stacking region and the hetero-stacking region (i.e., cubic-perovskite-like region). In other words, Ba3Y4O9 is classified as a layered perovskite compound. The stacking behavior is similar to other layered perovskites such as Ruddlesden–Popper phases (e.g., Srn+1TinO3n+1 (n = 1, 2, 3, and ∞) which consists of the stacking of a rock-salt structure region and a perovskite-structure region).22 The stacking direction of cationic layers is different between the Ruddlesden–Popper phase ((100) plane is stacked along the c-axis) and the substituted Ba3Y4O9 phase ((111) plane is stacked along the c-axis). However, as far as we know, there was little attention paid to the stacking sequences of not only AO3 layers but also B layers for describing the perovskite-related structure (AxByOz) in the previous studies. As the target material in this work, the substitution effect on the perovskite-related structure is not always simple, and the methodology we adopted in this work is very useful for understanding the diffraction peaks attributed to the long-range order (so-called superlattice reflection) from a viewpoint of cationic elementary units.
As mentioned above, the substitution effect on the structure significantly influences other properties such as chemical stability and ionic-conduction behavior. We believe that the interpretation methodology for layered perovskites consisting of bivalent and trivalent cations in this paper helps to design and develop new perovskite-related materials.
4 Conclusion
In this work, we investigated the structural properties of Ba3Y4O9 with/without Zr substitution for Y. For a comprehensive understanding of the Ba3Y4O9 structure, we adopted another description of perovskite(-related) structures based on cationic stacking sequences from the viewpoint of the BCC structure. In the description, the crystal structure of Ba3Y4O9 consists of two regions: the hetero-stacking region (Ba–Y–Ba–Y–Ba) and the homo-stacking region (Ba–Y–Y–Ba). The hetero-stacking region is similar to the cubic perovskite structure.First, we revisited the crystal structure of Ba3Y4O9 by focusing on the unindexed diffraction peak in a previous study. The revised unit cell of Ba3Y4O9 is double along the c-axis compared to the reported structure, and the BaO3 triangles in the BaO3 layers are alternately oriented along the c-axis. Besides, we theoretically and experimentally revealed that Zr tends to substitute Y in the hetero-stacking region in the Ba3Y4O9 structure, and therefore the local environment of Zr in Ba3Y4O9 is similar to that in BaZrO3. Moreover, an increase in the Zr substitution level causes a decrease in the frequency of the homo-stacking region in the stacking sequences. This is why some of the X-ray diffraction peaks exhibited irregular behavior that cannot be explained only by the change in the lattice parameters of Ba3Y4O9.
In our previous work, the Zr substitution for Y in Ba3Y4O9 leads to the enhancement of chemical stability at intermediate temperatures. Based on the present study, the structural change induced by the Zr substitution is probably responsible for the stability of the material. Now we are preparing a further publication focusing on the conductivity behavior and the chemical stability of Zr-substituted Ba3Y4O9.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding authors on reasonable requests.Author contributions
Katsuhiro Ueno: conceptualization, data curation, investigation, methodology, supervision, visualization, writing – original draft, and writing – review & editing. Atsunori Hashimoto: data curation, investigation, visualization, writing – original draft, and writing – review & editing. Kazuaki Toyoura: conceptualization, investigation, methodology, resources, software, supervision, writing – original draft, and writing – review & editing. Naoyuki Hatada: investigation and writing – review & editing. Shigeo Sato: methodology and writing – review & editing. Tetsuya Uda: resources, funding acquisition, project administration, supervision, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by Sumitomo Electric Industries, Ltd, IHI Corporation, Mitsui Mining & Smelting Co., Ltd, and Tokyo Gas Co., Ltd. The synchrotron radiation experiments were performed at the BL14B2 of Spring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2021B1865). The authors would like to thank Dr Hironori Ofuchi for technical assistance with the EXAFS experiments.References
- T. Mori, H. Yamamura, H. Ogino, H. Kobayashi and T. Mitamura, J. Ceram. Soc. Jpn., 1994, 102, 1047–1050 CrossRef CAS.
- S. Fang, A. Takagaki, M. Watanabe and T. Ishihara, Catal. Sci. Technol., 2020, 10, 2513–2522 RSC.
- S. Fang, A. Takagaki, M. Watanabe, J. T. Song and T. Ishihara, Catal. Sci. Technol., 2020, 117743 CAS.
- S. Devi, A. Khatkar, A. Hooda, V. B. Taxak, P. Boora, P. Dhankhar and S. P. Khatkar, J. Solid State Chem., 2020, 121333 CrossRef CAS.
- A. Hooda, S. P. Khatkar, A. Khatkar, R. K. Malik, M. Kumar, S. Devi and V. B. Taxak, J. Lumin., 2020, 217, 116806 CrossRef CAS.
- A. Hooda, A. Khatkar, P. Boora, S. Singh, S. Devi, S. P. Khatkar and V. B. Taxak, Optik, 2021, 228, 166176 CrossRef CAS.
- J. Li, R. Pang, Z. Yu, L. Liu, H. Wu, H. Li, L. Jiang, S. Zhang, J. Feng and C. Li, J. Rare Earths, 2018, 36, 680–684 CrossRef CAS.
- K. Li, H. Lian, M. Shang and J. Lin, Dalton Trans., 2015, 44, 20542–20550 RSC.
- S. Liu, J. Cui, L. Liu, W. You, M. C. Parmar, Q. Zeng, R. Wang and X. Ye, J. Lumin., 2019, 213, 174–183 CrossRef CAS.
- S. Liu, H. Ming, J. Cui, S. Liu, W. You, X. Ye, Y. Yang, H. Nie and R. Wang, J. Phys. Chem. C, 2018, 122, 16289–16303 CrossRef CAS.
- J. B. Goodenough, A. Manthiram, M. Paranthaman and Y. S. Zhen, Mater. Sci. Eng., B, 1992, 12, 357–364 CrossRef.
- T. Mori and H. Yamamura, Netsu Sokutei, 1996, 23, 20–28 CAS.
- M. Feng and J. B. Goodenough, Solid State Ionics, 1994, 68, 269–277 CrossRef CAS.
- K. Ueno, N. Hatada and T. Uda, Solid State Ionics, 2021, 368, 115709 CrossRef CAS.
- K. Ueno, N. Hatada, D. Han, K. Toyoura and T. Uda, J. Solid State Electrochem., 2020, 24, 1523–1538 CrossRef CAS.
- L. M. Lopato, Ceramurgia Int., 1976, 2, 18–32 CrossRef CAS.
- B. Szymanik, R. G. Buckley, H. J. Trodahl and R. L. Davis, Solid State Ionics, 1998, 109, 223–228 CrossRef CAS.
- J. Darriet and M. A. Subramanian, J. Mater. Chem., 1995, 5, 543 RSC.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- L. Katz and R. Ward, Inorg. Chem., 1964, 3, 205–211 CrossRef CAS.
- A. Guinier, G. B. Bokij, K. Boll-Dornberger, J. M. Cowley, S. Ďurovič, H. Jagodzinski, P. Krishna, P. M. De Wolff, B. B. Zvyagin, D. E. Cox, P. Goodman, Th. Hahn, K. Kuchitsu and S. C. Abrahams, Acta Crystallogr., Sect. A: Found. Crystallogr., 1984, 40, 399–404 CrossRef.
- R. J. D. Tilley, Perovskites: Structure-Property Relationships, John Wiley & Sons, Inc., West Sussex, 1st edn, 2016 Search PubMed.
- P. Babilo, T. Uda and S. M. Haile, J. Mater. Res., 2007, 22, 1322–1330 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357–361 CrossRef CAS.
- G. Oszlányi and A. Sütő, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 134–141 CrossRef PubMed.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kern, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8551–8559 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- B. H. Toby, Powder Diffr., 2006, 21, 67–70 CrossRef CAS.
- Blender Foundation, blender.org – Home of the Blender project – Free and Open 3D Creation Software, https://www.blender.org/, accessed March 7, 2023.
- K. Katahira, Y. Kohchi, T. Shimura and H. Iwahara, Solid State Ionics, 2000, 138, 91–98 CrossRef CAS.
- Y. Guo, Y. Lin, R. Ran and Z. Shao, J. Power Sources, 2009, 193, 400–407 CrossRef CAS.
- W. Zhang and K. Osamura, Mater. Trans., JIM, 1991, 32, 1048–1052 CrossRef CAS.
- J. Šesták, J. Kamarád, P. Holba, A. Tříska, E. Pollert and M. Nevřiva, Thermochim. Acta, 1991, 174, 99–114 CrossRef.
- K. Kawata, H. Maekawa, T. Nemoto and T. Yamamura, Solid State Ionics, 2006, 177, 1687–1690 CrossRef CAS.
- K. Saito, K. Fujii and M. Yashima, J. Solid State Chem., 2021, 122733 Search PubMed.
- D. Han, K. Kishida, K. Shinoda, H. Inui and T. Uda, J. Mater. Chem. A, 2013, 1, 3027 RSC.
- D. Han and T. Uda, ACS Appl. Mater. Interfaces, 2019, 11, 3990–4000 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt03544a |
| ‡ The attempts to synthesise of a single-phase sample of Ba-def Ba3Y4-Zr0 at 1600 °C often were not successful under either dry reducing atmospheres or dry oxidizing atmospheres. The low repeatability of the synthesis of the sample without the Zr substitution (Ba-def Ba3Y4-Zr0) is probably due to its chemical instability. In fact, Ba3Y4O9 is thermodynamically stable at 985–2140 °C and is expected to be decomposed into other oxides of barium and yttrium (e.g., BaY2O4) and/or barium (per)oxide below 985 °C.40,41 However, some groups reported their success in the preparation of the polycrystalline sample of Ba3Y4O9 by the solid-state reaction method similar to us.13,17 Therefore, the polycrystalline Ba3Y4O9 sample is considered to be kinetically metastable even at room temperature. In this work, we adopt only the Ba-def Ba3Y4-Zr0 sample which was successfully synthesized in this investigation. |
| § The structural information of Ba3Y4O9 in the database is based on the powder XRD with neutron scattering measurements by Szymanik et al. in 1998,17 but the database commented that “standardized atom coordinates of some site(s) differ by >0.1 from the type-defining data set” in the Powder Diffraction File card. The structural model for the fitting in the paper was Ba3Y2Yb2O9 whose structure was determined from single-crystal XRD by H. K. Müller-Buschbaum and O. Schrandt in 1993.36 Besides, before the crystallographic report of Ba3Y2Yb2O9, the crystal structure of Ba3Sc4O9 was reported by L. M. Kovba and M. V. Paromova in 1970 and that of Ba3Yb4O9 was reported by J. Krüger and H. K. Müller-Buschbaum in 1983.37,38 Both of the groups asserted the existence of Sc3+ and Yb3+ with trigonal-prismatic coordination by the determination of the oxygen ion sites using only the X-ray measurement with different Fourier synthesis, not the neutron diffraction measurement. |
¶ The structural refinements of the Ba-deficient Ba3Y4O9 samples with/without Zr substitution were performed using the powder XRD patterns collected with a laboratory X-ray source (CuKα1). However, we could not obtain thermal displacement parameters in the refinements because some of the parameters were refined to be negative (even though the lower limits of the parameters were set to be 0). This possibly suggests the necessity of the powder XRD patterns with higher S/N ratios and/or the use of standard samples for the equipment. Hence, we set the thermal displacement parameters to 0.01 for all atoms in the refinements in this work. Noteworthy, Ba3Y4O9_R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c_predicted.cif in the ESI† is a predicted structure by first-principles calculation, not an experimentally determined structure of Zr-unsubstituted Ba3Y4O9. In particular, for the determination of the crystal structure of Ba3Y4O9 and the investigation of the influence of barium deficiency on its structural properties, the preparation of a high-purity (and, ideally, a single-crystal) sample with a stoichiometric composition is needed. Besides, in order to determine the position and occupancy of O ions more accurately, solid-state nuclear magnetic resonance (NMR) spectroscopy for 89Y and the powder neutron diffraction measurement are powerful tools.42,43 Moreover, the usage of synchrotron radiation for the XRD measurement is recommended in terms of the observation of diffraction peaks with quite low intensities and the usage of anomalous X-ray scattering to distinguish between Y and Zr ions.44,45 c_predicted.cif in the ESI† is a predicted structure by first-principles calculation, not an experimentally determined structure of Zr-unsubstituted Ba3Y4O9. In particular, for the determination of the crystal structure of Ba3Y4O9 and the investigation of the influence of barium deficiency on its structural properties, the preparation of a high-purity (and, ideally, a single-crystal) sample with a stoichiometric composition is needed. Besides, in order to determine the position and occupancy of O ions more accurately, solid-state nuclear magnetic resonance (NMR) spectroscopy for 89Y and the powder neutron diffraction measurement are powerful tools.42,43 Moreover, the usage of synchrotron radiation for the XRD measurement is recommended in terms of the observation of diffraction peaks with quite low intensities and the usage of anomalous X-ray scattering to distinguish between Y and Zr ions.44,45 |
| || The periodic stackings of A-atom layers and B-atom layers in perovskite ABO3 along the 〈111〉 axis are not equal to the closest packing although both A-atom layers and B-atom layers are a two-dimensional hexagonal (triangular) lattice. The comparison of the stacking sequence between the BCC (e.g., α-Fe, ferrite) and the FCC (e.g., γ-Fe, austenite) is shown in Fig. S25 in the ESI.† For the {111} stacking sequence, the BCC unit cell is composed of the stacking of six layers (–α–γ–β–α–γ–β–) while the FCC unit cell is composed of the stacking of three layers (–A–B–C–). |
| ** To determine the Zr substitution site in the substituted Ba3Y4O9 structures (Fig. 12(b)–(d)), the curve-fittings of FT EXAFS spectra collected at the Zr K-edge seem to be useful. However, in fact, it is too difficult to discuss the stable site of Zr in the substituted Ba3Y4O9 structure from the fittings because of the complex structure of the substituted Ba3Y4O9. For example, Fig. S32 and Table S15 in the ESI† show the fitting result of the Ba-def Ba3Y4-Zr30 sample by assuming a Y3 site in the substituted structure (Fig. 12(d)) as an absorption site. The R-factor of the fitting was 0.0055, which is conventionally regarded as well-fitted. On the other hand, the uncertainty of the fitting parameters was significantly large relative to that obtained in the fitting with the BaZrO3 structure (Table S4†). It is probably because the number of parameters is too high for the curve fitting of the spectra even though we used the bare minimum parameters to represent the local environment of the Y3 site. Therefore, we adopted the fitting results with the BaZrO3 structure for the identification of the local environment of Zr in the substituted Ba3Y4O9. |
| This journal is © The Royal Society of Chemistry 2024 |