Open Access Article
Open Access ArticleCompetitive adsorption mechanisms of Cd(II), Cu(II) and Pb(II) on bioinspired mesoporous silica revealed by complementary adsorption/isothermal titration calorimetry studies†
Cléophée
Gourmand
 *a,
Caroline
Bertagnolli
*a,
Caroline
Bertagnolli
 a,
Bénédicte
Prelot
a,
Bénédicte
Prelot
 b,
Anne
Boos
a,
Véronique
Hubscher-Bruder
b,
Anne
Boos
a,
Véronique
Hubscher-Bruder
 a and
Jérémy
Brandel
a and
Jérémy
Brandel
 *a
*a
aUniversité de Strasbourg, CNRS, IPHC UMR 7178, F-67000 Strasbourg, France. E-mail: jbrandel@unistra.fr
bICGM, Univ Montpellier, ENSCM, CNRS, Montpellier, France
First published on 31st January 2024
Abstract
This study presents the adsorption properties of a bioinspired grafted mesoporous silica material and the competitive effects between Cd(II) or Cu(II) and Pb(II) during the adsorption process. Glutathione, a natural antioxidant known for its metal binding properties, has been successfully grafted to SBA-15 mesoporous silica and the optimum adsorption parameters were determined. This original and multidisciplinary approach combines classical adsorption studies with thermodynamic investigations to understand the adsorption behavior of Cd(II), Cu(II) and Pb(II) on this material. To this end, isothermal titration calorimetry (ITC) has been used to elucidate the mechanisms of single-metal and two-metal adsorption. The results showed affinity in the order Pb(II) > Cu(II) > Cd(II) in single metal systems. Cd(II) adsorption relied mainly on physical contributions while Cu(II) and Pb(II) adsorption was shown to be chemically driven. Two-metal systems highlighted that Cd(II) and Pb(II) are adsorbed on the same coordination sites, whereas Cu(II) and Pb(II) are adsorbed on different sites. The material showed good selectivity and encouraging results were obtained on real effluents.
1. Introduction
Metals are natural components of the Earth's crust which can be easily released into the environment.1 Fluxes between the different Earth layers are controlled by natural events such as erosion, volcanic activity or natural wildfires.2,3 However these fluxes have found themselves greatly affected by the increase of anthropic activity in the past few decades.4,5 Indeed, the development of industrial activity leads to the release of large volumes of wastewater contaminated with multiple metal ions, leading states and non-governmental organizations to take preventive measures against water contamination.6–8 Despite the high percentage of treated water in high-income countries, the pollutants are not always fully removed from wastewater regardless of the treatment method,9,10 hence leading to the presence of micro-pollutants at the outlet of wastewater treatment plants. For instance, in the EU, out of the almost 3 kilotons (kt) of metallic contaminants reportedly emitted, around half of them (1.276 kt) are released in the environment after treatment, according to the European Pollutant Release and Transfer Register (E-PRTR) monitoring.11 These pollutants generate water or soil pollution and can enter the organism through food since more and more traces of metallic elements are found in food,12–15 and by inhalation or skin absorption of air pollution.16–18 Their accumulation and the prolonged exposition of living organisms can lead to harmful toxic effects.3,19 The most common metallic contaminants released in the environment are arsenic, cadmium, chromium, copper, lead, nickel, platinum, silver, tin, titanium, vanadium and zinc.3,18,20,21 Thus, metallic pollution has become an important societal issue as some of these pollutants are highly toxic even at low concentrations.In the last few years in Europe, among all these pollutants, copper, lead and cadmium compounds are respectively the second, fifth and seventh most emitted metallic pollutants, according to the E-PRTR database. Lead compounds are widely used in industry: car batteries, electroplating, electronics, paints, steel, ceramics, pigment and fertilizers are among the main industrial uses of lead.18,22–26 In the case of cadmium, its main industrial uses are in metallurgy, dyes and paints, pesticides and fertilizers, in Ni–Cd batteries and as an anticorrosive agent.18 These two elements which have no known function in the organism3 are now classified by the International Agency for Research on Cancer as “carcinogenic to humans” (Cd-group 1) and “probably carcinogenic to humans” (Pb-group 2A).25,27 Unlike lead and cadmium, copper is considered as an essential element for the organism as many enzymes and proteins are copper-dependent.3,28 The high concentrations and the constant presence of copper in wastewater originate from its wide use, mainly in electroplating, electronic, ore mining, steel, refinery, dye, pesticide and plastic industries.18,21–24 On top of all the industrial uses of copper, it is also found domestically in coins, constructions and electrical systems.29,30 This may explain the presence of copper in rain waters, sometimes in higher concentrations than the permitted emission limit.31,32 Thus, it is essential to remove metallic pollutants such as cadmium, copper and lead from wastewater.
Conventional treatment methods are chemical precipitation, flotation, ion exchange, coagulation/flocculation, electrochemical removal and membrane technology.18,23,24,33,34 Despite their high efficiency, these current technologies show several drawbacks. They can be expensive to operate and/or maintain (membranes, ion exchange, electrochemistry), energy intensive (membranes, electrochemistry), can lead to a huge amount of waste and sludge that cannot be recovered (chemical precipitation, coagulation/flocculation) or need a large amount of chemicals (chemical precipitation). Adsorption appeared as a good economically and technically viable alternative because of its simplicity, low operating costs, waste production and energy consumption, while achieving adequate metal removal.35
In order to obtain an efficient and selective material for the adsorption process, the metal binding ability involved in the phytoremediation phenomenon of plants was combined with the porous properties of mesoporous silica. Glutathione (GSH – Fig. 1) plays a central role in phytoremediation as an essential metal chelator.36 This well-known cellular reagent is of high importance in cellular metabolism. It is a tripeptide, γ-L-glutamyl-L-cysteinyl-glycine, with high affinity for metallic ions, due to its multiple chelating functions, such as a thiol group on the cysteine amino acid, two amide groups, two carboxylic groups and an amine, all these chemical groups constituting potential metal binding sites.36–39 That is why an adsorbent based on highly porous SBA-15 silica combined with the binding and metal removal properties of glutathione has been developed.40
The characterization of the material and its adsorption capacities for Cd(II) were presented in a previous study.40 However, the use of an adsorbent in real effluents is conditioned to its ability to either be selective towards certain valuable elements, or remove all the toxic contaminants present in it.40 Therefore, it is necessary to understand the phenomena involved in the adsorption process and to gain insights into the competitive effects between different pollutants. Isothermal titration calorimetry (ITC) appeared as a good technique to obtain information both on the adsorption thermodynamics and competitive effects in this system.41 Originally designed for liquid–liquid thermodynamic studies, the recent years have seen an increase in the use of ITC for solid–liquid interactions35,41–46 but to the best of our knowledge, very few studies have focused on the application of ITC for solid–liquid interactions on grafted mesoporous silica.
In this work, the adsorption properties of the SBA-15-glutathione system for Cu(II) and Pb(II) will be described and discussed relative to the results obtained previously for Cd(II).40 To assess the role and impact of the grafting of GSH, the results were compared with non-grafted SBA-15. The combination of adsorption and ITC studies of these systems allowed gaining insights into the mechanisms of adsorption and particularly into the competitive effects on the adsorption of Pb(II) in the presence of other metallic ions such as Cd(II) and Cu(II). To show the applicability of this material in real industrial effluents, the material was tested on battery recycling wastewater.
2. Experimental section
2.1. Reagents
The following reagents were purchased from Sigma-Aldrich: (3-aminopropyl)triethoxysilane (APTES, ≥98%), cadmium nitrate (tetrahydrate, 98%), dichloromethane (≥99.8%), diethylether (≥99.8%), ethanol (≥99.8%), glutaraldehyde (25% in H2O), glutathione (GSH, ≥98%), hydrochloric acid (37%), nitric acid (68%), Pluronic® 123 (P123), sulfuric acid (95–97%), tetraethylorthosilicate (TEOS, 98%), and toluene (anhydrous, ≥99.8%). The remaining reagents were from Merck: cadmium nitrate (tetrahydrate, 98%), copper nitrate (trihydrate, >98%), disodium phosphate (dodecahydrate, >99%), lead nitrate (>99.5%), potassium diphosphate (≥99.5%), sodium nitrate (>99%) and tris(hydroxymethyl)aminomethane (Tris, 99.7%).2.2. Synthesis and characterization of the glutathione functionalized adsorbent
The synthesis of the glutathione grafted SBA-15 adsorbent has already been described in detail elsewhere.40 Briefly, SBA-15 silica is synthesized using a P123 non-ionic surfactant in acidic media using tetraethylorthosilicate as the silica precursor. Glutathione is grafted in three steps which correspond to the grafting of (1) APTES, (2) glutaraldehyde and finally (3) glutathione. SBA-15 silica-based materials will be designated hereafter as SBA-15 (unmodified silica) or SBA-GSH (glutathione grafted). SBA-GSH synthesis and structure are shown in Fig. 1.The specific surface area, pore size and volume have been determined by nitrogen physisorption at 77 K using a Micromeritics Tristar II Plus instrument. Prior to the measurement, samples were outgassed at 120 °C for 6 hours. The specific surface area was calculated according to the BET method with the relative pressure p/p0 ranging from 0.05 to 0.3. The pore size distribution was calculated using the BJH equation on the desorption branch and the total pore volume was determined at p/p0 = 0.95.
The quantity of grafted glutathione was determined by the elemental analysis of sulfur carried out using a Flash 2000/ThermoFisher CHN-S analyzer.
2.3. Batch adsorption experiments
All metal solutions were prepared in 0.1 M NaNO3 to fix the ionic strength. The effects of equilibrium pH, pHeq, contact time and initial metal concentration on adsorption have been investigated for Cu(II), Pb(II) and Cd(II). Tests are performed with a sorbent dosage of 10 g L−1 under 250 rpm magnetic stirring at a temperature maintained at 25 ± 1 °C. pH was adjusted using 1 M NaOH solution. Once the adsorption equilibrium was reached, the adsorbent was separated from the solution by centrifugation for 10 min at 15000g. The supernatants were then collected and unbound metal ions were quantified by inductively coupled plasma atomic emission spectroscopy (ICP-AES) analysis with a Varian 720 ES instrument.The adsorption capacity (q) and adsorption percentage (%ADS) were determined using eqn (1) and (2), respectively:
 | (1) |
 | (2) |
Adsorption isotherm data have been fitted with the Langmuir model describing adsorption on one type of adsorption site according to eqn (3)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 and with a bi-Langmuir model considering two types of adsorption sites (eqn (4)).48,49 The Langmuir model, although originally developed for gas adsorption, is one of the most widely used models for modeling adsorption isotherms in solution. Even if the basic assumptions are not completely fulfilled, the Langmuir model has been used to determine the adsorption parameters and compare the various systems.
47 and with a bi-Langmuir model considering two types of adsorption sites (eqn (4)).48,49 The Langmuir model, although originally developed for gas adsorption, is one of the most widely used models for modeling adsorption isotherms in solution. Even if the basic assumptions are not completely fulfilled, the Langmuir model has been used to determine the adsorption parameters and compare the various systems.
 | (3) |
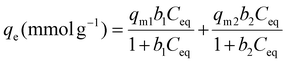 | (4) |
Adsorption isotherms have been recorded at pH 4 for Cd(II), Cu(II) and Pb(II) and at pH 7 for Cd(II). Comparisons with the non-grafted SBA-15 material have also been performed. For two-metal isotherms, the initial solutions contain an equimolar quantity of each element.
2.4. Isothermal titration calorimetry (ITC)
To measure the enthalpy of displacement accompanying adsorption reactions of different metal ions on non-grafted SBA-15 and SBA-GSH materials, a TAM 2277 differential calorimeter, based on the heat flow principle and operating in the dynamic correction mode, was used. ITC measurements were performed at 25 °C. In a typical experiment, 8 mg of silica material and 0.8 mL of 0.1 M NaNO3 were introduced in a glass ampoule to reproduce the solid/liquid ratio of the adsorption tests. The glass ampoule was equipped with a gold paddle stirrer to ensure homogeneity of the suspension and placed in the microcalorimeter for an equilibrium time of 2 hours prior to the measurement. 25 aliquots of 10 μL of single- or two-metal ion solution in 0.1 M NaNO3 are successively injected at a speed of 1 μL s−1. Stock solution concentrations are 20 mM for each element, including bimetal solutions. The time between two injections was set to 45 min, to ensure that the adsorption equilibrium is reached. The experimental enthalpy changes for adsorption were corrected from dilution effects by injecting the corresponding metal ion(s) solution into the ampoule containing 0.1 M NaNO3 without an adsorbent. pH remained within 0.5 units during the measurements. The cumulative enthalpy of displacement ΔdplHcum per unit mass of the adsorbent was calculated according to the method of Prelot and Zajac (2023) and Prelot et al. (2018), summing the enthalpy changes corresponding to each injection.41,50 All measurements were repeated 2 to 5 times to ensure reproducibility. The molar enthalpy effect was calculated at low surface coverage using the slope of the curve representing ΔdplHcum (J g−1) as a function of the adsorption capacity (mmol g−1). ΔdplHcum was evaluated with a precision of ±2 J g−1 and the calculation of the slope was performed in the adsorption capacity range where the precision is ±1 Jg−1. The results are given with a maximum incertitude of ±10%.3. Results and discussion
The SBA-GSH material presents a specific surface area of 187 m2 g−1 with a pore size of 51 Å and a pore volume of 0.26 cm3 g−1, as reported previously.40 The grafting of GSH was assessed by CHNS elemental analysis and FT-IR which showed the presence of oxygen, sulfur and nitrogen and confirmed the presence of 300 mmol kg−1 GSH in the material. FT-IR also highlighted the presence of residual silanol groups in the grafted material that may contribute to metal adsorption. GSH functional groups and more specifically C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, S–H, O–H and N–H are all able to provide free pairs of electrons, which may interact with the empty orbital of metal ions to form complexes, thus bringing an important contribution to the metal removal process.51
O, S–H, O–H and N–H are all able to provide free pairs of electrons, which may interact with the empty orbital of metal ions to form complexes, thus bringing an important contribution to the metal removal process.51
3.1. Adsorption studies of Cd(II), Cu(II) or Pb(II) (= M(II))
 | ||
| Fig. 2 Effect of pH on Cd(II), Cu(II) and Pb(II) adsorption percentages on SBA-GSH (C0: 1.5 mmolCd L−1; 1.5 mmolCu L−1; 5.3 mmolPb L−1; 10 g L−1 SBA-GSH; medium: 0.1 M NaNO3; stirring speed: 500 rpm; 25 ± 1 °C; contact time: 120 minutes). Experimental error: 4% for Cu(II), 3% for Cd(II) and 1% for Pb(II). Data for Cd(II) are from ref. 40. | ||
It can be observed that the three metal ions present different adsorption behaviors on SBA-GSH. Indeed, Cu(II) adsorption is more influenced by pH than Pb(II) adsorption, which is taking place on a much wider range of pH values. Optimal adsorption pH is above 3 for Pb(II), between 4 and 5 for Cu(II) and around 7 for Cd(II). Besides, at these concentrations, all elements are present in the M2+ or M(NO3)+ form at the studied pH value (Fig. S1†). Considering these results, for the adsorption studies, pH 4 was chosen for Cu(II) and Pb(II) and pH 7 was chosen for Cd(II).
Unlike Cd(II), the adsorption of Pb(II) and Cu(II) on non-grafted SBA-15 (Fig. S2, S3 and S4†) was not efficient with adsorption capacities below 1 mmol kg−1, and thus the effect of pH was not studied in these cases. Adsorption percentages and capacities of both materials are given and compared for both grafted and non-grafted materials in Table 1. As can be noted, SBA-15 adsorbs very low amounts of Pb(II) and Cu(II) (respectively <1 mmolPb kg−1 and 3 mmolCu kg−1) at pH 4 while SBA-GSH adsorbs 155 mmolPb kg−1 and 94 mmolCu kg−1 under identical conditions, due to the contribution of GSH functional groups to M(II) adsorption. In contrast, at its optimal adsorption pH (pH 7), Cd(II) was already adsorbed to a level of 63 mmolCd kg−1 (55%) on the non-grafted SBA-15 material but the grafting of GSH allowed reaching 116 mmolCd kg−1 (80%). As for the non-grafted material the adsorption can only be attributed to interactions with silanol groups, and these results suggest different mechanisms for Pb(II) and Cu(II) compared to Cd(II). Moreover, the higher capacity observed for Pb(II) with SBA-GSH also suggests that the sorption mechanism could be different for Pb(II) and Cu(II).
| Material | Pb(II) pHeq = 4 | Cu(II) pHeq = 4 | Cd(II) pHeq = 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
|||
|---|---|---|---|---|---|---|
| SBA-15 | SBA-GSH | SBA-15 | SBA-GSH | SBA-15 | SBA-GSH | |
| Adsorption capacity (mmol kg−1) | <1 | 155 | 3 | 94 | 63 | 116 |
| Adsorption percentage (%) | <0.1 | >99.9 | 2 | 75 | 55 | 80 |
Adsorption isotherms on SBA-GSH have been determined at pH = 4 for single-metal Cu(II), Pb(II) (Fig. 3), and Cd(II) (Fig. S6†) systems and two-metal Cu(II)–Pb(II) and Cd(II)–Pb(II) (Fig. 4) systems. Both Cu(II) and Pb(II) present an “H” isotherm (Fig. 3) according to the classification of Giles, meaning that the adsorption is most likely chemically driven with high affinity between the surface and the adsorbate.52
Cu(II) and Pb(II) adsorption capacities at pHeq = 4 were investigated in different concentration ranges ensuring no M(OH)2 precipitation during the test. Cu(II) and Pb(II) adsorption isotherms were fitted with Langmuir and bi-Langmuir models. All models allowed a good fit of the isotherm and gave similar results for Cu(II) adsorption (Table 2). When compared with the glutathione amount grafted on silica (300 mmol kg−1), adsorption of approximately 0.5 Cu(II) per glutathione can be calculated.
| Metal | q m (mmol kg−1) | b (L mmol−1) | R 2 |
|---|---|---|---|
| Langmuir model | |||
| Cu(II) | 142 | 3.30 | 0.972 |
| Pb(II) | 695 | 2.35 | 0.904 |
| Metal | q m1 + qm2 (mmol kg−1) | b 1 + b2 (L mmol−1) | R 2 |
|---|---|---|---|
| Bi-Langmuir model | |||
| Cu(II) | 146 | 61.9 | 0.978 |
| Pb(II) | 711 | 277.2 | 0.982 |
The bi-Langmuir model seems the best fitting for Pb(II) adsorption on SBA-GSH. A maximum adsorption capacity of 711 mmolPb kg−1 has been calculated, in accordance with the experimental capacity (704 mmolPb kg−1) and corresponds to around 2.3 Pb(II) per glutathione.
The Cd(II) adsorption isotherm showed little adsorption at pHeq = 4 (Fig. S6†) on SBA-GSH. At pHeq = 6.6, the Cd(II) adsorption isotherm was fitted with the Langmuir model for a maximum adsorption capacity of 1040 mmolCd kg−1 (ref. 40) corresponding to about 3.5 Cd(II) per glutathione. The calculated M(II) to GSH ratio highlights again different adsorption mechanisms for each metal. Higher M(II) to GSH ratios result from interactions with different types and/or number of binding groups of the ligand and/or by the affinity of metal ions with residual silanol groups.
To further investigate these different behaviors, two-metal adsorption isotherms have also been recorded (Fig. 4) to discuss potential competitive effects between Pb(II) and Cd(II) or Pb(II) and Cu(II). It has been postulated that in the presence of another metal in the system, the amount of a given adsorbed metal can decrease.41 In the presence of both added metals in the system (Cu(II) or Cd(II)), the maximum adsorption capacity (qm) for Pb(II) (red circles) decreases from around 700 mmolPb kg−1 to approximately 500 mmolPb kg−1 and the Pb(II) adsorption isotherm retains its “H” form. In contrast, in the presence of Pb(II), the Cu(II) adsorption isotherm shifts from an “H” isotherm in the single-metal system to an “L” shaped isotherm in the two-metal system (blue triangles). This could lead to the hypothesis that Cu(II) binds to different sites in the two-metal system compared to the single-metal system. Indeed, Pb(II) could be preferentially adsorbed on the binding sites used by Cu(II) in the single-metal system, thus forcing Cu(II) to move to other sites.
The observed Cd(II) isotherm at pH 4 in the presence of Pb(II) is different from the one in the single-metal system (Fig. S6†) and cannot be classified. Indeed, the occurrence of adsorption is observed for low Cd(II) equilibrium concentrations in solution, followed by a decrease above 1.9 mmolCd L−1 when a plateau is reached for Pb(II). This leads to the hypothesis that (i) cooperative adsorption of Cd(II) and Pb(II) and/or (ii) an identical adsorption site for Cd(II) and Pb(II) occurs on SBA-GSH under these conditions, with much higher affinity for Pb(II), preventing Cd(II) adsorption when saturation of the material by Pb(II) is reached (at pH = 4, there is little adsorption of Cd(II)). The maximum experimental adsorption capacities are 469 mmolPb kg−1 for Pb(II) and 47 mmolCd kg−1 for Cd(II) in the Cd(II)–Pb(II) system and 464 mmolPb kg−1 for Pb(II) and 138 mmolCu kg−1 for Cu(II) in the Cu(II)–Pb(II) system. To understand the underlying mechanisms resulting in these differences, isothermal titration calorimetry (ITC) studies were carried out which allowed the determination of the thermodynamic parameters of the adsorption process.
3.2. Isothermal titration calorimetry (ITC) study of Pb(II), Cd(II) and Cu(II) adsorption
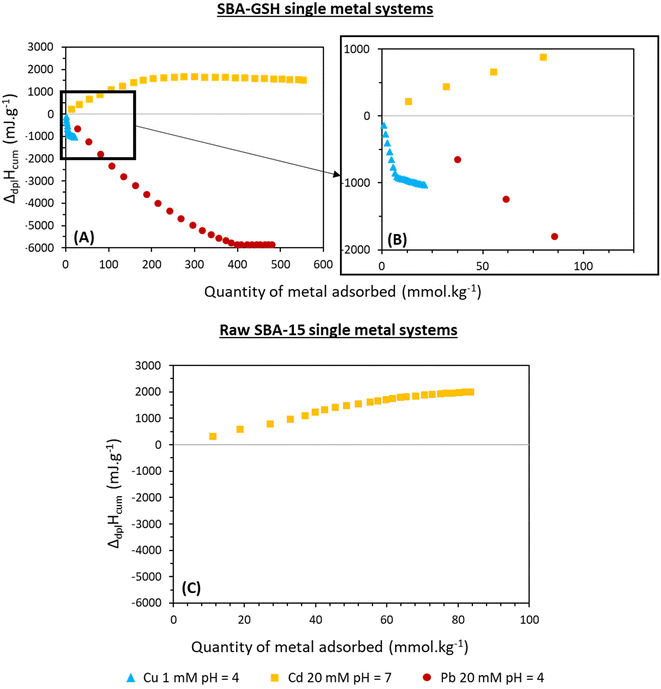
ITC measurements have been performed both on non-grafted SBA-15 and SBA-GSH materials at pH 4 for Cd(II), Cu(II) and Pb(II) and at pH 7, the optimal adsorption pH for Cd(II). Raw thermograms for single-metal adsorption and the corresponding dilution experiments are shown in Fig. 5 for SBA-GSH and Fig. 6 for SBA-15. Thermograms represent the overall heat of reaction generated (exothermic) or absorbed (endothermic) when adding aliquots of a metal salt solution to a suspension of the material, as a function of time. | ||
| Fig. 6 Thermograms for Cd(II) (A), Cu(II) (B) and Pb(II) (C) adsorption onto non-grafted SBA-15 (25 °C; 25 injections of 10 μL; medium: 0.1 M NaNO3; glass ampoule with a 10 g L−1 suspension). Dilution experiments are identical to the ones presented in Fig. 5. All curves are plotted with respect to the same y-axis scale. EXO defines the direction of the exothermic signal. | ||
To determine the contribution of the interaction of the metal with the material, thorough control experiments were carried out. Firstly, the injection of aliquots of the solvent (0.1 M NaNO3) in a suspension of SBA-GSH in 0.1 M NaNO3 was tested and did not lead to a substantial heat signal (Fig. S7†). Therefore, the dilution effect of NaNO3 in the suspension was considered negligible in data treatment. In contrast, injections of metal ion solutions prepared in 0.1 M NaNO3 into the same medium (0.1 M NaNO3) lead to weakly exothermic heat effects for all considered elements (Fig. 5(F)–(J)). The cumulative enthalpy effect of dilution of metal ion solutions is shown in Fig. S8,† as a function of the equilibrium molality for all experimental conditions. The thermal effect of dilution of the metal ion solutions in the NaNO3 medium increases in the order Pb(II) < Cu(II) < Cd(II) under identical conditions (20 mM, pH 4). This thermal effect will be referred to as “metal ion dilution” in the rest of the article.
Thermograms of the adsorption of Pb(II) on SBA-GSH (Fig. 5(E)) showed exothermic adsorption signals with decreasing intensities until reaching the signal intensity corresponding to metal ion dilution after 16 injections, indicating that no more adsorption occurred above the corresponding Pb(II) addition amount (400 mmolPb kg−1). The exothermic nature of the signals suggested that chemical contributions such as the metal ion reaction with the functional groups of glutathione are the main adsorption contributors. The Cu(II) adsorption experiment performed at the same concentration as that of Pb(II) (20 mM) led to one first strong exothermic peak followed by weak decreasing endothermic effects until reaching the signal intensity due to metal ion dilution alone (Fig. 5(C)), suggesting that the adsorption sites of the material were rapidly saturated with Cu(II) after the first injection, in accordance with its lower adsorption capacity for this ion. This hypothesis was confirmed by running the same experiment with 1 mM Cu(II) solution which showed a similar trend to the one observed with Pb(II) solution, namely several exothermic peaks due to the contribution of the chemical phenomenon (Fig. 5(D)). In contrast, Cd(II) adsorption was endothermic at pH 7 (Fig. 5(A)). However, Chekmeneva et al. showed that Cd(II) complexation with free GSH presents an exothermic effect, suggesting that this contribution may not be the predominant one in our system.53 At pH 4, Cd(II) ITC adsorption signals are equivalent to the signal of Cd(II) dilution, in accordance with the fact that Cd(II) was barely adsorbed at this pH (Fig. 5(B)).40
The same experiments were carried out on non-grafted SBA-15 silica to determine the contribution of the grafted GSH to the adsorption process. Pb(II) adsorption on SBA-15 at pH 4 showed a slightly endothermic heat effect (Fig. 6(C)), different from the exothermic metal ion dilution and most likely corresponding to residual contributions such as cation dehydration or Na–Pb ionic exchange. The Cu(II) adsorption experiment on SBA-15 at pH 4 (Fig. 6(B)) did not show any significant sign of adsorption, as shown by the signal intensity being similar to that in the metal ion dilution experiment (Fig. 5(G)). All these results show that ITC data correlate very well with the adsorption data and help to understand the adsorption mechanism. Finally, Cd(II) adsorption on the non-grafted SBA-15 material at pH 7 resulted in an endothermic effect, comparable to the one observed with SBA-GSH (Fig. 6(A)). Though the two contributions cannot be fairly compared due to the difference in the number of available silanol sites between the two materials, it is still possible to affirm that adsorption by silanol sites and contributions such as the displacement of protons are deeply influencing the adsorption phenomenon of Cd(II) in both materials. However, the endothermic effect with both SBA-15 and SBA-GSH materials confirmed that the precipitation of solid Cd(OH)2 (exothermic) is minimal or non-existent in this system and would not have any impact on other contributions. These results illustrate perfectly the ones obtained in batch adsorption studies.
For calorimetry data treatment applied to adsorption, it is necessary to take into account the quantity of metal ions effectively adsorbed by the material with the given injection. Indeed, upon each injection, the n moles of metal ions injected are first diluted in the solvent and some of the metal ions are thereafter adsorbed onto the material, and the remaining ions remain in solution, as shown by the adsorption isotherm.
Fig. 7 shows the calculated cumulative enthalpy of displacement accompanying the adsorption reaction (ΔdplHcum) which is the global enthalpy effect representing all the contributions involved in adsorption calculated according to the method of Prelot and Zajac (2023) and Prelot et al. (2018).41,50 This global enthalpy effect was calculated only for the systems showing significant adsorption, namely Pb, Cu and Cd with SBA-GSH and Cd with SBA-15. All enthalpy curves have been corrected for metal ion dilution effects. The observed contributions can be either due to chemical contributions (metal ion interactions with functional groups, intermolecular hydrogen bonds, electrostatic interactions, or other chemical reactions such as precipitation) leading to an exothermic effect or to physical contributions (dehydration effects, structural rearrangement, electrostatic repulsion, confinement within the pores of the material, displacement of other compounds, electrostatic repulsion, adsorption of M(II) on silica) leading to endothermic effects.54
To analyze quantitatively the obtained curves in Fig. 7(B), the initial slope of the plot of ΔdplHcumversus the amount adsorbed corresponding to the molar enthalpy was calculated. The results are shown in Table 3.
| Element | Initial M(II) concentration (mM) | Material | pH | Molar enthalpy (kJ mol−1) |
|---|---|---|---|---|
| Cd | 20 | SBA-15 | 7 | 10 |
| Cd | 20 | SBA-GSH | 7 | 29 |
| Pb | 20 | SBA-GSH | 4 | −20 |
| Cu | 1 | SBA-GSH | 4 | −140 |
The negative values of molar enthalpies for Cu and Pb reflect the exothermic effect of adsorption on SBA-GSH for these metals. In the solution state, Cu2+ is known to react rapidly and stoichiometrically with the thiol group of GSH to form disulfides.55 To determine if this reaction is taking place in our material, FT-IR and XPS measurements were carried out to observe the sulfur environment, but the low sulfur content did not allow to elucidate the oxidation state of GSH. The anchoring of GSH on mesoporous silica in our SBA-GSH material has an influence on the orientation and proximity of the thiol groups in the material and could induce steric hindrance that may prevent that reaction. We thus cannot assess that this solution state phenomenon takes place in our solid/liquid system. Yet, the molar enthalpy determined for Cu(II) at pH 4 was highly exothermic and seven times stronger than the one observed for Pb(II), though the latter showed higher affinity for the material in the adsorption studies. ITC gives a measurement of the global heat effect of all reactions taking place during the adsorption phenomena, and this highly exothermic reaction energy may also be due to redox reactions between GSH and Cu(II) in our material, as commonly observed in the solution state.55 For Cd(II), the positive enthalpy values are characteristic of the strongly endothermic effect associated with its adsorption on both SBA-15 and SBA-GSH.
The molar enthalpy determined here for the Cd(II)–SBA-15 interaction at pH 7 is slightly lower than, but coherent with, the one obtained by Prelot et al. for Spherosil (17 kJ mol−1), most likely due to the different nature and higher density of silanols in SBA-15, implying more silanol binding sites.56 In their study, the authors showed that different contributions were participating in the adsorption of metal ions such as Cd(II) on SiO2, one of the main ones being cation dehydration and the deprotonation of silanols to create negatively charged sites, which can later interact with positively charged Cd(II) ions.56
The enthalpy values cannot be compared to each other as they may not reflect adsorption on the same sites. To study the mechanism of competitive adsorption in more detail, ITC measurements have also been performed in two-metal Cd(II)–Pb(II) and Cu(II)–Pb(II) systems.
3.3. ITC study of adsorption with two-metal solutions
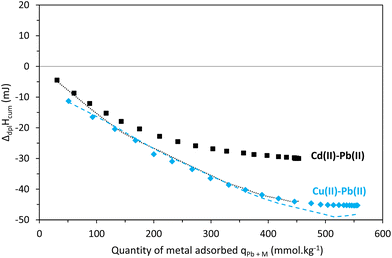
Raw adsorption and dilution thermograms of two-metal Cd(II)–Pb(II) and Cu(II)–Pb(II) systems are shown in Fig. 8. The adsorption heat effect of both two-metal experiments is very similar to the one of Pb(II) alone (Fig. 5(E)). In both cases, the only significant difference is in the first injection peak for the Cu(II)–Pb(II) system. All effects are exothermic, as a result of the contribution of metal ion binding to the material's functional groups, as well as potential side contributions such as intermolecular hydrogen bonds and other chemical reactions.In order to discuss the competitive effects, the cumulative enthalpy of displacement accompanying the adsorption as a function of the total quantity of metal adsorbed was calculated for both experiments, corrected from the dilution effect (Fig. S8B†) and superimposed with the sum of individual enthalpy plots extracted from Fig. 8 (Fig. 9).
In the case of the Pb(II)–Cu(II) system, the sum of individual contributions and the experimental plots are similar up to 400 mmolPb+M kg−1. Prelot et al. (2018)41 postulated that in multicomponent systems, the contributions are not only coming from the affinity between the metal ions and the adsorbent surface but also include the interactions between cations themselves. The additivity rule was used to characterize the competitive effects.41 Following this, it is possible to suggest that below an adsorption capacity of 400 mmolPb+M kg−1, each of the two metal ion adsorptions is independent. Once the plateau is reached, a difference of 6 to 8% is observed between the sum of individual contributions and the two-metal experimental values. This difference is not necessarily significant (within experimental error) as similar differences can usually be observed when the plateau is reached.
For the Cd(II)–Pb(II) system, the difference between the sum of individual contributions and the two-metal experimental values is significant and varies from 8% at the early stages of adsorption to 32% on the plateau. This indicates, for the lower quantities of Cd(II) adsorbed, a competition occurs between both elements resulting in the preferential adsorption of Pb(II), in accordance with the adsorption isotherm in Fig. 4, which showed a decrease of Cd(II) adsorption capacities when the Cd(II) concentration in solution increases. The binding sites of Cd(II) and Pb(II) are therefore the same under these conditions. According to the HSAB theory, Cd(II) is considered a soft element and thus shows affinity for sulfur, while Cu(II) and Pb(II) are both considered borderline and can show affinity for both hard and soft coordination groups.57 As our results highlighted a competition between Cd(II) and Pb(II), we can thus suggest that Pb(II) behaves as a soft metal in our system and under experimental conditions. Moreover, a solution complexation study of Pb(II) by GSH showed that above pH 4 complexes are formed with the thiol donor as the primary anchor of the metal ion.58
This combined adsorption/ITC study showed that, in synthetic solutions, the SBA-GSH material adsorbed Pb(II), Cu(II) and Cd(II) by different mechanisms, with a preference for Pb(II) in the presence of Cu(II) and Cd(II). Thus, selectivity for certain metal ions would be expected in complex aqueous solutions. This selectivity, as well as the applicability of the SBA-GSH material to remove traces of metallic ions in complex matrixes, was then investigated on a battery recycling effluent after primary treatment.
3.4. Application of the SBA-GSH material with an industrial effluent
The industrial effluent in battery recycling wastewater was obtained after chemical precipitation and decantation. The composition of this effluent for p- and d-block elements, before and after adsorption experiments at pH 5.6, are given in Table 4. The concentration of Cu, Fe, Pb and Zn is strongly reduced after treatment with SBA-GSH, to reach 77 and 75 μg L−1 for Pb (%ADS = 68%) and Zn (%ADS = 63%), respectively, and the limit of detection of 1 μg L−1 for Cu and Fe (%ADS ≥ 99.9%). The weaker removal of Pb in this effluent can be explained by the presence of high quantities of sulfur (total sulfur: 1000 mg L−1) in the effluent, which could lead to the formation of stable Pb(II)–sulfur complexes, competitive with GSH–Pb(II) binding. Al and Cd were less affected by the contact with SBA-GSH as the final concentration was only slightly lower than the initial concentration with an adsorption of 32% (Al) and 42% (Cd). Final concentrations of Cd and Zn were lower when the test was performed at pH 7, reaching 8 and 17 μg L−1, respectively, under conditions more adapted to their removal. These observations well illustrate the results previously described (Sections 3.1 to 3.4) for synthetic binary solutions, namely the pH dependence, the different mechanisms and the competitive effects between some elements. This therefore led to selectivity for some ions under these conditions. Indeed, the material remained very selective for p- and d-block metals in the presence of higher concentrations of s-block elements as shown by little to no adsorption of alkaline and alkaline earth elements (Table 4). These results showed the potential of this material as a way of depollution of industrial effluents.| Concentration before adsorption (μg L−1) | Concentration after adsorption (μg L−1) | |
|---|---|---|
| p and d-block elements | ||
| Al | 56 ± 5 | 38 ± 10 |
| Cd | 26 ± 1 | 15 ± 1 |
| Cu | 35 ± 1 | ≤1 |
| Fe | 17 ± 1 | ≤1 |
| Pb | 237 ± 3 | 77 ± 39 |
| Zn | 207 ± 4 | 75 ± 30 |
| s-block elements | ||
| Ba | 40 ± 4 | 42 ± 15 |
| Ca | (578 ± 49) × 103 | (599 ± 34) × 103 |
| K | (36 ± 3) × 103 | (39 ± 6) × 103 |
| Li | (3.0 ± 0.2) × 103 | (2.7 ± 0.7) × 103 |
| Mg | (46 ± 3) × 103 | (46 ± 2) × 103 |
| Na | (602 ± 114) × 103 | (605 ± 86) × 103 |
| Sr | 684 ± 200 | 655 ± 92 |
4. Conclusions
Detailed adsorption and ITC studies of different metals on glutathione grafted mesoporous silica (SBA-GSH) and its non-grafted equivalent (SBA-15) were carried out. Both studies gave fully consistent results and their combination allowed gaining a deep understanding of the adsorption mechanism. It has been observed that Cd(II) adsorption relied mainly on physical contributions (at pH 7) while the adsorption of Pb(II) and Cu(II) (at pH 4) depended mainly on chemical interactions between the metal ions and the functional groups of glutathione. The adsorbent thus presents better affinity for Pb(II) than Cu(II) and Cd(II) at pH 4. ITC also allowed elucidating the mechanism of competitive adsorption between Cd(II), Cu(II) and Pb(II). Data showed independent adsorption for Cu(II) and Pb(II) and competitive adsorption for Cd(II) and Pb(II) at pH 4 in the two-metal system, confirming that this material showed selectivity for Pb(II), a doorway for its use in industrial effluent treatment. Experiments performed on a battery recycling industrial effluent highlighted the preferential adsorption of some p- and d-block elements in the presence of s-block elements and confirmed the interest of this material for depollution purposes. This study also highlighted that this material could therefore be used in clean technologies to selectively remove Pb(II) from contaminated waters containing other metal ions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. G. would like to thank the University of Strasbourg for the PhD grant and Sylvia Michel for the technical assistance with calorimetric experiments.References
- A. A. Yaroshevsky, Geochem. Int., 2006, 44, 48–55 CrossRef.
- J. O. Nriagu, Nature, 1989, 338, 47–49 CrossRef CAS.
- H. Ali, E. Khan and I. Ilahi, J. Chem., 2019, 2019, e6730305 Search PubMed.
- Metals in Society and in the Environment: A Critical Review of Current Knowledge on Fluxes, Speciation, Bioavailability and Risk for Adverse Effects of Copper, Chromium, Nickel and Zinc, ed. L. Landner and R. Reuther, Springer Netherlands, Dordrecht, 2004 Search PubMed.
- F. T. Mackenzie, R. J. Lantzy and V. Paterson, Math. Geol., 1979, 11, 99–142 CrossRef CAS.
- Guidelines for drinking-water quality, World Health Organization, 3rd edition, 2008, vol. 1 Search PubMed.
- European Union, Directive 2010/75/EU of the European Parliament and of the Council of 24 November 2010 on industrial emissions (integrated pollution prevention and control), 2010 Search PubMed.
- European Union, Directive (EU) 2020/2184 of the European Parliament and of the Council of 16 December 2020 on the quality of water intended for human consumption, 2020, vol. L435/1 Search PubMed.
- T. Sato, M. Qadir, S. Yamamoto, T. Endo and A. Zahoor, Agric. Water Manag., 2013, 130, 1–13 CrossRef.
- S. Rojas and P. Horcajada, Chem. Rev., 2020, 120, 8378–8415 CrossRef CAS PubMed.
- European Environment Agency, Industrial waste water treatment pressures on environment, European Environment Agency, 2018 Search PubMed.
- R. Massoud, M. R. Hadiani, P. Hamzehlou and K. Khosravi-Darani, Electron. J. Biotechnol., 2019, 37, 56–60 CrossRef CAS.
- S. Kumar, S. Prasad, K. K. Yadav, M. Shrivastava, N. Gupta, S. Nagar, Q.-V. Bach, H. Kamyab, S. A. Khan, S. Yadav and L. C. Malav, Environ. Res., 2019, 179, 108792 CrossRef CAS PubMed.
- J. E. Gall, R. S. Boyd and N. Rajakaruna, Environ. Monit. Assess., 2015, 187, 201 CrossRef PubMed.
- A. Zwolak, M. Sarzyńska, E. Szpyrka and K. Stawarczyk, Water, Air, Soil Pollut., 2019, 230, 164 CrossRef.
- J. Baby, J. S. Raj, E. T. Biby, P. Sankarganesh, M. V. Jeevitha, S. U. Ajisha and S. S. Rajan, Int. J. Biol. Chem. Sci., 2010, 4, 939–952 Search PubMed.
- P. Govind and S. Madhuri, Res. J. Anim. Vet. Fishery Sci., 2014, 2, 17–23 Search PubMed.
- R. Shrestha, S. Ban, S. Devkota, S. Sharma, R. Joshi, A. P. Tiwari, H. Y. Kim and M. K. Joshi, J. Environ. Chem. Eng., 2021, 9, 105688 CrossRef CAS.
- M. R. Schock, R. N. Hyland and M. M. Welch, Environ. Sci. Technol., 2008, 42, 4285–4291 CrossRef CAS PubMed.
- M. Jaishankar, T. Tseten, N. Anbalagan, B. B. Mathew and K. N. Beeregowda, Interdiscip. Toxicol., 2014, 7, 60–72 CrossRef PubMed.
- S. A. Al-Saydeh, M. H. El-Naas and S. J. Zaidi, J. Ind. Eng. Chem., 2017, 56, 35–44 CrossRef CAS.
- Q. Gao, J. Xu and X.-H. Bu, Coord. Chem. Rev., 2019, 378, 17–31 CrossRef CAS.
- C. F. Carolin, P. S. Kumar, A. Saravanan, G. J. Joshiba and Mu. Naushad, J. Environ. Chem. Eng., 2017, 5, 2782–2799 CrossRef CAS.
- M. A. Barakat, Arabian J. Chem., 2011, 4, 361–377 CrossRef CAS.
- V. Kumar, S. K. Dwivedi and S. Oh, J. Water Process. Eng., 2022, 45, 102518 CrossRef.
- M. Ghorbani, O. Seyedin and M. Aghamohammadhassan, J. Environ. Manage., 2020, 254, 109814 CrossRef CAS PubMed.
- International Agency for Research on Cancer (WHO), List of Classifications – IARC Monographs on the Identification of Carcinogenic Hazards to Humans, https://monographs.iarc.who.int/list-of-classifications/, (accessed January 24, 2022).
- T. Attar, Chem. Rev. Lett., 2020, 3, 117–130 CAS.
- L. Li, G. Liu, D. Pan, W. Wang, Y. Wu and T. Zuo, Resour., Conserv. Recycl., 2017, 126, 132–140 CrossRef.
- F. Beauchesne, J. N. Barrandon, L. Alves, F. B. Gil and M. F. Guerra, Archaeometry, 1988, 30, 187–197 CrossRef CAS.
- C. E. Chubaka, H. Whiley, J. W. Edwards and K. E. Ross, Int. J. Environ. Res. Public Health, 2018, 15, 1551 CrossRef PubMed.
- P. Orlović-Leko, K. Vidović, I. Ciglenečki, D. Omanović, M. D. Sikirić and I. Šimunić, Atmosphere, 2020, 11, 144 CrossRef.
- F. Fu and Q. Wang, J. Environ. Manage., 2011, 92, 407–418 CrossRef CAS PubMed.
- T. A. Kurniawan, G. Y. S. Chan, W.-H. Lo and S. Babel, Chem. Eng. J., 2006, 118, 83–98 CrossRef CAS.
- G. Darmograi, B. Prelot, G. Layrac, D. Tichit, G. Martin-Gassin, F. Salles and J. Zajac, J. Phys. Chem. C, 2015, 119, 23388–23397 CrossRef CAS.
- C. S. Seth, T. Remans, E. Keunen, M. Jozefczak, H. Gielen, K. Opdenakker, N. Weyens, J. Vangronsveld and A. Cuypers, Plant, Cell Environ., 2012, 35, 334–346 CrossRef CAS PubMed.
- A. Devez, E. Achterberg and M. Gledhill, Met. Ions Life Sci., 2009, 5, 441–481 CAS.
- R. Shankar, P. Kolandaivel and L. Senthil kumar, Inorg. Chim. Acta, 2012, 387, 125–136 CrossRef CAS.
- R. Gusmão, C. Ariño, J. M. Díaz-Cruz and M. Esteban, Anal. Bioanal. Chem., 2009, 394, 1137–1145 CrossRef PubMed.
- C. Gourmand, C. Bertagnolli, J. Brandel, V. Hubscher-Bruder and A. Boos, Ind. Eng. Chem. Res., 2022, 61, 8188–8203 CrossRef CAS.
- B. Prelot, M. Araïssi, P. Gras, F. Marchandeau and J. Zajac, Thermochim. Acta, 2018, 664, 39–47 CrossRef CAS.
- L. Giraldo and J. C. Moreno-Piraján, J. Chem., 2012, 2013, e267464 Search PubMed.
- D. S. Almeida, C. J. Penn and C. A. Rosolem, Geoderma, 2018, 312, 64–73 CrossRef CAS.
- J.-P. Morel, V. Marry, P. Turq and N. Morel-Desrosiers, J. Mater. Chem., 2007, 17, 2812–2817 RSC.
- W.-Y. Chen, M.-S. Lin, P.-H. Lin, P.-S. Tasi, Y. Chang and S. Yamamoto, Colloids Surf., A, 2007, 295, 274–283 CrossRef CAS.
- S. G. Lanas, M. Valiente, M. Tolazzi and A. Melchior, J. Therm. Anal. Calorim., 2019, 136, 1153–1162 CrossRef CAS.
- M. A. Al-Ghouti and D. A. Da'ana, J. Hazard. Mater., 2020, 393, 122383 CrossRef CAS PubMed.
- D. Graham, J. Phys. Chem., 1953, 57, 665–669 CrossRef CAS.
- F. Gritti and G. Guiochon, Anal. Chem., 2013, 85, 8552–8558 CrossRef CAS PubMed.
- B. Prelot and J. Zajac, Chapter 2. Contribution of isothermal titration calorimetry to elucidate the mechanism of adsorption from dilute aqueous solutions on solid surfaces: data processing, analysis, and interpretation, in: Thermal Analysis and Calorimetry, ed. A. Aline and D.-V. Ljiljana, De Gruyter, Berlin, Boston, 2023, pp. 47–90 Search PubMed.
- F. Yang, S. Zhang, Y. Sun, K. Cheng, J. Li and D. C. W. Tsang, Bioresour. Technol., 2018, 265, 490–497 CrossRef CAS PubMed.
- C. H. Giles, D. Smith and A. Huitson, J. Colloid Interface Sci., 1974, 47, 755–765 CrossRef CAS.
- E. Chekmeneva, R. Prohens, J. M. Díaz-Cruz, C. Ariño and M. Esteban, Anal. Biochem., 2008, 375, 82–89 CrossRef CAS PubMed.
- B. Prelot, S. Lantenois, M.-C. Charbonnel, F. Marchandeau, J. M. Douillard and J. Zajac, J. Colloid Interface Sci., 2013, 396, 205–209 CrossRef CAS PubMed.
- (a) R. Smith, V. Reed and W. Hill, Phosphorus, Sulfur Silicon Relat. Elem., 1994, 90, 147–154 CrossRef CAS; (b) A. V. Kachur, C. J. Koch and J. E. Biaglow, Free Radical Res., 1998, 28(3), 259–269 CrossRef CAS PubMed.
- B. Prelot, S. Lantenois, M.-C. Charbonnel, F. Marchandeau, J. M. Douillard and J. Zajac, J. Colloid Interface Sci., 2013, 396, 205–209 CrossRef CAS PubMed.
- J. Duffus, Pure Appl. Chem., 2002, 74, 793–807 CrossRef CAS.
- A. Krezel and W. Bal, Acta Biochim. Pol., 1999, 46(3), 567–580 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt03210h |
| This journal is © The Royal Society of Chemistry 2024 |