Computation of ³¹P NMR chemical shifts in Keggin−based lacunary polyoxotungstates

Abstract

Density Functional Theory (DFT) calculations were employed to systematically study the accuracy of various exchange-correlation functionals in reproducing experimental ³¹P NMR chemical shifts, δ_Exp(³¹P) for Keggin, [PW₁₂O₄₀]³⁻ and corresponding lacunary clusters: [PW₁₁O₃₉]⁷⁻, [A-PW₉O₃₄]⁹⁻, and [B-PW₉O₃₄]⁹⁻. Initially, computed chemical shifts, δ_Calc(³¹P) were obtained with without neutralising their charge in which associated error, δ_Error(³¹P), decreased as a function of Hartree–Fock (HF) exchange, attributed to constriction of the P–O tetrahedron. By comparison, δ_Calc(³¹P) performed with explicitly located counterions to render the system charge neutral, reduced discrepancies, δ_Error(³¹P) by 1–2 ppm. However, uncertainties in δ_Calc(³¹P) remain, particularly for [B-PW₉O₃₄]⁹⁻ anions attributed to direct electrostatic interactions between the counterions and the central tetrahedron. Optimal results were achieved using the PBE/TZP//PBE0/TZP method, achieving a mean absolute error (MAE) and a mean squared error (MSE) of 4.03 ppm. Our results emphasize that understanding the nature of the electrolyte and solvent environment is essential to obtaining reasonable agreement between theoretical and experimental results.

---

Introduction

Polyoxometalates (POMs) are a large group of discrete, polynuclear metal–oxo clusters comprised of early transition-metal (addenda) and oxide atoms.^1–6 Addenda atoms are fully oxidized to d⁰ electron configurations capable of forming various topologies employing {MO_x} as the principal building block.^1–6 Polyoxo clusters are formed from the one-pot acidification of aqueous molybdate or tungstate oxoanions.^6–8 Self-assembly can be controlled by several synthetic variables including but not limited to: (i) concentration/type of metal oxide anion; (ii) pH and type of acid; (iii) presence of reducing agent; (iv) heteroatom concentration; (v) and solvent.^6–10 The synthesis and self-assembly mechanism of POMs requires a complex network of interdependent reactions, in which any slight variation to the listed five experimental variables can change the dominant species of the combinatorial library. Hence the outcome is often hard to predict.¹¹ Recent work exploiting the self-assembly properties of POMs with non-ionic organic matter was employed to enhance the structural and functional diversity of cyclodextrin-based open frameworks.¹²

Partial hydrolysis of poly-oxo clusters is achieved through the controlled addition of base produces lacunary clusters^9,10 Lacunary clusters formally ‘lose’ one or several M=O vertices and possess reactive cavities with high charge density around the defective region due to the negatively charged oxygen ligands.^13–17 The defect can react with transition-metal cations forming a new class of compounds, an example shown are mono-transition-metal-substituted polyoxotungstates posessing the general formula [XW₁₁M(L)O₃₉]^q− (X = e.g. P(V), Si(IV), L = H₂O, DMSO, etc.).^13–18

Nuclear magnetic resonance (NMR) of active nuclei has been routinely employed for characterising molecular structures in solution and solid state.¹⁹ The employment of ¹H, ²⁹Si, and ³¹P nuclei are common, producing resonance signals across a wide range of chemical shifts providing direct information of the chemical environment. For some cases, poorly sensitive nuclei (¹⁷O, ¹⁸³W) require high concentrations (≥ 0.1 M) coupled with long acquisition times.¹⁹ By contrast, ³¹P is a highly sensitive nucleus with 100% abundance, requiring significantly lower acquisition time and concentrations (< 0.01 M).¹⁹ This spectroscopy provides structural information reflecting in the range of −350 to 300 ppm, relative to 85% H₃PO₄. A fundamental variable of POM chemistry is controlling solubility achieved through the incorporation of inorganic and organic counterions.⁹ Their tuneable solubility in aqueous and organic media makes them suitable precursors for ³¹P NMR investigations.⁹ For decades, ³¹P NMR has been used to identify intermediates to understand self-assembly mechanisms in POMs,²⁰ for example, the base degradation of H₃PW₁₂O₄₀ and the formation of high-nuclearity clusters such as [P₈W₄₈O₁₈₄]⁴⁰⁻ wheels.^20,21

Early computational work in POMs has primarily focused on charged systems without implicit solvation models; see Fig. 1, in which we summarise the insights gained over the past 20-years regarding computed chemical shifts in POMs. In 2002, Bagno and co-workers calculated ⁹⁹Ru chemical shifts in [PW₁₁Ru(DMSO)O₃₉]⁵⁻ without accounting for counterions, solvation, relativistic corrections.²² The authors shown that shortening of d(Ru–S) by 0.045 Å induced shielding of the ⁹⁹Ru nucleus by 235 ppm.²² These approximations produced results that were significantly underestimated with respect to experimental ⁹⁹Ru chemical shifts, obtained at 7737 ppm.²³ Later, Bagno and co-workers computed ¹⁸³W NMR signals in [W₅O₁₈]⁶⁻, [Ru(DMSO)PW₁₁O₃₉]⁵⁻, and [PW₁₁O₃₉]⁷⁻ clusters accounting for relativistic effects using zero-order regular scalar approximations.²³ The authors reported the computed W1–W5 signals were deshielded relative to W6; only W2 and W3 reproduced trends shown by experimental work.²³ Counterion dependence of approx. 53 ppm was accounted for modelling with the [LiPW₁₁O₃₉]⁶⁻ adduct.²³ The adduct demonstrated improved ordering of the signals, however, such chemical shifts did not accurately reproduce experimental work. Later, Bagno reported that incorporation of spin–orbit (SO) corrections, coupled with implicit solvation, provided optimal (average) accuracy for ¹⁸³W chemical shifts, determined at 35 ppm.²³ In 2009, Kortz and co-workers performed relativistic ¹⁸³W NMR calculations for the mono-lacunary clusters, [GeW₁₀X(H₂O)O₃₆]⁷⁻ (X⁺ = Li, Na, K) which incorporated counterions with explicitly located water.²⁴ The ordering of three resonances in [GeW₁₀K(H₂O)O₃₆]⁷⁻ was successfully reproduced; although slightly shielded, replicated the experimental distance between W(B) and W(C) signals (Δδ = 26 ppm vs. 29 ppm).²⁴ The influence of counterions was shown by Δδ which was reduced to 19 ppm for [GeW₁₀O₃₆]⁸⁻ systems.²⁴ Vilà-Nadal and co-workers rationalised these observations in [XW₁₂O₄₀]^q− (X = B, Al, Si, P, Ga, Ge, As, Zn) by showing ¹⁸³W chemical shifts  were linearly correlated with the tungsten-bridging oxygen (O_b and O_c) bond distances.²⁵ The authors proposed that the contraction of the WO₆ polyhedral increased the energy gap between the occupied and unoccupied orbitals involved in electronic transition, hence, the principal contribution to paramagnetic shielding, U_ai, becomes less negative, deshielding the nucleus.²⁵

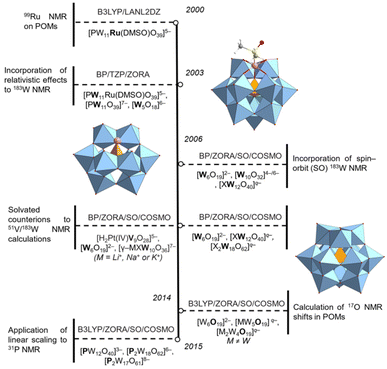Fig. 1 Timeline showing the progression of NMR calculations in polyoxometalates.^22–29

Linear scaling has been employed to reduce mean absolute error (MAE) of computed chemical shifts. In 2014, Pascual-Borràs and co-workers calculated ¹⁷O chemical shifts for [W₆O₁₉]²⁻ including spin–orbit corrections and implicit solvation providing an average mean absolute error of 39 ppm.²⁶ By incorporating scaling corrections, MAE was reduced to approx. 26 ppm across 75 signals.²⁶ Later, Pascual-Borràs and co-workers calculated ³¹P chemical shifts in Keggin, [PW₁₂O₄₀]³⁻, and Wells–Dawson, [P₂W₁₈O₆₂]⁶⁻ anions reporting MAE values of 2.62 ppm. The authors performed a systematic benchmark employing several exchange−correaltion (x-c) functionals and concluded that the optimal methodology was TZP/PBE//TZ2P/OPBE (NMR//optimization step)coupled with spin–orbit (SO) corrections and implicit solvation. Linear scaling corrections were applied which further reduced MAE to 0.57 ppm.²⁷ The authors rationalised chemical shifts with orbital gaps as an approximation to the probability of electronic transition. For example, chemical shifts became more positive as a function of metal oxidation state (X = W(VI) > V(V) > Sn(IV) > Ru(II)) in [P₂W₁₇M(H₂O)O₆₁]^q− anions.²⁷

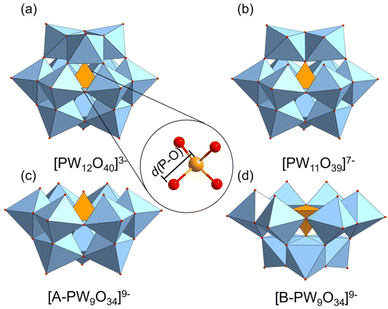
Contemporary quantum chemical calculations have focused on charged systems with spin–orbit (SO) corrections and implicit solvation models. Obtaining accurate models for computing ³¹P chemical shifts is crucial for spectral assignments of experimental data. The role of counterions in computed ³¹P chemical shifts have not been throughly investigated. DFT calculations currently rely on linear scaling to obtain sufficiently accurate results requiring a significant number of calculations to generate these regression models. In this work, we have employed density functional theory (DFT) calculations to reproduce experimental ³¹P NMR shifts in Keggin and corresponding mono- and tri-lacunary clusters, see Fig. 2. The present work will assess the accuracy of various exchange-correlation functionals and applied basis sets in reproducing experimental ³¹P NMR chemical shifts and provide a detailed analysis on the effect of the geomtric factors controlling it.

Fig. 2 Polyhedral representations of the hydrolytic conversions of [PW₁₂O₄₀]³⁻ to lacunary: [PW₁₁O₃₉]⁷⁻, [A-PW₉O₃₄]⁹⁻, and [B-PW₉O₃₄]⁹⁻ clusters. Colours corresponding to W = cyan, O = red, and P = orange.

Experimental

Materials and methods

All reagents and solvents were supplied by Sigma Aldrich Chemical Company Ltd, Thermo Fisher Scientific, and Cambridge Isotope Laboratories. All materials were used without further purification.

FT-IR spectra were recorded on a Nicolet 170SX-FT/IR spectrometer in the range of 400–4000 cm⁻¹. UV-Vis spectra of the prepared compounds were measured in the region (200–400) nm for 30 μM solutions in distilled water at 25 °C using a Shimadzu 1800 spectrophotometer matched quartz cell. All ³¹P NMR spectroscopy was performed using a Bruker DPX 400 spectrometer with 85% phosphoric acid as an external standard. All spectra were recorded using 50 mg samples dissolved in D₂O. All tetrabutylammonium (TBA) salts were recorded using 50 mg samples dissolved in CD₃CN. Electrospray ionization mass spectrometry (ESI-MS) was obtained in negative-ion mode on the Agilent Q-TOF 6520 LC/MS mass spectrometer. The electrospray ionization source conditions: V_cap, 3500 V; skimmer, 65 V; nebulizer, 30 psi; drying and nebulizer gas, N₂; drying gas flow, 10 L min⁻¹; drying gas temperature, 300 °C; fragmentor, 80 V; scan range 100–2000 m/z. The sample solutions with the concentration of approximately 1000 ppm were made and analysed by direct injection using an automatic sampler with a flow rate of 0.2 mL min⁻¹.

Preparation

Preparation of Li₃[PW₁₂O₄₀]. This was prepared in accordance with the literature.²⁸ Phosphotungstic acid hydrate (5.0 g, 1.74 mmol) was dissolved in water (20 mL). LiCl (0.22 g, 5.21 mmol) was dissolved in the phosphotungstic solution, under stirring for 1 h. The solvent was evaporated off at 373 K producing a white crystalline powder (5.05 g, 98.6%).

Preparation of Na₃[PW₁₂O₄₀]. This was prepared in accordance with the literature.²⁸ Phosphotungstic acid hydrate (5.0 g, 1.74 mmol) was dissolved in water (20 mL). NaCl (0.10 g, 5.21 mmol) was dissolved in the phosphotungstic solution, under stirring for 1 h. The solvent was evaporated off at 373 K producing a white crystalline powder (4.97 g, 98.6%).

Preparation of [(n-C₄H₉)₄N]₃[PW₁₂O₄₀]. This was prepared in accordance with the literature.²⁹ Phosphotungstic acid hydrate (5.0 g, 1.74 mmol) was dissolved in water (20 mL). (n-C₄H₉)₄NBr (TBABr) (1.67 g, 5.21 mmol) was dissolved in the phosphotungstic solution, under stirring for 1 h. The precipitate was collected, washed, and then dried with gentle heating producing a white crystalline powder (5.74 g, 85.9%).

Preparation of Li₇[PW₁₁O₃₉]. This was prepared in accordance with the adapted literature.³⁰ Phosphotungstic acid hydrate (5.0 g, 1.74 mmol) was dissolved in water (20 mL). LiCl (0.22 g, 5.21 mmol) was dissolved in the phosphotungstic solution. Aqueous solution of 1 M lithium hydrogencarbonate (6.79 g, 100 mL) was added dropwise until pH of the suspension reached pH 4.80. The crystalline salt was isolated by solvent evaporation and recrystallised from hot water. The crystals were dried with gentle heating producing a white crystalline powder (4.13 g, 87.1%).

Preparation of Na₇[PW₁₁O₃₉]. This was prepared in accordance with the adapted literature.³⁰ Phosphotungstic acid hydrate (5.0 g, 1.74 mmol) was dissolved in water (20 mL). NaCl (0.10 g, 5.21 mmol) was dissolved in the phosphotungstic solution. Aqueous solution of 1 M sodium hydrogencarbonate (8.40 g, 100 mL) was added dropwise until pH of the suspension reached pH 4.80. The crystalline salt was isolated by solvent evaporation and recrystallised from hot water. The crystals were dried with gentle heating producing a white crystalline powder (4.02 g, 81.4%).

Preparation of K₇[PW₁₁O₃₉]. This was prepared in accordance with the literature.³⁰ Phosphotungstic acid hydrate (25.0 g, 8.68 mmol) was dissolved in distilled water (100 mL). KCl (1.94 g, 26.04 mmol) was then added to the phosphotungstic solution. Aqueous solution of 1 M potassium hydrogencarbonate (10.01 g, 100 mL) was added dropwise until pH of the suspension reached pH 4.80. The filtrate was concentrated and allow to cool to room temperature. The white crystalline salt was recrystallised from hot water. The crystals were dried with gentle heating producing a white crystalline powder (24.70 g, 94.6%).

Preparation of Na₈H[Δ-PW₉O₃₄]. This was prepared in accordance to the literature.³¹ Sodium tungstate dihydrate (12.0 g) was dissolved in distilled water (14.8 mL) with stirring, then was added to 85% ortho-phosphoric acid (0.25 mL) followed by glacial acetic acid (2.2 ml). Gentle stirring produced a white precipitate which was isolated by filtration and washed for drying. The isomer was obtained depended on drying temperature. Drying between 20 < T < 80 °C obtained Na₈H[A-PW₉O₃₄], whilst at T > 80 °C, Na₈H[B-PW₉O₃₄] isomer appeared in the product. Complete isomerism was conducted at T = 140 °C for several hours.

Computational details

All computational results were obtained using the ARCHIE-WeSt High-Performance Computer based at the University of Strathclyde. Density Functional Theory (DFT) calculations were performed using the Amsterdam Modelling Suite (AMS 2020.1) package.³² In this work, two classes of exchange–correlation (x–c) functionals were employed, which include: (i) generalized gradient approximation (GGA); (ii) and hybrid methodologies. GGA functionals considered were Perdew–Burke–Ernzerhof (PBE).³³ The hybrid x–c functionals considered were: (i) Becke, 3-parameter, Lee–Yang–Parr (B3LYP*,³⁴ B3LYP³⁵); (ii) Perdew–Burke–Ernzerhof (PBE0);³⁶ (iii) and Becke's half-and-half (BH&H).³⁷ Hybrid functionals were selected on their contributions of Hartree–Fock (HF) exchange (15% B3LYP*, 20% B3LYP, 25% PBE0, and 50% BH&H). We employed Slater basis sets comprising: (i) triple-ζ polarization (TZP); (ii) triple-ζ plus polarization (TZ2P); (iii) and quadruple-ζ plus polarization (QZ4P).^38,39 Relativistic corrections were included by means of the zeroth order regular approximation (ZORA) formalism.⁴⁰ The effects of aqueous solvent were approximated by using the conductor-like screening model (COSMO), as implemented by AMS.⁴¹

³¹P-NMR signals were computed using several x–c functionals with varying degrees of HF exchange (0% PBE, 15% B3LYP*, 20% B3LYP, 25% PBE0, 50% BH&H). Also, the effect of larger basis sets (TZ2P & QZ4P) was investigated, restricted to the GGA–PBE level of theory. Relativistic corrections were included by the zeroth order regular approximation (ZORA) formalism and the aqueous solution was approximated by using the conductor-like screening model (COSMO), as implemented by AMS. Thereafter, single-point calculations were employed to calculate ³¹P-NMR parameters (hyperfine couplings and isotropic shielding constants) with spin–orbit (SO) corrections. The notation for this procedure is expressed throughout the text as Functional^NMR/Basis^NMR//Functional^OPT/Basis^OPT. Herein, all ³¹P NMR calculations were performed using PBE/TZP. The chemical shifts were referenced to 85% H₃PO₄ using PH₃ as a secondary standard following the method suggested by van Wüllen:⁴²

δ(X_Calc) = σ(PH_3Calc) − σ(X_Calc) − 266.1 (1)

where X is the phosphorus atom in the model system of interest and 266.1 is the difference in ppm between the absolute experimental chemical shielding of PH₃ (594.5 ppm) and 85% H₃PO₄ (328.4 ppm) at 300 K.⁴³ The use of a secondary standard for ³¹P has become a frequent model of choice, as the theoretical chemical shielding for 85% H₃PO₄ is difficult to obtain.⁴⁴

The chemical shift of a nucleus is dependent on the magnetic shielding tensor, σ. The shielding tensor can be rewritten in terms of the diamagnetic, paramagnetic, and spin–orbit contributions, see below:

σ = σ^d + σ^p + σ^SO (2)

σ_d corresponds to the diamagnetic tensor which depends on the electron density at the ground state. σ_p equates to the paramagnetic tensor which depends on the excited states of the unperturbed system. Conventionally, σ_d is analogous across chemical environments so changes in chemical shift is usually attributed to the paramagnetic part. The paramagnetic tensor can be expressed as:where ε⁰_i and ε⁰_a are the orbital energies of the occupied and unoccupied MOs involved in a given electronic transition, and the integral in the numerator is the first-order magnetic coupling between these orbitals.

Finally, to evaluate the discrepancy of the calculated vs. experimental chemical shifts, we employed the mean unassigned error (MUE), the mean signed error (MSE) obtained as:

where δ_Calc and δ_exp are the calculated and experimental chemical shifts, respectively.

Results and discussion

Anionic model

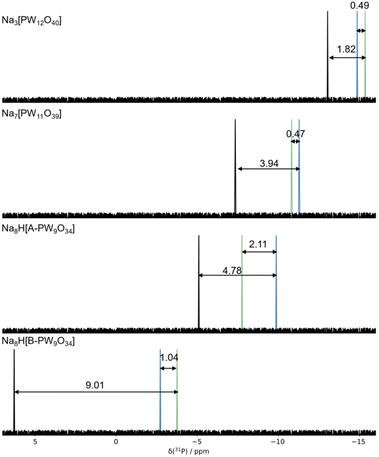
In this section, we seek to establish an optimal computational practise for calculating ³¹P NMR signals by using several x–c functionals with varying contributions of exact Hartree–Fock (HF) exchange (0% PBE, 15% B3LYP*, 20% B3LYP, 25% PBE0, 50% BH&H). The influence of applied basis set (TZ2P & QZ4P) was restricted to the GGA–PBE functional. Our initial work focussed on anionic systems, shown in Fig. 3.

Fig. 3 Computed chemical shift, δ_Calc(³¹P), plotted as a function of P–O distance for the hydrolytic conversions of (a) [PW₁₂O₄₀]³⁻ to lacunary: (b) [PW₁₁O₃₉]⁷⁻, (c) [A-PW₉O₃₄]⁹⁻, and (d) [B-PW₉O₃₄]⁹⁻ clusters. Optimisations were performed x–c functionals with varying degrees of Hartree–Fock (HF) exchange (0% PBE–50% BH&H). All NMR calculations were performed using PBE/TZP.

Computed δ(³¹P) signals for Keggin, [PW₁₂O₄₀]³⁻ and their corresponding lacunary: [PW₁₁O₃₉]⁷⁻, [A-PW₉O₃₄]⁹⁻, and [B-PW₉O₃₄]⁹⁻ clusters are presented in Fig. 3. δ_Calc(³¹P) for Keggin, [PW₁₂O₄₀]³⁻, were reproduced within ca. 8 ppm across all methods with respect to the experimental, δ_exp(³¹P) – see Table 1. δ_Calc(³¹P) for anionic Keggin systems, [PW₁₂O₄₀]³⁻ were in closer agreement with δ_exp(³¹P) of Na₃[PW₁₂O₄₀]. The discrepancy between δ_Calc(³¹P) and δ_Exp(³¹P) was represented by δ_Error(³¹P). Herein, δ_Error(³¹P) decreased as a function of exact Hartree–Fock (HF) exchange which was attributed shortening of P–O distances. For example, as exchange was increased from 15% (B3LYP*) to 50% (BH&H), P–O in  [PW₁₂O₄₀]³⁻ decreased by 0.026 Å, reflecting in the range of 7.87 ppm. All computed entries for [PW₁₂O₄₀]³⁻ produced P–O geometries in the region of 1.519–1.545 Å, closely replicating the crystallographic structure of 1.530 Å.⁴⁵

Table 1 Computed δ_Calc(³¹P) signals for Keggin, [PW₁₂O₄₀]³⁻ and their corresponding lacunary: [PW₁₁O₃₉]⁷⁻, [A-PW₉O₃₄]⁹⁻ with [B-PW₉O₃₄]⁹⁻ clusters and their corresponding salts (X = Li⁺, Na⁺, K⁺, TBA⁺). All NMR calculations were performed as single point calculations using PBE/TZP with spin orbit correction (SO-ZORA)

PBE^NMR/TZP^NMR//Functional^OPT/Basis^OPT	δ Calculated(^31P)						δ Experimental(^31P)
	PBE/TZ2P	PBE/QZ4P	B3LYP*/TZP	B3LYP/TZP	PBE0/TZP	BH&H/TZP	Our work	Lit.^19,46
a Protonated species. (Value) Discrepancy values in parentheses calculated using: δExp(^31P) minus δCalc(^31P).
[PW12O40]^3−/H2O	−7.56	−9.66	−9.63	−10.43	−11.30	−17.50		−14.60^a
Li3[PW12O40]	−7.90 (7.5)	−10.22 (5.2)	−10.27 (5.1)	−11.03 (4.4)	−12.84 (2.6)	−18.55 (3.1)	−15.41
Na3[PW12O40]	−8.28 (7.1)	−10.80 (4.6)	−10.65 (4.7)	−11.39 (4.0)	−13.04 (2.3)	−19.04 (3.7)	−15.36
[PW12O40]^3−/MeCN	−7.55	−9.62	−9.27	−9.97	−11.38	−17.50
TBA3[PW12O40]	−8.25 (7.1)	−11.40 (4.0)	−9.75 (5.6)	−10.68 (4.7)	−12.33 (3.0)	−19.65 (4.3)	−15.35
[PW11O39]^7−/H2O	−2.29	−4.43	−4.21	−5.00	−6.59	−14.35
Li7[PW11O39]	−3.47 (8.2)	−5.38 (6.3)	−5.35 (6.3)	−6.16 (5.5)	−7.27 (4.4)	−14.92 (3.5)	−11.65	−11.20
Na7[PW11O39]	−2.33 (8.5)	−4.65 (6.2)	−4.58 (6.2)	−5.37 (5.5)	−7.35 (3.5)	−14.28 (3.5)	−10.82	−10.65
K7[PW11O39]	−3.40 (7.7)	−6.06 (5.1)	−6.05 (5.1)	−6.82 (4.3)	−8.5 (2.6)	−16.28 (5.2)	−11.13	−10.80
[A-PW9O34]^9−/H2O	0.55	−1.00	−0.86	−1.61	−3.87	−13.86
Na8H[A-PW9O34]	−0.99 (6.8)	−2.34 (5.4)	−2.39 (5.4)	−3.24 (4.5)	−5.10 (2.7)	−12.83 (5.1)	−7.76	−7.10
[B-PW9O34]^9−/H2O	3.41	1.89	2.33	1.60	−1.96	−11.64
Na8H[B-PW9O34]	11.05 (14.8)	9.23 (13.0)	9.17 (12.9)	8.15 (11.9)	6.28 (2.5)	−2.96 (0.8)	−3.76	−3.00
MAE	8.65	6.37	6.61	5.79	4.03	3.74
MSE	8.65	6.37	6.61	5.79	4.03	−3.54
STD	2.54	2.83	2.66	2.58	2.53	1.57

---

Computed chemical shifts, δ_Calc(³¹P), will be rationalised as a function of structural geometry. The magnetic shielding tensor, σ, is comprised of the sum of three contributions: (i) diamagnetic; (ii) paramagnetic; (iii) and the spin–orbit (SO) correction – see eqn (2). The diamagnetic contribution to shielding is dominated by core orbitals contributions which are largely unaffected by the chemical environment. Hence, δ_Calc(³¹P) can be attributed to the paramagnetic term, σ_p. eqn (3) shows the principal contributor to the paramagnetic term is u_ai, which depends on the reciprocal of the energy gap between the occupied and virtual orbitals involved in transition. HOMO LUMO gaps are not the same as transitions atttributed to the P nucleus!

Generally, employment of hybrid x–c functionals proved superior and were in closer agreement with δ_exp(³¹P) with respect to GGA-PBE coupled with triple-ζ plus polarization (TZ2P) or quadruple-ζ plus polarization (QZ4P) basis sets. This observation was attributed to an over-expansion of the PO₄ tetrahedron. Our computed signals shown an inverse correlation with Hartree–Fock (HF) exchange, shown in Fig. 3. The contraction of the PO₄ tetrahedron induced shielding of the nucleus. Consequently, the energy gap between the occupied and virtual orbitals involved in transition have increased with contraction of the P–O distances. One would expect that for small energy gaps, this will reinforce σ_p (more negative), and the shielding tensor, σ, becomes less positive, displacing δ_Calc(³¹P) to more positive regions. Hence, the energy gap between the occupied and virtual orbitals increases and u_ai becomes less negative.

Incorporation of alkali metal cations

In this work, we have explicitly located alkali metal (X = Li⁺, Na⁺, K⁺) cations to render our systems charge neutral. On the surface of the molecule, the counterion can interact with 4-fold (pocket A–F) or 3-fold pockets – see Fig. S9.†¹⁴ The 4-fold pockets feature four oxygen atoms capable of interacting with counterions, whilst 3-fold pockets are comprised of three adjacent oxygen atoms which assume a triangular shape. In our previous work, we established alkal-.metal counterions preferentially interact with the 4-fold pockets because of improved Coulomb interactions.¹⁴ Herein, we have explicitly located alkali metal (X = Li⁺, Na⁺, K⁺) cations into 4-fold hollow sites, unless specified otherwise, to render the system neutral.

Computed δ(³¹P) signals for Keggin, X₃[PW₁₂O₄₀] and their corresponding lacunary: X₇[PW₁₁O₃₉], X₉[A-PW₉O₃₄], and X₉[B-PW₉O₃₄] (X = Li⁺, Na⁺, K⁺, TBA⁺) clusters are presented in Table 1. Incorporation of counterions to [PW₁₂O₄₀]³⁻ induced (minimal) deshielding by approx. 0.5–1.5 ppm. The active nuclei in X₃[PW₁₂O₄₀] (X = Li⁺, Na⁺) became more shielded (0.3 – 0.5 ppm) as the ionic radii of alkali–metal cation was increased from ca. 2.125 to 2.250 Å (Li⁺to Na⁺). δ_Calc(³¹P) calculated using PBE0/TZP produced the strongest agreement with δ_Exp(³¹P) shifted upfield by 2.5 ppm, relative to experimental data.

The accuracy of x–c functionals was assessed, in which, increasing HF exchange progressively shifted signals upfield from −10.27 (15% B3LYP*) to −18.55 ppm (50% BH&H) in Li₃[PW₁₂O₄₀]³⁻ salts and −10.80 (15% B3LYP*) to −19.04 ppm (50% BH&H) in Na₃[PW₁₂O₄₀], salts. Negligible effects to δ(³¹P) were induced by changing the implicit solvent (H₂O → MeCN) shown for [PW₁₂O₄₀]³⁻ in which Δδ(³¹P) did not exceed 0.5 ppm.

Assessment of the lacunary, X₇[PW₁₁O₃₉] (X = Li⁺, Na⁺) clusters were shifted downfield by 4.0–5.0 ppm with respect to Keggin, X₃[PW₁₂O₄₀]. δ(³¹P) signal in Na₇[PW₁₁O₃₉] clusters were shifted upfield by 1.0–1.5 ppm, with respect to Li₇[PW₁₁O₃₉] clusters. Conversely, δ(³¹P) signals in K₇[PW₁₁O₃₉] clusters were shifted downfield by ca. 1.0 ppm relative to Na₇[PW₁₁O₃₉] revealing the overall trend: K⁺ (upfield) > Li⁺ > Na⁺ (downfield). Unfortunately, our computational model is unable to replicate the order of δ_Exp(³¹P) values in X₇[PW₁₁O₃₉]: Li⁺ (upfield) > K⁺ > Na⁺ (downfield). This is probably since our model overlooks the ion pairing effect in aqueous solutions of polyoxometalate anions with different cations. In 2008 Poblet and co-workers studied the delicate interplay between electrostatic interactions and the proximity effect in the aqueous solutions of three different POMs, [PW₁₂O₄₀]³⁻, [SiW₁₂O₄₀]⁴⁻, and [AlW₁₂O₄₀]⁵⁻, with respect to three different monovalent cations Li⁺, Na⁺, and K⁺.⁴⁷ Later, Nyman and co-workers successfully investigated the ion-pairing effect in  Mo− based Lindqvist([(CH₃)₄N]⁺,Cs)₈[M₆O₁₉] (M = Nb, Ta), combining experiments and theory. Their system is particularly challenging as the clusters water solubility increases with stronger ion-pairing, contrary to most ionic salts.⁴⁸ Although, the best overall computational methodology was not consistent across the lacunary clusters. The influence of exact exchange progressively shielded δ(³¹P) values, for example: from −5.35 (15% B3LYP*) to −14.92 ppm (50% BH&H) in Li₇[PW₁₁O₃₉], salts. Generally, optimisations using PBE0/TZP (20% exchange) accurately replicated the experimental, reporting a mean absolute error (MAE) of 4.03 ppm. Computation with BH&H/TZP demonstrated the lowest value of MAE (3.74 ppm), attributed to an excellent replication of δ(³¹P) in Na₈H[B-PW₉O₃₄].

Incorporation of alkylammonium cations

To further this work, we have explicitly incorporated alkylammonium cations, neutralising our systems to: [(n-C_xH_2x+1)₄N]₃[PW₁₂O₄₀]; where x = 1–4 (Table 2). The alkylammonium cations adopted a triangular arrangement around the Keggin, [PW₁₂O₄₀]³⁻ in which the central heteroatom is co-planar with the cations, see Fig. S10.†

Table 2 Computed, δ_Calc(³¹P) for alkyl ammonium Keggin, [(n-C_xH_2x+1)₄N]₃[PW₁₂O₄₀] salts, reported in ppm. The difference in, δ_Calc(³¹P) relative to [(n-C₄H₉)₄N]₃[PW₁₂O₄₀] is represented by Δδ_Calc(³¹P). Optimizations were performed using PBE0/TZP level of theory. All NMR calculations were performed using PBE/TZP

[(n-CxH2x+1)4N]^+	δ Calc(^31P)	ΔδCalc(^31P)
[NH4]^+	−13.00	0.67
[(n-CH3)4N]^+	−12.68	0.35
[(n-C2H5)4N]^+	−12.70	0.37
[(n-C3H7)4N]^+	−12.83	0.50
[(n-C4H9)4N]^+	−12.33	0.00

---

The arrangement of [(n-C_xH_2x+1)₄N]₃ can be assessed by the average central heteroatom (P) – nitrogen (ammonium) distance calculated at 5.601, 7.227, 8.003, 7.919, and 8.043 Å for NH₄⁺, n-(CH₃)₄⁺, n-(C₂H₅)₄⁺, n-(C₃H₇)₄⁺, and n-(C₄H₉)₄⁺, respectively. Optimizations using PBE0/TZP for [(n-C₄H₉)₄N]₃[PW₁₂O₄₀] produced δ(³¹P) with reasonable agreement with the experimental (ca. 3.0 ppm). However, optimizations of [(n-C_xH_2x+1)₄N]₃[PW₁₂O₄₀] (x = 3 or 4) with hybrid x–c functionals is CPU expensive, hence, we explored the sensitivity of δ(³¹P) of alkyl chain length in [(n-C_xH_2x+1)₄N]₃. Computed δ_Calc(³¹P) was shielded by 0.67 ppm from −12.33 ([(n-C₄H₉)₄N]⁺) to −13.00 ([NH₄]⁺). Interestingly, optimisations using [NH₄]⁺ cations yielded the closest agreement with the experimental values.

Empirical scaling was performed to correct the discrepancies between the computed and experimental work. The present work employed data points obtained using the PBE/TZP//PBE0/TZP methodology, thereby computed isotropic shielding (σ) was plotted taking the form δ = bσ + a, in which the slope, b, is the scaling factor, see Fig. 4. Table S2† reports the comparison between experimental, δ_Exp, computed, δ_Comp, and fitted, δ_Fitted, chemical shifts (Fig. 5).

Fig. 4 Computed isotropic shielding, σ_Calc using the PBE/TZP//PBE0/TZP methodology, plotted as a function of experimental δ_Exp(³¹P) values.

Fig. 5 Computed (black), δ_Exp(³¹P), fitted (blue), δ_Fitted(³¹P), and experimental (green), δ_Exp(³¹P), signals for Keggin, Na₃[PW₁₂O₄₀] and their corresponding lacunary: Na₇[PW₁₁O₃₉], Na₉[A-PW₉O₃₄], and Na₉[B-PW₉O₃₄] clusters. All NMR calculations were performed using PBE/TZP.

The fitted values, δ_Fitted(³¹P), revealed significantly lower MAE values of 0.86 and were not systematically underestimated shown by MSE of −0.02 ppm. δ_Fitted(³¹P) replicated the order of δ(³¹P) values in X₇[PW₁₁O₃₉] (X = Li⁺, Na⁺, K⁺) replicating the experimental within ca. 0.9 ppm, see Fig. 4 and Table S2.† A significant improvement for the tri-lacunary: Na₈H[A-PW₉O₃₄] and Na₈H[B-PW₉O₃₄] clusters were observed, in which δ_Error(³¹P) was reduced from 2.66 and 10.04 using PBE/TZP//PBE0/TZP to 2.11 and 1.04 using fitted values, δ_Fitted(³¹P). Computed δ(³¹P) signals for Na₈H[B-PW₉O₃₄] were challenging to accurately compute without correctional fitting. No correlation between ion-pair proximity and chemical shift was observed, contrasted to redox potentials shown in our previous work. The effect of the functional outweighs the effect of the counterions.

Conclusions

In this work, we have employed Density Functional Theory (DFT) calculations to systematically study the accuracy of exchange– correlation functionals and applied basis sets for reproducing experimental chemical shift, δ_Exp(³¹P) values. Our objective has been to establish a methodology for obtaining accurate δ_Calc(³¹P) signals in Keggin-based clusters and to provide an insight into the geometric factors controlling it.

Computation of δ_Exp(³¹P) for Keggin, [PW₁₂O₄₀]³⁻, were in closer agreement to δ_Calc(³¹P) obtained for Na₃[PW₁₂O₄₀]. Generally, discrepancies between δ_Calc(³¹P) and δ_Exp(³¹P) represented by δ_Error(³¹P) decreased as a function of Hartree–Fock (HF) exchange, attributed to shortening of P–O. Explicitly located counterions reduced discrepancies by 1.0–2.0 ppm across all Keggin and corresponding lacunary compounds which was attributed to their deshielding effect. However, obtaining accurate approximations for for [B-PW₉O₃₄]⁹⁻ remains a challenge due to direct electrostatic interactions between the located counterions and central tetrahedron. Optimal results were achieved using the PBE/TZP//PBE0/TZP method, achieving an MAE and MSE of 4.03 ppm. Linear scaling was performed to reduce discrepancies between the computed and experimental work,in which δ_Fitted(³¹P), revealed lower MAE values of 0.86 ppm and were not systematically underestimated shown by MSE of −0.02 ppm.

Data availability

The datasets generated using DFT calculations are available in the ioChem-BD database: https://iochem-bd.bsc.es/browse/handle/100/312985

Author contributions

L.V.-N. conceived the idea together with J. A. T. who designed the modelling approach, performed all calculations, synthesised, and fully characterised all the compounds and analysed all the data. J. A. T. wrote the paper and made all tables and figures in the manuscript with input from L.V.-N.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support for this work was provided by University of Glasgow and the Engineering and Physical Sciences Research Council Grants (EP/S030603/1; EP/V048341/1; EP/S031170/1), Royal Society of Chemistry RSC Hardship Grant (COVID-19). We thank the EPSRC Doctoral Training Partnership (DTP) funding received by the University of Glasgow for Jake A. Thompson PhD studentship ‘Exploring N₂ fixation with metal oxides’ project 2442596 (EP/R513222/1; EP/T517896/1). We also thank the University of Glasgow (UofGla) Early Career Development Programme (ECDP) 2021, the UofGla Reinvigorating Research Scheme 2022, and the School of Chemistry for long-lasting support. We thank ScotCHEM for 2022 ECR equipment funding and we also thank the Cronin Group for upcylced glassware and equipment. Finally, we thank Mr Alec Mungall, for help collecting NMR samples, and all the technical staff in the School of Chemistry for support during this work. Results were obtained using the ARCHIE-WeSt High-Performance Computer (https://www.archie-west.ac.uk) based at the University of Strathclyde.

References

1. A. V. Anyushin, A. Kondinski and T. N. Parac-Vogt, Chem. Soc. Rev., 2020, 49, 382–432.
2. N. I. Gumerova and A. Rompel, Chem. Soc. Rev., 2020, 49, 7568–7601.
3. N. V. Izarova, M. T. Pope and U. Kortz, Angew. Chem., Int. Ed., 2012, 51, 9492–9510.
4. A. Proust, B. Matt, R. Villanneau, G. Guillemot, P. Gouzerh and G. Izzet, Chem. Soc. Rev., 2012, 41, 7605–7622.
5. A. S. Cherevan, S. P. Nandan, I. Roger, R. Liu, C. Streb and D. Eder, Adv. Sci., 2020, 7, 1903511.
6. S. M. Wilson, B. E. Petel, E. Schreiber, M. L. Maiola, P. Su, E. M. Matson and J. Laskin, Chem. – Eur. J., 2023, 29, 1–10.
7. C. P. Pradeep, D. L. Long and L. Cronin, J. Chem. Soc., Dalton Trans., 2010, 39, 9443–9457.
8. M. S. Balulla, J. A. Gamelas, H. M. Carapuça, A. M. V. Cavaleiro and W. Schlindwein, Eur. J. Inorg. Chem., 2004, 619–628.
9. A. Misra, K. Kozma, C. Streb and M. Nyman, Angew. Chem., Int. Ed., 2020, 59, 596–612.
10. D.-L. Long, E. Burkholder and L. Cronin, Chem. Soc. Rev., 2007, 36, 105–121.
11. H. N. Miras, L. Vilà-Nadal and L. Cronin, Chem. Soc. Rev., 2014, 43, 5679–5699.
12. S. Khlifi, J. Marrot, M. Haouas, W. E. Shepard, C. Falaise and E. Cadot, J. Am. Chem. Soc., 2022, 144, 4469–4477.
13. S. Azuma, T. Kadoguchi, Y. Eguchi, H. Hirabaru, H. Ota, M. Sadakane, K. Yanagisawa, T. Hasegawa and T. Ueda, Dalton Trans., 2020, 49, 2766–2770.
14. J. A. Thompson, R. González-Cabaleiro and L. Vilà-Nadal, Inorg. Chem., 2023, 62, 12260–12271.
15. D. Laurencin, R. Thouvenot, K. Boubekeur, P. Gouzerh and A. Proust, C. R. Chim., 2012, 15, 135–142.
16. M. Sadakane, D. Tsukuma, M. H. Dickman, B. Bassil, U. Kortz, M. Higashijima and W. Ueda, Dalton Trans., 2006, 4271–4276.
17. P. Klonowski, J. C. Goloboy, F. J. Uribe-Romo, F. Sun, L. Zhu, F. Gándara, C. Wills, R. J. Errington, O. M. Yaghi and W. G. Klemperer, Inorg. Chem., 2014, 53, 13239–13246.
18. R. González-Cabaleiro, J. A. Thompson and L. Vilà-Nadal, Front. Chem., 2021, 9, 742565.
19. R. I. Maksimovskaya and G. M. Maksimov, Coord. Chem. Rev., 2019, 385, 81–99.
20. L. Vilà-Nadal and L. Cronin, Nat. Rev. Mater., 2017, 2, 17054.
21. R. Contant and A. Tézé, Inorg. Chem., 1985, 24, 4610–4614.
22. A. Bagno and M. Bonchio, Eur. J. Inorg. Chem., 2002, 1475–1483.
23. (a) A. Bagno, M. Bonchio, A. Sartorel and G. Scorrano, Eur. J. Inorg. Chem., 2000, 17–20; (b) A. Bagno, M. Bonchio, A. Sartorel and G. Scorrano, ChemPhysChem, 2003, 4, 517–519; (c) A. Bagno, M. Bonchio and J. Autschbach, Chem. – Eur. J., 2006, 12, 8460–8471.
24. N. Vankova, T. Heine and U. Kortz, Eur. J. Inorg. Chem., 2009, 5102–5108.
25. L. Vilà-Nadal, J. P. Sarasa, A. Rodríguez-Fortea, J. Igual, L. P. Kazansky and J. M. Poblet, Chem. – Asian J., 2010, 5, 97–104.
26. M. Pascual-Borràs, X. López, A. Rodríguez-Fortea, R. J. Errington and J. M. Poblet, Chem. Sci., 2014, 5, 2031–2042.
27. M. Pascual-Borràs, X. López and J. M. Poblet, Phys. Chem. Chem. Phys., 2015, 17, 8723–8731.
28. J. A. Dias, S. C. L. Dias, E. Caliman, J. Bartis and L. Francesconi, Keggin Structure Polyoxometalates, Inorg. Synth., 2014, 36, 210–217.
29. J. A. Gamelas, F. A. S. Couto, M. C. N. Trovão, A. M. V. Cavaleiro, J. A. S. Cavaleiro and J. D. P. de Jesus, Thermochim. Acta, 1999, 326, 165–173.
30. N. Haraguchi, Y. Okaue, T. Isobe and Y. Matsuda, Inorg. Chem., 1994, 33, 1015–1020.
31. B. Moore and K. Foger, Inorg. Chim. Acta, 1991, 181, 201–205.
32. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 3865–3868.
34. M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55.
35. C. Lee, E. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 37, 785.
36. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
37. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
38. R. Sure, J. G. Brandenburg and S. Grimme, ChemistryOpen, 2016, 5, 94–109.
39. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
40. E. Van Lenthe, J. Chem. Phys., 1999, 110, 8943–8953.
41. C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408.
42. C. Van Wüllen, Phys. Chem. Chem. Phys., 2000, 2, 2137–2144.
43. D. B. Chesnut, J. Phys. Chem. A, 2005, 109, 11962–11966.
44. J. Přecechtělová, P. Novák, M. L. Munzarová, M. Kaupp and V. Sklenář, J. Am. Chem. Soc., 2010, 132, 17139–17148.
45. G. M. Brown, M.-R. Noe-Spirlet, W. R. Busing and H. A. Levy, Acta Crystallogr., 1977, 1038–1046.
46. M. Kozik, C. F. Hammer and L. C. W. Baker, J. Am. Chem. Soc., 1986, 108, 7627–7630.
47. F. Leroy, P. Miró, J. M. Poblet, C. Bo and J. Bonet-Ávalos, J. Phys. Chem. B, 2008, 112(29), 8591–8599.
48. J. Sures, S. A. Serapian, K. Kozma, P. I. Molina, C. Bo and M. Nyman, Phys. Chem. Chem. Phys., 2017, 19, 8715–8725D.

---

Footnote

† Electronic supplementary information (ESI) available: Selected structural parameters for Keggin, [PW₁₂O₄₀]³⁻ and corresponding lacunary: [PW₁₁O₃₉]⁷⁻, [A-PW₉O₃₄]⁹⁻, and [B-PW₉O₃₄]⁹⁻ clusters. Experimental ³¹P NMR, IR, UV, and ESI-MS spectra. See DOI: https://doi.org/10.1039/d3dt02694a

---