 Open Access Article
Open Access ArticleRegio-MPNN: predicting regioselectivity for general metal-catalyzed cross-coupling reactions using a chemical knowledge informed message passing neural network†
Baochen
Li‡
 a,
Yuru
Liu‡
a,
Yuru
Liu‡
 a,
Haibin
Sun
a,
Rentao
Zhang
a,
Yongli
Xie
a,
Klement
Foo
a,
Haibin
Sun
a,
Rentao
Zhang
a,
Yongli
Xie
a,
Klement
Foo
 b,
Frankie S.
Mak
b,
Ruimao
Zhang
c,
Tianshu
Yu
c,
Sen
Lin
a,
Peng
Wang
a and
Xiaoxue
Wang
b,
Frankie S.
Mak
b,
Ruimao
Zhang
c,
Tianshu
Yu
c,
Sen
Lin
a,
Peng
Wang
a and
Xiaoxue
Wang
 *a
*a
aChemLex Technology Co., Ltd, 1976 Gaoke Mid. Rd, Shanghai, China 201210. E-mail: wxx@chemlex.tech
bExperimental Drug Development Centre (EDDC), Agency for Science, Technology and Research (A*STAR), 10 Biopolis Road, #05-01, Chromos, 138670, Singapore
cSchool of Data Science, The Chinese University of Hong Kong, Shenzhen (CUHK-SZ), 2001 Longxiang Boulevard, Shenzhen, China 518172
First published on 3rd September 2024
Abstract
As a fundamental problem in organic chemistry, synthesis planning aims at designing energy and cost-efficient reaction pathways for target compounds. In synthesis planning, it is crucial to understand regioselectivity, or the preference of a reaction over competing reaction sites. Precisely predicting regioselectivity enables early exclusion of unproductive reactions and paves the way to designing high-yielding synthetic routes with minimal separation and material costs. However, it is still at the emerging state to combine chemical knowledge and data-driven methods to make practical predictions for regioselectivity. At the same time, metal-catalyzed cross-coupling reactions have profoundly transformed medicinal chemistry, and thus become one of the most frequently encountered types of reactions in synthesis planning. In this work, we for the first time introduce a chemical knowledge informed message passing neural network (MPNN) framework that directly identifies the intrinsic major products for metal-catalyzed cross-coupling reactions with regioselective ambiguity. Integrating both first principles methods and data-driven methods, our model achieves an overall accuracy of 96.51% on the test set of eight typical metal-catalyzed cross-coupling reaction types, including Suzuki–Miyaura, Stille, Sonogashira, Buchwald–Hartwig, Hiyama, Kumada, Negishi, and Heck reactions, outperforming other commonly used model types. To integrate electronic effects with steric effects in regioselectivity prediction, we propose a quantitative method to measure the steric hindrance effect. Our steric hindrance checker can successfully identify regioselectivity induced solely by steric hindrance. Notably under practical scenarios, our model outperforms 6 experimental organic chemists with an average working experience of over 10 years in the organic synthesis industry in terms of predicting major products in regioselective cases. We have also exemplified the practical usage of our model by fixing routes designed by open-access synthesis planning software and improving reactions by identifying low-cost starting materials. To assist general chemists in making prompt decisions about regioselectivity, we have developed a free web-based AI-empowered tool. Our code and web tool have been made available at https://github.com/Chemlex-AI/regioselectivity and https://ai.tools.chemlex.com/region-choose, respectively.
1 Introduction
Regioselectivity describes the preference of a reaction to occur at a specific site within a molecule when multiple sites are available (Fig. 1a). Accurately predicting regioselectivity for chemical reactions is crucial for designing feasible and high-yielding synthetic routes with minimal separation and material costs.4 Though human experts have accumulated rich experience during practice, predicting regioselectivity is still highly challenging for most experts, especially for molecules where competing reactive centers have subtle differences in intrinsic stereoelectronic reactivity. Conventionally, when given a new reaction with undetermined regioselectivity concerns, human experts need to study the mechanism of the reaction and conduct small-scale experiments to determine the results. Given such challenges often arise when the target molecule reaches a level of substantial complexity, any chemical material generated would often be considered precious, thus making such experimental approaches expensive. Moreover, this single-step product optimization may take several days, significantly hindering the process of synthetic route determination. Therefore, a fast computational tool to assist human experts during this process would have an invaluable impact and be in high demand. | ||
| Fig. 1 Regioselectivity in metal-catalyzed cross-coupling reactions. (a) An example of regioselectivity challenge in a Suzuki–Miyaura reaction. In the heteroaryl halide, there are two competing coupling sites, marked by blue and red circles. As reported by Saxty et al.,1 the blue circle denotes the major coupling site with the corresponding major product (with a yield of 82%) highlighted in the blue rectangle; (b) the general mechanism for Metal-Catalyzed Cross-Coupling Reactions (MCCCRs); (c) an overview of this work. The dataset comprising 9734 MCCCRs with regioselectivity ambiguity is licensed from Pistachio2 and CAS Content Collection.3 Calculated descriptors, together with atom and bond features are passed through Regio-MPNN to get the predicted probability for each candidate product. A steric hindrance checker guarantees that the predicted major reaction site is within the “safe” steric hindrance range. Black circles stand for carbon atoms, blue circles stand for nitrogen atoms, green circles stand for chlorine atoms, brown circles stand for bromine atoms, and filled circles stand for neighboring atoms considered at each message-passing step. | ||
Concurrently, the recent integration of artificial intelligence (AI) into computer-aided synthesis planning (CASP) has profoundly revolutionized early-stage drug discovery and preclinical manufacturing process development.5–13 Not only useful for saving opportunity and tangible costs for bench scientists, fast and accurate computational methods to determine regioselectivity are also critical for designing green and efficient synthetic routes in CASP.14–16 Aligning with such unmet needs, computational methods to predict regioselectivity for various organic chemistry reactions have been long pursued. However, despite relentless endeavors over decades, developing high-performing predictive computational tools for regioselectivity remains a significant challenge. In the 1990s, with limited computational power, scientists focused on using feature engineering to learn the correlation between molecular descriptors and regioselectivity.17 Oslob and co-workers18 used the Quantitative Structure–Activity Relationship (QSAR) to predict the regioselectivity for palladium-catalyzed allylations. They calculated the energy for steric probing, the bond length from palladium to the reacting center carbon, and two dihedral angles, to fit the experimental selectivity data. Nonetheless, to ensure the performance, data points with relatively high activation energy were removed from their dataset, limiting their method's application and imposing unresolved bias. Banerjee and co-workers19 used various Machine Learning (ML) tools to analyze the outcome of catalytic regioselective difluorination reactions of alkenes and decipher the complex interplay of various molecular parameters and their non-linear dependencies. In their work, they used density functional theory (DFT) to compute molecular parameters for 66 alkenes and further discovered the dependencies between these molecular parameters and regiochemical outcomes. However, computing these parameters via DFT is relatively time-consuming, underscoring the need for more efficient approaches. To enhance the computational efficiency, Hong et al.20 used ML models trained on DFT results to predict descriptors of interest. They combined 32 key physical organic descriptors and developed a regression algorithm to predict regioselectivity for radical C–H functionalization of heterocycles. Their work achieved a rapid and reliable prediction of descriptors through ML models successfully. However, the approach of featurizing reactants solely with physical organic descriptors may lead to missing critical structural information about molecules. Ree and co-workers21 calculated Charge Model 5 (CM5)22 atomic charges and used them to predict the regioselectivity of electrophilic aromatic substitution reactions with a light gradient boosting machine. Similarly, Tomberg et al.23 also focused on electrophilic aromatic substitution reactions. They computed the Fukui coefficient, partial charge, bond orders, and atomic solvent accessible surface for each aromatic carbon and found that random forest models achieved the best performance for classifying carbons as active or inactive in electrophilic aromatic substitution. Guan et al.17 introduced a new method that combines graph-based molecular representation with simulated chosen quantum mechanical descriptors to predict regioselectivity in substitution reactions. After that, they focused on the regioselectivity problem in nucleophilic aromatic substitution (SNAr) reactions and attached a checker at the end of their model to distinguish the possible products with similar predictive scores.24 In Ree's, Tomberg's, and Guan's work, they all treated the electronic properties as the major factors for regioselectivity in their interested reactions and did not take steric effects into account explicitly. Currently, there is no predictive model available that combines both electronic and steric effects with data-driven deep learning methods.
On the other hand, medicinal chemistry has been profoundly reshaped by metal-catalyzed cross-coupling reactions (MCCCRs) due to their impressive ability to forge carbon–carbon/carbon–heteroatom bonds between diverse chemical moieties, enabling the creation of compounds that are otherwise challenging to obtain.25 Palladium-catalyzed cross-coupling reactions, such as the Suzuki–Miyaura, Buchwald–Hartwig, Heck, and Stille reactions, have stood among the most popular reaction types in medicinal chemistry.25 As shown in Fig. 1b, the mechanism of MCCCRs generally involves:26 (1) oxidative addition converting an organic halide (RX) to L(n)MR(X) in the presence of catalyst L(n)M (L = spectator ligand). (2) Transmetallation converting L(n)MR(X) to L(n)MR(R′), where the source of R′(−) varies in different metal coupling reactions. For Suzuki, R′(−) comes from a boronic acid or the corresponding ester. For Buchwald, Heck, Sonogashira, Negishi, Stille, Hiyama, and Kumada reactions, the sources are amines, alkenes, alkynes, organozinc, -tin, and -silicon reagents and Grignard reagents, respectively. (3) Reductive elimination of L(n)MR(R′) to regenerate catalyst L(n)M and to release the resulting product R–R′. Among the three steps, oxidative addition is generally considered the rate-limiting step for most MCCCRs.27 The extent of this step is heavily influenced by the leaving group ability of X and the steric hindrance around the C–X bond.26 Therefore, it is possible to use quantitative descriptors, e.g. partial charge, Fukui index, and volumetric measures from conformational analysis, to describe the properties of the rate-limiting step, and further characterize the different kinetics between competing reaction sites where regioselectivity is considered. Additionally, regioselectivity-related experimental results have been widely reported in the literature, enabling data-driven methods to mine statistical rules behind the literature data. As a result, a computational model that accurately predicts the regioselectivity is thus made possible by both theoretical analysis and data-driven machine learning.
In this work, we propose Regio-MPNN, Message Passing Neural Network (MPNN) backbone combined with chemical descriptors, to directly predict intrinsic major products for MCCCRs with regioselectivity risks, as shown in Fig. 1c. We use computed atomic charges, Fukui index, Nuclear Magnetic Resonance (NMR) chemical shift, and bond length through DFT calculation to train an MPNN model based on the graph representation of a molecule, and examine the steric hindrance effect on possible reactive sites through a steric hindrance checker. It is worth noting that in practice, regioselectivity can also be affected by reaction conditions.28–30 However, literature has limited reported records on the relationship between regioselectivity and reaction conditions, making it difficult to capture this effect using data-driven methods. Therefore, in this work, we only focus on the intrinsic properties of reactants and ignore the differences caused by reaction conditions. Our model exhibits an overall accuracy of 96.51% on a test set comprising eight types of metal-catalyzed cross-coupling reactions, demonstrating the capability for practical usage. Our model architecture outperforms other frequently used model types, including Extended-Connectivity Fingerprint (ECFP)31 based multilayer perceptron (MLP), descriptor based MLP, sequence based model + MLP, and ml-QM-GNN,17 regarding prediction accuracy and robustness. We have also demonstrated that our steric hindrance checker is able to detect regioselectivity solely induced by steric hindrance regardless of electronic effects. Furthermore, we invited 6 experimental organic chemists with an average working experience of over 10 years in industry to compete with our model on regioselectivity tests. In this test, we randomly picked 100 reactions from the test set and collected the predictions of major products from the chemists and our model. Our model significantly outperformed human chemists, demonstrating the advantage of using machine learning methods with first-principles results. In the end, we show the practical usage cases of our model on synthesis planning and material cost saving by finding more accessible starting materials. Our Regio-MPNN model is designed to predict the regioselectivity of a given MCCCR, however, it does not guarantee the feasibility of the MCCCR. Therefore, if the feasibility of the MCCCR is a concern, a separate reaction yield prediction model should be used. It is worth noting that reaction yield prediction can be considerably challenging and is beyond the scope of this work.32–34
2 Methods
2.1 Data preparation
Data used in this manuscript came from two commercial datasets: Pistachio2 and Chemical Abstracts Service (CAS) Content Collection.3 For the Pistachio dataset, we first used NameRxn numbers provided together with the data to pick out each cross-coupling reaction, the Buchwald, Heck, Hiyama, Kumada, Negishi, Sonogashira, Stille, and Suzuki reactions, respectively. Then, for each reaction type, we applied several filters to get a dataset with 8923 data points. The filters added are discussed in detail in the following paragraph. To enhance the data balance among different metal-catalyzed cross-coupling reactions, we also licensed 811 curated data points from CAS Content Collection, producing a dataset with 9734 data points.The data cleaning process is as follows. Here we take the Suzuki–Miyaura cross-coupling reactions as examples. First, we removed the duplicate reactions. Then we filtered out reactions with yields less than 40% to ensure that the product in the dataset is indeed the preferred reacting site. Next, we used SMARTS to match each reactant and classify reactants into two types: organohalides or organoboron.35 The SMARTS of the reactant organohalides is defined as “[F,Cl,Br,I,$(OS(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)(
O)(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C(F)(F)F)][#6]”, which covers aryl halides and allyl halides. Here, the “generalized” halides are not limited only to halogens but also include halogen-like functional groups, e.g. trifluoromethane sulfonate (OTf). SMARTS of reactant organoboron is defined as “B(O)O”, which matches boronic acid or boronate ester. In order to be identified as Suzuki reactions, all reactions should have at least one organohalide and one boronic substance. Then another filter was applied to pick only organohalides with more than 2 halogen and halogen-like leaving groups. Finally, we use the rdkit.Chem.rdChemReactions module to enumerate all possible products.36 The SMIRKS we used for the Suzuki reactions is: “B(O)(O)([#6:1]).[Cl,Br,I, $(OS(
O)C(F)(F)F)][#6]”, which covers aryl halides and allyl halides. Here, the “generalized” halides are not limited only to halogens but also include halogen-like functional groups, e.g. trifluoromethane sulfonate (OTf). SMARTS of reactant organoboron is defined as “B(O)O”, which matches boronic acid or boronate ester. In order to be identified as Suzuki reactions, all reactions should have at least one organohalide and one boronic substance. Then another filter was applied to pick only organohalides with more than 2 halogen and halogen-like leaving groups. Finally, we use the rdkit.Chem.rdChemReactions module to enumerate all possible products.36 The SMIRKS we used for the Suzuki reactions is: “B(O)(O)([#6:1]).[Cl,Br,I, $(OS(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)(
O)(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C(F)(F)F)][#6:2] ≫ [#6:1]–[#6:2]”. For all the obtained products after applying the reaction SMIRKS, the product that is the same as in the reaction dataset is labeled with 1, which is the ground truth, and all the rest of the possible products are labeled as 0. Other types of MCCRs other than Suzuki reactions were treated similarly with their own chemical definitions respectively. The corresponding SMIRKS for each reaction type can be found in our GitHub repository.37
O)C(F)(F)F)][#6:2] ≫ [#6:1]–[#6:2]”. For all the obtained products after applying the reaction SMIRKS, the product that is the same as in the reaction dataset is labeled with 1, which is the ground truth, and all the rest of the possible products are labeled as 0. Other types of MCCRs other than Suzuki reactions were treated similarly with their own chemical definitions respectively. The corresponding SMIRKS for each reaction type can be found in our GitHub repository.37
2.2 Density functional theory (DFT) calculation
Reaction data were extracted from the aforementioned commercial datasets according to the reaction SMARTS templates. Then the reactants were extracted from those reactions for further DFT calculations. The DFT descriptors used in the model were calculated by an automated computational workflow developed as in Guan et al.17,38 The input for the workflow is a list of SMILES. The output for the workflow is the atom descriptors of each molecule. First, each of the SMILES strings was processed by RDKit36 using the Merck Molecular Force Field (MMFF94s) to obtain initial structure coordinates for each molecule.39 Then the molecular structure was optimized at the GFN2-xtb level of theory.40–42 We made sure there were no imaginary frequencies to guarantee the structure was correctly optimized. Next, the optimized structure was used to calculate the Fukui index with density functional theory (DFT). The DFT calculations were performed using Gaussian 16,43 with the B3LYP functional and def2svp basis set. Then, the target descriptors, Hirshfeld partial charge, Fukui index, and bond lengths were extracted from the Gaussian outputs. Details of the DFT descriptors are included in the ESI “Details of the DFT descriptors” section.† Following the approach in ml-QM-GNN,17 which employs a machine learning model named qmdesc to replace DFT calculations and reduce the computing time, we also use the qmdesc model instead of DFT calculations in Regio-MPNN. However, the Fukui index and Hirshfeld partial charge of MCCCRs' reactants cannot be accurately predicted by qmdesc. For example, ethylmagnesium chloride is a potential reactant for the Kumada reaction. The Fukui electrophilicity index, Fukui nucleophilicity index, and Hirshfeld partial charge of the carbon atom attached to the magnesium element, calculated by DFT, are −0.191, −0.064, and −0.209, respectively, while those predicted by the qmdesc model are −0.051, −0.040, and −0.039, respectively. This discrepancy may be attributed to certain elements or functional groups in reactant molecules involved in MCCCRs, such as the magnesium element in this example, being underrepresented in the qmdesc training set. The coefficient of determination between DFT calculations and qmdesc results is 0.39 for the Fukui electrophilicity index, 0.21 for the Fukui nucleophilicity index, and 0.96 for the Hirshfeld partial charge. Therefore, we treat the qmdesc model as a pre-trained model and use the DFT-calculated Fukui index and Hirshfeld partial charge as new data to update the weights in qmdesc. This fine-tuned qmdesc model is called Fqmdesc. The Fukui electrophilicity index, Fukui nucleophilicity index, and Hirshfeld partial charge of the carbon atom attached to the magnesium element in ethylmagnesium chloride, predicted by the Fqmdesc model, are −0.179, −0.057, and −0.207, respectively. The coefficient of determination between DFT calculations and Fqmdesc results is 0.73 for the Fukui electrophilicity index, 0.75 for the Fukui nucleophilicity index, and 0.99 for the Hirshfeld partial charge. Detailed comparisons between target descriptors predicted by qmdesc and Fqmdesc are given in ESI Fig. S1.† The Fukui index and Hirshfeld partial charge predicted by Fqmdesc are much closer to the DFT results compared to those predicted by qmdesc. Additionally, NMR chemical shifts and bond length matrices predicted by qmdesc closely match the DFT results, so we use the qmdesc predictions for these properties in our work.2.3 MPNN for regioselectivity prediction
MPNN is a type of graph neural network suitable to learn molecular features wherein atoms are vertices and bonds are edges.44–46 Concretely, a molecule can be represented as a graph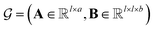 , where A is the matrix of atom features and B is the adjacency tensor of bond features. Here, l is the number of atoms in the molecule, a is the dimension of atom features, and b is the dimension of bond features. Such a graph
, where A is the matrix of atom features and B is the adjacency tensor of bond features. Here, l is the number of atoms in the molecule, a is the dimension of atom features, and b is the dimension of bond features. Such a graph  serves as the input for the MPNN framework. In an MPNN layer, there are two fundamental steps for a forward pass: a message-passing step and an update step. The number of stacked MPNN layers typically depends on the number of connected bonds to be considered around the central atom.44 Besides the conventional graph pairwise sum aggregator used in the message-passing step, other graph aggregators, such as the graph pooling aggregator and gated attention aggregator47 are also implemented to verify the impact of different graph aggregators on model performance.
serves as the input for the MPNN framework. In an MPNN layer, there are two fundamental steps for a forward pass: a message-passing step and an update step. The number of stacked MPNN layers typically depends on the number of connected bonds to be considered around the central atom.44 Besides the conventional graph pairwise sum aggregator used in the message-passing step, other graph aggregators, such as the graph pooling aggregator and gated attention aggregator47 are also implemented to verify the impact of different graph aggregators on model performance.
A message-passing step with the pairwise sum aggregator reads,
 | (1) |
 denotes the new message of atom v at the next time step t + 1 with dimension lm; N(v) denotes the neighboring atom indices of v;
denotes the new message of atom v at the next time step t + 1 with dimension lm; N(v) denotes the neighboring atom indices of v;  denotes the hidden state for atom v at time step t with dimension lh;
denotes the hidden state for atom v at time step t with dimension lh;  denotes the corresponding atom features for atom n at time step t where n ∈ N(v); the initial hidden states
denotes the corresponding atom features for atom n at time step t where n ∈ N(v); the initial hidden states  and
and  are vectors of length a that denotes the vth and nth elements of atom features matrix A, correspondingly;
are vectors of length a that denotes the vth and nth elements of atom features matrix A, correspondingly;  is a vector of length b that denotes the (v, n) element of the adjacency tensor B; ‖ denotes the operation of vector concatenation; M is the message neural network as a mapping, M(xM) = ReLU(WM·xM + bM), ReLU is the rectified linear unit activation function, and
is a vector of length b that denotes the (v, n) element of the adjacency tensor B; ‖ denotes the operation of vector concatenation; M is the message neural network as a mapping, M(xM) = ReLU(WM·xM + bM), ReLU is the rectified linear unit activation function, and  and
and  are the weights and bias of M respectively.
are the weights and bias of M respectively.
A message-passing step with the graph pooling aggregator reads,
| mvt+1 = M(hvt‖pooln∈N(v)(P(hnt‖B(v,n)))) | (2) |
 and
and  are the weights and bias of P respectively; pooln∈N(v) is the pool operator, which can be average pooling or max pooling along all neighbouring atoms; M is the message neural network as a mapping, M(xM) = ReLU(WM·xM + bM), and
are the weights and bias of P respectively; pooln∈N(v) is the pool operator, which can be average pooling or max pooling along all neighbouring atoms; M is the message neural network as a mapping, M(xM) = ReLU(WM·xM + bM), and  and
and 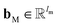 are the weights and bias of M respectively.
are the weights and bias of M respectively.
A message-passing step with the gated attention aggregator reads,
 | (3) |
 ; H is the number of heads in the attention mechanism, used to capture features from different representation subspaces; σ is the sigmoid function; G and F are single fully-connected layers; Qk is a linear map,
; H is the number of heads in the attention mechanism, used to capture features from different representation subspaces; σ is the sigmoid function; G and F are single fully-connected layers; Qk is a linear map,  , for computing the query vector of head k; Kk is a linear map,
, for computing the query vector of head k; Kk is a linear map,  , for computing the key vector of head k; Vk is a linear map,
, for computing the key vector of head k; Vk is a linear map,  , for computing the value vector of head k;· represents the dot product between two vectors; M is the message neural network as a mapping, M(xM) = ReLU(WM·xM + bM), and
, for computing the value vector of head k;· represents the dot product between two vectors; M is the message neural network as a mapping, M(xM) = ReLU(WM·xM + bM), and 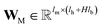 and
and  are the weights and bias of M respectively.
are the weights and bias of M respectively.
In the update step,
| hvt+1 = U(hvt‖mvt+1) | (4) |
 and
and  are the weights and bias of the update neural network U respectively.44
are the weights and bias of the update neural network U respectively.44
An overall pipeline of our model with the gated attention aggregator is shown in Fig. 2. At the beginning, input reactant pairs were fed into the DFT computation module or finetuned qmdesc model (Fqmdesc)17 to obtain atom-wise descriptors (Hirshfeld partial charge, nucleophilicity, and electrophilicity) and bond-wise descriptors (bond length). At the same time, atom and bond features of input reactant pairs were extracted using RDKit.36 Extracted atom and bond features are described in ESI Table S2.† Atom features were concatenated with atom descriptors and bond features were concatenated with bond descriptors. Together, the concatenated atom and bond features were fed into the MPNN module, with different aggregation strategies, as the input A and B, respectively, to perform representation learning for atoms. The representations of reaction center atoms were recorded at each step and these representations were max-pooled among different steps. The final atom representation was gained through a single fully-connected layer which took average-pooled representations and its corresponding atom descriptors as input. At the same time, the rxnfp48 of the interested reaction was also calculated to incorporate reaction details into our model. Unlike Guan et al.'s previous work on aromatic substitution reaction regioselectivity,17 which applies global attention between atom representation and reactant molecules to capture the possible impact of atoms beyond the immediate neighbors considered in the message passing section, we used a multi-head attention layer between atom representation and reaction rxnfp to capture the various possible relationships between the reaction center atoms and the entire reaction. The final atom representation together with the attention vector was used to compute the probability of being the main product for each candidate product. This probability was estimated as follows. We first calculated a score for each candidate product using eqn (5),
 | (5) |
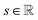 is the resulting score;
is the resulting score;  is the hidden state of atom c learned by the MPNN at time step t, c belongs to reaction center atoms, reaction center atoms are the atoms which undergo changes in their bonding pattern during the course of MCCCRs, for example, the carbon atom attached to the boronic acid or the corresponding ester group and the carbon atom attached to the reacting halogen or OTf group in a Suzuki–Miyaura reaction are the reaction center atoms;
is the hidden state of atom c learned by the MPNN at time step t, c belongs to reaction center atoms, reaction center atoms are the atoms which undergo changes in their bonding pattern during the course of MCCCRs, for example, the carbon atom attached to the boronic acid or the corresponding ester group and the carbon atom attached to the reacting halogen or OTf group in a Suzuki–Miyaura reaction are the reaction center atoms;  is the QM computed or Fqmdesc computed atom descriptors with a dimension of ld for atom c; R is a neural network as a mapping, R(xR) = WR·xR,
is the QM computed or Fqmdesc computed atom descriptors with a dimension of ld for atom c; R is a neural network as a mapping, R(xR) = WR·xR,  is the weights of the neural network; Qh is a linear map,
is the weights of the neural network; Qh is a linear map,  , for computing the query vector of head h; Kh is a linear map,
, for computing the query vector of head h; Kh is a linear map, 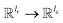 , for computing the key vector of head h; Vh is a linear map,
, for computing the key vector of head h; Vh is a linear map,  , for computing the value vector of head h; lr is the length of the reaction rxnfp; D is the number of heads in the attention mechanism; S is a neural network as a mapping, and
, for computing the value vector of head h; lr is the length of the reaction rxnfp; D is the number of heads in the attention mechanism; S is a neural network as a mapping, and  and
and 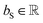 are the weights and bias of the neural network. After computing the scores for each candidate product, the probabilities of being the main product for each candidate product were calculated by feeding the concatenation of the scores through a softmax activation function.
are the weights and bias of the neural network. After computing the scores for each candidate product, the probabilities of being the main product for each candidate product were calculated by feeding the concatenation of the scores through a softmax activation function.
 | ||
| Fig. 2 Architecture of Regio-MPNN. We calculate the atom and bond descriptors using density functional theory (DFT) or a finetuned qmdesc model(Fqmdesc),17 at the same time the atom features and bond features are computed using RDKit. We combine the quantum mechanics (QM) descriptors with the features and feed the overall input into the MPNN network, which outputs a learned embedding of the reaction center atom. We then use this embedding together with the atom descriptors to predict the probabilities for candidate products. A steric hindrance checker (shown in Fig. 1c) is used after Regio-MPNN to filter out steric hindered results. | ||
2.4 Steric hindrance checker
As described in Oslob et al.,18 the steric effect has a significant impact on selectivity results in the oxidative addition step of MCCCRs. Therefore, a steric hindrance checker was attached to filter out heavily steric-hindered reactive sites in the inference stage. To compute the steric hindrance effect of the reactive sites, a conformer of the molecule was generated by the ETKDG method from RDKit.49 We located the reaction center carbon with the carbon–halogen bond or carbon–triflate bond, placed this carbon atom as the center, and considered a sphere with a radius equal to 5 Å. We defined the steric hindrance value as the occupied volume by other atoms (calculated using van der Waals radii) in the sphere divided by the total volume of the sphere. We then analyzed the steric hindrance values for all metal-catalyzed cross-coupling reaction entries in Pistachio2 and CAS Content Collection,3 chose 95% percentile of the steric hindrance values and got 0.60 as the maximum “safe” steric hindrance value. After removing carbon-halogen or carbon-triflate sites with steric hindrance values greater than the threshold, we determined the product with the highest probability in the remaining candidates as the predicted main product.2.5 Human chemists' composition and question design
A total of 6 chemists at Chemlex participated in this study. These chemists, who had educational backgrounds in organic chemistry and an average of over 10 years of bench experience in the chemical synthesis contract research organization (CRO) industry, were included. For the study, we randomly selected 100 reactions with regioselectivity risks from the stratified-split test set. The number of reactions for each reaction type was chosen to reflect the proportion of each type in the entire Pistachio + CAS Content Collection dataset, as shown in Fig. 3. Detailed numbers for each reaction type in the question set are listed in the ESI “Human chemist test and results” section.† We generated out all possible reaction outcomes based on the specific reaction type and asked the chemists to identify the main product from the generated candidate products for each reaction. The choices made by these chemists were based solely on their background knowledge and working experiences, without the use of any chemical reaction databases, such as SciFinder.50 The regioselective data are all licensed from commercial databases Scifinder and Pistachio, and are unfortunately not allowed to be published. However, we have listed out the reactants with regioselectivity issues which at least one chemist made incorrect predictions in the ESI “Human chemist test and results” section† to show the difficulty of this test. The correct results can be obtained using the web UI based on the model reported in this work.3 Results and discussion
3.1 Analysis of reaction data
We first analyze the reaction data in our cleaned commercially available dataset. Fig. 3a shows the distribution of data from each reaction type extracted from the Pistachio dataset. Suzuki coupling reactions overweight all the other seven coupling reactions in terms of volume. The phenomenon is not unexpected as the Suzuki coupling reaction has been extensively used in the synthesis of various compounds in synthetic organic chemistry.51,52 In order to improve the data balance, we supplement the data for Heck, Hiyama, Kumada, and Negishi reactions using data from the CAS Content Collection.3Fig. 3b shows the distribution of data from each reaction type in the dataset combining both Pistachio and CAS Content Collection datasets. After adding high-quality data from the CAS Content Collection, there is an increase in the data portion of Heck, Hiyama, Negishi and Kumada coupling reactions. Specifically, the portion of Heck reaction increased from 0.2% to 4.6%. Considering the various catalysts used in MCCCRs, we also analyze the data distribution of metals used in the datasets. Most reactions extracted from Pistachio use palladium-based catalysts and only Sonogashira reactions use zinc-based catalysts. In total, 11 different metals are used as catalysts in selected CAS Content Collection data. A summary of different metal elements used as catalysts in CAS Content Collection data is provided in Table S1.†To get a deeper understanding of our dataset, we plot the competing reaction sites with regioselectivity risks in the overall cross-coupling reaction dataset in Fig. 3c. The vertical axis denotes the ground-truth halogens or halogen-like groups corresponding to the major product, and the horizontal axis denotes other potential reactive sites present in the same reactant. For instance, the deepest blue section in the heatmap represents that the most commonly seen competing site pair in MCCCRs is Br vs. Cl (3599 data points), where the actual reactions occur at the bromine-substituted sites. The total number in the heatmap exceeds the total number of our datasets (9734) because there may be more than two competing sites in one molecule.
3.2 Analysis of model performance
We split the combined dataset comprising 9734 data points from Pistachio2 and CAS Content Collection3 into training/validation/test by a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. To ensure the fidelity of the estimation of our model's generalization ability, we incorporated a stratified sampling strategy.53 In other words, reactions in the test set do not contain any reactants that are seen in the training or validation sets. In addition, we made sure that each reaction type is distributed among the three sets according to their distribution in the overall dataset shown in Fig. 3b.
1. To ensure the fidelity of the estimation of our model's generalization ability, we incorporated a stratified sampling strategy.53 In other words, reactions in the test set do not contain any reactants that are seen in the training or validation sets. In addition, we made sure that each reaction type is distributed among the three sets according to their distribution in the overall dataset shown in Fig. 3b.
We implement different model architectures to predict the main product for MCCCRs with regioselectivity risks (Table 1). The random guess refers to randomly picking a product from the candidate products and treating it as the main product. Besides the aforementioned graphical representation in the MPNN framework, other frequently used representations for chemical compounds or reactions, such as Extended-Connectivity Fingerprints (ECFPs),31 Simplified Molecular Input Line Entry System (SMILES) sequence,54 and chemical descriptors, are used to do the same prediction task. Detailed implementation of each representation is illustrated in the ESI “Details for implementation of other models” section.† The robustness of each model is evaluated by a five-fold cross-validation in which the data splitting also follows the stratified sampling strategy.53 Accuracy for each model is the average accuracy of the model running on different data splits for five times and robustness for each model is the maximum deviation between the average accuracy and a one-time running accuracy. Accuracy and robustness results for different models are shown in Table 1. The overall accuracy on the test set using only MPNN is 62.33%, while the overall accuracy can increase to 95.83% when integrating Fqmdesc-calculated descriptors into the MPNN, emphasizing the necessity of introducing chemical descriptors to the model. The accurate results of the MPNN + DFT model and MPNN + Fqmdesc model indicate that the difference between using DFT- vs. Fqmdesc-calculated descriptors is negligible. Therefore, Fqmdesc can be an effective alternative to the DFT calculation for inference, reducing the total inference time by ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times. Putting this into context, calculating descriptors with DFT takes 1.5 days vs. 6 seconds with Fqmdesc for the same data in the test set. To compare the impact of aggregation functions in the message passing step, we implement the aggregation functions mentioned in Section 2.3 in our Regio-MPNN model. This comparison is made using Fqmdesc-calculated atom descriptors. The performance of each aggregation function is shown in Table 1. Among these functions, the gated attention aggregator (eqn (3)) exhibits the highest accuracy and strongest robustness. To verify the effectiveness of the Regio-MPNN model, we also conduct an experiment where the multi-head attention mechanism in the score calculation section was removed. In this variant, the final atom representation is directly concatenated with the reaction's rxnfp and fed into the fully connected layer, resulting in a model with an accuracy of 96.32 ± 0.86%. Another experiment involves changing the max-pooling of reaction center atom representations after T steps to average-pooling, resulting in a model with an accuracy of 96.33 ± 0.96%. Additionally, we implement the state-of-the-art regioselectivity determination model, ml-QM-GNN17 which is designed for substitution reactions, in the metal-catalyzed cross-coupling reactions. We find that Regio-MPNN, using the gated attention aggregator, outperforms ml-QM-GNN in this task.
000 times. Putting this into context, calculating descriptors with DFT takes 1.5 days vs. 6 seconds with Fqmdesc for the same data in the test set. To compare the impact of aggregation functions in the message passing step, we implement the aggregation functions mentioned in Section 2.3 in our Regio-MPNN model. This comparison is made using Fqmdesc-calculated atom descriptors. The performance of each aggregation function is shown in Table 1. Among these functions, the gated attention aggregator (eqn (3)) exhibits the highest accuracy and strongest robustness. To verify the effectiveness of the Regio-MPNN model, we also conduct an experiment where the multi-head attention mechanism in the score calculation section was removed. In this variant, the final atom representation is directly concatenated with the reaction's rxnfp and fed into the fully connected layer, resulting in a model with an accuracy of 96.32 ± 0.86%. Another experiment involves changing the max-pooling of reaction center atom representations after T steps to average-pooling, resulting in a model with an accuracy of 96.33 ± 0.96%. Additionally, we implement the state-of-the-art regioselectivity determination model, ml-QM-GNN17 which is designed for substitution reactions, in the metal-catalyzed cross-coupling reactions. We find that Regio-MPNN, using the gated attention aggregator, outperforms ml-QM-GNN in this task.
| Model | Structure info | Descriptors used | Aggregator in message passing steps | Accuracy% |
|---|---|---|---|---|
| Random guess | ✗ | ✗ | ✗ | 41.74 ± 4.83 |
| ECFP based MLP | ✓ | ✗ | ✗ | 46.34 ± 2.56 |
| Descriptor based MLP | ✗ | DFT | ✗ | 60.52 ± 5.98 |
| ✗ | Fqmdesc | ✗ | 61.40 ± 1.93 | |
| Sequence based model + MLP | ✗ | ✗ | ✗ | 62.53 ± 5.32 |
| ✗ | DFT | ✗ | 71.65 ± 3.05 | |
| ✗ | Fqmdesc | ✗ | 73.51 ± 2.63 | |
| Regio-MPNN | ✓ | ✗ | Pairwise sum aggregator | 62.33 ± 1.74 |
| ✓ | DFT | Pairwise sum aggregator | 95.61 ± 0.97 | |
| ✓ | Fqmdesc | Pairwise sum aggregator | 95.83 ± 0.95 | |
| Regio-MPNN | ✓ | Fqmdesc | Average pooling aggregator | 95.51 ± 0.97 |
| Regio-MPNN | ✓ | Fqmdesc | Max pooling aggregator | 94.68 ± 1.13 |
| Regio-MPNN | ✓ | Fqmdesc | Gated attention aggregator | 96.51 ± 0.87 |
| Regio-MPNN (w.o. multi-head attention) | ✓ | Fqmdesc | Gated attention aggregator | 96.32 ± 0.86 |
| Regio-MPNN (average-pooling after T steps) | ✓ | Fqmdesc | Gated attention aggregator | 96.33 ± 0.96 |
| ml-QM-GNN17 | ✓ | Fqmdesc | Pairwise sum aggregator | 96.13 ± 0.91 |
We also evaluated the accuracy of prediction among different cross-coupling reaction types in the test set. As shown in Fig. 4a, four reaction types with relatively fewer data points (as shown in Fig. 3b), Kumada, Hiyama, Negishi, and Heck, have relatively higher percentages of erroneous regioselectivity prediction. This could be rationalized by the lack of data in the data set for these reaction types (Fig. 3b). Even though we have combined all the relevant data from Pistachio and CAS Content Collection3 datasets, the extent of data imbalance is still significant. To mitigate this, data scientists typically use measures such as data augmentation,55 under-sampling,56 and weighted loss.57 However, data augmentation may not be a suitable solution for the task at hand, because regioselectivity may vary even with small structural changes, which means the generation of new data points from scratch or from existing data points for rare reaction types would not be feasible. Under-sampling the majority reaction type leads to a small training set and would significantly reduce the ability to generalize our model (detailed under-sampling experiments are shown in the ESI “Experiment on under-sampling training set” section†). Unlike classification tasks, the scaling strategy in the loss function cannot be applied to our model either. Thus, in the future, the best solution to the data imbalance is to intentionally acquire more wet lab data from high throughput experiments, as proposed by recent literature.58–60 However, this approach is out of the scope of this work.
The reaction type that challenged our prediction model the most was Kumada coupling reactions (Fig. 4a). Surprisingly, as shown in Fig. 3b, Kumada reactions are not the rarest reaction type in the dataset. In order to understand the uniqueness of Kumada reactions, we conduct a fine-grained analysis of the data distributions. We notice the obvious difference in competing site distribution between all reactions in the overall dataset and Kumada reactions as shown in Fig. 3c and d. To quantify this difference, the Kullback–Leibler (KL) divergence,61 Jensen–Shannon (JS) divergence,62 and Bhattacharyya coefficient63 are computed with eqn (6) and the difference of competing site pairs among different reaction types is shown in Table 2.
 | (6) |
| Reaction type | KL divergence | JS divergence | Bhattacharyya coefficient |
|---|---|---|---|
| Buchwald | 0.065 | 0.027 | 0.941 |
| Heck | 0.127 | 0.052 | 0.930 |
| Hiyama | 0.114 | 0.054 | 0.936 |
| Kumada | 0.219 | 0.101 | 0.876 |
| Negishi | 0.068 | 0.033 | 0.945 |
| Sonogashira | 0.164 | 0.058 | 0.909 |
| Stille | 0.142 | 0.058 | 0.919 |
| Suzuki | 0.035 | 0.011 | 0.975 |
Among the 8 reaction types, Kumada reactions exhibit the highest KL and JS divergence as well as the lowest Bhattacharyya coefficient compared to the entire dataset, which indicates that the competing site pairs in Kumada reactions are significantly different from those in the entire dataset. To better understand this difference, we calculate an approximation of the posterior probability of reaction type k given competing site pairs i, j using eqn (7), and this posterior probability for Kumada reactions is shown in Fig. 4b.
 | (7) |
An interesting fact is discovered that the competition between Br vs. OTf with Br as the preferred site is a signature of Kumada reactions. This is unexpected since the reactivity for Bromine sites and that for OTf sites in MCCCRs are normally considered as closely similar and hard to distinguish,64 which could be attributable to the relatively low accuracy for predicting regioselectivity for Kumada reactions. Moreover, among all the reaction types we are considering, the Kumada reactions require strict experimental condition control owing to the high reactivity of Grignard reagent with water or with functional groups in other reactants,65 which also makes Kumada reactions unique among MCCCRs. Figures of competing site pair distribution and approximated posterior probability for other reactions are available in ESI Fig. S4–S10.†
3.3 Steric hindrance checker case study
To examine the effectiveness of our steric hindrance checker, we conduct a case study of a couple of MCCCRs whose regioselectivity is dominantly affected by the steric hindrance. In Fig. 5, four reported Suzuki–Miyaura reactions with regioselectivity risks are shown.66 These four reactions undergo the same reaction conditions but result in different primary reacting sites. The main products for the first three reactions correspond to the reaction site at the ortho-position with respect to the X group (circled in blue), while the main product for the last reaction corresponds to the meta-chlorine. Spivey et al. attribute this difference to the steric hindrance effect.66 Based on their analysis, we extract the steric hindrance values of carbon atoms highlighted by the blue circle in Fig. 5 for these four reactions. The steric hindrance values for the first three reactions are 0.456, 0.507, 0.477, respectively, while the steric hindrance value for the last reaction is 0.603, above our steric hindrance threshold (0.6) determined by the statistics on the MCCCRs in Pistachio2 and CAS Content Collection.3 The first three reactants are “safe” in terms of steric hindrance at the ortho-chlorine, but the last reaction is under the steric hindrance “risk” at the same reaction site. Therefore, our model predicts that the main products of the first three reactants are products with R2 as the reacting site and the main product of the last reactant is product with R1 as the reacting site, which agrees with experimental results. | ||
| Fig. 5 Case study of steric impact on a series of Suzuki–Miyaura reactions. Regioselectivity may vary due to the crowded chemical environment around the reacting halogen group. Our steric hindrance checker can successfully capture this change. The yield reported here is from the literature.66 | ||
3.4 Contest between human chemists and Regio-MPNN
To compare model performance with predictions made by senior chemists, we randomly picked 100 reactions with regioselectivity risks from the test set and invited six senior chemists working at ChemLex to identify the main products for these reactions independently. The accuracy of predictions made by the chemists varies from 74% to 94%, while the accuracy of predictions made by our model is 100%, as shown in Table 3. Fig. 6 shows some examples in which at least three senior chemists have made incorrect predictions. These examples indicate that predicting regioselectivity between reaction sites substituted by the same kind of halogen atoms remains a challenge for some human chemists. In contrast, our model can successfully determine the regioselectivity for these situations. More examples related to this contest are included in ESI Fig. S11–S15.† We have developed a web tool72 empowered by Regio-MPNN to assist organic chemists when they encounter regioselectivity problems.| Test taker | Accuracy |
|---|---|
| Chemist_1 | 94% |
| Chemist_2 | 91% |
| Chemist_3 | 81% |
| Chemist_4 | 80% |
| Chemist_5 | 78% |
| Chemist_6 | 74% |
| Regio-MPNN | 100% |
 | ||
| Fig. 6 Examples of erroneous predictions made by at least half of the human chemists. The reactions are from the 100 randomly sampled reactions with regioselectivity issues from the test set. The ground-truths are shown as the product;67–71 the sites predicted by our model are marked by blue circles; the sites erroneously predicted by human chemists are marked by red circles. | ||
3.5 Model application case study
To further exemplify the practical application of our proposed model, we demonstrate two cases where Regio-MPNN can facilitate synthetic route planning for bench chemists in Fig. 7a–c. Fig. 7a–b show an example where Regio-MPNN can potentially improve the performance of existing CASP systems. Recent open-source CASP software packages, e.g. ASKCOS,5 AiZynthFinder,12 and RXN for Chemistry,7 have made a significant impact on the synthesis planning industry and have facilitated the process of organic synthesis profoundly. However, mistakes can still happen in regioselectivity prediction for AI-embedded CASP systems. For example, Fig. 7a shows an erroneously planned Buchwald–Hartwig reaction with regioselectivity issues, recommended during synthesis planning using an open source CASP software package. Integration of a regioselectivity model in such systems will be useful. This is exemplified when the correct prediction of the same Buchwald–Hartwig reaction was performed by our model as shown in Fig. 7b, demonstrating the ability of our model to mitigate the regioselectivity issue for CASP systems. The second case is shown in Fig. 7c, demonstrating that the determination of regioselectivity can be useful in industrial process development. In Fig. 7c, the original reaction from an industrial process74 involves a reactant containing different halogen groups, chlorine and iodine, with a price of $83 per g.50 Typically such hetero-substituted starting materials are expensive and short in stock. Our regioselectivity model suggests an alternative starting material substituted with two chlorine atoms. The price of the latter compound is $14 per g (ref. 50) and the yield is not significantly affected according to the literature75 as shown in the ESI “Details for the alternating reactant example” section.† Thus, our model provides a potentially more economical method to develop new process routes with more accessible starting materials by leveraging fast and accurate predictions of regioselective preferences over competing reaction sites. Based on our model, a web tool72 (Fig. 7b) has been made available to assist general bench chemists in making quick decisions about regioselectivity. | ||
| Fig. 7 Applications of the Regio-MPNN model. (a) An example of a regioselectivity mistake made by an AI-driven CASP system. This Buchwald–Hartwig reaction is used in a route designed by a CASP system with open online access. However, the ground truth73 demonstrates that the blue-circled site is more active than the mistakenly chosen red-circled one; (b) a snapshot of the prediction result from our Regio-MPNN web tool for the Buchwald–Hartwig reaction in (a), showing that our model can fix the above regioselectivity mistake; (c) an example of how regioselectivity models can potentially save material costs by replacing expensive starting materials (upper reaction scheme)74 with economical ones (lower) without significantly affecting the yield. | ||
4 Conclusions
We analyzed metal-catalyzed cross-coupling reactions with regioselectivity issues from the Pistachio and CAS Content Collection and applied MPNN together with DFT calculated descriptors or Fqmdesc computed descriptors to identify the correct main product. We also developed a statistical checker to take the steric hindrance effect into consideration. The overall accuracy on a stratified sampled test set for the plain Regio-MPNN model is 62.33% and the accuracy is significantly boosted to >96% by adding DFT or Fqmdesc calculated descriptors together with the implementation of efficient message-passing aggregator methods and reaction fingerprints. Our model outperformed other commonly used model architectures in terms of accuracy and robustness. We have also demonstrated that our steric hindrance checker is able to identify the cases where regioselectivity is solely induced by steric hindrance effects. On the basis of the superior performance of our model, we showed that intrinsic weaknesses in literature datasets, e.g. insufficient training data for rare competition pairs of reaction sites and data imbalance, are major reasons for relatively weaker predictions for certain types of reactions, proposing the potential approaches to collect experimental data in order to further advance the current method. In addition, we conducted a fine-grained analysis of the data distributions and demonstrated that Kumada reactions might pose unique challenges to regioselectivity prediction tasks compared to other types of metal-catalyzed cross-coupling reactions. We also collected the results of a set of regioselectivity challenges from 6 senior level organic chemists, and found that our model outperformed the human chemists in this test. Based on the high accuracy of our model and the results of the competition with human chemists, we demonstrate that our model can help senior chemists determine the regioselectivity in metal-catalyzed cross-coupling reactions in synthesis planning efficiently and accurately. We have also made a web based regioselectivity prediction tool for general chemists to use.Data availability
The source code is available at https://github.com/Chemlex-AI/regioselectivity upon request. A Regio-MPNN based wet tool is also available at https://ai.tools.chemlex.com/region-choose. All reaction data used in the paper are available from commercial databases Pistachio2 and CAS Content Collection.3Author contributions
B. L. and X. W. conceived the project. B. L. and H. S. carried out the experiments. Y. L. processed the data and performed the DFT calculations. R. T. Z. and Y. X. organized the human chemist test under the supervision of P. W. and S. L. K. F. and F. M. proposed the model application and reviewed the medicinal chemistry part. R. M. Z. and T. Y. discussed and guided the machine learning studies with B. L. and X. W. X. W. supervised the project. B. L., Y. L. and X. W. prepared the manuscript. All authors discussed the results and contributed to the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank members of the organic chemistry team at ChemLex for their insights on regioselectivity issues in metal-catalyzed cross-coupling reactions and feedback on the 100-example test. We acknowledge the software development team at Chemlex for making our model available on the website. The authors would like to acknowledge that the data from the CAS Content Collection were provided under license for this study by CAS. CAS is a division of the American Chemical Society and provider of SciFinder®, STN®, and CAS Custom Services. https://www.cas.org/.Notes and references
- G. Saxty, C. W. Murray, V. Berdini, G. E. Besong, C. C. F. Hamlett, S. J. Woodhead, Y. A. E. Ligny and P. R. Angibaud, Substituted quinoxalines as FGFR kinase inhibitors, US Pat., US9290478B2, 2016 Search PubMed.
- R. A. Sayle, J. W. Mayfield, I. Lagerstedt and R. Pirie, Nextmove Software Pistachio, 2022, http://www.nextmovesoftware.com/pistachio.html Search PubMed.
- CAS Content Collection, CAS Content Collection through CAS Custom Services, https://www.cas.org/cas-data.
- J. Li and M. D. Eastgate, React. Chem. Eng., 2019, 4, 1595–1607 RSC.
- C. Coley, connorcoley/ASKCOS: First public release of ASKCOS, 2019, https://zenodo.org/record/3261361 Search PubMed.
- C. W. Coley, W. H. Green and K. F. Jensen, Acc. Chem. Res., 2018, 51, 1281–1289 CrossRef PubMed.
- P. Schwaller, R. Petraglia, V. Zullo, V. H. Nair, R. A. Haeuselmann, R. Pisoni, C. Bekas, A. Iuliano and T. Laino, Chem. Sci., 2020, 11, 3316–3325 RSC.
- R. Irwin, S. Dimitriadis, J. He and E. J. Bjerrum, Mach. Learn.: Sci. Technol., 2022, 3, 015022 Search PubMed.
- K. Lin, Y. Xu, J. Pei and L. Lai, Chem. Sci., 2020, 11, 3355–3364 RSC.
- C. Shi, M. Xu, H. Guo, M. Zhang, J. Tang, A Graph to Graphs Framework for Retrosynthesis Prediction, arXiv, 2020, preprint, arxiv:2003.12725, DOI:10.48550/arXiv.2003.12725.
- M. H. S. Segler, M. Preuss and M. P. Waller, Nature, 2018, 555, 604–610 CrossRef.
- S. Genheden, A. Thakkar, V. Chadimová, J.-L. Reymond, O. Engkvist and E. Bjerrum, J. Cheminf., 2020, 12, 70 Search PubMed.
- T. Klucznik, B. Mikulak-Klucznik, M. P. McCormack, H. Lima, S. Szymkuć, M. Bhowmick, K. Molga, Y. Zhou, L. Rickershauser, E. P. Gajewska, A. Toutchkine, P. Dittwald, M. P. Startek, G. J. Kirkovits, R. Roszak, A. Adamski, B. Sieredzińska, M. Mrksich, S. L. Trice and B. A. Grzybowski, Chem, 2018, 4, 522–532 Search PubMed.
- X. Wang, Y. Qian, H. Gao, C. W. Coley, Y. Mo, R. Barzilay and K. F. Jensen, Chem. Sci., 2020, 11, 10959–10972 RSC.
- P.-S. Wang and L.-Z. Gong, Acc. Chem. Res., 2020, 53, 2841–2854 CrossRef CAS PubMed.
- P. Beak, A. Basu, D. J. Gallagher, Y. S. Park and S. Thayumanavan, Acc. Chem. Res., 1996, 29, 552–560 CrossRef CAS.
- Y. Guan, C. W. Coley, H. Wu, D. Ranasinghe, E. Heid, T. J. Struble, L. Pattanaik, W. H. Green and K. F. Jensen, Chem. Sci., 2021, 12, 2198–2208 RSC.
- J. D. Oslob, B. Åkermark, P. Helquist and P.-O. Norrby, Organometallics, 1997, 16, 3015–3021 CrossRef.
- S. Banerjee, A. Sreenithya and R. B. Sunoj, Phys. Chem. Chem. Phys., 2018, 20, 18311–18318 RSC.
- X. Li, S.-Q. Zhang, L.-C. Xu and X. Hong, Angew. Chem., Int. Ed., 2020, 59, 13253–13259 CrossRef PubMed.
- N. Ree, A. H. Göller and J. H. Jensen, Digital Discovery, 2022, 1, 108–114 RSC.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS.
- A. Tomberg, M. J. Johansson and P.-O. Norrby, J. Org. Chem., 2018, 84, 4695–4703 CrossRef.
- Y. Guan, T. Lee, K. Wang, S. Yu and J. C. McWilliams, J. Chem. Inf. Model., 2023, 63, 3751–3760 CrossRef CAS PubMed.
- M. J. Buskes and M.-J. Blanco, Molecules, 2020, 25, 3493 CrossRef CAS.
- M. Busch, M. D. Wodrich and C. Corminboeuf, ACS Catal., 2017, 7, 5643–5653 CrossRef CAS.
- L. Kurti and B. Czako, Strategic Applications of Named Reactions in Organic Synthesis, Elsevier Academic Press, 2005 Search PubMed.
- I. N. Houpis, R. Liu, Y. Wu, Y. Yuan, Y. Wang and U. Nettekoven, J. Org. Chem., 2010, 75, 6965–6968 CrossRef CAS PubMed.
- J. P. Norman, N. G. Larson, E. D. Entz and S. R. Neufeldt, J. Org. Chem., 2022, 87, 7414–7421 CrossRef CAS PubMed.
- C. Cai, J. Y. L. Chung, J. C. McWilliams, Y. Sun, C. S. Shultz and M. Palucki, Org. Process Res. Dev., 2007, 11, 328–335 CrossRef CAS.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS.
- D. Probst, P. Schwaller and J.-L. Reymond, Digital Discovery, 2022, 1, 91–97 RSC.
- V. Voinarovska, M. Kabeshov, D. Dudenko, S. Genheden and I. Tetko, J. Chem. Inf. Model., 2024, 64, 42–56 CrossRef CAS.
- J. Schleinitz, M. Langevin, Y. Smail, B. Wehnert, L. Grimaud and R. Vuilleumier, J. Am. Chem. Soc., 2022, 144, 14722–14730 CrossRef CAS.
- Daylight Theory Manual, Chapter 4: SMARTS – A Language for Describing Molecular Patterns, https://daylight.com/dayhtml/doc/theory/theory.smarts.html, accssed: 2023-10-01.
- G. Landrum, P. Tosco, B. Kelley, Ric, Sriniker, Gedeck, R. Vianello, N. Schneider, E. Kawashima, A. Dalke, N. Dan, D. Cosgrove, B. Cole, M. Swain, S. Turk, A. Savelyev, G. Jones, A. Vaucher, M. Wójcikowski, I. Take, D. Probst, K. Ujihara, V. F. Scalfani, G. Godin, A. Pahl, F. Berenger, JLVarjo, strets123, JP and DoliathGavid, rdkit/rdkit: 2022_03_1 (Q1 2022) Release, 2022, DOI:10.5281/zenodo.6388425.
- Regioselectivity code on Github, https://github.com/Chemlex-AI/regioselectivity.
- O. W. Yanfei Guan and D. Ranasinghe, QM descriptors calculation, 2020, https://github.com/yanfeiguan/QM_descriptors_calculation.
- P. Tosco, N. Stiefl and G. Landrum, J. Cheminf., 2014, 6, year Search PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef.
- P. Pracht, E. Caldeweyher, S. Ehlert and S. Grimme, A Robust Non-Self-Consistent Tight-Binding Quantum Chemistry Method for large Molecules, ChemRxiv, 2019 DOI:10.26434/chemrxiv.8326202.v1.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian ∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, G. E. Dahl, Neural Message Passing for Quantum Chemistry, arXiv, arXiv, 2017, preprint, arXiv:1704.01212 DOI:10.48550/arXiv.1704.01212.
- M. Withnall, E. Lindelöf, O. Engkvist and H. Chen, J. Cheminf., 2020, 12, 1 Search PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef PubMed.
- J. Zhang, X. Shi, J. Xie, H. Ma, I. King and D. Yeung, Proceedings of the Thirty-Fourth Conference on Uncertainty in Artificial Intelligence, 2018, pp. 339–349 Search PubMed.
- P. Schwaller, D. Probst, A. C. Vaucher, V. H. Nair, D. Kreutter, T. Laino and J.-L. Reymond, Nat. Mach. Intell., 2021, 3, 144–152 CrossRef.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef PubMed.
- SciFinder, https://scifinder-n.cas.org/?referrer=scifinder.cas.org.
- I. P. Beletskaya, F. Alonso and V. Tyurin, Coord. Chem. Rev., 2019, 385, 137–173 CrossRef.
- M. Farhang, A. R. Akbarzadeh, M. Rabbani and A. M. Ghadiri, Polyhedron, 2022, 227, 116124 CrossRef.
- J. Xu, D. Kalyani, T. Struble, S. Dreher, S. Krska, S. L. Buchwald, K. F. Jensen, Roadmap to Pharmaceutically Relevant Reactivity Models Leveraging High-Throughput Experimentation, ChemRxiv, 2022, DOI:10.26434/chemrxiv-2022-x694w.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef.
- X. Xu, W. Chen and Y. Sun, JSEE, 2019, 30, 1182–1191 Search PubMed.
- C. Seiffert, T. M. Khoshgoftaar, J. V. Hulse and A. Napolitano, IEEE Trans. Syst. Man Cybern. A:Syst. Hum., 2010, 40, 185–197 Search PubMed.
- S. H. Khan, M. Hayat, M. Bennamoun, F. A. Sohel and R. Togneri, IEEE Transact. Neural Networks Learn. Syst., 2018, 29, 3573–3587 Search PubMed.
- N. S. Eyke, B. A. Koscher and K. F. Jensen, Trends Chem., 2021, 3, 120–132 CrossRef.
- D. F. Nippa, K. Atz, R. Hohler, A. T. Müller, A. Marx, C. Bartelmus, G. Wuitschik, I. Marzuoli, V. Jost, J. Wolfard, M. Binder, A. F. Stepan, D. B. Konrad, U. Grether, R. E. Martin and G. Schneider, Nat. Chem., 2023, 239–248 Search PubMed.
- S. A. Biyani, Y. W. Moriuchi and D. H. Thompson, Chem.: Methods, 2021, 1, 323–339 Search PubMed.
- S. Kullback and R. A. Leibler, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- J. Lin, IEEE Trans. Inf. Theory, 1991, 37, 145–151 CrossRef.
- A. Bhattacharyya, Sankhya, 1946, 7, 401–406 Search PubMed.
- Z. Chen, C. Gu, O. Y. Yuen and C. M. So, Chem. Sci., 2022, 13, 4762–4769 RSC.
- S. E. Denmark, Organic Reactions, Wiley, 2019 Search PubMed.
- J. Almond-Thynne, D. C. Blakemore, D. C. Pryde and A. C. Spivey, Chem. Sci., 2017, 8, 40–62 RSC.
- S. Schann, S. Mayer and B. Manteau, Substituted tricyclic 1,4-benzodiazepinone derivatives as allosteric modulators of group ii metabotropic glutamate receptors, US Pat., US20180346468A1, 2021 Search PubMed.
- H. Loozen, H. Stock and C. Timmers, Ring-annulated dihydropyrrolo[2,l-a isoquinolines, EP2459560B1, 2015.
- B. Seshadri, C. Darne, H. Rahaman, J. Warrier, M. Kamble, P. Liu, R. Mannoori, R. Borzilleri and U. Velaparthi, Tgf beta receptor antagonists, US Pat., US20190337942A1, 2019 Search PubMed.
- C. Tang, J. Yin, K. Yi, Q. Ren, X. Lin and Y. Zhang, Inhibitors of influenza virus replication, application methods and uses thereof, US Pat., US20180346463A1, 2018 Search PubMed.
- B. Wei, D. Ortwine, J. Crawford and W. Young, Heteroaryl pyridone and aza-pyrodine compounds, US Pat., US20190194203A1, 2019 Search PubMed.
- Regioselectivity Analyzer web tool, https://ai.tools.chemlex.com/region-choose.
- D. S. Choi and Y. H. Cho, Preparation of aromatic amine compounds for organic light emitting device comprising organic solar cell, electronic paper, an organic photoconductor or an organic transistor, 2015, https://scifinder-n.cas.org/patent-viewer?docuri=gWep6ap-cBSz8swSpe1GUAII8baFQvVxG5F0ETKig5I%26markedFullTextKey=Ea8sHV9JXE8n-plFFGaRhEr9f2lHT06emPlpj8oMv7A.pdf%26fullTextKey=OkeY4Y8TltkYQTyRmPQqbAOTxGN1_Co3lXnr6ndqwtQ.pdf.
- S. Karlsson, H. Benson, C. Cook, G. Currie, J. Dubiez, H. Emtenäs, J. Hawkins, R. Meadows, P. D. Smith and J. Varnes, Org. Process Res. Dev., 2021, 26, 601–615 CrossRef.
- G. Beaton, S. B. Ravula, F. Tucci, S. J. Lee and C. R. Shah, Pyrimidine and pyridine amine compounds and usage thereof in disease treatment, 2022, https://worldwide.espacenet.com/patent/search/family/084323512/publication/WO2022256075A1?q=WO2022256075A1.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00244j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |


