Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
MolBar: a molecular identifier for inorganic and organic molecules with full support of stereoisomerism†
Nils
van Staalduinen
 and
Christoph
Bannwarth
and
Christoph
Bannwarth
 *
*
Institute of Physical Chemistry, RWTH Aachen University, Melatener Str. 20, 52074 Aachen, Germany. E-mail: bannwarth@pc.rwth-aachen.de
First published on 10th October 2024
Abstract
Before a new molecular structure is registered to a chemical structure database, a duplicate check is essential to ensure the integrity of the database. The Simplified Molecular Input Line Entry Specification (SMILES) and the IUPAC International Chemical Identifier (InChI) stand out as widely used molecular identifiers for these checks. Notable limitations arise when dealing with molecules from inorganic chemistry or structures characterized by non-central stereochemistry. When the stereoinformation needs to be assigned to a group of atoms, widely used identifiers cannot describe axial and planar chirality due to the atom-centered description of a molecule. To address this limitation, we introduce a novel chemical identifier called the Molecular Barcode (MolBar). Motivated by the field of theoretical chemistry, a fragment-based approach is used in addition to the conventional atomistic description. In this approach, the 3D structure of fragments is normalized using a specialized force field and characterized by physically inspired matrices derived solely from atomic positions. The resulting permutation-invariant representation is constructed from the eigenvalue spectra, providing comprehensive information on both bonding and stereochemistry. The robustness of MolBar is demonstrated through duplication and permutation invariance tests on the Molecule3D dataset of 3.9 million molecules. A Python implementation is available as open source and can be installed via pip install molbar.
1 Introduction
When enrolling a compound in a chemical database system or registry, it is customary to initially verify the novelty of its structure. Checking for duplicates, the molecular structure of the compound to be registered is compared with the structures already present in the database. To represent the molecular structure, connection table (CT) formats, which have been used since the early days of cheminformatics, are the most widely used in computer systems.1–3 The molecular structure is represented as an undirected graph, with the atoms serving as nodes and the bonds as edges.4 This approach goes back to the pioneering work of August Kekulé5 and Gilbert N. Lewis,6 who introduced the structural formula as a mathematical graph for chemical structures. The graphical representation of molecules has the advantage that duplicate identification is equivalent to determining whether the two graph representations are identical, a concept known as isomorphism in graph theory. Since most applications of chemoinformatics relate to organic molecules with well-defined covalent bonds, graph representation is a practical choice.4 Classical cheminformatics representations rely on alphanumeric string line notations, such as SMILES7 and InChI,8 to only name two representations, which are derived from the CT representation. Line notations are widely used in cheminformatics and are supported by most chemical database systems. Several chemical line notation systems were proposed in the 1950s and 1960s, but the Wiswesser Line-formula Notation (WLN), introduced in 1949, became the most widely used.9–11 The WLN remained popular until the early 1980s, when more flexible systems such as SMILES began to replace it. The WLN used simple digits 1–9 to represent unbranched alkyl chains and capital letters to denote individual atoms or common substructures, making it a compact and efficient system. However, the WLN eventually fell out of favor due to its inability to represent complex features such as stereochemistry and its reliance on rigid, complicated rules.12 The Simplified Molecular Input Line Entry System (SMILES) was created by David Weininger in 1986 and is based on a few basic rules.7 Molecules are depicted by a chain of connected atoms. The atoms themselves are denoted by their atomic symbols. Hydrogen atoms are omitted, since free valences are assumed to be saturated with hydrogen atoms. Only double and triple bonds are portrayed by their symbols and
and  . Atoms in aromatic substructures are expressed by lowercase atom symbols. Branches are illustrated by brackets around the branch, and digits are used to denote ring closures. In addition, stereochemistry is represented by the symbols
. Atoms in aromatic substructures are expressed by lowercase atom symbols. Branches are illustrated by brackets around the branch, and digits are used to denote ring closures. In addition, stereochemistry is represented by the symbols  and
and  for tetrahedral chiral centers and
for tetrahedral chiral centers and  and
and  for double bonds. SYBYL Line Notation (SLN), originally inspired by SMILES, has since diverged significantly from it.13,14 A key difference lies in the treatment of valence and aromaticity. SMILES allows implicit valences as part of the language structure, while SLN makes no assumptions about the valence of an atom. In addition, aromaticity is treated differently: SMILES treats aromaticity as an atomic property, while SLN explicitly assigns aromaticity to bonds. Another notation system, the Representation Of Structure Diagram Arranged Linearly (ROSDAL), was developed facilitating searches in the Beilstein database.15 The IUPAC International Chemical Identifier (InChI) is a non-proprietary identifier for chemical substances, developed since 2000 and nowadays used in many chemical database systems.8 The InChI is generated based on a workflow that includes normalization, followed by a canonicalization and finally a serialization of the structure. Normalization intends to unify different input representations of single compounds, such as different tautomeric or mesomeric structures by applying a consistent chemical model. Canonicalization ensures a unique numbering of the atoms to be independent of the order of the input atoms. Finally, the canonicalized structure is serialized to a string, which is the InChI. Serialization refers to the process of converting the labeled atoms to a string line notation. The InChI is a hierarchical identifier, which consists of several layers, each of which is separated by a forward slash delimiter. The main layer consists of the chemical formula of the compound, the connection layer /c and the hydrogen layer /h. Further layers include the charge layer (charge sublayer /q and proton sublayer /p), the stereochemical layer representing double bond stereoconfiguration (/b) and tetrahedral stereochemistry (/t). Non-standard InChI can be used to distinguish between tautomers by the fixed-H layer (/f), for example.
for double bonds. SYBYL Line Notation (SLN), originally inspired by SMILES, has since diverged significantly from it.13,14 A key difference lies in the treatment of valence and aromaticity. SMILES allows implicit valences as part of the language structure, while SLN makes no assumptions about the valence of an atom. In addition, aromaticity is treated differently: SMILES treats aromaticity as an atomic property, while SLN explicitly assigns aromaticity to bonds. Another notation system, the Representation Of Structure Diagram Arranged Linearly (ROSDAL), was developed facilitating searches in the Beilstein database.15 The IUPAC International Chemical Identifier (InChI) is a non-proprietary identifier for chemical substances, developed since 2000 and nowadays used in many chemical database systems.8 The InChI is generated based on a workflow that includes normalization, followed by a canonicalization and finally a serialization of the structure. Normalization intends to unify different input representations of single compounds, such as different tautomeric or mesomeric structures by applying a consistent chemical model. Canonicalization ensures a unique numbering of the atoms to be independent of the order of the input atoms. Finally, the canonicalized structure is serialized to a string, which is the InChI. Serialization refers to the process of converting the labeled atoms to a string line notation. The InChI is a hierarchical identifier, which consists of several layers, each of which is separated by a forward slash delimiter. The main layer consists of the chemical formula of the compound, the connection layer /c and the hydrogen layer /h. Further layers include the charge layer (charge sublayer /q and proton sublayer /p), the stereochemical layer representing double bond stereoconfiguration (/b) and tetrahedral stereochemistry (/t). Non-standard InChI can be used to distinguish between tautomers by the fixed-H layer (/f), for example.
While connection tables like Molfiles or SDFiles are extensively employed in cheminformatics, their utilization is not as prevalent in the realm of quantum chemistry.16 In quantum chemistry, the molecular structure is typically conveyed through a list of atoms along with their Cartesian coordinates without any explicit information about the connectivity of the atoms. Recent algorithmic advances have facilitated the automatic generation of molecular structures from quantum chemical calculations such as ab initio reaction and molecule discovery workflows,17–19 conformer ensemble sampling tools20 or ab initio electron ionization mass spectra,21,22 pinpointing novel structures as local minima on the potential energy surface represented by their Cartesian coordinates. However, registering these structures in a quantum chemical database system would then require relying on additional pre-processing software to assess the connectivity of the atoms before generating an identifier. More critically, these black-box tools can generate structures that are drastically different from the input. These cases are not always related to changing stereoinformation, as the resulting structures may have chemically unreasonable geometries. In other cases, the VSEPR geometry of metal centers may change from square-planar to tetrahedral due to an insufficient level of theory to describe the underlying electronic structure. Automated information about molecular shape changes is crucial for evaluating the correctness of the vast number of generated structures. Furthermore, existing approaches reach their limits when it comes to supporting all possible inorganic stereochemistries and accounting for non-central chirality in (in)organic molecules. While SMILES supports an incomplete set of inorganic stereochemistry,23 InChI separates all bonds to metals, resulting in a complete loss of such information.8 Both SMILES and InChI take an atom-centric Lewis picture, making them unable to effectively represent non-central chirality, such as axial or planar chirality, where the stereochemistry information may relate to a group of atoms rather than a single atom.24
2 Design goals of the molecular barcode
This motivates the introduction of a new concept for a molecular identifier, inspired by the principles of electronic structure theory and optimized for quantum chemical structure databases and chemical space exploration with electronic structure theory methods. To fulfill the criteria for use in computational chemistry, the identifier must effectively differentiate between structures that are separated by a reasonably high potential energy surface barrier. Consequently, the identifier must not only distinguish between constitutional isomers and stereoisomers, but by default also between (prototropic) tautomers, explicitly considering hydrogen atoms. The identifier must retain information about the molecular shape, e.g., including VSEPR geometries, but at the same time, different conformations should be mapped to a single identifier. To achieve this, the identifier should integrate an evaluation of molecular topology using a black-box approach. This ensures clarity and prevents divergent interpretations of atomic connectivity. This level of distinction is crucial for the individual registration of these structures in quantum chemical database systems. Such precision facilitates computational studies, as each minimum on the potential energy surface possesses unique and distinguishable properties from electronic structure theory. However, the identifier should follow a hierarchical approach with different levels to categorize the relationship between different stored structures, e.g. tautomerism, which is crucial for the evaluation of the correctness of the generated structures. For comprehensive utility in organic and inorganic molecular computational studies, the identifier must describe all forms of stereochemistry, including tetrahedral/center, axial, and planar chirality. In addition to an atom-centric approach, the identifier should adopt a fragment-centric perspective capable of characterizing the stereochemistry of a group of atoms.3 Theory of the molecular barcode
3.1 Topology: describing atomic connectivity
The description of molecular topology is a crucial first step in the creation of a molecular identifier. The covalent bonds determine how atoms are connected to each other and how they share their electrons, and form the basis of a molecule's identity.The specification of bonds already allows to differentiate between constitutional isomers, since their differences are based on different connectivity of atoms (Fig. 1). As discussed before, simple structure diagrams of molecules can be interpreted mathematically as graphs. A set of vertices vi ∈ Vatoms and a set of edges eij ∈ Eatoms is called a graph Gatoms = (Vatoms, Eatoms). The adjacency matrix A ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) natoms×natoms is a mathematical representation of a graph G, which describes, in analogy to the Hückel matrix, if two atoms are adjacent. If both atoms vi and vj are connected by a bond eij, the matrix element aij is one (eqn (1)).
natoms×natoms is a mathematical representation of a graph G, which describes, in analogy to the Hückel matrix, if two atoms are adjacent. If both atoms vi and vj are connected by a bond eij, the matrix element aij is one (eqn (1)).
 | (1) |
 | ||
| Fig. 1 Example of two constitutional isomers of a silver complex. Both structures differ by different connected atoms while sharing the same molecular formula. | ||
The disadvantage of the matrix graph representation is that its size grows quadratically with the system size and the matrix itself is not permutation invariant with respect to the atomic order. Interchanging atoms is equivalent to interchanging rows and columns in the adjacency matrix, resulting in a different matrix representation. However, coming back to the analogy of the Hückel matrix, the sorted eigenvalue spectrum of such a matrix is independent of the atomic order. By calculating the spectrum of an adjacency matrix in general, the molecular topology can be represented in an a priori permutation invariant vector.25,26 Furthermore, this representation does not grow quadratically with system size and corresponds to a desired line notation. Yet, a simple adjacency matrix contains no information about the nature of the involved atoms. If one element were replaced by another, the adjacency matrix would remain the same and so would the spectrum. Therefore, a modified adjacency matrix must include atomic information. For a topology representation, we introduce a modified extended adjacency matrix that is inspired by the Hückel matrix. In analogy, the diagonal elements of the modified extended adjacency matrix thus contain atomic information in form of the atomic number and the coordination number of the atom to represent its local environment. The coordination number CNi is the number of bonds in which atom vi is involved. If two atoms are bonded, the respective off-diagonal element is the arithmetic mean of the respective diagonal elements. The matrix elements of the topology matrix Htopology are given by:
 | (2) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) natoms leads to a representation of the molecular topology that is invariant to the atomic order.25,26 To obtain a spectrum composed only of integers, we multiply the eigenvalues by a factor of ten and round them to the nearest integer values.
natoms leads to a representation of the molecular topology that is invariant to the atomic order.25,26 To obtain a spectrum composed only of integers, we multiply the eigenvalues by a factor of ten and round them to the nearest integer values.
3.2 Topography: describing spatial atomic arrangement
While the topology is sufficient for the distinction of constitutional isomers, stereoisomers require additional criteria, since they do not differ in their atomic connectivity. For this purpose, the atoms' spatial arrangement has to be taken into account. The adjacency matrix does not contain any information about the 3D position of atoms in space. Two molecules with the same topology that differ in their relative configurations, such as in Fig. 2, cannot be distinguished as their topological spectra are the same. In the field of molecular machine learning, 3D representations have been used to describe the shape of the molecule and correlate them with various molecular properties.29–31 3D representations are derived from the molecular structure as an object in Cartesian space and include information about the relative positions of the atoms to each other. Those representations can be divided into local (nearer atomic vicinity) and global (considering the whole molecule) types of representations.32 For a molecular identifier, in general, global representations are of interest as they capture the shape of molecules as a whole as they describe the long-range interactions. | ||
| Fig. 2 Configurational isomers of two platinum complexes. Both complexes have the same atomic connectivity as indicated by the same eigenvalue spectrum σ(Htopology) of eqn (2), but differ generally in the relative position of the nitrogen atoms (blue-colored atoms). The eigenvalue spectrum was rounded to integer values for clarity reasons. | ||
A global 3D descriptor was introduced in the work of Rupp et al. in the context of machine learning for molecular atomization energies. The Coulomb matrix (CM) representation is defined by:27
 | (3) |
The diagonal elements describe a polynomial fit of atomic energies to the nuclear charge Zi. The off-diagonal elements of the matrix contain the Coulomb repulsion operator with the inverse of the Cartesian distance Rij between pairs of atoms, allowing the characterization of the molecular shape. Since the relative positions, e.g., of the nitrogen atoms differ for the complexes in Fig. 2, resulting in different interatomic distances and molecular shape, such a representation is able to distinguish between the two. In literature, it has been proven to be effective in describing constitutional isomers and diastereomers with the spectrum of the matrix as a permutation-invariant descriptor for the molecular shape.33 However, it is important to note that this matrix is not invariant in conformational space and thus impractical to be used as molecular identifier on its own. To yield a conformer-independent representation, modifications to eqn (3) are required. Overall, conformers exhibit variations primarily due to rotations around single bonds, resulting in different Coulomb spectra with evolving off-diagonal matrix elements within eqn (3) as the interatomic distance changes. This is illustrated by the highlighted off-diagonal matrix elements in Fig. 3 for two conformers of 1,2-difluoroethane.
 | ||
| Fig. 3 Conformational dependence of the Coulomb matrix in eqn (3) (ref. 27) for two conformers of 1,2-difluoroethane optimized at the GFN2-xTB level of theory.28 Rotation around the C–C single bond changes the distance between the two fluorine atoms, leading to different off-diagonal matrix elements (highlighted in darker blue). | ||
Nevertheless, the particular spatial orientation of these fluorine atoms with respect to each other has no significance for the identification of the molecule as 1,2-difluoroethane. This is because the transition between conformers is rapid and primarily reflects conformational changes rather than changes in the fundamental identity of the molecule. A simple strategy to achieve conformational independence is to allow interatomic interactions in the CM matrix only if the relative distances between the atoms remain unchanged under rotations around the respective single bonds. Therefore, we introduce a matrix similar to the eqn (2) by including the inverse atomic distances (eqn (4)). However, this CM matrix contains only off-diagonal nonzero elements between atoms that form rigid substructures within the molecule and will be denoted by the indicator function I(vi, vj) in the following. If two atoms belong to the same rigid fragment, the indicator function yields I(vi, vj) = 1. Conversely, if the spatial distance between two atoms in the conformational space changes, the indicator function is I(vi, vj) = 0. These rigid fragments are thus defined as substructures within the molecule if the relative positions of the atoms can be consistently unified into identical relative three-dimensional positions regardless of the current conformation of the whole molecule. The expression for the indicator function and the structure unification workflow will be discussed in Section 4. The matrix elements of Btopography are given by the following expression
 | (4) |
![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) natoms×natoms to obtain its spectrum σ(Btopography) ∈
natoms×natoms to obtain its spectrum σ(Btopography) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) natoms, which leads to a vector representation of the molecular topography that is invariant to the atomic order and invariant to rotation and translation in Cartesian space.26,27,33
natoms, which leads to a vector representation of the molecular topography that is invariant to the atomic order and invariant to rotation and translation in Cartesian space.26,27,33
3.3 Chirality: describing absolute configuration
Chirality is of extraordinary importance in various fields of chemistry and biochemistry, as it strongly influences molecular properties.34 Enantiomers possess the ability to have different pharmacological activities, variations in chemical reactivity, and exhibit different circular dichroism spectra.34 Chirality occurs in a variety of forms, with chiral carbon atoms being the most common (c.f.Fig. 4a), although the center of chirality does not to be located on a single atom, as illustrated by the example of tetrasubstituted adamantane (c.f.Fig. 4b).34In addition, chirality can originate either from an axis, where atoms arrange sequentially clockwise or counterclockwise around an axis (c.f.Fig. 4c) or from a plane with atoms located on one side or the other with respect to a chiral plane (c.f.Fig. 4d).34 Chiral molecules exhibit rigidity within the specific molecular segment that defines the chirality – whether it is a chiral center, axis, or plane. This property can be exploited by the introduced concept of rigid fragments in eqn (4), which only allows interactions between atoms that are within the boundaries of the same rigid fragment. To characterize the absolute configuration for the whole molecule, the inherent rigidity of these fragments can be effectively utilized by solely characterizing the absolute configuration of these fragments. In general, two enantiomers have the same topology and topography (after structure unification), but cannot be superimposed. As a result, the spectra of the topology matrix of eqn (2) (blue spectrum in Fig. 5) and of the topography matrix in eqn (4) (red spectrum in Fig. 5) are identical.
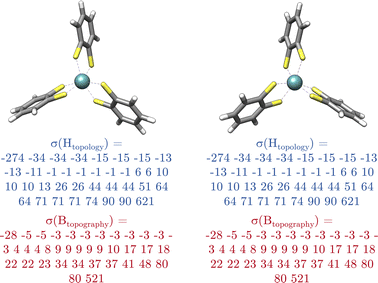 | ||
| Fig. 5 Two enantiomers of a technetium complex exhibiting axial chirality. Both complexes have identical topology and topography, so they cannot be distinguished based on the spectra of the matrices of the eqn (2) (blue spectrum) and (4) (red spectrum). The eigenvalue spectra were rounded to integer values for clarity reasons. | ||
Therefore, an additional matrix is needed to fully describe chirality. To design an identifier that also covers axial and planar chirality, a matrix of size natoms × natoms describing only atomic properties is not sufficient, since in these cases the chiral properties cannot be assigned to individual atoms. Therefore, an alternative to the atomic matrix based on rigid fragments is obligatory. This matrix has the dimensions of nfragments × nfragments, where nfragments indicates the number of rigid fragments in the molecule.
In this matrix, the diagonal elements describe the absolute configuration of the individual fragments, while the off-diagonal elements represent the relationships between the (a)chiral fragments. In this context, the variable Ga ∈ {–1, 0, 1} serves as a chirality index and determines whether fragment a is achiral (0) or one of its enantiomers (−1 or 1). An expression for Ga is discussed in Section 4. The parameter pa denotes the priority of the fragment a, analogous to the Cahn–Ingold–Prelog rules but extended to the entire fragment in the molecule. This parameter characterizes each unique fragment in the molecule. More details on the concept behind the fragment priority can be found in Section 4. Since the relative arrangements of rigid fragments can change due to conformational changes, dab denotes the graph distance between two fragments, which is the number of edges along the shortest path between them.
Diagonalizing Gchirality, we obtain the spectrum σ(Gchirality) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) nfragments, which decomposes the absolute configuration of the molecule into contributions of different fragments and is not restricted to describing a chiral center located on an atom. Following the eqn (4), we hereby introduce the absolute configuration matrix tailored to these fragments, denoted Gchirality, where gaa and gbb are the diagonal matrix elements.
nfragments, which decomposes the absolute configuration of the molecule into contributions of different fragments and is not restricted to describing a chiral center located on an atom. Following the eqn (4), we hereby introduce the absolute configuration matrix tailored to these fragments, denoted Gchirality, where gaa and gbb are the diagonal matrix elements.
 | (5) |
4 Implementation of the molecular barcode
In a nutshell, MolBar uses a set of matrices, more precisely their rounded eigenvalue spectra, to represent the topology, topography of the molecule as well as the absolute configuration of fragments. The latter two matrices rely on a partitioning procedure that decomposes the molecule into rigid substructures. This facilitates the representation of the molecule as a 3D object consistent within the conformational space. In the following sections, the comprehensive MolBar workflow (Fig. 6) and the algorithms used to obtain the 3D molecular information required for matrix construction are discussed in more detail. The molbar implementation is provided via an open-source Python module that is partially written in Fortran to handle resource-intensive tasks. The program package and its documentation are available at https://git.rwth-aachen.de/bannwarthlab/molbar. The molbar package is installable via the Python package index (PyPI) using the command pip install molbar. The package takes 3D coordinates of the molecule with explicit hydrogen atoms as input, supporting various file formats as defined in the documentation.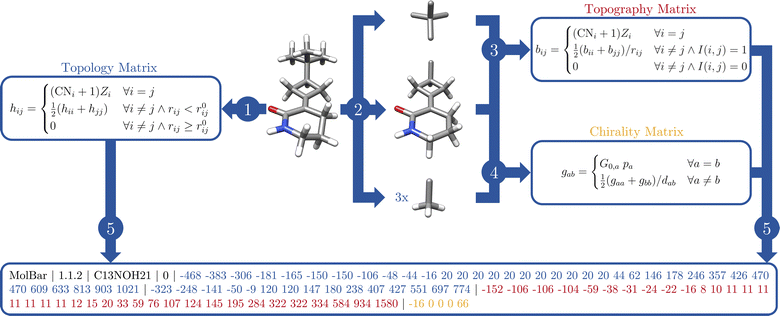 | ||
| Fig. 6 Flowchart for MolBar generation: (1) use of an extended adjacency matrix (eqn (2)) to represent the molecular topology. Identification of bonds by comparing Cartesian distances rij with reference values r0ij.35 (2) Partitioning of the molecule into rigid fragments using bond orders and ring structures, then 3D structure unification of fragments using a specialized force field. (3) Use of a modified Coulomb matrix (eqn (4)) to describe the 3D atomic arrangement in the unified fragments. (4) Describing absolute configuration based on Osipov–Pickup–Dunmur indices {G0,a}36 for each fragment, incorporated into an additional matrix. (5) Concatenation of the eigenvalue spectra of the matrices to yield MolBar. All eigenvalue spectra are first multiplied by ten and then rounded to the nearest integer. These spectra are preceded by the identifier name, version, the chemical formula, and its (user-specified) charge. | ||
4.1 Step 1: topology
To construct the topology matrix according to eqn (2), it is important to determine which atoms are bonded. Starting from 3D coordinates, the connectivity evaluation can be carried out by comparing the Cartesian distance rij between the two atoms with a certain reference value r0ij.35 For a given molecular geometry represented by Cartesian coordinates X in 3D space, a molecular graph G can therefore be constructed:| E = {(vi,vj)|vi,vj ∈ Vatoms∧rij < r0ij} | (6) |
This reference value r0ij can be a simple scaled summation of the two tabulated covalent radii, as used in the DFT-D3 dispersion,37 or a more elaborate expression that takes into account the chemical environment of the individual atoms, as used in the force field GFN-FF by the Grimme group.35 While the former approach is found to be appropriate for organic chemistry molecules, the latter approach was chosen for the molbar implementation. This choice allows for a more satisfactory treatment of metal complex systems. Here, the precalculated reference value r0ij describes the usual bonding distance between these two atoms in their actual environment. Those values had been fitted to reproduce equilibrium bond lengths at the PBEh-3c38/B97-3c39 level of theory. More information can be found in the ESI† of ref. 35. This force field has been successfully applied in computational studies across a wide range of chemical fields, including metal–organic frameworks,40 transition metal complexes,41 and supramolecular systems and biological macromolecules.42 These applications demonstrate the force field's reliability in accurately defining molecular topologies, which is why it has been adapted as a standalone implementation within MolBar. By implementation of the same bond identification routine, MolBar does not rely on external packages to determine the topology in molecules. Furthermore, only atomic information such as the coordination number CNi of atom vi and its nuclear charge Zi are required. The nuclear charges are tabulated for each element and are assigned by the element information specified in the input file.
4.2 Step 2.1: fragmentation
The introduction of the concept of rigid fragments in eqn (4) allows a consistent representation of the atomic 3D positions in conformational space. Consequently, a rigidity analysis must be conducted prior to constructing the topography and absolute configuration matrix in eqn (4) and (5). For that, in the following, the indicator function I(vi, vj) is defined that states if two atoms are part of the same fragment.In general, bonds with a bond order higher than one are considered as rigid substructures. The restriction of rotational motion around a multiple bond arises from the intrinsic nature of the π-bond.43 This rigidity leads to important structural properties such as E–Z isomerism, which is distinguishable in the topography matrix, where interactions are allowed exclusively between atoms with more or less fixed relative positions. Therefore in I(vi, vj), information about bond orders must be included. For a molecular graph G, we define the function w, which gives the integer bond order for the bonds in Eatoms.
w: Eatoms → ![[Doublestruck Z]](https://www.rsc.org/images/entities/i_char_e17d.gif) | (7) |
Following, we define a set of bonds with a bond order greater than one to only include bonds where the rotation around the bond is restricted.
| M = {w(eij) > 1|eij ∈ Eatoms} | (8) |
Furthermore, ring structures can be considered as rigid substructures in the molecule. At first glance, this is particularly evident in aromatic rings, but as well as in aliphatic ring structures, where the alteration of dihedral angles within the system is limited, ensuring the integrity of the rings. To start, we define a set C as the set of all possible cycles ca in the graph G:
| C = {ca, cb, …, cz} | (9) |
| ca = (vi, vj, vk, …, vi) ∈ Vatoms × Vatoms × … × Vatoms | (10) |
| f(vi) = argmin{|ca|∀ca ∈ C, vi ∈ ca} | (11) |
With that given function, we define the subset of chemical meaningful cycles Cs.
| Cs = {f(vi)|vi ∈ Vatoms} | (12) |
With that we also can define a subset of Eatoms termed Esatoms, containing edges that make up the chemical cycles in Cs.
| Esatoms = {eij|vi ∈ ca∧vj ∈ ca∧ca ∈ Cs} | (13) |
Now, two vertices belong to the same fragment if no edge in the shortest path connecting them is a non-cycle edge with a bond order of 1. A path ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) a ∈ P(vi, vl) is in general defined as a sequence of vertices connecting two vertices vi and vl, where P(vi, vl) is a set of all possible paths between the two vertices.
a ∈ P(vi, vl) is in general defined as a sequence of vertices connecting two vertices vi and vl, where P(vi, vl) is a set of all possible paths between the two vertices.
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) a = (vi,vj,vk, …, vl) ∈ Vatoms × Vatoms × … × Vatoms a = (vi,vj,vk, …, vl) ∈ Vatoms × Vatoms × … × Vatoms | (14) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) s(vi,vl) = argmin{|pa∥∀ s(vi,vl) = argmin{|pa∥∀![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) a ∈ P(vi,vl)} a ∈ P(vi,vl)} | (15) |
With this, we can now define the indicator function I(vi, vj) needed for the eqn (4). So that two vertices are part of the same rigid fragment, the function returns the value one if all edges on the shortest path between both vertices either have a bond order greater than one or are part of a cycle. Also, the function returns the value one if both vertices are adjacent (number of vertices in ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) s is equal to two), so that there is an overlap between the vertices of the fragment. This is done so that there is an interaction between the fragments and information about the relation between two fragments is still included in eqn (4) (the matrix does not consist entirely of block matrices). On the other hand, if there is at least one non-cyclic single bond between the two edges or if the two vertices are not adjacent, the value zero is returned.
s is equal to two), so that there is an overlap between the vertices of the fragment. This is done so that there is an interaction between the fragments and information about the relation between two fragments is still included in eqn (4) (the matrix does not consist entirely of block matrices). On the other hand, if there is at least one non-cyclic single bond between the two edges or if the two vertices are not adjacent, the value zero is returned.

| (16) |
Before the indicator function can be applied, the bond orders must first be assigned to the bonds and cycles determined according to their definition in eqn (12). Bond orders can be calculated by quantum mechanical calculations such as the Wiberg (or Mayer) bond orders (WBO).44,45 However, because of computational cost, such a quantum mechanical calculation is not preferable for a molecular identifier. In the past, an algorithm based on graph theory was proposed by Y. Kim and W. Y. Kim, requiring only information about the edges present and element-specific parameters such as the number of possible valences for a given element and the number of valence electrons.46 This algorithm has already been implemented in xyz2mol47 and RDKit48 and is also implemented in a modified version in molbar. To find the minimum size cycles (eqn (12)) for a graph, several algorithms have been developed in the past. In the implementation, the algorithm proposed by Kavitha et al.49 as implemented in the Python package networkx50 is used. In the context of solving the shortest path problem, the standard Dijkstra algorithm51 is implemented using the networkx library as well.
Since the fragmentation into rigid substructures is based solely on bond orders and ring structures, atropisomerism cannot be automatically captured with this rigidity function in its current form in MolBar. Atropisomerism refers to restricted rotation around a single bond.34 For example, this fragmentation procedure applied to [1,1′-binaphthalene]-2,2′-diol in Fig. 4c would result in two separate 2-naphthol units, losing the chirality information. While atropisomerism cannot yet be handled automatically, the Python implementation allows for manual input to specify rigidity and thus accurately describe atropisomerism. An additional consequence of this current fragmentation algorithm is the separation of mechanically interlocked molecular architectures, such as catenanes,52 rotaxanes,53 or molecular knots,54 into their covalent substructures. As a result, MolBar in its current form cannot capture the spatial arrangements of these architectures.
To illustrate the concept of fragmentation, consider the second step in Fig. 6, in which the molecule 3-(3-tert-butylcyclo-butylidene)-piperidin-2-one is fragmented. This results in four tetrahedral fragments and one larger fragment consisting of two rings linked by a double bond. The definition of the indicator function in eqn (16) leads to overlapping fragments where the atoms are shared by several fragments, due to the rule that adjacent atoms always belong to the same fragment.
4.3 Step 2.2: structure unification
After fragmentation to eliminate the conformational dependence of the eqn (4), multiple fragments are obtained with their respective 3D coordinates. However, structural differences between identical fragments of the same molecule may remain due to variations attributable to different sources of the coordinates provided. For example, the application of different DFT functionals in a geometry optimization may result in different bond lengths, angles, and dihedral angles for the same molecule.38,55,56 To obtain a uniform identifier for all input structures of the same molecule, structural unification of bond lengths, angles, and dihedral angles is essential. An effective method to achieve this unification is to use force field optimization characterized by harmonic potentials.57 By using such harmonic terms of the form of k(x0 − x)2 with sufficiently large force constants, the system can be forced to a reference value x0: | (17) |
E bond sums harmonic terms for each edge eij ∈ Eatoms to constrain the actual bond length to an element-pair specific reference value rcovij as the sum of the covalent radii proposed by Pyykkö and Atsumi.58Eangle sums harmonic terms for all angles that can be defined for each fragment atom vi as the central atom. The reference angle α0 is derived, e.g., from the basic VSEPR theory but also adapted from more distorted geometries, with the values described in the ESI.†59 Future developments will also include reference geometries other than VSEPR, such as those required for metal complexes. Currently, such systems with unknown VSEPR reference, will be treated exclusively via the distance constraints and the repulsive term.
Consequently, a method is needed to represent the structural arrangement of neighboring atoms around an atom vi and assign a reference geometry classification to it. For example, the Smooth-Overlap of Atomic Positions (SOAP) descriptor can be used to evaluate and compare different chemical environments around an atom.60 This is done by creating a neighborhood density around the atom by summing Gaussian functions centered on neighboring atoms by spherical harmonics and radial basis functions. The resulting expansion coefficients cnlm then find application in a similarity kernel equation for comparing different chemical environments:
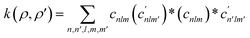 | (18) |
 | (19) |
Here,
 | (20) |
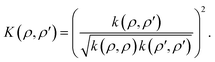 | (21) |
When calculating the power spectrum in eqn (20) for each vi, the real geometry is compared with ideal reference structures by the similarity measure in eqn (21), which ranges from 0 (not similar) to 1 (very similar). The overall workflow for finding the best set of reference angles {α0ijk} is shown in Fig. 8. Since the assignment of the reference angles is not straightforward for distorted geometries or such ones, where not all angles are identical, several steps are necessary. First, the workflow cuts out the immediate neighborhood of the target atom from the overall structure, taking into account the coordinates of both the central atom and the adjacent atoms (as shown in the first step of Fig. 8). In preparation for the power spectrum calculations, all bond lengths are set uniformly to 1 Å, and placeholder elements are introduced that align with the ideal reference structure, as shown in the second step of Fig. 8. This alignment is crucial because the calculation of the power spectrum depends on the atomic elements and bond lengths.
In the next step, the power spectrum given in eqn (20) is calculated for the rescaled local structure in question. Then, using the SOAP kernel described in eqn (21), a comparison of this power spectrum with those of the ideal reference structures is performed. This process is illustrated in the third step of Fig. 8. Once the best match to an ideal geometry class is identified, the Kabsch algorithm is used to calculate the optimal rotation matrix to rotate the real structure into the ideal geometry.61 This matrix facilitates the mapping of the atoms of the real structure to the corresponding atoms in the ideal geometry. In this alignment process, both the real local geometry and the reference geometry are shifted so that their center of mass coincides with the origin of the coordinate system. Then, a covariance matrix labeled H is computed in eqn (22), where Preal and Q0 are the centered Cartesian coordinates of the two structures as matrices of dimensions natoms × 3 (fourth step of the Fig. 8).
| H = PTrealQ0 | (22) |
The optimal rotation matrix ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) to rotate Preal into Q0 can be determined with a Singular Value Decomposition (SVD) of the covariance matrix H.
to rotate Preal into Q0 can be determined with a Singular Value Decomposition (SVD) of the covariance matrix H.
| H = UΣVT | (23) |
The rotation matrix then follows by
 | (24) |
| d = sign(det(VUT)) | (25) |
Since Preal and Q0 must be in the same atomic order, all atomic permutations of Preal must be considered to find the best match. In the final step, the best reference angles are determined by using the angles between the mapped atoms in the ideal geometry after aligning them with the atoms in the real structure. Nitrogen is an exception to the above procedure as its usual trigonal pyramidal geometry can easily be inverted. Therefore, nitrogen always obtains angular constraints for a trigonal planar structure. Stereocenters involving nitrogen can occur when the configuration is fixed by a ring structure or other constraints.
E
dihedral sums the harmonic terms for all dihedral angles used to constrain different structures within the molecule. For example, the dihedral constraint ensures that C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds and aromatic rings are constrained to be planar. Furthermore, these terms are also used to planarize aliphatic ring structures so that different conformations of, for example, cyclohexane are unified into a single structure. The resulting unified structure does not need to be physically meaningful, since the crucial information is retained even after structure unification, namely whether the atoms are above or below the ring plane. Thus, the topography matrix in eqn (4) is conformer-independent even for non-aromatic ring systems and still contains the information necessary to distinguish cis/trans isomers for example. The sine and cosine basis was chosen to prevent unreasonably high energy contributions upon geometry optimization, due to a possible sign change of a dihedral angle close to 180°. When using the sine and cosine basis, as shown in eqn (17), the sign reversal problem is circumvented and a more stable representation of the dihedral angles is obtained as sin(180°) = sin(−180°) = 0 and cos(180°) = cos(−180°) = −1.
C double bonds and aromatic rings are constrained to be planar. Furthermore, these terms are also used to planarize aliphatic ring structures so that different conformations of, for example, cyclohexane are unified into a single structure. The resulting unified structure does not need to be physically meaningful, since the crucial information is retained even after structure unification, namely whether the atoms are above or below the ring plane. Thus, the topography matrix in eqn (4) is conformer-independent even for non-aromatic ring systems and still contains the information necessary to distinguish cis/trans isomers for example. The sine and cosine basis was chosen to prevent unreasonably high energy contributions upon geometry optimization, due to a possible sign change of a dihedral angle close to 180°. When using the sine and cosine basis, as shown in eqn (17), the sign reversal problem is circumvented and a more stable representation of the dihedral angles is obtained as sin(180°) = sin(−180°) = 0 and cos(180°) = cos(−180°) = −1.
E Coulomb is introduced to enforce repulsive interatomic interactions, which results in maximizing the interatomic distance under constraints. Thus, ECoulomb sums over all atom–atom combinations with system-independent scaling constant Q. Table 1 shows the default values for the parameters used in the force field to unify the input structures. The geometry optimization is performed with a Newton-CG algorithm62 as implemented in the scipy package.63 The gradients and the Hessian matrix are calculated analytically, and the derivatives can be found in the ESI.†
| Constant | Default value |
|---|---|
| k bond | 1 × 106 Å−2 |
| k angle | 2 × 103 rad−2 |
| k dihedral | 2 × 103 |
| Q | 1 × 102 Å |
4.4 Step 3: topography matrix
After the fragmentation and structure unification of all fragments, the matrix of eqn (4) can be set up by calculating the interatomic distances for the atoms within a fragment. The coordination number and the nuclear charges are already known from the first step. In contrast to Fig. 3 with the CM matrix in eqn (3) by Rupp et al.,27 the topography matrix is conformer independent due to fragmentation and structure unification (c.f.Fig. 7). The rotation around a C–C single bond changes the interatomic distances between the substituents of the two carbon atoms. The fact that the substituents of the carbon atoms in 1,2-difluoroethane do not belong to the same molecular fragment, e.g., for the two fluorine atoms I(1, 6) = 0, does not lead to any change in the matrix despite the inherent changes in the spatial arrangement. Consequently, for the substituents of the two carbon atoms represented by zero entries in the matrix, no 3D information of those two atoms is kept in the MolBar topography matrix, leading almost to a set of block matrices. The complete formation of block matrices is prevented only by the overlapping of the fragments, since the adjacent carbon atom belongs in each case to the fragment of the other carbon atom. | ||
| Fig. 7 Conformational independence of the topography matrix in eqn (4) for two conformers of 1,2-difluoroethane optimized at the GFN2-xTB level of theory. In general, rotation around the C–C single bond changes the distance between the two fluorine atoms, but since the two fluorine atoms are not part of the same fragment, i.e., I(1, 6) = 0. In MolBar, we enforce no 3D information between atoms of two different fragments by zeroing out the corresponding Coulomb matrix elements. This mimics the effect of conformational averaging and, thus, changing the F–F distance does no longer affect the topography matrix. | ||
 | ||
| Fig. 8 Flowchart to determine the best set of reference angles {α0ijk}: (1) isolation of local structure. (2) Insertion of dummy elements and rescaling all bond lengths to 1 Å. (3) Calculate eqn (20) and select the most resembling reference geometry class based on eqn (21). (4) Apply Kabsch algorithm for optimal rotation matrix.61 (5) Obtain best reference angles by comparing mapped real and ideal structure. | ||
4.5 Step 4: absolute configuration matrix
Moreover, the absolute configuration matrix in eqn (5) can be constructed once the fragments are defined and their structures are unified. Unlike eqn (4), the matrix contains the fragmentary information rather than the atomic information. For this purpose, a fragment graph is constructed where each vertex va ∈ Vfragments represents a fragment and each edge eab ∈ Efragment describes whether two fragments are adjacent, i.e., there is an overlap between the atoms vi ∈ Vatoms in both fragments (cf.Fig. 9). The interaction between two fragments va and vb is described by the graph distance dab. Thus, dab is the number of edges in the shortest path between two fragments va and vb, calculated by the standard Dijkstra algorithm.514.6 Step 4.1: chirality index
Each fragment va, must be characterized in terms of its absolute configuration with an index, denoted Ga. Requirements for such an index are that it must be zero for nonchiral and non-zero for chiral fragments. Moreover, it should change sign upon spatial inversion of a chiral fragment, which allows the determination of an absolute configuration.64 Various chirality indices have been proposed in the past such as the Hausdorff measure,65,66 the helicity tensor of Ferrarini and Nordio67 or a measure based on mean torsion in a molecule by Luzanov and Babich.68Another approach is to derive a chirality index based on optical activity theory, since chiral molecules have different specific angle of rotation for example. Therefore, it is logical to start with an optical activity tensor to derive a geometric chirality measure. Osipov, Pickup, and Dunmur stated that the pseudoscalar behaviour of a chiral molecule described by its Cartesian coordinates X can be described by the trace of the gyration tensor G (eqn (26)),36
 | (26) |
 | (27) |
 | (28) |
For the purpose of the identifier, only the sign is of interest, so the used expression for the chirality index Ga of a fragment, described with the Cartesian coordinates after the unification process Xunia, writes as:
 | (29) |
However, Millar, Weinberg, and Mislow have pointed out that the utilization of pseudoscalar functions as measures of chirality theoretically leads to situations where a chirality index becomes zero, even when the object is inherently chiral.64 The argument is that for each enantiomer X, there exists a path of geometric distortion transforming it into its enantiomer ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) , where only chiral objects exist along that path. As there must be change of sign for G0, there must also be chiral structure with G0 = 0. Future research needs to investigate whether this occurrence is frequent, as current tests show its usefulness to describe the absolute configuration of unified fragments (c.f. Section 5). The unification process, which precludes any geometric distortion path between X and
, where only chiral objects exist along that path. As there must be change of sign for G0, there must also be chiral structure with G0 = 0. Future research needs to investigate whether this occurrence is frequent, as current tests show its usefulness to describe the absolute configuration of unified fragments (c.f. Section 5). The unification process, which precludes any geometric distortion path between X and ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) , as every input fragment structure is unified into either Xunia or
, as every input fragment structure is unified into either Xunia or ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) unia, may potentially reduce the incidence of chiral zeros.
unia, may potentially reduce the incidence of chiral zeros.
4.7 Step 4.2: priorities
The process requires the use of pseudo masses pi for an atom vi in eqn (28). If the atomic masses mi were employed, identical atoms of the same element but in different environments would be treated as equivalent. In the case of fragment b in Fig. 9, the four adjacent carbon atoms are not equivalent due to their substituents, since three carbon atoms belong to a methyl group and one to a ring system. Therefore, we introduce a pseudo mass pi termed as the atomic priority for each atom vi in the molecule, which takes the atom itself and its environment into account. In theory, this priority can be anything as long as it groups equivalent atoms together. Coming from theoretical chemistry and quantum mechanics, equivalent atoms share the same atom-partitioned electron density. The Mulliken population analysis is often used in quantum chemistry to get the number of electrons associated to individual atoms in a molecule.57 The total electron density is partitioned into atomic contributions based on the coefficients of the atomic orbitals that contribute to each molecular orbital. The analysis provides insights into the distribution of electrons across the atoms within a molecule, aiding in understanding bonding characteristics and reactivity. The partitioning reads as follows: | (30) |
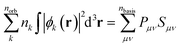 | (31) |
 | (32) |
 | (33) |
| HtopographyC = EC | (34) |
These orbitals can then be used to calculate an artificial electron density at each atom. Determining how to populate the MolBar orbitals is challenging since the topography matrix lacks physical significance. In electronic structure theory, the lowest eigenvalues are populated according to the Aufbau principle, as this corresponds to the most stable occupation. In MolBar, however, the orbitals with highest eigenvalues show fewer nodal planes. Hence, all orbitals with positive eigenvalues are occupied, with each orbital having an arbitrarily chosen occupation number nk of two. This ensures a defined rule, with degenerate orbitals (capturing symmetry information) always occupied in the same manner. This process results in the formulation of the MolBar density matrix, denoted as PMolBar:
| PMolBar = CNoccC⊺ | (35) |
 | (36) |
Further, as the topography matrix has the dimensions natoms × natoms, equivalent to a minimal basis set, the artificial atomic density for each atom just simply the density matrix element:
| PMolBarμμ = ρi | (37) |
Based on that procedure, each atom {vi} gets assigned an artificial electron density ρi. These densities are ranked yielding a set of atomic priorities {pi}. The priorities obtained naturally include information about connectivity, but even if two branches differ only in the configuration of the double bond, using the topography matrix as a source for the orbitals. Equivalent atoms have the same density so they get assigned the same priority, while non-equivalent atoms receive different priorities. For the absolute configuration matrix in eqn (5), not atomic priorities but fragment priorities {pa} are needed. Those fragment priorities are obtained by comparing atomic priorities of fragments (c.f.Fig. 10). The highest atomic priority within a fragment is compared to the highest atomic priority of another fragment. The fragment with the highest atomic priority is then assigned the highest fragment priority. In case of a tie between several fragments, the comparison continues with the evaluation of the second highest priority until all fragments receive different priorities or are considered equal.
4.8 Step 5: concatenation of modified eigenvalue spectra and MolBar generation
In the final step, the eigenvalue spectra of the matrices from eqn (2), (4), and (5) are combined to generate MolBar. The eigenvalues are first multiplied by ten and then rounded to the nearest integer in order to minimize the size of the MolBar. Previous results have shown that it is not necessary to use more digits. We term this the “modified eigenvalue spectra”. A MolBar example can be found in Table 2 using 3-(3-tert-butylcyclobutylidene)piperidin-2-one as an example (c.f.Fig. 6).| MolBar | Example |
|---|---|
| Version | 1.1.2 |
| Molecular formula | C13NOH21 |
| Total molecular charge | 0 |
| Topology | −468 −383 −306 −181 −165 −150 −150 |
| −106 −48 −44 −16 20 20 20 20 20 20 20 20 | |
| 20 20 20 44 62 146 178 246 | |
| 357 426 470 470 609 633 813 903 1021 | |
| Heavy atom topology | −323 −248 −141 −50 −9 120 120 147 |
| 180 238 407 427 551 697 774 | |
| Topography | −152 −106 −106 −104 −59 −38 −31 −24 −22 −16 |
| 8 10 11 11 11 11 11 11 11 12 15 20 33 59 | |
| 76 107 124 145 195 284 322 322 334 | |
| Chirality | −16 0 0 0 66 |
The first segment contains the version number, the molecular formula and the total molecular charge. The purpose of specifying the version is to ensure that only MolBar identifiers with the same version are compared, taking into account that future changes or bug fixes may result in different spectra. The concatenation of eigenvalue spectra follows a specific order: λtopology, λtopology,Zi>ZH, λtopography, and λchirality. First, the eigenvalue spectra λtopology of the topology matrix (eqn (2)) are shown, followed by the spectra of the topology matrix without hydrogen atoms. By explicitly including hydrogen atoms in one matrix and excluding them from the other, it is possible to classify two different molecules as prototropic tautomers. By default, therefore, tautomeric structures are given a different MolBar identifier. This approach is advantageous for quantum chemical structure databases, as it guarantees that each structure receives a unique database entry, since it is characterized by its unique properties derived from electronic structure theory. Prototropic tautomers exist when, under the same molecular formula, the total topology spectrum is different but the heavy atom topology spectrum is identical. It must be kept in mind that the tautomeric picture is rather simplistic, as it does not take into account large energy barriers for hydrogen shifts,69 but it is sufficient for quantum chemical structure databases. Then the topography spectrum λtopography is given (eqn (4)), followed by the absolute configuration spectrum (eqn (5)).
5 Results and discussion
5.1 Topology test
Many approaches for describing molecular topologies are based on graph relaxation algorithms to create a canonical atomic order.70 The classical Morgan algorithm1 faces challenges with molecules with high topological symmetry.71 Since then many improved algorithms have been published that benchmark their approaches on such highly symmetrical molecules.70,72,73 Unlike these methods, MolBar does not rely on any canonicalization process. MolBar starts with the topology matrix defining the molecular graph. The corresponding topology matrix is then diagonalized to obtain the sorted eigenvalues as a permutation invariant vector. In this approach, each eigenvalue represents a topological substructure composed of multiple atoms, rather than focusing on individual atoms. To test MolBar on systems with difficult topology and high symmetry, the topology barcode was tested on the set of 1812 unique isomers of C60 fullerene.74 In fact, all 1812 topology barcodes generated by MolBar were unique. Thus, MolBar is able to identify each isomer even though the topology is very similar. Moreover, considering the full barcode, within these isomers, 1722 are identified as chiral, exhibiting non-central chirality. Barcodes and structures for all these isomers are included in the ESI.†As a side note, in general, two distinct graphs can be isospectral, meaning they possess the same eigenvalue spectrum. This situation is particularly common when using only the adjacency matrix to represent the graph. However, the probability of finding isospectral graphs is highly dependent on the employed type of matrix. The number of such isospectral graphs can be significantly reduced by using a Laplacian matrix or by combining the eigenvalue spectra from several different matrices.75 However, MolBar addresses this issue by using three matrices to describe molecular connectivity and is not purely graph-based: the topology matrix, the heavy atom topology matrix, and the non-graph-based topography matrix, the latter of which encodes information indirectly through bonding force field constraints. For two distinct molecules to be isospectral within MolBar, they would need to have identical eigenvalues across all three matrices, thereby minimizing the likelihood of such occurrences. So far, in all tested cases, including in the dataset of the duplication test discussed below and other cases beyond it, no instances of such isospectral molecules have been identified. However, continued research is necessary to further explore the robustness of this approach.
5.2 Duplication test
Molecular identifiers play a critical role in merging of and eliminating duplicate entries in molecular databases. A benchmark set is critical for evaluating different molecular identifiers in database deduplication tasks because it provides a standardized test bed that allows for fair and consistent comparisons. To our knowledge, there is no existing benchmark set for deduplication tasks. However, several datasets containing millions of molecules have been proposed, particularly in the field of molecular machine learning, where molecular structures are represented by 3D coordinates. Such a dataset has been proposed by Xu et al. with the benchmark set Molecule3D for predicting 3D geometries from molecular graphs.76 It consists of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899
899![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 molecules with ground state 3D molecular geometries with an average of 29.11 atoms per molecule, an average of 14.08 heavy atoms and an average of 29.53 bonds. The source of the molecular data is the PubChemQC database,77 with optimized molecular structures at the B3LYP/6-31G* level of theory.78–90
647 molecules with ground state 3D molecular geometries with an average of 29.11 atoms per molecule, an average of 14.08 heavy atoms and an average of 29.53 bonds. The source of the molecular data is the PubChemQC database,77 with optimized molecular structures at the B3LYP/6-31G* level of theory.78–90
A pickle file molecule3D.pkl with all molecular 3D coordinates of that dataset is provided in the ESI.† Throughout the benchmark tests, the molecules are named by the ID specified in the Molecule3D dataset. As a side note, this ID initially corresponds to the CID in the PubChem database, but due to structural modifications, the structures may differ from the database in some cases due to factors such as hydrogen shifts or inversion of the absolute configuration of stereocenters. This discrepancy is not investigated further in this work, as the correspondence of the structures to the PubChem database is not relevant to the following discussion.
The Molecule3D dataset contains organic molecules with typical 2c–2e bonding patterns. The stereoisomerism in this dataset is present through stereocenters as well as E/Z and cis/trans isomerism, aspects that are captured by the InChI identifier in a highly robust manner.8 This robustness and reliability in representing chemical structures makes InChI an ideal reference for evaluating MolBar on standard organic molecules with typical stereochemistry. To provide a reliable reference, the InChI identifier is generated using RDKit 2023.09.02 and OpenBabel 3.1.0 with the FixedH option to differentiate between tautomers. Typically, the input for InChI is a Molfile, for example, but since MolBar is designed to be generated from 3D coordinates, which is the starting point for computational chemists, Cartesian coordinates are used as the input for both MolBar and InChI. Using these two different tools with RDKit and OpenBabel helps to eliminate potential misinterpretations of the 3D geometry prior to InChI generation from the discussion. In 8.4% of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899
899![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 molecules, the InChIs generated by RDKit and OpenBabel are different. These differences could stem from a variety of reasons, likely unrelated to InChI itself. For instance, they may arise from the process of converting Cartesian coordinates into connectivity, bonding, and stereochemistry information before inputting them into InChI. To streamline the discussion, these molecules are excluded from the duplication test, resulting in a final count of 3
647 molecules, the InChIs generated by RDKit and OpenBabel are different. These differences could stem from a variety of reasons, likely unrelated to InChI itself. For instance, they may arise from the process of converting Cartesian coordinates into connectivity, bonding, and stereochemistry information before inputting them into InChI. To streamline the discussion, these molecules are excluded from the duplication test, resulting in a final count of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570
570![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657 molecules (referred to as filtered_molecule3D.pkl in the ESI†).
657 molecules (referred to as filtered_molecule3D.pkl in the ESI†).
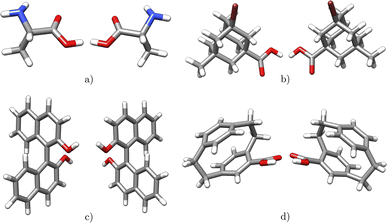
First, we examine unique dataset entries identified by both MolBar and InChI. The Molecule3D dataset initially includes a variety of molecules, including constitutional isomers and stereoisomers. To explore the basic properties of MolBar and demonstrate its ability to discriminate between stereoisomers, several examples of stereoisomerism are presented in Fig. 11. Typically, these stereoisomers have the same topology barcode but differ in their topography and chirality barcodes.
The first two examples show classical cases with carbon stereocenters. In Fig. 11a, the topography barcodes are identical, which means that the interatomic distances within the rigid fragments are the same. Here, the fragments consist mainly of the benzene ring, while the remaining atoms form monoatomic fragments, as the atoms are all connected by rotatable bonds. However, the chirality barcodes differ only in sign, indicating that the molecules are enantiomers, as the absolute configurations of the two chiral fragments are interchanged. In Fig. 11a, with two chiral fragments, this results in four non-zero eigenvalues, while in Fig. 11b, with one chiral fragment, only two eigenvalues are non-zero.
The examples in Fig. 11c and d show cases where the topography barcodes differ, indicating that the interatomic distances within the rigid fragments are not the same. In both cases, this corresponds to a different configuration of a double bond: the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond in Fig. 11c and the C
N double bond in Fig. 11c and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond in Fig. 11d. In addition, the chirality barcodes in both examples consist only of zeros, which indicates that all fragments are achiral.
C double bond in Fig. 11d. In addition, the chirality barcodes in both examples consist only of zeros, which indicates that all fragments are achiral.
In Fig. 11e and f the topography barcodes differ again, but here due to a different relative configuration of the ring substituents. These two examples also make it clear that the chirality barcodes can only be compared if the topography barcodes are the same. Although the absolute configuration of a chiral carbon center is different in both structures in Fig. 11f, the chirality barcode remains unchanged. In Fig. 11e, the chirality barcodes differ in sign, but both structures are not enantiomers. In Fig. 11e and f, the stereocenters are located within larger fragments (here the ring structures), which changes the interatomic distances. This changes the 3D shape of the fragments, which is then captured by the topography barcode. In general, it can be said that the sign determined by the Osipov–Pickup–Dunmur index strongly depends on the 3D shape of the fragment, and small changes can lead to different signs. Since the Osipov–Pickup–Dunmur index is derived from the theory of optical activity, this is comparable to how ECD spectra differ in orientation for two conformers.
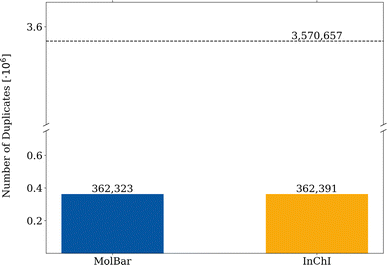
For the duplication test, a molecule is considered a duplicate if it shares the same respective identifier with another molecule. From 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570
570![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657 molecules in the filtered Molecule3D dataset, around 162
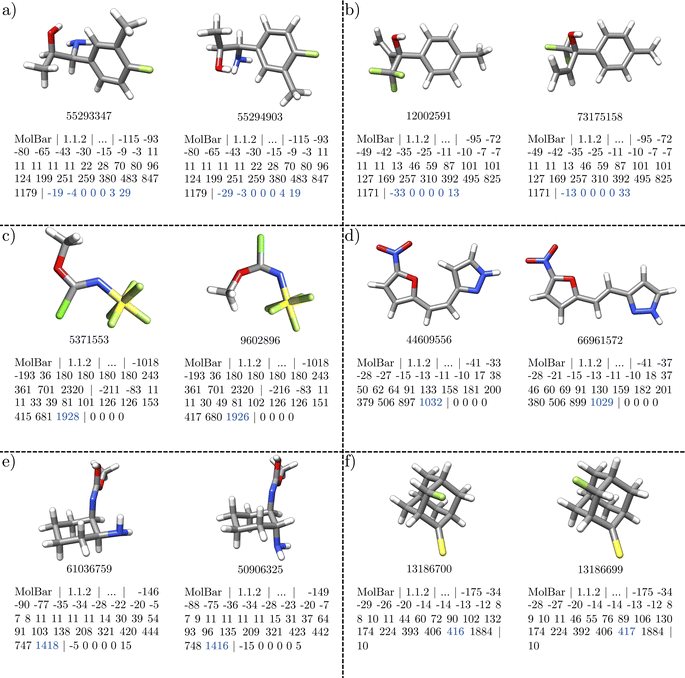
657 molecules in the filtered Molecule3D dataset, around 162![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 duplicates are found by both identifiers, which corresponds to a duplication rate of 4.5% (see Fig. 12). Therefore, the MolBar identifier is able to identify duplicates with a similar performance to InChI. However, in 70 instances, MolBar and InChI identify different duplicates. This means that one identifier recognizes a molecule as a duplicate, while the other does not. Only one molecule is identified as a MolBar-exclusive duplicate. This case involves a different bonding motif in the InChI for the first and duplicate dataset entry, despite nearly identical 3D geometries. This discrepancy is likely due to the conversion tool from coordinates to bonding information rather than an issue with InChI. Therefore, it should not be discussed here but can be found in the ESI.† In contrast, 69 molecules are identified as InChI-exclusive duplicates. The 69 differences can be divided into eight different classes, the examples of which are shown in Fig. 13. All cases are categorized in their class and provided as XYZ files in the ESI.†
300 duplicates are found by both identifiers, which corresponds to a duplication rate of 4.5% (see Fig. 12). Therefore, the MolBar identifier is able to identify duplicates with a similar performance to InChI. However, in 70 instances, MolBar and InChI identify different duplicates. This means that one identifier recognizes a molecule as a duplicate, while the other does not. Only one molecule is identified as a MolBar-exclusive duplicate. This case involves a different bonding motif in the InChI for the first and duplicate dataset entry, despite nearly identical 3D geometries. This discrepancy is likely due to the conversion tool from coordinates to bonding information rather than an issue with InChI. Therefore, it should not be discussed here but can be found in the ESI.† In contrast, 69 molecules are identified as InChI-exclusive duplicates. The 69 differences can be divided into eight different classes, the examples of which are shown in Fig. 13. All cases are categorized in their class and provided as XYZ files in the ESI.†
Fig. 13a shows a case in which both structures are enantiomers and exhibit axial chirality through the ring scaffold (1 case). Since the entire structure is a single fragment, the chirality barcode consists of only one eigenvalue. Therefore, the entire fragment is characterized by a chirality index, and this type of decentralized chirality can be detected. The two chirality barcodes differ only in the sign between the enantiomers. Fig. 13b, on the other hand, shows a case of centro-chirality with phosphorus or sulfur (18 cases). In this example with phosphorus, the atom has four different substituents, indicating that it is a stereocenter. However, this case can also be considered as two tautomers, where the hydrogen atom can be exchanged between the oxygen groups. Consequently, the hydrogen position can change rapidly, inverting the absolute configuration. For InChI, the structures are therefore considered identical. For MolBar, however, the tautomers are always treated explicitly. The distinction between 11506511 and 16072129 is desirable, as both structures have different properties for the calculation of e.g. ECD spectra. Fig. 13c shows a case of chiral structures with two nitrogen stereocenters (1 case). Both structures are diastereomers. Normally, the nitrogen in a trigonal pyramidal geometry is not a stereocenter because it is rapidly transformed by pyramidal inversion. In this case, however, the configuration of the stereocenters is fixed by the ring structure. Fig. 13d and e highlight the importance of preserving 3D shape information for identifiers in computational chemistry and why MolBar's motivation deviates from InChI in some cases. Modern tools like CREST20 and Nanoreactor17 produce new structures as 3D point clouds, either during conformational sampling or reaction discovery. Given the vast number of generated geometries, manually verifying their chemical correctness is impractical. Fig. 13d demonstrates a scenario where the sulfur atom's geometry is trigonal planar in one structure and trigonal pyramidal in another (15 instances). MolBar identifies these differences using eqn (21) and applies distinct force field constraints to eqn (17), resulting in varied unified structures, topography matrices, and final barcodes. Fig. 13e shows a chemically unreasonable geometry, far from the global minimum (21 cases). Here, hydrogen atoms on one carbon point towards the center of the ring, unlike in the other structure. The examples given by Fig. 13d and e can also occur during black-box structure generation. For example, CREST allows users to define a starting structure with a specific geometry, but during its black-box conformational search, the geometry might change depending on the theoretical level used. Users need to be notified if the geometry alters during optimization or sampling processes. Identifying such discrepancies is crucial for ensuring the chemical reasonableness of geometries generated during black-box chemical space exploration. Further evaluation of this use case is discussed in Section 5.5.
Fig. 13f shows chemically unreasonable, broken structures, either missing hydrogen atoms or with open ring structures (5 instances). Fig. 13g and h highlight cases where MolBar needs improvement. In Fig. 13g, both structures are identical, but MolBar identifies one case where phosphorus atoms are closer than the threshold defined by connectivity evaluation. As only 6 out of 162![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324 duplicate structures are effected by this, this indicates a rare issue. In general, it was found that the covalent radii of phosphorus or sulfur are too large for the connectivity evaluation and need to be adjusted.
324 duplicate structures are effected by this, this indicates a rare issue. In general, it was found that the covalent radii of phosphorus or sulfur are too large for the connectivity evaluation and need to be adjusted.
Fig. 13h shows a case where, despite applying identical force field constraints, the exact same energetic minimum in the force field unification is not achieved (2 out of 162![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324 duplicate structures). This issue is attributed to convergence issues with the optimizer used for the force field optimization. Overall the duplication test demonstrates that MolBar is capable of differentiating between stereoisomers and constitutional isomers and identifying duplicates with a similar performance to InChI. Differences between MolBar and InChI are mainly due to the different motivation from which the identifiers were developed, as MolBar treats all 3D structures explicitly.
324 duplicate structures). This issue is attributed to convergence issues with the optimizer used for the force field optimization. Overall the duplication test demonstrates that MolBar is capable of differentiating between stereoisomers and constitutional isomers and identifying duplicates with a similar performance to InChI. Differences between MolBar and InChI are mainly due to the different motivation from which the identifiers were developed, as MolBar treats all 3D structures explicitly.
5.3 Permutation invariance test
Registry and storage systems require a unique and unambiguous identifier, where uniqueness requires a one-to-one correspondence between the identifier and a distinct molecular structure. In the context of a molecule consisting of n atoms, there are n! possible permutations of these atoms. With InChI, a canonicalization procedure is applied to obtain a unique numbering of the atoms. As demonstrated in previous studies, InChI is permutation-invariant.91 To evaluate the robustness of MolBar against changes in atomic order, a permutation test was conducted on 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 randomly selected molecules from Molecule3D. The atomic numbering of these molecules was randomly permuted five times. For each permutation, the MolBar identifiers were generated and compared to the original identifiers. In the sample set, no permutation errors were found for MolBar. Dataframes containing the original and permuted geometries, as well as the calculated MolBar identifiers, are available in the ESI.† At first glance, this might seem straightforward, as eigenvalue spectra in MolBar are inherently permutation invariant. However, it is essential that the entries in the different MolBar matrices also maintain permutation invariance. For example, an identical set of flexible, freely rotatable bonds is crucial for fragmenting the molecule consistently into matching sets of fragments, regardless of atomic order. Additionally, force field constraints must be defined in a permutation-invariant manner to ensure a consistently unified structure. While the permutation invariance test shows that MolBar is generally robust against shuffling atomic order, some exceptional cases may still occur.
000 randomly selected molecules from Molecule3D. The atomic numbering of these molecules was randomly permuted five times. For each permutation, the MolBar identifiers were generated and compared to the original identifiers. In the sample set, no permutation errors were found for MolBar. Dataframes containing the original and permuted geometries, as well as the calculated MolBar identifiers, are available in the ESI.† At first glance, this might seem straightforward, as eigenvalue spectra in MolBar are inherently permutation invariant. However, it is essential that the entries in the different MolBar matrices also maintain permutation invariance. For example, an identical set of flexible, freely rotatable bonds is crucial for fragmenting the molecule consistently into matching sets of fragments, regardless of atomic order. Additionally, force field constraints must be defined in a permutation-invariant manner to ensure a consistently unified structure. While the permutation invariance test shows that MolBar is generally robust against shuffling atomic order, some exceptional cases may still occur.
5.4 Examples of metal complex isomerism and non-central chirality
MolBar departs from the conventional atomic description and instead attempts to characterize the relative and absolute configuration of entire fragments. Therefore, MolBar is theoretically able to represent a wide range of molecules, including both organic and inorganic variants, and going beyond the limits of centrochirality. The data set considered so far, Molecule3D, contains mainly molecules that do not require a decentralized description, such as classical organic molecules with stereocenters as well as E/Z-configured double bonds. In the following, some cases are examined where the atomistic description reaches its limits, taken from the tmQM dataset.92 For example, Fig. 14 shows stereoisomers involving both inorganic and organic molecules, as well as examples of planar and axial chirality. The first example (Fig. 14a) shows two stereoisomers of a tungsten complex with octahedral coordination geometry. For MolBar, the central fragment corresponds to the octahedron itself. The different ligand arrangements within the octahedron distinguish the stereoisomers; in particular, the position of a carbon monoxide ligand is exchanged with that of a hydroxide ligand. As a result, the interatomic distances in the topography matrix vary, allowing MolBar to discriminate between the two stereoisomers. A parallel scenario unfolds in Fig. 14b, where a square-planar platinum complex exhibits cis/trans isomerism. The stereoisomers in Fig. 14c show an octahedral osmium complex with two bidentate dithiocarbamate ligands and two phosphine ligands. Depending on the arrangement of the ligands, the complex can be chiral or achiral. Axial chirality occurs when the two bidentate ligands are not in the same plane. In such cases, the complex consists of a single chiral fragment, the octahedron with the metal atom at the center. The absolute configuration spectra of the two enantiomers, therefore, differ only in sign. If both bidentate ligands are in the same plane, the complex is considered achiral. The achiral variant has different relative ligand positions within the octahedron compared to both chiral complexes, which can be seen in the topography spectrum. Achirality is captured by the absolute chirality spectrum, which consists exclusively of zeros. A similar example is shown in Fig. 14d, which shows the classic example of Δ/Λ isomerism with tris(ethylenediamine)cobalt(III). In contrast to the previous case, the entire molecule corresponds to a singular fragment characterized by a single eigenvalue in the absolute configuration spectrum. Another stereogenic unit can occur in metallocenes, as shown in Fig. 14e, where complexation of the iron atom to one side of a suitably substituted aromatic ring results in planar chirality. The chirality of the hexahelicene in Fig. 14f results from the tendency to relieve steric tension. This leads to a right- or left-handed helical form within the polyaromatic ring system. Another notable example is the chiral fullerene C76 (Fig. 14g), which exists in two enantiomeric forms. The absolute configuration of hexahelicenes and fullerenes is correctly described by the Osipov–Pickup–Dunmur index, which characterizes a single fragment and leads to a differentiation of the respective enantiomers with MolBar.5.5 Conformational invariance and application to chemical space exploration
The fragmentation of molecules into rigid substructures was performed to ensure the MolBar identifier remains conformationally invariant. An additional step of force field unification was undertaken to map structural variances of the input to a consistent structure. To demonstrate the practical application of this concept, molecular dynamics (MD) simulations were conducted on two examples. The first example, labeled 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 628
628![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081 in Fig. 13, is an organic molecule featuring freely rotatable bonds and two connected rings. The second example, an achiral osmium complex representative of inorganic chemistry, was already discussed in Fig. 14c. The MD simulations were conducted using the GFN2-xTB level of theory with xtb 6.6.1 and standard settings.28 The results are illustrated in Fig. 15, where the energies of different MD snapshots are presented. The MolBar was calculated for each snapshot and compared to the original MolBar of the input structure. For both examples, the MolBar values remained constant throughout the simulation, demonstrating the conformational invariance of MolBar for those examples. This demonstrates that the chosen reference values in the force field, such as VSEPR geometries, are robust for the two examples. Despite fluctuations in geometry during the simulations, the same force field parameters, including the angles derived from VSEPR theory, were consistently applied. This resulted in the exact same unified structure after force field optimization, ensuring identical MolBar identifiers throughout the molecular dynamics simulation. This robustness of the references is also proven by the duplication test as otherwise MolBar would not be able to find the same duplicates as InChI. However, the example in Fig. 13h may also be considered as showing conformational variance due to convergence issues during geometry optimization. Such cases are rare but can occur.
081 in Fig. 13, is an organic molecule featuring freely rotatable bonds and two connected rings. The second example, an achiral osmium complex representative of inorganic chemistry, was already discussed in Fig. 14c. The MD simulations were conducted using the GFN2-xTB level of theory with xtb 6.6.1 and standard settings.28 The results are illustrated in Fig. 15, where the energies of different MD snapshots are presented. The MolBar was calculated for each snapshot and compared to the original MolBar of the input structure. For both examples, the MolBar values remained constant throughout the simulation, demonstrating the conformational invariance of MolBar for those examples. This demonstrates that the chosen reference values in the force field, such as VSEPR geometries, are robust for the two examples. Despite fluctuations in geometry during the simulations, the same force field parameters, including the angles derived from VSEPR theory, were consistently applied. This resulted in the exact same unified structure after force field optimization, ensuring identical MolBar identifiers throughout the molecular dynamics simulation. This robustness of the references is also proven by the duplication test as otherwise MolBar would not be able to find the same duplicates as InChI. However, the example in Fig. 13h may also be considered as showing conformational variance due to convergence issues during geometry optimization. Such cases are rare but can occur.
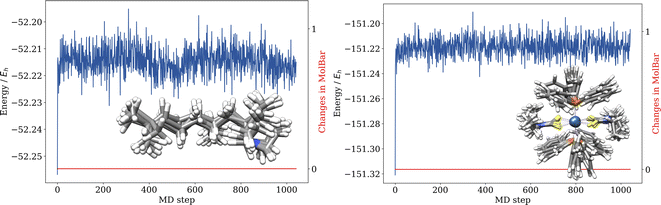 | ||
| Fig. 15 Conformational invariance of MolBar: (a) MD simulation of an organic molecule with freely rotatable bonds, taken from Fig. 13c, (b) MD simulation of an achiral osmium complex, see Fig. 14c. No changes in the MolBar identifier are observed. The MDs were all carried out on the GFN2-xTB level of theory. | ||
The duplication test highlighted the importance of retaining 3D shape information for molecular identifiers used in computational chemistry. This is particularly important for identifiers used in conformational sampling or reaction discovery, where novel structures are generated as 3D coordinates in a black-box fashion. In some cases, the generated structures may not be chemically reasonable, as shown in Fig. 13e. In other cases, the VSEPR geometry may change due to the level of theory used during the structure optimization, as shown in Fig. 13d. Given the large number of generated geometries, manual verification of their chemical correctness is impractical. Fig. 16 shows another example. The input structure is a Pt complex with a square planar geometry. The conformer ensemble was generated at the GFN-FF level of theory using the crest software 3.0.1,20 with a charge of 0 and the ALPB solvation model for water.35,93 The MolBar identifier was calculated for each conformer and compared to the MolBar of the input structure. None of the structures in the ensemble were identical to the input structure. Further evaluation revealed that the square planar geometry was not preserved in the conformer ensemble. However, all structures in the ensemble shared the same topography and topology. Unlike the input structure, the conformer ensemble consisted of structures with tetrahedral geometry. In addition, since the metal has four different ligands, the metal center became a stereocenter in the generated conformer ensemble, resulting in two enantiomers. Consequently, the entire ensemble can be separated into two enantiomeric ensembles. This example highlights the importance of identifying discrepancies in the geometry of generated structures during black-box conformational sampling.
 | ||
| Fig. 16 Conformational sampling of a Pt complex with square planar geometry was performed using the crest20 software. The input structure is displayed in the top left corner. The resulting conformer ensemble consists of structures with tetrahedral geometry, which can be divided into two enantiomeric sub-ensembles. | ||
5.6 Computational cost
To evaluate the computational cost of MolBar, the time required to calculate the identifier was measured using a random sample of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules from the Molecule3D dataset. The calculations were conducted on Apple Silicon M1 hardware using the molbar Python package version 1.1.2 with the function get_molbar_from_coordinates. The timing measurements were performed three times for each molecule, and the results were averaged. Additionally, the average time was calculated for molecules with the same number of atoms. It is important to note that the time required to calculate the MolBar identifier depends on several factors, including the number of rings, the rigidity of the molecule, and the number of freely rotatable bonds, which can lead to varying calculation times for molecules with the same number of atoms. In result, those timings are only indicative, should be interpreted with caution and highly depend on the specific molecule. The results are presented in Fig. 17, where the number of atoms includes the heavy and hydrogen atoms.
000 molecules from the Molecule3D dataset. The calculations were conducted on Apple Silicon M1 hardware using the molbar Python package version 1.1.2 with the function get_molbar_from_coordinates. The timing measurements were performed three times for each molecule, and the results were averaged. Additionally, the average time was calculated for molecules with the same number of atoms. It is important to note that the time required to calculate the MolBar identifier depends on several factors, including the number of rings, the rigidity of the molecule, and the number of freely rotatable bonds, which can lead to varying calculation times for molecules with the same number of atoms. In result, those timings are only indicative, should be interpreted with caution and highly depend on the specific molecule. The results are presented in Fig. 17, where the number of atoms includes the heavy and hydrogen atoms.
 | ||
| Fig. 17 Computational cost of MolBar for the Molecule3D dataset. The time required to calculate the MolBar identifier is shown for molecules with the same number of atoms. | ||
The overall computational cost of MolBar scales to the power of 0.93 for molecules. The computational cost is higher compared to the generation of SMILES and InChI. However, for its primary application in chemical space exploration with quantum chemical or reactive force field methods, MolBar is practical and never poses a rate-limiting step in these workflows. Nonetheless, the algorithm is continuously being developed to reduce computational overhead, making it more suitable for applications outside of quantum chemistry requiring lower computational costs. The most computationally demanding aspect of MolBar is the force field geometry optimization step during structure unification, which ensures the input structure is mapped to a consistent form. The cost of the geometry optimization process largely depends on the optimizer and the convergence criteria. Currently, the Newton-CG optimizer from the scipy package is used.63 More specialized convergence criteria, such as convergence based on the stability of the rounded eigenvalue spectrum, could significantly reduce the computational burden. Additionally, while the analytical gradient and Hessian of the MolBar force field are implemented in Fortran, they are currently accessed through Python's scipy optimizer, which introduces overhead. Future improvements will focus on using a dedicated optimizer directly in Fortran without using external packages with MolBar-specific convergence criteria. The other steps, such as the diagonalization of the topography and chirality matrices, are less computationally demanding and negligible in comparison.
As mentioned earlier, the Molecule3D dataset consists of structures with an average of 29.11 atoms per molecule, with no molecule exceeding 45 atoms in this analysis. To account for larger systems in the computational cost analysis, we also examined a supramolecule and a protein. The Cucurbit[6]urils host with n-butylammonium as a guest (BuNH4+@CB6), containing 125 atoms, took an average of 2.4 seconds to compute.94,95 Meanwhile, the photoactive yellow protein, consisting of 1931 atoms, required approximately 141 seconds on average to calculate the MolBar identifier.96
6 Conclusions
We introduced a unique molecular identifier named the Molecular Barcode (MolBar), which is designed to comprehensively describe both organic and inorganic molecules. MolBar includes full support for stereochemistry beyond the constraints of 2c–2e bonds and atom-centered stereochemistry. This identifier takes a unique approach to describe molecules with eigenvalue spectra from a Hückel-like adjacency matrix and Coulomb-inspired matrix. Using the Coulomb-inspired matrix, MolBar retains information about molecular shape, including local atom geometries, while mapping different conformations to a single identifier. This is achieved by fragmenting the molecule into rigid substructures and applying geometry optimization with a specialized force field for additional structural uniformity. The 3D structure of these unified fragments is then described by the Coulomb-inspired matrix. Thus, MolBar relies on a fragmentary picture rather than solely on an atomistic description, unlike standard molecular identifiers. This fragmentary approach allows MolBar to describe a wide range of molecules, both organic and inorganic, surpassing the limits of centrochirality. MolBar excels in distinguishing (in)organic molecules characterized by non-local chirality, such as axial or planar chirality in hexahelicene or chiral substituted ferrocene derivatives. MolBar distinguishes between tautomers by default, which is essential for quantum chemical structural databases since these structures have different electronic properties. The robustness of MolBar was demonstrated in deduplication tasks and permutation invariance tests on a dataset of approximately 3.9 million molecules. Differences in identifying duplicates between MolBar and InChI were observed, which are explainable by the different design strategies behind the identifiers and considerations of non-central chirality.In future updates, we plan to address existing limitations, particularly those arising from significant deviations in coordination geometry from the VSEPR reference. Challenges also arise with η bonds, as small changes in the metal–ligand distance can easily affect the coordination sphere of the metal center. Caution is advised when dealing with metal complexes with η bonds, and additional analysis, such as examining geometry optimization trajectories for each fragment provided by the molbar package, should be performed if necessary.
In addition, the current rigidity analysis is based on bond orders and ring structures. Consequently, in cases of atropisomerism, such as in the case of 1,1′-bi-2-naphthol, the analysis does not account for rotational hindrance around covalent single bonds. This omission results in the loss of information about the configuration of the atropisomer, as both 2-naphthol substructures are split into two fragments, and axial chirality is not detected. Currently, the molbar implementation allows the user to set an additional constraint to account for this barrier. However, an upcoming update will provide automatic detection of atropisomerism and appropriate constraints.
While the procedure for defining molecular topology is generally robust, challenges in determining whether two atoms are bonded may still arise, as discussed by rare the cases. This is particularly true in situations where the bonding is ambiguous, especially when working with systems beyond organic chemistry. However, users can verify the topology through the debug options provided in the Python package.
All in all, a novel molecular identifier able to distinguish different stereoisomers based only on their 3D geometry is presented here. To our knowledge, it is more capable than any other identifier for computational chemistry currently in use. It can be used as a gatekeeper to avoid data duplicates in quantum chemical structure databases and to evaluate geometries in electronic structure theory-based exploration of chemical space.
Looking ahead, our future developments aim to introduce a MolBar version that supports Molfiles without 3D coordinates, along with the ability to convert MolBar strings back to the input structure. Additionally, our next focus will be on streamlining the MolBar string, as topology information is redundantly encoded in the topography spectrum by force field bond constraints. Nevertheless, the topology spectrum will be retained for the time being, as we are considering the potential benefits of back-converting from this spectrum.
Author contributions
C. B. conceived the initial concepts of the MolBar identifier and functioned as academic supervisor. Both authors contributed equally to the further conceptual development of the MolBar algorithm in its current form. The code development including the derivation of the unifying force field, implementation and benchmark of the MolBar package was carried out by N. v. S. He also prepared the manuscript and all figures with support from C. B. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. B. gratefully acknowledges the support of the Ministry of Culture and Science of the State of North Rhine-Westphalia (MKW) through the NRW Rückkehrprogram. The authors thank Sonja Herres-Pawlis and Ulrich Schatzschneider for helpful discussions. Furthermore, we thank Ying Chen, Alessandro Currà, Felix Bröcker, Hannah Schulz, and Janis Sprenger from the Bannwarth group at RWTH Aachen University as well as Johannes Gorges (University of Bonn) for testing.References
- H. L. Morgan, J. Chem. Doc., 1965, 5, 107–113 CrossRef CAS.
- M. F. Lynch, J. Chem. Doc., 1968, 8, 130–133 CrossRef CAS.
- A. E. Petrarca, M. F. Lynch and J. E. Rush, J. Chem. Doc., 1967, 7, 154–165 CAS.
- T. Engel, in Chemoinformatics: Basic Concepts and Methods, ed. T. Engel and J. Gasteiger, Wiley-VCH, Weinheim, 1st edn, 2018, ch. 2, p. 15 Search PubMed.
- A. Kekulé, Liebigs Ann. Chem., 1872, 162, 77–124 Search PubMed.
- G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- S. R. Heller, A. McNaught, I. Pletnev, S. Stein and D. Tchekhovskoi, J. Cheminf., 2015, 7, 1–34 CAS.
- W. J. Wiswesser, Chem. Eng. News, 1952, 30, 3523–3526 CrossRef CAS.
- W. J. Wiswesser, J. Chem. Doc., 1968, 8, 146–150 CrossRef CAS.
- W. J. Wiswesser, J. Chem. Inf. Comput. Sci., 1982, 22, 88–93 CrossRef CAS.
- W. A. Warr, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 557–579 CAS.
- S. Ash, M. A. Cline, R. W. Homer, T. Hurst and G. B. Smith, J. Chem. Inf. Comput. Sci., 1997, 37, 71–79 CrossRef CAS.
- R. W. Homer, J. Swanson, R. J. Jilek, T. Hurst and R. D. Clark, J. Chem. Inf. Model., 2008, 48, 2294–2307 CrossRef CAS PubMed.
- J. M. Barnard, C. J. Jochum and S. M. Welford, in Chemical Structure Information Systems, ed. W. A. Warr, ACS Publications, 1989, ch. 8, pp. 76–81 Search PubMed.
- T. Verstraelen, W. Adams, L. Pujal, A. Tehrani, B. D. Kelly, L. Macaya, F. Meng, M. Richer, R. Hernández-Esparza and X. D. Yang, et al. , J. Comput. Chem., 2021, 42, 458–464 CrossRef CAS PubMed.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Nat. Chem., 2014, 6, 1044–1048 CrossRef CAS PubMed.
- R. Xu, J. Meisner, A. M. Chang, K. C. Thompson and T. J. Martínez, Chem. Sci., 2023, 14, 7447–7464 RSC.
- G. N. Simm, A. C. Vaucher and M. Reiher, J. Phys. Chem. A, 2018, 123, 385–399 CrossRef PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Grimme, Angew. Chem., Int. Ed., 2013, 52, 6306–6312 CAS.
- C. A. Bauer and S. Grimme, J. Phys. Chem. A, 2016, 120, 3755–3766 CrossRef CAS PubMed.
- M. Quirós, S. Gražulis, S. Girdzijauskaitė, A. Merkys and A. Vaitkus, J. Cheminf., 2018, 10, 1–17 Search PubMed.
- A. H. Cheng, A. Cai, S. Miret, G. Malkomes, M. Phielipp and A. Aspuru-Guzik, Digital Discovery, 2023, 2, 748–758 CAS.
- R. Merris, Linear Algebra Appl., 1994, 197, 143–176 CrossRef.
- G. Strang, Linear Algebra and Its Applications, Harcourt Brace Jovanovich, San Diego, 1988 Search PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. von Lilienfeld, A. Tkatchenko and K.-R. Müller, J. Chem. Theory Comput., 2013, 9, 3404–3419 CrossRef CAS PubMed.
- G. Ferré, T. Haut and K. Barros, J. Chem. Phys., 2017, 146, 114107 CrossRef PubMed.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. von Lilienfeld, J. Chem. Theory Comput., 2017, 13, 5255–5264 CrossRef CAS PubMed.
- M. F. Langer, A. Goeßmann and M. Rupp, npj Comput. Mater., 2022, 8, 41 CrossRef.
- J. Schrier, J. Chem. Inf. Model., 2020, 60, 3804–3811 CrossRef CAS PubMed.
- L. Poppe and J. Nagy and G. Hornyánszky and Z. Boros, in Stereochemistry and Stereoselective Synthesis: An Introduction, ed. L. Poppe and J. Nagy, Wiley-VCH, Weinheim, 2018, ch. 2, pp. 44–46 Search PubMed.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- M. Osipov, B. Pickup and D. Dunmur, Mol. Phys., 1995, 84, 1193–1206 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- S. Spicher, M. Bursch and S. Grimme, J. Phys. Chem. C, 2020, 124, 27529–27541 CrossRef CAS.
- M. Bursch, A. Hansen, P. Pracht, J. T. Kohn and S. Grimme, Phys. Chem. Chem. Phys., 2021, 23, 287–299 RSC.
- S. Spicher and S. Grimme, J. Phys. Chem. Lett., 2020, 11, 6606–6611 CrossRef CAS PubMed.
- S. S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, John Wiley & Sons, Hoboken, NJ, 2007 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- I. Mayer, in Simple Theorems, Proofs, and Derivations in Quantum Chemistry, Springer US, Boston, MA, 2003, pp. 227–249 Search PubMed.
- Y. Kim and W. Y. Kim, Bull. Korean Chem. Soc., 2015, 36, 1769–1777 CrossRef CAS.
- Jensen Group, xyz2mol, https://github.com/jensengroup/xyz2mol, accessed: 25 September 2024 Search PubMed.
- RDKit Community, RDKit: Open-source cheminformatics, https://www.rdkit.org, accessed: 25 September 2024 Search PubMed.
- T. Kavitha, K. Mehlhorn, D. Michail and K. E. Paluch, Algorithmica, 2008, 52, 333–349 CrossRef.
- A. A. Hagberg, D. A. Schult and P. J. Swart, Exploring Network Structure, Dynamics, and Function using NetworkX, Python in Science Conference, Pasadena, CA, USA, 2008, pp. 11–15 Search PubMed.
- E. W. Dijkstra, Numer. Math., 1959, 1, 269–271 CrossRef.
- P. R. Ashton, C. L. Brown, E. J. T. Chrystal, T. T. Goodnow, A. E. Kaifer, K. P. Parry, D. Philp, A. M. Z. Slawin, N. Spencer, J. F. Stoddart and D. J. Williams, J. Chem. Soc., Chem. Commun., 1991, 634–639 RSC.
- I. T. Harrison and S. Harrison, J. Am. Chem. Soc., 1967, 89, 5723–5724 CrossRef CAS.
- O. Lukin and F. Vögtle, Angew. Chem., Int. Ed., 2005, 44, 1456–1477 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- C. Zhao, R. Wu, S. Zhang and X. Hong, J. Phys. Chem. A, 2023, 127, 6791–6803 CrossRef CAS PubMed.
- F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, Hoboken, NJ, 2nd edn, 2017 Search PubMed.
- P. Pyykkö and M. Atsumi, Chem. - Eur. J., 2009, 15, 186–197 CrossRef PubMed.
- R. J. Gillespie, Chem. Soc. Rev., 1992, 21, 59–69 RSC.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B, 2013, 87, 184115 CrossRef.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 922–923 CrossRef.
- J. Nocedal and S. J. Wright, in Numerical Optimization, Springer New York, New York, NY, 2006, pp. 101–134 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- G. Millar, N. Weinberg and K. Mislow, Mol. Phys., 2005, 103, 2769–2772 CrossRef CAS.
- A. B. Buda and K. Mislow, J. Am. Chem. Soc., 1992, 114, 6006–6012 CrossRef CAS.
- A. B. Buda, T. A. der Heyde and K. Mislow, Angew. Chem., Int. Ed., 1992, 31, 989–1007 CrossRef.
- A. Ferrarini and P. L. Nordio, J. Chem. Soc., Perkin Trans. 2, 1998,(2), 455–460 RSC.
- A. V. Luzanov and E. N. Babich, J. Mol. Struct.: THEOCHEM, 1995, 333, 279–290 CrossRef CAS.
- R. A. Sayle, J. Comput.-Aided Mol. Des., 2010, 24, 485–496 CrossRef CAS PubMed.
- N. Schneider, R. A. Sayle and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2111–2120 CrossRef CAS PubMed.
- M. Randić, J. Chem. Inf. Comput. Sci., 1975, 15, 105–108 CrossRef.
- M. Randic, G. M. Brissey and C. L. Wilkins, J. Chem. Inf. Comput. Sci., 1981, 21, 52–59 CrossRef CAS.
- Z. Ouyang, S. Yuan, J. Brandt and C. Zheng, J. Chem. Inf. Comput. Sci., 1999, 39, 299–303 CrossRef CAS.
- R. Sure, A. Hansen, P. Schwerdtfeger and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 14296–14305 RSC.
- R. C. Wilson and P. Zhu, Pattern Recognit., 2008, 41, 2833–2841 CrossRef.
- Z. Xu, Y. Luo, X. Zhang, X. Xu, Y. Xie, M. Liu, K. Dickerson, C. Deng, M. Nakata and S. Ji, arXiv, preprint, 2021, DOI:10.48550/arXiv.2110.01717.v1.
- M. Nakata and T. Shimazaki, J. Chem. Inf. Model., 2017, 57, 1300–1308 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. S. Binkley and J. A. Pople, J. Chem. Phys., 1977, 66, 879–880 CrossRef CAS.
- J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222 Search PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984 CrossRef CAS.
- J. M. Goodman, I. Pletnev, P. Thiessen, E. Bolton and S. R. Heller, J. Cheminf., 2021, 13, 40 CAS.
- D. Balcells and B. B. Skjelstad, J. Chem. Inf. Model., 2020, 60, 6135–6146 CrossRef CAS PubMed.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- R. Sure and S. Grimme, J. Chem. Theory Comput., 2015, 11, 3785–3801 CrossRef CAS PubMed.
- W. L. Mock and N. Y. Shih, J. Am. Chem. Soc., 1989, 111, 2697–2699 CrossRef CAS.
- S. Rajagopal and K. Moffat, Proc. Natl. Acad. Sci. U.S.A., 2003, 100, 1649–1654 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The ESI encompasses the first and second derivatives of the bond, angle, dihedral, and Coulomb terms of the unification force field. It also contains the specified ideal geometries for matching the actual structure to a reference structure (SI.pdf). Additional ESI material further contains the full and the filtered benchmark dataset as pickle files with 3D coordinates of the molecules (molecule3D.pkl and filtered_molecule3D.pkl). Further, each dataset entry discussed in this work is presented as XYZ files, identifiable by their ID of the Molecule3D dataset. Additionally, the data from permutation test is provided (permutation_data.pkl) and from the timings (timings.pkl). The ESI material contains the Python code for generating the identifiers (generate_identifiers.py) and running the tests (run_duplication_test.py, run_permutation_test.py, run_timing_test.py). Finally, the MolBar package in the version used in this work is provided as a ZIP file. All if this additional data can be obtained from https://zenodo.org/records/13827787. See DOI: https://doi.org/10.1039/d4dd00208c |
| This journal is © The Royal Society of Chemistry 2024 |