High-throughput quantum theory of atoms in molecules (QTAIM) for geometric deep learning of molecular and reaction properties

Abstract

We present a package, generator, for geometric molecular property prediction based on topological features of quantum mechanical electron density. Generator computes quantum theory of atoms in molecules (QTAIM) features, via density functional theory (DFT), for sets of molecules or reactions in a high-throughput manner, and compiles features into a single data structure for processing, analysis, and geometric machine learning. An accompanying graph neural network package can be used for property prediction and allows users to readily use computed features for learning tasks. To test the efficacy of electron density-based data for machine learning, we benchmark several datasets including QM8, QM9, LIBE, Tox21, and a Green 2022 reaction dataset. This wide dataset diversity underscores the flexibility of QTAIM descriptors and our package. In addition, we made our code compatible with new versions of BondNet and ChemProp architectures to allow for both reaction and molecular property prediction out-of-the-box. To motivate the use of QTAIM features for varied prediction tasks, we also perform extensive benchmarking of our new models against several existing models as well as to our models without QTAIM features. We show that almost universally, QTAIM features improve model performance on our algorithms, ChemProp, and BondNet. We also determine that QTAIM can aid in generalizing model performance to out-of-domain (OOD) datasets and improve learning at smaller data regimes. Combined, we hope that this framework could enable QTAIM-enhanced structure-to-property predictions – especially in domains with less data, including experimental or reaction-level datasets with complex underlying chemistries.

---

QTAIM is an storied methodology for deriving insight from the electronic density distribution of a molecule.¹ QTAIM assigns the electronic density ρ to particular atoms and delineates bonding interactions between them. By topological analysis, QTAIM partitions ρ into atomic basins bounded by zero-flux surfaces S(Ω) that satisfy ∇ρ(r)·n(r) = 0. Integrating electronic properties over each enclosed basin yields descriptors such as atomic energies and electron delocalization. Similarly, QTAIM identifies critical points (CP) at nuclei and between them where ρ is maximized according to its second derivative; these nuclear (NCP), bond (BCP), ring (RCP), and cage (CCP) critical points are differentiated by how many spatial dimensions exhibit local maxima in ρ. Properties of the density measured at CPs provide a compact set of descriptors that encapsulate the molecule's electronic distribution. Furthermore, a unique path of steepest ascent in ρ (i.e., the gradient path) exists from each bond CP to its two adjacent nuclear CPs, thereby linking neighboring atoms with a bonding interaction. In other words, QTAIM yields bonding networks as well as higher-order information about a molecule's electronic structure.

As a density-based theory, QTAIM builds upon either theoretical calculations or X-ray diffraction data, and is thus applicable across computational and experimental disciplines.² Exemplar studies utilize QTAIM to understand ligand–receptor interactions in biological systems,³ predict chemical activation barriers,⁴ describe toxicity,⁵ and estimate spectroscopic parameters in organic compounds.²Table 1 displays a representative set of descriptors alongside the properties they measure. Given QTAIM's high descriptiveness and prior usage in quantitative structure activity relationship (QSAR) models, we believe that it can be leveraged to improve machine-learned predictions of molecular, protein, and periodic system properties. QTAIM's unique bond definitions, rooted in quantum chemical information, can also serve as powerful alternatives to cheminformatic heuristics such as bond cutoffs⁶ for resolving bonding in difficult chemistries involving aromaticity, multi-center bonds, and metals. Several studies have utilized QTAIM as a fine-grained analytical tool for bonding analysis of both covalent and non-covalent interactions. Bader previously investigated how Ti bonds to cyclopentadienyl and a substituted dienyl fragment, with QTAIM differentiating whether or not a C bonds to Ti by the presence or absence of a bonding interaction.⁷ Farruga et al. also compared the covalency of transition metal–carbon bonds based on density, alongside other QTAIM values, at bond critical points.⁸ Given these examples, we also probe whether QTAIM features could improve performance for datasets containing metals.

Table 1 A set of QTAIM features and their previous interpretations

QTAIM value	Derived concepts
Electron density (ρ)	Bond order/strength^14,15
Laplacian (∇^2ρ)	Atomic graph, electrophilic/nucleophilic sites^11
Electrostatic potential (ϕ)	Interaction strengths w/nuclei, other electrons^12,13
Kinetic energy density (KED)	Valence shell polarization^14,15
Ellipticity (ε)	π-Character^16
ETA index (η)	Interaction type^17
Electron localization function (ELF)	Electrophilic/nucleophilic sites^9,10
Localized orbital locator (tσ)	Electron localization^18

---

Our goal is to merge the interpretive richness and relevance of QTAIM descriptors with powerful geometric learning algorithms. Previous QTAIM/ML approaches incorporated a limited set of hand-selected features based on existing heuristics,^4,19–21 and thus, potentially missed leveraging many useful features. With our approach, we integrate a rich set of over 20 atom and 20 bond critical point features for an exhaustive toolkit of electronic descriptors (Table S1†). Integrating these features into graph neural networks (GNNs) allows for greater applicability to systems with varying chemical structures and unexplored chemical motifs where heuristics have not yet been developed.²² In addition, graphs are a flexible data structure that can readily intake spatial information such as atomic positions and/or bond lengths to further inform predictions. Given the power and ubiquity of geometric learning in chemical spaces, coupling them to electronic structure-informed features could extend their applicability and ability to generalize on smaller datasets.^23–26 Notably, graph neural networks (GNNs) often perform poorly under low data regimes^27,28 — regimes where experimental and high-accuracy quantum chemical calculations may operate and electronic descriptors could offer a strategy for suitable performance. Furthermore, GNNs suffer from poor out-of-domain (OOD) extrapolation and we probe whether QTAIM features can help alleviate this shortcoming.²⁷ We note one other study²⁹ that takes a somewhat similar approach to using QTAIM for geometric machine learning; our work differs by including benchmarks on standard cheminformatic datasets, testing on spin/charge-varying datasets, testing out-of-domain performance, and providing tools for generating and training QTAIM-informed geometric learning models for both molecules and reactions.

We make a few important advances to the utilization of QTAIM in machine learning. First, we create a set of easy-to-use, pythonic tools for computing QTAIM descriptors at scale and using them for machine learning tasks. These tools include high-throughput job-runners for calculating QTAIM values, visualization tools for descriptive statistics, parsing utilities for compiling data into single data structures, and ready-to-use graph neural network architectures. These tools work together in an ecosystem for harnessing QTAIM in geometric learning. We also compute QTAIM values on several datasets chosen for benchmarking or developing algorithms to handle tricky chemical domains with varying charges, spins, and reactivities. In addition, we benchmark the usage of QTAIM features to demonstrate their ability to improve overall model performance, learning on smaller datasets, and out-of-domain predictions. We hope that these contributions can serve as an important foundation for further studies using hybrid QTAIM/ML approaches to tackle machine learning in difficult chemical domains with experimental or small datasets. In addition, these tools can serve as an important basis for developing more advanced QTAIM-enabled machine learning algorithms.

1. Methods

1.1 Quantum chemical calculations

QTAIM calculations build on top of quantum chemical density calculations. Our package can intake any format compatible with Multiwfn³⁰ or Critic2 ³¹ and thus could use a number of DFT codes such as Q-Chem³² or Gaussian.³³ We use ORCA³⁴ as it is open-source, free under academic licenses, and implements a wide range of basis sets and levels of theory. For now, we have implemented options files that allow the user to write a wide-range of custom ORCA input files, including relativistic corrections, individual atomic basis sets, and parallelization options. Generalization to other quantum chemical packages requires new methods for writing input files but otherwise can fit into our ecosystem for high-throughput QTAIM and molecular/reaction graph neural networks. We chose differing levels of theory for our dataset construction, considering the relative expense of computed properties in each dataset — we wanted to ensure that the cost of DFT and subsequent QTAIM calculations did not rival the expense of computed properties. We outline the different levels of theory below for each dataset.

1.2 QTAIM calculations

Our current implementation uses critic2 ³¹ or Multiwfn³⁰ to handle QTAIM calculations. All datasets here, however, leverage Multiwfn due to its richer set of QTAIM descriptors, including spin information, energies, etc. (Table S1†). These calculations intake any density file format supported by Multiwfn including .cube and .wfn files and yield a single text file for analysis.

1.3 Dataset construction

We format our datasets into standard JSONs constructed either by standard tools from RDKit³⁵ and pymatgen⁶ or by our built-in scripts for construction and formatting (Fig. 1). These scripts parse molecular charge and spin information from xyz files and produce a database. Initial guesses at bonding can optionally be handled by RDKit. The resulting JSON includes the following notable data structures in order to write DFT input files and perform subsequent machine learning: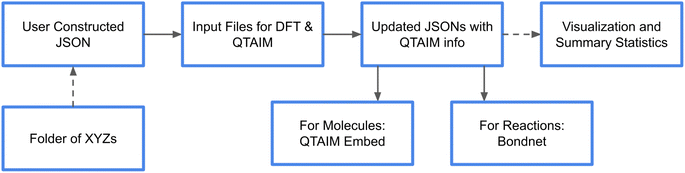

Fig. 1 An outline of the current workflow for QTAIM property prediction. Users can either start from a JSON of data or use our helpers to parse xyz files into compatible JSON formats.

Molecules (pymatgen molecules) – Pymatgen molecules, without bonding information, used to featurize the molecules for machine learning and write input files with coordinates at atomic sites.

Molecular graphs (pymatgen MoleculeGraphs) – Pymatgen molecular graphs with added bonding information from molecules.

IDs – index of the molecule in the JSON, can be user specified.

Names (for xyz construction) – name of the file from which a datapoint is constructed.

Spin (if specified) – molecular spin state, otherwise singlet.

Charge (if specified) – molecular charge, otherwise neutral.

Bonds (if specified) – We include an option to specify bonding with RDKit's tools but any user-specified bonds work. These bonds can be optionally overwritten by the bond paths determined by QTAIM.

Given the dataset, our script reads in several options, including information on writing DFT input files, QTAIM parser information, and reaction/molecular options. Users can also specify custom options for executables used in running DFT and/or QTAIM calculations. Folders of input files become jobs for a high-throughput job manager/runner in our package. This runner randomly selects folders and checks for pending QTAIM and DFT jobs. Incomplete tasks are performed and the implementation allows for concurrent jobs on high-performance computing resources.

Finalized directories of QTAIM properties contain either JSONs (critic2) or text files (Multiwfn) with QTAIM information including bonding, energetics, and critical point types. Our script intakes these folders and merges QTAIM information into the original JSON. This merge process involves parsing a user-specified set of QTAIM features, and optionally, imputation. We compile all of the QTAIM values for the dataset and use them to compute mean and median values for imputation where information is missing or where QTAIM and prior bond definitions are not in alignment. The user can also update bond definitions using QTAIM BCPs and whether to parse the dataset as a dataset of molecules or reactions. Atom and bond mappings are computed between final bond definitions and features. This is vital for the construction of reaction-property datasets where atom/bond-mapping across different numbers of reactions/products is non-trivial. The finalized output of these processes is a new JSON containing pymatgen objects, bonding information, QTAIM features, mappings, and optional features such as spin and charges. The entire pipeline allows for QTAIM calculations at scale, and as such, we include several large datasets for further experimentation and development.

1.4 Dataset visualization and statistics

Included in our toolkit are also basic visualization scripts that compute summary statistics such as mean, mode, median for debugging and visualization purposes. We compute these features for each element in the dataset and output a breakdown of statistics at the elemental level as well. For visualization, we break down QTAIM descriptors at the global and element level with log scaling for highly-variable features. These tools were created to allow users to filter features with low variability and heavy outliers.

2. Datasets

We selected key datasets across varying levels of computational complexity and computed properties to highlight the flexibility of our package. Key considerations for these datasets and the level of theory for subsequent QTAIM calculations were the following: first, we wanted to highlight important features of our package, such as support for reactions and spin/charge. Second, we informed the level of theory in our QTAIM calculations with the relative expense of computed properties. In other words, inexpensive orbital energies of organic molecules only justified a modest level of theory in our dataset construction. Conversely, more expensive vertical excitation or vibrationally-corrected free energies on metal-containing complexes justified more expensive calculations. We wanted to reflect real use cases where computing descriptors should be considerably less expensive than the properties they are used to predict. Finally, we sought to integrate datasets that are either already in use by the community or could be adopted readily to test the limits of new models on domains such as molecules with varying spins and charges, transition metals, and reactions. Towards understanding the relationship of individual QTAIM features to individual target variables, we conducted a simple correlatory study. Here we mean-pooled each QTAIM across individual molecules and correlated these values with labels in molecular property datasets. We briefly describe the datasets that we based our QTAIM datasets upon as well as the labels used to test and validate the application of QTAIM descriptors in machine learning.

2.1 QM9

Perhaps the most widely-adopted dataset for structure-to-property benchmarking, QM9 is a dataset of optimized, small organic compounds consisting of 134 000 structures.^36,37 These structures are limited to up to 9 heavy (CONF) atoms and up to 29 atoms including H. We constructed a train-test split of 90/10 and the validation set was constructed from the training set with a split of 80/20 for model selection and hyperparameter tuning. We benchmarked on 3 of the reported properties in the dataset, namely the energy of highest occupied molecular orbital (ε_HOMO), energy of lowest unoccupied molecular orbital (ε_LUMO), and the HOMO–LUMO gap (Δ_ε). We used this limited set as it included only size-intensive properties. Algorithms were trained in a multi-task fashion to predict all three properties. QTAIM properties for this dataset were computed at TPSS³⁸/def2-SVP³⁹ with D3BJ⁴⁰ dispersion. Here we aimed to study the efficacy of QTAIM features at lower levels of theory, given the comparatively low level of theory and cost of computed target values.

2.2 QM8

QM8 encompasses a set of time-dependent density functional theory (TD-DFT) calculations of electronic excited states.^37,41 The dataset contains 22 000 molecules, which are a subset of QM9 with up to 8 CONF atoms, and further refinement for strained geometries. Computed properties include the vertical excitation energies for the two lowest-lying excited states and corresponding oscillator strengths. For benchmarking, we only trained/tested on the excitation energies at second-order approximate coupled-cluster (CC2)⁴²/def2-TVZP⁴³ level of theory, yielding two target variables. We constructed a random train-test split of 90/10 and the validation set was constructed from the training set with a random split of 80/20 for model selection and hyperparameter tuning. Algorithms were trained in a multi-task fashion to predict both properties. QTAIM properties for this dataset were computed at PBE0 ⁴⁴/def2-TZVP³⁹ level of theory. Here we aimed to study the efficacy of QTAIM features at higher levels of theory (hybrid functionals via PBE0) given the expense of vertical excitation properties (labels for machine learning).

2.3 Tox21

The Toxicology in the 21st Century (Tox21) dataset measures the toxicity of 8000 compounds across 12 different toxicity targets including nuclear receptors and stress response pathways.^45,46 Structures in this dataset are provided as SMILES structures with RDKit³⁵ embedding their geometries prior to optimization. GFN2-xTB⁴⁷ further optimized these structures prior to DFT and QTAIM. We constructed a random train-test split of 90/10 and the validation set was constructed from the training set with a split of 80/20 for model selection and hyperparameter tuning. Algorithms were trained in a multi-task fashion to predict all 12 properties (toxicity toward 12 targets). QTAIM properties for this dataset were computed at TPSS³⁸/def2-SVP³⁹ with D3BJ⁴⁰ dispersion following geometry optimization. The dataset consists of various missing values across the 12 labels so we imputed mode values for training but at testing no imputation was performed. Here we aimed to study the efficacy of QTAIM features at high levels of theory given the experimental nature of this dataset. We did, however, use a relatively cheap method for geometry optimizations to probe how robust QTAIM is to the quality of the geometry.

2.4 LIBE

Lithium-ion battery electrolyte (LIBE) is a dataset composed of a diverse set of lithium-ion battery solid electrolyte interface (SEI) species. These structures were generated via fragmentation and combination operations on the principal molecules known to be present in the Li-ion battery SEIs. The dataset contains 17 000 structures of varying spin and charge states “labeled” with both raw and corrected enthalpies, entropies, and free energies.⁴⁸ We used the rigid-rotor harmonic oscillator (RRHO) approximated free energies⁴⁹ as a training target, units are reported in eV as in the original publication (Fig. S2†). To approximate molecular formation energies, we performed an energy correction calculation via linear regression to approximate individual atomic energies at infinite separation (Fig. S3 and Table S4†). We constructed a random train-test split of 90/10 and the validation set was constructed from the training set with a random split of 80/20 for model selection and hyperparameter tuning. The inclusion of the LIBE dataset was also of note as there is currently no benchmark predicting molecular properties on this dataset and it would allow us to test the ability of QTAIM descriptors to generalize across different charge and spin states. LIBE also contains metals with nonstandard bonding interactions – an instance where QTAIM's rigorous bonding definitions should fare well. QTAIM properties for this dataset were computed at TPSS³⁸/def2-SVP³⁹ with D3BJ⁴⁰ dispersion.

2.5 Grambow 2022

To test QTAIM performance on predicting reaction-level properties we benchmarked a dataset recently published by Green et al.⁵⁰ This dataset consists of 12 000 reactions with barrier heights and reaction enthalpies computed at three levels of theory. Reactions in the dataset involve only C, N, O, and/or H atoms with up to 7 heavy atoms. We benchmarked predicting activation energies at the highest level of theory they were computed (CCSD(T)-F12a⁵¹/def2-TZVP³⁹). We constructed a random train-test split of 90/10 and the validation set was constructed from the training set with a random split of 80/20 for model selection and hyperparameter tuning. QTAIM here was computed at TPSS³⁸/def2-SVP³⁹ with D3BJ⁴⁰ dispersion level of theory given the large number of individual molecules in the entire dataset.

3. Models

A host of geometric learning algorithms were developed or adapted to interoperate with our QTAIM generation framework: molecular graph neural networks spanning graph convolutional networks (GCNs), residual convolutions, heterograph graph attention (GAT) layers, ChemProp (albeit only for molecular property predictions with atomic QTAIM features), and a variant of the BondNet architecture for reaction-level property predictions. Further details on each architecture implementation follow.

3.1 Molecular representation

Molecules, and molecules within reactions, are represented similarly as heterographs with atom, bond, and global feature nodes (Fig. 2). Heterographs, as opposed to homographs with bonds as edges, allow for separate relationships between each different edge type and enable the addition of a separate global node type to store important molecular-level information. Graphs (G = (B, A, g)) consist of B as bond information vectors, A is atom-level information, and g is the molecular-level feature vector. This followed prior work that also featurized molecules as complex knowledge graphs.^52–55 Notably, we also intake user information on molecular charge and spin information, and transform it into one-hot encoded vectors in the global feature vector g. Features from the original graph encoding are transformed via iterative message-passing steps to yield an updated molecular graph G′ = (B′, A′, g′) with updated node features B′, A′, g′. These features are embedded into a fixed-size vector prior to a dense, feedforward network for property prediction similar to other molecular property graph neural networks.²⁷

Fig. 2 The heterograph construction of our molecular property prediction algorithm.

3.2 Molecular-property graph neural network

Our graph neural network models rely on complex encoder architectures where raw features are embedded to a fixed-size vector at each node prior to neural message passing. This amounts to a rectifying step that allows for greater parameterization in our models at the node level.⁵² Message passing is then used to update a rich set of features in a graph. The final, updated graph is passed through a global graph pooling operation to readout the graph into a meaningful, learned vector representation (Fig. 3). Under the message passing paradigm, these updates are computed as a function of differentiable update and aggregate functions on neighbor features. These functions can take an arbitrary number of forms and herein lies much of the rich diversity of developed graph neural networks.^56,57 Typically, these functions are applied in various successive rounds to propagate information further across the initial graph. A pitfall lies with the potential of over smoothing, where features become uniform across the graph. This updated graph is then embedded into vectors using one of a number of different methods we implemented to make it amenable to traditional neural networks for supervised learning tasks. These embedding schemes have also been an active area of research with schemes such as set2set,⁵⁸ setTransformers,⁵⁹ and self-attention graph (SAG) pooling⁶⁰ created to balance computational complexity with expressiveness. In particular, we implmented MeanPooling, WeightedMeanPooling, self-attention pooling,⁶⁰ and set2set pooling⁵⁹ as a diverse set of pooling approaches.

Fig. 3 The full framework of our molecular property algorithms. Several different message passing and global pooling operations are implemented for intensive and extensive molecular properties.

We implemented several graph neural network architectures in our approach to ensure a wide-range of algorithms were benchmarked with/without QTAIM descriptors. These architectures included different update and pooling functions to ensure that relatively up-to-date models were compared. For update functions, we used traditional graph convolutions,⁶¹ graph attention mechanisms,⁶² and residual convolutions.⁶³ These layers were selected for their diversity and ability to learn at different model depths with attention and residual connections typically being more resistant to oversmoothing.⁶⁴ These layers have use across the chemical structure-to-property domain with strong results in cases including predicting aqueous solubility,⁶⁵ reactivity,⁶⁶ and synthesis cost.⁶⁷ Pooling functions ultimately intake raw or processed graphs and compute a fixed-sized representation for visualization or tasks via a dense neural network. These layers are highly important and vary in complexity from simple sum operations to complex setTransformer architectures incorporating attention and beyond.^59,68 Here we integrate four such operations into our potential space of graph neural networks: global summing, weighted global summing, set2set, and global attention pooling. These layers were selected to span a space of expressiveness and cost for our benchmarking and provide a wide toolkit for future QTAIM-enabled machine learning experiments. In order to merge QTAIM-features with nodes in our heterographs, we parsed Multiwfn's outputs to map features at NCP/BCPs to nodes based on “attractors” that aligned with atomic positions. For BCPs, Multiwfn also outputs NCPs that terminate bond paths, which we parsed to their respective bonds. This avoided any non-nuclear “attractors” (NNAs) appearing as atom nodes in our graphs.

3.3 ChemProp

ChemProp is a flexible framework for computing a host of different molecule-level and reaction-level properties.⁵³ The algorithm incorporates a local embedding from atom/bond features, a graph-level embedding function that transforms finalized representation graphs to a fixed-size vector, and a standard feed-forward neural network for property prediction. We adopted our QTAIM generator to construct atom-level QTAIM features in a format compatible with ChemProp's featurization. Here we limit ourselves to atom-level molecular features, excluding both bonds and reactions due to the inflexibility of ChemProp for user-defined bonds and the added complexity of atom-mappings. Hyperparameter optimization was performed using their convenient Bayesian optimization functionalities.

3.4 BondNet

BonDNet is a reaction-property graph neural network originally constructed for the prediction of reaction ΔG_rxn values in single bond dissociation reactions. It consists of two modules, the graph-to-graph and graph-to-property modules, where each constitute the processing of the original feature graph towards the final prediction. The graph-to-graph module intakes the original knowledge graph G(B, A, g) and transforms it, via successive message-passing steps, to the final graph G(B′, A′, g′). Updates are performed on each separate reaction molecule prior to the construction of a global reaction difference graph. The reaction graph is constructed via the mapping of atoms and bonds in reactants to corresponding atoms in the products prior to a simple subtraction. The finalized reaction graph is embedded into a fixed-size vector via a global embedding set2set layer prior to feed-forward neural network layers for property prediction. Here QTAIM descriptors offer a promising avenue for highlighting nuanced changes in electronic structure between products and reactants, even at distal locations from the reaction site. We adapted our code to work natively with newer variants of the BonDNet architecture. This architecture was recently updated to improve generalizability for custom user descriptors and arbitrary reaction molecularity – essential quality of life updates that make it a prime model for testing an integrated QTAIM/ML approach.⁶⁹ Furthermore, this updated architecture allows for custom bond definitions, thus, we integrate QTAIM bond path connectivities to define bonds within our molecular graphs.

3.5 Benchmarks

QTAIM-enabled algorithms were pitted against a diverse set of molecular-graph property algorithms. Our aim here was not necessarily to outperform SOTA models but to demonstrate that models with QTAIM features could approach these models in performance and thus serve as the basis for more-advanced QTAIM-enabled algorithms. Benchmarks on molecular properties were performed using SchNet, PaiNN, and ChemProp. We briefly overview SchNet and PaiNN here. The SchNet architecture introduced the concept of continuous convolution filters. These convolution operations allow for the arbitrary position of atoms within the model representation and give SchNet improved performance over their direct legacy algorithms, Deep Tensor Neural Networks (DTNNs). PaiNN is an equivariant neural network architecture, it couples ideas from SchNet to new representations, enabling more data-efficient learning. Perhaps the biggest algorithmic development of PaiNN is the use of equivariant message passing functions that incorporate not only rotationally invariant distances but also rotationally equivariant neighbor directions as part of the message-passing update function. This allows the algorithm to predict tensorial properties, as well as generalize well with less data. Its efficient representations also allow for effective models with fewer parameters and shorter inference times. We note that our baseline GNN architectures are comparatively less sophisticated than many of these algorithms, and as such, we hope to bridge performance gaps with these models via the inclusion of QTAIM features alone. These models were benchmarked competitively on QM8 and QM9 as the remaining datasets required spin/charge information or covered reaction-level properties.

Other benchmarks to note are the use of our QTAIM-enabled algorithms vs. those without on the LIBE, Green, and Tox21 datasets. Here we opted to remove the above benchmark datasets to avoid added complexities in treating classification tasks, reaction-property predictions, and spin/charge-varying molecules with algorithms that cannot encode this information. For Tox21, both models sets of models perform comparably and we include both the dataset and performance in ESI (Table S25†). To gauge the effect of QTAIM on model learning, we benchmarked model test performance on LIBE, QM8, and QM9 given 10², 10³, 10⁴, (and 10⁵ for QM9) training data points. These learning curves are often used in machine learning to measure the learning capacity of a model and extrapolate to how accuracy varies with dataset size (Table 2).

Table 2 Test performance (MAE, Hartrees) of various geometric learning algorithms on orbital energies in QM9

Model	HOMO	LUMO	Gap	Average
SchNet	0.0109	0.0115	0.0151	0.0125
PaiNN	0.0136	0.0148	0.0158	0.0147
ChemProp (w/out QTAIM)	0.0028	0.0031	0.0038	0.0032
Our best (w/out QTAIM)	0.0058	0.0076	0.0090	0.0075
ChemProp (w/QTAIM)	0.0030	0.0035	0.0042	0.0036
Our best (w/QTAIM)	0.0028	0.0036	0.0042	0.0035

---

4. Results and discussion

In addition to the experiments that follow, we evaluated a classifier variant of our model on the Tox21 dataset with and without QTAIM features (Table S25†). Here we see marginal but comprehensive improvements in performance with QTAIM features.

4.1 QM9

Evaluating model performance on QM9, we note how our QTAIM-enhanced models are able to compete with the performance of the otherwise best-performing model, ChemProp (Table 3). We also augmented ChemProp with QTAIM NCP-only features but here we actually see a slight drop in testing performance. We emphasize that ChemProp does not include vital BCP QTAIM features and thus does not leverage the comprehensive set of QTAIM descriptors. Even here, the performance difference between QTAIM-enabled and non-QTAIM ChemProp models is quite small and also suggests the model is near or at capacity – not that QTAIM features are not informative. Analyzing scatterplots of QM9 test performance, we can also determine the robustness of QTAIM-informed models with few outlier points between predicted and true labels. Interestingly, our outlier points are generally some of the heaviest molecules in QM9. It is also worth noting that the QM9 dataset constitutes a comparatively-simple dataset for machine learning with the difference between the top-performing models being relatively small. Observing correlations of target variables to individual QTAIM values – QM9 exhibits the highest correlations of any of our datasets (though still quite low). Here several values emerge as important, these include electron localization values and bond Lagrangian values (Fig. S44 and S45†).

Table 3 Test performance (MAE, Hartrees) of various geometric learning algorithms on orbital energies in QM8

Model	E1-CC2	E2-CC2	Average
SchNet	0.517	0.379	0.448
PaiNN	0.0133	0.0145	0.0139
ChemProp (w/out QTAIM)	0.0373	0.0270	0.0322
Our best (w/out QTAIM)	0.0130	0.0130	0.0130
ChemProp (w/ QTAIM)	0.0052	0.0060	0.0056
Our best (w/ QTAIM)	0.0062	0.0067	0.0064

---

In addition, we examine the learning curves of our models with and without QTAIM features. To give each set of models even footing, we conducted hyperparameter tuning on models with and without QTAIM features separately and thus these curves (and overall test performance) correspond to the best models for each descriptor set. We see QTAIM yielding a distinctive improvement in performance in the low data regime with consistent advantages in test performance across all training set sizes (Fig. S30†). Beyond 10 000 structures, however, there is little improvement in test performance of the QTAIM-informed model suggesting the model is at capacity or that mainly irreducible errors remain.

4.2 QM8

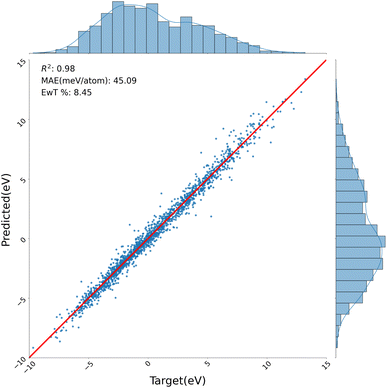
Across both tasks (first and second vertical excitation energies) QTAIM-enabled models were the top-performing algorithms (Table 3). ChemProp and our models with QTAIM yielded improved test errors over all other models with a notable gap in performance between QTAIM/ML models and all others. Again, we note that ChemProp's QTAIM featurization was limited to only QTAIM NCP features, and even then, this led to increased performance. Finally, when examining predicted versus true plots of our models, it becomes evident that QTAIM-enhanced models exhibit greater robustness, displaying fewer outlier residual errors compared to their non-QTAIM equivalent (Fig. S5, S6, S52, and S53†). Our correlation study (Fig. S42 and S43†) also shows remarkably low correlations between vertical excitation energies and any one QTAIM value – underlying the relative complexity of this property. We do note that some of the highest correlations are with BCP QTAIM features, suggesting ChemProp could improve with these features (Table 4).

Table 4 Test performance of our geometric learning algorithms on formation energies in LIBE

Model	MAE (meV per atom)
QTAIM-embed (ours, No QTAIM)	76.26
QTAIM-embed (ours, QTAIM)	45.09

---

The learning curves further reinforce the advantage of QTAIM-enabled models, illustrating a consistent improvement in performance across varying training set sizes (Fig. S29†). Additionally, the learning curves for both QTAIM and non-QTAIM models do not appear to reach saturation, implying that additional training data could potentially lead to further reductions in prediction errors for both types of models (Fig. 4).

Fig. 4 Parity plot of our model, with QTAIM, on the QM9 test set. The equivalent model, without QTAIM can be found in S8.†

4.3 LIBE

The LIBE dataset presents a more challenging task due to its inclusion of spin-varying and charged species. Moreover, the dataset exhibits a wide range of molecular free energies which further add to the difficulty of learning energetics here. In pitting QTAIM/ML versus non-QTAIM models we note that our non-QTAIM models do directly describe spin and charge as one-hot encoded global features while the QTAIM/ML models add QTAIM features, including α spin, β spin, and spin density at each critical point, to further inform learning. Both models perform quite well with the top QTAIM/ML model yielding a reduced error on formation energies from 76.26 meV per atom to 45.09 meV per atom and an increased proportion of predicted energies within chemical accuracy to true labels (8.5% vs. 5.4%) versus its non-QTAIM equivalent (Table 5). Analyzing correlation values (Fig. S47†) we see again that electron localization functions and electrostatic potentials, specifically at BCPs, emerge as the most correlated features to formation energies. This interpretation in agreement with previous studies that leveraged both electron localization and electrostatic potential values to analyzed bonding strength and orbital interactions.^70,71

Table 5 MAE performance of our model with/without QTAIM on Green 2022 barriers

Model	Test MAE (kcal mol^−1)
BondNet (w/out QTAIM)	4.18
BondNet (w/QTAIM)	2.60

---

In addition, no discernible trends can be gleaned across predicted vs. true values for the QTAIM/ML models while non-QTAIM models perform slightly worse on low spin, positively-charged species (Fig. 5 and S12†). Learning curves here present a more obfuscated picture with the non-QTAIM model outperforming the QTAIM/ML model on the smallest training set (Fig. S26†). This narrative shifts at larger dataset sizes as the QTAIM/ML model, again, outperforms the top non-QTAIM model. Here, there is no pronounced improvement in the learning curves between the two sets of models as QTAIM models have a slightly more aggressive learning curve – indicative of their ability to increase model generalizability at lower data regimes.

Fig. 5 Parity plot of our model, with QTAIM, on the LIBE test set. The equivalent model, without QTAIM can be found in S12–S14.†

4.4 Green 2022

The Green 2022 dataset represents a comprehensive compilation consisting of approximately 12 000 gas-phase reactions, meticulously calculated at high-level theory (CCSD(T)-F12a⁵¹/def2-TZVP³⁹). This dataset was constructed to facilitate transfer learning approaches by incorporating two lower levels of theory (ωB97X-D3 (ref. 72)/def2-TZVP,⁴³ and B97-D3 (ref. 73)/def2-mSVP⁴³). Remarkably, our experimental results demonstrate a performance on par with the original authors' findings, achieving comparable results without necessitating a transfer learning approach at lower levels of theory.⁷⁴ Notably, the original authors employ significantly higher levels of theory for transfer learning, specifically ωB97X-D3/def2-TZVP⁴³ and B97-D3 (ref. 73)/def2-mSVP.⁴³ In contrast, our descriptors are limited to the TPSS³⁸/def2-SVP⁴³ level, yet they enable us to attain comparable performance. It would be intriguing for the original authors to explore and compare the transfer learning process from the lowest level of theory to the highest level of theory (without the intermediate-level of theory). This would effectively simulate the relative performance of QTAIM versus transfer-learning labels at inference time. Furthermore, when evaluating their non-transfer learned models, it's observed that those roughly align (4.17 kcal mol⁻¹versus 4.07 kcal mol⁻¹) with our Bondnet training without QTAIM integration (Table 6). The incorporation of QTAIM features with BondNet, however, elevates its performance, surpassing the non-transfer learned models with a reduced mean absolute error (MAE) of 2.6 kcal mol⁻¹ (Fig. S15 and S16†). This discrepancy underscores the advantageous impact of QTAIM integration in enhancing model accuracy and predictive capabilities.

Table 6 Test performance (MAE, Hartrees) of various geometric learning algorithms on orbital energies in QM9 OOD

Model	HOMO	LUMO	Gap	Average
Our best (w/out QTAIM)	0.0177	0.0320	0.0376	0.0291
Our best (w/ QTAIM)	0.0155	0.0243	0.0330	0.0243

---

4.5 OOD tests

Beyond a measure of train/test performance, we wanted to gauge whether QTAIM could functionalize machine learning models to make out-of-domain predictions. We conducted two sets of experiments here. First, we trained/tested models with/without QTAIM features on the LIBE dataset where the training set was trimmed to only include examples of neutral molecules and the test set was refined to only include test molecules with charges ∈ {−1, 1}. The baseline model included only a one-hot encoding of molecular charge in the global feature node; the QTAIM-enabled model adds QTAIM features to the model. None of the prior benchmark models include native support for spin and charge; therefore we only conducted this experiment on our own architecture. Second, we tested model performance of our GNNs with/without QTAIM features on sub-selected variants of QM9 train/test sets. Here we stratified the datasets along molecular size: molecules in the training set with fewer than 13 atoms included were included in the OOD training set and those with more than 13 atoms in the original test set included in the OOD test set.

For QM9 stratification, there is a significant decline in model performance between both QTAIM and non-QTAIM models (Fig. S23 and S24†). Despite this, QTAIM-informed models demonstrate a moderate ability to generalize to much larger molecules despite being trained entirely on small molecules. We also note that the filtering of the QM9 dataset to only molecules with fewer than 13 atoms results in a training set of only 4000 molecules. This comparatively small (2 orders of magnitude smaller than the full QM9 test set) training set also shows how QTAIM could be an effective tool for leveraging smaller datasets. We note the systematic overprediction of the LUMO/gap energies and underprediction of the HOMO energies in the QTAIM informed model, and couple this to the mean values for each label in the training and testing set: −0.263 Ha, −0.057 Ha, 0.206 Ha in training and −0.239 Ha, 0.0131 Ha, 0.252 Ha in the test set for HOMO, LUMO, gap respectively (Fig. S23 and S24†). Here these systematic changes can be partially attributed to the difference between the two label distributions as well as to the model itself. The mean absolute error (MAE) values highlight the effectiveness of QTAIM, with an average MAE of 0.0243 Ha compared to 0.0291 Ha without QTAIM (Table 7). LIBE OOD tests also show a marked drop in testing performance, though not to the extent of the QM9 OOD test (Table 7). The QTAIM model here remains quite serviceable while the model without QTAIM features is drastically worse versus in-domain testing. Changes in performance can be partially attributed to the reduction in training data (only 5200 molecules in training). This notion is somewhat qualified by our learning tests (Fig. S26†) where non-QTAIM models had better test errors (<125 meV per atom) with only 1000 training examples. Notably, both models exhibited a trend of overpredicting for positively charged molecules and underpredicting for those with a −1 charge, yet this deviation was less pronounced in QTAIM-informed models where a greater portion of test examples were within chemical accuracy (2.88% vs. 1.35%) (Fig. 6). These results show that QTAIM can be an effective method for improving model robustness in out-of-domain experiments, especially in the context of charged species.

Table 7 Test performance of our geometric learning algorithms on formation energies in LIBE OOD

Model	MAE (meV per atom)
QTAIM-embed (ours, No QTAIM)	191.65
QTAIM-embed (ours, QTAIM)	119.13

---

Fig. 6 Parity plot of our model, with QTAIM (a) and without QTAIM (b).

5. Conclusions

Here we present a framework for leveraging QTAIM descriptors as general, robust features for geometric machine learning tasks. Our framework extends to both molecular and reaction-level predictive tasks, making it applicable for a wide-range of use cases. We created tools for both high-throughput calculation of QTAIM descriptors and a custom machine learning package for easily implementing models with these features.

Furthermore, we performed extensive testing to demonstrate how QTAIM can functionalize machine learning models to perform better on out-of-domain tasks and smaller datasets. In the case of QM8, our test showed that QTAIM features helped both our architectures and ChemProp improve model performance given identical datasets – suggesting our featurization package could be used with outside machine learning models as well. In the future, we plan on writing more “translation” functionalities to allow users of other architectures to leverage QTAIM features for their learning tasks.

Future work in this space should see further integration beyond algorithms to include more databases and DFT codes. For example, the native dovetailing of this software into the larger Materials Project ecosystem could see QTAIM integrated into their workflows. At present, the Materials Project only natively supports Q-Chem³² (for molecular DFT) as a DFT software – a commercial software we aimed to avoid to increase accessibility. Additional work could also see the integration of input files and execution scripts for other DFT packages such as Gaussian, NWChem, etc. We also implement reaction parsing and processing with compatibility for BondNet and ChemProp (to a lesser extent) but native dataset compatibility for more algorithms could facilitate benchmarking and development.

Also in development are graph-neural networks that could leverage QTAIM-descriptors while avoiding computationally-expensive message-passing graph neural networks. The aim here would be to rely on QTAIM descriptors to capture distal relationships between nodes (atom, bonds) rather than using iterative message-passing steps to achieve this task. From a conceptual DFT standpoint, the native integration of parsers and data structures that support ring and cage critical points would be beneficial.

Data availability

Code for generating QTAIM datasets can be found at: https://github.com/santi921/qtaim_generator. Code for performing molecular machine-learning can be found at: https://github.com/santi921/qtaim_embed. Code for reaction-property machine-learning can be found at: https://github.com/santi921/bondnet. Datasets are available here: https://figshare.com/projects/qtaim-generator/196192.

Author contributions

S. V. contributed to conceptualization, analysis, writing, visualization, validation, methodology, and software. W. G. contributed in conceptualization, writing, and software. A. A. contributed resources, supervision, and writing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. V. was supported by the Department of Energy Computational Science Graduate Fellowship under grant DE-SC0021110. This work was supported by the NSF CHE-2203366 grant to A. N. A.

Notes and references

1. R. F. W. Bader, Chem. Rev., 1991, 91(5), 893–928.
2. C. F. Matta and A. A. Arabi, Future Med. Chem., 2011, 3, 969–994.
3. S. Rojas, O. Parravicini, M. Vettorazzi, R. Tosso, A. Garro, L. Gutiérrez, S. Andújar and R. Enriz, Eur. J. Med. Chem., 2020, 208, 112792.
4. S. Vargas, M. R. Hennefarth, Z. Liu and A. N. Alexandrova, J. Chem. Theory Comput., 2021, 17, 6203–6213.
5. U. J. Rangel-Peña, L. A. Zárate-Hernández, R. L. Camacho-Mendoza, C. Z. Gómez-Castro, S. González-Montiel, M. Pescador-Rojas, A. Meneses-Viveros and J. Cruz-Borbolla, J. Mol. Model., 2023, 29, 217.
6. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
7. R. F. W. Bader and C. F. Matta, Inorg. Chem., 2001, 40, 5603–5611.
8. L. J. Farrugia, C. Evans, D. Lentz and M. Roemer, J. Am. Chem. Soc., 2009, 131, 1251–1268.
9. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
10. Y. Grin, A. Savin and B. Silvi, The ELF Perspective of Chemical Bonding, 2014,  DOI:10.1002/9783527664696.ch10.
11. R. F. W. Bader, P. J. MacDougall and C. D. H. Lau, J. Am. Chem. Soc., 1984, 106, 1594–1605.
12. P. Balanarayan, R. Kavathekar and S. R. Gadre, J. Phys. Chem. A, 2007, 111, 2733–2738.
13. S. R. Gadre, C. H. Suresh and N. Mohan, Molecules, 2021, 26, 3289.
14. P. Carpio-Martínez, J. E. Barquera-Lozada, A. M. Pendás and F. Cortés-Guzmán, ChemPhysChem, 2019, 21, 194–203.
15. D. I. Ramírez-Palma and F. Cortés-Guzmén, Phys. Chem. Chem. Phys., 2020, 22, 24201–24212.
16. F. Cortés-Guzmán, J. I. Rodríguez and J. S. Anderson, in Introduction to QTAIM and Beyond, Elsevier, 2023, pp. 1–19.
17. B. Niepötter, R. Herbst-Irmer, D. Kratzert, P. P. Samuel, K. C. Mondal, H. W. Roesky, P. Jerabek, G. Frenking and D. Stalke, Angew. Chem., Int. Ed., 2014, 53, 2766–2770.
18. H. Schmider and A. Becke, J. Mol. Struct.: THEOCHEM, 2000, 527, 51–61.
19. E. E. Ondar, M. V. Polynski and V. P. Ananikov, ChemPhysChem, 2023, 24, e202200940.
20. M. Gallegos, J. M. Guevara-Vela and M. Pendás, J. Chem. Phys., 2022, 156, 014112.
21. V. V. Petrova, A. V. Domnin, Y. B. Porozov, P. O. Kuliaev and Y. V. Solovev, J. Comput. Chem., 2023, 45, 170–182.
22. W. L. Hamilton, Synthesis Lectures on Artificial Intelligence and Machine Learning, 2020, vol. 14, pp. 1–159.
23. J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural Message Passing for Quantum Chemistry, 2017.
24. J. Gasteiger, J. Groβ and S. Günnemann, Directional Message Passing for Molecular Graphs, 2022.
25. Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530.
26. S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453.
27. S. M. Vadaddi, Q. Zhao, B. M. Savoie, ChemRxiv, 2023,  DOI:10.26434/chemrxiv-2023-tdl2v.
28. M. Wen, S. M. Blau, X. Xie, S. Dwaraknath and K. A. Persson, Chem. Sci., 2022, 13, 1446–1458.
29. C. Isert, K. Atz, S. Riniker and G. Schneider, RSC Adv., 2024, 14, 4492–4502.
30. T. Lu and F. Chen, J. Comput. Chem., 2011, 33, 580–592.
31. A. Otero-de-la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
32. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince III, R. A. DiStasio Jr, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard III, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock III, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian – Revision C.01, Gaussian Inc., Wallingford CT, 2016.
34. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
35. RDKit: Open-source Cheminformatics, https://www.rdkit.org.
36. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022.
37. L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875.
38. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
39. A. Hellweg and D. Rappoport, Phys. Chem. Chem. Phys., 2015, 17, 1010–1017.
40. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
41. R. Ramakrishnan, M. Hartmann, E. Tapavicza and O. A. von Lilienfeld, J. Chem. Phys., 2015, 143, 1.
42. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
43. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
44. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
45. A. Mayr, G. Klambauer, T. Unterthiner and S. Hochreiter, Front. Environ. Sci., 2016, 3, 1.
46. R. Huang, M. Xia, D.-T. Nguyen, T. Zhao, S. Sakamuru, J. Zhao, S. A. Shahane, A. Rossoshek and A. Simeonov, Front. Environ. Sci., 2016, 3, 1.
47. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
48. E. W. C. Spotte-Smith, S. M. Blau, X. Xie, H. D. Patel, M. Wen, B. Wood, S. Dwaraknath and K. A. Persson, Sci. Data, 2021, 8, 203.
49. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
50. K. Spiekermann, L. Pattanaik and W. H. Green, Sci. Data, 2022, 9, 417.
51. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
52. M. Wen, S. M. Blau, E. W. C. Spotte-Smith, S. Dwaraknath and K. A. Persson, Chem. Sci., 2021, 12, 1858–1868.
53. E. Heid, K. P. Greenman, Y. Chung, S.-C. Li, D. E. Graff, F. H. Vermeire, H. Wu, W. H. Green and C. J. McGill, J. Chem. Inf. Model., 2023, 64, 9–17.
54. C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572.
55. P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro, R. Faulkner, C. Gulcehre, F. Song, A. Ballard, J. Gilmer, G. Dahl, A. Vaswani, K. Allen, C. Nash, V. Langston, C. Dyer, N. Heess, D. Wierstra, P. Kohli, M. Botvinick, O. Vinyals, Y. Li and R. Pascanu, Relational Inductive Biases, Deep Learning, and Graph Networks, 2018.
56. K. T. Schütt, O. T. Unke and M. Gastegger, Equivariant Message Passing for the Prediction of Tensorial Properties and Molecular Spectra, 2021.
57. K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890.
58. O. Vinyals, S. Bengio and M. Kudlur, Order Matters: Sequence to Sequence for Sets, 2016.
59. J. Lee, Y. Lee, J. Kim, A. R. Kosiorek, S. Choi and Y. W. Teh, Set Transformer: A Framework for Attention-based Permutation-Invariant Neural Networks, 2019.
60. J. Lee, I. Lee and J. Kang, International Conference on Machine Learning, 2019, pp. 3734–3743.
61. T. N. Kipf and M. Welling, Semi-Supervised Classification with Graph Convolutional Networks, 2017.
62. P. Veličković , G. Cucurull, A. Casanova, A. Romero, P. Liò and Y. Bengio, International Conference on Learning Representations, 2018.
63. K. He, X. Zhang, S. Ren and J. Sun, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016.
64. T. K. Rusch, M. M. Bronstein and S. Mishra, A Survey on Oversmoothing in Graph Neural Networks, 2023.
65. C. W. Coley, R. Barzilay, W. H. Green, T. S. Jaakkola and K. F. Jensen, J. Chem. Inf. Model., 2017, 57, 1757–1772.
66. K. Riedmiller, P. Reiser, E. Bobkova, K. Maltsev, G. Gryn’ova, P. Friederich and F. Gräter, Chem. Sci., 2024, 15, 2518–2527.
67. R. Sanchez-Garcia, D. Havasi, G. Takács, M. C. Robinson, A. Lee, F. von Delft and C. M. Deane, Digital Discovery, 2023, 2, 103–111.
68. A. M. Schweidtmann, J. G. Rittig, J. M. Weber, M. Grohe, M. Dahmen, K. Leonhard and A. Mitsos, Comput. Chem. Eng., 2023, 172, 108202.
69. R. D. Guha, S. Vargas, E. W. C. Spotte-Smith, A. R. Epstein, M. C. Venetos, M. Wen, R. Kingsbury, S. M. Blau and K. Persson, AI for Accelerated Materials Design – NeurIPS 2023 Workshop, 2023.
70. D. Ferro-Costas, M. Pendás, L. González and R. A. Mosquera, Phys. Chem. Chem. Phys., 2014, 16, 9249–9258.
71. A. R. E. Mountain and N. Kaltsoyannis, Dalton Trans., 2013, 42, 13477–13486.
72. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
73. A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560.
74. K. A. Spiekermann, L. Pattanaik and W. H. Green, J. Phys. Chem. A, 2022, 126, 3976–3986.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00057a

‡ These authors contributed equally to this work.

---