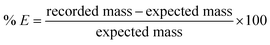Open Access Article
Open Access ArticleOptimization of liquid handling parameters for viscous liquid transfers with pipetting robots, a “sticky situation”†
Pablo
Quijano Velasco
 *a,
Kai Yuan Andre
Low
*a,
Kai Yuan Andre
Low
 b,
Chang Jie
Leong
b,
Chang Jie
Leong
 a,
Wan Ting
Ng
a,
Selina
Qiu
a,
Shivam
Jhunjhunwala
a,
Bryant
Li
a,
Anne
Qian
a,
Kedar
Hippalgaonkar
a,
Wan Ting
Ng
a,
Selina
Qiu
a,
Shivam
Jhunjhunwala
a,
Bryant
Li
a,
Anne
Qian
a,
Kedar
Hippalgaonkar
 ab and
Jayce Jian Wei
Cheng
ab and
Jayce Jian Wei
Cheng
 *a
*a
aInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), Singapore 138634, Singapore. E-mail: pablo_quijano_velasco@imre.a-star.edu.sg; jayce_cheng@imre.a-star.edu.sg
bDepartment of Materials Science and Engineering, Nanyang Technological University, Singapore 117575, Singapore
First published on 17th April 2024
Abstract
Automated air-displacement pipettes have become a standard equipment for the transfer of liquids in laboratory settings. However, these tools fail to perform accurate and precise transfers of liquids with viscosities greater than 100 cP. In this study, we report a systematic protocol for optimizing the liquid-handling parameters of automated pipettes to achieve accurate and precise transfers of viscous liquids (within 5% of percentage transfer error) with viscosities as high as 1275 cP using minimal transfer times. The protocol is based on the iterative gravimetric testing of different combinations of aspiration and dispense rates obtained by a Multi-Objective Bayesian Optimization (MOBO) algorithm. We demonstrate that optimal solutions obtained through MOBO can match or outperform solutions derived from human intuition, showing a consistent performance even when different pipetting equipment and tip geometries are used. Finally, we demonstrate that the protocol can be performed in a fully automated, closed-loop fashion by integrating an automated mass balance, increasing the manpower efficiency of the method. This offers a valuable advancement in the accurate manipulation of highly viscous liquids, with broad applications for the automation of various laboratory experiments.
Introduction
Automation of wet chemistry experiments has shown the potential to accelerate chemical discovery by increasing efficiency, throughput, safety, and repeatability of results. Currently, to automate chemical experiments researchers must buy or build different tools that are put together as modules, each replicating a single task normally performed in laboratory settings for a specific experiment (such as solid and liquid mass transfer, heating, stirring, filtration, etc.). While a plethora of automated tools are now commercially available or have been reported in the literature,1–7 many basic tasks that are performed in a laboratory setting remain challenging to implement through automated methods. In particular, the transfer of liquids with viscosities larger than 100 cP is a task that is still challenging to automate,8 while being of high relevance to the fields of biology, polymer, and formulation sciences.Air-displacement pipettes have become a ubiquitous tool in laboratory settings. The working principle of air-displacement pipettes can be divided in an aspiration and a dispense step. During aspiration, the piston is first protracted to displace a target volume of air within the pipette barrel. While the piston is held in place, the pipette tip is placed inside a vessel containing the target liquid to be transferred, leaving an air-cushion between the piston and the liquid. Afterwards, the piston is retracted creating a negative pressure difference between the air cushion within the pipette barrel and the atmosphere, which causes the flow of liquid into the pipette tip until the pressure difference has been equalized. Finally, during the dispense step the piston is once again protracted compressing the air-cushion inside the pipette barrel and raising the internal pressure of the system. Due to the force applied by the plunger movement, the liquid is expelled from the pipette tip until the pressure inside the pipette barrel is once again equalized with the atmosphere. Today there is a wide range of affordable fully automated electronic air-displacement pipettes commercially available such as the Opentrons OT2 platform, Hamilton ZEUS, Sartorius rLine series and Tricontinent Air-Z series. However, these tools are rated by the manufacturers for the transfer of liquids with viscosities less than 100 cP due to the observation of transfer errors when handling liquids with high viscosities.
When air-displacement pipettes are used to transfer viscous liquids, there is a high likelihood of undesirable occurrences happening during each of the transfer steps (Fig. 1). The first issue arises during aspiration when the piston moves much faster than the liquid flow into the pipette tip. When this event occurs, the pipetting robot will move prematurely out of the liquid causing air to flow into the tip due to the unequalized pressure difference between the pipette barrel and the atmosphere. This leads to an incomplete aspiration and if the volume of air is large enough, it may even break down the liquid meniscus and cause an uncontrolled aspiration event that may damage the equipment. Similarly, during the dispense step it is crucial that the speed of the piston closely matches the flow rate of the liquid to avoid a rapid increase in the pressure of the air cushion located between the plunger and the liquid. If this condition is not maintained, the pressure build-up causes the meniscus of the liquid to break, leading to an uncontrolled dispense of the liquid. Thus, it is key to select aspiration and dispense rates that match the flow rate of the liquid within the pipette tip to enable the accurate transfer of viscous liquids with air-displacement pipettes.
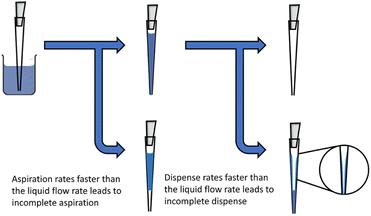 | ||
| Fig. 1 Schematic representation of the challenges faced by air-displacement pipettes during the aspiration and dispense step. | ||
Opentrons Labworks have published applications notes and released webinars to help researchers find appropriate liquid handling parameters for the transfer of viscous liquids using their OT2 pipetting robot.9 Their proposed optimization protocol consists in non-systematic trial-and-error testing of different combinations of parameters that are set by the user's intuition. This approach is likely to lead to results that depend mainly on the prior experience of the experimenter and the resulting parameters may not be fully optimized due to lack of extensive exploration of the parametric space. In addition, this methodology does not consider the existence of multiple combinations of aspiration and dispense rates that would satisfy the requirements for accurate transfer of the target liquid (i.e. aspiration and dispense rates slower than the liquid flow rate within the pipette tip). Thus, this protocol may lead to solutions that accurately transfer a liquid in an unnecessarily long transfer time, decreasing the experimental throughput of the workflow. Hence, there is a need for protocols that aim to optimize the liquid handling parameters of viscous liquids that consider both transfer error and transfer time as optimization objectives.
Here, we propose a new protocol that allows researchers to obtain optimized liquid handling parameters (defined by aspiration and dispense rates) capable of transferring liquids with viscosities as high as 1275 cP within 5% of percentage transfer error. This protocol enables the optimization of liquid handling parameters using suggestions generated by a Multi-Objective Bayesian Optimization (MOBO) algorithm that aims to minimize the absolute value of percentage transfer error and time to transfer 1000 μL. These objectives were formulated in mind for experimentalists to attain accurate liquid handling procedures with minimal transfer time, such that the optimized protocol is amenable for integration into high-throughput setups. The protocol commences with an initialization step that narrows the range of flow rates for aspiration and dispense closer to the optimal values. This is followed by an iterative gravimetric testing procedure that first explores the boundaries of the parametric step and then refines the aspiration and dispense rates using suggestions derived by a MOBO algorithm. We successfully demonstrated the optimization of liquid handling parameters of four viscosity standards ranging from 204 to 1275 cP for two automated pipettes from different manufacturers. The performance of the MOBO was benchmarked against an optimization guided by human intuition. Our results demonstrate that MOBO matches and can outperform human-based intuition by obtaining liquid handling parameters that result in higher accuracy and/or speed of transfer. Finally, we incorporate an automated mass balance to demonstrate full closed-loop optimization of pipetting parameters for liquids with unknown viscosity.
Experimental
Materials and equipment
General-purpose Newtonian fluid viscosity standards of approximately 204, 505, 817 and 1275 cP were purchased from Paragon Scientific and used as received at 25 °C. Full specifications of the viscosity standards can be found in the ESI (Table S1).† Optimization experiments of liquid handling parameters for the transfer of viscous liquid standards were performed on an Opentrons OT-2 robot using a single channel P1000 gen2 pipette and an in-house assembled platform made of a Sartorius rLine1000 electronic pipette attached to a Dobot M1 SCARA robotic arm (Fig. S1†). The pipette tips used during the experiments were OT-2 1000 μL and Eppendorf epT.I.P.S 1000 for each pipette respectively. To interface with the robotic platforms control-lab-ly (an in-house developed Python package https://pypi.org/project/control-lab-ly/) was used to control the Sartorius rLine1000 pipette and the Dobot M1 SCARA robotic arm. The OT2 robot was controlled via Jupyter Notebooks using the Python API from Opentrons. To augment the feasible aspiration and dispense flow rates in the Sartorius rLine1000 pipette, a protocol was implemented using a combination of plunger movement and waiting time to obtain an apparent flow rate; full details of the protocol can be found in the ESI (Section S2.2†). The files used to perform the experiments can be found in our GitHub repository (https://github.com/Quijanove/LiqTransferOptimizer).Gravimetric testing
Gravimetric testing was used to evaluate the accuracy for each combination of liquid handling parameters used during the optimization campaigns. The test started by measuring the height of the viscous liquid column within the glass vial container. After that, the pipette tip was submerged into the source vial at a predetermined distance from the surface of the viscous liquid (15 and 5 mm for P1000 gen2 and rLine1000 respectively). After each transfer, the column height was automatically updated by the expected height decrease after each aspiration (2 mm per mL for the vials used in this study). The pipette was then programmed to aspirate a target volume using a specific aspiration rate. After the aspiration step was completed, the pipette was left idle for a specific number of seconds (5 and 10 seconds for P1000 gen2 and rLine1000 respectively) to allow the pressure of the air cushion between the piston and the liquid to equilibrate. Then, the pipette was moved to touch the four walls of the vial with its tip to remove any excess of liquid coating its exterior. Regardless of the volume of liquid actually aspirated with these parameters, the target volume was then dispensed using a specific dispense rate at a position of 5 mm below the top of a second glass vial that was previously weighed. After the dispense step was completed, the pipette was once again left idle for a specific number of seconds (5 and 10 seconds for P1000 gen2 and rLine1000 respectively). After the transfer of the target volume, the pipette was moved to the top of the source container. The change in mass in the destination vial was recorded after the transfer of the viscous liquid by either an automated balance or by manually measuring with a standard balance. The percentage transfer error (% E) was calculated as follows:where the expected mass value was calculated from the liquid density and the target volume for the transfer.
The pipette was programmed to perform six cycles of blowouts and piston-homing into the source vial to eliminate any remaining liquid still present after the transfer. For each combination of aspiration and dispense rates, this procedure was used to test the transfer of 1000, 500 and 300 μL. Finally, the average % E for the transfers of the three volumes was calculated for each set of parameters. A detailed workflow diagram of the gravimetric testing can be found in the ESI (Fig. S3).†
Calibration of optimized liquid handling parameters
Once a set of optimal aspiration and dispense rates were selected, the accuracy and precision of the transfers were obtained through a modified protocol based on ISO8655.10 At the beginning of each calibration experiment the pipette would be prewetted with an unrecorded transfer using the optimal liquid handling parameters found during the optimization campaign. Subsequently, ten repetitions of gravimetric testing would be performed for transfers of 1000, 500 and 300 μL. Between each transfer (including the prewetting step) the pipette was programmed to perform six cycles of blowouts and piston-homing into the source vial to eliminate any remaining liquid still present after the liquid transfer. The mean % E for the transfers of each target volume was calculated to obtain the systematic error (accuracy) of the transfer, while the percentage standard deviation of % E was used to obtain the random error (precision) of the transfer.Optimization protocol of liquid handling parameters
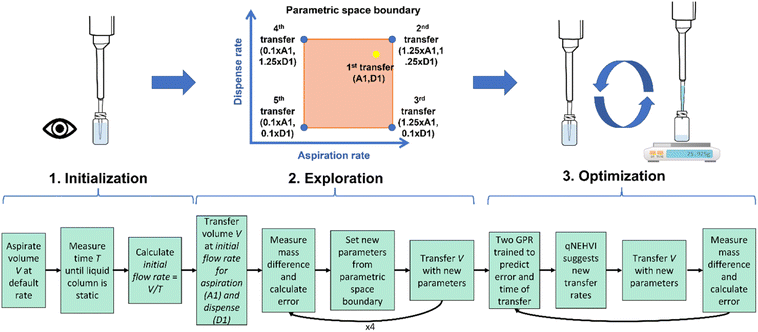
Our protocol for the optimization of the liquid handling parameters (defined as a combination of aspiration and dispense rates for this study) for accurate viscous liquid transfer is shown in Fig. 2. We have divided the protocol into three different steps: initialization, exploration, and optimization. The objective of the initialization step is to provide an aspiration and dispense rate based on a coarse approximation of the flow rate of the target liquid within the pipette tip for a specific aspiration rate. The initialization step consists of aspirating 1000 μL at the default flow rate as established by the pipette manufacturer (273.15 μL s−1 for P1000 gen2 and 260 μL s−1 for rLine1000). After the aspiration of the liquid is triggered, the robot is programmed to maintain the tip submerged in the liquid even after the piston stops moving. As the pipette piston moves the liquid will flow upwards into the pipette tip until the pressure between the air cushion inside the pipette tip and the atmospheric pressure has been equilibrated. A timestamp (ti) is automatically recorded when the aspiration of the viscous liquid started, and a second timestamp (tf) is recorded by the user, when it has determined by visual inspection that the column of liquid seems static. The approximated flow rate of the liquid inside the tip is calculated as follows:Then the viscous liquid is dispensed into the same vial at a dispense rate equal to the flow rate obtained in the previous step. The initialization step therefore provides a sensible starting point for the optimization of the liquid handling parameters, leading to a reduced number of iterations required to obtain parameters with low transfer errors. In addition, the initialization step acts as a safety protocol, where we obtain an aspiration rate that will not lead to a meniscus breakdown that can lead to uncontrolled aspiration that can cause damage to the equipment.
The second and third steps of the protocol focus on optimizing the liquid handling parameters using gravimetric testing (see the Experimental section for details). In these steps several combinations of aspiration and dispense rates are tested and the percentage transfer error (% E) for each transfer is calculated. The exploration step consists of testing five combinations of liquid handling parameters that explore the boundaries of the parametric space where the best liquid handling parameters are likely to be found. The first combination of liquid handling parameters to be tested is aspiration and dispense rates equal to the approximated flow rate obtained in the initialization step. Afterwards, the approximated flow rate is multiplied by a factor of 1.25 and 0.1 to set the maximum and minimum values of aspiration and dispense rates for the optimization. These values have been set as the limits of the parametric space based on previous knowledge obtained from the optimization of liquid handling parameters of viscous liquids. Then the four permutations of aspiration and dispense rates of these two limit values are gravimetrically tested (Fig. 2).
In the optimization step, new values for aspiration and dispense are proposed for evaluation with the objectives of minimizing (1) the transfer error (% E) and (2) time required to aspirate 1000 μL (t1000 μL). A machine learning driven optimization was implemented using the BoTorch Python package to implement MOBO utilizing the q-Noisy Expected Hypervolume Improvement (qNEHVI) algorithm. The qNEHVI algorithm was chosen due to its fast convergence on multi-objective problems and robustness in observation of noise,10 which is a concern for this use case since small variations in volume caused by liquid dripping or air bubbles can have a large impact on the transfer errors at the microliter scale. Since BoTorch is implemented for maximization problems, our optimization task is formulated to maximize the negative value of the absolute percentage error (−|% E|) (set as absolute to accommodate positive and negative percentage errors) and maximize the negative value of the time to transfer 1000 μL (−t1000 μL). To benchmark the performance of the algorithm, we performed in parallel a human-driven optimization where a scientist starts the optimization with the five data points collected during the exploration step. Based on their intuition, the next set of aspiration and dispense rates were selected and tested gravimetrically.
To start the MOBO, two independent Gaussian process regressors were trained on the first five data points obtained during the exploration step to predict −|% E| and −t1000 μL. Sobol sampling is used to propose a discrete candidate set of n different combinations of aspiration and dispense rates to be evaluated for optimization (n = 1024 for our study). The regressors predict the objective values for these candidates, which are then computed on the qNEHVI acquisition function to consider which candidate has the highest likely gain. The parameter set with the highest qNEHVI acquisition value is therefore evaluated in the next iteration of gravimetric testing. This process of training the model, sampling new candidates and greedy maximization on qNEHVI is repeated for each iteration, updating the dataset with each new evaluation. In our study, the procedure for machine and human-driven optimization was performed for a minimum of five iterations or up to a threshold of 5% absolute percentage error.
During the optimization campaign, the reference point for time was kept constant to the −t1000 μL for the set of transfer parameters equal to 0.1 times the flow rate obtained in the initialization step, which is equal to the longest value of time tested. In order to find solutions that prioritize minimal error, we implemented a dynamic reference point to pressure the algorithm to explore solutions that minimized error instead of time. Previous studies using MOBO have used this approach to avoid undesirable solutions for one of the objectives of the optimization.11 Thus, the reference point for error was updated at each iteration to be 1.25 times the maximum −|% E| observed so far in the data set. In this way, we allowed for bias towards solutions that minimize error while maintaining reasonable time, rather than considering the entire Pareto front where time minimization may be favored.
Results and discussion
Semi-automated optimization of liquid handling parameters
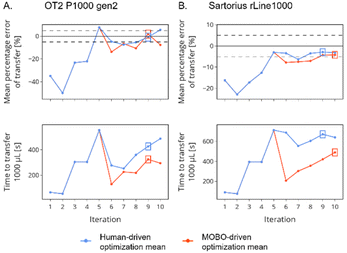
In Fig. 3 we display the mean change per iteration in % E and t1000 μL for the optimizations driven by human intuition and MOBO algorithm using the OT2 P1000 (Fig. 3A) and Sartorius rLine1000 (Fig. 3B) pipettes. For each graph, the first five iterations represent the transfers performed during the exploration step. By examining these first five iterations, we can find some trends that were present for each pipette and for every liquid (the plots for all liquids can be found in Fig. S6 in the ESI†). Firstly, it can be observed that as t1000 μL increases (i.e. decreasing the aspiration and dispense rates), the % E approaches values closer to zero. This observation is expected since the slower piston movement enables a more controlled flow of the liquid within the pipette tip and a smooth equalization of pressure. However, when the OT2 P1000 pipette is used there is a critical point where the further decrease in aspiration and dispense rates leads to volume transfers higher than the expected value (i.e. positive % E). On the other hand, the error associated with the transfer of the Sartorius rLine1000 pipette always remains negative. Considering that the viscosity standards have a lower density in comparison to water (<∼15%), the observation of positive % E at low transfer rates is not surprising. During aspiration, a specific mass of liquid needs to be withdrawn to equalize the pressure difference between the pipette barrel and the atmospheric pressure. Since the pipettes are optimized to transfer water, it is expected that liquids with lower density than water require a larger volume to match the mass required to equalize the pressure difference, thus leading to positive % E.12,13 However, the rLine1000 pipette tips have a narrower tip profile in comparison to the tips used with the OT2 P1000 pipette. It is conceivable that the smaller diameter of the pipette tip enables the equalization of pressure of the pipette barrel with a smaller amount of liquid, explaining why the rLine1000 pipette only displayed negative values for % E.Second, the values for aspiration and dispense rate have a distinct impact on the % E. This can be observed from the % E obtained in iterations three and four, where the values of aspiration and dispense have been interchanged. In iteration number three the aspiration and dispense rates are respectively equal to 1.25 and 0.1 times the approximated flow rate obtained in the initialization step, while the inverted values were tested in iteration number four. We can observe that while both iterations have the same time of transfer for 1000 μL there is a significant decrease in the % E when the aspiration rate is larger than the dispense rate. The observation that the % E is improved with slower dispense rates may be due to the lower surface tension the viscosity standards used in this study have in comparison to water. A low surface tension liquid will be more likely to wet the walls of the pipette tip, causing the liquid in contact with the walls to flow at a lower rate in comparison to the bulk due to adhesive interactions with the plastic walls.13
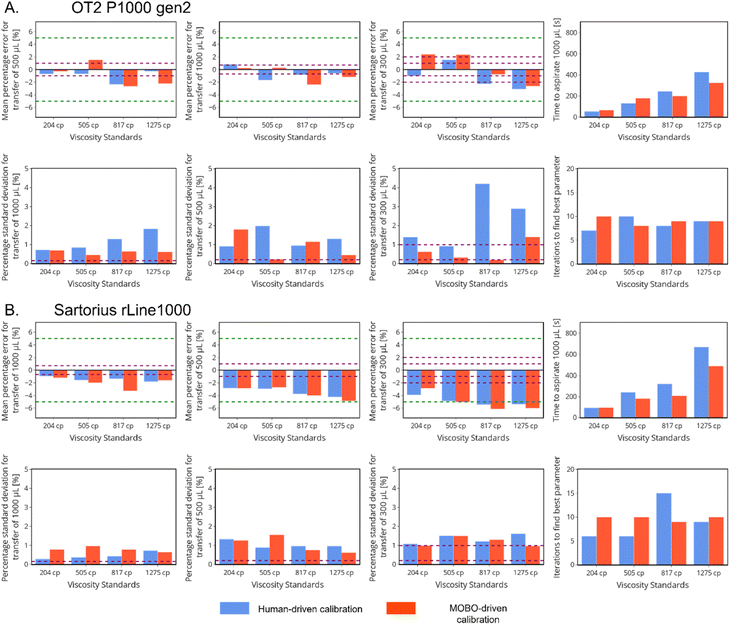
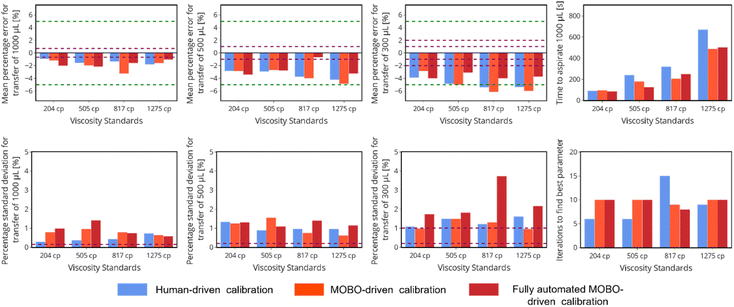
After the first five initial points, the next liquid handling parameters tested were either generated by a MOBO algorithm or human intuition for a minimum of five iterations or until the absolute value of % E was within 5%. The criteria for the selection of the best optimized parameters were the set of aspiration and dispense rates that displayed maximum mean −|% E|, since this was the objective to be optimized by the MOBO algorithm. After the optimal parameters were selected, a calibration test was performed to determine their accuracy and precision (see further details in the Experimental section). In Fig. 4 we present a summary of the performance of the best optimized liquid handling parameters for each of the tested liquids. It can be observed that for both pipettes the best parameters found by both human and MOBO algorithm for each viscous liquid were within the target of 5% experimental error (excluding the transfer of 300 μL for liquids with viscosities ≥817 cP). In addition, the number of iterations to achieve the best transfer parameters were all greater than five, meaning that both human intuition and MOBO were able to discover liquid handling parameters with a % E closer to zero and shorter transfer times in comparison to the best parameters found during the exploration step of the protocol.
As expected, for both pipettes the systematic errors (characterized by the mean % E) increased with viscosity due to the inherent limitations of air-displacement pipettes to accurately transfer viscous liquids. In addition, the systematic errors became larger as smaller volumes of liquid were transferred due to the greater impact that dripping and incomplete volume transfers have on the value of % E. The increase of error with smaller transfer volumes is a behavior that is also expected for non-viscous liquids and even the pipette manufacturers increase the threshold for tolerance of systematic error when small volumes of water are transferred (these thresholds are highlighted in Fig. 4 as purple dashed lines). The random error obtained from the percentage standard deviation of % E the transfers reflects the precision of the liquid handling parameters. For all parameters obtained with MOBO, we can observe that they were below 2.5% and were similar for both pipettes. Similar to the observations in systematic error, larger random errors were observed with increasing viscosities and decreasing transferred volumes. Both random and systematic errors in all cases are within ten times above the reported values for the transfer of water by the manufacturer. Considering that there is an increase of two to three orders of magnitude in the viscosity of the tested samples in comparison to water, we deem as acceptable the observed increase in the systematic and random error.
When the performance of the MOBO and human-driven optimization is compared, we observe that for the OT2 P1000 pipette the liquid handling parameters obtained by MOBO displayed shorter transfer times than human-driven optimization for the two most viscous liquids, with a maximum decrease of approximately 40% for the 1275 cP viscosity standard. For the 204 and 505 cP viscosity standards, the human-driven optimization demonstrated a quicker transfer time (27% decrease for the 505 cP viscosity standard) in comparison to the parameters obtained through MOBO. In relation to transfer errors, the liquid handling parameters obtained through human intuition had smaller systematic errors in comparison to the parameters obtained from MOBO, especially for volume transfer of 500 and 300 μL. On the other hand, for the rLine1000 pipette it can be observed that in all cases MOBO of the liquid handling parameters displayed similar or shorter transfer times than human-driven optimization, with a maximum reduction of approximately 36% in time for the transfer of the 817 cP viscosity standard. Both human-driven optimization and MOBO presented similar systematic errors, while falling short of meeting the target of 5% error of the transfer of 300 μL for the 817 and 1275 cP viscosity standards.
In general, MOBO performed similarly irrespective of the equipment used during the optimization. It was found that MOBO found the optimal parameters between 7 and 10 iterations. The main difference between the pipettes was that the OT2 P1000 pipette presented smaller systematic errors for the transfer of 300 μL for all liquids. This may be due to the different pipette geometry since the profile of the tip used by the OT2 P1000 pipette has a more gradual increase in radius and a wider bore, which are regarded as favorable attributes to transfer viscous liquids. In contrast, the performance of the human-driven optimization varied greatly depending on the equipment used. The number of iterations to obtain the best parameters varied from 6 to 15 when human intuition was driving the optimization of the rLine1000 pipette, while the number of iterations was between 7 and 10 when the OT2 P1000 pipette was used. The larger differences in performance of the human-driven optimization in comparison to MOBO for each equipment suggest that MOBO allows for a standardized protocol with consistent performance irrespective of the equipment used. On the other hand, human-driven optimization will vary highly depending on the ability and experience of the experimenter with the equipment.
Fully automated optimization of liquid handling parameters
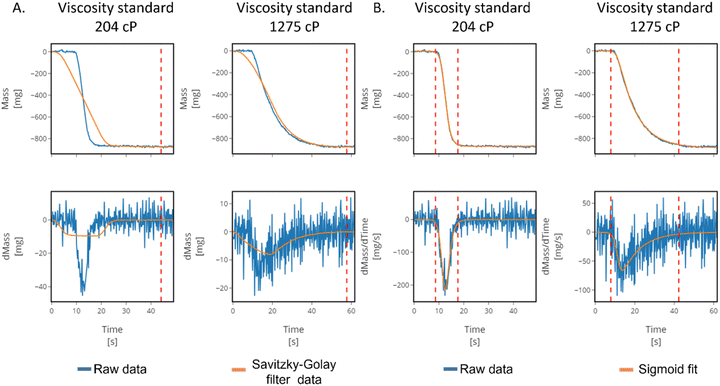
So far, we have described a protocol based on a MOBO algorithm that can be used to optimize the liquid handling parameters of any automated pipette and tip combination. The only requirements for the protocol are that the pipette is capable of adjusting the plunger flow rate and that a human experimenter is running the initialization step and gravimetric testing. Although we have shown that this procedure can match or outperform the optimization guided by human intuition, the protocol still requires spending manpower in tedious and time-consuming experimental tasks. Incorporating automated methods to perform the initialization step and the gravimetric testing in our protocol would minimize the need of a human experimenter, leading to a protocol that allows more efficient allocation of manpower. To achieve full automation, we incorporated an automated mass balance into the workflow that can perform the initialization step and the gravimetric testing without human intervention, thus closing the loop of the optimization of liquid handling parameters.Our manual initialization step is based on a qualitative approach to measure the time required to aspirate 1000 μL of liquid by visual inspection. An alternative way to measure the flow rate of liquid inside the pipette tip is to measure the mass change of a reservoir of liquid on top of a mass balance during the aspiration step. Based on this approach, the following protocol was implemented using the rLine1000 setup. After picking up a new tip, the robot moved the pipette into a container with the specific viscous liquid placed on top of an in-house built automated mass balance (see ESI Section S1.3† for further details on the automated mass balance). The balance was zeroed and started to record the mass of the vial for 10 s to establish a baseline. As the balance was still recording, the pipette was instructed to aspirate 1000 μL of the viscous liquid using the default aspiration flow rate of 260 μL s−1. Fig. 5 displays the mass change over time during the aspiration of 1000 μL for two liquids with viscosities of 204 (Fig. 5A top left) and 1275 cP (Fig. 5B top right). The mass decrease over time displays an asymmetric S-shaped curve, where a sharp mass change is observed at the start of aspiration and then it smoothly levels as the aspiration of the liquid is close to completion. When the shape of the curve between both liquids is compared, it can be observed that the asymmetry of the curve increases with viscosity leading to a more dampened mass change at the later stages of aspiration for liquids with high viscosity.
A two-step protocol is used to get an approximated liquid flow rate from the mass–time curve. First, during the aspiration of the target liquid the protocol requires that recording automatically stop when the target volume has been fully aspirated. As the live mass change is recorded by the automated balance, the mass change (dm) with respect to time (t) is simultaneously calculated and used as a parameter to stop the recording when this value reaches a threshold approaching zero (Fig. 5 bottom). As can be observed in Fig. 5a, the mass readings need to be smoothed with a Savitzky–Golay filter to reduce the impact of the noise of the mass measurements on the dm calculation. The amount of filtering required increases with viscosity since the rate of mass change will be inherently slower for these liquids. However, our protocol must be agnostic to the viscosity of the liquids thus a high filtering regime was implemented in order to accommodate the procedure for high viscosity liquids. Once the smoothed mass change surpasses a preset threshold (−0.05 mg) represented by the dashed vertical red lines in Fig. 5a, the measurement is considered completed. This protocol tends to overestimate the time required to aspirate the target volume as observed in Fig. 5a, and the overestimation increases with decreasing liquid viscosity. Another condition that can be used to assess if the aspiration has finished is to stop recording once the total mass difference is equal to or smaller than the density of the liquid. This procedure would have the advantage of not overestimating the time required to aspirate the target volume. However, air-displacement pipettes are known to under-aspirate when liquids denser than water are handled,13 making this condition likely to lead to an infinite loop. Hence, in order to obtain an accurate value of the time of aspiration for the target volume a second step is required.
The objective of the second step is to obtain the time required to aspirate 1000 μL from the recorded mass–time curve. By fitting an asymmetric sigmoid function to the experimental data we can obtain a smooth mass–time curve that closely resembles the recorded data. As can be observed in Fig. 5b, the sigmoid fit can be derived without concern of noise into a dm/dt curve and has smaller deviations from the experimental data in comparison to the curves obtained through Savitzky–Golay filtering. In this way we manage to circumvent the overestimation of the time required to fully aspirate the target liquid by the first step. Finally, we determined that the time required to aspirate 1000 μL will be equal to the time where the dm/dt value is equal to or smaller than 5% of the maximum recorded dm/dt value since it represents approximately 99% of the change of the output (i.e. mass) for a symmetric sigmoid function. Full details of the data processing and a step-by-step diagram of the automated initialization can be found in the ESI (see Section S2.3).†
Once the initialization step is completed the optimization of the liquid handling parameters is performed using the same procedure described previously. The mass measurements during the gravimetric testing of the exploration and optimization steps are automatically recorded using the mass balance, the error associated with the transfers is calculated and the MOBO algorithm suggests the new set of parameters to be tested, all without human intervention. The fully automated protocol was implemented to optimize the liquid handling parameters for all four viscous liquid standards. A remarkable observation was that the approximated flow rates obtained through the measurement of mass change were very similar to the flow rates obtained through visual inspection of the column of liquid, further supporting our user initialized protocol (see Fig. S7 of the ESI†). The performance of the liquid handling parameters obtained through the fully automated protocol matched or outperformed the parameters obtained through the user initialized methods (Fig. 6). The only metric where the fully automated protocol considerably underperformed was the standard deviation of the transfer of 300 μL of the standard with viscosity of 817 cP. However, this was not a metric that we were set to minimize and further optimization iterations would likely be able to discover parameters with an improved precision.
Prospects and future directions
Considering that most automated air-displacement pipettes are manufactured with the intention to transfer aqueous-like liquids, we envision that this protocol could become a common practice in labs using liquid handling automated tools to verify and improve their liquid transfers. This would not only give greater statistical confidence to their results but also ensure the repeatability of their experiments. We believe that fields of formulation, polymer, colloidal and biological sciences would benefit the most by the adoption of this protocol. For example, Chitre et al.5 recently reported the development of an automated tool that adjusts the pH of shampoo-like formulations. However, the platform still requires a liquid handling system that can accurately transfer the viscous reagents to complete a self-optimizing loop. This drawback could be solved by incorporating an automated air-displacement pipette that uses our protocol to optimize the liquid handling parameters for each of the viscous liquids required for the shampoo fomulations. Beaucage and Martin14 recently published an autonomous formulation platform to study colloidal and polymeric solutions. For their platform, the authors used an OT2 robot to prepare solutions containing the viscous colloids. However, they limited their reagents to liquids with viscosities in the order of 136 cP due to the loss of pipetting accuracy with liquids with higher viscosities. Implementing our optimization protocol could expand the design space for their colloidal formulations. Finally, biological assays may involve the transfer of viscous fluids (e.g. biological fluids, glycated liquids, surfactants, oils, etc.) that currently rely on manual optimization of the liquid handling parameters.15,16 Our protocol would benefit by increasing the level of automation of these tasks and improving the repeatability of the assays.We also envision several avenues that could be explored to further improve our optimization protocol. Future work on the application of MOBO algorithms that can handle categorical variables to add blowout steps could potentially increase the accuracy of the transfers and would be able to obtain liquid handling parameters for accurate transfer of liquids with even higher viscosities. The transfer of non-Newtonian fluids was out of the scope of this study, thus further research is required to verify and improve the applicability of this protocol for the transfer of this kind of liquids. We also believe that the ability of air-displacement pipettes to accurately transfer liquids with high viscosity will be limited and there will exist highly viscous liquids that will not be suited for these tools even after optimization. Further research and development of reliable and accessible automated positive displacement pipettes is still required to offer liquid transfer solutions for this sort of liquids.
Conclusions
Herein we described an optimization protocol that can be used to obtain aspiration and dispense rates that can transfer Newtonian liquids with viscosities as high as 1275 cP within 5% of systematic error, while simultaneously minimizing the time required to transfer the liquids. Our optimization protocol can be applied irrespective of the liquid handling robot used, as long as the aspiration and dispense rates of the equipment can be controlled. We found that when the protocol was implemented with a MOBO algorithm, it could match and outperform the liquid handling parameters obtained through human-driven optimization. In addition, the MOBO algorithm was able to discover liquid handing parameters with similar performance independent of the tool used, making it a reliable and consistent protocol. Finally, we demonstrated that with the addition of an automated mass balance the protocol can be completely executed in a closed-loop framework with minimal human intervention. We believe that this protocol will be a significant tool for research in formulation science involving viscous liquids, and ultimately will be used to fully automate workflows and improve manpower efficiency.Data availability
Data, processing scripts and code to execute the experiments for this paper are available at LiqTransferOptimizer at https://github.com/Quijanove/LiqTransferOptimizer.Author contributions
P. Quijano Velasco: conceptualization, methodology, formal analysis, data curation, investigation, software, visualization, writing – original draft, writing – review and editing. K. Y. A. Low and C. J. Leong: software, writing – review and editing. W. T. Ng, S. Qiu, S. Jhunjhunwalaa, B. Li and A. Qian: software, investigation. K. Hippalgaonkar: supervision, writing – review and editing. J. J. W. Cheng: methodology, project administration, resources, software, supervision, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Aniket Chitre and Riko I. Made for their initial comments on the application of Bayesian optimization during the conceptualization of the project. This work was supported by A*STAR under an MTC AME Programmatic Grant (Grant number A20H3b0140) for Structural Power for portable and electrified transportation.Notes and references
- S. H. Needs, T. T. Diep, S. P. Bull, A. Lindley-Decaire, P. Ray and A. D. Edwards, PLoS One, 2019, 14, e0224878 CrossRef CAS PubMed.
- P. Dettinger, T. Kull, G. Arekatla, N. Ahmed, Y. Zhang, F. Schneiter, A. Wehling, D. Schirmacher, S. Kawamura, D. Loeffler and T. Schroeder, Nat. Commun., 2022, 13, 2999 CrossRef CAS PubMed.
- F. Barthels, U. Barthels, M. Schwickert and T. Schirmeister, SLAS Technol., 2020, 25, 190 CrossRef CAS PubMed.
- Y. Jiang, H. Fakhruldeen, G. Pizzuto, L. Longley, A. He, T. Dai, R. Clowes, N. Rankin and A. I. Cooper, Digital Discovery, 2023, 2, 1733 RSC.
- A. Chitre, J. Cheng, S. Ahamed, R. C. M. Querimit, B. Zhu, K. Wang, L. Wang, K. Hippalgaonkar and A. A. Lapkin, Chem.: Methods, 2023, e202300043 Search PubMed.
- N. Yoshikawa, K. Darvish, M. G. Vakili, A. Garg and A. Aspuru-Guzik, Digital Discovery, 2023, 2, 1745 RSC.
- B. W. Soh, A. Chitre, W. Yang Lee, D. Bash, J. N. Kumar and K. Hippalgaonkar, Digital Discovery, 2023, 2, 481 RSC.
- M. Christensen, L. P. E. Yunker, P. Shiri, T. Zepel, P. L. Prieto, S. Grunert, F. Bork and J. E. Hein, Chem. Sci., 2021, 12, 15473 RSC.
- A. Kanase and K. Watson, Viscous Handling Automation using Opentrons OT2, Opentrons Application Note, 2022 Search PubMed.
- A. K. Y. Low, E. Vissol-Gaudin, Y.-F. Lim and K. Hippalgaonkar, J. Mater. Inf., 2023, 3, 11 CrossRef.
- B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott, T. D. Morrissey, T. H. Haley, O. Proskurin, M. B. Rooney, N. Taherimakhsousi, D. J. Dvorak, H. N. Chiu, C. E. B. Waizenegger, K. Ocean, M. Mokhtari and C. P. Berlinguette, Nat. Commun., 2022, 13, 995 CrossRef CAS PubMed.
- S. Koivisto, Technical Note, Thermo Fisher Scientific, 2009, vol. 151, p. 7160 Search PubMed.
- K. Ewald, Eppendorf Userguide, 2015, vol. 21, p. 1 Search PubMed.
- P. A. Beaucage and T. B. Martin, Chem. Mater., 2023, 35(3), 846 CrossRef CAS.
- R. Cao, N. T. Li, S. Latour, J. L. Cadavid, C. M. Tan, A. Forman, H. W. Jackson and A. P. McGuigan, Adv. Healthcare Mater., 2023, 12, 2202422 CrossRef CAS PubMed.
- J. J. Caponi, J. Shmushkis, H. Geissler, M. J. Post, L. Jackisch and E. M. Mall, STAR Protoc., 2023, 4, 102143 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00255a |
| This journal is © The Royal Society of Chemistry 2024 |