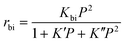Combining computational and experimental studies to gain mechanistic insights for n-butane isomerisation with a model microporous catalyst

Abstract

Microporous solid acid catalysts are widely used in industrial hydrocarbon transformations in both the fuels and petrochemical industries. The specific choice of microporous framework often dictates the acidic properties of the system, such as acid site strength and concentration. In this work we have explored the influence of acid site concentration on butane isomerisation activity and the mechanistic pathway by controlling the quantity of magnesium doped into an aluminophosphate, keeping the acid site strength and framework topology constant. By combining experimental kinetic studies, and theoretical mechanistic studies, we conclude that isobutane formation, from n-butane, predominantly proceeds through a bimolecular pathway. Specifically, the activity of the system is strongly linked to the presence of alkenes, and herein the precise mechanistic roles of the alkenes are explored.

---

Introduction

Solid acid catalysis plays a vital role in the transformation of alkane hydrocarbon species, which supply the global demand for polymer precursors and petrochemical feedstocks. The activity of such catalysts is not just determined by acid site strength and concentration, but also the location of acid sites, and the space around them. One process which has been explored with a wide variety of solid acid catalysts, is the isomerisation of n-butane to isobutane, a precursor for high octane alkyl fuels and chemical intermediates, also a widely used propellant and a calibrant.^1–3 The chemical equilibrium of butane isomerisation typically favours isobutane below 250 °C, making it an interesting challenge for designing solid acid catalysts.² Ideally the catalyst must be able to operate at low enough temperatures to exploit the chemical equilibrium, while also being able to activate the relatively inert butane molecule at milder temperatures. As a result, a wide range of solid acid catalysts have been explored for this reaction including alumina,⁴ zirconia,⁵ silicas,⁶ molybdena⁷ and zeolites.^8,9

Microporous materials, particularly zeolites (aluminosilicates), are widely used for the transformation of light alkanes in the petrochemical industry.^10,11 Doping heteroatoms into the zeolite framework creates Brønsted acid sites, which can catalyse chemical transformations. The strength of these acid sites depends on the precise framework topology, and the quantity of dopants in the framework.^12,13 Thus, it is challenging to change just a single variable, such as acid site concentration in zeolite materials.^10,11 Aluminophosphates (AlPOs) are structurally similar to zeolites, but are made of alternating AlO₄ and PO₄ units, forming identical frameworks.^14,15 Like zeolites AlPOs create Brønsted acid sites by substituting framework atoms with dopant heteroatoms. While silicon is the most common dopant, the strongest acid sites occur when magnesium (Mg²⁺) is doped into the framework, replacing Al³⁺ to form MgAlPOs.^16,17 Here the substitution of Mg²⁺, for an Al³⁺ framework species, leads to a charge imbalance, which is countered by the formation of a Brønsted acid site on an oxygen adjacent to the Mg²⁺ dopant (Fig. S1†). This can, in some cases, also lead to Lewis acid sites forming due to the dehydration of this site, leading to oxygen vacancies (Fig. S1†).^14–17 Due to the alternating Al/P nature of AlPOs, this means that any magnesium dopant must be separated by a minimum of four bonds, leading to isolated active sites. Here we chose to study magnesium doped AlPOs (MgAlPO-5) as a model system.

AlPO-5 is also one of the larger AlPO frameworks (7.3 × 7.3 Å pore diameter), meaning that there will be little steric hindrance around the acid site, and reactants and products can readily ingress and egress out of the pores. The combination of these factors, and the relative strength of MgAlPOs compared to other doped AlPO systems, makes this an excellent model system for exploring solid acid catalysed processes.

Most alkane isomerisations proceed through a substituted carbenium intermediate,^8,18–22 however when n-butane is used, this would lead to a primary methylpropane carbenium ion, destabilising the reaction pathway. Instead, two primary reaction pathways are proposed for butane isomerisation; a monomolecular (Scheme 1A) and bimolecular pathway (Scheme 1B), along with C–C cracking to form by-products (Scheme 1C).^18–21 The exact isomerisation pathway (Scheme 1A or B) is discussed in the catalysis literature and varies depending on the catalyst choice and experimental parameters such as temperature, butane concentration and flow rate.^8,18–21 Mordenite zeolite (MOR) has been the most studied microporous catalyst for butane isomerisation,^23–26 due to its high activity. The one-dimensional MOR channels (7.0 × 6.5 Å) possess strong acid sites that can activate n-butane. Common observations include that high conversion leads to high propane selectivity, principally due to the bimolecular pathway (Scheme 1B). In principle, the bimolecular pathway, where uneven scission occurs, should form equimolar quantities of propane and pentane by-products.^23,24 However, pentane is more reactive than butane, and performs further reactions with an activated C₄ species, forming a C₉ species. This subsequently decomposes into a C₆ species and propane, and then eventually into three C₃ species.²⁷ Propane however is less reactive than butane, and significantly less reactive than pentane, and as such acts as a ‘product sink’, thus higher conversions ultimately lead to higher propane selectivity.²⁸ Many studies have focussed on the influence of Si/Al ratio in MOR samples, showing that higher Si/Al species follow the bimolecular pathway, with the rate of reaction following the number of acid sites (or substituted aluminium species) squared.^26,29–31 However, it is argued that as these studies focus on dealuminated MOR samples, there are other factors to consider. Primarily dealumination is known to increase the strength of Brønsted acid sites and create mesopores. Both factors can greatly influence the choice of mechanism. Others have focussed on isotopically labelled n-butane to probe the mechanism.^{18,24,32–34} In a monomolecular mechanism there is no possible exchange of carbons, thus di-isotopically labelled ¹³C₂¹²C₂H₁₀n-butane would be expected to form C₄ products that are strictly di-isotopically labelled. However, if a bimolecular reaction was occurring, then exchange of carbons is possible. C₄ species could then contain a variety of ¹³C species, ultimately ending up in a binomial distribution, known as carbon scrambling. Evidence of carbon scrambling has clearly been seen in MOR species, pointing to a bimolecular pathway,¹⁸ whilst the monomolecular pathway is still known to play an important role in MOR.^24,29 In contrast ZSM-5 primarily shows a bimolecular pathway,^27,28 due to the additional space afforded at channel intersections, often recording reaction orders of around 1.5, suggesting a strong bimolecular contribution.³⁵

Scheme 1 Showing prominent reaction pathways which occur in n-butane isomerisation, A) monomolecular, B) bimolecular and C) cracking pathways.

Many have attempted to interpret experimentally determined reaction orders, which only rarely yield expected integer values. A reaction order of 1.5, for example, could simply be interpreted as a combination of monomolecular (1.0) and bimolecular (2.0) pathways. However, a range of equations and kinetic models have been used to describe the bimolecular pathway which can account for this behaviour.²⁸ Notably the work from Wang et al. describes how differences in pressure can lead to a bimolecular pathway yielding a reaction order of 1.0, depending on the quantity and type of surface intermediates.²⁷

To understand the influence of acid sites, researchers have employed theoretical quantum chemical calculations to inform which intermediate species are likely to form.^36,37 Typically these studies consider the possibility of an alkoxide forming (typically 2-butoxide), bound to the zeolite, or carbenium ion formation.^8,38 Primarily these works focus on butene isomerisation,^39–46 however recent work by us explores the likelihood of bimolecular reactions between activated species, as shown in Scheme 1.⁴⁷ Typically butane and butene skeletal isomerisation over zeolite species were found to go via an alkoxy route, where two steps; 2-butoxide to isobutoxide, and isobutoxide to an isobutyl carbenium ion were found to be the rate determining steps, with very similar activation energies. However the conclusions from multiple studies highlighted the strong influence that framework topology and acid-site strength had on the mechanistic pathway followed.^39–45,47 As such in this work we will probe the catalytic pathway of n-butane isomerisation using MgAlPO-5, a model catalyst where acid site quantity can be varied whilst retaining the characteristics of the acid site, leading to structure–property relationships relevant to optimising solid acid catalysts by combining experimental and theoretical techniques.

Experimental methods

Synthesis

3 different MgAlPO-5 systems were made, denoted as 1, 3 and 6%, corresponding to the mol% of Mg in the synthesis gel. The procedure for 3 mol% MgAlPO-5 is described below, with variations for 1 and 6 mol% outlined:

11.54 g of 85 wt% Phosphoric Acid in H₂O (ACS Reagent Grade, Sigma Aldrich), was mixed with 41.2 mL of deionised water, and stirred in a Teflon beaker, in an ice bath for 15 minutes. 5.25 g of hydrated aluminium hydroxide (Sigma Aldrich 50–57.5% Al₂O₃; 5.35 g for 1%, 5.08 g for 6%) was added slowly to the diluted phosphoric acid, forming a white suspension, and left to stir for 15 minutes. A solution of 0.284 g of magnesium(II) acetate tetrahydrate (Sigma Aldrich, ≥99% purity; 0.142 g for 1%, 0.852 g for 6%), dissolved in 5 mL of deionised water was added dropwise to the gel, and left to stir for a further 15 minutes. 5.4 g of triethylamine (Sigma Aldrich ≥99% purity) was then added dropwise to the white gel, then the Teflon beaker was then removed from the ice bath, and the white gel stirred for a further 2 hours. Giving gel ratios of:

1% MgAlPO-5 = 1.5 P : 0.99 AI : 0.01 Mg : 0.8 TEA : 40 H₂O

3% MgAlPO-5 = 1.5 P : 0.97 AI : 0.03 Mg : 0.8 TEA : 40 H₂O

6% MgAlPO-5 = 1.5 P : 0.94 AI : 0.06 Mg : 0.8 TEA : 40 H₂O

The homogeneous white gel was then split between three 100 mL Teflon-lined steel autoclaves, which were sealed, and then heated to 200 °C, under autothermal pressure, in a preheated oven for two hours. On removal the autoclaves were quenched in ice-cold water. Once cooled, the contents of each autoclave was filtered, and washed with 1000 mL of deionised water. The resulting white powders were dried overnight at 70 °C, and then calcined in a tube furnace under a flow of air, ramping at 2.5 °C min⁻¹ up to 600 °C, and held for 16 hours, yielding a white powder, which was confirmed as AFI using a range of characterisation techniques, as details in the ESI.†

n-Butane isomerisation catalysis measurements

0.6 g of microporous 3 mol% MgAlPO-5 was pelletised at 3 tons of pressure, into 7 mm circular pellets, containing 50 mg of catalyst per pellet. These were then sieved between 300–500 μm, and used as the catalyst bed, typically 4 cm in height, within a quartz reactor. Glass beads were put above and below the catalyst bed to ensure the bed was in the isothermal range of the reactor, and that dead-space was minimised in the system. The catalyst was dried in the reactor under a flow of 30 mL min⁻¹ of nitrogen, for 1 hour at 400 °C, at a ramp rate of 20 °C min⁻¹. After drying, the n-butane (99%, BOC) and nitrogen (99.98%, BOC) flows were set, with a combined total of between 3.91 and 3.94 mL min⁻¹, corresponding to the desired partial pressure.

An online Arnel 4035 light hydrocarbon analyser system (Perkin Elmer Clarus 590 gas chromatogram with single FID detector and autosampler) was used to analyse the reactor output, with a 250 μL sample loop, that was constantly refreshed, and injected every 17.5 minutes. The parameters for the GC experiment are as follows: injector temperature = 200 °C, FID detector temperature = 250 °C, flow rates = 30 mL min⁻¹ of hydrogen and 450 mL min⁻¹ of air, carrier gas pressure = 7.5 psi, helium split flow = 50 mL min⁻¹. A Perkin Elmer alumina sulfate PLOT column was used, 50 m in length, and an internal diameter of 0.53 mm. The GC method was: hold at 100 °C for 1 min, heat up to 120 °C at a rate of 2.5 °C min⁻¹, then heat to 190 °C at a rate of 20 °C min⁻¹ and hold for 5 minutes for a total run time of 17.5 minutes.

Reaction samples were taken at 17.5 minute intervals, from 10 minutes to 185 minutes. The first four data points (10, 27.5, 45 and 62.5 minutes) were excluded as the system reached equilibrium, with the remaining 7 data points (80, 97.5, 115, 132.5, 150, 167.5 and 185 minutes) being averaged to reach the final catalytic values, with errors translating as the standard deviation. Conversion and selectivity values were constant over these values, confirming there was no deactivation.

Computational details

An AFI unit cell containing 48 T-sites; HAl₂₃MgO₉₆P₂₄ was used to model MgAlPO-5 in this work, with lattice parameters of a = b = 13.863 Å, c = 16.832 Å, V = 2801.361 ų. On substituting Mg into the framework, there are four crystallographically distinct O-sites for H to occupy, so calculations have been performed with H occupying the lowest energy O-site (determined by calculations, Table S1†). Geometry optimizations and energy calculations of all periodic structures were performed using the VASP program package connected with the atomic simulation environment (ASE) Python library.⁴⁸ For optimization of the structures, a GGA PBE-D3 approach^49,50 employing standard PAW-potentials and a convergence criterion of 0.001 eV Å⁻¹ is used. The Brillouin-zone was only sampled at the Γ-point. Search of transition states has been performed with the automated relaxed potential energy surface scan script (ARPESS) by Plessow.⁵¹ All structures were confirmed to be a minimum or, in case of transition states, a saddle point on the potential energy surface by vibrational calculations. Here transition states must have one imaginary frequency, and all other species none. For this, only vibrational modes for the adsorbent as well as the acid site (Mg) and its four neighbouring oxygen and phosphorus atoms are calculated; all other atoms are constrained. The free energy of the vibrations calculated at the given temperature and within the harmonic approximation is added to the periodic PBE-D3 energy to account for entropy. For this, all frequencies under a threshold of 12 cm⁻¹ are treated as 12 cm⁻¹ to avoid possible entropic inaccuracies due to low frequencies.^52,53

After optimisation of the periodic structure, DFT energies were calculated by using a smaller T46 cluster model of the structure, terminated with hydrogen, which encompasses the channel structure of the zeotype. Al–H and P–H bond distances for termination of Al and P have been taken from the optimized structures of AlH₃ (1.595 Å) and PH₃ (1.431 Å), respectively. Hydrogen termination has been performed so that there are at least 4 atoms between the active Mg site and a terminating hydrogen, so the reactive environment is properly described. As AFI has a channel structure, the cluster model has four layers of O-connected Al and P atoms, as shown in Fig. S2–S5.† The size was chosen to be as large as necessary so that the periodic images of the adsorbents are sufficiently far away from each other to avoid interactions between them along the channel and preserve the numerical accuracy, whilst minimizing computational costs.

Single point energies of these cluster model structures are calculated with the PBE-D3 functional within VASP, and also with the highly accurate M06 hybrid functional⁵⁴ and the def2-TZVPP basis set^55,56 within the TURBOMOLE program package.^57,58 The periodic energies are then corrected in the following way:

E = E^PBC_PBE-D3 + E^T46_{M06/def2-TZVPP} − E^T46_{PBE-D3/def2-TZVPP}

It has been shown by Goncalves et al. that correcting the periodic energies this way drastically improves the accuracy in zeolite catalysis, as the pure periodic PBE-D3 energies can have errors of up to 40 kJ mol⁻¹.⁵⁹ All energies were calculated within the harmonic oscillator approximation and at T = 400 °C and p = 1 bar.

Results and discussion

Confirming catalyst integrity

The three MgAlPO-5 samples were successfully synthesised, all exclusively showing X-ray diffraction signals that are attributed to the intended AFI structure (Fig. S6A†), confirming phase purity of the crystalline material.¹⁷ Nitrogen physisorption (Fig. S6B†) confirms the species are primarily microporous, due to the rapid uptake of nitrogen at lower pressures, with a slight hysteresis in all cases, typical of surface roughness. Calculated surface areas (Table S2†) showed little variation on incorporation of Mg from 308 m² g⁻¹ for 1% MgAlPO-5, to 285 m² g⁻¹ for 6% MgAlPO-5, which are within the expected range for a crystalline AlPO-5 material.¹⁷ Total pore volumes also varied from 0.25 to 0.21 cm³ g⁻¹, which was primarily micropore volume (Table S2†). Calculated pore-width distributions show no significant or ordered mesoporosity being present, confirming the microporous nature of the systems (Fig. S6†). Scanning electron microscopy images (Fig. S7†) showed spherical/barrel-like particles between 5 and 10 μm in size for all three systems, made from agglomerations of rod-like crystals with similar surface texture and roughness. Solid state ²⁷Al and ³¹P nuclear magnetic resonance (Fig. S8†) confirmed that Al and P primarily exist as tetrahedral oxides,¹⁵ in all three systems, as expected.

The Mg content of the systems varied as anticipated from 0.15, 0.46 to 0.95 wt% for the 1, 3 and 6% systems respectively (Table S2†), accompanied by a similar decrease in the Al content, suggesting Mg had indeed substituted into the framework, in the place of Al, as intended. Overall, the structural integrity of the three MgAlPO-5 systems was confirmed, with little variation in physicochemical properties between the system, allowing for accurate comparison of catalytic data.

The influence of incorporating Mg²⁺ into an AlPO-5 framework to form MgAlPO-5 was explored using pyridine-probed diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS), comparing MgAlPO-5 and undoped AlPO-5 (Fig. S9†). The addition of Mg²⁺ leads to a significant increase in signals attributed to Brønsted acid sites (ν_8a; 1633 and ν_19b; 1541 cm⁻¹).^60–62 However the increase in Lewis acidity, on introducing Mg²⁺ was far more subtle with slight increases in signals at 1608 and 1447 cm⁻¹ (ν_8a and ν_19b respectively).^60–62 This confirms that the introduction of Mg²⁺ has predominantly led to an increase in the number of Brønsted acid sites, with a slight increase in Lewis acidity. Additionally, we computed the shift of the ν_19b vibrational mode of adsorbed pyridine on MgAlPO-5, compared to pyridine in the gas phase (1438 cm⁻¹) to be 118 cm⁻¹ (final value of 1556 cm⁻¹). According to a recent study on surface Lewis and Brønsted acid sites in zeolite catalysis, this shift indicates a Brønsted acid site, therefore substantiating the aforementioned experimental findings.⁶³

Ammonia-temperature programmed desorption (NH₃-TPD) experiments were used to probe the strength and quantity of acid sites in the three MgAlPO-5 systems (Fig. 1). The data shows two clear peaks, corresponding to low temperature physisorbed ammonia (0–80 minutes) and a high-temperature Brønsted acid peak (80–150 minutes). For probing the Brønsted acidity we focus on the latter peak. The acid site quantity, from the second peak, was found to be 118, 234 and 496 μmol g⁻¹ (Table S3†). This is in good agreement with the expected acidity (82, 246 and 492 μmol g⁻¹).

Fig. 1 NH₃-TPD data of MgAlPO-5 samples describing acid site quantity and strength.

The maximum temperature for the three systems was found to be 433, 417 and 421 °C, showing that similar strength acid sites were present in all three systems. As such the strength of the acid sites did not vary significantly with increasing Mg loading, however the acid site quantity increased as expected, which appears to be the only consequence of the varying Mg loading in the three MgAlPO-5 catalysis. Based on the pyridine-probed infrared measurements (Fig. S9†) we believe the vast majority of these sites are Brønsted acid sites.

Catalysis data

Initially 3% MgAlPO-5 was tested at low partial pressures of n-butane, (0.05 to 0.20 bar, Table S4†), with the influence of partial pressure observed on conversion and product yields (Fig. 2A and S8†). As the n-butane partial pressure increases, the conversion also increases (Fig. S10A†). This suggests that n-butane has a positive reaction order, with regards to the total conversion of n-butane, as expected given the two likely reaction pathways, i.e. monomolecular (theoretical reaction order of 1) or bimolecular (theoretical reaction order of 2).

Fig. 2 Catalytic data of 3% MgAlPO-5 showing the variation the product yield of main products between A) a n-butane partial pressure between 0.05 and 0.20 bar (flow rates as per Table S4†), and B) n-butane partial pressure between 0.30 and 1.00 bar (flow rates as per Table S5†). Conditions: 0.6 g of catalyst, 400 °C.

Focussing on the product yields shows that isobutane is the main product, indicating that, at low conversions (<5 mol%), MgAlPO-5 is very selective for isobutane, whilst propane and pentane are also formed in reasonable quantities. We note that the conversion of MgAlPO-5 (3.7 mol%) is notably higher than that of undoped AlPO-5 (1.7 mol%) and the blank reaction (0.6 mol%, Fig. S10A†), showing the importance of adding strong Brønsted acid sites into AlPO-5, on doping Mg into the framework. Without the Mg, far more modest conversions are achieved, likely due to surface Al–OH and P–OH defect sites. C₁–C₅ products were readily identifiable, with only trace quantities of pentenes and hexanes observed. Isobutane, propane and pentane yields increase with increasing partial-pressure, whereas the yield of cracking products (methane, ethane, ethene, propene and butene) decreases.

Cracking is known to be a monomolecular process (Scheme 1C), whereas propane and particularly pentane formation mainly occur from the bimolecular C₈ intermediate (Scheme 1B).^{8,18,24,29,32,38,64} Here the behaviour of isobutane yield follows a similar trend to the bimolecular propane and pentane yields (increasing with increasing partial pressure), suggesting in this case, that isobutane is at least in part formed through a bimolecular process. Likely this is a result of the larger AlPO-5 pore aperture (7.3 × 7.3 Å), permitting the formation of the bulkier C₈ intermediate.

Scheme 1B shows that pentane and propane should be formed in equal molar amounts from the bimolecular pathway, however here the propane/pentane molar ratio varies from 4.2 at 0.056 bar, to 2.8 at 0.194 bar (Fig. S10B†). As propane cannot be formed through cracking, the uneven molar ratio is likely due to pentane undergoing secondary reactions.^{8,18,24,29,32,38,64} pentane has been found to be five times more reactive than n-butane, and, as such is susceptible to further reactions, even if formed in low quantities. Likely this will be either through a C₉ intermediate, as discussed above, leading to excess propane, or through monomolecular cracking of pentane to give C₁/C₄ or C₂/C₃ pairs. Wang et al. suggest that the propane/pentane molar ratio is a function of the maximum free sphere that can fit within a microporous channel.²⁷

Though the precise experimental conditions differ, the propane/pentane ratios of our MgAlPO-5 lie in the same region as frameworks with comparable sizes such as zeolite's Y and beta from their work, supporting this theory.²⁶

Investigating the distribution of cracking products (Fig. S10C†) shows similar quantities of ethane and ethene being formed, as expected. However, we see significantly more methane than propene, likely due to the subsequent reactions of propene. Unsurprisingly there is a greater quantity of butene than the other olefins, given the high concentration of n-butane precursor. It is possible that monomolecular cracking of pentane is contributing to the uneven molecular ratios. Converting the reaction data to formation rates (Fig. S11†) shows that the rates of all our products increase with increasing partial pressure, even for our cracking products, despite decreasing yields. This is a direct consequence of the conversion increasing with partial pressure, thus greater conversion, of more n-butane, leads to higher formation rates.

At higher partial pressures we expect to see a greater influence of the bimolecular pathways, due to the higher reaction order of n-butane. We separately focussed on the 0.30–1.00 bar region with 3% MgAlPO-5 (Fig. 2B and S12†). Conversion largely increases with n-butane partial pressure, but plateaus at 0.80 bar, and decreases at 1.00 bar were observed (Fig. S12A†).

Despite this, a larger absolute quantity of n-butane is still being converted (Fig. S13A†), though it is a smaller proportion of the total amount of n-butane, hence the perceived decrease in overall conversion. Careful inspection of the butane reaction rate (Fig. S13A†) does show it slowing down between 0.80 and 1.00 bar, likely as the catalyst is reaching its maximum possible activity, under these conditions. We note the formation of isobutane is well below the equilibrium limitations for this reaction, which previous work suggests would lead to equilibrium quantities of 47 mol% n-butane, and 53 mol% isobutane.⁶⁵ The product yields (Fig. 2B) all show similar trends to the conversion but comparing the high and low partial pressure data (Fig. 2) shows a significant decrease in the amount of cracking products, compared to the other products. This is again a result of higher partial pressure favouring bimolecular products more than the monomolecular (cracking) products. We observe a much greater yield of isobutane, again suggesting a significant bimolecular contribution.

The propane to pentane ratio (Fig. S12B†) drops from 2.6 at 0.30 bar to 2.0 at 1.00 bar, again decreasing with increasing partial pressure, suggesting that monomolecular cracking is a significant contributor to the uneven propane to pentane ratio. The distribution of cracking products at higher pressures (Fig. S12C†) resembles the lower pressures (Fig. S10C†), with methane, ethane and ethene having similar quantities, and similar relative amounts of olefins. Again, converting the product yields into reaction and formation rates (Fig. S13†), shows that the rates of all products increase with partial pressure, owing to gains in conversion and n-butane reaction rates.²⁷

By comparing the high and low partial pressure data we can explore how the experimental reaction orders change with pressure (Fig. 3, S14† and Table 1). The different species can be divided into those with reaction order < 1, namely methane, ethane, ethene, propene and butene, and those with reaction order > 1; i.e. propane, isobutane, pentane. Again, this confirms that the cracking products are primarily formed through the monomolecular mechanism, but the reaction orders are generally lower than the theoretical first order. The reaction order of propane, isobutane and pentane is significantly less than two, as would be expected for a bimolecular pathway. One may speculate that these products are being formed by a combination of monomolecular and bimolecular pathways, as such providing an intermediate number. However, this is inconsistent with the order decreasing with increased partial pressure. Increased n-butane partial pressure would result in a greater contribution from the bimolecular pathway, compared to the monomolecular, and an increase in reaction order. As we observe the opposite, we dismiss this idea. Instead, our findings are consistent with those of Wang et al. who studied n-butane isomerisation over ZSM-5, where the reaction orders were also found to decrease from the 0–0.1 bar region, to the 0.2–1.0 bar region. Wang et al. ascribed this to their derived rate law equation for the bimolecular pathway:²⁷

where r_bi is the rate of the bimolecular reaction, P is the partial pressure of n-butane.

Fig. 3 Deriving the reaction orders with respect to n-butane for isobutane formation, as a function of n-butane partial pressure between 0.05 and 0.20 bar, and 0.30 and 1.00 bar. Conditions: 0.6 g of catalyst, 400 °C, flow rates as per Tables S4 and S5.†

Table 1 Calculated reaction orders with respect to n-butane for 3% MgAlPO-5 at 400 °C, summarising findings from Fig. S14†

Reaction	Calculated reaction order
	0.05–0.20 bar	0.30–1.00 bar
n-Butane consumption	1.43	1.13
Methane formation	0.96	0.75
Ethane formation	1.00	0.82
Ethene formation	0.86	0.56
Propane formation	1.47	1.12
Propene formation	0.69	0.60
Isobutane formation	1.56	1.15
Butene formation	0.92	0.90
pentane formation	1.79	1.36

---

The K′P term represents the surface coverage of activated propane, n-butane, isobutane and pentane intermediates, whereas the K′′P² term represents the surface coverage of the C₈ intermediate. The K_bi term is a simplification term, containing several rate constants and equilibrium constants for various elementary steps. For further details on the equation and derivation we refer the reader to the original publication by Wang et al.²⁷

The valuable feature of this equation is its ability to describe behaviour at both high and low n-butane partial pressure. At low partial pressures, the surface coverage of any species, be it C₃–C₅, or C₈, will be incredibly low. Therefore, the K′P and K′′P² terms will also be low, compared to the constant of 1, which will dominate the denominator. As such the equation simplifies to being second order with respect to n-butane partial pressure (P). However, at higher pressures the acid sites will be saturated, and therefore the K′P and K′′P² terms will dominate the denominator, leading to less than second order behaviour. This describes the behaviour we see, with reaction order decreasing as the partial pressure increases.

To test this description further we now explore the behaviour of the 1% and 6% MgAlPO-5 systems. The number of acid sites is directly correlated to the quantity of activated surface species that can form, and therefore dictates the partial pressure at which the surface becomes saturated. As such higher dopant loading samples should have higher reaction orders, than lower loading samples, over the same partial pressure range. This is due to higher loading samples retaining the second order behaviour at higher pressures, due to the greater availability of acid sites.

Comparing the behaviour of 1% and 6% MgAlPO-5 under identical conditions (Fig. 4 and S15†) shows, as expected, the 6% MgAlPO-5 system has a higher conversion than the 1% MgAlPO-5 system; likely a function of having a greater quantity of acid sites (Table S2†). However, the overall order of conversion is that 3% > 6% > 1% (Fig. S10A and S15A†), suggesting conversion is not solely influenced by the quantity of acid sites. As the framework is unchanged and the acid site strength is similar for the 3% and 6% MgAlPO-5 systems, then the space around the active site, nor acid site strength can be contributing factors to the differences in conversion.

Fig. 4 Catalytic data of A) 1% MgAlPO-5, and B) 6% MgAlPO-5, showing the variation in product yield of main products, as a function of n-butane partial pressure between 0.05 and 0.20 bar. Conditions: 0.6 g of catalyst, 400 °C, flow rates as per Table S3.†

Instead, these findings suggest that the distribution and density of acid sites must be a contributing factor to the overall activity, with the 3% MgAlPO-5 system being a more active system. The overall product yields show similar trends to the 3% system, with isobutane being the main product, followed by the cracking products, propane and finally pentane. The lower conversion (and more isolated acid sites) in 1% MgAlPO-5 means that the selectivity for cracking is close to isobutane, but as the conversion increases, the isobutane becomes the more dominant product.

Comparing the data of all three systems at low pressure (Fig. 2A and 4) shows that with conversion increases, the selectivity to bimolecular products also increases. This is due to a greater quantity of activated n-butane molecules, capable of forming the C₈ species, leading to the bimolecular pathway, as suggested in other works. Comparing the C₃/C₅ ratios (Fig. S10B and S15B†) shows that all systems have similar values and trends, suggesting that the ratio is independent of conversion, or acid site density. As such, key factors affecting this ratio are more likely to be framework choice, temperature, partial pressure, and the acid site strength, all of which were kept constant in this study. The distribution of cracking products varies with conversion, where low conversion strongly favours butene formation (1% MgAlPO-5, Fig. S15C†).

Likely this is due to the absence of other activated species for butene to react with, or, cracking to butene and hydrogen just being the favoured route. As conversion increases, a more even distribution of cracking products occurs (Fig. S15D†), with more methane and ethene occurring. This may also be linked to the higher yields of pentane, which then undergoes a secondary reaction. Plotting the data as reaction rates (Fig. S16†) again shows similar trends to the 3% MgAlPO-5 systems (Fig. S11 and S13†).

On calculating the reaction orders with respect to metal loading (and acid site density) for each product (Fig. 5 and S17†) confirms our earlier hypothesis. Indeed, lower metal loadings, with fewer acid sites, translates to faster saturation, and a lowering of the reaction order.²⁷ The order for the monomolecular cracking products (methane, ethane, ethene, propene and butene) tends towards one, whilst the order for bimolecular products (propane, isobutane and pentane) tend towards two. Here the prevailing mechanism for isobutane formation appears to be bimolecular, in agreement with previous findings with ZSM-5, and in contrast to mordenite. This aligns with hypotheses from previous work suggesting the larger cavities in ZSM-5 allowed the larger C₈ intermediates to form unhindered, hence favouring the bimolecular processes.^27,28,66 Whereas the channels in the mordenite framework hindered the formation of larger intermediates, favouring monomolecular transformations instead, similar to small pore-type zeolites.^66–68 Extending this notion, we would also expect the large-pored AlPO-5 framework (7.3 × 7.3 Å) to permit the formation of larger intermediates, and therefore also allow the bimolecular reaction to prevail, similar to ZSM-5.^27,28

Fig. 5 Schematic summary of the variation in reaction orders with respect to n-butane partial pressure (0.05–0.20 bar), as a function of metal loading. Conditions: 0.6 g of catalyst, 400 °C, flow rates as per Table S4.†

We attempted to fit the 3% MgAlPO-5 data to the equation of Wang et al. over the whole 0–1 bar n-butane partial pressure range, though this led to significant errors in the K′ term (Table S6,† B).²⁷ Modifying the equation shows that our data fit well to an equation of the form:

where A and C are fitted parameters linked to K_bi and K′′. While this equation explains the change in reaction order with temperature, this is missing the K′P term (the surface coverage of C₃ and C₅ species) from the model of Wang et al. This suggests that in the present work the surface coverage of C₃–C₅ species, is constant and does not change with n-butane partial pressure.²⁷ However, despite this, the coverage of the C₈ species does still change with pressure and influence the kinetics.

In the work of Wang et al., olefins are purposefully removed from the feedstock, to limit their influence on the kinetics. Indeed, their mechanism does not consider the possibility of activated species forming from butene, or them contributing to C₈ formation:

C₄H₈ + HZ → C₄H₉⁺Z⁻

C₄H₈ + C₄H₉⁺Z⁻ → C₈H₁₇⁺Z⁻

As such, we believe the deviation in our data from the model of Wang et al. is due to the role of olefins being present, either as impurities in the feed or being formed in the reaction.²⁷ To investigate the role of olefins, particularly n-butene, on the reaction mechanism we probed the interactions of various butene isomers with the Brønsted acid sites of MgAlPO-5, using DFT calculations. We first focussed on the isomerisation of butene, rather than butane, as this is the reactive intermediate. Two mechanistic pathways were considered, the monomolecular skeletal isomerisation of n-butene, and the bimolecular pathway where two butenes form a C₈ intermediate which isomerises, and then cracks to yield isobutene and butene, as stated in previous work on H-SSZ-13.⁴⁷ We note here that we have also investigated the direct dehydrogenation of butane to butene and H₂, but have found it to be unfavourable, with a free energy barrier of 232 kJ mol⁻¹. In the monomolecular pathway, only 1-butene has been considered as a starting reactant.

Previous investigations have concluded that the activation energy of the skeletal isomerisation of butenes⁴⁷ is notably higher than of both double-bond migration and stereochemical isomerisation,⁶⁹ thus the various butene isomers will rapidly interconvert between 1-butene, cis-2-butene and trans-2-butene. While a skeletal isomerization (e.g. the n-butane isomerisation) describes a change in the branching degree of a hydrocarbon, a stereochemical isomerisation entails the change of the stereochemistry, i.e. the positioning of branching groups. For all pathways shown in this work we have chosen the most stable gas-phase species as the reference, which is trans-2-butene. For the monomolecular mechanism, the most favourable obtained transition state, starting from 1-butene is depicted (Fig. 6). As discussed above, the barrier for isomerization between 1-butene and 2-butene catalyzed by MgAlPO-5 is low (139 kJ mol⁻¹) and hence omitted in the figure, all energies are referenced to trans-2-butene. Both the mono- and biomolecular isomerisation are shown below (Fig. 6) at 400 °C and 1 bar of pressure.

Fig. 6 Free energy diagram comparing the monomolecular (black) to the bimolecular (red) butene isomerization mechanism, calculated at T = 400 °C and 1 bar. ΔG‡ values for the rate determining transition states are given explicitly. All intermediate energies and barriers are referenced to the empty zeolite and 2-butene in the gas phase, and are given in kJ mol⁻¹. Isomerization of 2-butene to 1-butene for the monomolecular pathway is omitted in the figure as the barriers are low (see text). Intermediate structures are shown in the graph; images of the transition state structures are shown below, with important bond distances given in pm.

In the monomolecular pathway (Fig. 6, black) 1-butene adsorbs onto the MgAlPO-5 active site with a free energy of 65 kJ mol⁻¹ (referenced to 2-butene). 1-butene then reacts through a single transition state (TS.U1) to form an isobutoxide, with a free energy barrier of 147 kJ mol⁻¹ (shown in more detail in Fig. S18 in the ESI†). This is followed by a hydride shift and desorption to form an unstable tert butyl cation. This process has a free energy barrier of 148 kJ mol⁻¹, similar as reported in previous work.⁴⁷ The tert butyl cation then transfers a proton back to the zeolite, leading to a bound isobutene, which then subsequently desorbs from the active site, yielding isobutene. Carbonium ions like the methylcyclopropanes formed in TS.U1 and also TS.B2 have been discussed to be important for the n-butane isomerization reaction.^8,24,70–72

In the bimolecular pathway (Fig. 6, red) two molecules of trans-2-butene sequentially co-adsorb at the active site, with free energy values of 45 and 101 kJ mol⁻¹, respectively. The large increase in free energy on adsorbing the second butene is largely driven by the entropic contribution (−TΔS = 219 kJ mol⁻¹). Once co-adsorbed at the MgAlPO-5 active site, a C–C bond readily forms, leading to a C₈ intermediate (shown in more detail in Fig. S19 in the ESI†), which then undergoes a methyl shift (ΔG‡ = 155 kJ mol⁻¹) and then a hydride shift. The C₈ species then undergoes β-scission, yielding isobutene and a 2-butyl cation. The 2-butyl cation then transfers a proton back to MgAlPO-5, recovering the Brønsted acid site and giving 2-butene. The two alkene species are then subsequently desorbed. The free energy values of the highest barriers of the two mechanisms (148 kJ mol⁻¹, monomolecular and 155 kJ mol⁻¹, bimolecular) differ by only 7 kJ mol⁻¹, and can thus be seen as competing under the given reaction conditions.

We now discuss the hydrogen transfer mechanism for the formation of isobutane from n-butane. In this mechanism, adsorbed isobutene reacts with n-butane via two hydrogen transfers to isobutane and n-butene, see Fig. 7. Co-adsorption of isobutene and then subsequently n-butane occurs with free energy values of 38 and 114 kJ mol⁻¹, again due to the entropic contribution (−TΔS = 217 kJ mol⁻¹). Isobutene is then protonated by the Brønsted acid site to form a tert-butyl cation. In a further transition state (189 kJ mol⁻¹, TS.H2) a hydride is transferred from n-butane to the tert-butyl cation, yielding isobutane. Simultaneously n-butane is deprotonated to recover the Brønsted acid site on MgAlPO-5, yielding 2-butene (shown in more detail in Fig. S20 in the ESI†). This barrier was calculated to be 180 kJ mol⁻¹, and the C–H length between the two hydrocarbons is 193 pm. However, we need to stress that no initial olefins can be produced through this mechanism. For this reaction to take place, very small initial amounts of olefins are sufficient, which are usually present in the n-butane feed even when utilizing a butene trap, as has been shown by Wulfers et al.¹⁸

Fig. 7 Free energy diagram of the intramolecular hydrogen transfer (HT) mechanism, calculated at T = 400 °C and 1 bar. The ΔG‡ value for the rate determining transition states is given explicitly. All intermediate energies and barriers are referenced to the empty zeolite and isobutene and n-butane in the gas phase, and given in kJ mol⁻¹. Intermediate structures are shown in the graph; images of the transition state structures are shown below, with important bond distances given in pm.

Note, that within this mechanism even small amounts of olefins catalyze the n-butane isomerization process. This aligns with our experimental findings which also confirms their importance and clarifies the roles they play.

Conclusions

Microporous catalysts are promising candidates for promoting n-butane isomerisation to isobutane. Whilst not necessarily the optimal system for industrial use, MgAlPO-5 serves as an excellent model system owing to its active site uniformity, isolated acid sites and (comparatively) large pore diameter of 7.3 × 7.3 Å. In this work we have demonstrated that, unlike many microporous zeolite systems, we can vary the acid site concentration of MgAlPO-5. By controlling the quantity of Mg substituting Al in the AlPO-5 framework (1, 3, or 6%), different quantities of acid sites can be created, without significant changes to the properties of the active sites. This allows direct correlations to be made between catalytic performance and the number of active sites, only. By probing the reaction order of the different products, we determined that the olefinic products and methane formed almost exclusively via a monomolecular pathway, whereas isobutane, propane, and pentane were primarily formed via a bimolecular pathway. Previous work suggests the precise pathway for isobutane formation in microporous catalysts depends on the framework topology, particularly the size of the pore diameter. Here we believe the larger AlPO-5 pore diameter (7.3 × 7.3 Å) doesn't notably hinder two n-butane molecules coming together, thereby permitting the bimolecular pathway more than smaller pores in other microporous systems. These observations were further tested by exploring the influence of butane partial pressure on conversion, and product selectivity, which led to notable improvements in isobutane formation, though had less influence on products formed via the monomolecular pathway.

Notably the bimolecular pathway requires olefinic butene species, which may be present either as impurities in the butane feed or could be formed within the reaction itself. As such we have combined theoretical and experimental data to explore the reaction pathways that operate in MgAlPO-5, with emphasis on the butene species. The calculated free energies of the monomolecular and bimolecular pathways were found to differ by less than 7 kJ mol⁻¹, suggesting both pathways would be competitive, under these conditions. This was in good agreement with the experimental findings that showed the formation of isobutane was primarily bimolecular, but still had monomolecular contributions. Overall through combining experimental and theoretical results, we have been able to demonstrate the influence of acid site quantity and n-butane partial pressure on reaction pathways in a larger microporous MgAlPO-5 catalyst, which can now be readily compared with previous work on other microporous zeolite systems.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

M. E. P. wrote the manuscript and performed the experimental work. L. S. performed the computational work and helped write the manuscript. P. N. P. helped write, review, and edit the manuscript. E. B. M. and M. C. collected SEM and NMR characterisation data. A. E. O., T. B., and J. H. C. collected and analysed the pyridine DRIFTS data. B. D. V. and K. M. K. helped write, review, and edit the manuscript. F. S., B. D. V., and R. R. helped with funding acquisition, supervision and to review and edit the manuscript. All authors have approved and contributed to the final manuscript.

Conflicts of interest

The authors declare that this study received funding from TotalEnergies OneTech Belgium. The funder had the following involvement in the study: discussion and interpretation of data, as well as the decision to submit and support in writing the publication.

Acknowledgements

This study was conducted as part of the Consortium of Metal Nanocatalysis funded by TotalEnergies OneTech Belgium. The authors acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology. Support from TotalEnergies through Houston HPC computational resources is greatly acknowledged. Prof. Graham Hutchings is thanked for kind access to his groups DRIFTS equipment at Cardiff University.

Notes and references

1. M. Amer, E. Z. Wojcik, C. Sun, R. Hoeven, J. M. X. Hughes, M. Faulkner, I. S. Yunus, S. Tait, L. O. Johannissen, S. J. O. Hardman, D. J. Heyes, G.-Q. Chen, M. H. Smith, P. R. Jones, H. S. Toogood and N. S. Scrutton, Energy Environ. Sci., 2020, 13, 1818–1831.
2. M. E. Potter, J. J. M. Le Brocq, A. E. Oakley, E. B. McShane, B. D. Vandegehuchte and R. Raja, Catalysts, 2020, 10, 1099.
3. P. Wang, M. Zhang, W. Zhang, C. Yang and C. Li, Ind. Eng. Chem. Res., 2017, 56, 8456–8464.
4. V. Adeeva and W. M. H. Sachtler, Appl. Catal., A, 1997, 163, 237–243.
5. G. A. Urzhuntsev, E. V. Ovchinnikova, V. A. Chumachenko, S. A. Yashnik, V. I. Zaikovsky and G. V. Echevsky, Chem. Eng. J., 2014, 238, 148–156.
6. V. Nieminen, N. Kumar, T. Salmi and D. Y. Murzin, Catal. Commun., 2004, 5, 15–19.
7. P. Del Gallo, F. Meunier, C. Pham-Huu, C. Crouzet and M. J. Ledoux, Ind. Eng. Chem. Res., 1997, 36, 4166–4175.
8. P. Cañizares, A. de Lucas, F. Dorado and D. Pérez, Appl. Catal., A, 2000, 190, 233–239.
9. T. Kurniawan, O. Muraza, A. S. Hakeem, I. A. Bakare, T. Nishitoba, T. Yokoi, Z. H. Yamani and A. M. Al Amer, Energy Fuels, 2017, 31, 12691–12700.
10. M. Shamzhy, M. Opanasenko, P. Concepcion and A. Martinez, Chem. Soc. Rev., 2019, 48, 1095–1149.
11. J. Shi, Y. Wang, W. Yang, Y. Tang and Z. Xie, Chem. Soc. Rev., 2015, 44, 8877–8903.
12. I. Lezcano-Gonzalez, E. Campbell, A. E. J. Hoffman, M. Bocus, I. V. Sazanovich, M. Towrie, M. Agote-Aran, E. K. Gibson, A. Greenaway, K. De Wispelaere, V. Van Speybroeck and A. M. Beale, Nat. Mater., 2020, 19, 1081–1087.
13. I. Lezcano-González, P. Cong, E. Campbell, M. Panchal, M. Agote-Arán, V. Celorrio, Q. He, R. Oord, B. M. Weckhuysen and A. M. Beale, ChemCatChem, 2022, 14, e202101828.
14. H. O. Pastore, S. Coluccia and L. Marchese, Annu. Rev. Mater. Res., 2005, 35, 351–395.
15. M. E. Potter, ACS Catal., 2020, 10, 9758–9789.
16. F. Corà, M. Alfredsson, C. M. Barker, R. G. Bell, M. D. Foster, I. Saadoune, A. Simperler and C. R. A. Catlow, J. Solid State Chem., 2003, 176, 496–529.
17. E. Gianotti, M. Manzoli, M. E. Potter, V. N. Shetti, D. Sun, J. Paterson, T. M. Mezza, A. Levy and R. Raja, Chem. Sci., 2014, 5, 1810–1819.
18. M. J. Wulfers and F. C. Jentoft, J. Catal., 2015, 330, 507–519.
19. M. Gešvandtnerová, T. Bučko, P. Raybaud and C. Chizallet, J. Catal., 2022, 413, 786–802.
20. J. Rey, A. Gomez, P. Raybaud, C. Chizallet and T. Bučko, J. Catal., 2019, 373, 361–373.
21. J. Rey, P. Raybaud, C. Chizallet and T. Bučko, ACS Catal., 2019, 9, 9813–9828.
22. X. Gong, M. Caglayan, Y. Ye, K. Liu, J. Gascon and A. Dutta Chowdhury, Chem. Rev., 2022, 122, 14275–14345.
23. R. A. Asuquo, G. Eder-Mirth, K. Seshan, J. A. Z. Pieterse and J. A. Lercher, J. Catal., 1997, 168, 292–300.
24. R. A. Asuquo, G. Edermirth and J. A. Lercher, J. Catal., 1995, 155, 376–382.
25. M. E. Potter, J. J. M. Le Brocq, A. E. Oakley, H. Cavaye, B. D. Vandegehuchte and R. Raja, Chem. Commun., 2022, 58, 10659–10662.
26. M. T. Tran, N. S. Gnep, G. Szabo and M. Guisnet, J. Catal., 1998, 174, 185–190.
27. P. Wang, W. Zhang, H. Zhu, P. Yuan, C. Yang, C. Li and X. Bao, Appl. Catal., A, 2019, 584, 117135.
28. P. Wang, S. Wang, Y. Yue, T. Wang and X. Bao, Microporous Mesoporous Mater., 2020, 292, 109748.
29. P. Cañizares, A. de Lucas and F. Dorado, Appl. Catal., A, 2000, 196, 225–231.
30. M. T. Tran, N. S. Gnep, G. Szabo and M. Guisnet, Appl. Catal., A, 1998, 170, 49–58.
31. M. J. Wulfers, G. Tzolova-Müller, J. I. Villegas, D. Y. Murzin and F. C. Jentoft, J. Catal., 2012, 296, 132–142.
32. X. Li, K. Nagaoka, L. Simon, R. Olindo and J. Lercher, J. Catal., 2005, 232, 456–466.
33. M. V. Luzgin, A. G. Stepanov, S. S. Arzumanov, V. A. Rogov, V. N. Parmon, W. Wang, M. Hunger and D. Freude, Chemistry, 2005, 12, 457–465.
34. L. Zhang, Y. Ren, B. Yue and H. He, Chem. Commun., 2012, 48, 2370–2384.
35. P. Wang, W. Zhang, Q. Zhang, Z. Xu, C. Yang and C. Li, Appl. Catal., A, 2018, 550, 98–104.
36. P. Cnudde, M. Waroquier and V. Van Speybroeck, Catal. Sci. Technol., 2023, 13, 4857–4872.
37. W. Chen, X. Yi, Z. Liu, X. Tang and A. Zheng, Chem. Soc. Rev., 2022, 51, 4337–4385.
38. S. Li, J. Cao, Y. Liu, X. Feng, X. Chen and C. Yang, Catal. Today, 2020, 355, 171–179.
39. M. Boronat, P. Viruela and A. Corma, Phys. Chem. Chem. Phys., 2001, 3, 3235–3239.
40. F. Ferrante, T. Rubino and D. Duca, J. Phys. Chem. C, 2011, 115, 14862–14868.
41. D. Gleeson, J. Phys. Chem. A, 2011, 115, 14629–14636.
42. M. He, J. Zhang, R. Liu, X. Sun and B. Chen, Catalysts, 2017, 7, 11.
43. M. John, K. Alexopoulos, M.-F. Reyniers and G. B. Marin, Catal. Sci. Technol., 2017, 7, 1055–1072.
44. C. Wattanakit, S. Nokbin, B. Boekfa, P. Pantu and J. Limtrakul, J. Phys. Chem. C, 2012, 116, 5654–5663.
45. J. Wei, M. Zheng, D. Chen, C. Wei, Y. Bai, L. Zhao, J. Gao and C. Xu, Ind. Eng. Chem. Res., 2022, 61, 5429–5441.
46. X. Zhang, H. Li, Y. Du, X. Chen, P. Wang, L. Wang, X. Feng, C. Yang and S. Li, Fuel, 2023, 339, 127397.
47. L. Spiske, P. N. Plessow, K. Kazmierczak, B. D. Vandegehuchte and F. Studt, Front. Catal., 2023, 3, 1213803.
48. A. Hjorth Larsen, J. Jorgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiotz, O. Schutt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
49. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
51. P. N. Plessow, J. Chem. Theory Comput., 2018, 14, 981–990.
52. R. Y. Brogaard, R. Henry, Y. Schuurman, A. J. Medford, P. G. Moses, P. Beato, S. Svelle, J. K. Nørskov and U. Olsbye, J. Catal., 2014, 314, 159–169.
53. R. Y. Brogaard, C.-M. Wang and F. Studt, ACS Catal., 2014, 4, 4504–4509.
54. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
55. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
56. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
57. M. Von Arnim and R. Ahlrichs, J. Comput. Chem., 1998, 19, 1746–1757.
58. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
59. T. J. Goncalves, P. N. Plessow and F. Studt, ChemCatChem, 2019, 11, 4368–4376.
60. D. Padovan, A. Al-Nayili and C. Hammond, Green Chem., 2017, 19, 2846–2854.
61. D. S. A. Silva, W. N. Castelblanco, D. H. Piva, V. de Macedo, K. T. G. Carvalho and E. A. Urquieta-González, Mol. Catal., 2020, 492, 111026.
62. R. K. Parsapur and P. Selvam, Sci. Rep., 2018, 8, 16291.
63. P. Huber, F. Studt and P. N. Plessow, J. Phys. Chem. C, 2022, 126, 5896–5905.
64. K. Surla, H. Vleeming, D. Guillaume and P. Galtier, Chem. Eng. Sci., 2004, 59, 4773–4779.
65. S. S. Chen, R. C. Wilhoit and B. J. Zwolinski, J. Phys. Chem. Ref. Data, 1975, 4, 859–870.
66. W. Zhang, P. Wang, C. Yang and C. Li, Catal. Lett., 2019, 149, 1017–1025.
67. D. Jo and S. B. Hong, ChemCatChem, 2016, 9, 114–116.
68. D. Jo, S. B. Hong and M. A. Camblor, ACS Catal., 2015, 5, 2270–2274.
69. M. Kangas, N. Kumar, E. Harlin, T. Salmi and D. Y. Murzin, Ind. Eng. Chem. Res., 2008, 47, 5402–5412.
70. T. Suzuki and T. Okuhara, Chem. Lett., 2000, 29, 470–471.
71. N. Lohitharn, E. Lotero and J. Goodwinjr, J. Catal., 2006, 241, 328–341.
72. M. Boronat and A. Corma, Appl. Catal., A, 2008, 336, 2–10.

---

Footnote

† Electronic supplementary information (ESI) available: Including experimental methods, catalyst characterisation data, further catalysis data and DFT calculations. See DOI: https://doi.org/10.1039/d4cy01035c

---