 Open Access Article
Open Access ArticleApplication of machine learning to discover new intermetallic catalysts for the hydrogen evolution and the oxygen reduction reactions†
Carmen
Martínez-Alonso
 abc,
Valentin
Vassilev-Galindo
abc,
Valentin
Vassilev-Galindo
 a,
Benjamin M.
Comer
c,
Frank
Abild-Pedersen
c,
Kirsten T.
Winther
c and
Javier
LLorca
a,
Benjamin M.
Comer
c,
Frank
Abild-Pedersen
c,
Kirsten T.
Winther
c and
Javier
LLorca
 *ad
*ad
aIMDEA Materials Institute, C/Eric Kandel 2, 28906 – Getafe, Madrid, Spain. E-mail: javier.llorca@upm.es; javier.llorca@imdea.org
bDepartment of Inorganic Chemistry, Complutense University of Madrid, 28040 Madrid, Spain
cSUNCAT Center for Interface Science and Catalysis, Department of Chemical Engineering, SLAC National Accelerator Laboratory, Stanford University, Menlo Park, Stanford, California 94305, USA
dDepartment of Materials Science, Polytechnic University of Madrid, E. T. S. de Ingenieros de Caminos, 28040 Madrid, Spain
First published on 4th June 2024
Abstract
The adsorption energies for hydrogen, oxygen, and hydroxyl were calculated by means of density functional theory on the lowest energy surface of 24 pure metals and 332 binary intermetallic compounds with stoichiometries AB, A2B, and A3B taking into account the effect of biaxial elastic strains. This information was used to train two random forest regression models, one for the hydrogen adsorption and another for the oxygen and hydroxyl adsorption, based on 9 descriptors that characterized the geometrical and chemical features of the adsorption site as well as the applied strain. All the descriptors for each compound in the models could be obtained from physico-chemical databases. The random forest models were used to predict the adsorption energy for hydrogen, oxygen, and hydroxyl of ≈2700 binary intermetallic compounds with stoichiometries AB, A2B, and A3B made of metallic elements, excluding those that were environmentally hazardous, radioactive, or toxic. This information was used to search for potential good catalysts for the HER and ORR from the criteria that their adsorption energy for H and O/OH, respectively, should be close to that of Pt. This investigation shows that the suitably trained machine learning models can predict adsorption energies with an accuracy not far away from density functional theory calculations with minimum computational cost from descriptors that are readily available in physico-chemical databases for any compound. Moreover, the strategy presented in this paper can be easily extended to other compounds and catalytic reactions, and is expected to foster the use of ML methods in catalysis.
Introduction
Further expansion of the application of renewal energy sources is limited because the power provided by solar and wind energy (as opposed to coal, natural gas, and nuclear) is intermittent and has to be associated with large energy storage capabilities. Hydrogen energy storage offers a unique combination of scalability, long-term storage, and portability, leading to the so-called hydrogen economy. In this model, renewable energy sources are used to split water into hydrogen and oxygen. The hydrogen is stored for later use in fuel cells or gas-fired turbines to generate electricity without the emission of pollutants.1–6 In fact, the limitations to implementing the hydrogen economy are not with the storage but with the production of hydrogen from water and the generation of energy by the oxidation of hydrogen into water. The efficiency and kinetics of the former process are controlled by the hydrogen evolution reaction (HER) and those of the latter by the oxygen reduction reaction (ORR). Platinum (Pt) is the best catalyst in both cases (HER and ORR) and allows high reaction rates to be reached in an acidic environment with very small overpotentials.7–10 However, the cost and scarcity of Pt is one of the main factors that limits the widespread application of these technologies to use hydrogen as a clean energy source.Obviously, the search for efficient and affordable catalysts for the HER and the ORR is a critical priority to ensure the success of the hydrogen economy, and the research effort has been very large (see, for instance, ref. 11). The final goal is to modify the catalyst's electronic structure to achieve an optimum performance and this can be achieved by adding other elements to form an alloy or compound,12–19 introducing defects in the crystal lattice or changing the surface facets20,21 and also through the application of elastic strains.22–25 The combination of all these variables gives rise, however, to endless possibilities that cannot be explored experimentally without computational tools to guide research towards more promising materials and structures.
The extraordinary progress of ab initio calculation methods based on density functional theory (DFT) to calculate the electronic structure has opened the door for the virtual design of catalysts from computer simulations.26 There are examples in the scientific literature in which the entire kinetics of a catalytic reaction (including the determination of the activation states as well as the activation and reaction energies and the corresponding entropic contributions) have been determined from DFT calculations and Monte Carlo simulations,27,28 but it is necessary to recognize that the evaluation by first principles of the kinetics of all the reactions in a catalytic process is –in most cases– an impossible task. Therefore, the discovery of new catalysts through simulations is usually carried out based on the rational definition of different descriptors related to various stages of the catalytic process that allow determining the stages that control the kinetics of said reaction. The identification of these descriptors can be simplified because the activation energies of the elemental reactions on the catalyst surface are proportional to the adsorption energies according to the Brønsted–Evans–Polanyi principle.29 In this regard, the accuracy associated with DFT in the calculation of adsorption energies is in the range of 0.1 eV30 and this strategy has been used in the HER and the ORR reactions with good agreement between theoretical and experimental results.26,31 Moreover, DFT calculations have been used recently by us to analyze the effect of elastic strains on the catalytic activity of transition metals for the HER and ORR, providing good agreement with the experimental evidence available in the literature.24,32,33
However, the computational cost of DFT-scales as O(n3), with n being the number of electrons in the system34 – prevents a detailed exploration of the chemical compound space spanned by all possible intermetallic materials.35 This limitation has encouraged the use of strategies based on artificial intelligence, namely machine learning (ML), in the prediction of new materials in different fields, including catalysis.36–40 Nevertheless, the application of ML tools to assess catalytic processes involving hydrogen is scarcely explored41,42 due to three main limitations: the first one is the lack of large and robust databases that can be used to train ML algorithms that can deal with different geometries, stoichiometries, and surfaces.43,44 The second limitation is the lack of accuracy of the ML model predictions, which provide mean absolute errors (MAEs) equal to or higher than 0.16 eV for H,45 and 0.23 eV for O and OH adsorption energies,46 too large to predict the catalytic activity. Finally, information about the influence of elastic strains on the catalytic activity is missing.
The objective of this investigation is to overcome these limitations and develop an accurate ML model to describe the adsorption processes for the HER and the ORR in intermetallic compounds. To this end, a large database of the adsorption energies of H, O, and OH was computed by DFT in 24 pure metals and 332 binary intermetallic compounds with different lattice structures, stoichiometries, and surfaces, including the effect of biaxial elastic strains. This information was used to train a random forest model to predict the adsorption energy of ≈2700 binary intermetallic compounds including the effect of elastic strains using descriptors that can be obtained for each compound and surface from physico-chemical databases. A short list of candidates presented similar adsorption energies to Pt, indicating their potential to replace Pt-group metals as catalysts in these reactions. Overall, this investigation demonstrates a strategy based on the synergistic application of high-throughput DFT calculations and artificial intelligence tools to discover new catalysts for the HER and ORR that can be easily employed for other catalytic processes.
Results
Screening and database
In order to build a database of adsorption energies able to cover intermetallic compounds of transition metals, 24 pure metals were included in the database. The most stable (minimum energy) surface was selected for each element according to the information available in the Materials Project database47 and the reference of experimental data.48 That led us to five different slab geometries: fcc(111) for Ag, Au, Cu, Ir, Ni, Pd, Pt, and Rh, bcc(110) for Cr, Fe, Mo, Nb, Ta, and W, bcc(100) for V, hcp(0001) for Cd, Co, Hf, Os, Re, Ru, Zn, and Zr, and hcp(1010) for Y. Regarding binary intermetallic compounds, the screening depicted in Fig. 1 was carried out to select the best candidates to include in the database. Starting from all the possible binary intermetallic compounds available in the Materials Project database,47 some restraints were included to eliminate elements that are not suitable as catalysts. Thus, environmentally hazardous (Hg, Pb, P, and As), radioactive (Tc, Fr, Ra, Po, At, Rn, Rf, Db, Sg, Bh, Hs, Mt, Ds, Rg, Cn, Nh, Fl, Mc, Lv, Ts, and Og), and toxic (Be, Tl, and Se) elements were excluded from the database. Moreover, unstable binary intermetallic compounds (energy above hull ≠ 0)47 were also excluded, leading to 2458 possible binary intermetallic compounds. For keeping computational costs as low as possible without compromising the completeness of our database, we computed the adsorption energy for the three adsorbates (H, O, OH) on different adsorption sites only for a diverse and representative subset of the starting list of compounds. Firstly, only compounds with the most common AnB stoichiometries: AB, A2B, and A3B, which comprise 62% of the total number of binary intermetallic compounds, were included. The other 38% was composed of the rest of the AnB (A4B 1.9%, A5B 2.8%, A6B 0.7%, A7B 0.2%, A8B 0.1%, A9B 0%), and AnBm (32.3%) stoichiometries. Even though the compounds with AnBm stoichiometry stand for a considerable amount of the available binary intermetallic materials, the combinations between n and m are that different, that is not possible to find a general trend in the adsorption energy for them. Furthermore, the crystal lattices are very specific on each candidate – orthorhombic, monoclinic, tetragonal, triclinic and a proper grouping between candidates is not possible to study them. Thus, restricting our study to AB, A2B, and A3B materials allows us to cover the majority of the surfaces commonly used in catalysis as well as a significant percentage of the existing binary intermetallics. | ||
| Fig. 1 Flowchart for the database generation: strategy to select the binary intermetallic compounds for the database of adsorption energies. | ||
For each stoichiometry, only the most stable lattice and the lowest energy surface were considered for the calculations, namely 117 AB bcc(101), 9 AB fcc(101), 24 A2B hcp(0001), 118 A3B fcc(111), and 20 A3B hcp(0001) compounds were found, leading to a total of 332 compounds. From those, we randomly selected 106 compounds to compute by DFT the adsorption energy of H, O, and OH with and without the application of biaxial strains. Adsorption is a very localized process since the adsorption energy depends on the local atomic environment of the adsorption site. Therefore, we explored all possible adsorption sites for both the pure metals and binary intermetallic compounds (see Fig. 2). The main adsorption sites for pure metals (Fig. 2a–e) are FCC, HCP, ONTOP, and BRIDGE. At FCC and HCP positions, the adsorbate is placed on a hole between three atoms. At FCC, there is no atom in the second layer below, while at HCP, a metal atom is present right under the adsorbate. ONTOP refers to the adsorption above an atom of the first layer, and BRIDGE describes the adsorption at the bond between two atoms. For bcc(100) surfaces we must discriminate between SHORTBRIDGE and LONGBRIDGE, as there are two different bond distances on the surface. HOLLOW refers to the adsorption site in the hole between four atoms. For most pure metals, the most favorable adsorption sites (lowest adsorption energies) were FCC and HCP. In contrast, BRIDGE and ONTOP positions were higher in energy and, in some cases, they were unstable (i.e., the adsorbate moved to another position during the geometry optimization). Those cases where the adsorbate moved were not included in the database since they corresponded to repeated entries. For the binary intermetallic compounds (Fig. 2f–j), the number of possible adsorption sites was bigger, as we had to discriminate between A and B atoms on the surface. Here, we studied different FCC and HCP possibilities depending on the three atoms around the hole –AAA, AAB, or ABB–. Similarly, the ONTOP positions could occur above an atom A or an atom B, and BRIDGE sites between two atoms AA, BB, or AB. In AB bcc(101) samples, an extra position appeared: THREEFOLD. It stands for a hole between three atoms where the atom in the second layer below is at an intermediate position between FCC and HCP. The most favorable binding site for binary intermetallics was highly dependent on the affinity of the adsorbate towards A or B.
The adsorption energy varies significantly with the adsorption site. For instance, we found that the adsorption energy can change in more than 1 eV between a hole between three atoms (FCC, HCP, THREEFOLD) to a bond between two atoms (BRIDGE, LONGBRIDGE, SHORTBRDIGE) or ONTOP a single atom. Additionally, the specific atoms around the adsorption site are also very relevant. For instance, in the adsorption process on a THREEFOLD position in a binary compound AnB, the three atoms around the adsorbate can be AAA, AAB, or ABB and the adsorption energy can change in more than 0.5 eV by changing one single atom.
The results of the DFT calculations are included in two different databases: one with EHads and the other with EOads and EOHads. Given that EOads and EOHads are linearly correlated49 and that OH binds to the surface by the O atom, it was expected that one single model could be able to predict the adsorption energy of both adsorbates. A total of 130 different pure metals and binary intermetallic compounds were included: 24 pure metals, 58 AB bcc(101), 8 AB fcc(101), 6 A2B hcp(0001), 26 A3B fcc(111), and 8 A3B hcp(0001). The total number of entries in the two databases was 942 and 1699, respectively, considering the different adsorption sites and strain states. The distribution and the number of entries of the database are shown in Fig. 3. A tabulated version can be found in Table S2 of the ESI.† The inputs and the outputs of the DFT calculations for the adsorption energies can be found in Catalisys-Hub.org43via the link https://www.catalysishub.org/publications/AlonsoStrain2023.
Feature selection
Selection of the most appropriate descriptors is a key step to improve the accuracy of a ML model. Previous works on catalysis have focused on descriptors of many different types. Tehrani et al.50 included the group and period number, the polarizability, the melting point, the boiling point, the specific heat, the crystal system, and the electron density. Wang et al.51 used the formation enthalpy, the surface energy, and the Bader charge, among others. Hansen et al.52 and Lamoureux et al.53 considered the distance between atoms, the bulk formation energies, and the surface termination atoms. Additionally, other authors include descriptors based on the d-bands, such as the band gap, the d-band center, or the d-band width.46,54 All of these were considered and finally discarded by either redundancy or because they needed DFT calculations to be determined.Following these previous references, 9 descriptors from 3 different types were chosen as features in our ML model. Two of them are characteristic of each adsorption site on the surface of the intermetallic compound and describe the geometry configuration of the adsorption site and the chemical environment around the site. The third descriptor is extrinsic and indicates the biaxial elastic strain applied to the surface. The nine geometrical, electronic, and strain descriptors are depicted in Table 1. One important condition for the intrinsic descriptors is that they can be calculated for any compound, surface, and adsorption site from data available in structural and electronic databases. In fact, the values for the atomic radii, the electronegativity, and the first ionization energy were taken from the Mendeleev Python package,55 whereas the unit cell volume was taken from the Materials Project database.47 Although additional descriptors (such as the d-band center and the d-band width) can provide a better description of the local chemical environment,56–58 they require expensive DFT calculations that would hinder an efficient exploration of thousands of intermetallic compounds. Finally, an extra descriptor was needed to describe the prediction of either O or OH in the database for the adsorption energy of O and OH. It was a categorical and binary descriptor with a value of 0 for O and 1 for OH adsorption. The reason for employing a Boolean descriptor over more elaborate physical or categorical features to encode the information of the adsorbate is simple. The adsorption of OH always happens with the O atom close to the surface and the H atom above it, while O is a single atom interacting with the surface. Thus, there are no other relevant degrees of freedom that characterize adsorbate-slab interactions apart from the position of the adsorbates above the surface (already included in the information of other descriptors that will be described later, such as the generalized coordination number and Ψ). A Boolean descriptor (0/1), which in this scenario is formally equivalent to a categorical feature with values O and OH, serves to encode the only missing information: the identity of the adsorbate. Before feeding the descriptors to train the RF models, all non-categorical descriptors were scaled to a [0,1] range with a MinMax scaler.
| Geometric descriptors | Unit cell volume |
| Weighted atomic radius (WAR) | |
| Generalized coordination number (GCN) | |
| Electronic descriptors | Weighted electronegativity (WEN) |
| Weighted first ionization energy (WIE) | |
| Outer electrons of A (SA) | |
| Outer electrons of B (SB) | |
| Ψ | |
| Strain descriptor | Biaxial strain |
Geometric descriptors
The geometric descriptors contain information related to the stoichiometry of the binary intermetallic compound, the size of the supercell, the adsorption plane, and the properties of the binding site. The unit cell volume – expressed in Å3 – corresponds to the volume of the unit cell of the bulk that can be retrieved from the Materials Project database.47 We considered normalizing the unit cell volume to the number of atoms, but as 98% of the surfaces included have exactly 16 atoms on the supercell, this approximation does not affect the overall performance of our models. It gives information related to the bond distance and the spacing between layers, which plays a significant role in the adsorption process. The weighted atomic radius (WAR) provides information on the individual size of the atoms by weighting the atomic radius of atoms A and B according to the stoichiometry of the system. The size of the atoms is an indirect measurement of the distance between their nucleus and their electrons in the valence shell, which plays a major role in the binding energy. For a binary intermetallic compound AnBm, it is calculated as: | (1) |
The generalized coordination number (GCN) is the feature employed to describe the adsorption plane as well as the binding site where the adsorption takes place. Each adsorption site at a specific surface plane has a unique GCN, which allows our model to discriminate between geometries and facets. It can be computed as:59
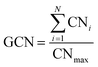 | (2) |
Other geometrical features, such as the lattice parameters, the cell size, and the area of the adsorption hole, were explored but they provided information equivalent to that of the unit cell volume. The molecular mass was also included but it did not correlate with the adsorption phenomena.
Electronic descriptors
This second set of descriptors aims to describe the electronic properties of the binary intermetallic compounds and of the binding site where the adsorption occurs. The weighted electronegativity (WEN) is analogous to the WAR and can be defined as: | (3) |
The weighted first ionization energy (WIE) can similarly be expressed as:
 | (4) |
The outer electrons of A and B range from 1 to 12 and reflect the electronic properties of the valence layer for element A and element B, respectively. These are the electrons that interact with the adsorbate and, therefore, influence the adsorption energy.
The last descriptor of this set is Ψ that was proposed by Gao et al.60 according to
 | (5) |
The magnetic moment of the intermetallic compounds was also explored as an additional electronic feature but it had very low importance in the description of the adsorption process and the errors of the model experimented no variation when this feature was included. Thus, it was not included among the descriptors.
Strain descriptor
The final descriptor is the biaxial elastic strain applied to the system. It is defined as a percentage with negative values for compressive strains and positive values for tensile strains. This is an extrinsic descriptor, in contrast to the rest of the features, which are intrinsic properties of the materials. The strain descriptor is defined as ε (×100) in the deformation gradient F applied to the supercell (see Methods section) and stands as the normal strain applied to the surface of the metallic materials. The stresses perpendicular to the surface plane have been considered equal to zero. The range of strain applied vary from −8% compression to 8% tension as it has been proven to be an stable window in previous publications.25,61Descriptor analysis
The maximum and minimum values and the units for each descriptor are shown in the ESI† Table S1. We can expect the predictions of our models not to be reliable for binary intermetallic compounds whose descriptors' values are outside the ranges of the dataset. However, the ranges are very wide, and it is difficult to find binary intermetallics outside those limits. Hence, it is more informative to look at the shape of the distributions for anticipating model performance. In principle, our models should behave correctly for compounds whose features lie within the limits of the distributions. Nevertheless, some distributions have non-uniform shapes. This indicates that training sets must be selected carefully, ensuring the inclusion of compounds from less populated regions. Otherwise, a poor model performance could be obtained even for compounds with features within the distributions. The distribution of all the 9 descriptors for EadsH and EadsO and EadsOH are shown in Fig. S1 and S2 of the ESI,† respectively. The general conclusion is that all the descriptors present a pseudo-normal distribution focused on one or two central values. All intervals within the distributions are populated in most descriptors both for the H and the O/OH databases in the case of the outer electrons of A and B, the range from 2 to 12 is well described. It is notable that in the case of outer electrons of B, elements with more than half-filled shells are more common. The majority of compounds in our database have a cell volume between 10 and 100 Å3, which is a very large range considering intermetallics with only 5 geometries and stoichiometries. The WEN, WIE, and WAR are also homogeneously distributed in the complete range, while the GCN and the applied strain have discrete values between 0.25–5.25 and −8–8, respectively. The values of PSI are well distributed among the total range with a slightly higher count in values from 5 to 50.The Pearson correlation indexes between all the features (in the complete H and O/OH database) in Table 1 were calculated to make sure that they provide unique information to the model and avoid features that were strongly correlated. They are presented in Fig. 4. The results are similar for both the hydrogen and the oxygen and hydroxyl descriptors: the most correlated features are Ψ and the outer electrons of A (SA), which is coherent with the description of Ψ. As shown in eqn (6), SA is included in the numerator, which explains a positive value of the correlation. Additionally, the WIE is relatively correlated with SA and Ψ due to the definition of ionization energy (energy that an isolated, gaseous atom in the ground electronic state must absorb to discharge an electron). Conversely, WAR and WEN are correlated with a negative index of −0.6, which is in accordance with the basis of chemistry: the larger the atomic radius of an element, the lower the tendency to attract electrons to itself. Finally, the categorical feature adsorbate in the model for oxygen and hydroxyl (b) is not related to any other descriptor because it does not represent any chemical property of the binary intermetallic compounds. All in all, we can conclude the final set of 9 descriptors were not correlated with each other.
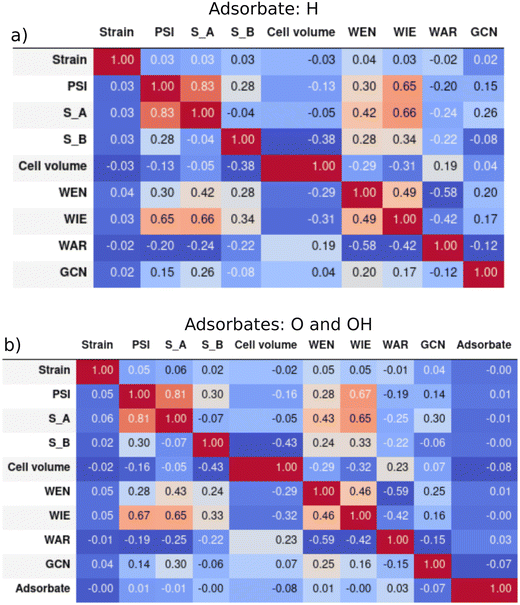 | ||
| Fig. 4 Pearson correlation matrixes of the features: a) hydrogen adsorption and b) oxygen and hydroxyl adsorption. | ||
Model results
Two RF models were trained with the two datasets of hydrogen and oxygen/hydroxyl adsorption. All pure metal samples were included in the training set, as well as all AnBm samples with sites fccXXX, hcpXXX, longbridgeX, and ontopX if X (either A or B) was not available as pure metal in the datasets. The parity plots that show the correspondence between the adsorption energies calculated by DFT and by the RF model are shown in Fig. 5a) and c) for the hydrogen adsorption and in Fig. 5b) and d) for the oxygen and hydroxyl adsorption. The training data are indicated by blue dots while those not included in the training data (testing data) are shown with red dots. A representation of the learning curves for both ML models is illustrated in the ESI† Fig. S3.The adsorption energies in the dataset range from −2 to 2 eV in the case of hydrogen and from −8 to 7 eV in the case of oxygen and hydroxyl (Fig. 5). Overall, the accuracy of the predictions of the RF is excellent according to various statistical parameters, such as R2, MAE, RMSE, and MAD of the testing set, that are indicated in Fig. 5a) and b). The MAE is 0.07 eV for hydrogen, and MAE = 0.18 eV for oxygen and hydroxyl. Considering that the error of the DFT calculations in the adsorption energy is assumed to be 0.1 eV,30 these models are able to predict the adsorption energy with a similar degree of accuracy. It should be noted that the MAE in the model for O/OH was higher than for the H model due to the wider range of its predictions (−8 to 7 eV vs. −2 to 2 eV). For approximately the same amount of data in the training, the O/OH model is required to predict a larger scope of energies, thus, the amount of entries at each energy is lower, leading to higher MAE. Hence, more entries in the oxygen and hydroxyl database should be included to achieve a similar performance as that obtained from hydrogen adsorption.
Moreover, the standard deviations from the mean of the testing data are plotted in Fig. 5c) and d) for the sake of clarity. These error bars have been calculated using the Jackknife or “leave one out” procedure. This is an iterative cross-validation technique that gives an estimate of the sampling variance of the random forest. Firstly, each point is estimated from all the data available in the dataset. Then it is recalculated, dropping out one by one other entries in the training. The difference between the whole sample estimate and the partial estimate is calculated and its standard deviation is used to estimate the error and the confidence intervals. In other words, the error bars are a measurement of how much the RF predictions would change if we trained it on a different training set. The results in Fig. 5c) and d) give a reference of two uncertainty quantifications that are crucial in machine learning: calibration, and dispersion. Calibration (or honesty) compares the difference among error bars. A “well-calibrated” model has entries whose standard deviations are close to the model's predicted standard deviations. This means that for those points that are further away from the diagonal in the parity plots, the confidence intervals should be broader. In contrast, the error bars are very small for those entries in which the DFT calculated and the ML predicted adsorption energies are very similar. Thus, it can be concluded from this data that the calibration of our model is correct. Secondly, the models present reasonable error bars along all the range of energies (limited dispersion), especially in the middle, because the datasets are well distributed. In the case of the hydrogen model, it can be observed that the error bars are significantly larger at larger energies (between 0.5 and 1 eV) because of the lower number of data in this range. All in all, our model has consistent uncertainty metrics.
As expected, the surfaces and geometries with more entries in the dataset –fcc(111) and bcc(101)– are the ones that are more accurately described by our models. Among the total data for intermetallics, A3B fcc(111) represents the 32.5% and AB bcc(101) the 56.2%. Yet AB fcc(101), A2B hcp(0001), and A3B hcp(0001), only represent the 1.4%, 1.9%, and 8.0%, respectively. The entries in the test set with the highest errors were A2B hcp(0001), and A3B hcp(0001).
Feature importance
The role of the descriptors in describing the adsorption energies of binary intermetallic compounds can be assessed from the feature importance, which is plotted in Fig. 6a) and b) for the hydrogen and oxygen/hydroxyl adsorption, respectively. It is measured in % and obtained from the Gini impurity measure, which is one of the methods used in decision-tree ML algorithms to decide the optimal split of the trees.62 The feature importances are computed as the mean and standard deviation of that impurity decrease within each tree. Fundamentally they describe which feature is the most useful for the model to distinguish between the samples and give an idea of how it is contributing to the RF output. | ||
| Fig. 6 Features importances for the RF models: prediction of a) hydrogen and b) oxygen and hydroxyl. | ||
The features with the highest weight for the hydrogen adsorption are GCN and PSI (Fig. 6a). These descriptors contain information about the local geometrical and chemical environment of the adsorption site and this result demonstrates that the adsorption energy of the small hydrogen atoms onto a surface is highly dependent on the specific adsorption site. Regarding the oxygen and hydroxyl adsorption (Fig. 6b), the most relevant descriptor is the type of adsorbate (either O or OH). The second most important feature is the WEN. This was expected because the adsorption of oxygen will be disfavored on a surface with high WEN because oxygen is very electronegative, whereas electropositive surfaces will favor the adsorption. The influence of GCN and PSI is smaller –compared to the hydrogen adsorption– because, larger adsorbates such as O and OH are not as dependent on the local geometric and chemical features of the binding site as H. Regarding the outer electrons, it can be observed that in both cases SA has a higher weight than SB. This reflects that in most cases the proportion of A is larger than B (A3B, A2B), and consequently, the feature describing A is somehow more important than the feature for B. Finally, WAR, WIE, and the volume of the cell have a smaller influence on the adsorption energy, with the exception of WIE in the case of hydrogen, which has a significant weight. As the H atom only has one proton and one electron, the quantity of energy that is absorbed to discharge an electron, which corresponds to the definition of IE, is more relevant.
The importance of the strain descriptor is the smallest in both models. It indicates that biaxial strains in the range applied have a limited effect on the adsorption energy as compared with other features, such as GCN, PSI, or WEN. This is expected since the variation in adsorption energy is larger between different chemical compositions compared to the variation due to strain within one given composition. However, these changes in the adsorption energies (either positive or negative) of 0.1–0.2 eV in the case of hydrogen and of 0.4–0.8 eV in the case of oxygen and hydroxyl61 can be introduced to any intermetallic surface. Thus, the capability of the RF models to account for elastic strains can be very useful to study their effect on the catalytic behavior of the particular compounds.25 It indicates that biaxial strains in the range applied have a limited effect on the adsorption energy as compared with other features, such as GCN, PSI, or WEN. This is expected since the variation in adsorption energy is larger between different chemical compositions compared to the variation due to strain within one given composition. However, these changes in the adsorption energies (either positive or negative) of 0.1–0.2 eV in the case of hydrogen and of 0.4–0.8 eV in the case of oxygen and hydroxyl61 can be introduced to any intermetallic surface. Thus, the capability of the RF models to account for elastic strains can be very useful to study their effect on the catalytic behavior of the particular compounds.25
Model validation
To assess the accuracy of the RF models, the adsorption energies of H, O, and OH of 30 candidates, randomly selected from the 2458 compounds, were calculated by DFT with and without strain. The adsorption energies predicted by the RF models and by DFT are indicated in Table 2, together with the difference between them. The upper part of the table summarizes intermetallic compounds and binding sites in which the RF model is expected to provide accurate results as both A and B are present as pure elements in the training set of the database. Moreover, several results with and without strain were included to demonstrate that the RF model is able to predict accurately the variation in the adsorption energy induced by tensile/compressive elastic strains.| System | Adsorbate | Strain | Binding site | E ads (ML) | E ads (DFT) | Error |
|---|---|---|---|---|---|---|
| Ce3Sn | H | 0 | fccAAA | −0.47 | −0.71 | 0.24 |
| Ce3Sn | H | 0 | hcpAAA | −0.50 | −0.71 | 0.21 |
| Ce3Sn | OH | 0 | fccAAA | −2.09 | −2.05 | −0.04 |
| Ir3Sc | OH | −1 | fccAAA | 1.19 | 1.42 | 0.23 |
| Nd3In | OH | 0 | fccAAB | −2.00 | −2.13 | 0.14 |
| Ni3Pt | H | −3 | fccAAB | −0.41 | −0.44 | −0.04 |
| Ni3Pt | O | −5 | fccAAB | −1.94 | −2.05 | −0.11 |
| Pd3Ce | H | 1 | fccAAA | −0.44 | −0.54 | −0.10 |
| Pd3Sc | H | −5 | fccAAA | −0.47 | −0.34 | 0.13 |
| Pd3Sc | H | −5 | hcpAAA | −0.51 | −0.70 | 0.20 |
| Pd3Sc | O | −5 | hcpAAA | −1.68 | −1.58 | −0.10 |
| Pd3Sc | OH | −5 | fccAAA | 1.00 | 1.08 | −0.08 |
| Pt3Dy | H | 0 | hcpAAA | −0.68 | −0.49 | 0.19 |
| Pt3Dy | OH | 0 | hcpAAA | 1.01 | 1.23 | −0.22 |
| Pt3Mn | OH | 1 | ontopA | 0.99 | 0.74 | 0.25 |
| Pt3Mn | OH | 1 | hcpAAA | 1.17 | 1.15 | 0.02 |
| Pt3Sn | O | 5 | fccAAA | −1.64 | −1.39 | −0.25 |
| Pt3Y | H | 1 | hcpAAA | −0.50 | −0.70 | −0.20 |
| Ir3Sc | O | −3 | ontopB | −1.94 | −0.79 | 1.15 |
| Nd3In | H | 0 | hcpAAA | −0.46 | −0.83 | 0.38 |
| Ni3Ga | O | −3 | ontopB | −1.60 | 0.08 | −1.68 |
| Pt3Mn | O | 1 | hcpAAA | −1.69 | −1.43 | −0.26 |
| Pt3Mn | OH | 1 | ontopB | 1.09 | 0.59 | 0.50 |
| Pr3In | H | 3 | hcpAAA | −0.46 | −0.79 | 0.34 |
| Pr3In | H | 3 | fccAAA | −0.46 | −0.78 | 0.32 |
| Pr3In | OH | 3 | fccAAB | −2.07 | −2.07 | 0.00 |
| Pr3In | OH | 3 | fccAAA | −1.97 | −2.30 | 0.32 |
| SmRh | H | 0 | longbridgeA | −0.46 | 0.02 | 0.48 |
| Sn3Pr | H | 5 | fccAAB | −0.45 | 0.32 | −0.77 |
| Sn3Pr | O | 5 | ontopB | −1.60 | −2.41 | 0.81 |
In contrast, the second part of the table shows candidates who were expected to give inaccurate predictions and, thus, highlights the limitations of the RF models. These candidates contain Al, Dy, Sc, Nd, In, Ga, Mn, Pr, Sm, and Sn, which were not included in the database of 24 pure elements for which the adsorption energy of H, O, and OH was computed. The RF models cannot predict accurately the adsorption energies in fccAAA, hcpAAA, longbridgeA, or ontopA locations if the adsorption energy of pure element A is not included in the dataset because the chemical environment in these sites (which is determined by element A) has not been included enough in the training set. The differences between the adsorption energies calculated by RF and DFT were much higher in these sites and reached >1 eV in some cases, although the differences were below 0.34 eV for Pr3In, even though pure Pr and In were not included in the database. The parity plot representing the 30 verification candidates is shown in the ESI† Fig. S4.
Prediction of new catalysts for the HER and ORR
The RF models presented above were used to predict the adsorption energies of hydrogen, oxygen, and hydroxyl of 175 binary intermetallic candidates with and without strain. Those candidates met the criteria indicated in Fig. 1 and present stoichiometries and geometries equal to the ones included in the databases at the lowest energy surfaces (AB bcc, AB fcc, A2B hcp, A3B fcc, and A3B hcp). It must be kept in mind, that after considering the different adsorption sites and strain states, the number of predictions is nearly 2700. The values of the descriptors and the code for the ML model can be found in https://zenodo.org/doi/10.5281/zenodo.11486422.HER
In the case of the HER, Pt(111) is known to be the optimum catalyst and it was decided to select compounds and surfaces whose adsorption energy for H was that of Pt ±0.05 eV. We chose this value, instead of 0.07 eV (the MAE of the RF model) to leave all the pure metals that were not Pt or Pd out of range. In this way, the list of possible candidates was set to 25 compounds, which are indicated in Table 3. All of them present an A3B stoichiometry with fcc lattice and fcc(111) geometry. Only 11 do not contain either Pt or Pd, which makes them potentially interesting to replace these metals. It should be noted that adsorption takes place at FCC or HCP adsorption sites in all candidates, which are the optimum ones at fcc(111) geometries. The results are in agreement with the previous DFT screening conducted by Norskov,63 where most of the candidates obtained contain Pt in their structure. Additionally, Ce3Ga, Ce3In, Ce3Sn, Nd3In, Ni3Fe, Pr3In, Rh3Mo, Sm3In, Sn3Nd, Sn3Sm, and Zn3Ti were found to have adsorption energies of H similar to those of Pt. Among them, candidates containing Ce, Nd, Pr, or Sm should be discarded because of their extremely negative normal reduction potentials. However, we see Zn3Ti as a particularly interesting material to further study as the oxidation potential of Zn is closer to that of Pt.| Material | Adsorption site | E Hads (eV) | Material | Adsorption site | E Hads (eV) |
|---|---|---|---|---|---|
| Pt | FCC | −0.49 | Pt | FCC | −0.49 |
| Ce3Ga | hcpAAA | −0.45 | Pd3Nd | hcpAAA | −0.53 |
| fccAAA | −0.45 | Pd3Sm | hcpAAA | −0.52 | |
| Ce3In | hcpAAA | −0.46 | fccAAA | −0.52 | |
| fccAAA | −0.45 | fccAAB | −0.51 | ||
| Ce3Sn | hcpAAA | −0.50 | Pd3Y | fccAAA | −0.52 |
| fccAAB | −0.48 | Pr3In | hcpAAA | −0.45 | |
| Nd3In | hcpAAA | −0.46 | Pt3Co | hcpAAA | −0.49 |
| Ni3Fe | fccAAB | −0.53 | fccAAB | −0.49 | |
| hcpAAB | −0.49 | fccAAA | −0.49 | ||
| Ni3Pt | fccAAA | −0.48 | Pt3Dy | hcpAAA | −0.49 |
| hcpAAA | −0.48 | fccAAA | −0.47 | ||
| fccAAB | −0.47 | Pt3Sc | hcpAAA | −0.53 | |
| Pd3Ce | hcpAAA | −0.53 | fccAAA | −0.51 | |
| fccAAA | −0.53 | fccAAB | −0.51 | ||
| fccAAB | −0.50 | Pt3Sn | fccAAA | −0.53 | |
| Pd3Dy | hcpAAA | −0.47 | Pt3Y | fccAAA | −0.51 |
| fccAAA | −0.46 | hcpAAA | −0.48 | ||
| Pd3Fe | fccAAA | −0.53 | fccAAB | −0.45 | |
| Pd3Pr | fccAAA | −0.53 | Rh3Mo | fccAAA | −0.46 |
| hcpAAA | −0.53 | Sm3In | hcpAAA | −0.46 | |
| fccAAB | −0.52 | Sn3Nd | fccAAB | −0.45 | |
| Pd3Sc | fccAAA | −0.52 | Sn3Sm | fccAAB | −0.49 |
| hcpAAA | −0.51 | Zn3Ti | fccAAB | −0.48 | |
| fccAAB | −0.48 | hcpAAB | −0.44 |
From the experimental viewpoint, Baibars et al.65 proved that a NiFeOxHy/Ni3Fe interface designed via electropassivation could provide superior catalysis of the HER. Additionally, Cu3Pt is one of the candidates that has been studied experimentally as a potential candidate to replace Pt, although its application has been hindered by dealloying and passivation phenomena.66–69
The application of elastic strains introduces two more candidates with adsorption energies ±0.05 eV that of Pt(111): Pt3Sm and Ir3W. The difference in the adsorption energy of H for both candidates is reduced to 0.01 eV and 0.03 eV in the presence of −3% and −5% compression strains, respectively. Moreover, the candidates whose adsorption energies were close to Pt could get even closer (≈0.03 eV) under the application of biaxial strains. This is the case of Ir3W, Pd3Ce, Pd3Fe, Pd3Nd, Pd3Pr, Pd3Sc, Pd3Sm, Pd3Y, Pt3Sc, Pt3Sm, Pt3Sn, and Zn3Ti that become closer to Pt in the presence of compressive strains, while Ce3Ga, Ce3In, Ce3Sn, Nd3In, Ni3Pt, Pd3Dy, Pr3In, Sm3In, Sn3Nd, and Sn3Sm get closer to Pt under tensile strains. Ni3Fe, Pt3Co, Pt3Dy, Pt3Y, and Rh3Mo are the only candidates whose adsorption energies for hydrogen are closer to Pt at zero strain. The optimum applied strain state and adsorption site for each candidate, and a representation of the variation of EHads with strain are shown in Table S5, and Fig. S5 of the ESI,† respectively. This fact supports the potential of elastic strains to tune the catalytic properties of materials, because changes of a few tenths of eV may lead to important changes in the catalytic activity.24–26
ORR
The criteria to select potential catalysts for the ORR were similar to those in the case of the HER. Compounds and surfaces whose adsorption energies for O and OH were within ±0.2 eV of that for Pt(111) were selected from those reported in https://zenodo.org/doi/10.5281/zenodo.11486422. This magnitude is equivalent to the MAE of the RF model for oxygen and hydroxyl. 13 candidates were identified in this range. All of them were A3B with an fcc(111) geometry and one (ZnAu) was AB bcc(101). The adsorption energies as well as the adsorption sites of these compounds are indicated in Table 4. It is worth noting that the adsorption sites are generally not the same for O and OH even in the same material. Among the 13, only 2 candidates do not contain Pd or Pt on their structure: Ir3Sc and ZnAu.| Material | Adsorption site | E Oads (eV) | Adsorption site | E OHads (eV) |
|---|---|---|---|---|
| Pt | FCC | −1.79 | FCC | 1.19 |
| Cu3Pt | fccAAB | −1.82 | ontopA | 1.3 |
| hcpAAA | −1.92 | ontopB | 1.38 | |
| Ir3Sc | ontopB | −1.95 | fccAAA | 1.21 |
| Ni3Pt | hcpAAA | −1.99 | ontopB | 1.37 |
| Pd3Dy | fccAAA | −1.88 | fccAAA | 1.19 |
| fccAAB | −1.83 | hcpAAA | 1.10 | |
| ontopA | 1.37 | |||
| Pd3Sc | hcpAAA | −1.73 | fccAAA | 1.00 |
| Pd3Sn | fccAAB | −1.94 | fccAAA | 1.30 |
| hcpAAA | 1.06 | |||
| Pt3Co | fccAAA | −1.61 | fccAAB | 1.37 |
| fccAAB | −1.64 | hcpAAA | 1.24 | |
| Pt3Dy | fccAAA | −1.76 | fccAAA | 1.14 |
| fccAAB | −1.78 | hcpAAA | 1.01 | |
| hcpAAA | −1.82 | ontopA | 1.28 | |
| ontopB | 1.36 | |||
| Pt3Mn | fccAAA | −1.67 | fccAAA | 1.36 |
| fccAAB | −1.71 | fccAAB | 1.06 | |
| hcpAAA | −1.69 | hcpAAA | 1.22 | |
| ontopA | 1.05 | |||
| ontopB | 1.15 | |||
| Pt3Sc | fccAAB | −1.96 | fccAAA | 1.21 |
| Pt3Sn | fccAAB | −1.99 | fccAAA | 1.23 |
| Pt3Y | hcpAAA | −1.63 | fccAAA | 1.06 |
| ZnAu | threefoldAAB | −1.82 | longbridgeB | 1.36 |
Another suitable candidate, Ag3In fcc(111), appears for the ORR if the effect of elastic strains is considered. In this case, the EOads is within the ranges of energies close to Pt when 5% of tension strain is applied, while EOHads needs a −5% compression to be similar to Pt. Among the rest of the candidates, strain drives the adsorption energy up to 0.15 eV closer to Pt. The optimum applied strain level and the specific adsorption sites for each compound are indicated in Table S6 of the ESI.† Compressive strains bring the EOads closer to Pt in Cu3Pt, Ir3Sc, Ni3Pt, Pd3Dy, Pd3Sn, Pt3Dy, Pt3Sc, and Pt3Sn, while tensile strains have the same result for Ag3In, Pd3Sc, Pt3Co, Pt3Mn, Pt3Y, and ZnAu. Compressive strains are favorable for EOHads in Ag3In, Ir3Sc, Pd3Sc, Pt3Co, and Pt3Sn, whereas tensile strains bring Cu3Pt, Ni3Pt, Pd3Sn, Pt3Dy, Pt3Mn, and Pt3Sn. Only Pd3Dy, Pt3Y, and ZnAu are closer to the EOHads of Pt at zero strains. A representation of the variation of EOads and EOHads for the candidates with strain, can be found in the ESI† Fig. S6 and S7, respectively. These results indicate again the potential of the elastic strains to improve the catalytic performance of good catalysts.
Experimentally, core–shell nanoparticles of Ni3Pt have demonstrated good catalytic performance for the ORR by Godínez-Salomón et al.,70 but they observed a strong segregation of Ni on the topmost layer. Similarly, Pd3Fe, Pd3Y, Pt3Sc, and Pt3Y have been proven to be an efficient catalyst for ORR.71–76 Stamenkovic et al.33 also measured that Pt3Co exhibits a similar catalytic activity to Pt, in the ORR. Although there is still little experimental evidence of the effect of elastic strains on the catalytic activity of the ORR, Escudero-Escribano et al.24 proved experimentally that the catalytic activity of Pt5Dy, Pt5Ce, and Pt5Sm compounds was enhanced by a factor of 3 to 6 over Pt. These studies match our DFT calculations and ML predictions and therefore represent a starting point for the use of binary intermetallic compounds and elastic strain engineering in the catalysis of the HER and the ORR.
Discussion
The adsorption energy for H, O, and OH was calculated by means of DFT on the lowest energy surface of 24 pure metals and 106 binary intermetallic compounds with stoichiometries AB, A2B, and A3B taking into account the effect of biaxial elastic strains. This information was used to train two RF regression models, one for hydrogen adsorption and another for oxygen and hydroxyl adsorption. These models predicted the adsorption energies based on 9 descriptors that characterized the geometrical and chemical features of the adsorption site as well as the applied strain. All the descriptors for each compound in the models could be obtained from physico-chemical databases. The MAE of the predictions of the RF models was excellent (0.07 and 0.18 eV for the adsorption of hydrogen and oxygen/hydroxyl, respectively) and, in addition, the accuracy of the results was validated against the adsorption energies of 30 randomly selected binary intermetallic compounds.The ML models were used to predict the adsorption energy for hydrogen, oxygen, and hydroxyl of ≈2700 binary intermetallic compounds with stoichiometries AB, A2B, and A3B made of metallic elements, excluding those that were environmentally hazardous, radioactive, or toxic. This information was used to search for potential good catalysts for the HER and ORR from the criteria that their adsorption energy for H and O/OH, respectively, should be close to that of Pt, which is the best-known catalyst for both reactions. Including the effect of elastic strains, 27 potential candidates were reported for the HER and 14 for the ORR. The few of them that have been explored experimentally have shown good catalytic performance, validating our methodology.
The results of this investigation provide a large database of adsorption energies of H, O, and OH in pure metals and binary intermetallic compounds (including the effect of elastic strains) that can be very useful for training other data-driven strategies to search for new catalysts. Moreover, it demonstrates that the ML models –suitably trained– can predict adsorption energies with an accuracy not far away from density functional theory calculations with minimum computational cost from descriptors that are readily available in physico-chemical databases for any compound. Finally, the expansion of the strategy presented in this paper to ternary intermetallic compounds, oxides, etc. for other catalytic reactions is straightforward and is expected to foster the use of these methods in catalysis.
Methods
DFT calculations
Adsorption energies of H, O, and OH on intermetallic surfaces were determined from DFT plane wave simulations using the GPU-accelerated version of Quantum Espresso.77 The electron exchange–correlation was described using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional78 and the calculations were carried out using ultrasoft pseudopotentials.79 Brillouin zone calculations were performed using a Marzari–Vanderbilt–DeVita–Payne cold smearing of 0.015 Ry.80 The plane-wave basis was expanded to a cutoff energy of 80 Ry, and the Monkhorst–Pack k-points were sized (4 × 4 × 1) for the pure metallic supercells, and (6 × 6 × 1) for all the binary intermetallic compounds with the exception of A2B stoichiometry in which (8 × 8 × 1) was used due to the higher number of atoms involved.The adsorption of H, O, and OH was modeled on four-layer slabs (2 × 2) generated with the atomic simulation environment (ASE)81 from the equilibrium lattice parameters obtained in the Materials Project database.47 The equilibrium lattice parameters were calculated by DFT for a number of random candidates with all the stoichiometries. The differences between the calculated and the database values of the lattice parameters were negligible in all cases and can be found in the ESI† Table S4. Thus, the lattice parameters from the Materials Project database were used to avoid an unnecessary waste of computational time. The periodic slabs were separated by 10 Å of vacuum in the direction perpendicular to the surface and adsorption energies were calculated for each chemical species assuming a coverage of 1/4 monolayers. All metal atoms in the half-top of the slab and all adsorbed H, O, and OH were fully relaxed, while the positions of metal atoms in the half-bottom layers were fixed. The adsorption energy of H, O, and OH was calculated following the methodology in ref. 61. The expression used for the H and the O adsorption was:
 | (6) |
Similarly, the adsorption energy of OH was calculated as:
 | (7) |
The effect of elastic strains was assessed by imposing biaxial strains on the surface plane. The deformation gradient F applied to the supercell was
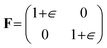 | (8) |
Machine learning
Different types of Machine Learning models have been used to describe the adsorption phenomena that occur in heterogeneous catalysis. They include support vector regression (SVR),50K-nearest neighbors (KNN),51 convolutional neural network,54 and Gaussian process regression.52Among all, the state-of-the-art MAE of ML model predictions for the adsorption energy is in the range of 0.16–0.3 eV.45,46 In our case, random forest (RF) regressor models were built separately for the datasets of EHads and of EOads/EOHads. RF is a part of a family of methods known as ensemble methods. Ensemble methods combine the predictions of different base estimators. In RF models, the ensemble consists of a collection of decision trees that are trained independently using random subsets of both features and training data. Each decision tree predicts the target variable by learning simple decision rules inferred from the features. In regression tasks, the final prediction of a RF model is the average of the predictions made by each tree in the forest. RF models are generally robust to overfitting, can handle outliers, and provide information about the importance of each feature in the descriptor, which can be useful for feature selection and for elucidating the model's behavior. RFs are known to be versatile to different datasets without requiring an expensive hyperparameter tuning. We chose a RF regressor as the algorithm for this work due to the size of our database (useful with small- –hundred– or medium-sized –thousand– databases), the quick training, and the good accuracy obtained. Under the same conditions, we trained our databases with a Gaussian process regressor algorithm, however, the MAE was 0.2 eV higher on average. We did not consider graph neural networks due to the diversity and size of our databases. In our RF model, the training set was 85% of the data and the remaining 15% conformed the test set. The training set was used to optimize the hyperparameters with a k-fold grid-search cross-validation (K = 5) and they can be found in Table S3 in the ESI.† For that, we constructed a parameters grid and optimize it with the GridSearchCV routine as implemented in the Scikit-learn library.82
The accuracy of the model was analyzed with the coefficient of determination R2, the MAE, the root mean squared error (RMSE), and the median absolute error (MAD). The algorithm selected was ExtraTreesRegressor and was constructed and analyzed using the Scikit-learn library.82
Data availability statement
The database of DFT adsorption energy calculations is made openly available at the Catalysis-Hub platform43via the link https://www.catalysishub.org/publications/AlonsoStrain2023, and the values of the descriptors along with the ML code are published in https://zenodo.org/doi/10.5281/zenodo.11486422.Author contributions
J. LL. and K. W. conceived the idea of this work, who was supervised by J. LL. in Spain and F. A. and K. W. in the USA. C. M. and V. V. carried out DFT calculation to create the dataset. C. M. designed the machine learning model under the advice of V. V. and B. C. The results were analyzed and discussed by all authors. C. M. wrote the original draft of the manuscript which was reviewed by all authors.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This investigation was supported by the project High-Throughput Strategies for The Discovery of New Catalysts for The Hydrogen Economy Through Elastic Strain Engineering (CATbyESE) funded in the call for Oriented Projects for the Ecological and Digital Transition, Spanish Ministry of Science and Innovation (TED2021-129497B-I00). VV-G acknowledges support from the European Union through the Marie Sklodowska-Curie Actions (MSCA) Postdoctoral Fellowship HighHydrogenML (grant agreement 101105610). Computational resources and technical assistance provided by the Centro de Supercomputación Visualización de Madrid (CeSViMa) and by the Spanish Supercomputing Network (projects QS-2021-1-0013, QHS2021-3-0019, and QHS-2023-2-0001) are gratefully acknowledged. Additional computational resources were provided by the HPC Vega, Institute of Information Science, Maribor, Slovenia through the European High-Performance Computing Joint Undertaking, PRACE project REG-2022R01-040. CMA also acknowledges the support from the Spanish Ministry of Education through the Fellowship FPU19/02031 and the US-Spain Fulbright Commission. The technical assistance of Dr. J. M. Guevara-Vela and Dr. T. Xie to create some entries of the database is also appreciated.References
- O. Bičáková and P. Straka, Int. J. Hydrogen Energy, 2012, 37, 11563–11578 CrossRef.
- A. Steinfeld, Solar Hydrogen, Sol. Energy, 2005, 78, 603–615 CrossRef CAS.
- P. de Wild and M. Verhaak, Catal. Today, 2000, 60, 3–10 CrossRef CAS.
- A. P. Reverberi, J. J. Kleme
![[s with combining breve]](https://www.rsc.org/images/entities/char_0073_0306.gif) , P. S. Varbanov and B. Fabiano, PRES'15: Cleaner energy planning, management and technologies, J. Cleaner Prod., 2016, 136, 72–80 CrossRef CAS.
, P. S. Varbanov and B. Fabiano, PRES'15: Cleaner energy planning, management and technologies, J. Cleaner Prod., 2016, 136, 72–80 CrossRef CAS. - S. Fukuzumi, Y. Yamada and K. D. Karlin, Electrochim. Acta, 2012, 82, 493–511 CrossRef CAS PubMed.
- C. L. Zitnick, L. Chanussot, A. Das, S. Goyal, J. Heras-Domingo, C. Ho, W. Hu, T. Lavril, A. Palizhati, M. Riviere, M. Shuaibi, A. Sriram, K. Tran, B. Wood, J. Yoon, D. Parikh and Z. Ulissi, An Introduction to Electrocatalyst Design using Machine Learning for Renewable Energy Storage, 2020 Search PubMed.
- Y. Li, L. Yang, H. He, L. Sun, H. Wang, X. Fang, Y. Zhao, D. Zheng, Y. Qi, Z. Li and W. Deng, Nat. Commun., 2022, 13, 1355 CrossRef CAS PubMed.
- Y. Chen, S. Ji, W. Sun, Y. Lei, Q. Wang, A. Li, W. Chen, G. Zhou, Z. Zhang, Y. Wang, L. Zheng, Q. Zhang, L. Gu, X. Han, D. Wang and Y. Li, Am. Ethnol., 2019, 132, 1311–1317 Search PubMed.
- F. Li, D. H. Kweon, G.-F. Han, H.-J. Noh, W. Che, I. Ahmad, H. Y. Jeong, Z. Fu, Y. Lu and J.-B. Baek, ACS Nano, 2023, 17, 2923–2931 CrossRef CAS PubMed , PMID: 36722955.
- D. Hyung Kweon, I.-Y. Jeon and J.-B. Baek, Adv. Energy Sustainability Res., 2021, 2, 2100019 CrossRef CAS.
- J. Yu, Y. Dai, Q. He, C. Cheng, Z. Shao and M. Ni, Appl. Phys. Rev., 2020, 7, 4 Search PubMed.
- J. Li, Z. Xi, Y.-T. Pan, J. S. Spendelow, P. N. Duchesne, D. Su, Q. Li, C. Yu, Z. Yin, B. Shen, Y. S. Kim, P. Zhang and S. Sun, J. Am. Chem. Soc., 2018, 140, 2926–2932 CrossRef CAS PubMed.
- Y. Shi, T.-T. Zhai, Y. Zhou, W.-X. Xu, D.-R. Yang, F.-B. Wang and X.-H. Xia, J. Electroanal. Chem., 2018, 819, 442–446 CrossRef CAS.
- H. Liu, K. Liu, P. Zhong, J. Qi, J. Bian, Q. Fan, K. Ren, H. Zheng, L. Han, Y. Yin and C. Gao, Chem. Mater., 2018, 30, 7744–7751 CrossRef CAS.
- H. El-Deeb and M. Bron, J. Power Sources, 2015, 275, 893–900 CrossRef CAS.
- R. Lin, T. Zhao, M. Shang, J. Wang, W. Tang, V. E. Guterman and J. Ma, J. Power Sources, 2015, 293, 274–282 CrossRef CAS.
- R. Tian, S. Shen, F. Zhu, L. Luo, X. Yan, G. Wei and J. Zhang, ChemSusChem, 2018, 11, 1015–1019 CrossRef CAS PubMed.
- J. Ying, X.-Y. Yang, Z.-Y. Hu, S.-C. Mu, C. Janiak, W. Geng, M. Pan, X. Ke, G. Van Tendeloo and B.-L. Su, Nano Energy, 2014, 8, 214–222 CrossRef CAS.
- B. Chen, D. Cheng and J. Zhu, J. Power Sources, 2014, 267, 380–387 CrossRef CAS.
- K. Li, Y. Li, Y. Wang, F. He, M. Jiao, H. Tang and Z. Wu, J. Mater. Chem. A, 2015, 3, 11444–11452 RSC.
- C. Fu, C. Liu, T. Li, X. Zhang, F. Wang, J. Yang, Y. Jiang, P. Cui and H. Li, Comput. Mater. Sci., 2019, 170, 109202 CrossRef CAS.
- I. Shuttleworth, Appl. Surf. Sci., 2016, 378, 286–292 CrossRef CAS.
- I. Shuttleworth, Surf. Sci., 2017, 661, 49–59 CrossRef CAS.
- M. Escudero-Escribano, P. Malacrida, M. H. Hansen, U. G. Vej-Hansen, A. Velazquez-Palenzuela, V. Tripkovic, J. Schiotz, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Science, 2016, 352, 73–76 CrossRef CAS PubMed.
- C. Martínez-Alonso, J. M. Guevara-Vela and J. LLorca, Phys. Chem. Chem. Phys., 2022, 24, 4832–4842 RSC.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Science, 2005, 307, 555–558 CrossRef CAS PubMed.
- S. Kandoi, J. Greeley, M. A. Sanchez-Castillo, S. T. Evans, A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, Top. Catal., 2006, 37, 17–28 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333–1360 RSC.
- M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Muller and K. Burke, Nat. Commun., 2020, 11, 5223 CrossRef CAS PubMed.
- B. Hammer and J. Nørskov, in Advances in Catalysis, Elsevier, 2000, pp. 71–129 Search PubMed.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086 RSC.
- V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241–247 CrossRef CAS PubMed.
- N. Schuch and F. Verstraete, Nat. Phys., 2009, 5, 732–735 Search PubMed.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- J. Wei, X. Chu, X.-Y. Sun, K. Xu, H.-X. Deng, J. Chen, Z. Wei and M. Lei, InfoMat, 2019, 1, 338–358 CrossRef CAS.
- D. Morgan and R. Jacobs, Annu. Rev. Mater. Res., 2020, 50, 71–103 CrossRef CAS.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- X. Wan, Z. Zhang, W. Yu and Y. Guo, Machine Learning and Artificial Intelligence for Energy Materials, Mater. Rep.: Energy, 2021, 1, 100046 CAS.
- B. Han, Sci. Talks, 2022, 2, 100019 CrossRef.
- N. K. Pandit, D. Roy, S. C. Mandal and B. Pathak, J. Phys. Chem. Lett., 2022, 13, 7583–7593 CrossRef CAS PubMed.
- J. Kim, M. Rweyemamu and B. Purevsuren, Sci. Technol. Nucl. Install., 2022, 2022, 1–9 CAS.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Sci. Data, 2019, 6, 75 CrossRef PubMed.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS.
- K. Tran and Z. W. Ulissi, Nat. Catal., 2018, 1, 696–703 CrossRef CAS.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, npj Comput. Mater., 2020, 6, 177 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 1 Search PubMed.
- E. Belin-Ferré, Surface properties and engineering of complex intermetallics, World Scientific Publishing Co. Pte. Ltd., 2010 Search PubMed.
- H. Li, S. Dai, Y. Wu, Q. Dong, J. Chen, H. T. Chen, A. Hu, J. Chou and T. Chen, Adv. Sci., 2023, 10, 156857 Search PubMed.
- A. M. Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, J. Am. Chem. Soc., 2018, 140, 9844–9853 CrossRef PubMed.
- Y. Wang, T. Xie, Q. Tang, M. Wang, T. Ying, H. Zhu and X. Zeng, J. Magnesium Alloys, 2022, 1 Search PubMed.
- M. H. Hansen, J. A. G. Torres, P. C. Jennings, Z. Wang, J. R. Boes, O. G. Mamun and T. Bligaard, An Atomistic Machine Learning Package for Surface Science and Catalysis, arXiv, 2019, preprint, arXiv:1904.00904, DOI:10.48550/arXiv.1904.00904.
- P. S. Lamoureux, K. T. Winther, J. A. GarridoTorres, V. Streibel, M. Zhao, M. Bajdich, F. Abild-Pedersen and T. Bligaard, ChemCatChem, 2019, 11, 3581–3601 CrossRef.
- V. Fung, G. Hu, P. Ganesh and B. G. Sumpter, Nat. Commun., 2021, 12, 88 CrossRef CAS PubMed.
- T. Mentel, Mendeleev – A Python Package with Properties of Chemical Elements, Ions, Isotopes and Methods to Manipulate and Visualize Periodic Table, 2021, https://github.com/lmmentel/mendeleev Search PubMed.
- S. Singh, M. Pareek, A. Changotra, S. Banerjee, B. Bhaskararao, P. Balamurugan and R. B. Sunoj, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 1339–1345 CrossRef CAS PubMed.
- X. Ma, Z. Li, L. E. K. Achenie and H. Xin, J. Phys. Chem. Lett., 2015, 6, 3528–3533 CrossRef CAS PubMed.
- Z. Li, S. Wang, W. S. Chin, L. E. Achenie and H. Xin, J. Mater. Chem. A, 2017, 5, 24131–24138 RSC.
- F. Calle-Vallejo, J. I. Martinez, J. M. Garcia-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- W. Gao, Y. Chen, B. Li, S.-P. Liu, X. Liu and Q. Jiang, Nat. Commun., 2020, 11, 1196 CrossRef CAS PubMed.
- C. Martínez-Alonso, J. M. Guevara-Vela and J. LLorca, Phys. Chem. Chem. Phys., 2021, 23, 21295–21306 RSC.
- J. L. Grabmeier and L. A. Lambe, Int. J. Bus. Intell. Data Min., 2007, 2, 213 Search PubMed.
- J. Greeley and J. K. Norskov, Surf. Sci., 2007, 601, 1590–1598 CrossRef CAS.
- K. Trepte and J. Voss, J. Comput. Chem., 2022, 43, 1104–1112 CrossRef CAS PubMed.
- I. O. Baibars, M. G. Abd El-Moghny and M. S. El-Deab, J. Environ. Chem. Eng., 2022, 10, 108736 CrossRef CAS.
- D. Wang, Y. Yu, J. Zhu, S. Liu, D. A. Muller and H. D. Abruña, Nano Lett., 2015, 15, 1343–1348 CrossRef CAS PubMed.
- D. Wang, Y. Yu, H. L. Xin, R. Hovden, P. Ercius, J. A. Mundy, H. Chen, J. H. Richard, D. A. Muller, F. J. DiSalvo and H. D. Abruña, Nano Lett., 2012, 12, 5230–5238 CrossRef CAS PubMed.
- L. Han, H. Liu, P. Cui, Z. Peng, S. Zhang and J. Yang, Sci. Rep., 2014, 4, 6414 CrossRef CAS PubMed.
- N. Cheng, L. Zhang, S. Mi, H. Jiang, Y. Hu, H. Jiang and C. Li, ACS Appl. Mater. Interfaces, 2018, 10, 38015–38023 CrossRef CAS PubMed.
- F. Godínez-Salomón, M. Hallen-López and O. Solorza-Feria, Int. J. Hydrogen Energy, 2012, 37, 14902–14910 CrossRef.
- W.-P. Zhou, X. Yang, M. B. Vukmirovic, B. E. Koel, J. Jiao, G. Peng, M. Mavrikakis and R. R. Adzic, J. Am. Chem. Soc., 2009, 131, 12755–12762 CrossRef CAS PubMed.
- D. N. Son, P. Van Cao, T. T. T. Hanh, V. Chihaia and M. P. Pham-Ho, Electrocatalysis, 2017, 9, 10–21 CrossRef.
- X. Yang, J. Hu, J. Fu, R. Wu and B. E. Koel, Angew. Chem., 2011, 123, 10364–10367 CrossRef.
- R. Brandiele, V. Amendola, A. Guadagnini, G. A. Rizzi, D. Badocco, P. Pastore, A. A. Isse, C. Durante and A. Gennaro, Electrochim. Acta, 2019, 320, 134563 CrossRef CAS.
- N. Lindahl, B. Eriksson, H. Grönbeck, R. W. Lindström, G. Lindbergh, C. Lagergren and B. Wickman, ChemSusChem, 2018, 11, 1438–1445 CrossRef CAS PubMed.
- F. Qian, C. Hu, W. Jiang, J. Zhang, L. Peng, L. Song and Q. Chen, Chem. Eng. J., 2023, 468, 143665 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- N. Marzari, D. Vanderbilt, A. D. Vita and M. C. Payne, Phys. Rev. Lett., 1999, 82, 3296–3299 CrossRef CAS.
- S. Bahn and K. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00491d |
| This journal is © The Royal Society of Chemistry 2024 |



