Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correction: Nonequilibrium thermodynamic model of thermoelectricity and thermodiffusion in semiconductors
Semen N.
Semenov
 *a and
Martin E.
Schimpf
*a and
Martin E.
Schimpf
 b
b
aInstitute of Biochemical Physics RAS, Kosygin Street 4, 119334, Moscow, Russia. E-mail: sem@triniti.ru
bDepartment of Chemistry, Boise State University, Boise, ID, USA. E-mail: mschimpf@boisetstate.edu
First published on 31st July 2024
Abstract
Correction for ‘Nonequilibrium thermodynamic model of thermoelectricity and thermodiffusion in semiconductors’ by Semen N. Semenov et al., Phys. Chem. Chem. Phys., 2023, 25, 6790–6796, https://doi.org/10.1039/D2CP05065J.
The authors would like to make changes to eqn (2), (3), (5), (28), (29) and Table 2 in the published manuscript. The corrections pertain to the term ∓ne(h)e0∇Φ (where ne(h) is the numeric concentration of electrons (holes), e0 is the elementary charge, and Φ is the electric potential), inserted into eqn (3) by analogy with the literature. However, a difference in the present work is that the effect described by this term is already taken into account in eqn (2) and (3) by the use of the electrochemical potential
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e(h) = μe(h) ∓ e0Φ [where μe(h) is the chemical potential of the electron (hole)]. There is no need for this term in the open-circuit systems, although its presence as the ohmic voltage in the closed circuits causes no objections.
e(h) = μe(h) ∓ e0Φ [where μe(h) is the chemical potential of the electron (hole)]. There is no need for this term in the open-circuit systems, although its presence as the ohmic voltage in the closed circuits causes no objections.
Eqn (2) expresses the gradient of the electrochemical potential of the electron or hole:
 | (2) |
However, the electrochemical potential is the thermodynamic function of the temperature and concentration and can change in space only through the change of these physical parameters. The term ∓e0∇Φ should be written as 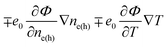 . Since the considered thermoelectric potential demonstrates no concentration dependence, eqn (2) should be written correctly as
. Since the considered thermoelectric potential demonstrates no concentration dependence, eqn (2) should be written correctly as
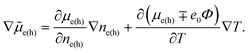 | (corrected 2) |
Substituting the corrected eqn (2) into the equation for the electron or hole flux
 | (3) |
 | (corrected 3) |
 | (corrected 3′) |
The calculations of the electron and hole chemical potentials yielding eqn (15) keep the validity:
 | (15) |
 | (28) |
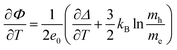 | (corrected 28) |
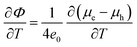 | (29) |
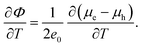 | (corrected 29) |
The revised versions of the concluding expression for the Seebeck coefficient (eqn (28)) and the relevant columns of Table 2 are shown below. The values of the Seebeck coefficient have doubled after correction.
The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.
| This journal is © the Owner Societies 2024 |