 Open Access Article
Open Access ArticleProton transport in liquid phosphoric acid: the role of nuclear quantum effects revealed by neural network potential†
Pei
Liu
,
Wei
Li
 * and
Shuhua
Li
* and
Shuhua
Li
 *
*
Key Laboratory of Mesoscopic Chemistry of Ministry of Education, New Cornerstone Science Laboratory, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing, Jiangsu 210023, People's Republic of China. E-mail: shuhua@nju.edu.cn; wli@nju.edu.cn
First published on 11th February 2025
Abstract
Pure phosphoric acid exhibits high proton conductivity and is widely used in modern industry. However, its proton transport mechanism remains less understood compared to that of water, which presents a significant challenge for advancing technologies like phosphoric acid fuel cells. In this study, we utilize machine learning potentials and molecular dynamics (MD) simulations to investigate the proton diffusion mechanisms in liquid phosphoric acid systems. The neural network potentials we developed demonstrate quantum chemical accuracy and stability across a range of temperatures. Our simulations reveal continuous proton hopping between phosphoric acid anions. Moreover, the radial distribution functions and diffusion coefficients obtained from ring polymer MD—a variant of path-integral MD—exhibit improved alignment with experimental values compared to classical MD results, as ring polymer MD inherently accounts for nuclear quantum effects on proton behavior. Additionally, we employed neural networks combined with the charge equilibration method to predict the charge distribution in liquid phosphoric acid, examining the proton transport mechanism through vibrational spectra analysis.
1. Introduction
Phosphoric acid, a widely used inorganic acid, plays a pivotal role in modern industry as an essential chemical substance.1 It has attracted considerable attention across various disciplines, including atmospheric science,2 environmental science,3 and astrophysics.4 Notably, phosphoric acid fuel cells represent the first generation of commercialized fuel cell technology.5 Due to its exceptional proton conductivity,6,7 pure phosphoric acid has found extensive application in energy technologies, such as proton exchange membrane fuel cells8–10 and phosphoric acid fuel cells.11,12 Additionally, phosphate-based systems are crucial in biological processes;13 the synthesis of adenosine triphosphate (ATP) is driven by proton concentration gradients between cellular compartments, with proton transport (PT) occurring near the surface of the phospholipid membrane.14 Therefore, investigating the physicochemical properties of phosphoric acid can provide valuable insights into the PT mechanisms in more complex materials and biological systems, underscoring its scientific importance.To gain deeper insights into the properties and behavior of liquid phosphoric acid systems, molecular dynamics (MD) simulations are a commonly employed approach. Classical force fields (FFs), such as GROMOS15 and COMPASS,16 are typically used to explore the structural and dynamical properties of liquid phosphoric acid systems.17–19 These classical FFs can reproduce experimental radial distribution functions (RDFs) and densities,17 For example, Zhu et al. utilized classical FFs to investigate the microscopic structure and hydrogen bonding characteristics of pristine and phosphoric acid doped polybenzimidazoles.18 However, these classical FFs have precision limitations and are incapable of describing chemical reactions, making them inadequate for accurately modeling proton transfer processes in liquid phosphoric acid systems. In contrast, ab initio MD (AIMD) simulations are capable of describing chemical reactions with higher precision, providing detailed results such as vibrational spectra,20 PT chains,6 and intermediate scattering functions21 of phosphoric acid. Nonetheless, the computational cost of AIMD scales significantly with system size, often limiting simulations to small systems and time scales of only a few ps.
To overcome these limitations and bridge the gap between efficiency and accuracy, various machine learning (ML) algorithms have been developed to construct FFs with ab initio accuracy by learning from reference ab initio data.22–27 ML potential (MLP)-based MD simulations combine the efficiency of classical FF methods with the precision of AIMD.25,26,28–32 In these methods, the local atomic environment of each atom serves as the input, and the total energy of a large system is calculated by summing the atomic energy contributions, which depend on the local environment. Equivariant neural networks (NNs), such as NequIP,33 Allegro,34 and MACE,35 are employed to construct equivariant interatomic potentials. These potentials rely on relative interatomic position vectors and higher-order geometric tensors, rather than just scalar distances or angles. This enables the network to capture more complex geometric relationships and exhibit both rotational and translational equivariance. Compared to conventional neural network potentials (NNPs), this results in superior predictive accuracy and significantly higher sample efficiency. Jinnouchi utilized ML potentials to conduct MD simulations of liquid phosphoric acid to investigate its proton conduction properties.36 However, the obtained RDFs and diffusion coefficients showed discrepancies compared to experimental values. We attribute these discrepancies to the neglect of nuclear quantum effects (NQEs) associated with protons in the simulations, which have been shown in previous studies to significantly impact PT.37–39
In this work, we combined path-integral MD (PIMD) with NNPs, based on hybrid density functional theory (DFT), to construct a dataset for liquid phosphoric acid at multiple temperatures. This dataset was then used to train NNPs for liquid phosphoric acid. We conducted classical Born–Oppenheimer MD, abbreviated as MD, simulations and ring polymer MD (RPMD)40 simulations utilizing our NNP. The results indicate that the impact of NQEs is clearly observed due to the substantial presence of protons. These NQEs significantly influence the structure and atomic arrangement of liquid phosphoric acid, thereby affecting the RDFs. Proton diffusion coefficients in the RPMD simulations were higher than those in the MD simulations, as NQEs lower the energy barriers for PT in liquid phosphoric acid. Additionally, the simulated vibrational spectra revealed overlapping P–O peaks and a broad O–H peak, reflecting the presence of hydrogen-bonding networks in liquid phosphoric acid, which facilitates long-range PT.
2. Methodology and computational details
2.1 Liquid phosphoric acid models
All liquid phosphoric acid systems were modeled with unit cells under three-dimensional periodic boundary conditions (PBCs). First, we optimized the structure of gaseous phosphoric acid molecules at the PBE0/def2-SVP level of theory. Packmol software41 was used to randomly pack the optimized structures into cubic boxes. To simulate the diffusion behavior of liquid phosphoric acid at different temperatures, we generated three boxes of varying sizes, with densities derived from experimental and theoretical studies of liquid phosphoric acid at 298.15 K, 333.15 K, and 350.15 K (1.874 g cm−3, 1.830 g cm−3, and 1.804 g cm−3, respectively).36,42,43 As shown in Fig. 1, each box contains 38 phosphoric acid molecules.To obtain equilibrium lattice structures, we employed the SCC-DFTB44 semi-empirical method to optimize the three initial configurations and performed NVT MD simulations at 298.15 K, 333.15 K, and 350.15 K for 200 ps each using the CP2K software.45 In the MD simulations, the time step was set to 1 fs for efficient structural relaxation. We randomly sampled 200 structures from the last 100 ps of each trajectory to create an initial dataset, which was then used to train preliminary NNs for subsequent active learning iterations.
2.2 Neural network potential generations
To construct a high-accuracy NNP for liquid phosphoric acid, we employed an active learning approach using committee NNs for iterative sampling.46,47 After each round of NNP training, we conducted MD simulations on three different initial structures at three temperatures under PBCs. The initial simulated trajectories lasted a few ps and were extended to 1 ns as the iterations increased. Configurations were extracted at 100 fs intervals during each sampling round as candidate samples. Four models were trained on the same dataset, forming the committee NNs. These committee NNs evaluated all candidate configurations by calculating the maximum standard deviation of atomic forces. Approximately 500 configurations with the largest force deviations were selected for further sampling. We then calculated the energy, atomic forces, and atomic charges of the selected configurations, adding these results to the dataset. This iterative process was repeated until the NNs converged on the test set.Fig. 1 illustrates the periodic structure of liquid phosphoric acid in the dataset. All calculations in this study were performed at the Gamma point. Single-point calculations were carried out using the CP2K software with the mixed Gaussian and plane wave (GPW) method at the PBE0-D3(BJ)/TZVP-MOLOPT-GTH level.48–50 The auxiliary density matrix method (ADMM)51 was applied with admm-dzp as the auxiliary basis set. The Coulomb truncation of the hybrid functional was set to 6.0 Å, while the plane wave cutoff was established at 550 Rydberg, with convergence tests for the cutoff energy shown in Fig. S1 and Table S1 of the ESI.† Atomic charges were calculated using the Hirshfeld-I method.52
The NN model used in this work is the MACE equivariant graph NN (GNN). In the MACE equivariant GNN, the interatomic graph comprises atomic nodes and edges connecting these atoms.35,53 An atom j near atom i is included in the graph if it is within the truncation radius rij, which is a hyperparameter of the NN. The features of node i are represented by  , where t denotes the layer number, k indexes this series of features, which also corresponds to the number of chemical channels. L specifies the feature set of node i as well as the transformation of
, where t denotes the layer number, k indexes this series of features, which also corresponds to the number of chemical channels. L specifies the feature set of node i as well as the transformation of  :
:
 | (1) |
 represents an L-th order Wigner D-matrix, and Q denotes a set of rotational transformations applied to atomic coordinates. When all features are labeled as L = 0, they represent invariant scalars. For L > 0, they correspond to tensors of the respective order: vectors for L = 1, matrices for L = 2, and higher-order tensors for larger values of L.
represents an L-th order Wigner D-matrix, and Q denotes a set of rotational transformations applied to atomic coordinates. When all features are labeled as L = 0, they represent invariant scalars. For L > 0, they correspond to tensors of the respective order: vectors for L = 1, matrices for L = 2, and higher-order tensors for larger values of L.
The network outputs the atomic energy EA for each atom A based on the local environment descriptors of the atoms. The total energy E is the sum of the atomic energies in the system:
 | (2) |
The atomic force FA on atom A is the negative gradient of the total energy with respect to the position of atom A.
The NNP developed for liquid phosphoric acid is termed PBE0-NN. Additionally, we combined the MACE model with the charge equilibration (Qeq) method to develop a NN for predicting the charge distribution within liquid phosphoric acid systems, termed Qeq-NN. In Qeq-NN, atomic charges are determined by minimizing a simplified energy expression:
 | (3) |
 | (4) |
 | (5) |
 | (6) |
The hyperparameters are provided in Table 1:
| Model | Cutoff radius r/Å | Chemical channels k | Max L |
|---|---|---|---|
| Qeq-NN | 4.5 | 16 | 1 |
| PBE0-NN | 4.5 | 128 | 1 |
Following several rounds of active learning, the final dataset for liquid phosphoric acid comprised 4947 energies, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511
511![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 atomic forces, and 1503
664 atomic forces, and 1503![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888 atomic charges. This dataset was randomly split into a training set and a validation set with an 88% to 12% ratio and was used to train the MACE equivariant GNNs, PBE0-NN and Qeq-NN. The test set, consisting of 600 frames of periodic liquid phosphoric acid systems, was randomly sampled from all six trajectories, which included both MD and RPMD ones at three different temperatures.
888 atomic charges. This dataset was randomly split into a training set and a validation set with an 88% to 12% ratio and was used to train the MACE equivariant GNNs, PBE0-NN and Qeq-NN. The test set, consisting of 600 frames of periodic liquid phosphoric acid systems, was randomly sampled from all six trajectories, which included both MD and RPMD ones at three different temperatures.
We evaluated the predictive accuracy of the two NNs. For the test set, the correlation coefficient (R2) between the atomic forces predicted by PBE0-NN and the reference values was 99.84% (see Fig. S3, ESI†), demonstrating excellent predictive performance. The mean absolute errors (MAEs) for energies and atomic forces were 0.238 meV per atom and 35.13 meV Å−1, respectively, closely aligned with the errors observed on the training and validation sets (see Table S2, ESI†). This consistency suggests that the NNP has achieved quantum chemical accuracy. Additionally, the MAE of atomic partial charge predictions in the periodic liquid phosphoric acid system, obtained using the Qeq-NN model, was as low as 0.003 e. This indicates that we can efficiently and accurately predict the distribution of partial charges throughout the trajectory, enabling precise analysis in subsequent trajectory studies. To assess the computational speed improvement of NNP MD simulations using PBE0-NN compared to AIMD, we tested systems of three different sizes (see in Fig. S4 and Table S4, ESI†). The results showed that our NNP achieved a performance efficiency improvement of at least 2400-fold over AIMD on CPU. Given that the NNP is deployed to run on GPUs, the computational efficiency in actual simulations is even more substantial. The computational resources for generating the dataset and training the ML model are compared in Section S3 of the ESI.†
2.3 Analysis methods
The trajectories obtained from MD simulations can be used to calculate the RDF, gA-B(r). The RDF describing the density of atoms of element B around atoms of element A and is defined as follows: | (7) |
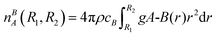 | (8) |
The diffusion of molecules and atoms in liquid phosphoric acid is crucial for understanding its transport properties. Given the strong PT capabilities of phosphoric acid under standard conditions, investigating the proton diffusion coefficient provides valuable insights into the mechanisms that facilitate efficient PT in liquid phosphoric acid. In condensed-phase systems, the diffusion coefficient for a specific atomic species can be derived from the slope of the mean square displacement (MSD) of the corresponding atoms:
 | (9) |
 | (10) |
The vibrational density of states (VDOS) is a tool used in MD simulations to analyze the dynamic properties of a system. The VDOS can be calculated from the autocorrelation function of atomic velocities, vi(t), obtained from the MD trajectories:
 | (11) |
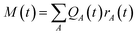 | (12) |
 | (13) |
The RPMD-simulated dynamical properties of liquid phosphoric acid are calculated by first averaging the coordinates, velocities, and dipole moments of different beads. These averaged values are then substituted into the corresponding formulas to obtain the desired dynamical properties.
2.4 Simulation details
We performed canonical ensemble MD simulations using the trained PBE0-NN model at three temperatures (298.15 K, 333.15 K, and 350.15 K) each for a duration of 1 ns. Additionally, we conducted canonical ensemble RPMD simulations with 12 beads at the same three temperatures for 100 ps, utilizing the PBE0-NN to explore NQEs in the phosphoric acid system. All NNP-based MD and RPMD simulations were performed with the i-PI software.57,58 For comparison, we also carried out a CVFF-based59 MD simulation of phosphoric acid at 298.15 K starting from the same initial structure and applying identical MD simulation parameters with the LAMMPS software.60 A Langevin thermostat61 was used to control the temperature in all MD simulations in this work. The computational resources for simulations and DFT calculations are compared in Section S3 of the ESI.†3. Results and discussions
3.1 Radial distribution functions
To verify the accuracy of the PBE0-NN MD simulation trajectories and to characterize the simulated structural information, we calculated the RDFs from the MD simulations of the phosphoric acid system and compared the results with those obtained from neutron scattering experiments,43 as shown in Fig. 2 and Table 2. It should be mentioned that all experimental data presented in our study were obtained using pure phosphoric acid. | ||
| Fig. 2 Radial distribution function of the phosphoric acid system at 333.15 K, obtained from PBE0-NN MD and RPMD simulations, compared with the experimental data.43 The variable X represents oxygen (O) and phosphorus (P) atoms. | ||
| Peaka | Position/Å | Average CNsb | Assignment |
|---|---|---|---|
| a Peak labels as shown in Fig. 2, where X represents O and P atoms. b Values presented before and after the slash correspond to MD and RPMD simulations, respectively. Experimental values of pure phosphoric acid from ref. 43 are provided in parentheses. n.m.: not meaningful. | |||
| gX–X (1) | 1.57 (1.54) | 1.10/1.19 (1.16) | P–O bonds |
| gX–X (2) | 2.55 (2.51) | 3.80/3.84 (3.82) | O–O intramolecular |
| gH–X (1) | 1.00 (0.98) | 0.95/0.95 (0.95) | H–O bonds |
| gH–X (2) | 1.53 (1.54) | 0.73/0.76 (0.75) | H–O through hydrogen bonds |
| gH–X (3) | 2.20 (2.20) | n.m. | H–P intramolecular |
| gH–X (4) | 2.80 (2.80) | n.m. | H–O intramolecular |
| gH–H (1) | 1.90–2.60 | n.m. | H–H across hydrogen bond |
| gH–H (2) | 2.60–4.10 | n.m. | H–H intramolecular and intermolecular |
Fig. 2 illustrates that the PBE0-NN MD results align closely with experimental RDFs, particularly in terms of peak positions for gX–X, gH–X, and gH–H in the phosphoric acid system. However, there are some discrepancies in the shape and intensity of these peaks. The first peak in gX–X, located at 1.57 Å in the PBE0-NN MD simulations, corresponds to the P–O bond within the phosphoric acid molecule and shows a minor deviation of 0.03 Å from the experimental value. In gas-phase phosphoric acid, P–O bonds are classified into single bonds (1.60 Å) and double bonds (1.46 Å).20 In the condensed-phase phosphoric acid system, however, only a single peak appears in the RDFs due to the influence of a strong hydrogen-bonding network. The second peak in gX–X, at 2.55 Å, represents O–O intramolecular correlations, with a 0.04 Å deviation from the experimental value. Overall, the deviations between PBE0-NN MD-simulated and experimental gX–X peak positions are small. Additionally, there is little difference between RPMD and MD results for gX–X, as NQEs are less significant for heavier atoms like O and P.
The gH–X peaks from both MD and RPMD simulations are similarly positioned and closely match experimental values. The first peak at 1.00 Å in gH–X corresponds to the covalent O–H bond, with a deviation of only 0.02 Å from the experimental value. RPMD simulations provide a more accurate depiction of peak intensity and width compared to MD. The second peak in gH–X, located at 1.53 Å, represents the intermolecular O⋯H–O hydrogen bond, deviating by 0.01 Å from the experimental value. The overlap of these two peaks in gH–X suggests frequent proton transfers along strong O⋯H–O hydrogen bonds in liquid phosphoric acid. However, RPMD might slightly overestimate this overlap compared to experimental data. The third and fourth peaks in gH–X reflect non-bonded intramolecular H–P and H–O interactions, respectively, with RPMD providing a significantly better representation of these interactions than MD.
The first peak in gH–H, spanning 1.90 to 2.60 Å, captures H–H correlations across adjacent hydrogen bonds. The MD simulations, however, tend to overestimate the intensity of this peak, indicating that the hydrogen-bond network in phosphoric acid appears more structured in simulations than in experimental measurements. Nonetheless, the gH–H peaks from both MD and RPMD simulations qualitatively agree with experimental data.
As presented in Table 2, the average coordination numbers calculated (CNs) from RPMD and MD simulations show no significant differences, indicating that PBE0-NN accurately predicts the structure and local atomic environment of phosphoric acid. Furthermore, the gH–X RDFs in Fig. 2 reveal that RPMD, which accounts for NQE, produces RDFs with peak intensities and shapes that are more consistent with experimental values. The overlap of the O–H bond and O⋯H–O hydrogen bond peaks suggests a lower energy barrier for proton transfer between oxygen atoms, potentially indicating increased proton diffusion and hopping in RPMD simulations. This aspect will be explored in the following section.
3.2 Proton diffusion
Fig. 3 illustrates the snapshots extracted from PBE0-NN MD trajectories at 298.15 K. These four panels sequentially display the transfer of three protons along a hydrogen bond chain to new oxygen atoms. Fig. 3(a) shows the initial 0 ps snapshot, where four phosphoric acid molecules or ions form a chain-like structure stabilized by hydrogen bonds. According to the Grotthuss mechanism,62 protons are transported through this hydrogen bond network by the continuous breaking and reforming of hydrogen bonds. Fig. 3(b) illustrates a later snapshot in which a proton (highlighted in yellow) has transferred from one oxygen atom to another along the hydrogen bond. About 3 ps later, as shown in Fig. 3(c), a second proton undergoes a similar transfer. Four ps after that, a third proton transfer occurs, depicted in Fig. 3(d).According to previous studies,21 proton transfer predominantly occurs through the hydrogen bond network rather than a molecular vehicle, as illustrated in Fig. 3. To investigate this, we tracked the motion of a single proton. Fig. 4 depicts its bonding to various oxygen atoms over time, excluding transfers to the same oxygen atom to provide a clearer view of directional PT within the hydrogen bond network. The transport distance of this proton is approximately 2 Å, contributing significantly to the high conductivity observed in liquid phosphoric acid.
Fig. 5 compares the proton diffusion coefficients at different temperatures from both PBE0-NN MD simulations and experimental data, with specific values listed in Table 3. The diffusion coefficients from the PBE0-NN MD simulations show a clear upward trend with increasing temperature. In RPMD simulations, the diffusion coefficients exhibit an exponential increase with temperature, aligning well with the experimental results.
 | ||
| Fig. 5 Comparison of proton diffusion coefficients in the phosphoric acid system obtained from PBE0-NN MD and RPMD simulations at various temperatures, alongside experimental values of pure phosphoric acid from ref. 63. | ||
| Temperature/K | D/10−10 m2 s−1 | |
|---|---|---|
| H | P | |
| a Values presented before and after the slash correspond to MD and RPMD simulations, respectively. Experimental values of pure phosphoric acid from ref. 63 are provided in parentheses. | ||
| 298.15 | 0.16/0.21 (0.40) | 0.04/0.06 (0.09) |
| 333.15 | 0.38/0.66 (1.27) | 0.06/0.22 (0.21) |
| 350.15 | 0.55/1.20 (2.02) | 0.11/0.39 (0.57) |
Table 3 also reveals that the diffusion coefficient of P is much smaller than that of H. This supports the conclusion that PT in phosphoric acid primarily follows a hopping mechanism, consistent with the mechanism shown in Fig. 3. The differences between simulated and experimental diffusion coefficients are within an order of magnitude. At temperatures of 298.15 K, 333.15 K, and 350.15 K, experimental diffusion coefficients for hydrogen in phosphoric acid were determined to be 0.40 × 10−10 m2 s−1, 1.27 × 10−10 m2 s−1, and 2.02 × 10−10 m2 s−1, respectively. Corresponding MD values were 0.16 × 10−10 m2 s−1, 0.38 × 10−10 m2 s−1, and 0.55 × 10−10 m2 s−1, while RPMD values were 0.21 × 10−10 m2 s−1, 0.66 × 10−10 m2 s−1, and 1.20 × 10−10 m2 s−1. Similar to previous simulations of liquid water systems, RPMD results show enhanced hydrogen diffusion coefficients compared to MD, highlighting the significant impact of NQEs on phosphoric acid dynamics. Both RPMD and MD simulations predict lower diffusion coefficients than the experimental values at corresponding temperatures. As shown in Fig. 2, the first H–H peak intensities predicted by both MD and RPMD simulaions are higher than experimental observations, which suggests that this discrepancy does not arise from the neglect of NQEs in the MD simulations. Similar discrepancy have been observed in previous PBE-based AIMD simulations of liquid phosphoric acid systems.20 This discrepancy may stem from the inherent limitations of the DFT method, as several studies have pointed out that DFT often struggles to accurately predict hydrogen bonding and tends to underperform relative to more advanced methods like MP2.64,65 This effect could result in protons becoming “trapped” in the simulations, leading to slower diffusion than in experiments, where additional bond-breaking and reforming events enhance proton mobility.
Fig. 2 also shows that the RDFs for hydrogen bonds and covalent bonds exhibit greater overlap in RPMD than in MD. This overlap lowers the energy barrier for proton hopping between oxygen atoms, facilitating proton diffusion. In contrast, MD predicts sharper, more intense RDF peaks for covalent bonds, hydrogen bonds, and H–O and H–P correlations, reflecting a denser phosphoric acid configuration that restricts proton mobility. By incorporating NQE, RPMD provides a more accurate representation of these interactions, which is crucial for capturing proton dynamics in phosphoric acid.
3.3 Vibrational spectra
We compared the VDOS and IR spectra of phosphoric acid at 298.15 K from MD simulations with experimental data, as shown in Fig. 6 and 7. Fig. 6 shows the PBE0-NN MD simulated VDOS for phosphoric acid along with experimental Raman peaks at 298.15 K.66 In Fig. 6(a), the MD-simulated VDOS does not display distinct vibrational peaks in the low- and mid-frequency regions. By contrast, Fig. 6(b) shows the VDOS from RPMD simulations, which features three distinct peaks, with those at 496 cm−1 and 359 cm−1 closely aligning with experimental observations. This alignment suggests that incorporating NQEs enhances the accuracy of vibrational energy spacing, evidenced by the sharper, more defined peaks in the RPMD spectrum. The simulated peak for P–O single bond stretching at 910 cm−1 matches the experimental value well in both MD and RPMD simulations, though the P–O double bond stretching exhibits a blue shift of approximately 100 cm−1. The overlapping vibrations of P–O single and double bonds, due to frequent proton transfers within phosphate, obscure distinct spectral features. While no discrete O–H bond stretching peaks were observed in the experimental Raman spectra, the simulations reveal a broad peak between 2400 and 4000 cm−1, significantly red-shifted compared to the sharp O–H stretching peak seen in gas-phase phosphoric acid.20 This broadening and red shift can be attributed to strong hydrogen bonding in liquid phosphoric acid, which weakens the O–H bond and suppresses a well-defined stretching mode. | ||
| Fig. 6 Comparison of the VDOS predicted by PBE0-NN MD (a) and RPMD (b) simulations with experimentally observed vibrational frequencies of pure phosphoric acid from ref. 66. Green arrows indicate vibrational frequencies observed in the experimental Raman spectra of liquid phosphoric acid. | ||
 | ||
| Fig. 7 Comparison of the IR spectra of pure phosphoric acid predicted by PBE0-NN MD and RPMD, and CVFF MD simulations with experimental data of pure phosphoric acid from ref. 67. | ||
Fig. 7 illustrates the IR spectra for phosphoric acid at 298.15 K, as predicted by PBE0-NN and CVFF MD simulations, compared with experimental attenuated total reflectance IR spectra.67 In the 400–1400 cm−1 region, the classical CVFF predicts two absorption peaks: one at 460 cm−1 with greater intensity than the 915 cm−1 peak. However, these peaks differ significantly from experimental data in terms of frequency, shape, and intensity. In contrast, PBE0-NN simulations, both MD and RPMD, produce an absorption peak at 490 cm−1 that closely matches the experimental peak in both frequency and shape. The experimental peak at 915 cm−1, associated with P–O bond vibrations, is more intense than in PBE0-NN simulations, with the RPMD-predicted peak exhibiting a red shift of about 30 cm−1, bringing it closer to the experimental frequency (Table 4).
| Peaks | Experiment | PBE0-NN RPMD | PBE0-NN MD | CVFF MD |
|---|---|---|---|---|
| 1 | 470 | 490 | 490 | 460 |
| 2 | 915 | 885 | 1030 | 915 |
| 3 | 2780 | 2800 | 3270 | 3060/3750 |
At high frequencies, the PBE0-NN simulations produce a broad absorption band from 2000 to 3800 cm−1, consistent with the experimentally observed broad peak. In contrast, absorption peaks from classical FF are much narrower, showing two distinct peaks that fail to capture the complex hydrogen-bonding network in phosphates. The PBE0-NN method weakens the O–H bond force constant and enhances dipole moment changes during vibration, leading to broader, stronger absorption features. Specifically, PBE0-NN MD simulations reveal a prominent absorption peak at 3270 cm−1, which is blue-shifted by approximately 490 cm−1 from the experimental value. In comparison, PBE0-NN RPMD, which accounts for NQEs of light atoms such as hydrogen, predicts O–H stretching peaks in the range of 2000 to 3500 cm−1. The shape and intensity of this RPMD-predicted peak align well with experimental data, with only a 20 cm−1 blue shift at the peak's maximum.
These findings underscore the critical role of NQEs in influencing proton vibrational properties in liquid phosphoric acid. Classical MD, which neglects NQEs, underestimates the impact of strong hydrogen bonding on O–H vibrations in liquid phosphoric acid. In contrast, RPMD effectively captures these effects by modeling protons as a series of “beads” forming a ring polymer. Overall, these results highlight the strong predictive performance of the PBE0-NN method for the vibrational spectra of phosphoric acid and emphasize the indispensable role of NQEs in facilitating PT within liquid phosphoric acid systems.
4. Conclusion
In this work, we developed a NNP for phosphoric acid based on a high-precision dataset generated using the PBE0 hybrid functional. Long-time simulations were conducted at three temperatures using both RPMD and MD simulations. The simulated RDFs closely align with experimental results, validating that the PBE0-NN model accurately captures the structural characteristics of phosphoric acid. Notably, the gH–X curves from RPMD match experimental data more closely than those from MD, highlighting the significant impact of NQEs on structural properties. Furthermore, analysis of the MD trajectories reveals continuous directional proton transfer along hydrogen-bond networks, indicating that PT in phosphoric acid follows the Grotthuss mechanism (similar to liquid water), where protons hopping through hydrogen bond breaking and reformation.Comparing proton diffusion coefficients obtained from RPMD and MD at various temperatures confirmed that NQEs significantly enhance PT. Additionally, RPMD reproduces the vibrational density of states and IR spectra with greater accuracy in both shape and frequency. Our results show that RPMD not only provides more accurate vibrational energy spacing but also captures the effects of strong hydrogen bonding and proton tunneling on the transport and vibrational properties of phosphoric acid. These findings offer valuable insights and a robust foundation for further exploration of NQEs in the conductive properties of phosphoric acid and related materials. Building on this work, future research could explore the integration of NNP and PIMD simulations with low-scaling electron correlation methods.68 This would enable the construction of datasets at the MP2 or CCSD(T) level, thus achieving more accurate NNP-based MD simulations. Additionally, we aim to develop NNs capable of predicting system pressure, which will enable pressure-controlled simulations. This approach will allow us to simulate the viscosity of phosphoric acid and phosphate systems across a range of temperatures and concentrations, thus providing a more comprehensive theoretical framework for understanding their properties.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 22273038, 22033004), Jiangsu Province Innovation Support Program (Soft Science Research) Special Funding (no. BK20232012), and Nanjing University AI&AI for Science Special Project.References
- R. Gilmour, Purification, Uses, Technology and Econimics, USA, 2013, pp.11–12 Search PubMed.
- J. Elm, N. Myllys and T. Kurtén, Mol. Phys., 2017, 115, 2168–2179 CrossRef CAS.
- M. Zeng, B. Liao, M. Lei, Y. Zhang, Q. Zeng and B. Ouyang, J. Environ. Sci., 2008, 20, 75–79 CrossRef CAS PubMed.
- M. Millan, S. Teinturier, C. A. Malespin, J. Y. Bonnet, A. Buch, J. P. Dworkin, J. L. Eigenbrode, C. Freissinet, D. P. Glavin, R. Navarro-González, A. Srivastava, J. C. Stern, B. Sutter, C. Szopa, A. J. Williams, R. H. Williams, G. M. Wong, S. S. Johnson and P. R. Mahaffy, Nat. Astron., 2022, 6, 129–140 CrossRef.
- H. Abdi, R. Rasouli Nezhad and M. Salehimaleh, in Distributed Generation Systems, ed. G. B. Gharehpetian and S. M. Mousavi Agah, Butterworth-Heinemann, 2017, pp. 221–300 Search PubMed.
- L. Vilčiauskas, M. E. Tuckerman, G. Bester, S. J. Paddison and K.-D. Kreuer, Nat. Chem., 2012, 4, 461–466 CrossRef PubMed.
- K.-D. Kreuer, Chem. Mater., 1996, 8, 610–641 CrossRef CAS.
- Q. Li, J. O. Jensen, R. F. Savinell and N. J. Bjerrum, Prog. Polym. Sci., 2009, 34, 449–477 CrossRef CAS.
- K. H. Lim, I. Matanovic, S. Maurya, Y. Kim, E. S. De Castro, J.-H. Jang, H. Park and Y. S. Kim, ACS Energy Lett., 2023, 8, 529–536 CrossRef CAS.
- G. Skorikova, D. Rauber, D. Aili, S. Martin, Q. Li, D. Henkensmeier and R. Hempelmann, J. Membr. Sci., 2020, 608, 118188 CrossRef CAS.
- H. R. Kim, J. H. Lee and T. S. Kim, J. Mech. Sci. Technol., 2020, 34, 3863–3874 CrossRef.
- S. V. Kanuri and S. Motupally, in Fuel Cells and Hydrogen Production: A Volume in the Encyclopedia of Sustainability Science and Technology, ed. T. E. Lipman and A. Z. Weber, Springer, New York, New York, NY, 2nd edn, 2019, pp. 515–530 Search PubMed.
- F. H. Westheimer, Science, 1987, 235, 1173–1178 CrossRef CAS PubMed.
- J. Heberle, J. Riesle, G. Thiedemann, D. Oesterhelt and N. A. Dencher, Nature, 1994, 370, 379–382 CrossRef CAS PubMed.
- W. F. van Gunsteren and H. J. C. Berendsen, Biochem. Soc. Trans., 1987, 15, 303–306 CrossRef.
- H. Sun, P. Ren and J. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246 CrossRef CAS.
- S. A. H. Spieser, B. R. Leeflang, L. M. J. Kroon-Batenburg and J. Kroon, J. Phys. Chem. A, 2000, 104, 7333–7338 CrossRef CAS.
- S. Zhu, L. Yan, D. Zhang and Q. Feng, Polymer, 2011, 52, 881–892 CrossRef CAS.
- S. Li, J. R. Fried, J. Sauer, J. Colebrook and D. S. Dudis, Int. J. Quantum Chem., 2011, 111, 3212–3229 CrossRef CAS.
- E. Tsuchida, J. Phys. Soc. Jpn., 2006, 75, 054801 CrossRef.
- I. Popov, Z. Zhu, A. R. Young-Gonzales, R. L. Sacci, E. Mamontov, C. Gainaru, S. J. Paddison and A. P. Sokolov, Commun. Chem., 2023, 6, 77 CrossRef CAS PubMed.
- M. Sun, A. W. Dougherty, B. Huang, Y. Li and C. H. Yan, Adv. Energy Mater., 2020, 10, 1903949 CrossRef CAS.
- V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765 CrossRef CAS PubMed.
- T. C. Ricard, X. Zhu and S. S. Iyengar, J. Chem. Theory Comput., 2023, 19, 8541–8556 CrossRef CAS PubMed.
- Z. Yan, D. Wei, X. Li and L. W. Chung, Nat. Commun., 2024, 15, 4181 CrossRef CAS PubMed.
- J. Liu, J. Lan and X. He, J. Phys. Chem. A, 2022, 126, 3926–3936 CrossRef CAS PubMed.
- Y. Chen, Y. Ou, P. Zheng, Y. Huang, F. Ge and P. O. Dral, J. Chem. Phys., 2023, 158, 074103 CrossRef CAS PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- J. Zeng, D. Zhang, D. Lu, P. Mo, Z. Li, Y. Chen, M. Rynik, L. A. Huang, Z. Li, S. Shi, Y. Wang, H. Ye, P. Tuo, J. Yang, Y. Ding, Y. Li, D. Tisi, Q. Zeng, H. Bao, Y. Xia, J. Huang, K. Muraoka, Y. Wang, J. Chang, F. Yuan, S. L. Bore, C. Cai, Y. Lin, B. Wang, J. Xu, J.-X. Zhu, C. Luo, Y. Zhang, R. E. A. Goodall, W. Liang, A. K. Singh, S. Yao, J. Zhang, R. Wentzcovitch, J. Han, J. Liu, W. Jia, D. M. York, W. E, R. Car, L. Zhang and H. Wang, J. Chem. Phys., 2023, 159, 054801 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- J. Daru, H. Forbert, J. Behler and D. Marx, Phys. Rev. Lett., 2022, 129, 226001 CrossRef CAS PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14, 579 CrossRef CAS.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, NeurIPS, 2022, 35, 11423–11436 Search PubMed.
- R. Jinnouchi, Phys. Chem. Chem. Phys., 2022, 24, 15522–15531 RSC.
- Y. Kawashima, K. Sawada, T. Nakajima and M. Tachikawa, J. Comput. Chem., 2019, 40, 172–180 CrossRef CAS.
- M. Heres, Y. Wang, P. J. Griffin, C. Gainaru and A. P. Sokolov, Phys. Rev. Lett., 2016, 117, 156001 CrossRef CAS PubMed.
- Y. Nishimura and H. Nakai, J. Chem. Phys., 2023, 158, 164101 CrossRef CAS PubMed.
- F. Paesani, W. Zhang, D. A. Case, T. E. Cheatham, III and G. A. Voth, J. Chem. Phys., 2006, 125, 184507 CrossRef PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- N. C. f. B. Information, PubChem Compound Summary for CID 1004, Phosphoric Acid., https://pubchem.ncbi.nlm.nih.gov/compound/Phosphoric-Acid, (accessed July 25, 2024).
- R. H. Tromp, S. H. Spieser and G. W. Neilson, J. Chem. Phys., 1999, 110, 2145–2150 CrossRef CAS.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- C. Schran, K. Brezina and O. Marsalek, J. Chem. Phys., 2020, 153, 104105 CrossRef CAS PubMed.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- D. P. Kovács, J. H. Moore, N. J. Browning, I. Batatia, J. T. Horton, V. Kapil, I.-B. Magdău, D. J. Cole and G. Csányi, arXiv, 2023, preprint, arXiv:2312.15211 DOI:10.48550/arXiv.2312.15211.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS.
- A. Y. Toukmaji and J. A. Board, Comput. Phys. Commun., 1996, 95, 73–92 CrossRef CAS.
- V. Agarwal, G. W. Huber, W. C. Conner, Jr. and S. M. Auerbach, J. Chem. Phys., 2011, 135, 134506 CrossRef PubMed.
- V. Kapil, M. Rossi, O. Marsalek, R. Petraglia, Y. Litman, T. Spura, B. Cheng, A. Cuzzocrea, R. H. Meißner, D. M. Wilkins, B. A. Helfrecht, P. Juda, S. P. Bienvenue, W. Fang, J. Kessler, I. Poltavsky, S. Vandenbrande, J. Wieme, C. Corminboeuf, T. D. Kühne, D. E. Manolopoulos, T. E. Markland, J. O. Richardson, A. Tkatchenko, G. A. Tribello, V. Van Speybroeck and M. Ceriotti, Comput. Phys. Commun., 2019, 236, 214–223 CrossRef CAS.
- M. Ceriotti, J. More and D. E. Manolopoulos, Comput. Phys. Commun., 2014, 185, 1019–1026 CrossRef CAS.
- P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Proteins, 1988, 4, 31–47 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford Univ. Press., 2017 Search PubMed.
- D. Marx, ChemPhysChem, 2007, 8, 209–210 CrossRef CAS.
- T. Dippel, K. D. Kreuer, J. C. Lassègues and D. Rodriguez, Solid State Ionics, 1993, 61, 41–46 CrossRef CAS.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- A. D. Boese, ChemPhysChem, 2015, 16, 978–985 CrossRef CAS PubMed.
- A. Simon and G. Schulze, Z. Anorg. Allg. Chem., 1939, 242, 313–368 CrossRef CAS.
- Y. A. Fadeeva, I. V. Fedorova, M. A. Krestyaninov and L. P. Safonova, J. Mol. Liq., 2020, 300, 112342 CrossRef CAS.
- W. Li, G. Wang and J. Ma, Natl. Sci. Rev., 2023, 10, nwad335 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04195j |
| This journal is © the Owner Societies 2025 |



