Influence of symmetry breaking on the absorption spectrum of crystal violet: from isolated cations at 5 K to room temperature solutions

Abstract

We report the resolution of a long-standing puzzle in molecular spectroscopy: the origin of the shoulder in the room temperature solution absorption spectrum of crystal violet (CV) - an archetypal cationic triphenylmethane dye. This was achieved by comparing experimental and theoretical results for CV in solution at room temperature and as an isolated cation in gas-phase at 5 K. The two lowest energy electronically excited states involved in the visible region absorption are degenerate and coupled via a Jahn–Teller (JT) mechanism involving phenyl torsions, making CV particularly sensitive to environmental perturbations. The shoulder is absent in the low-temperature isolated cation spectrum, and vibronic simulations based on time dependent density functional theory (TD-DFT) indicate negligible JT effects under these conditions. Combining vibronic simulations with molecular dynamics, demonstrates that in water and toluene solution at room temperature the shoulder arises mainly from an intermolecular, Jahn–Teller-like symmetry-breaking effect induced by the fluctuating electrostatic potential of the disordered solvent environment, rather than from molecular distortions.

---

Introduction

The broad, visible-region, room temperature solution absorption band of hexamethyl pararosaniline chloride (commonly known as crystal violet, CV⁺…Cl⁻) shows a shoulder to higher energy which depends sensitively on solvent polarity (see ref. 1 and references therein). The origin of crystal violet's shoulder has been the subject of controversy since G. N. Lewis proposed that the propeller-shaped, chiral molecular cation (CV⁺, see insert in Fig. 1(a) and (c)) can exist in an equilibrium of two different isomeric forms in solution. One isomer is symmetric with each of its three arms rotated by the same dihedral angle (of about 33 degrees) out of the molecular plane and the other isomer was thought to have one arm twisted in the opposite direction.² More than 80 years later, after many spectroscopic^1–13 and theoretical^11–16 studies of the corresponding electronic transition from S₀ to the degenerate pair (in D₃ symmetry) of S₁ and S₂ states, using increasingly complex methods, it still remains unclear whether distinct isomers, torsional disorder and/or other types of symmetry breaking are responsible for the shoulder of CV⁺. The peculiarity of this molecule is that the pair of degenerate S₁ and S₂ states can undergo Jahn–Teller (JT) distortions and therefore have an intrinsic tendency to symmetry breaking which is likely enhanced by environmental perturbations like non-covalent interactions with the solvent and counterions.

Fig. 1 Panel (a) comparison of computed and experimental spectra (S₁ + S₂) at 0 K, using the vertical gradient (VG) approach and the linear vibronic coupling (LVC) approach within quantum dynamics (QD) and the experimental spectrum recorded at 5 K, respectively. The computed VG spectrum was determined with CAM-B3LYP/cc-pVDZ, including all normal coordinates and shifted by −0.54 eV to match the main experimental peak and it was broadened with a Gaussian with FWHM = 65 cm⁻¹. The QD-LVC spectrum was computed as discussed above by considering the contribution of the seven normal coordinates reported in Table S2 (ESI†). Gas-phase experimental data at 5 K obtained with the He-TAG setup are shown in black. The inset represents the CV⁺ chemical structure. (b) The main stick bands of the computed VG spectrum are assigned with labels p^x, where p is the normal mode and x the number of quanta (e.g., 5¹, 5² represent the 1st and 2nd vibrational excitations associated to mode 5). C₀ band is the transition between the ground vibrational states (0–0). Different shades of green instead distinguish stick bands to final states belonging to class C_n, where “n” is the number of simultaneously excited normal modes in the excited state (i.e., C₁ represent vibrational excitations of a single mode at a time, while C₂ represent simultaneous excitation of two vibrational modes at a time).¹⁷ (c) Visual representations of the modes responsible for the most extensive vibronic progressions (related movies are uploaded in the ESI†).

For example, Vauthey et al.¹³ recently studied CV⁺ in solutions using both time and frequency domain spectroscopic methods together with time dependent density functional theory (TD-DFT) calculations including a polarizable continuum model (PCM)^18,19 to approximate solvent effects. They concluded that the splitting in the absorption spectrum is mainly due to symmetry breaking via torsional disorder. This has been recently disputed by Zuehlsdorff et al., who have computed the solution spectra at room temperature by using molecular dynamics (MD) and a cumulant approach.¹⁶ Results suggest that in polar solvents there are contributions to the shoulder from both torsional disorder and non-covalent interactions with solvent. Both effects serve to break the symmetry of the CV⁺ ground state. In non-polar solvents by contrast, the main contribution to spectral splitting appears to be interaction with the chloride counterion which forms a contact pair (while this interaction is essentially completely shielded in polar solution). These conclusions depend on the accuracy with which electronically excited states and vibronic coupling effects can be described at the TD-DFT level, as well as on the accuracy of the configuration sampling and the description of related solvent interactions. Therefore, to definitively disentangle the contribution of intra-molecular and inter-molecular factors to the shoulder in the absorption spectrum, better-defined experimental benchmarks and new theoretical calculations are needed.

To this end, in this work, we combined high-resolution experimental techniques with state-of-the-art calculations, including non-adiabatic JT couplings, solvent, temperature, and electrostatic effects, all of which play an important role in the photophysics of the CV⁺ molecule as we show here. In particular, we experimentally studied the CV⁺ dye under isolated conditions without counterion at low vibrational temperature thus accessing its vibronically resolved absorption features for the first time. Loison et al.¹¹ had previously recorded an essentially unresolved photodissociation (PD) spectrum of isolated CV⁺ near room temperature (including also a PD spectrum of [CV⁺…H₂O]). Some of us have recently implemented an experimental setup allowing PD measurements of isolated ions tagged with one helium atom at 5 K which we have used to study the absorption spectra of a range of organic dye cations – notably rhodamine B,²⁰ pyronin Y²¹ and acriflavine.²² Here we report an analogous PD spectroscopy study of isolated [CV⁺…He].

Our calculations showed that despite that low-frequency torsions are found to be active in JT couplings,²³ JT effects are very minor at 5 K and the spectrum of the isolated CV⁺ molecule can be well described by vibronic calculations performed in the harmonic approximation. In this way, we could single out the modes responsible for the observed vibronic structure. Interestingly, this shows no sign reminiscent of the shoulder found in room-temperature solution.²⁴ To consistently include the effect of temperature, molecular flexibility and solvent fluctuations, we further employed a mixed quantum classical approach where vibronic computations are performed on top of snapshots extracted from classical molecular dynamics (MD),^25,26 allowing to predict spectra in gas-phase as well as in explicit water and toluene solution at room temperature. Notably, we performed MD production runs up to 10 ns to ensure a thorough sampling of the configurational space by building and using quantum mechanically derived force fields.^27,28 The results satisfactorily describe the absorption measurements performed in solution and are analysed to dissect the role of intra-molecular flexibility and environment-induced symmetry breaking in both the ground and excited states on the absorption properties of this well-known chromophore.

Results and discussion

Photodissociation experiments at 5 K

The visible region PD spectrum of isolated hexamethyl pararosaniline cation tagged with one helium atom ([CV⁺…He]) at 5 K is presented in Fig. 1 (see also Fig. S1 and Table S1 for peak positions, ESI†). It was obtained with an instrumental setup for one-photon laser PD spectroscopy of mass-selected ions complexed with helium atoms (He-TAG) which has been described elsewhere.²⁰ Briefly, after electrospray, mass-selection and accumulation, the ions are trapped in a radio-frequency ion trap with helium as a buffer gas. At wall temperatures of 3–5 K, adducts of the ions and He are then formed. Such adducts are irradiated with a tuneable, nanosecond pulsed laser having a spectral resolution of 5 cm⁻¹ (FWHM). The number of remaining He-tagged ions is recorded using a second quadrupole mass filter and an ion counter. Assuming no significant competing processes, the wavelength dependent depletion of tagged ions resulting from one photon absorption can be converted into a normalized absorption cross section as plotted in Fig. 1. We probed [CV⁺…He] and compared this to the slightly shifted spectra of adducts with more than one helium atom (see Fig. S2, ESI†). Before performing the PD measurement, the mass composition of the sample was checked via mass spectrometry (see Fig. S3 and S4, ESI†) and the isomeric composition of the isolated CV⁺ sample generated by electrospray from solution was checked via cyclic traveling wave ion mobility spectrometry (see Fig. S5 (ESI†) and also ref. 22, 29 and 30). Only one isomer was observed with a calibrated collision cross section³¹ in good agreement with the ground state structure obtained from theory. The He-TAG spectrum shows an unusual vibronic pattern, with the strongest transition at ν_max = 18 468 cm⁻¹ followed by a long progression in a ∼194 cm⁻¹ vibration (with up to eight monotonically damped features) towards higher energy. Notably, there is no indication of a higher-energy shoulder, as observed in the room temperature solution absorption spectrum (see below). Interestingly, the vibronic features seen in the 5 K spectrum are significantly broadened (FWHM of 93 cm⁻¹) relative to the laser resolution limited bandwidths (of about 5 cm⁻¹) typically seen by us and others in previous measurements of structurally rigid, cationic chromophores at low vibrational temperatures.^20–22,32 We will return to this point below.

Theoretical description of the 5 K spectrum and assignment of vibronic features

To understand the vibronically resolved 5 K electronic spectrum of isolated [CV⁺…He] (and its relation to the red shifted solution spectra) we next turn to theory. The ground-state optimized structure of CV⁺ exhibits D₃ symmetry, characterized by a doubly degenerate irreducible representation E, which results in the degeneracy of the two lowest-lying dipole-allowed excitations, S₁ and S₂. TD-DFT calculations on the optimized chromophore in the ground state in gas-phase reveal that these two states arise from a combination of transitions from HOMO and HOMO−1 to LUMO (see Table S2, ESI†) and that their degeneracy is due to the degeneracy of two specific canonical Kohn–Sham molecular orbitals (MOs): the HOMO and HOMO−1 orbitals.^13,14,16

When considering Fig. 1 it is important to note that, the two degenerate excited electronic states can undergo vibrationally coupled E⊗e JT distortion. The two adiabatic potential energy surfaces (PES) form a conical intersection (CI) in D₃ symmetry, which takes on the characteristic shape of a Mexican hat^12,23 and consequently vibronic states that span the region of the coordinate space where the CI is located are expected to be affected by nonadiabatic couplings. Therefore, in principle, to accurately compute the absorption spectra of such JT systems, non-adiabatic approaches are required. Specifically, we incorporated the couplings between the two states of the degenerate pair using a linear vibronic coupling (LVC) model. The LVC Hamiltonian is built from quadratic expansions of the diabatic potentials assuming that they have the same Hessian of the ground state and adding linear potential couplings between the states as explained in ESI† Section S3. Here, the Hamiltonian was parameterized using TD-DFT calculations and the diabatic states reconstructed through a maximum-overlap diabatization technique implemented in our freely distributed code, Overdia.^33,34 In order to compute the nonadiabatic spectrum, quantum dynamics propagation on the coupled diabatic PES are used to numerically compute the time evolution of the electron-nuclear wavepackets and the associated correlation functions weighted by the electric transition dipole moments of the corresponding states.³⁵ These simulations were performed accounting for the seven most relevant degrees of freedom (see below) and using the MCTDH method³⁶ and in particular its implementation in QUANTICS.³⁷ Details are given in ESI† Section S3.

Using this approach, we found JT couplings involving concerted rotations of the phenyl rings, but they have a very small impact on the shape of the spectrum at 5 K. This is illustrated in Fig. S6 (ESI†), where we show that the spectra with and without linear JT couplings are essentially the same. Therefore, in the following steps of our analysis of the CV⁺ spectrum we neglected JT couplings. In this way, the LVC model simplifies into the straightforward vertical gradient (VG) model.³⁸ VG is an adiabatic model which neglects non-adiabatic couplings between states and assumes that the final-state PES has the same normal modes and frequencies as the initial-state.^24,39 Thus, it only accounts for the effect of the displacement of the equilibrium position that is estimated with a harmonic model from the excited vertical gradient at the ground state geometry. This model can be easily utilized in combination with analytical methods for the computation of optical spectra,^24,39 including the effect of all normal coordinates. For such computations we adopted our code FCclasses3.0²⁴ (see ESI† Section S3). A comparison of the computed VG spectrum with that obtained with LVC quantum dynamics simulations and the He-TAG experiment is shown in Fig. 1(a). The VG approach successfully replicates the peak spacing, vibronic pattern/progression, and the broadening of the experimental bands. This holds for both well-known CAM-B3LYP⁴⁰ and ωB97X-D⁴¹ long-range corrected functionals, which give similar Huang–Rhys factors and normal mode vibrational frequencies (see Table S3 and Fig. S7, ESI†). By contrast, absolute transition energies are predicted ca. 0.5–0.6 eV too high depending on the functional – reflecting well-known systematic errors of TD-DFT in combination with long-range corrected functionals when applied to molecules of this type.^42,43 In Fig. S8 (ESI†), we also show that at low temperature S₁ and S₂ degenerate states yield the same spectrum.

To understand the origin of the experimental vibronic features characterizing the low-temperature He-TAG spectrum, we show the main modes responsible for the main vibronic progressions in Fig. 1b. The 0–1 band at about 18 648 cm⁻¹ (2.31 eV) is due to the fundamental of the totally symmetric breathing mode 18 (Fig. 1c), yielding an energy spacing of ∼194 cm⁻¹, with some contribution from the fundamental of mode 22 (see Table S3, ESI†). The 0–2 band at about 18 861 cm⁻¹ (2.34 eV) is due to both the overtone of mode 18 and the fundamental of mode 36. Each experimentally visible vibronic feature conceals a progression along very low-frequency modes. Among these, mode 5 for CV⁺, which involves a concerted rotation of the phenyl rings (a “torsion” mode, see Fig. 1c) brings a sizable Huang–Rhys factor. We note that, mode 5 belongs to a degenerate pair, together with mode 4 of E symmetry (see Fig. 1c) and they are involved in the E⊗e JT system discussed above (note that these low-frequency modes together with modes number 2 and 3 were considered in our LVC model as well, see ESI† Section S4 and Fig. S6).

Rationalizing the intrinsic broadening of the lowest energy features in the 5 K spectrum

We next focus on the fine details of the 5 K He-TAG spectrum. On closer inspection the first peak whose overall width is 92 cm⁻¹ actually shows two partially resolved peaks with maxima separated by about 44 cm⁻¹ (see Fig. 2 and Fig. S2, ESI†), each of them having a FWHM of around 43 cm⁻¹. As noted, the latter value is still significantly larger compared to the 5 cm⁻¹ laser bandwidth-limited vibronic features observed in analogous helium tagging PD studies.^20–22,32 What is the origin of the splitting and the broadening?

Fig. 2 (a) Averaged spectrum over two different conformers found for the [CV⁺…He] complex, simulated at CAM-B3LYP/cc-pVDZ level. The spectrum for each conformer is computed taking the AS (w/o He) spectrum and shifting the vertical energies according to the single point TD-DFT calculations of the conformer. Each conformer is weighted according to Boltzmann populations at 5 K (ConfA : ConfB = 1 : 2). Panels (b) and (c) represent the optimized structures at CAM-B3LYP/cc-pVDZ of the two conformers. The helium atom is shown in orange. The computed spectra were shifted by −0.54 eV to match the experiment.

Our spectral simulations suggest that the two features observed in the 0–0 band come from the progression along one of the torsional E-symmetry modes, with a frequency consistent with the separation of nearly 40 cm⁻¹. This frequency and corresponding progression are rather sensitive to slight changes in the displacement of the torsional degrees of freedom. To estimate this dependence, we compared the VG predictions with those of an analogous approach for reconstructing the excited-state PES, known as the adiabatic shift (AS) as well as both CAM-B3LYP and ωB97X-D functionals. Notably, like VG the AS model only accounts for vibronic effects due to equilibrium geometry displacements, however it computes these displacements through direct optimization of the final state, rather than relying on a harmonic approximation of the PES.

In Fig. 2, panel (a), we show that CAM-B3LYP when using the AS model – taking the B-symmetry stationary-point as a reference structure to expand the final state PES (more details below) – correctly describes a significantly large displacement along the low frequency torsional modes and gives an especially good agreement with the experiment. On the contrary, ωB97X-D functional underestimates this displacement (see Fig. S9, ESI†). The progression predicted by the VG model is significantly lower in intensity, despite the torsional displacements being only slightly smaller compared to those computed with the AS model. It is important to remark that these torsional degrees of freedom are the same modes involved in the E⊗e JT effect. Overall, the present results not only prove that the two bands with a 44 cm⁻¹ spacing arise from progressions around such E-symmetry low frequency modes, but they also demonstrate that accurately reproducing them is quite challenging due to the anharmonicities and couplings of the S₁ and S₂ surfaces.

After clarifying the origin of the splitting of the 0–0 bands, we now focus on explaining the significant broadening of each partially resolved peak. To understand the physical reasons for this loss of resolution, we first take a deeper look at the electronic states of CV⁺. Our computational study shows that symmetry breaking from D₃ to C₂ splits the degenerate E pair into two states belonging to B and A irreducible representations (irreps). The optimization of the B-symmetry state reaches a stationary-point consistent with that predicted by the VG model (see Fig. S10 and S11, ESI†), while the A-symmetry one follows a barrierless decay to a dark CT state, with nearly zero oscillator strength. The minimum of the latter state is mainly characterized by a large rotation around the torsion of one of the rings (see Fig. S12a, ESI†), eventually reaching a nearly perpendicular orientation (see Fig. S13a, ESI†). Moreover, it is also worth noting that even the stationary point located for the B-state is actually a transition state, as it displays an imaginary frequency over a non-totally symmetric stretching mode, involving the distortion of the central C–C bonds, which further lowers the symmetry to C₁. A new optimization of the system after a small displacement along this mode results in decay towards the dark CT state as shown in Fig. S10 and S11 (ESI†), proving that the two states are coupled even far from the D₃ JT conical intersection. It is conceivable that the coupling between the B and A states and the A-symmetry path toward the dark CT state provide a fast non-radiative channel able to reduce the lifetime of the bright state and, in turn, increases the natural broadening. This fact can qualitatively explain some of the unusually large broadening observed in the experiment.

Another potential source of broadening could be related to the intrinsic tendency of the molecule to undergo symmetry breaking due to JT instability mentioned before. This effect could be induced by inter-molecular factors, for instance the weak interaction of the He atoms used in our He-TAG measurements with the CV⁺ molecule. Until now, we have neglected this possibility in our theoretical treatment by calculating only the isolated CV⁺. Consequently, we now explore the potential effect of He atoms attached to the CV⁺ cation. First, we identified two stable conformers of the [CV⁺…He] adducts depicted in Fig. 2, panels (b) and (c). These structures, with the He located either near to the nitrogen atom or to the aromatic ring (the latter being the global minimum), are quite close in energy (ΔE = 2.3 cm⁻¹). At temperatures as low as 5 K, their relative Boltzmann populations are nearly 1 : 2. The presence of the He atom breaks the D₃ symmetry in the excited states and thus introduces a slight splitting of S₁ and S₂ that could lead to spectral broadening. We attempted to apply the AS vibronic model by optimizing the excited bright state, including the He atom. However, this procedure proved very challenging and ultimately unsuccessful due to the complex characteristics of the S₁ and S₂ PES discussed above. Therefore, we adopted an alternative, simplified approach. Specifically, the spectral shapes for both the S₁ and S₂ states were taken from those of the isolated species (w/o He) using the AS model (red dashed line in Fig. 2), which includes a Gaussian broadening with FWHM = 26 cm⁻¹ (chosen smaller than the experimental width of FWHM = 43 cm⁻¹). Then, for each of the two stable [CV⁺…He] adducts, we considered the contributions of the S₁ and S₂ states to the spectrum and shifted them according to the computed effect of symmetry breaking caused by the He atom on the transition energies. The resulting predicted spectrum, indicated with the orange line in Fig. 2, panel (a), qualitatively supports the idea that part of the experimentally observed shift and broadening also results from symmetry-breaking induced by the He atom.

Shoulder of the solution absorption spectrum at room temperature

We now turn to the analysis of the effect of temperature and solvent on the spectral features of the CV⁺ molecule. Fig. 3 presents the electronic absorption spectra of hexamethyl pararosaniline chloride in water and toluene solutions (CV⁺(solv), room temperature). The experimental spectra (dashed lines) were recorded using a Cary 500 (Varian) UV/VIS spectrometer (for details see ESI† Section S1) and are consistent with previous literature.^3,44 The same batch of crystal violet from Sigma Aldrich was used without further purification throughout (incl. He-TAG). Fig. 3 also includes the gas-phase photodissociation spectrum at room temperature previously obtained by Loison et al.¹¹ as well as our 5 K He-TAG measurement. In going from 5 K to room temperature in gas-phase we note a dramatic increase in spectral broadening associated with essentially complete loss of vibronic structure and a red shift of about −0.065 to −0.070 eV. The broadening is a consequence of the wider geometrical distributions accessed by higher vibrational temperatures. Interestingly, no shoulder is yet distinguishable in the gas phase spectrum at room temperature.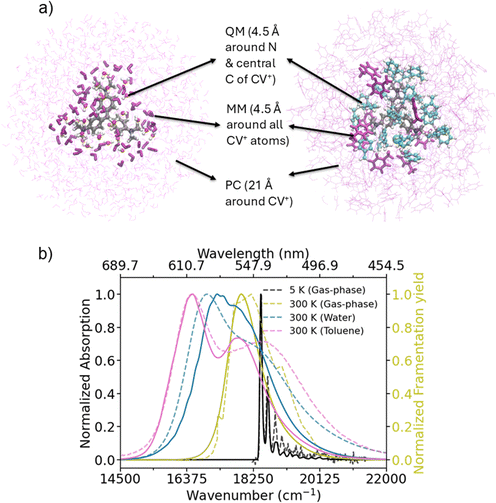

Fig. 3 (a) Representation of the various layers characterizing the ONIOM QM/MM approach^45,46 used for the description of the CV⁺ snapshots extracted from long (10 ns) MD trajectories in water (left) and in toluene (right). Details are given in ESI† Section S4. A CV⁺ molecule is included in the QM region together with explicit solvent molecules within 4.5 Å from the nitrogen atoms and the central carbon atom of the CV⁺ molecule (Corey–Pauling–Koltun (CPK) and related colour scheme). The other solvent molecules within 4.5 Å from any other CV⁺ atom were included at MM level (thick purple representation) using the same force-field adopted in the MD simulation. Finally, all the rest of the solvent molecules within 21 Å around the chromophore are treated as atomic point charges (PC) placed at the different atomic positions extracted from the MD (thin purple representation). The charges were obtained using the restrained electrostatic potential (RESP) procedure⁴⁷ to fit the electronic density as explained in ESI† Section S4. The chloride ion (typically proximal to CV⁺, see also Fig. S20) is represented in green. (b) Comparison between computed (solid lines) and experimental (dashed lines) spectra in different temperature and solvent conditions. Ad-MD|gVG simulations were ran adopting the ONIOM QM/MM partition represented in panel (a) to obtain RT data in water and toluene, represented with pink and blue lines, respectively. The same Ad-MD|gVG computation was used to obtain the spectrum in gas-phase by performing MD simulations at room temperature of CV⁺ in isolation as described in the Methods (ESI† Section S3). Note, that all the simulated data are obtained using ωB97X-D level of theory as explained in the main text. The spectra at RT were all shifted to the red by −0.7 eV, while the data at 5 K were shifted by −0.581 eV to match the experiment (yellow and black lines). Experimental RT data in toluene and water were obtained as described in the text, while the RT experimental data in gas-phase were taken from ref. 11 (Fig. 4; experimental fragmentation yield).

Compared to the gas-phase room temperature spectrum of CV⁺, CV⁺Cl⁻ dissolved in the polar solvent water shows further spectral broadening and a solvatochromic red shift by ∼−0.12 eV. Importantly, in water we note the appearance of a second band/shoulder at higher energy (0.17 eV shift). In toluene, which is less polar than water, the spectral broadening increases further, and we observe an even larger splitting between the lower and the higher energy band - with respect to the water solution. Moreover, the spectrum shifts even further towards the red. What causes the increased broadening when transitioning from the gas phase to the solution? Why does a second band appear at higher energy in the solvent but remain invisible in the gas phase, even at room temperature? Why does the high-energy band appear in both polar and non-polar solvents, with the latter showing even greater spectral broadening?

To answer these questions and complement the analysis in the gas phase at low temperature, we computed the room temperature absorption spectrum of CV⁺ in the gas phase, in water and in toluene. For this we used a mixed quantum-classical scheme that some of us have recently developed, called the adiabatic molecular dynamics generalized vertical gradient (Ad-MD|gVG)^25,26 approach (see ESI† Section S3).^6,7 In brief, we first parameterize an accurate quantum-mechanical force field (QMD-FF^27,28) for the ground-state potential of CV⁺ (see ESI† Section S4) and then, after system equilibration, we run long (10 ns) MD trajectories to extract a representative number of snapshots for excited state calculations. The computation of the spectrum is based on an adiabatic assumption: the solvent and the soft (torsional) degrees of freedom of the molecule are considered slow compared to the stiff (high-frequency) modes. The contribution of slow modes to the spectrum is accounted for classically by MD sampling, whereas the contribution of stiff modes is included at the quantum level by computing vibronic spectra on VG models specifically built for each configuration of the slow coordinates (each snapshot). The final spectrum is the average of the vibronic spectra computed for different snapshots. In Fig. 3, we show that the computed results effectively reproduce the key experimental findings at 300 K: the spectrum broadens and progressively red-shifts as we move from the gas phase to water and then to toluene. In both water and toluene, but not in gas-phase, the spectrum also splits into two bands, with the spacing between them being larger in toluene than in water as observed experimentally. These results and the approach adopted are qualitatively similar to those already used recently by Zuehlsdorff et al.¹⁶ in solution phase. Quantitatively, our computations can reproduce the fact that no shoulder appears in gas-phase and accurately capture the relative positions of the spectra in the three different media, although they slightly underestimate the width of the room temperature spectra and the splitting of the two bands in water and toluene. These discrepancies can likely be attributed to limitations in TD-DFT. Indeed, moderately different results are obtained using the two different long-range corrected functionals used so far, CAM-B3LYP and ωB97X-D (see Fig. S15, ESI†). We present the results obtained with ωB97X-D in Fig. 3, as they better match the experimental data. Our computation does not fully capture the red-shift observed in the experimental gas-phase spectra when moving from 5 K to room temperature, underestimating this shift by 0.12 eV at the ωB97X-D level of theory. However, it is important to note that despite these differences, the main conclusions of this work remain robust and independent of the functional used, as will be clarified below.

In the gas phase, we observe a small splitting between the S₁ and S₂ states, with the lower-energy state consistently less intense across all snapshots extracted along the MD trajectory (see Fig. S14, ESI†). Despite the thermal structural fluctuations that the molecule undergoes along its dynamics, the energy splitting between the S₁ and S₂ is so small that the two bands effectively cannot be resolved in the simulations, in good agreement with what has been observed by Loison et al.¹¹ in PD gas-phase experiment at 300 K (see Fig. 3). As mentioned before, the situation in solution is quite different, leading to a larger splitting (of 0.17 eV in water and 0.25 eV in toluene) with the higher-energy state generally being less intense in experimental spectra. Our calculations not only reproduce the experimental trend (see Fig. 3), but also reveal that the appearance of the two bands both in water and toluene is due to a larger energy splitting of the contributions from the S₁ and S₂ states and that the magnitude of this gap is environment dependent. This is clearly demonstrated by plotting the individual bands of the two states, as shown in Fig. S14 and S15 (ESI†). The S₁ and S₂ spectra are nearly unchanged when the CV⁺ molecule is simulated in isolation (gas-phase) and the splitting progressively increases from water to toluene. This solvent-driven splitting can already be seen at a classical level without considering vibronic contributions, simply by inspecting the distribution of the differences in the S₁ and S₂ transition energies across different snapshots from the MD simulations (see Fig. S14d, ESI†).

Importantly, in Fig. S16 (ESI†), we highlight that if one performs MD in an explicit solvent and then removes the solvent before calculating the spectrum for each snapshot, the splitting disappears, and results are essentially the same as those obtained by sampling the conformations of the molecules from an MD in the gas-phase. This finding clearly indicates that the splitting is not due to an indirect effect of the solvent on the movement of the flexible degrees of freedom of the CV⁺ structure as it was recently hypothesized by Vauthey et al.¹³ Instead, it must be directly related to the explicit fluctuations in the solvent configuration. Notably, Fig. S17 (ESI†) also demonstrates that the splitting in water is not reintroduced when the explicit solvent molecules are replaced by a mean-field continuum model like PCM.^18,19 These observations highlight that the splitting of the S₁ and S₂ states is due to the positional disorder of the solvent molecules during the MD simulations.

Rationalizing the solvent symmetry breaking effect

To further understand the reason for the origin and solvent-dependent magnitude of the energy splitting we provide a microscopic explanation of the main underlying factors contributing to this in Fig. 4. We note in passing that while finalizing this manuscript, we noticed that a similar, but independent, representation was recently provided by Zuehlsdorf et al.¹⁶ The horizontal bars in Fig. 4 represent the energies of the molecular orbitals involved in the two electronic transitions of representative snapshots. Fig. 4 also displays these orbitals for CV⁺ in gas-phase and, with respect to what given in ref. 16 it adds a representation of the local electrostatic field exerted by the solvent environment on the CV⁺ solute at the specific representative snapshot. Analysis of the orbital energies clearly shows that the degeneracy of the HOMO−1 and HOMO orbitals is lifted primarily by dynamic fluctuations of the environment. Consequently, the splitting is small in the gas phase, where it is connected to the intra-molecular JT effect, substantial in water, and even larger in toluene. The two orbitals exhibit distinct distributions of electron density across the three arms of the molecule. Specifically, one of the orbitals is primarily localized on one arm (HOMO-1 in the selected snapshot), while the other orbital is distributed across the remaining two arms. Consequently, the clearly visible negative and positive regions of the instantaneous electrostatic potential of the environment affects the two orbitals differently.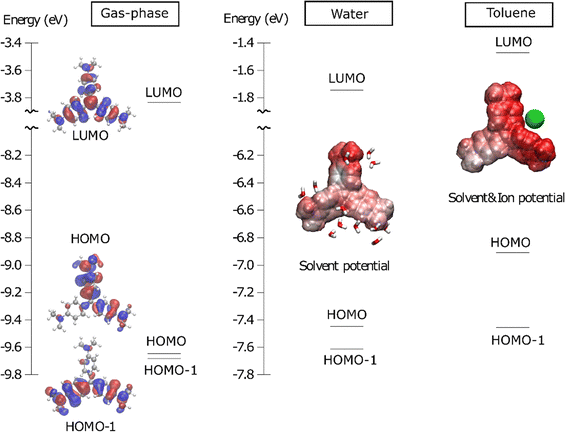

Fig. 4 Molecular orbital (MO) diagrams from representative snapshots of MD trajectories in gas-phase, water and toluene, including orbitals from HOMO−1 to LUMO computed with ωB97X-D/cc-pVDZ. Horizontal lines represent the energy of each MO. The MOs are shown in gas-phase only (they are similar in the other environments, see Fig. S18, ESI†). The electrostatic potential exerted by the environment (here fully represented as point charges for representation purpose) around CV⁺ is depicted as a colour map from −0.1 a.u. (red) to +0.1 a.u. (blue). The solvent molecules (as ball and stick models) within 4.5 Å of the CV⁺ are shown for the representation in water, while the chloride ion (green sphere) is included for that in toluene.

Fig. 4 also illustrates that, in the selected snapshot, the water environment creates a negative potential mainly on the upper arm. This potential destabilizes the HOMO relative to HOMO−1, lowering the energy of the state corresponding to the HOMO → LUMO transition. This effect is responsible for the splitting observed in the polar water solvent. Interestingly, as discussed by Zuehlsdorf et al.,¹⁶ the situation in apolar toluene is somewhat different from that in water. In water, the CV⁺/Cl⁻ pair is dissolved (and well separated) and the splitting is induced by the electrostatic field of the water molecules, whereas in toluene, the chloride ion remains very close to CV⁺ (forming a contact ion-pair) and this is primarily responsible for the S₁–S₂ splitting. As shown in Fig. 4, in the selected snapshot, the chloride ion is positioned between the upper and rightmost arms, creating a negative potential that once again destabilizes the HOMO. The electrostatic effect of the close-lying anion in toluene is therefore stronger than that exerted by proximal water molecules, resulting in a larger splitting in toluene than in water. Fig. S19 in the ESI† shows that most of this effect is captured even when describing the chloride ion at the MM level (as compared to a QM description). This indicates that the polarization of the chloride's electronic density due to its interaction with the solute is not crucial for explaining the splitting, which is here also primarily due to configurational variety of the solvent. The diversity of configurations for the chloride ion is illustrated in Fig. S20 (ESI†).

Conclusions

We have used helium tagging photodissociation spectroscopy to study the visible region electronic absorption of the isolated crystal violet cation complexed with a helium atom ([CV⁺…He]) and held at 5 K in an electrodynamic ion trap. The measurement shows a long damped vibrational progression with its lowest energy and strongest absorption feature centered at 18 468 cm⁻¹. The spectrum differs strongly from CV⁺ dissolved in water and toluene at room temperature which show a broad absorption with a high energy shoulder. The origin of this shoulder in the solution absorption spectrum of crystal violet has been controversially discussed for many decades.

Here we have clarified the underlying photophysics by applying a comprehensive theoretical approach which can consistently describe both the gas-phase and solution measurements. The approach uses the low temperature, gas-phase measurement to benchmark a TD-DFT based description incorporating vibronic effects. This can satisfactorily replicate the peak spacing, vibronic pattern/progression, and the broadening of the 5 K He-TAG spectrum. To describe the solution spectra on this basis we then used the Ad-MD|gVG mixed quantum-classical scheme that was recently developed by some of us. Here 10 ns long MD trajectories are run in an explicit solvent environment to extract a representative number of snapshots for appropriate excited state calculations. Moreover, in the computation of the spectrum, the contribution of solvent and soft solute modes is treated at classical level and the one of the stiff solute modes at quantum (vibronic) level.

The underlying electronic transition takes the molecule from its ground state to a pair of nominally degenerate states, S₁ and S₂. These degenerate states can undergo vibrationally coupled E⊗e JT distortion and symmetry breaking associated with a conical intersection between the two adiabatic potential energy surfaces (PES). Theoretical modelling implies that the small spectral splitting due to this “intrinsic” intra-molecular JT effect is not directly observable in the 5 K measurement but, interestingly, it is connected to the observed spectral broadening together with other factors such as an environmental symmetry breaking effect associated with complexation of helium.

These theoretical conclusions highlight the fact that in CV⁺, the S₁/S₂ degeneracy is inherently unstable and easily lifted, making the molecule extremely sensitive to intra-molecular and inter-molecular perturbations. In fact, in the condensed phase at room temperature, the perturbation from the environment is much stronger than the “intrinsic” intra-molecular JT effect, resulting in a significant energy gap between the S₁ and S₂ states. This gap is primarily due to fluctuations in the instantaneous configuration of the environment, which includes the solvent and counterion, rather than distortions of the molecular structure. Thus, the symmetry-breaking phenomenon can be described as a kind of inter-molecular JT effect induced (and amplified) by the environmental electrostatic potential. More specifically, the splitting occurs due to the stabilization and destabilization of the HOMO−1 and HOMO orbitals, caused by fluctuations in the electrostatic field generated by the surrounding environment. This effect is more pronounced in the apolar solvent toluene than in water. This happens because in toluene the counterion remains close to the CV⁺ cation and forms a contact ion-pair, whereas in water cation and counterion are well solvated and remain separate.

In summary comparison of low-temperature spectra of the isolated species and room temperature spectra in solution allows us to definitively conclude that crystal violet's solution shoulder primarily reflects configurational disorder of the environment – torsional disorder of the molecule itself plays a comparatively minor role. As a corollary, the characteristic spectral shape reflects the local (dis)order of the solvent molecules about the dye cation. Absorption spectra of a series of appropriately functionalized conjugated triphenylmethane dyes could in this sense provide a novel avenue to sense solution structure on the subnanoscale.

Data availability

Data are available from the corresponding authors upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. K. thanks Karlsruhe Institute of Technology, Land Baden-Württemberg and DFG (CRC 1573, project C3) for financial support in constructing, testing and running the He-TAG machine and for funding of a Cyclic IMS (Art. 91b GG). A. S. acknowledges support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through Grant No. INST 40/575-1 FUGG (JUSTUS 2 cluster). We thank Regina Fischer for the assistance in obtaining solution spectra. F. S. and S. G. thank the support of ICSC – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU – PNRR, Missione 4 Componente 2 Investimento 1.4. S. G. holds a FNRS Charge’ de Recherches and acknowledges LUCIA Tier-1 supercomputer and the Walloon Region.

Notes and references

1. S. Lovell, B. J. Marquardt and B. Kahr, Crystal Violet's Shoulder, J. Chem. Soc., Perkin Trans. 2, 1999, 2241–2247.
2. G. N. Lewis, T. T. Magel and D. Lipkin, Isomers of Crystal Violet Ion. Their Absorption and Re-Emission of Light, J. Am. Chem. Soc., 1942, 64, 1774–1782.
3. J. Korppi-Tommola and R. W. Yip, Solvent Effects on the Visible Absorption Spectrum of Crystal Violet, Can. J. Chem., 1981, 59, 191–194.
4. J. Korppi-Tommola, E. Kolehmainen, E. Salo and R. Yip, The Temperature-Dependent Red-Shift of the Visible Absorption Spectra of Crystal Violet in Alcohol Solutions, Chem. Phys. Lett., 1984, 104, 373–377.
5. V. Sundström and T. Gillbro, Effects of Solvent on TMP Photophysics. Transition from No Barrier to Barrier Case, Induced by Solvent Properties, J. Chem. Phys., 1984, 81, 3463–3474.
6. F. Clark and H. Drickamer, High-Pressure Study of Triphenylmethane Dyes in polymeric and Aqueous Media, J. Phys. Chem., 1986, 90, 589–592.
7. D. Ben-Amotz and C. Harris, Torsional Dynamics of Molecules on Barrierless Potentials in Liquids. I. Temperature and Wavelength Dependent Picosecond Studies of Triphenyl-Methane Dyes, J. Chem. Phys., 1987, 86, 4856–4870.
8. H. B. Lueck, J. L. McHale and W. Edwards, Symmetry-breaking Solvent Effects on the Electronic Structure and Spectra of a Series of Triphenylmethane Dyes, J. Am. Chem. Soc., 1992, 114, 2342–2348.
9. M. Ishikawa and Y. Maruyama, Femtosecond Spectral Hole-Burning of Crystal Violet in Methanol. New Evidence for Ground State Conformers, Chem. Phys. Lett., 1994, 219, 416–420.
10. Y. Maruyama, M. Ishikawa and H. Satozono, Femtosecond Isomerization of Crystal Violet in Alcohols, J. Am. Chem. Soc., 1996, 118, 6257–6263.
11. C. Loison, R. Antoine, M. Broyer, P. Dugourd, J. Guthmuller and D. Simon, Microsolvation Effects on the Optical Properties of Crystal Violet, Chem. – Eur. J., 2008, 14, 7351–7357.
12. E. C. Wu, Q. Ge, E. A. Arsenault, N. H. Lewis, N. L. Gruenke, M. J. Head-Gordon and G. R. Fleming, Two-Dimensional Electronic-Vibrational Spectroscopic Study of Conical intersection Dynamics: an Experimental and Electronic Structure Study, Phys. Chem. Chem. Phys., 2019, 21, 14153–14163.
13. J. Sissaoui, D. S. Budkina and E. Vauthey, Torsional Disorder, Symmetry Breaking, and the Crystal Violet Shoulder Controversy, J. Phys. Chem. Lett., 2023, 14, 5602–5606.
14. J. Campo, A. Painelli, F. Terenziani, T. Van Regemorter, D. Beljonne, E. Goovaerts and W. Wenseleers, First Hyperpolarizability Dispersion of the Octupolar Molecule Crystal Violet: Multiple Resonances and Vibrational and Solvation Effects, J. Am. Chem. Soc., 2010, 132(46), 16467–16478.
15. F. Terenziani, C. Sissa and A. Painelli, Symmetry Breaking in Octupolar Chromophores: Solvatochromism and Electroabsorption, J. Phys. Chem. B, 2008, 112, 5079–5087.
16. D. Bashirova and T. J. Zuehlsdorff, First-Principles Modeling of the Absorption Spectrum of Crystal Violet in Solution: The Importance of Environmentally Driven Symmetry Breaking, J. Phys. Chem. A, 2024, 128, 5229–5242.
17. F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, Effective Method to Compute Franck-Condon Integrals for Optical Spectra of Large Molecules in Solution, J. Chem. Phys., 2007, 126(8), 084509.
18. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3094.
19. B. Mennucci, Polarizable Continuum Model, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404.
20. S. Debnath, A. Schäfer, K. A. Haupa, D. Strelnikov, J. Roithová, J. Jašík, S. Lebedkin and M. M. Kappes, Vibrationally Resolved Electronic Spectroscopy of Rhodamine B Cation at Less Than 5 K: Combining Gas Phase Absorption and Matrix Isolation Fluorescence Spectroscopy, Mol. Phys., 2024, 122, e2223072.
21. S. Debnath, A. Schäfer, S. Ito, D. Strelnikov, R. Schneider, K. A. Haupa and M. M. Kappes, Vibrationally Resolved Absorption, Fluorescence, and Preresonance Raman Spectroscopy of Isolated Pyronin Y Cation at 5 K, J. Phys. Chem. Lett., 2023, 14, 10553–10560.
22. A. Schäfer, S. Debnath, J. Tränkle, T. Mohr and M. M. Kappes, Acriflavine Is More than It Seems: Resolving Optical Properties of Multiple Isomeric Constituents at 5 K, J. Phys. Chem. Lett., 2024, 15, 7295–7301.
23. W. Domcke, D. Yarkony and H. Köppel, Conical Intersections: Electronic Structure, Dynamics & Spectroscopy, World Scientific, 2004.
24. J. Cerezo and F. Santoro, FCclasses3: Vibrationally-Resolved Spectra Simulated at the Edge of the Harmonic Approximation, J. Comput. Chem., 2023, 44, 626–643.
25. J. Cerezo, D. Aranda, F. J. Avila Ferrer, G. Prampolini and F. Santoro, Adiabatic-Molecular Dynamics Generalized Vertical Hessian Approach: a Mixed Quantum Classical Method to Compute Electronic Spectra of Flexible Molecules in the Condensed Phase, J. Chem. Theory Comput., 2019, 16, 1215–1231.
26. J. Cerezo, J. Gierschner, F. Santoro and G. Prampolini, Explicit Modelling of Spectral Bandshapes by a Mixed Quantum-Classical Approach: Solvent Order and Temperature Effects in the Optical Spectra of Distryrylbenzene, ChemPhysChem, 2024, e202400307.
27. I. Cacelli and G. Prampolini, Parametrization and Validation of Intramolecular Force Fields Derived from DFT Calculations, J. Chem. Theory Comput., 2007, 3, 1803–1817.
28. J. Cerezo, G. Prampolini and I. Cacelli, Developing Accurate Intramolecular Force fields for Conjugated Systems Through Explicit Coupling Terms, Theor. Chem. Acc., 2018, 137, 1–15.
29. F. Hennrich, S. Ito, P. Weis, M. Neumaier, S. Takano, T. Tsukuda and M. M. Kappes, Cyclic Ion Mobility of Doped [MAu₂₄L₁₈]²⁻ Superatoms and Their Fragments (M = Ni, Pd and Pt; L = alkynyl), Phys. Chem. Chem. Phys., 2024, 26, 8408–8418.
30. K. Giles, J. Ujma, J. Wildgoose, S. Pringle, K. Richardson, D. Langridge and M. Green, A Cyclic Ion Mobility-Mass Spectrometry System, Anal. Chem., 2019, 91, 8564–8573.
31. S. M. Stow, T. J. Causon, X. Zheng, R. T. Kurulugama, T. Mairinger, J. C. May, E. E. Rennie, E. S. Baker, R. D. Smith and J. A. McLean, An Interlaboratory Evaluation of Drift Tube Ion Mobility–Mass Spectrometry Collision Cross Section Measurements, Anal. Chem., 2017, 89, 9048–9055.
32. E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Laboratory Confirmation of C₆₀⁺ as the Carrier of Two Diffuse Interstellar Bands, Nature, 2015, 523, 322–323.
33. M. Yaghoubi Jouybari, Y. Liu, R. Improta and F. Santoro, Ultrafast Dynamics of the Two Lowest Bright Excited States of Cytosine and 1-methylcytosine: A Auantum Dynamical Study, J. Chem. Theory Comput., 2020, 16, 5792–5808.
34. J. A. Green, M. Yaghoubi Jouybari, H. Asha, F. Santoro and R. Improta, Fragment Diabatization Linear Vibronic Coupling Model for Quantum Dynamics of Multichromophoric Systems: Population of the Charge-Transfer State in the Photoexcited Guanine–Cytosine Pair, J. Chem. Theory Comput., 2021, 17, 4660–4674.
35. A. Segalina, D. Aranda, J. A. Green, V. Cristino, S. Caramori, G. Prampolini, M. Pastore and F. Santoro, How the Interplay Among Conformational Disorder, Solvation, Local, and Charge-Transfer Excitations Affects the Absorption Spectrum and Photoinduced Dynamics of Perylene Diimide Dimers: A Molecular Dynamics/Quantum Vibronic Approach, J. Chem. Theory Comput., 2022, 18, 3718–3736.
36. M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, The Multiconfiguration Time-Dependent Hartree (MCTDH) Method: a Highly Efficient Algorithm for Propagating Wavepackets, Phys. Rep., 2000, 324, 1–105.
37. G. Worth, Quantics: A General Purpose Package for Quantum Molecular Dynamics Simulations, Comput. Phys. Commun., 2020, 248, 107040.
38. D. Aranda and F. Santoro, Vibronic Spectra of π-Conjugated Systems with a Multitude of Coupled States: A Protocol Based on Linear Vibronic Coupling Models and Quantum Dynamics Tested on Hexahelicene, J. Chem. Theory Comput., 2021, 17, 1691–1700.
39. F. J. A. Ferrer and F. Santoro, Comparison of Vertical and Adiabatic Harmonic Approaches for the Calculation of the Vibrational Structure of Electronic Spectra, Phys. Chem. Chem. Phys., 2012, 14, 13549–13563.
40. T. Yanai, D. P. Tew and N. C. Handy, A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
41. J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
42. C. Adamo and D. Jacquemin, The Calculations of Excited-State Properties with Time-Dependent Density Functional Theory, Chem. Soc. Rev., 2013, 42, 845–856.
43. A. D. Laurent and D. Jacquemin, TD-DFT Benchmarks: a Review, Int. J. Quantum Chem., 2013, 113, 2019–2039.
44. T. Heidari, F. Ghasemi-Moghaddam and M. Chamsaz, Application of Differential Spectra from Two Different Environments in Simultaneous Quantification of New Fuchsine, Crystal Violet and Malachite Green in the Presence of Unmodeled Interferents Using First Order Multivariate Calibration Method, J. Anal. Chem., 2015, 70, 44–49.
45. L. W. Chung, W. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke and F. Liu, The ONIOM Method and Its Applications, Chem. Rev., 2015, 115, 5678–5796.
46. H. M. Senn and W. Thiel, QM/MM Methods for Biomolecular Systems, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
47. C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: the RESP Model, J. Phys. Chem., 1993, 97, 10269–10280.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03825h

‡ A. S. and S. G. contributed equally to this work.

---