Influence of solution stoichiometry on the thermodynamic stability of prenucleation FeS clusters

Abstract

The significance of iron sulphide (FeS) formation extends to “origin of life” theories, industrial applications, and unwanted scale formation. However, the initial stages of FeS nucleation, particularly the impact of solution composition, remain unclear. Often, the iron and sulphide components' stoichiometry in solution differs from that in formed particles. This study uses ab initio methods to computationally examine aqueous FeS prenucleation clusters with excess Fe(II) or S(−II). The results suggest that clusters with additional S(−II) are more likely to form, implying faster nucleation of FeS particles in S(−II)-rich environments compared to Fe(II)-rich ones.

---

1 Introduction

Iron sulphides are a complex group of minerals which can go through a variety of (metastable) phases.¹ FeS clusters found in nature are often linked to “origin of life” theories^2,3 and their distinct chemical properties also make iron sulphides promising materials for industrial applications related to energy storage,^4,5 CO₂ conversion,⁶ and environmental remediation.^7,8 However, their formation in natural waters can be problematic in piping in for instance geothermal energy systems due to scale formation.^9,10 Hence, there is a need for knowledge and control on their formation in natural or engineered waters. The effect of solution stoichiometry on nucleation and the formation of prenucleation clusters in particular is poorly understood,¹¹ even though in natural waters the concentration ratio between Fe(II) and S(−II) ions forming the materials might vary. For example, Fe(II) concentrations range from 75–200 μmol L⁻¹ in sediment pore samples¹² and 6–20 mmol L⁻¹ in ground water rich with Fe(II).¹³ S(−II) concentration ranges from 0.05–100 μmol L⁻¹ in layers of marine sediments depending on oxygen level¹⁴ and 17 mmol L⁻¹ in high-temperature hydrothermal vent fluid.¹⁵ Hence the Fe(II) : S(−II) concentration ratio of (mixed) natural waters might range between 10⁻⁵ and 10³.

For several other minerals we have shown the importance of solution stoichiometry for nucleation and the formation of prenucleation clusters.^16–18 In particular, the stability and lifetime of triple ion complexes from Ba²⁺, Ca²⁺, CO₃²⁻ and SO₄²⁻ determined by molecular dynamics simulations,¹⁸ was correlated to a stoichiometric effect on nucleation of minerals formed from these ions examined with, among others, dynamic light scattering. Therefore it is interesting to investigate how triple ion complexes with Fe(II) and S(−II) would form and if FeS nucleation would be similarly impacted by solution stoichiometry. Several reaction mechanisms for FeS formation have been proposed depending on pH.¹ Our goal is to elucidate the mechanism of formation of FeS prenucleation clusters by determining the thermodynamic stability of intermediate states that might occur in excess of Fe(II) or S(−II) on path to nucleation. This should give an indication of how fast the first steps towards nucleation might occur in excess of either ion. Since here we focus our calculations on the prenucleation clusters of FeS, our work is mostly related to the formation of mackinawite (stoichiometric FeS), which is the first phase that forms in anoxic environments with Fe(II) and S(−II) ions and can transform to other phases like greigite or pyrite.¹ As the most current FeS force field to our knowledge,¹⁹ is not developed enough for a bias-enhanced exploration of triple ion clusters with molecular dynamics calculation, we used ab initio methods. We reviewed several previously used ab initio methods for FeS complexes and calculated the reaction free energy of formation and thus stability of triple ion complexes with different stoichiometry with the goal to examine the effect of excess in Fe(II) or S(−II) on path to nucleation.

2 Methodology

2.1 Triple ion complexes

At stoichiometric conditions it is often assumed that first ion pairs are formed, which can then be treated as monomers following classical nucleation theory.²⁰ However, here we assume that at non-stoichiometric conditions when either ion is in a large excess, it is more likely for nucleation to occur via single-ion addition. This leads initially to triple ion complexes. Note that we will also assume an anoxic environment and no redox reactions involving Fe(II) and S(−II).

To obtain a more complete overview of a possible stoichiometry effect, we have looked into the reaction free energy to form triple ion complexes from three different cation–anion combinations. In one case we assume the divalent ions Fe²⁺ and S²⁻, which form an FeS ion pair and either Fe₂S²⁺ or FeS₂²⁻ triple ion complexes. This case is most similar to our previous research on triple ion complexes with Ba²⁺, Ca²⁺, SO₄²⁻, and CO₃²⁻¹⁸ as both the cation and anion are divalent. This ensures charge effects are similar in a surplus of either Fe(II) or S(−II). This ion pair however has limited direct experimental relevance since the presence of a S²⁻ ion is questionable in most or all environments.²¹ With a pK₁ of around 7 at 25 °C and 1 atm,²² H₂S is expected to be the dominant species in acidic environments, while HS⁻ would be dominant in alkaline environments. Within the scope of this work we only focused on alkaline environments. Hence as a second case, we investigated the pair of Fe²⁺ or HS⁻, which forms an FeSH⁺ ion pair and either Fe₂SH³⁺ or Fe(SH)₂ triple ion complexes. Due to the large difference in charge between these three triple ion complexes, it is expected that the neutral Fe(SH)₂ would be more favourable to form. As a last case, we examined the FeOH⁺ and HS⁻ ions, which form FeOHSH and subsequently either (FeOH)₂SH⁺ or FeOH(SH)₂⁻ complexes. Fe(II) can be present as FeOH⁺ in alkaline environments.²³ As FeOH⁺ can already be classified as an ion pair, technically we are now looking into the formation of triple and quintuple ion complexes instead. For simplicity in comparisons between the different cases we will consider FeOHSH as the ion pair and (FeOH)₂SH⁺ or FeOH(SH)₂⁻ as triple ion complexes. Since now both triple ion complexes are monovalent, the charge is of equivalent magnitude in both cases. Note that in all cases we neglected any intermediate steps that might occur such as FeOHSH → FeSH⁺ + OH⁻ or FeSH⁺ → FeS + H⁺, which would change one complex into another. We assume that by examing these distinct cases, we have also captured the behaviour involved for these cross reactions.

2.2 Computational details

We used several ab initio methods, which have been employed previously in related Fe(II) or FeS research.^24–27 We have excluded multi-reference methods as these would be computationally unaffordable for larger clusters explicitly including the surrounding water. However, the reported methods have compared favourably to experimental or CCSD data on related complexes justifying the use of these single reference methods. Using the different levels of theory we computed the geometry and J-coupling for an Fe₂S₂ complex in the gas phase and the solvation free energy of H₂O, HS⁻, OH⁻, and Fe²⁺ to determine which method is most appropriate. Additionally, we performed initial computations with all methods for the reaction free energy in one case (Fe²⁺ and S²⁻) to see if any stoichiometry effect would be influenced by the method. Lastly we performed more extensive computations with the most appropriate method on all three distinct cases.

Using Gaussian16²⁸ we have used mPW1B95 hybrid-meta-DFT method²⁹ with a basis set of 6-31+g(d,p),^30–32 which was applied previously to calculate the reaction free energy for a number of FeS complexes.²⁴ MPW1B95 is a hybrid meta-GGA density functional that has proven to be quite effective for a variety of chemical systems, particularly in the areas of thermochemistry, kinetics, and non-covalent interactions.³³ Therefore, we choose mPW1B95 for its ability to predict reaction energies. Furthermore, we have employed the MP2^34–38 method with a basis set of 6-31++g(d,p)^30–32 which has recently been used to examine the configuration of H₂O around Fe^2+ 26 and the corresponding solvation energy.²⁷ They have shown that MP2, a post-Hartree Fock method, is capable of predicting binding, clustering, and solvation energy of Fe²⁺ in line with experimental results, making it a suitable option for further reaction energy predictions. We will refer to the former method as mPW and the latter as MP2. While both methods use a different basis set for consistency with the original papers, it is unlikely this is of much influence as it only concerns the long-range interactions between hydrogen atoms and any observed differences in results is likely attributed to the difference in method. The total spin was fixed at high or low spin and the state with the lowest electronic energy was used. In cases with two Fe(II) we also computed the broken symmetry state, where the spin states on the two Fe(II) are antiparallel. We have accounted for solvent effects with a cluster–continuum model³⁹ as detailed later on which combines explicit considerations of nearby H₂O molecules with a continuum solvation model. For the continuum solvation model we used PCM with the integral equation formalism variant.⁴⁰ As an alternative we have also used the SMD variation,⁴¹ which Gaussian16 recommends for computing the solvation energy. Geometry optimisations and frequency calculations were either performed in gas phase or continuum solvent as will be mentioned accordingly.

With VASP 6.4^42–44 we employed a DFT+U approach⁴⁵ characterised by U = 5 with a PBE functional⁴⁶ and the PAW method.^47,48 This was previously used for calculations on the Fe₂S₂ complex²⁵ and their results compared favourably to experimental data of the biological Fe₂S₂ complex.⁴⁹ As a reference we also performed calculations without this Hubbard correction. We will refer to either U = 5 or PBE to denote the calculation with or without the inclusion of the U correction. We used a plane wave cutoff of 550 eV and PAW potentials considering 4s and 3d electrons of Fe, the 3s and 3p of S, the 2s and 2p of O, and the 1s of H as valence electrons. The calculations were performed at Γ-point and a Grimme correction (D2) was included to account for dispersion forces.⁵⁰ To compensate for charge effects within the periodic boundary conditions implemented in VASP, we use a first order dipole correction^51,52 and a box of 28 × 28 × 28 Å.⁵³ The total spin was optimised during the calculation starting from a high spin configuration. In cases with two Fe(II) atoms we performed an additional computation starting from a broken symmetry state and continued with the state that had the lowest electronic energy. For a continuum solvation model we used VASPsol.^54,55 Geometry optimisations and frequency calculations were only performed in gas phase, but single point calculations were performed in the solvent phase. VASPkit⁵⁶ was used to extract the energy corrections from the frequency calculations, which uses the same equations as Gaussian16.

Magnetic coupling constants J were determined for Fe₂S₂ as described previously using:²⁵

where E_BS and E_HS are the zero-point energies of the broken symmetry and high spin states and the maximum total spin S_max = 4. Examples of input for all methods are found in Supplementary Information S1 and S2 (ESI†).

2.3 Reaction free energy

To obtain the reaction free energy for reaction A + B → C we used:where ΔE_el is the difference in the electronic gas phase energy, the difference in the vibrational, rotational, and translational contributions in the gas phase at 298 K under a standard-state pressure of 1 atm, the difference in the solvation free energy going from 1 mol L⁻¹ gas to 1 mol L⁻¹ in solution, and 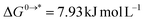is associated to the standard-state conversion of 1 atm to 1 mol L⁻¹. The solvation free energy was obtained by a cluster–continuum model,³⁹ which combines explicit inclusion of water molecules near the complexes with an implicit continuum solvent model. This relates the solvation energy of a solute X to the cluster formation X + nH₂O → X(H₂O)_n, where n is the amount of explicit water molecules considered. 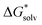is then given by³⁹:where ΔE_el,cl(X(H₂O)_n) and (X(H₂O)_n) are based on the clustering reaction and 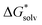(X(H₂O)_n) is the solvation free energy of the entire cluster obtained from calculations with the continuum solvent model. 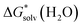The vaporisation free energy of water ΔG_vap(H₂O) is given by:³⁹where is the solvation free energy of H₂O from calculations with the continuum solvent model, R is the ideal gas constant, T is the temperature 298 K, and [H₂O] = 55.5 mol L⁻¹.

The amount of H₂O molecules n is of importance for the exact value of and 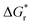. According to Pliego and Riveros,³⁹ by varying n and exploring all possible configurations a minimum in solvation free energy should be found. For the initial computations with all different methods, we instead used the same number of H₂O and did not search for this optimum for each separate method. In Table 1 we show the amount of H₂O used for each species. For OH⁻, HS⁻, and Fe²⁺ this number was based on the coordination number observed from coordination analysis of the radial distribution function in a preliminary short ab initio simulation using the PBE functional in VASP6.4. Starting configurations were based on a snapshot of this simulation. For FeS, Fe₂S²⁺, and FeS₂²⁻ this number was based on the coordination found in similar complexes.²⁴ For S₂²⁻ it was chosen to be the same as FeS₂²⁻ as this would be consistent with the cationic complex where Fe²⁺ and Fe₂S²⁺ also had the same coordination number.

Table 1 Number of H₂O n used in the cluster–continuum models for all comparative calculations between the various methods

	n		n
Fe^2+	6	Fe2S^2+	6
S2^2−	2	FeS2^2−	2
HS^−	6	FeS	3
OH^−	4

---

For the more extensive calculations using a single method for all three distinct reaction schemes, we did vary n and explored possible configurations. The amount n for most FeS complexes needed to be large to get close to an optimum, making the number of possible configurations large. To reduce the computational effort of exploring all configurations, we first performed several computations in a range of n and estimated possible configurations and from that used a more systematic approach. Starting from the minimum configuration of the initial assessment we added H₂O where it increases the coordination around S, Fe, OH, or H₂O in the first coordination shell and in such a way that it has the most hydrogen bonds. Then we determined which configuration had the lowest solvation free energy and added the next H₂O to this configuration. If increasing a certain coordination was unfavourable for the addition of multiple H₂O in a row, we did not add H₂O in that specific coordination. This process continued until either decreased minimally for multiple H₂O or up to n ≈ 13–16, where the calculation became unmanageable. Note that we only checked the electronic energy of different spin states for small n and used the most stable spin state at small n for calculations at higher n. For the final configuration at high n we confirmed whether the other spin state was more stable or not.

3 Results and discussion

3.1 Method comparison

3.1.1 Fe₂S₂ complex. First we computed the gas-phase geometry and magnetic coupling constant J for a high spin Fe₂S₂ complex with the results shown in Table 2. We have compared them to the results of a CCSD calculation which would be the most accurate.²⁵ The Hubbard parameter U was calibrated to these CCSD calculations in the original paper,²⁵ so the geometry of U = 5 compares well. Additionally, MP2 leads to a very similar geometry. The geometry of PBE and mPW is quite different, suggesting that these are not adequate in describing complexes with two Fe(II). Lastly, the biological Fe₂S₂ complex is expected to be in a low spin state,⁴⁹ meaning J should be negative. This is correctly predicted by U = 5, MP2, and mPW.

Table 2 Comparison of the gas-phase geometry (bond length in Å, dihedral angle in°) and magnetic coupling J (cm⁻¹) of a high spin Fe₂S₂ complex for various levels of theory

	CCSD^25	PBE	U = 5	mPW	MP2
d(Fe–Fe)	2.58	2.21	2.56	2.20	2.56
d(Fe–S)	2.27	2.20	2.27	2.21	2.27
θ(Fe–S–Fe–S)	0.0	22.9	0.17	18.6	0.04
J	—	+192	−103	−181	−60

---

3.1.2 Solvation free energy. To test how well the solvation models work for the different methods, we compared the solvation free energy of a number of compounds with previously reported values in Table 3. The reference values are all based on a combination of experiments and theoretical considerations as they cannot be measured directly. For Fe²⁺ there is a larger discrepancy in literature and we have shown a minimum and maximum value in the Table, but −1860⁵⁷ and −1890⁵⁸ kJ mol⁻¹ have also been reported. For all ionic species we have incorporated the cluster–continuum model with the same number of H₂O as described in Table 1. We have also noted which continuum solvation model was used in Gaussian16 and whether the geometry optimisation and frequency calculations were performed in the gas phase or solvent phase. We did not vary the solvation models for mPW as MP2 was shown to be more promising following the results on the Fe₂S₂ complex. Additionally, we did not optimise the geometry for U = 5 in the solvent phase as this prove to be unaffordable. Furthermore, in all cases the Fe²⁺ ion is in the high spin state for all methods.

Table 3 Comparison of solvation free energies in kJ mol⁻¹ obtained by a number of methods

	Ref.	PBE gas	U = 5 gas	mPW gas SMD	MP2 gas SMD	MP2 solv. SMD	MP2 gas PCM	MP2 solv. PCM
H2O	−26^59	−30	−30	−37	−38	−39	−22	−22
OH^−	−438^59	−360	−360	−384	−379	−416	−402	−431
HS^−	−302^59	−266	−266	−219	−216	−250	−269	−296
Fe^2+	−1840^60 to −1949^61	−2056	−2114	−1918	−1881	−1927	−1808	−1824

---

It seems that VASPsol poorly describes the solvation free energy for all ionic species. It is possible that VASPsol is less accurate for charged species and/or requires additional considerations accounting for charge. The SMD solvation model only performs well for the Fe²⁺-ion. This is somewhat surprising as it is the recommended solvation model by Gaussian16 for calculation of the solvation free energy. The discrepancy for OH⁻ and HS⁻ is likely exacerbated from the fact that the H₂O solvation free energy is not well described and the cluster–continuum model relies on this value for the computation of all other solvation free energies. Overall MP2 with the PCM solvation model and geometry optimisation in the solvent phase performs the best. Unsurprisingly, this corresponds to the same solvation settings used to determine solvation energies of Fe²⁺ with MP2 using a slightly different cluster–continuum model.²⁷ There they included up to 13 H₂O molecules around the Fe²⁺-ion and found a value of −1889 kJ mol⁻¹ after extrapolation, which is in line with the reference values. Hence it was expected that a more accurate value would be found in our calculations with MP2 and PCM if the number of H₂O molecules are optimised. As MP2 also described the Fe₂S₂ complex adequately, this seemed the most appropriate method to do our more extensive calculations on.

To get an indication whether some of the results in Table 3 are not biased because the number of H₂O molecules is not optimal, we varied this number in the case of HS⁻ between 1 and 6 for MP2 with the two different solvation methods (SMD and PCM) and the two types of geometry optimisation (gas and solvent). For all solvation methods the optimal number of H₂O was 2 and the solvation free energy changed (in the same order as the Table) to −270, −278, −289, and −300 kJ mol⁻¹. While this is an improvement for all cases, it is still the best for MP2 with PCM and solvent-phase geometry. The fact that the energy also changes less than the other methods for different amounts of water, shows that it would be more robust. From now on, when we discuss MP2 the optimal solvation method (PCM and solvent-phase geometry) is implied.

3.1.3 Reaction free energy. As a final comparison, we looked into how each method would describe the effect of stoichiometry with the ions Fe²⁺ and S²⁻. The reaction free energy for the pair formation and triple ion complexes is shown in Table 4. Almost all complexes with Fe(II) are in high spin, except for PBE and U = 5 where Fe₂S²⁺ is in broken symmetry. While the discrepancy between the methods is significant, it is also smaller than for the solvation energy. This is likely because the solvation energy on both sides of the reaction have a similar discrepancy and some of this error cancels out. Some of the trends between the different methods in Table 3 do seem to correlate with the results in Table 4. In particular, for U = 5, which had the largest solvation energy for Fe²⁺ compared to other methods, it is less favourable to reduce the number of coordinated H₂O to form new bonds, which is reflected by the smaller values for the reaction free energy.

Table 4 Comparison of reaction free energy in kJ mol⁻¹ for the pair formation of FeS and the addition of either Fe²⁺ or S²⁻ obtained by a number of methods

Method		Triple ion complex formation via:
	Pair formation	Fe(II) addition	S(−II) addition
PBE	−94	−47	−141
U = 5	−28	−23	−111
mPW	−138	−75	−130
MP2	−137	−48	−127

---

For all methods there is a strong difference between Fe(II) or S(−II) addition with S(−II) addition being favoured. For PBE and U = 5, S(−II) addition is favoured over pair formation, while for mPW and MP2 it is in a similar range. These initial results suggest that the prenucleation cluster formation might be more rapid in the presence of an excess of S(−II) as opposed to an excess of Fe(II). One could argue that this result might be expected because it is known that S²⁻ is an unstable ion in water²¹ and therefore it would be highly favourable to form any kind of new bond. Hence in the next section, the other reaction schemes are also examined.

3.2 Triple ion complexes

This section follows a more thorough analysis of the pair formation and triple ion complexes using only MP2 with PCM solvation and solvent-phase geometry. First the optimal amount of H₂O n is examined by varying the configurations and coordination of water for all relevant complexes and ions in the reaction schemes. Then reaction free energies are presented and discussed.

3.2.1 Solvation free energy. In Fig. 1 the solvation free energy from the cluster–continuum model is plotted as a function of number n of H₂O that is considered explicitly. The black datapoints represent the most stable configuration computed for that number n, while the grey datapoints represent less stable configurations. In some graphs less grey datapoints are included than others, because either there were fewer possible different configurations or, especially in the case of the complexes with two Fe(II), the computation could not converge in other geometries even when changing various settings. All complexes with Fe(II) are presented in high spin, though complexes in broken symmetry state differed less than 1 kJ mol⁻¹ from a high spin state. The geometries of the most stable configurations are presented in Supplementary Information S3 (ESI†). We have also included a linear fit for the decrease in 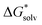as in most cases the decrease was fairly linear (as indicated by R²). In some cases we only fitted until the dashed line as from that point increasing n did not lower 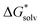by as much. The dashed line was drawn at the minimum obtained and n_min indicates where the two lines cross and represents a minimal amount of H₂O needed to describe the solvation free energy. For Fe²⁺, S²⁻, and (FeOH)₂SH⁺ we did not include the data for n < 2 in the linear fit as they are significant outliers where the first H₂O seemed to have a stronger effect. Additionally, for Fe²⁺, S²⁻, and FeOH⁺n_min is quite close to their computational limit of n ≈ 16 and one could argue that 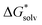would still be lower for more n. However, additional H₂O would either be added in equivalent positions as the configurations for n = 15 and 16 or in a further coordination shell (see Fig. S3–S5, ESI†) and therefore would likely only contribute to a small decrease in .

Fig. 1 The solvation free energy in kJ mol⁻¹ is shown as a function of the number n of explicit H₂O around the ion/complex. The black datapoints represent the most stable configuration computed for that number n, while the grey datapoints represent less stable configurations. The lines represent a fit for the most stable configurations.

Now we look into the ions also shown in Table 3 and how these results correlate to related complexes. It is clear that OH⁻ and HS⁻ only require few H₂O to adequately describe 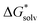and the graphs show that the values in Table 3 are representative for an optimal amount of H₂O as well. Hence the results in the Figure are also in good agreement with reference values.⁵⁹ As a consequence, most complexes with more than two of either OH⁻ and HS⁻ (Fe(SH)₂, FeOHSH, and FeOH(SH)₂⁻) require less n compared to the other complexes. The exception is (FeOH)₂SH⁺, which needs more H₂O as there are two Fe(II) present.

For Fe²⁺ our result in has lowered significantly compared to our result in Table 3, but the value is still in the expected reference range.^57,58,60,61 We also compared this result with reported solvation free energies of Fe²⁺ using the MP2 method.²⁷ Their 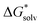decreased more slowly at n = 12 with a value . This discrepancy is either because of the difference in the cluster–continuum model, an unknown difference in certain settings in Gaussian16, or a difference in input geometry which they did not disclose. When Fe²⁺ is paired with a single OH⁻ or HS⁻ very similar configurations are stable as just Fe²⁺ (see Fig. S3, S5 and S7, ESI†) and hence a similar n_min is needed to adequately describe . The configuration of H₂O around FeS (see Fig. S6, ESI†) is quite different as much more is coordinated around the S(−II)-ion, but a similar n_min was obtained. It is striking that for S²⁻ a similarly large n was needed as for Fe²⁺ to adequately describe . This meant that for most complexes with two or more of either ions (Fe₂S²⁺, FeS₂²⁻, and Fe₂SH³⁺) a larger amount of n is needed than could be computed as multiple ions in the complex would require a significant amount of H₂O around them.

Extrapolation of for the complexes where we did not compute with enough n is tricky as it requires an estimation of n_min. For Fe₂SH³⁺ and (FeOH)₂SH⁺ a roughly estimated value for n_min could be argued from the configurations of FeSH⁺ and FeOHSH respectively. For FeSH⁺ only two H₂O are directly coordinated to the SH group and for FeOHSH no H₂O are directly coordinated around the SH group (see Fig. S7 and S8, ESI†). As an estimate for n_min, we could expect a similar coordination around Fe(II) in Fe₂SH³⁺ and around the FeOH groups in (FeOH)₂SH⁺. We would not expect direct H₂O coordination around the SH group at n_min as it is already bonded by two Fe(II) and this was not favourable in configurations we computed at lower n (see Fig. S7 and S8, ESI†). This would lead to n_min ≈ 2 × (13.3 − 2) ≈ 22.6 for Fe₂SH³⁺ and n_min ≈ 2 × 8.8 ≈ 17.6 for (FeOH)₂SH⁺. An extrapolation for Fe₂S²⁺ and FeS₂²⁻ based on the configuration of FeS alone is more challenging as the H₂O configuration around FeS is much more divided between the Fe(II) and S(−II) groups (see Fig. S6, ESI†). However, since n_min of FeS and FeSH⁺ is similar, it is reasonable to expect that upon addition of Fe₂²⁺n_min is also similar, hence we use the same estimate n_min ≈ 22.6 for Fe₂S²⁺. Furthermore, since Fe²⁺ and S²⁻ have a similar n_min, we also estimate n_min for Fe₂S²⁺ and FeS₂²⁻ to be the same.

3.2.2 Reaction free energy. In Table 5 we show the reaction free energies for the addition of the Fe(II) cation (Fe²⁺ or FeOH⁺) and the S(−II) anion (S²⁻ or HS⁻) to the ion pairs (FeS, FeSH⁺, or FeOHSH) using the minimal obtained and extrapolated values if applicable. We have included the formation free energy of the ion pair itself as a reference. In Fig. 2 we have also schematically illustrated our (extrapolated) results and how they position on the path to nucleation. When compared to the MP2 values in Table 4, we notice that all reaction free energies for Fe²⁺ and S²⁻ have higher absolute values in Table 5 than Table 4. Since all solvation energies 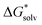have been lowered, it becomes less favourable to break bonds with H₂O to form new bonds. However, we still observe that S(−II) addition is strongly favoured over Fe(II) addition. For the other cases in Table 5 S(−II) addition is similarly favoured over Fe(II) addition.

Table 5 Comparison of reaction free energy in kJ mol⁻¹ for the pair formation and the addition of either the Fe(II) cation or S(−II) anion to the three different ion pairs

Ion pair		Triple ion complex formation via:
	Pair formation	Fe(II) addition	S(−II) addition
Fe^2+ + S^2−	−62	103	13
Extrapolation		16	−51
Fe^2+ + HS^−	−35	92	−29
Extrapolation		2
FeOH^+ + HS^−	−13	42	−30
Extrapolation		−1

---

Fig. 2 Schematic representation of the formation of FeS complexes.

For some of these reactions we can compare to literature values for (the logarithm of) stability constants log K, computed using the expression 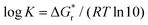. For FeSH⁺ formation, stability constants have been reported ranging from log K = 4.34 to 5.94 depending on experimental method and ionic strength.^62–65 Using −35 kJ mol⁻¹ we obtain log K = 6.05, which is quite close to experimental results. One report with log K = 5.07 also reported a stability constant for Fe₂SH³⁺(log K = 10.07).⁶⁴ We can compute this stability constant from our results by adding of the pair formation with the respective (extrapolated) value for ion addition leading to log K = 5.79. This is quite a different value indicating that for Fe₂SH³⁺ the estimated n_min might need to be higher. Increasing n_min by two H₂O molecules (n_min = 24.6) would lead to log K = 10.46, which is much more similar to the literature value. Additionally, for Fe(SH)₂ a stability constant of log K = 11.27 is obtained, which is of similar magnitude giving some validation to this value. For Fe(SH)₂ other values were also reported (log K = 6.45⁶⁶ or 8.9⁶⁷) which are substantially lower. However, in the same reports the stability constants for FeSH⁺ were considerably lower (log K < 3⁶⁶ or = 1.4⁶⁷) than most other reported values, which means these values are likely underestimated. Additionally, the existence of Fe(SH)₂ in their experiments is controversial.^64,66,67

For all cases, we find that S(−II) addition is favoured over Fe(II) addition, but this result is influenced by the estimate of n_min for the extrapolated values. Hence for the complexes with two Fe(II) we have calculated how much higher n_min needs to be for Fe(II) addition to become favoured over S(−II) addition. This means that should be lowered by at least 66 kJ mol⁻¹ for Fe₂S²⁺. Similarly, for Fe₂SH³⁺ should be lowered by 31 kJ mol⁻¹ and for (FeOH)₂SH⁺ by 28 kJ mol⁻¹. Using the linear fits for , we estimated that n_min should be increased respectively by 7.0, 2.3, and 3.1. For Fe₂S²⁺ such a large increase would be unlikely and therefore S(−II) addition should be more favourable in this case even with the optimal n_min. For Fe₂SH³⁺ and (FeOH)₂SH⁺, the increases in n_min are smaller, so there is a reasonable uncertainty in our conclusion on whether S(−II) addition would be favoured over Fe(II) addition. It is worth reminding that for Fe₂SH³⁺ our resulting stability constant log K = 11.27 for S(−II) addition is larger than the experimental result for Fe(II) addition (log K = 10.07), but we have overestimated other experimental values as well so this gives little confirmation for either conclusion.

Overall though, S(−II) addition seems favoured in most cases and for most methods, which would imply that in an alkaline environment there would be faster nucleation in an S(−II) excess with respect to an Fe(II) excess. Thus in an S(−II) excess you would expect a large amount of small particles and in an Fe(II) excess you would expect to form a smaller amount of large particles. Additionally, a negatively charged particle seems more favourable to form than a positively charged particle. These results could be related to density functional theory calculations on mackinawite surfaces.⁶⁸ Here an S-terminated {001} surface had the smallest surface energy and hence was the most stable surface, while an Fe-terminated {001} surface was the least stable.

4. Conclusions

We have computed the reaction free energy for the formation of complexes in excess of either Fe(II) or S(−II) using ab initio methods. Our results demonstrate that care should be taken when describing FeS complexes with ab initio methods in selecting the right ab initio method, solvation model, and explicit consideration of H₂O. However, with the MP2 method this lead to solvation free energies for HS⁻, OH⁻, Fe²⁺ in line with experimental results and a reaction free energy for FeSH⁺ in reasonable agreement with experiments. It seemed complexes with an additional S(−II) are overall more favourable to form suggesting that in alkaline environments an S(−II) excess leads to faster nucleation compared to an Fe(II) excess. These results again showcase the importance of solution stoichiometry in nucleation and warrant further experimental investigation of this effect on FeS formation in particular.

Author contributions

Vincent F. D. Peters: conceptualization, formal analysis, investigation, methodology, writing – original draft. Janou A. Koskamp: conceptualization, methodology. Devis di Tommaso: methodology, supervision, writing – review & editing. Mariette Wolthers: conceptualization, supervision, writing – review & editing.

Data availability

The data supporting this article have been included as part of the article and ESI.† Optimised structures are available at https://public.yoda.uu.nl/geo/UU01/HC7V0W.html.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank A. Muthuperiyanayagam and A. Živković for help with the ab initio calculations and A. Karami for discussions on FeS formation. This project has received funding to M. W., V. F. D. P., and J. A. K from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme (grant agreement no. 819588).

Notes and references

1. D. Rickard and G. W. Luther, Chem. Rev., 2007, 107, 514–562.
2. M. J. Russell and A. J. Hall, J. Geol. Soc., 1997, 154, 377–402.
3. C. Bonfio, L. Valer, S. Scintilla, S. Shah, D. J. Evans, L. Jin, J. W. Szostak, D. D. Sasselov, J. D. Sutherland and S. S. Mansy, Nat. Chem., 2017, 9, 1229–1234.
4. C. Modrzynski and P. Burger, Dalton Trans., 2019, 48, 1941–1946.
5. J. Zhao, J. Syed, X. Wen, H. Lu and X. Meng, J. Alloys Compd., 2019, 777, 974–981.
6. A. Roldan, N. Hollingsworth, A. Roffey, H.-U. Islam, J. Goodall, C. Catlow, J. Darr, W. Bras, G. Sankar, K. Holt, G. Hogarth and N. De Leeuw, Chem. Commun., 2015, 51, 7501–7504.
7. Y. Gong, J. Tang and D. Zhao, Water Res., 2016, 89, 309–320.
8. Y. Sun, J. Liu, X. Fan, Y. Li and W. Peng, Front. Environ. Sci., 2023, 11, 1212355.
9. J. Jamero, S. Zarrouk and E. Mroczek, Geothermics, 2018, 72, 1–14.
10. A. Hamza, I. Hussein, R. Jalab, M. Saad and M. Mahmoud, Energy Fuels, 2021, 35, 14401–14421.
11. Y. Liu, Z. Zhang, N. Bhandari, F. Yan, F. Zhang, G. Ruan, Z. Dai, H. Alsaiari, A. Lu, G. Deng, A. Kan and M. Tomson, SPE Int. Oilfield Chem. Symp. Proc., 2017, 2017-April, 361–376.
12. M. Ma, H. Wang, J. Xu, Y. Huang, D. Yuan, X. Zhang and Q. Song, ACS Omega, 2020, 5, 31551–31558.
13. C. Blodau, Acta Hydrochim. Hydrobiol., 2005, 33, 104–117.
14. Y. Zheng, R. Anderson, A. Van Geen and J. Kuwabara, Geochim. Cosmochim. Acta, 2000, 64, 4165–4178.
15. K. Ding, W. Seyfried Jr., M. Tivey and A. Bradley, Earth Planet. Sci. Lett., 2001, 186, 417–425.
16. S. Y. M. H. Seepma, S. E. Ruiz-Hernandez, G. Nehrke, K. Soetaert, A. P. Philipse, B. W. M. Kuipers and M. Wolthers, Cryst. Growth Des., 2021, 21, 1576–1590.
17. V. F. D. Peters, A. Baken, S. Y. M. H. Seepma, J. A. Koskamp, A. Fernández-Martínez, A. E. S. van Driessche and M. Wolthers, Ind. Eng. Chem. Res., 2024, 63, 78–88.
18. J. A. Koskamp, S. Y. M. H. Seepma, V. F. D. Peters, D. Toroz, D. Di Tommaso and M. Wolthers, Chem. – Eur. J., 2024, 30, e202303860.
19. E. Moerman, D. Furman and D. J. Wales, J. Chem. Inf. Model., 2021, 61, 1204–1214.
20. D. Kashchiev and G. M. Van Rosmalen, Cryst. Res. Technol., 2003, 38, 555–574.
21. P. May, D. Batka, G. Hefter, E. Königsberger and D. Rowland, Chem. Commun., 2018, 54, 1980–1983.
22. O. Suleimenov and T. Seward, Geochim. Cosmochim. Acta, 1997, 61, 5187–5198.
23. F. Furcas, B. Lothenbach, O. Isgor, S. Mundra, Z. Zhang and U. Angst, Cem. Concr. Res., 2022, 151, 106620.
24. S. Haider, D. Di Tommaso and N. H. De Leeuw, Phys. Chem. Chem. Phys., 2013, 15, 4310–4319.
25. U. Terranova and N. H. De Leeuw, Phys. Chem. Chem. Phys., 2014, 16, 13426–13433.
26. O. Boukar, J. J. Fifen, M. Nsangou, H. Ghalila and J. Conradie, New J. Chem., 2021, 45, 10693–10710.
27. O. Boukar, J. J. Fifen, J. Conradie and M. M. Conradie, J. Mol. Model., 2024, 30, 52.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian–16 Revision C.01, 2016, Gaussian Inc., Wallingford CT.
29. Y. Zhao and D. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667.
30. T. Clark, J. Chandrasekhar, G. Spitznagel and P. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
31. M. Frisch, J. Pople and J. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
32. V. Rassolov, M. Ratner, J. Pople, P. Redfern and L. Curtiss, J. Comput. Chem., 2001, 22, 976–984.
33. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918.
34. M. Head-Gordon, J. Pople and M. Frisch, Chem. Phys. Lett., 1988, 153, 503–506.
35. S. Sæbø and J. Almlöf, Chem. Phys. Lett., 1989, 154, 83–89.
36. M. Frisch, M. Head-Gordon and J. Pople, Chem. Phys. Lett., 1990, 166, 281–289.
37. M. Frisch, M. Head-Gordon and J. Pople, Chem. Phys. Lett., 1990, 166, 275–280.
38. M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122–128.
39. J. R. Pliego and J. M. Riveros, J. Phys. Chem. A, 2001, 105, 7241–7247.
40. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
41. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
42. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
43. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
44. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
45. S. Dudarev and G. Botton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
46. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257.
48. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
49. A. Albers, S. Demeshko, K. Pröpper, S. Dechert, E. Bill and F. Meyer, J. Am. Chem. Soc., 2013, 135, 1704–1707.
50. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
51. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
52. G. Makov and M. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022.
53. R. González Gómez, I. del Rosal, K. Philippot and R. Poteau, Theor. Chem. Acc., 2019, 138, 95.
54. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106.
55. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101.
56. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
57. Y. Marcus, Ions in Solution and their Solvation, Wiley Online Library, Hoboken, NJ, 1st edn, 2015, pp. 1–293.
58. R. Noyes, J. Am. Chem. Soc., 1962, 84, 513–522.
59. A. V. Marenich, C. P. Kelly, J. D. Thompson, G. D. Hawkins, C. C. Chambers, D. J. Giesen, P. Winget, C. J. Cramer and D. G. Truhlar, Minnesota Solvation Database (MNSOL) version 2012, 2020, Retrieved from the Data Repository for the University of Minnesota.
60. Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999.
61. W. R. Fawcett, J. Phys. Chem. B, 1999, 103, 11181–11185.
62. G. Luther and T. Ferdelman, Environ. Sci. Technol., 1993, 27, 1154–1163.
63. D. Wei and K. Osseo-Asare, J. Colloid Interface Sci., 1995, 174, 273–282.
64. G. W. Luther, D. Rickard, S. Theberge and A. Olroyd, Environ. Sci. Technol., 1996, 30, 671–679.
65. R. Al-Farawati and C. Van Den Berg, Mar. Chem., 1999, 63, 331–352.
66. W. Davison, N. Phillips and B. Tabner, Aquat. Sci., 1999, 61, 23–43.
67. D. Dyrssen, Mar. Chem., 1988, 24, 143–153.
68. A. J. Devey, R. Grau-Crespo and N. H. De Leeuw, J. Phys. Chem. C, 2008, 112, 10960–10967.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03758h

---