On the peculiar EPR spectra of P1 centers at high (12–20 T) magnetic fields

Abstract

The most common lattice defect in high-pressure high-temperature (HPHT) diamonds is the nitrogen substitution (P1) center. This is a paramagnetic defect with a single unpaired electron spin coupled to a ¹⁴N nuclear spin forming an S = 1/2, I = 1 spin system. While P1 centers have been studied by electron paramagnetic resonance (EPR) spectroscopy for decades, only recently did their behavior at ultra-high (>12 T) magnetic fields become of interest. This is because P1 centers were recently found to be very efficient polarizing agents in dynamic nuclear polarization (DNP) experiments, which are typically carried out at high magnetic fields. The P1 ultra-high field EPR spectra show multiple peaks which the lower fields spectra do not. In this paper, we present an account of the EPR spectra of P1 centers at ultra-high fields and show that the more complex spectra at 12–20 T are the result of significant state mixing in the m_S = +1/2 electron spin manifold. The state mixing is a result of fulfilling the cancellation condition, meaning the e–¹⁴N hyperfine interaction equals twice the Larmor frequency of the ¹⁴N nuclear spin. We illustrate the influence of the cancellation condition on the EPR spectra by comparing EPR spectra acquired at 6.9 and 13.8 T. While the former are similar to the consensus spectra observed at lower fields, the latter are very different. We present numerical simulations that quantitatively account for the experimental spectra at both 6.9 and 13.8 T. Finally, we use electron electron double resonance (ELDOR) measurements to show that the cancellation condition results in increased spectral diffusion in the 13.8 T spectrum. This work sheds light on the spin properties of P1 centers under DNP-characteristic conditions, which will be conducive to their efficient utilization in DNP.

---

Introduction

Defects in the diamond lattice have attracted research interest for years.¹ The most common impurities in synthetic diamonds are nitrogen-based, which are introduced during the synthesis due to the presence of nitrogen in the typical conditions used for the growth of high-pressure high-temperature (HPHT) lab diamonds.^2,3 The nitrogen concentration can vary from hundreds of ppm in HPHT diamonds to a few ppb in chemical vapor deposition (CVD) grown diamonds.² While recent advances allow for strict control over the presence of nitrogen impurities,⁴ such control is unnecessary for most applications, and the nitrogen substitutions are typically present in the hundreds of ppm concentrations in most industrial diamonds.⁵

The simplest nitrogen defect is nitrogen substitution, which is referred to as N_s defect, C-center, and P1 center in electron paramagnetic resonance (EPR) literature.⁶ Another nitrogen-based defect that is widely researched due to the unique coupling between its electron spin and optical properties is the negatively charged nitrogen-vacancy (NV) center.⁷ NV centers are a prime candidate for various quantum applications, e.g. quantum computing,^8–10 subpicotesla magnetometry,^11–13 quantum memories,¹⁴ microwave amplification,¹⁵ and teraherz radiation generation.¹⁶ They are fabricated from P1 centers with 25% efficiency at best¹⁷ and therefore P1 centers are present in large concentrations in NV-enriched samples. P1 centers are a source of relaxation for NV centers and their presence affects NV centers’ spin properties which can hamper their use in the aforementioned applications.^18,19 Characterization of both NV and P1 center populations is thus essential for the development of these fields. Since, unlike NV centers, the electron spin and optical properties of P1 centers are not coupled, P1 centers can only be investigated using magnetic resonance spectroscopy.

Both P1 and NV centers are also extensively investigated as polarizing agents for dynamic nuclear polarization (DNP) experiments, which have been actively developed over the past two decades due to their ability to enhance the nuclear magnetic resonance (NMR) signal by several orders of magnitude.^20–23 In a DNP experiment, nuclear polarization is enhanced by polarization transfer from unpaired electron spins, which have orders of magnitude higher thermal polarization due to their larger gyromagnetic ratio (e.g. γ_e/γ_¹³C ≈ 2600). Since pure diamonds are diamagnetic, the introduction of paramagnetic defects into the diamond lattice is required for DNP applications.

Diamonds are promising candidates for DNP as they provide several advantages over the organic radicals that currently dominate the DNP experiments.^24–29 Diamonds are chemically and thermally stable under a broad range of conditions. Large crystals (>few micrometers) have long electron spin relaxation times, which allow for room temperature DNP.^30–42 In addition, the ¹³C polarization inside the diamond lattice is very long-lived due to the low natural abundance of ¹³C and the scarcity of other magnetic nuclei. Recently, nanodiamonds were used to enhance protein signals in magic angle spinning (MAS)-DNP experiments,⁴³ and were shown to be compatible with in vivo applications due to their ability to enter the blood flow.⁴⁴

Since it is possible to optically polarize the electron spins in NV centers, which makes their electron spin polarization independent of the magnetic field strength, most of the NV center DNP research focused on low-field DNP experiments,^45–47 with some notable exceptions of 7 and 9.4 T experiments.^48,49 Similarly, P1 centers were subject to multiple DNP investigations at low magnetic fields.^30–33 Recently, efficient ¹³C hyperpolarization using P1 centers was reported at 3.3, 7, and 14 T for single crystals of HPHT diamonds and microdiamond powders.^36,38–42 The high hyperpolarization efficiency was a surprising observation since the solid effect (SE) DNP mechanism, which was expected to be the only active ¹³C DNP mechanism in these samples, scales as B₀⁻² and would have resulted in low DNP efficiency. These results prompted the investigation of the electron spin properties of P1 centers at ultra-high magnetic fields, thereby discovering exchange-coupled P1 center clusters in HPHT diamonds, which allow for the cross-effect (CE) DNP mechanism, which is much more efficient at high-field.^41,42 These results emphasized that a detailed understanding of the DNP mechanisms requires a detailed understanding of the electron spin properties of the polarizing agent under the same set of conditions.

While the diamond EPR spectra reported at 3.3 and 7 T are similar to the well-known P1 center spectra reported at lower fields, the spectra at 14 T are significantly more difficult to interpret with multiple additional resolved peaks which appear due to the ¹⁴N spin state mixing present in one of the electron spin manifolds. This paper elaborates on the EPR spectra of P1 centers at ultra-high (>12 T) magnetic fields. The paper is structured as follows. First, we briefly review the theory of the P1 center electronic structure and its EPR spectra. In the next section, we follow by presenting simulated EPR spectra, starting from the simplest case of an isolated P1 center and building up to simulating the spectra of single-crystal diamond and microcrystalline diamond powder samples, which account for powders of grain size larger than ∼1 μm.^35,50,51 Throughout this section, we highlight the differences between the EPR spectra at <12 T fields and those at 12–20 T fields. In the experimental section, we present continuous wave (CW) and pulsed EPR spectra measured at 6.9 and 13.8 T, of a single crystal HPHT diamond at several orientations, and of a microcrystalline diamond powder. The simulations from the preceding section quantitatively account for the observed effects. In the last section, we demonstrate that the state mixing not only affects the appearance of the EPR spectra, but also results in enhanced electron–electron spectral diffusion (eSD) at 13.8 T, as proven by electron electron double resonance (ELDOR) measurements.

Theory

The nitrogen atom has five valence electrons, compared to four of the carbon. Upon substitution for carbon in the diamond lattice, the nitrogen atom forms three bonding sp³ orbitals with three neighboring carbon atoms, and a fourth antibonding sp³ orbital, that is occupied by a lone pair of electrons, with a fourth carbon atom (colored light blue in Fig. 1a). The fourth neighboring carbon is thus left with an unpaired electron. While 75% of electron spin density is on the carbon atom, the main feature visible in the EPR spectra of P1 centers is the hyperfine interaction with the ¹⁴N nuclear spin, due to the natural abundance ratios of carbon and nitrogen isotopes.^52–54 This means the most commonly encountered P1 center is the one formed by a ¹²C, ¹⁴N pair (spin 0 and 1 respectively). Such a P1 center forms a two-spin (S = 1/2; I = 1) system with a spin Hamiltonian given by:⁵⁵Where Ŝ and Î are the electron and nuclear spin operators; g_N is the ¹⁴N g-factor, μ_β and μ_N are Bohr and nuclear magnetons; B₀ is the magnetic field vector; g_e is the electron axial g-tensor with g_⊥ = 2.00220; g_‖ = 2.00218;⁴²A is the axial e–¹⁴N hyperfine interaction tensor with A_⊥ = 81.3; A_‖ = 114 MHz, Q is the axial nuclear quadrupole tensor with a coupling constant of −3.97 MHz.⁵⁵ All three tensors are collinear and are oriented along the unique ¹²C–¹⁴N antibonding orbital. We will refer to the angle between the vector oriented along this orbital and the direction of the static magnetic field B₀ as θ (Fig. 1a). Following a standard treatment, the Hamiltonian can be expanded in the high-field approximation as follows:^56,57Where ν_e and ν_¹⁴N are the electron and ¹⁴N nuclear Larmor frequencies. For a given value of θ there are six energy levels corresponding to each of the |m_S, m_I〉 states. Note that due to the symmetry of the spin system and the axial symmetry of the magnetic field, P1 centers oriented with angles θ or 180° − θ are magnetically equivalent and have the same energies. The order of the |m_S, m_I〉 states depends on the strength of the hyperfine interaction relative to ν_¹⁴N. The energy diagram depicted in Fig. 1b left corresponds to the strong coupling case, encountered in EPR experiments on P1 centers at fields <12 T, where ν_¹⁴N < A_eff/2. Here, A_eff is the coefficient of the Ŝ_zÎ_z term in eqn (2), representing the effective hyperfine coupling for a specific value of θ. In the weak coupling case, ν_¹⁴N > A_eff/2 the order of the energy levels in the m_S = +1/2 manifold changes. This is depicted in the energy level diagram in Fig. 1b right. The intermediate case, where ν_¹⁴N ≈ A_eff/2, is known as the cancellation condition. 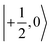The name refers to the vanishing effective field in one of the electron spin manifolds, where the nuclear Zeeman and hyperfine fields cancel each other.⁵⁸ In this case, the presence of the pseudo-secular Ŝ_zÎ_x term in the Hamiltonian, which connects the sublevel with the sublevels, results in the anticrossing depicted in Fig. 1c and d. While there is no general analytical solution for a S = 1/2; I = 1 spin system with anisotropic hyperfine and quadrupolar coupling,^59–62 a special case where the g-, hyperfine, and quadrupolar tensors are axial and colinear was treated analytically rather early in the EPR history.^63,64 Nowadays numerical simulations provide a much easier alternative to spectral fitting which does not rely on the approximations of the 2^nd order perturbation theory used to obtain the analytical expressions. We therefore utilize numerical simulations in this work.

Fig. 1 (a) Schematic diagram of a P1 center at an angle θ relative to the direction of the static magnetic field B₀. (b) Schematic energy level and transitions diagram for a single P1 center in the strong coupling (left) and weak coupling (right) regimes. (c) and (d) Energy levels diagrams, (e) and (f) transition probabilities, and (g) and (h) EPR spectra vs. field for (c), (e) and (g) θ = 70° and (d), (f) and (h) θ = 20°. The spectra in (g) and (h) were aligned by subtracting the central resonance frequency ν₀(θ) for each field.

Simulations

EPR spectra of a single P1 center

In this six-level system of a single P1 center, nine Δm_S = 1 transitions are observable in the EPR spectrum (Fig. 1b). The individual transitions will be referred to as v_i,j and the corresponding transition probabilities as P_i,j with i = 1,2,3 and j = 4,5,6. In the strong coupling case, there are three allowed transitions: ν_1,6, ν_2,5 and ν_3,4, one for each of the nuclear spin states m_I = +1, 0, −1, respectively, where Δm_I = 0. There are four forbidden EPR transitions: ν_1,5, ν_2,6, ν_2,4, and ν_3,5, where Δm_I = ±1, and two doubly forbidden EPR transitions: ν_1,4 and ν_3,6, where Δm_I = ±2 (Fig. 1b left). The Δm_I = ±1 and Δm_I = ±2 transitions become partially allowed due to the presence of the pseudo-secular term Ŝ_zÎ_x in the hyperfine interaction in eqn (2).⁵⁶

Ultimately, a typical EPR spectrum of an individual P1 center at the strong coupling regime consists of three lines of equal intensity, corresponding to the three Δm_S = 1, Δm_I = 0 EPR transitions. The four smaller peaks, corresponding to the Δm_I = ±1 EPR transitions, are also observed for the θ ≠ 0, 90° orientations of a P1 center. The transition probabilities of the Δm_I = ±2 transitions are typically too low for those transitions to be observed. Characteristic examples of simulated frequency swept EPR spectra at 7 T with θ = 70° and 20° are shown in Fig. 1g and h respectively. The frequency swept spectra are simulated at a constant magnetic field B₀ for a varying irradiation frequency ν. The spectra are aligned by subtracting the resonance frequency of the central m_I = 0 line ν₀(θ) = μ_βB₀g_eff(θ). The spectra at lower fields are very similar and are dominated by the triplet of the Δm_I = 0 transitions. With the increase in the magnetic field, the familiar shape of the spectrum begins to change. This is because starting with B₀ ≈ 13.5 T (ν_¹⁴N(B₀ = 13.5 T) = 41.55 MHz), the cancellation condition ν_¹⁴N ≈ A_eff/2 will be fulfilled for some θ values up to the field of B₀ ≈ 18.5 T (ν_¹⁴N(B₀ = 18.5 T) = 56.9 MHz). Near the cancellation condition, significant state mixing occurs, and the energy levels of the upper m_S = +1/2 manifold converge with an anticrossing at the exact cancellation condition (Fig. 1c and d). The transition probabilities, shown in Fig. 1e and f, change drastically, resulting in the differently looking P1 center spectra, as illustrated in Fig. 1g and h.

The hyperfine interaction is the smallest along the perpendicular direction, thus with an increase in the magnetic field the cancellation condition is first fulfilled for the P1 centers with θ = 90°. With a further increase of the magnetic field, the cancellation condition will be fulfilled for other θ values up to ∼18.5 T, at which the cancellation condition will occur for P1 centers oriented parallel to the magnetic field (θ = 0°). This effect is clearly visible in the spectra in Fig. 1g and h, where additional strong peaks appear in the spectra calculated at the fields of 12 and 14.5 T for θ = 70° (Fig. 1g), while in the spectra calculated for θ = 20°, additional peaks appear at the higher fields of 17 and 19.5 T (Fig. 1h). Note, that even though the cancellation condition is not strictly fulfilled below ∼13.5 T and above ∼18.5 T, the effects of the state mixing manifest themselves in the spectra down to ∼12 T and up until ∼20 T. This is because despite the exact cancellation condition not being fulfilled, the transition probabilities are still sufficiently high (>0.2), as can be seen in Fig. 1e and f.

Another way to observe the impact of the cancellation condition on the EPR spectra is by comparing the spectra simulated at 6.9 T in Fig. 2a, for selected values of θ, with the spectra simulated at 13.8 T in Fig. 2b. In the 6.9 T spectra, the expected three Δm_S = 1, Δm_I = 0 EPR transitions dominate and the outer lines relative position changes with the change of A_eff. On the other hand, in 13.8 T the spectra shift from strong coupling at θ = 0° to weak coupling at θ = 90° with more complex spectra with multiple additional peaks for θ = 40, 60, and 80°.

Fig. 2 Simulated changes in the EPR spectra vs. θ at (a) 6.9 T and (b) 13.8 T. The spectra were aligned by subtracting the central resonance frequency ν₀(θ) for each angle.

Next, we turn to a detailed discussion of the different EPR transitions and the dependence of their transition probabilities on θ at 13.8 T, where the experiments were performed. For simplicity, we begin with the model case of quadrupole interaction of Q = 0 MHz. At the field of 13.8 T, the cancellation condition is fulfilled for θ = 70.5°. This results in a peculiar situation where the P1 centers can shift between strong and weak coupling regimes based on θ. The transition probabilities P_i,j of the nine EPR transitions and the corresponding changes in the energy levels as a function of θ are presented in Fig. 3a and Fig. S1a in the ESI,† respectively. Interestingly, the shift from strong to weak coupling regimes is not apparent in the energy level diagram depicted in Fig. S1a (ESI†), with the change in the energy levels with θ being dominated by the change in the A_eff. For the Q = 0 case, P_1,6 and P_3,4 coincide as do the P_i,j for all four Δm_I = ±1 transitions and the P_1,4 and P_3,6 of the Δm_I = ±2 transitions; thus, only four different curves are visible in Fig. 3a. For θ = 0°, at 13.8 T the spin system is in the strong coupling regime (A_eff/2 = 57 MHz > ν_¹⁴N(B₀ = 13.8 T) = 42.5 MHz), and the P_i,j for the three allowed transitions equal one and the rest equal zero. With the increase in θ, the P_i,j of the allowed transitions decrease, with the P_2,5 decreasing faster than the P_1,6 and the P_3,4. Concurrently, the P_i,j for all the forbidden transitions increases. The P_1,4 and P_3,6 of the Δm_I = ±2 transitions remain close to zero up to θ ≈ 30°. This trend continues up to the cancellation condition at θ = 70.5°, at which P_2,5 = 0 and P_i,j for the Δm_I = ±1 transitions reach a maximum. Notably, at values of θ close to the cancellation condition, all nine EPR transitions have non-zero transition probabilities and will be visible in the spectra. With a further increase in θ, the spin system shifts to the weak coupling regime (for θ = 90° at 13.8 T, A_eff/2 = 40.7 MHz < ν_¹⁴N(B₀ = 13.8 T) = 42.5 MHz). In this regime, the ν_1,4 and ν_3,6 transitions become allowed, and correspondingly the P_1,4 and P_3,6 increase, reaching 1 for θ = 90°. The ν_1,6 and ν_3,4 transitions become doubly forbidden (Δm_I = ±2) transitions, and correspondingly P_1,6 and P_3,4 decrease to zero. Past the cancellation condition, the P_i,j of the Δm_I = ±1 transitions also decrease to zero at θ = 90° (Fig. 3a).

Fig. 3 Transition probabilities of the P1 center spin system at (a) B₀ = 13.8 T and Q = 0 MHz and (b) Q = −3.97 MHz, and at (c) B₀ = 6.9 T and Q = −3.97 MHz. The color coding of the P_i,j curves is consistent with the energy level diagram in Fig. 1b.

Next, we turn to analyze the complete P1 center spin system, with the real value of the quadrupolar coupling constant Q = −3.97 MHz. The main influence of the quadrupolar interaction is lifting the degeneracy between different transitions with the same Δm_I, resulting in more complex P_i,j dependence on θ. While the overall dependence of P_i,j on θ remains similar, the P_i,j of all nine EPR transitions are now distinct (Fig. 3b). This further complicates the appearance of the EPR spectra and their dependence on θ (the energy level diagram is shown in Fig. S1b, ESI†).

For comparison, in the case where the cancellation condition is not fulfilled for any θ, the P_i,j for the Q = −3.97 MHz at 6.9 T are presented in Fig. 3c, and the corresponding, much simpler, energy level diagram is presented in Fig. S1c (ESI†). In this case, the dependence of P_i,j on θ is very mild, P_i,j ≈ 1 for all the Δm_I = 0 transitions, and P_i,j ≈ 0 for all the other transitions. Note the inset in Fig. 3c showing a zoom-in of the transition probabilities.

EPR spectra of P1 centers in a single-crystal diamond

The diamond crystal belongs to the Fd3̄m space group, which has four symmetry-related sites that are resolved in the EPR spectra of P1 centers in a diamond crystal. The four sites can be visualized using the P1 center schematic in Fig. 1a, at which the carbon atom with an unpaired electron was colored light blue. In a lattice, any of the depicted four carbon atoms can be the one with an unpaired electron, giving rise to the four sites. Thus the unique antibonding orbitals can be oriented along any of the ¹²C–¹⁴N bond axes.^{52,54,65–67} In addition, the crystal orientation relative to the magnetic field, defined by three Euler angles (in the ZYZ convention for the following simulations), can be changed. Therefore, in the strong coupling regime, for an arbitrary orientation of the diamond crystal in the magnetic field, the EPR spectrum is composed of up to four resolved triplets. Such spectra are observed in all conventional EPR experiments; examples of the simulated EPR spectra at the magnetic field of 6.9 T for different crystal orientations are shown in Fig. 4a. For some orientations of the crystal, fewer peaks are present in the spectrum as several sites are magnetically equivalent. For example, if the diamond crystal is oriented with the B₀ field normal to the crystallographic (100) plane, two P1 defects have (also known as the “magic angle” in magnetic resonance literature) and two , making all four sites magnetically equivalent and the EPR spectrum reduces to a single triplet (Fig. 4a top). Alternatively, if the crystal is oriented at (0°, 58.2°, 0°), the four possible sites are magnetically equivalent to a pair of sites, site I with θ = 37.35° and site II with θ = 79.27°. This particular crystal orientation was used in the experiments presented in the Results section and will be referred to as orientation A. The 6.9 T EPR spectrum of the diamond crystal in orientation A consists of two triplets of equal intensity (Fig. 4a middle). The central (m_I = 0) line practically coincides for all orientations, and the small g-anisotropy only manifests itself as a small line broadening. A case where all four triplets are resolved for a crystal orientation (−85.8°, −12.6°, 24.8°), is depicted in Fig. 4a bottom. This will be referred to as orientation B. The separation of each of the spectra presented in Fig. 4 into the contributions from the four individual sites is shown in Fig. S2 (ESI†).

Fig. 4 Changes in the simulated EPR spectra of P1 centers in a single crystal diamond vs. crystal orientation for (a) 6.9 T and (b) 13.8 T, using Q = −3.97 MHz.

EPR spectra acquired at higher magnetic fields become more complex as one or several sites can be oriented such that they are near the cancellation condition for that particular field. In those cases, the EPR spectrum can consist of up to 36 lines, as up to nine transitions could be resolved per each of the four crystallographic sites. In practice, the spectra may feature fewer peaks, as not all the sites are near the cancellation conditions at the same time, two or more sites are magnetically equivalent, or not all lines are fully resolved. Examples of the EPR spectra simulated for B₀ = 13.8 T are shown in Fig. 4b. Even for the crystal orientation that resulted in the EPR spectra with the fewest peaks (normal to the 100 plane) at 6.9 T, the spectrum at 13.8 T is significantly more complex. While all four sites are magnetically equivalent to θ = 54.74°, and contribute an identical EPR spectrum, this spectrum consists of 9 resolved lines (Fig. 4b top). The spectrum in Fig. 4b middle is for the crystal at orientation A. It has two resolved sites oriented at θ_I = 37.35° and θ_II = 79.27°. Since the exact cancellation condition for 13.8 T is fulfilled for θ = 70.5°, site I is in the strong coupling regime, while site II is in the weak coupling regime. Nonetheless, both sites are close to the cancellation condition, and the EPR spectra consist of seven and nine lines for sites I and II, respectively. This is discussed in more detail in the Results section. Note the complexity of the spectra in Fig. 4b bottom, simulated for the crystal at orientation B which consists of 35 partially overlapping lines. The contributions from each of the four sites are detailed in Fig. S2f (ESI†).

EPR spectra of P1 centers in diamond powder

Another diamond sample commonly encountered in DNP and EPR experiments is the micro- or nanodiamond powder. In such samples, the P1 center EPR spectra consist of the contributions from P1 centers with a statistical distribution of all θ angles. In the strong coupling regime (low-field experiments), the EPR spectrum is almost symmetric with two broad lines for the m_I = ±1 manifolds, where there is an anisotropic hyperfine interaction, and a narrow central line for the m_I = 0 manifold, for which there is no hyperfine interaction (Fig. 5a). The lines of the m_I = −1 and +1 manifolds are formed by the powder patterns of the ν_3,4 and ν_1,6 transitions, respectively. The powder patterns have a familiar shape that is determined by the statistical probability of finding a P1 center at a specific orientation θ. The contribution of the Δm_I = ±1 transitions is small, though sometimes visible, and that of the Δm_I = ±2 is negligible (Fig. 5a). Unsurprisingly, the complex angular dependence of P_i,j on θ results in more complex spectra at 13.8 T (Fig. 5b). While the spectrum is still composed of three lines for the m_I = −1, 0 and +1 manifolds, each of those lines is now composed of three overlapping powder patterns. The powder patterns have a non-conventional shape that depends both on the P_i,j(θ) for that transition and on the statistical probability for that θ. For small θ values, the transitions that are allowed for the strong coupling case (ν_1,6,ν_2,5,ν_3,4) contribute the most to the EPR spectrum. At θ values closer to the cancellation condition, the Δm_I = ±1 transitions contribute the most, and at θ values approaching 90°, the contributions from the transitions allowed in the weak coupling case (ν_1,4,ν_2,5,ν_3,6) dominate (Fig. 5b). Note that the color codes of the different transitions in Fig. 5 correspond to the colors used in the energy level diagram in Fig. 1b. The color transitions in Fig. 5b correspond to transitions between strong and weak coupling regimes.

Fig. 5 Simulated EPR spectra of diamond powders at (a) 6.9 T and (b) 13.8 T. The color coding of the individual EPR transitions is consistent with the transitions in the energy level diagram in Fig. 1b.

Experimental results

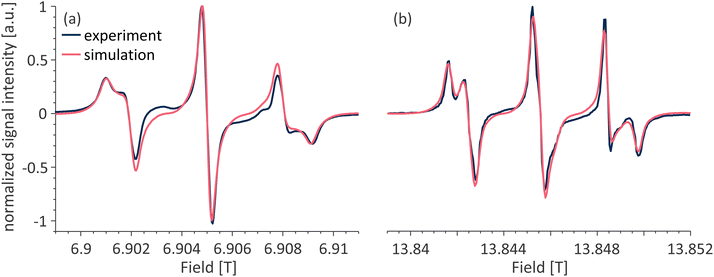
Fig. 6 presents a comparison between the EPR spectra recorded for a single crystal diamond at 6.9 and 13.8 T at orientation A. The continuous wave (CW) EPR spectra are presented in Fig. 6a and b for 6.9 and 13.8 T, respectively, and the echo-detected EPR spectra in Fig. 6c and d for the same fields. It is important to note that due to the way CW EPR spectra are acquired, the spectra are recorded as the derivative of the EPR line, while the echo-detected spectra are recorded as absorption. The simulated data is plotted as derivative or absorption to match the experimental data. The simulations performed, in accordance with the theory outlined in the previous section, show an excellent agreement with the experimental spectra. Note, that simulations presented in Fig. 6 and onward include the contribution from the P1 center pairs/clusters with strong dipolar and exchange couplings. These strongly coupled species do not contribute to the resolved signals in the EPR spectra of P1 centers but rather to the signal intensity at the bottom of and between the resolved signals.^41,42 The separation of each simulation of the experimental spectra into the relative contribution from each population is shown in Fig. S3–S5 (ESI†). These species with broad EPR signals will not be further discussed here.

Fig. 6 Overlay of the experimental and simulated spectra of a single crystal HPHT diamond at orientation A. CW EPR at (a) 6.9 T and (b) 13.8 T; echo-detected pulsed EPR at (c) 6.9 T and (d) 13.8 T. Simulated contributions from the individual sites for (c) and (d) shown below. The color coding of the individual EPR transitions is consistent with the transitions in the energy level diagram in Fig. 1b.

As mentioned in the previous section, the crystal at orientation A has two pairs of magnetically distinct P1 centers. While the spectra acquired at 6.9 T (Fig. 6a and c), as expected, consist of two triplets, one for each pair of sites, the spectra at 13.8 T are more complex. The individual contributions from sites I and II are shown in Fig. 6c and d at the bottom. While only the allowed transitions contribute to the EPR spectra of both sites at 6.9 T, the spectra at 13.8 T consist of all possible transitions. As discussed in the theory section, at 13.8 T for this crystal orientation, site I is in the strong coupling regime while site II is in the weak coupling one. In addition, both sites are close to the cancellation condition; thus, more than three transitions contribute to each site. For site I, the relative intensities of each transition are as expected, with the Δm_I = 0 transitions having the highest intensities and the Δm_I = ±2 transitions having a very small intensity. For site II, which is ∼9° away from strictly fulfilling the cancellation condition, this is not the case and the Δm_I = ±1 transitions dominate over both the Δm_I = 0 and Δm_I = ±2 transitions, for both m_I = 0 and m_I = +1 manifolds, and have the smallest contribution for the m_I = −1 manifold, which is consistent with the angular dependence of P_i,j presented in Fig. 3b.

A more complicated example of a 13.8 T EPR spectrum observed for a crystal at orientation B is shown in Fig. 7. In this crystal orientation, all four crystallographic sites are magnetically distinct. This results in a very crowded EPR spectrum, that does not resemble the single-crystal EPR spectra of diamonds at lower fields. The simulation includes the contribution from four different sites (θ_I,II,III,IV = 43.1°,51.3°,59.9°,66.6°) and reproduces the experimental spectrum. The contributions from the individual sites are detailed at the bottom part of Fig. 7.

Fig. 7 Overlay of experimental and simulated P1 center CW EPR spectra for a single crystal in orientation B (top). Simulated contributions from the individual sites (bottom). The color coding of the individual EPR transitions is consistent with the transitions in the energy level diagram in Fig. 1b.

In the next section, we present the P1 center CW EPR spectra of a microdiamond powder, recorded at 6.9 and 13.8 T, in Fig. 8a and b, respectively. As explained in the theory section, in this case, the spectrum at 6.9 T is composed almost entirely of the contribution from the Δm_I = 0 transitions with two almost symmetric powder patterns for the m_I = ±1 manifolds, and a sharp line in the center corresponding to m_I = 0. The spectrum at 13.8 T is also composed of three lines, corresponding to the three m_I manifolds. But, as explained in the theory section, each of those lines is composed of contributions from three distorted powder patterns, due to the complex dependence of P_i,j on θ. The changes are more striking when examining the simulated absorption spectra shown in Fig. 5, where in addition to the distortion in shape, the signal intensity difference in the m_I = ±1 manifolds relative to the m_I = 0 manifold changes drastically between the 6.9 and 13.8 T spectra. While the signal of the m_I = 0 line has three times the intensity of the m_I = ±1 lines in the EPR spectra acquired at 6.9 T, in the spectra acquired at 13.8 T all three lines have similar maximum intensities.

Fig. 8 Overlay of experimental and simulated CW EPR spectra of a microdiamond powder at (a) 6.9 and (b) 13.8 T.

The state mixing at high magnetic fields has further implications beyond the changes in the appearance of the EPR spectra: it results in increased electron–electron spectral diffusion (eSD). In this case, irradiation on one of the transitions immediately affects the polarization across other observable transitions. For example, while at low magnetic fields irradiation on any of the allowed transitions does not affect the polarization across any of the other allowed transitions of the same spin packet, at higher fields this is no longer the case. This can be seen in the ELDOR experiment presented in Fig. 9a. ELDOR is a pump–probe experiment. The influence of a long saturation pulse on electrons resonating at a frequency ν_pump over electrons resonating at a different frequency ν_probe is probed; the pulse sequence is shown in the inset in Fig. 9. The resulting ELDOR spectrum is normalized to the echo intensity with ν_pump away from the EPR signal with a change in the echo intensity indicating an interaction between the electrons at ν_pump and at ν_probe. In the ELDOR spectrum presented in Fig. 9a, ν_probe is set to the ν_3,4 transition belonging to site I at 193.515 GHz, labeled as 1 in the figure, while ν_pump is stepped over the entire EPR line. The largest signal occurs when ν_pump = ν_probe and the other three strong signals in this ELDOR spectrum are at 193.538, 193.549, and 193.586 GHz (labeled as 2–4 in the figure). The peak at 193.538 GHz (labeled 2) corresponds to the crosstalk between the allowed Δm_I = 0 transitions of different crystallographic sites via dipole–dipole driven eSD process. The signals at 193.549 and 193.586 GHz (labeled 3 and 4) correspond to altering the electron spin polarization across the forbidden (ν_3,5 and ν_2,4) transitions belonging to site I. This occurs because these Δm_I = ±1 transitions have a common energy level with the ν_3,4 Δm_I = 0 transition. The situation drastically changes at 13.8 T. Here, pumping at the same ν_3,4 transition at 387.995 GHz (labeled as 1 in the figure) strongly affects multiple transitions across the EPR spectrum. The signals at 388.011, 388.017, 388.087, and 388.183 GHz (labeled as 2–4 and 6) belong to the ν_3,5 transition of site I, ν_3,4 of site II, ν_2,4 of site I, and ν_1,4 of both sites, respectively. In addition, an electron spin hyperpolarization (ELDOR signal intensity > 1) appears at the frequencies of 388.109, and 388.205 GHz (labeled as 5 and 7) corresponding to the ν_2,6 transition of both sites and ν_1,6 transition of site I. While the exact mechanism underlying the hyperpolarized ELDOR signals in P1 centers is unclear, such signals can be either a result of nuclear spin relaxation⁶⁸ or the formation of electron spin dipolar order.⁶⁹ Regardless of the underlying mechanism, the ELDOR spectra reveal that electron spin saturation is spread much more efficiently across the EPR spectrum at 13.8 compared to 6.9 T.

Fig. 9 Overlay of the ELDOR and EPR spectra acquired at (a) 6.91 T; ν_probe = 193.515 GHz and (b) 13.85 T; ν_probe = 387.995 GHz for a single crystal HPHT diamond at orientation A.

Conclusions

The EPR spectra of P1 centers observed at 13.8 T greatly differ from those reported at lower fields. Additional lines are resolved in the EPR spectra of single-crystal diamonds, and the spectra of microdiamond powders become asymmetric. This is because at 13.8 T, up to nine resolved lines per P1 center orientation can be observed, instead of only three in spectra acquired at lower magnetic fields.

This is caused by the cancellation condition, ν_¹⁴N ≈ A_eff/2, being fulfilled at 13.5–18.5 T for some orientations of the diamond crystal relative to the magnetic field. The cancellation condition results in the energy levels of the m_S = +1/2 electron spin manifold becoming degenerate, which leads to drastic changes in the transition probabilities. The “forbidden transitions” become allowed, and the “allowed transitions” become forbidden. By calculating the transition probabilities, we showed the profound transformation that occurs in the spin system that shifts from the strong-coupling regime (ν_¹⁴N < A_eff/2) to the weak-coupling regime (ν_¹⁴N > A_eff/2) with the change of the crystal orientation under high magnetic fields. The simulations reveal that the magnetic field range over which forbidden transitions significantly contribute to the EPR spectra lies in the 12–20 T range, well beyond the 13.5–18.5 T range where the cancellation condition is strictly fulfilled, with the exact range of fields depending on the crystal orientation.

The utilization of the cancellation condition is not limited to the field of magnetic resonance. NV centers in diamonds are utilized around the cancellation condition of the zero-field splitting to allow for nuclear qubit manipulation.^70–72 For quantum information applications, other defects in their respective solid-state platforms are studied near or at various cancellation conditions for the varying benefits provided.^73–75

Finally, the effects of the cancellation condition are not limited only to changes in the shape of the EPR spectra. The degeneracy of the energy levels in the m_S = +1/2 manifold results in a connection between multiple transitions observed across the EPR spectrum, resulting in a strong spread of electron spin saturation known as eSD. The eSD was shown to have profound effects in DNP; indeed, in the presence of eSD, the excitation spreads across the EPR spectrum, thus allowing for more electron spins to participate in DNP.^76–78 This suggests that the DNP mechanisms behind the P1-DNP can differ at 13.8 T (and higher) magnetic fields compared to the ones investigated at 3.3 and 7 T. The influence of the effects described here on DNP at >12 T fields using P1 centers, and for other polarizing agents at or near the cancellation condition will require further investigation.

Materials and methods

All measurements presented were performed at room temperature using a home-built DNP/EPR spectrometer operating at 6.9 and 13.8 T. The design of the spectrometer and its CW-EPR⁷⁹ and pulsed-EPR capabilities⁴² were described in previous publications.

The parameters used for each CW-EPR spectrum are summarized in Table 1.

Table 1 Experimental parameters summary for the CW EPR spectra

Fig.	6a	6b	7	8a	8b
Frequency [GHz]	193.5	388		388	193.5
Field [T]			13.85
Modulation amplitude [mT]	0.27	0.27	0.054	0.16	0.27
Lock-in time constant [ms]	300	300	300	100	300
Acquisition time [min]	8.5	7	40	3	8.5

---

The echo-detected frequency stepped EPR spectra in Fig. 6c and d were measured using a t_p–τ–t_p–τ–echo sequence with the following 16-step phase cycle, used to account for mixer imperfections: ϕ_p1 = [0°₄,90°₄,180°₄,270°₄], ϕ_p2 = [0°,90°,180°,270°]₄, and ϕ_detection = ϕ_p1 − 2ϕ_p2. The measurements were performed using the parameters summarized in Table 2.

Table 2 Experimental parameters summary for the echo-detected pulsed EPR spectra

Fig.	6c	6d
Field [T]	6.91	13.85
t p [μs]	0.9	1.6
τ [μs]	1.2	0.5
Repetition time [ms]	3	2
Averages per point	50	50

---

The ELDOR spectra in Fig. 9 were measured using the pulse sequence shown in the inset of Fig. 9. The same 16-step phase cycle that was used in the echo-detected frequency stepped EPR spectra was used for the echo sequence at ν_probe. The phase of the pulse at ν_pump was not cycled. The experimental parameters are summarized in Table 3.

Table 3 Experimental parameters summary for the ELDOR spectra

Fig.	9a	9b
Field [T]	6.91	13.85
ν pump [GHz]	193.37	387.995
t pump [ms]	10	10
t p [μs]	0.9	1.6
τ [μs]	1.2	0.8
Repetition time [ms]	14	14
Averages per point	25	50

---

The single crystal sample used for measurements presented in Fig. 6, 7, and 9 is a 3.2 × 3.2 × 1.1 mm³ HPHT diamond with a uniform yellow color, purchased from element 6 and polished to the (100) face. The diamond has a boron concentration below 0.1 ppm and a nitrogen concentration below 200 ppm. The P1 center concentration is 20 ppm as determined by spin counting on a CW X-band Bruker Elexsys E500 spectrometer.

The diamond powder sample used for measurements presented in Fig. 8 is a HPHT diamond powder with consistent but irregular crystal shapes with a particle size of ∼15–25 μm, purchased from element 6 (MICRON+ MDA M1525). The P1 center concentration is 90 ppm as determined by spin counting on a CW X-band Bruker Elexsys E500 spectrometer.

The simulations were performed using the MATLAB EasySpin toolbox⁸⁰ using the resfreqs_matrix function for the transition probabilities simulations, the levels function for the energy levels diagrams, and the pepper function for solid-state EPR spectra simulations. All simulations used the g-tensor of (2.00220, 2.00220, 2.00218), the hyperfine tensor (81.3, 81.3, 114) MHz, and the quadrupole coupling constant of −3.973 MHz. Fig. 4, 6, and 7 used a crystal symmetry of Fd3̄m, and Euler angles of (45°,54.74°,0°) were used for the molecular frame orientation relative to the crystal frame. Fig. 6 and 7 used (0°,58.2°,0°) and (−85.8°,−12.6°,24.8°) respectively for the orientation of the crystal frame relative to the magnetic field. The experimental spectra simulations used three components accounting for isolated P1 centers, P1 centers pairs with dipolar coupling, and P1 centers clusters with an exchange coupling of 138 MHz and no dipolar interaction. Each component used an electron spin coupled to a single ¹⁴N spin, except for the P1 centers clusters which used two electrons, each coupled to a different ¹⁴N spin.⁴² The parameters used for each spectrum simulation are summarized in Table 4.

Table 4 Parameters summary of the simulated EPR spectra

Fig.	6a	6b	6c	6d	7	8a	8b
Isolated P1 centers
Line width peak-to-peak [MHz] (Gaussian|Lorentzian)	7.6|0	7.6|0	4.52|0	4.52|0	3.5|0	6.5|2.8	6.5|5.6
Relative weight	0.55	0.55	0.62	0.62	0.54	0.59	0.59
P1 center pairs
Line width [MHz]	29.9	29.9	29.9	29.9	20	28	28
Relative weight	0.4	0.4	0.34	0.34	0.46	0.36	0.36
P1 center clusters
Line width [MHz]	17.5	17.5	17.5	17.5	—	28	28
Relative weight	0.05	0.05	0.04	0.04	—	0.05	0.05

---

Author contributions

ONA investigation, methodology, formal analysis, software, writing – original draft. EL formal analysis, writing – original draft. MD investigation. NM supervision, writing – original draft. IK conceptualization, methodology, funding acquisition, supervision, writing – original draft.

Data availability

The data supporting this article have been included as part of the ESI.† The ESI† contains the energy levels for a single P1 center at 6.9 and 13.8 T, the simulated EPR spectra of P1 centers in a single-crystal diamond decomposed into the contributions of different crystallographic sites, and the contribution of isolated P1 centers, P1 pairs, and P1 clusters populations to the experimental EPR spectra. An example script with the code used for the simulations presented in this work can be found in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by THE ISRAEL SCIENCE FOUNDATION (grant No. 2149/19 and 1058/23). Orit Nir-Arad is a fellow of the Ariane de Rothschild Women's Doctoral Program. Dr Raanan Carmieli is acknowledged for helping with the spin counting experiments. Dr Daphna Shimon is acknowledged for providing the diamond powder samples and for fruitful discussions.

References

1. J. E. Shigley and C. M. Breeding, Optical Defects in Diamond: A Quick Reference Chart, Gems Gemol., 2013, 49(2), 107–111,  DOI:10.5741/GEMS.49.2.107.
2. M. N. R. Ashfold, J. P. Goss, B. L. Green, P. W. May, M. E. Newton and C. V. Peaker, Nitrogen in Diamond, Chem. Rev., 2020, 120(12), 5745–5794,  DOI:10.1021/acs.chemrev.9b00518.
3. H. P. Bovenkerk, F. P. Bundy, H. T. Hall, H. M. Strong and R. H. Wentorf, Preparation of Diamond, Nature, 1959, 184(4693), 1094–1098,  DOI:10.1038/1841094a0.
4. L. Chen, X. Miao, H. Ma, L. Guo, Z. Wang, Z. Yang, C. Fang and X. Jia, Synthesis and Characterization of Diamonds with Different Nitrogen Concentrations under High Pressure and High Temperature Conditions, CrystEngComm, 2018, 20(44), 7164–7169,  10.1039/C8CE01533C.
5. Y. N. Palyanov, Y. M. Borzdov, A. F. Khokhryakov, I. N. Kupriyanov and A. G. Sokol, Effect of Nitrogen Impurity on Diamond Crystal Growth Processes, Cryst. Growth Des., 2010, 10(7), 3169–3175,  DOI:10.1021/cg100322p.
6. F. Jelezko and J. Wrachtrup, Single Defect Centres in Diamond: A Review, Phys. Status Solidi A, 2006, 203(13), 3207–3225,  DOI:10.1002/pssa.200671403.
7. M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup and L. C. L. Hollenberg, The Nitrogen-Vacancy Colour Centre in Diamond, Phys. Rep., 2013, 528(1), 1–45,  DOI:10.1016/j.physrep.2013.02.001.
8. F. Jelezko, T. Gaebel, I. Popa, M. Domhan, A. Gruber and J. Wrachtrup, Observation of Coherent Oscillation of a Single Nuclear Spin and Realization of a Two-Qubit Conditional Quantum Gate, Phys. Rev. Lett., 2004, 93(13), 130501,  DOI:10.1103/PhysRevLett.93.130501.
9. N. Bar-Gill, L. M. Pham, A. Jarmola, D. Budker and R. L. Walsworth, Solid-State Electronic Spin Coherence Time Approaching One Second, Nat. Commun., 2013, 4(1), 1743,  DOI:10.1038/ncomms2771.
10. S. Pezzagna and J. Meijer, Quantum Computer Based on Color Centers in Diamond, Appl. Phys. Rev., 2021, 8(1), 011308,  DOI:10.1063/5.0007444.
11. F. Shi, Q. Zhang, P. Wang, H. Sun, J. Wang, X. Rong, M. Chen, C. Ju, F. Reinhard, H. Chen, J. Wrachtrup, J. Wang and J. Du, Single-Protein Spin Resonance Spectroscopy under Ambient Conditions, Science, 2015, 347(6226), 1135–1138,  DOI:10.1126/science.aaa2253.
12. T. Wolf, P. Neumann, K. Nakamura, H. Sumiya, T. Ohshima, J. Isoya and J. Wrachtrup, Subpicotesla Diamond Magnetometry, Phys. Rev. X, 2015, 5(4), 041001,  DOI:10.1103/PhysRevX.5.041001.
13. C. Zhang, F. Shagieva, M. Widmann, M. Kübler, V. Vorobyov, P. Kapitanova, E. Nenasheva, R. Corkill, O. Rhrle, K. Nakamura, H. Sumiya, S. Onoda, J. Isoya and J. Wrachtrup, Diamond Magnetometry and Gradiometry Towards Subpicotesla Dc Field Measurement, Phys. Rev. Appl., 2021, 15(6), 064075,  DOI:10.1103/PhysRevApplied.15.064075.
14. C. E. Bradley, J. Randall, M. H. Abobeih, R. C. Berrevoets, M. J. Degen, M. A. Bakker, M. Markham, D. J. Twitchen and T. H. Taminiau, A Ten-Qubit Solid-State Spin Register with Quantum Memory up to One Minute, Phys. Rev. X, 2019, 9(3), 031045,  DOI:10.1103/PhysRevX.9.031045.
15. A. Sherman, O. Zgadzai, B. Koren, I. Peretz, E. Laster and A. Blank, Diamond-Based Microwave Quantum Amplifier, Sci. Adv., 2022, 8(49), eade6527,  DOI:10.1126/sciadv.ade6527.
16. S. Kollarics, B. G. Márkus, R. Kucsera, G. Thiering, Á. Gali, G. Németh, K. Kamarás, L. Forró and F. Simon, Terahertz Emission from Diamond Nitrogen-Vacancy Centers, Sci. Adv., 2024, 10(22), eadn0616.
17. Y. Mindarava, R. Blinder, C. Laube, W. Knolle, B. Abel, C. Jentgens, J. Isoya, J. Scheuer, J. Lang, I. Schwartz, B. Naydenov and F. Jelezko, Efficient Conversion of Nitrogen to Nitrogen-Vacancy Centers in Diamond Particles with High-Temperature Electron Irradiation, Carbon, 2020, 170, 182–190,  DOI:10.1016/j.carbon.2020.07.077.
18. V. Stepanov and S. Takahashi, Determination of Nitrogen Spin Concentration in Diamond Using Double Electron–Electron Resonance, Phys. Rev. B, 2016, 94(2), 024421,  DOI:10.1103/PhysRevB.94.024421.
19. E. Bauch, S. Singh, J. Lee, C. A. Hart, J. M. Schloss, M. J. Turner, J. F. Barry, L. M. Pham, N. Bar-Gill, S. F. Yelin and R. L. Walsworth, Decoherence of Ensembles of Nitrogen-Vacancy Centers in Diamond, Phys. Rev. B, 2020, 102(13), 134210,  DOI:10.1103/PhysRevB.102.134210.
20. J. Eills; D. Budker; S. Cavagnero; E. Y. Chekmenev; S. J. Elliott; S. Jannin; A. Lesage; J. Matysik; T. Meersmann; T. Prisner; J. A. Reimer; H. Yang and I. V. KoptyugSpin Hyperpolarization in Modern Magnetic Resonance; preprint; Chemistry, 2022 DOI:10.26434/chemrxiv-2022-p7c9r.
21. T. Maly, G. T. Debelouchina, V. S. Bajaj, K.-N. Hu, C.-G. Joo, M. L. Mak-Jurkauskas, J. R. Sirigiri, P. C. A. van der Wel, J. Herzfeld, R. J. Temkin and R. G. Griffin, Dynamic Nuclear Polarization at High Magnetic Fields, J. Chem. Phys., 2008, 128(5), 052211,  DOI:10.1063/1.2833582.
22. C.-Y. Cheng and S. Han, Dynamic Nuclear Polarization Methods in Solids and Solutions to Explore Membrane Proteins and Membrane Systems, Annu. Rev. Phys. Chem., 2013, 64(1), 507–532,  DOI:10.1146/annurev-physchem-040412-110028.
23. A. S. Lilly Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Dynamic Nuclear Polarization for Sensitivity Enhancement in Modern Solid-State NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102(Supplement C), 120–195,  DOI:10.1016/j.pnmrs.2017.06.002.
24. C. Song, K.-N. Hu, C.-G. Joo, T. M. Swager and R. G. Griffin, TOTAPOL: A Biradical Polarizing Agent for Dynamic Nuclear Polarization Experiments in Aqueous Media, J. Am. Chem. Soc., 2006, 128(35), 11385–11390,  DOI:10.1021/ja061284b.
25. Y. Matsuki, T. Maly, O. Ouari, H. Karoui, F. Le Moigne, E. Rizzato, S. Lyubenova, J. Herzfeld, T. Prisner, P. Tordo and R. G. Griffin, Dynamic Nuclear Polarization with a Rigid Biradical, Angew. Chem., Int. Ed., 2009, 48(27), 4996–5000,  DOI:10.1002/anie.200805940.
26. A. Zagdoun, G. Casano, O. Ouari, M. Schwarzwälder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Copéret, A. Lesage, P. Tordo and L. Emsley, Large Molecular Weight Nitroxide Biradicals Providing Efficient Dynamic Nuclear Polarization at Temperatures up to 200 K, J. Am. Chem. Soc., 2013, 135(34), 12790–12797,  DOI:10.1021/ja405813t.
27. C. Sauvée, M. Rosay, G. Casano, F. Aussenac, R. T. Weber, O. Ouari and P. Tordo, Highly Efficient, Water-Soluble Polarizing Agents for Dynamic Nuclear Polarization at High Frequency, Angew. Chem., Int. Ed., 2013, 52(41), 10858–10861,  DOI:10.1002/anie.201304657.
28. F. Mentink-Vigier, I. Marin-Montesinos, A. P. Jagtap, T. Halbritter, J. van Tol, S. Hediger, D. Lee, S. T. Sigurdsson and G. De Paëpe, Computationally Assisted Design of Polarizing Agents for Dynamic Nuclear Polarization Enhanced NMR: The AsymPol Family, J. Am. Chem. Soc., 2018, 140(35), 11013–11019,  DOI:10.1021/jacs.8b04911.
29. A. Lund, G. Casano, G. Menzildjian, M. Kaushik, G. Stevanato, M. Yulikov, R. Jabbour, D. Wisser, M. Renom-Carrasco, C. Thieuleux, F. Bernada, H. Karoui, D. Siri, M. Rosay, I. V. Sergeyev, D. Gajan, M. Lelli, L. Emsley, O. Ouari and A. Lesage, TinyPols: A Family of Water-Soluble Binitroxides Tailored for Dynamic Nuclear Polarization Enhanced NMR Spectroscopy at 18.8 and 21.1 T, Chem. Sci., 2020, 11(10), 2810–2818,  10.1039/C9SC05384K.
30. J. Zhou, L. Li, H. Hu, B. Yang, Z. Dan, J. Qiu, J. Guo, F. Chen and C. Ye, Study of Natural Diamonds by Dynamic Nuclear Polarization-Enhanced ¹³C Nuclear Magnetic Resonance Spectroscopy, Solid State Nucl. Magn. Reson., 1994, 3(6), 339–351,  DOI:10.1016/0926-2040(94)90018-3.
31. B. Yang, J. Zhou, H. Hu, L. Li, J. Qiu, J. Guo, P. He, J. Lu and C. Ye, Study of Synthetic Diamonds by Dynamic Nuclear Polarization-enhanced ¹³C Nuclear Magnetic Resonance Spectroscopy, Appl. Magn. Reson., 1995, 9(3), 379–388,  DOI:10.1007/BF03161961.
32. E. C. Reynhardt and G. L. High, Dynamic Nuclear Polarization of Diamond. I. Solid State and Thermal Mixing Effects, J. Chem. Phys., 1998, 109(10), 4090–4099,  DOI:10.1063/1.477009.
33. E. C. Reynhardt and G. L. High, Dynamic Nuclear Polarization of Diamond. II. Nuclear Orientation via Electron Spin-Locking, J. Chem. Phys., 1998, 109(10), 4100–4107,  DOI:10.1063/1.477010.
34. G. J. Hill, J. Wu and M. J. R. Hoch, Satellite Structure of DNP Enhanced ¹³C NMR Spectra in Diamond, Hyperfine Interact., 1999, 120(1), 81–86,  DOI:10.1023/A:1017073912037.
35. L. B. Casabianca, A. I. Shames, A. M. Panich, O. Shenderova and L. Frydman, Factors Affecting DNP NMR in Polycrystalline Diamond Samples, J. Phys. Chem. C, 2011, 115(39), 19041–19048,  DOI:10.1021/jp206167j.
36. C. O. Bretschneider, Ü. Akbey, F. Aussenac, G. L. Olsen, A. Feintuch, H. Oschkinat and L. Frydman, On The Potential of Dynamic Nuclear Polarization Enhanced Diamonds in Solid-State and Dissolution ¹³C NMR Spectroscopy, ChemPhysChem, 2016, 17(17), 2691–2701,  DOI:10.1002/cphc.201600301.
37. A. M. Carroll Development of a Combined DNP/EPR Spectrometer for the Investigation of Small Volume Samples by Solid State NMR. PhD, Yale University, United States – Connecticut, 2018. https://www.proquest.com/docview/2184267171/abstract/4B057AB0E664647PQ/1 (accessed 2024-06-23).
38. D. Shimon, K. A. Cantwell, L. Joseph, E. Q. Williams, Z. Peng, S. Takahashi and C. Ramanathan, Large Room Temperature Bulk DNP of ¹³C via P1 Centers in Diamond, J. Phys. Chem. C, 2022, 126(41), 17777–17787,  DOI:10.1021/acs.jpcc.2c06145.
39. D. Shimon, K. Cantwell, L. Joseph and C. Ramanathan, Room Temperature DNP of Diamond Powder Using Frequency Modulation, Solid State Nucl. Magn. Reson., 2022, 122, 101833,  DOI:10.1016/j.ssnmr.2022.101833.
40. A. A. Nevzorov, A. Marek, S. Milikisiyants and A. I. Smirnov, Characterization of Photonic Band Resonators for DNP NMR of Thin Film Samples at 7 T Magnetic Field, J. Magn. Reson., 2021, 323, 106893,  DOI:10.1016/j.jmr.2020.106893.
41. S. Bussandri, D. Shimon, A. Equbal, Y. Ren, S. Takahashi, C. Ramanathan and S. Han, P1 Center Electron Spin Clusters Are Prevalent in Type Ib Diamonds, J. Am. Chem. Soc., 2024, 146(8), 5088–5099,  DOI:10.1021/jacs.3c06705.
42. O. Nir-Arad, D. H. Shlomi, N. Manukovsky, E. Laster and I. Kaminker, Nitrogen Substitutions Aggregation and Clustering in Diamonds as Revealed by High-Field Electron Paramagnetic Resonance, J. Am. Chem. Soc., 2024, 146(8), 5100–5107,  DOI:10.1021/jacs.3c06739.
43. K. Kato; H. Takahashi; H. Tamaki; T. Fujiwara and Y. Matsukiin situ. ChemRxiv, 2023, preprint DOI:10.26434/chemrxiv-2023-x9m17-v2.
44. F. Alexis, E. Pridgen, L. K. Molnar and O. C. Farokhzad, Factors Affecting the Clearance and Biodistribution of Polymeric Nanoparticles, Mol. Pharmaceutics, 2008, 5(4), 505–515,  DOI:10.1021/mp800051m.
45. R. Fischer, C. O. Bretschneider, P. London, D. Budker, D. Gershoni and L. Frydman, Bulk Nuclear Polarization Enhanced at Room Temperature by Optical Pumping, Phys. Rev. Lett., 2013, 111(5), 057601,  DOI:10.1103/PhysRevLett.111.057601.
46. J. Scheuer, I. Schwartz, Q. Chen, D. Schulze-Sünninghausen, P. Carl, P. Höfer, A. Retzker, H. Sumiya, J. Isoya, B. Luy, M. B. Plenio, B. Naydenov and F. Jelezko, Optically Induced Dynamic Nuclear Spin Polarisation in Diamond, New J. Phys., 2016, 18(1), 013040,  DOI:10.1088/1367-2630/18/1/013040.
47. A. Ajoy, K. Liu, R. Nazaryan, X. Lv, P. R. Zangara, B. Safvati, G. Wang, D. Arnold, G. Li, A. Lin, P. Raghavan, E. Druga, S. Dhomkar, D. Pagliero, J. A. Reimer, D. Suter, C. A. Meriles and A. Pines, Orientation-Independent Room Temperature Optical ¹³C Hyperpolarization in Powdered Diamond, Sci. Adv., 2018, 4(5), eaar5492,  DOI:10.1126/sciadv.aar5492.
48. J. P. King, P. J. Coles and J. A. Reimer, Optical Polarization of C 13Nuclei in Diamond through Nitrogen Vacancy Centers, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(7), 073201,  DOI:10.1103/PhysRevB.81.073201.
49. E. Scott, M. Drake and J. A. Reimer, The Phenomenology of Optically Pumped ¹³C NMR in Diamond at 7.05 T: Room Temperature Polarization, Orientation Dependence, and the Effect of Defect Concentration on Polarization Dynamics, J. Magn. Reson., 2016, 264, 154–162,  DOI:10.1016/j.jmr.2016.01.001.
50. Z. Peng, T. Biktagirov, F. H. Cho, U. Gerstmann and S. Takahashi, Investigation of Near-Surface Defects of Nanodiamonds by High-Frequency EPR and DFT Calculation, J. Chem. Phys., 2019, 150(13), 134702,  DOI:10.1063/1.5085351.
51. A. I. Shames, G. G. Zegrya, D. M. Samosvat, V. Y. Osipov and A. Y. Vul’, Size Effect in Electron Paramagnetic Resonance Spectra of Impurity Centers in Diamond Particles, Phys. E, 2023, 146, 115523,  DOI:10.1016/j.physe.2022.115523.
52. W. V. Smith, P. P. Sorokin, I. L. Gelles and G. J. Lasher, Electron-Spin Resonance of Nitrogen Donors in Diamond, Phys. Rev., 1959, 115(6), 1546–1552,  DOI:10.1103/PhysRev.115.1546.
53. H. J. Bower and M. C. R. Symons, Electron Spin Resonance Spectra Associated with Nitrogen in Diamonds, Nature, 1966, 210(5040), 1037–1038,  DOI:10.1038/2101037a0.
54. J. H. N. Loubser and J. A. van Wyk, Electron Spin Resonance in the Study of Diamond, Rep. Prog. Phys., 1978, 41(8), 1201–1248,  DOI:10.1088/0034-4885/41/8/002.
55. A. Cox, M. E. Newton and J. M. Baker, ¹³C, ¹⁴N and ¹⁵N ENDOR Measurements on the Single Substitutional Nitrogen Centre (P1) in Diamond, J. Phys.: Condens. Matter, 1994, 6(2), 551,  DOI:10.1088/0953-8984/6/2/025.
56. A. Schweiger and G. JeschkeChapter 3.5 Model System for Pulse EPR and ENDOR Experiments, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, 2001, pp. 58–66.
57. M. J. Duer Chapter 5.2.1 The Quadrupole Hamiltonian, Solid State NMR Spectroscopy: Principles and Applications, John Wiley & Sons, Incorporated, Chichester, United Kingdom, 2001, pp. 237–248.
58. A. Lai, H. L. Flanagan and D. J. Singel, Multifrequency Electron Spin Echo Envelope Modulation in S = 1/2, I = 1/2 Systems: Analysis of the Spectral Amplitudes, Line Shapes, and Linewidths, J. Chem. Phys., 1988, 89(12), 7161–7166,  DOI:10.1063/1.455293.
59. S. Stoll and D. GoldfarbEPR Interactions – Nuclear Quadrupole Couplings, eMagRes, John Wiley & Sons, Ltd, 2017, pp. 495–510 DOI:10.1002/9780470034590.emrstm1504.
60. H. L. Flanagan and D. J. Singel, Analysis of ¹⁴N ESEEM Patterns of Randomly Oriented Solids, J. Chem. Phys., 1987, 87(10), 5606–5616,  DOI:10.1063/1.453532.
61. E. J. Reijerse and C. P. Keijzers, Model Calculations of Frequency-Domain ESEEM Spectra of Disordered Systems, J. Magn. Reson., 1987, 71(1), 83–96,  DOI:10.1016/0022-2364(87)90129-6.
62. H.-I. Lee, P. E. Doan and B. M. Hoffman, General Analysis of ¹⁴N (I = 1) Electron Spin Echo Envelope Modulation, J. Magn. Reson., 1999, 140(1), 91–107,  DOI:10.1006/jmre.1999.1803.
63. B. L. Bleaney, Hyperfine Structure in Paramagnetic Salts and Nuclear Alignment, London, Edinburgh Dublin Philos. Mag. J. Sci., 1951, 42(328), 441–458,  DOI:10.1080/14786445108561175.
64. A. Schweiger, F. Graf, G. Rist and H. H. Günthard, Theory and Applications of Generalized Operator Transforms for Diagonalization of Spin Hamiltonians, Chem. Phys., 1976, 17(2), 155–185,  DOI:10.1016/0301-0104(76)80099-7.
65. J. H. N. Loubser and L. D. Preez, New Lines in the Electron Spin Resonance Spectrum of Substitutional Nitrogen Donors in Diamond, Br. J. Appl. Phys., 1965, 16(4), 457,  DOI:10.1088/0508-3443/16/4/307.
66. P. E. Klingsporn, M. D. Bell and W. J. Leivo, Analysis of an Electron Spin Resonance Spectrum in Natural Diamonds, J. Appl. Phys., 1970, 41(7), 2977–2980,  DOI:10.1063/1.1659347.
67. E. C. Reynhardt, G. L. High and J. A. van Wyk, Temperature Dependence of Spin–Spin and Spin–Lattice Relaxation Times of Paramagnetic Nitrogen Defects in Diamond, J. Chem. Phys., 1998, 109(19), 8471–8477,  DOI:10.1063/1.477511.
68. B. Epel, A. Pöppl, P. Manikandan, S. Vega and D. Goldfarb, The Effect of Spin Relaxation on ENDOR Spectra Recorded at High Magnetic Fields and Low Temperatures, J. Magn. Reson., 2001, 148(2), 388–397,  DOI:10.1006/jmre.2000.2261.
69. A. Equbal, C. Ramanathan and S. Han, Dipolar Order Induced Electron Spin Hyperpolarization, J. Phys. Chem. Lett., 2024, 15(20), 5397–5406,  DOI:10.1021/acs.jpclett.4c00294.
70. V. Jacques, P. Neumann, J. Beck, M. Markham, D. Twitchen, J. Meijer, F. Kaiser, G. Balasubramanian, F. Jelezko and J. Wrachtrup, Dynamic Polarization of Single Nuclear Spins by Optical Pumping of Nitrogen-Vacancy Color Centers in Diamond at Room Temperature, Phys. Rev. Lett., 2009, 102(5), 057403,  DOI:10.1103/PhysRevLett.102.057403.
71. A. Dréau, P. Spinicelli, J. R. Maze, J.-F. Roch and V. Jacques, Single-Shot Readout of Multiple Nuclear Spin Qubits in Diamond under Ambient Conditions, Phys. Rev. Lett., 2013, 110(6), 060502,  DOI:10.1103/PhysRevLett.110.060502.
72. M. Hirose and P. Cappellaro, Coherent Feedback Control of a Single Qubit in Diamond, Nature, 2016, 532(7597), 77–80,  DOI:10.1038/nature17404.
73. M. H. Mohammady, G. W. Morley and T. S. Monteiro, Bismuth Qubits in Silicon: The Role of EPR Cancellation Resonances, Phys. Rev. Lett., 2010, 105(6), 067602,  DOI:10.1103/PhysRevLett.105.067602.
74. M. Onizhuk, K. C. Miao, J. P. Blanton, H. Ma, C. P. Anderson, A. Bourassa, D. D. Awschalom and G. Galli, Probing the Coherence of Solid-State Qubits at Avoided Crossings, PRX Quantum, 2021, 2(1), 010311,  DOI:10.1103/PRXQuantum.2.010311.
75. B. Tissot, M. Trupke, P. Koller, T. Astner and G. Burkard, Nuclear Spin Quantum Memory in Silicon Carbide, Phys. Rev. Res., 2022, 4(3), 033107,  DOI:10.1103/PhysRevResearch.4.033107.
76. Y. Hovav, D. Shimon, I. Kaminker, A. Feintuch, D. Goldfarb and S. Vega, Effects of the Electron Polarization on Dynamic Nuclear Polarization in Solids, Phys. Chem. Chem. Phys., 2015, 17(8), 6053–6065,  10.1039/C4CP05625F.
77. A. Leavesley, D. Shimon, T. Ann Siaw, A. Feintuch, D. Goldfarb, S. Vega, I. Kaminker and S. Han, Effect of Electron Spectral Diffusion on Static Dynamic Nuclear Polarization at 7 Tesla, Phys. Chem. Chem. Phys., 2017, 19(5), 3596–3605,  10.1039/C6CP06893F.
78. D. Shimon and I. Kaminker, A Transition from Solid Effect to Indirect Cross Effect with Broadband Microwave Irradiation, Phys. Chem. Chem. Phys., 2022, 24(12), 7311–7322,  10.1039/D1CP05096F.
79. O. Nir-Arad, D. H. Shlomi, A. Israelstam, T. Amit, N. Manukovsky, A. B. Fialkov and I. Kaminker, The CW-EPR Capabilities of a Dual DNP/EPR Spectrometer Operating at 14 and 7 T, J. Magn. Reson., 2024, 360, 107635,  DOI:10.1016/j.jmr.2024.107635.
80. S. Stoll and A. Schweiger, EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR, J. Magn. Reson., 2006, 178(1), 42–55.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03055a

---