Spin labels for ¹⁹F ENDOR distance determination: resolution, sensitivity and distance predictability

Abstract

¹⁹F electron-nuclear double resonance (ENDOR) has emerged as an attractive method for determining distance distributions in biomolecules in the range of 0.7–2 nm, which is not easily accessible by pulsed electron dipolar spectroscopy. The ¹⁹F ENDOR approach relies on spin labeling, and in this work, we compare various labels’ performance. Four protein variants of GB1 and ubiquitin bearing fluorinated residues were labeled at the same site with nitroxide and trityl radicals and a Gd(III) chelate. Additionally, a double-histidine variant of GB1 was labeled with a Cu(II) nitrilotriacetic acid chelate. ENDOR measurements were carried out at W-band (95 GHz) where ¹⁹F signals are well separated from ¹H signals. Differences in sensitivity were observed, with Gd(III) chelates providing the highest signal-to-noise ratio. The new trityl label, OXMA, devoid of methyl groups, exhibited a sufficiently long phase memory time to provide an acceptable sensitivity. However, the longer tether of this label effectively reduces the maximum accessible distance between the ¹⁹F and the C_α of the spin-labeling site. The nitroxide and Cu(II) labels provide valuable additional geometric insights via orientation selection. Prediction of electron–nuclear distances based on the known structures of the proteins were the closest to the experimental values for Gd(III) labels, and distances obtained for Cu(II) labeled GB1 are in good agreement with previously published NMR results. Overall, our results offer valuable guidance for selecting optimal spin labels for ¹⁹F ENDOR distance measurement in proteins.

---

Introduction

Among the diverse physicochemical techniques available for elucidating the molecular structure of proteins and nucleic acids, electron paramagnetic resonance (EPR) techniques are valuable tools.^1–3 Specifically, pulsed dipolar EPR methods have become routine for determining distances in the 1.5–6.0 nm range,^4,5 and longer distances can be accessed by employing tailored pulse sequences^6,7 or by deuterating the macromolecule.^8,9 These distance determinations rely on measuring magnetic dipolar interactions between two paramagnetic moieties, either intrinsic to the system or chemically introduced spin labels.

To extract short-range distances, electron–nuclear (further referred to as e–n) interactions, i.e. hyperfine couplings, can be exploited via electron spin echo envelope modulation (ESEEM),¹⁰ electron–electron double resonance (ELDOR) detected NMR,¹¹ or electron–nuclear double resonance (ENDOR).^12,13 In the past, in the biological context, these approaches were used primarily for structural investigations of paramagnetic metal ions in metalloenzymes to map close-by atoms in their coordination shells (<5 Å).^14–17 More recently, ENDOR has also been applied to measure distances below 2.0 nm.^18,19 This requires introducing a fluorine atom into the molecule at a specific site, in addition to the spin label, to measure the hyperfine coupling between them. For proteins, the spin label can be attached to a native or an introduced cysteine residue, and a fluorinated amino acid is introduced at another position. For purely dipolar interactions, the value of the hyperfine splitting is given by:

where μ₀ is the vacuum magnetic permeability, g_e and g_n are electron and nuclear g-values, μ_B and μ_N are Bohr and nuclear magneton, respectively, h is the Planck constant, and r is the e–n distance.

The use of ¹⁹F for such measurements offers high sensitivity due to its high gyromagnetic ratio, approaching that of ¹H, as well as excellent selectivity since ¹⁹F is absent in all biomolecules, unlike the widely abundant ¹H.¹⁹ An additional advantage of spin label – ¹⁹F distance measurements is the small size of the fluorine atom, permitting labeling at sites where large spin labels may cause structural changes or in buried areas that are not easily accessible for labeling. Furthermore, introducing fluorine into small molecules, such as drugs, for investigating protein–ligand (protein–drug) interactions²⁰ is less perturbing than adding a larger spin label that may interfere with binding and/or alter binding affinity.

To date, a wide range of spin labels for ¹⁹F ENDOR distance determination have been reported, including nitroxide^19,21–23 and trityl^24,25 spin labels, intrinsic tyrosyl radicals,²⁶ as well as Gd(III)^27–29 and Cu(II)³⁰ chelates. In the case of Gd(III), in-cell measurements have also been demonstrated.²⁸ All these spin labels exhibit different chemical, spectroscopic and relaxation properties, and their advantages and disadvantages must be considered for each system. For proteins, the structure, size, length, and flexibility of the tether, chemical and environmental stability and compatibility, need to be considered. In addition, spin relaxation characteristics and the width of the EPR spectrum are also important. For ¹⁹F ENDOR, several additional points need to be assessed: (i) distance range and resolution for each specific label; (ii) sensitivity of ENDOR measurements; (iii) availability of suitable EPR instrumentation; (iv) prediction of possible distance distributions for assessing possible models based on ENDOR data. With regard to the latter, our recent Gd(III)–¹⁹F study demonstrated that distances obtained for two labeling sites in the model protein GB1 could be predicted accurately, while this was not the case for two labeling sites in ubiquitin.²⁸ This discrepancy raised a question whether a structural change induced by the Gd(III) tag or limitations in the predicted distance distributions based on crystal structures and rotamer libraries of the spin label were the cause.^31–33 We, therefore, decided to systematically compare several different spin labels in ¹⁹F ENDOR measurements, focusing mainly on the ¹⁹F ENDOR spectral resolution and the prediction of distances. In addition, we also obtained several conclusions regarding sensitivity at W-band.

Two proteins, the B1 domain of protein G (GB1) and ubiquitin (Ub) were used, each possessing a single ¹⁹F-labeled amino acid. The fluorinated residues were 5F-tryptophan (5F-Trp) for GB1 and p-trifluoromethyl phenylalanine (tFmPhe) for Ub. Using the trifluoromethyl group (in the latter case) increases the ENDOR efficiency since it scales with the number of ¹⁹F nuclei. However, distinctly different hyperfine splittings for each of the three fluorine atoms may complicate the data analysis for electron–nuclear distances shorter than ∼10 Å, as shown earlier.²⁷

The four protein variants were labeled with each of the three commonly used spin labels: nitroxide, trityl, and the Gd(III)-BrPSPyDO3A chelate³⁴ (further referred to as Gd-DO3A). All spin labels were attached to the same sites in each protein (Fig. 1). The use of two different spin labeling positions per protein and two different ¹⁹F labeled residues broadens the scope of variants and distances for which ENDOR data can be interrogated and compared, providing more general conclusions regarding sensitivity and resolution and allowing for future rational design and engineering of samples for optimal electron–nuclear distance measurements. Two distinct trityl labels, CT02MA³⁵ and OXMA, which differ in their phase memory time, were employed. In a newly synthesized spin label OXMA, the methyl groups of CT02MA are replaced with hydroxyethylene groups. MTSSL (methanethiosulfonate spin label)³⁶ was used as a nitroxide spin label, except for GB1 Q32C, which was labeled with 5-MSL (3-maleimido proxyl)³⁷ because of the higher labeling efficiency. Additionally, a double histidine variant of GB1 was labeled with Cu(II), capped with nitrilotriacetic acid (Cu–NTA),³⁸ to include Cu–¹⁹F ENDOR in the comparison. To our knowledge, this is the first attempt to use a Cu(II) spin label for ¹⁹F ENDOR distance determination in proteins, as prior applications dealt with DNA.³⁰ Nitroxide^19,23,39 and trityl²⁵ spin labels have also been mostly applied to nucleic acids, with one application to a protein.²⁴

Fig. 1 (A) Backbone structures in ribbon representation of ubiquitin (pdb id: 1UBQ⁴⁰) and GB1 (pdb id: 1GB1,⁴¹ model 3). The introduced cysteines and fluorine-containing side chains are shown in stick representation with the sulfur atoms in yellow and the fluorine atoms in green. Each variant contains one cysteine, but both are shown on the structure for space considerations. (B) Backbone structure in ribbon representation of GB1 (pdb id 1GB1) depicting the Cu–NTA (pink sphere and stick representation for NTA) and 5-fluoro tryptophan (5F in green). (C) Chemical structures of the reagents MTSSL, 5-MSL, BrPyDO3A-Gd(III) (Gd-DO3A), CT02MA, and OXMA after conjugation to cysteine residues. (D) Chemical structures of 5F-tryptophan (5F-Trp) and p-trifluoromethyl phenylalanine (tFmPhe).

Experimental details

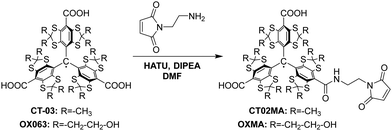
Synthesis of spin labels

Trityl radicals OX063^42,43 and CT-03^44–47 were synthesized according to previously reported procedures. All other reagents used were of commercial grade.

OXMA was synthesized using the somewhat modified method previously reported for other maleimide-conjugated trityl spin labels (Scheme 1).^48,49 In brief, to a solution of OX063 (50 mg, 36.74 μmol, 1 eq.) and N,N-diisopropylethylamine (DIPEA, 25.60 μL, 146.96 μmol, 4 eq.) in dry dimethylformamide (DMF, 5 mL) solution of hexafluorophosphate azabenzotriazole tetramethyl uronium (HATU, 13.27 mg, 34.91 μmol, 0.95 eq.) in DMF (0.5 mL) was added dropwise. The reaction mixture was stirred for 5 min, and then 1-(2-aminoethyl)-1H-pyrrole-2,5-dione (19.47 mg, 110.25 μmmol, 3 eq.) in DMF (0.5 mL) was added. After stirring at room temperature overnight, the reaction mixture was quenched by 3 M HCl to pH 5 and concentrated in vacuo. The crude product was purified by reversed-phase C-18 column chromatography eluted with 20 mM ammonium acetate/MeOH (9 : 1) to afford OXMA as a green solid (21 mg, 38%). HPLC analysis: retention time, 6.7 min; EPR analysis: α_N = 207 mG.

Scheme 1 Synthesis of trityl spin labels CT02M and OXMA.

CT02MA³⁵ was synthesized using the same procedure as for the synthesis of OXMA. CT02MA (60 mg) was obtained as a green solid from CT-03 (100 mg, 99.95 μmol, 1 eq.) in a yield of 54%. HPLC analysis: retention time, 13.7 min; EPR analysis: α_N = 211 mG.

High-resolution mass spectrometry (HRMS) of OXMA is presented in Fig. S1 (ESI†) and HPLC chromatograms and CW EPR spectra for OXMA and CT02MA are presented in Fig. S2 and S3 (ESI†), respectively.

Protein synthesis, spin labeling, and sample preparation

Proteins were prepared as described previously.^28,50 Ubiquitin T66C and M1C possess 4-trifluoromethyl phenylalanine (tFmPhe) at position 45 and GB1 K31C and Q32C contain 5-fluorotryptophan (5F-Trp) at position 43. The MTSSL,⁵¹ 5-MSL,³⁷ CT02MA,³⁵ OXMA (see above), or BrPSPyDO3A-Gd(III) (Gd-DO3A)³⁴ spin labels were attached to single cysteines in both proteins as described previously.²⁸ Cu(II) NTA labeled protein was prepared for the double histidine GB1/K28H/Q32H variant using a published procedure.⁵²

Proteins were dissolved in 25 mM D₂O-based phosphate buffer (pD 7.0), 150 mM NaCl, with 20 vol% glycerol-d₈ added as a cryoprotectant. For EPR measurements, solutions (ca. 3 μL) were placed in fused silica capillaries (inner diameter 0.6 mm) and sealed at one end with crytoseal. The protein concentrations used for ENDOR measurements differed between the samples (Table S4, ESI†), ranging from 8 to 13 μM for the Gd-DO3A labeled proteins, 50 to 120 μM for the nitroxide labeled proteins, 110 to 220 μM for the trityl labeled proteins (except for the OXMA labeled GB1 Q32C at 20 μM), and 420 μM for Cu–NTA labeled GB1 K28H Q32H. For Gd-DO3A labeled proteins, the chosen concentration was optimized for sensitivity, as demonstrated earlier.²⁸ For proteins labeled with nitroxide and trityl spin labels, the chosen concentrations were around 50–200 μM, which are known^53,54 to provide a good signal-to-noise ratio (SNR) and yet not lead to an extensive decrease of the phase memory time in pulsed dipolar EPR measurements. The lower concentration of OXMA labeled GB1 Q32C was due to the difficulties in the sample preparation. A higher concentration of Cu–NTA-labeled protein was used to provide the necessary SNR.

W-band pulsed EPR measurements

Pulsed EPR and ENDOR measurements were performed using two pulsed home-built W-band EPR spectrometers equipped with cylindrical TE₀₁₁ cavities and Helmholtz radiofrequency (RF) coils as described earlier.⁵⁵ The first spectrometer (referred to as 1) has a solenoid superconducting magnet (Cryomagnetics, Inc.), a 3 W pulsed microwave power amplifier (QPP95013530, Quinstar) and a pulsed 2 kW RF amplifier (BT02000-GammaS, TOMCO). The second spectrometer (referred to as 2) has a 0–5 T cryogen-free magnet with an integrated variable temperature unit and 300 mT sweep coil (J3678, Cryogenic Ltd),⁵⁶ is equipped with 2 W pulsed microwave power amplifier (QPP95023330-ZW1, Quinstar) and a 1 kW RF amplifier (3446 Herley-AMT). The frequency band of the signal channels of both spectrometers is approximately 94.7–95.3 GHz, and the bandwidth is limited by a band-pass filter PBS-10/94.9 (ELVA-1, bandwidth 500 MHz) and PIN phase modulator FPM-10-95-180 (Quinstar, bandwidth 300 MHz). Identical sample tubes were used in both spectrometers.

A comparison of the sensitivity of the two spectrometers for the same samples demonstrated that spectrometers 1 and 2 have comparable sensitivity, with the signal-to-noise ratio of the spectrometer (2) being ∼20% higher.

Echo-detected electron paramagnetic resonance (ED-EPR) spectra were recorded using the Hahn echo (π/2–τ–π–τ–echo) sequence. Mims ENDOR spectra were recorded using the sequence π/2–τ–π/2–T(π_RF)–π/2–τ–echo–[τ₂–π–τ₂–echo]_n with a four-step phase cycle⁵⁷ and a Carr–Purcell Meiboom–Gill (CPMG) detection train at the end to enhance the signal-to-noise ratio.⁵⁷ We used five CPMG echoes with τ₂ = 600 ns for detection. Each echo was integrated over a 20 ns window, optimized for the best signal-to-noise ratio. Random sampling of RF was employed,⁵⁸ with 5–10 shots acquired per frequency point in each scan. Microwave power was adjusted to result in a π pulse of 28–40 ns, using the Rabi nutation sequence, t_nut − t_wait–π/2–τ–π–τ–echo (t_nut was varied; t_wait was chosen such as to let for the decay of the transverse magnetization). RF power was adjusted to yield the desired π_RF pulse length, using a Rabi nutation sequence π/2–τ–π/2–T(t_RF)–π/2–τ–echo, with a constant mixing time T of 100 μs and varying RF pulse length, t_RF. The RF pulse length was set to be long enough to avoid significant broadening of the ENDOR spectrum while ensuring acceptable SNR. The mixing time T in the Mims ENDOR experiment was set to be 2 μs longer than the RF pulse length. The used τ values and RF pulse lengths are listed in Table S1 (ESI†).

Mims ENDOR spectra were recorded at different temperatures for different spin labels: 11 K for Gd-DO3A, 5 K for Cu–NTA, and 40 K for nitroxide and trityl radicals (except for Ub T66C MTSSL, measured at 25 K). For nitroxide DEER the optimal temperature was reported to be 40–50 K.⁵⁴ These temperatures were chosen to permit repetition times of approximately 5–15 ms to ensure efficient data acquisition without appreciable saturation. In addition, the shot repetition rate is limited by the spin–lattice relaxation rate. For Gd-DO3A, the temperature has to be high enough (higher than ∼6 K) to avoid significant loss of central transition intensity.

Phase memory times were estimated by recording a Hahn echo decay and fitting it to a stretched exponential function: I(τ) = A·exp[−(2τ/T_M)^β₂].

Spin–lattice relaxation times T₁ were estimated using an inversion recovery sequence, π–t_wait–π/2–τ–π–τ–echo, with varying t_wait. The recorded traces were fitted to a stretched exponential function to estimate T₁: I(t_wait) = I_∞ − (I_∞ − I₀)·exp[−(t_wait/T₁)^β₁], where I₀ and I_∞ are the echo intensities immediately after the inversion pulse, and after complete relaxation, respectively. Note that this approach leads to an underestimation of the spin–lattice relaxation time due to spectral diffusion. The length of the inversion pulse in the inversion recovery experiment was 28–32 ns.

Spectral acquisition parameters and experimental relaxation times are listed in Table S1 (Section S2, ESI†).

Results and discussion

Echo-detected EPR spectra and echo decays

The ¹⁹F-ENDOR sensitivity strongly depends on the spin label's spectral characteristics, its spin–lattice relaxation time, T₁, and phase memory time, T_M. For each of the spin labels used here, examples of the W-band echo-detected EPR (ED-EPR) spectra and the spin-echo decays for the proteins carrying the spin label are shown in Fig. 2. Note that measuring at W-band has the advantage that the ¹⁹F signals are well separated from the ¹H signals. Furthermore, the central transition (|−1/2〉 → |+1/2〉) for Gd(III) is narrow despite the whole spectrum being broad because of the zero-field splitting (ZFS). Here, we only report ENDOR data measured on the central transition. In contrast, W-band is less favorable for Cu(II); Cu–NTA has a very broad spectrum due to the pronounced g-anisotropy, leading to orientation selection. Namely, at each field position where the ENDOR measurements were carried out, only a sub-ensemble of Cu(II) complexes with a particular orientation relative to the direction of the magnetic field contributes to the ENDOR signal. Accordingly, determining a distance requires measurements at several magnetic fields within the EPR spectrum.³⁰ The nitroxide line shape (Fig. 2(A), black line) is also determined by the anisotropic Zeeman and hyperfine interaction and, therefore, can also exhibit orientation selection.¹⁹ Trityl lacks hyperfine interactions and has a very small g-anisotropy, which yields a narrow EPR spectrum also at W-band, thereby enhancing the sensitivity of the ENDOR measurements. The EPR spectra of the two trityl labels, CT02MA and OXMA, were identical (Fig. S4A, ESI†).

Fig. 2 (A) ED-EPR spectra of the proteins functionalized with different spin labels: nitroxide MTSSL (black line, 25 K, Ub T66C, 120 μM), trityl CT02MA (yellow line, 40 K, Ub M1C, 110 μM), Gd-DO3A (blue line, 10 K, Ub T66C, 40 μM) and double-histidine Cu–NTA (green line, 5 K, GB1 K28H Q32H, 420 μM). Arrows in corresponding colors mark the field positions at which the ENDOR spectra were recorded. (B) Spin echo decay traces, measured at maximum EPR intensity, for the spin-labeled proteins at the same temperatures as used for ENDOR spectra recording (see Table S4, ESI†). The dark-blue line in the upper panel in (B) corresponds to Ub M1C labeled with OXMA (40 K, 110 μM) and the black line overlaps with the green one. The corresponding T_M values are listed in Table S1 (ESI†).

To access long distances with Mims ENDOR, long T_M values are needed, and, therefore, deuterated solvents (D₂O/glycerol-d₈, 4 : 1 v/v) were used for all measurements. A comparison of the echo-decay rates (Fig. 2(B) and Table S1, ESI†) shows that Gd-DO3A has the longest T_M, partially due to the lower sample concentrations. The nitroxide spin labels MTSSL and MSL exhibited a somewhat faster echo decay rate than the Gd-DO3A. As expected, the two trityl spin labels have very different phase memory times, two to three times faster for CT02MA than for OXMA.⁵⁹ The enhanced phase memory relaxation in CT02MA is most likely caused by methyl group rotation.⁵⁹ The echo decay for Cu–NTA labeled GB1 is comparable to that of the nitroxide-labeled sample.

¹⁹F-ENDOR spectra

In Fig. 3, the ¹⁹F ENDOR spectra for all proteins with nitroxide, trityl, and Gd-DO3A labels are compared. For nitroxides, the traces shown are the sum of the spectra recorded at four different field positions (a–d, Fig. 2(A)), weighted by the EPR spectrum intensity. The individual spectra are shown in Fig. S5 (ESI†). For the same protein, the ¹⁹F-doublet splittings for the different labels are often different, possibly caused by differences in local structure imparted by the tether between the protein backbone and the radical (cf.Fig. 1(C)), leading to different e–n distances, where the distance deviation from the ¹⁹F–C_α distance is expected to be nitroxide < Gd(III) < trityl. For all samples, except for Ub T66C, the distances follow this expected trend, but for Ub T66C, the trityl yields the shortest distance, possibly caused by an interaction of the label with the protein.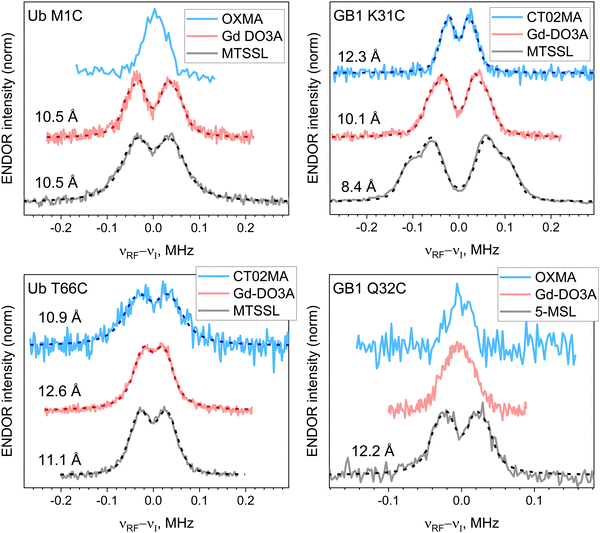

Fig. 3 Experimental (solid lines) and simulated (dashed lines) ¹⁹F ENDOR spectra of protein variants labeled with trityl (CT02MA or OXMA; blue), Gd-DO3A (red) and nitroxide (MTSSL or 5-MSL; black) tags. For nitroxide-labeled proteins, the weighed sum spectra over field positions a–d illustrated in Fig. 2(A) are shown. Electron–nuclear distances are listed next to the spectra; ν_I is the ¹⁹F Larmor frequency. The data for Gd-DO3A were previously reported.²⁸

The ENDOR doublets were resolved only for two out of four samples labeled with trityl radicals. Both of these happen to correspond to CT02MA labels. This is coincidental as it is unlikely that different distances should be found for OXMA and CT02MA labels since these labels only differ by substituents to the scaffold. In fact, essentially identical ENDOR spectra were obtained in the case of Ub M1C labeled with CT02MA and OXMA (see Fig. S4B, ESI†).

The e–n distances (Fig. 3) were extracted using nonlinear least-squares simulations of the spectra, where, for simplicity, the distance distribution was accounted for by varying the linewidth. In most cases, spectra were best reproduced using Lorentzian line shapes, probably due to the distance distribution and the 1/r⁶ dependence of the ENDOR efficiency¹⁸ that increases the intensity of the wings. The spectra were also simulated using Gaussian distance distributions (Fig. S6, ESI†), and all simulation parameters are given in Table S3 (ESI†). The Table (as well as Fig. 5 below) shows that for all cases the single distance, r, is smaller than the center of the Gaussian distribution, r₀ (r₀ > r). We attribute this discrepancy to the 1/r⁶ dependence of the ENDOR efficiency which affects the Gaussian distribution but not the single distance fit. This is consistent with the observation that the discrepancy is larger when the distribution width is large as observed for Ub M1C-MTSSL and Ub T66C (all labels).

Interestingly, Ub T66C exhibits the largest line width for all studied spin labels, consistent with the large Gaussian distance distribution (see Table S3, ESI†) and an earlier report for Gd-DO3A.²⁸ This extra broadening could be due to distinct distances to each of the ¹⁹F in the CF₃ group. However, the distance obtained is larger than 10 Å, and the effect was reported negligible for such a distance.²⁷ Furthermore, if this were the reason, we would expect to see it for Ub M1C.

For nitroxide-labeled GB1 K31C and Ub T66C, orientation selection was present, although in the latter case, it was less pronounced (see Fig. S5, ESI†). The spectra of the two other nitroxide-labeled proteins were essentially the same at all selected field positions (Fig. S5, ESI†). The spectra recorded at four field positions were jointly simulated in all cases. When orientation selection was apparent, this was explicitly included in the simulations using a previously developed method.^19,21 In essence, the echo-detected EPR spectrum was simulated to determine which orientations of the e–n pairs with respect to the magnetic field are excited at a given field position. These orientations were further used to calculate the ENDOR spectra. In the cases where orientation selection was absent, ENDOR spectra, recorded at different field positions, were simulated jointly, using the same hyperfine splitting for all spectra and taking into account all possible orientations. Details of spectral simulations are provided in Section S4 (ESI†). The simulation of individual spectra of nitroxide-labeled proteins is presented in Fig. S5 (ESI†), and the parameters used are listed in Table S2 (ESI†).

Note that in most cases the comparable quality of fit was observed when the spectra are simulated using a single-distance approach or a Gaussian e–n distance distribution. However, this was not the case for MTSSL-labeled GB1 K31C, where the quality of fit was lower and the obtained distribution width was unrealistically narrow.

Fig. 4 shows the ENDOR spectra recorded at the g_‖ (a), g_⊥ (g) and intermediate (b)–(f) field positions (marked in Fig. 2(A)) for GB1 K28H Q32H labeled with Cu–NTA. The spectra demonstrate a weak orientation selection effect, with the largest ENDOR splitting observed at position c. Simulations yielded a distance of 11.7 Å with a Gaussian ENDOR line width of 25.7 kHz and the e–n vector positioned at an angle of 50° to the g_‖ axis of the Cu–NTA. This distance agrees well with DFT calculations for an analogous Zn(II) complex (12.0 Å) and with the metal–fluorine distance obtained for the analogous Co(II) complex (12.9 Å) using ¹H pseudocontact shifts.⁵⁰ Here, the distance cannot be compared with those obtained for the other spin labels because the position of the spin label is not the same, although similar. Nevertheless, a comparison of the distance resolution, as judged by the ¹⁹F linewidth, can be performed (see Table S3, ESI†). No clear improvement in the ¹⁹F ENDOR spectral resolution can be seen.

Fig. 4 Experimental (black lines) and simulated (red lines) ¹⁹F ENDOR spectra of GB1 K28H Q32H labeled with Cu–NTA. The field positions a–g, at which the ENDOR spectra were recorded, are marked in Fig. 2(A). Dashed vertical lines are presented to guide the eye, their placement tentatively corresponds to the observed splitting at the g_‖ and g_⊥ field positions.

In silico predictions of e–n distances

We also tested how well the experimentally determined single distances can be predicted in silico. The calculations were performed using the ChiLife software,⁶⁰ and different approaches were tested, such as free rotation of dihedral angles,^32,61 rotamer library sampling,^62–64 and off-rotamer sampling.³³ The resulting e–n distance distributions obtained using the free rotation of dihedral angles are shown in Fig. 5. Distance distributions obtained with the other approaches were somewhat different (see Fig. S7, ESI†). However, none of these yielded better agreement with the experiment. For Gd(III), the agreement is satisfactory for all constructs except Ub M1C. The disagreement may be due to a structural change introduced by the label at this position.²⁸ A smaller deviation is noted for the nitroxide spin-labeled protein. For the protein constructs, GB1 K31C, GB1 Q32C and Ub T66C, the distance extracted for the nitroxide-labeled variants tends to be at the low end of the distance distribution. Trityl labeled Ub T66C and GB1 K31C yielded resolved spectra; however, the discrepancy between the in silico predicted distances and the experimentally extracted ones is large for both. The large linewidth for Ub M1C nitroxide, Ub T66C trityl and Gd(III) is consistent with the predicted width of the calculated distance distributions.

Fig. 5 Predicted electron–nuclear distance distributions obtained with the ChiLife software⁶⁰ and the free rotation of dihedral angles approach (ChiLife parameter “dihedral_sigma” set to infinity) for GB1 and ubiquitin labeled with trityl (blue), Gd-DO3A (red) and nitroxide (black) tags. Vertical lines correspond to the experimental distances obtained by simulation of ENDOR spectra using a single e–n distance approach, and the Gaussian curves correspond to experimental distance distributions obtained by simulation of ENDOR spectra using Gaussian e–n distance distribution. The experimental Gd–F distance for GB1 Q32C Gd-DO3A is shown as obtained from PRE²⁸ and ENDOR measurement on the satellite transitions of Gd(III).²⁹ The structures used for the modeling are 1GB1 (model 3)⁴¹ for GB1 and 1UBQ⁴⁰ for ubiquitin.

A comparison of the predicted distance distribution with the results of fitting the experimental ENDOR spectra with a Gaussian distance distribution is also shown in Fig. 5. Differences between the predictions and experimental distributions are similar to those discussed above for fitting with single distances, except for some improvement for UbT66C OXMA and Ub M1C MTSSL and a drop in agreement for Ub T66C Gd-DO3A, Ub T66C MTSSL.

Discussion

Here we discuss the ¹⁹F ENDOR results with different spin labels in terms of spectral resolution and sensitivity. We first present general considerations and then examine the relative pros and cons for each label. Generally, the e–n distance can be determined when the corresponding hyperfine splitting (eqn (1)) is resolved, namely, when it is larger than the linewidth. The intrinsic linewidth is determined by the ¹⁹F nuclear spin–spin relaxation, T_2n.⁶⁵ Time-domain ENDOR measurements (to be published separately) indicate that it is of the order of ∼350 μs for Gd(III) complexes and ∼2 ms for nitroxides. This implies that broadening due to this mechanism is very small, compared to the observed linewidths (13–35 kHz). Other broadening contributions include:

(a) ¹⁹F chemical shift anisotropy (CSA);²¹ the CSA for ¹⁹F nucleus is around 50 ppm for 5F-Trp residue^66,67 and around 40 ppm for 3FmPhe residue,⁶⁸ which correspond at W-band to a broadening of 7 and 5 kHz, respectively.

(b) Dipolar interactions with surrounding nuclei, depending on the ¹⁹F closest neighbors. For 5F-Trp the vicinal protons in the aromatic ring are ∼2.6 Å away from the ¹⁹F nuclei, which results in a dipolar interaction of ∼6 kHz. For 3FmPhe, the distance between the geminal ¹⁹F nuclei is 2.1 Å, corresponding to a dipolar interaction of ∼11 kHz.

(c) Broadening due to the finite length of the RF pulse in the Mims ENDOR sequence; the pulse length can be experimentally adjusted to prevent extensive broadening, albeit at the cost of lower SNR. For pulses of t_RF = 25–80 μs, as used here, the expected broadening is ∼1/2t_RF corresponding to 6.25–20 kHz. For Gd-DO3A labeled proteins, it has been previously shown experimentally that the pulse lengths do not contribute appreciably to spectral broadening (ref. 28 and Fig. S3, ESI†).

(d) Flexibility of the spin label, motional freedom of the ¹⁹F labeled amino acid, and backbone conformational variability, resulting in the distribution of e–n distances. Here, as spin labels were attached at the same position in the protein, it can be safely assumed that the label's conformational freedom causes any observed difference in linewidth between the spin labels.

Each stated mechanism adds up to the broadening, and careful examination of each contribution could be used to improve the resolution. The easiest to identify and overcome is mechanism (c), as measurements can be carried out with different RF pulse lengths. For mechanism (b), the broadening can be eliminated by isotopic substituting ¹H nuclei near the ¹⁹F nucleus with ²H.³⁹ The contribution of the CSA to the linewidth is expected to be smaller at a lower magnetic field. As for item (d), this can be minimized by using rigid spin labels.

When the broadening mechanisms (a–c) are known it is possible to obtain reliable distance distributions directly from ¹⁹F ENDOR spectra simulation. In the cases where the distance distributions are expected to be narrow, the simulation using a single distance is a generally applicable tool.

The signal-to-noise ratio (SNR) of Mims ENDOR per square root time depends on several experimental parameters given by:

where V₀ is the echo intensity at τ ∼ 0 and T ∼ 0. It accounts for the absolute EPR spectrum intensity of the spin label, which depends on the spectrum width, field position within the spectrum, the electron spin (sensitivity is higher for high-spin labels), the MW pulses bandwidth, the sample concentration and the spin labeling efficiency, Boltzmann population difference, and instrumental parameters. T₁ and T_M are the spin–lattice relaxation and phase memory times of the spin label, respectively, β₁ and β₂ are the corresponding stretched exponentials; τ and T are inter-pulse delays in the Mims ENDOR sequence (see Experimental details). F_ENDOR is the ENDOR efficiency defined as

F_ENDOR = (I_OFF − I_ON)/I_OFF, (3)

where I_OFF and I_ON are the spin echo intensities, with the RF pulse off- and on-resonance with respect to the nuclear transition. The ENDOR efficiency is roughly proportional to sin²(π·aτ), according to the Mims blind-spot behavior,⁶⁹ where a is hyperfine interaction constant. When a is due to a dipolar interaction, it is proportional to 1/r³ When a·τ ≤ 0.15, which holds for most of the variants studied in the present work, sin(π·aτ) ≈ π·aτ, which results in an approximate ∝1/r⁶ dependence of the ENDOR efficiency¹⁸ and, consequently, of the SNR. The experimentally observed efficiency depends on the details of the RF set-up and the RF pulse bandwidth. The term in eqn (2) accounts for the repetition rate, which has to be slower than ∼1/T₁ to prevent saturation, and SNR increases with the square root of the number of acquired shots. When the repetition rate is limited by the maximum duty cycle of the RF amplifier and not by T₁, as in the case of Gd(III), the efficiency of the data accumulation is reduced.

In Table S4 (ESI†) we present separately the calculated SNR_ENDOR and V₀ to highlight the different contributions to the EPR signal intensity and the specific ENDOR sensitivity, as well as the overall predicted SNR values based on eqn (2). Since the protein samples had varying concentrations and spin labeling efficiencies may also vary, we determined V₀ from a single shot echo intensity (measured with a short τ on the same spectrometer) for solutions of the various spin labels (not the labeled protein) at an identical concentration of 100 μM. The values of V₀ are listed in Table S4 (ESI†). The relative echo intensities obtained for the Gd-DO3A complex exceed those obtained for other labels, which explains the enhanced sensitivity of the measurements for Gd(III). The measurements were carried out at the same temperature as the ENDOR measurements. The estimates of SNR from eqn (2) are compared with the experimental SNRs of the ENDOR spectra, also given in Table S4 (ESI†). It lists the SNR of each ENDOR spectrum and normalized values, taking acquisition time, number of points in the experimental spectrum, and spin-label concentration into account. In the case of Cu(II) and nitroxides, where several spectra were recorded due to orientation selection, the time it takes to record all the needed spectra should also be borne in mind (the SNR values presented in Table S4 (ESI†) correspond to individual ENDOR spectra at each field position). Given the approximate nature of eqn (2), a reasonable correlation (R² = 0.84) between the experimental and the estimated values of SNR is observed (Fig. S8, ESI†).

Additionally, eqn (2) is relevant for optimizing SNR with respect to the delay time τ in the Mims ENDOR sequence. It is known¹⁸ that to determine long distances, long delays τ are necessary since the ENDOR efficiency F_ENDOR grows proportionally to sin²(π·aτ). On the other hand, SNR decreases for longer τ values due to phase memory decay, given by exp(−[2τ/T_M]^β₂) (see eqn (2)). Therefore, the highest SNR is achieved at intermediate values of τ. This is illustrated in Fig. S9 (ESI†) where SNRs of the ¹⁹F ENDOR spectra of GB1 K31C Gd-DO3A recorded with different values of τ are shown, alongside a theoretical estimate according to eqn (2). It can be appreciated that the optimal experimental τ value is somewhat shorter than the predicted theoretical value and that the experimental SNR decreases more abruptly for long τ values. This may be because the T_M values used in the prediction were measured for Hahn echo decays, and the stimulated echo decay may be faster due to spectral diffusion during the mixing period T.⁷⁰

Note that the protein concentration dependence of the ¹⁹F ENDOR signal is expected to be linear at small concentrations. Larger spin concentrations lead to the shortening of the phase memory time T_M by instantaneous and spectral diffusion mechanisms.⁷¹ Because measuring long e–n distances entails using longer τ values, this may lead to a significant decrease in spin echo intensity per unit concentration and, hence, a decrease in sensitivity. Therefore, optimization of the SNR for the protein concentration is necessary, as demonstrated previously.²⁸

Next, we discuss the virtues and limitations of the different spin labels for ¹⁹F ENDOR measurements at the W-band for the following characteristics: the spectral resolution (Fig. 3 and 4), in silico predictability of the experimentally derived distances from available structures (Fig. 5) and the SNR data (Table S4, ESI†).

Nitroxide spin labels

These labels seem to be the most versatile; they yielded resolved ENDOR doublets for all constructs due to the short tether; two nitroxide labeled proteins exhibited orientation selection, which provided additional geometric information. They also resulted in good SNR, although the need to record several spectra along the EPR powder patterns increases the total acquisition time, especially for the spectra recorded at the g_zz position. Regarding predicting distances, nitroxide spin labels were superior to trityl and comparable to Gd-DO3A.

Trityl spin labels

Resolved doublets were observed for two of the four samples. In these cases, the resolution was comparable to the other labels. In principle, the associated high V₀ values are expected to yield the best SNR. However, this is compromised by the shorter phase memory time. The OXMA spin label, which has a longer T_M, resulted in good SNR, higher than that for the nitroxides, but lower than that for Gd-DO3A. Significant differences between the experimental and the predicted e–n distances were observed for trityl spin labels, most likely because interactions between the label and protein side chains come into play. In addition, difficulties in estimating and accounting for the conformational flexibility of the tether have to be considered. Thus, trityl spin labels with shorter linkers may be more attractive, as this will allow accessing longer ¹⁹F–C_α distances.⁷²

Gd-DO3A label

This label proved to be the best regarding sensitivity. It provided the highest signal-to-noise ratio per unit concentration and unit square root time. This is mainly due to the more favorable Boltzmann population difference at low temperatures (10 K) made possible by the short T₁. Therefore, in principle, sensitivity can be further improved by increasing the repetition rate. This is currently limited by the RF amplifier duty cycle, not the T₁. The label also resulted in excellent resolution, although it produced longer distances than the nitroxides, effectively reducing resolution (see GB1 Q32C). However, it has been shown recently that significant improvements can be garnered by accessing other transitions and carrying out measurements below 6 K.²⁹ The predictability of distances for the specific proteins studied in this work is comparable, or even slightly better than nitroxides (the agreement for GB1 K31C and GB1 Q32C is better for Gd-DO3A than nitroxide, the agreement for Ub T66C is comparably decent, and for Ub M1C, the agreement is poor for both labels). Judd et al. also compared the sensitivity of ¹⁹F ENDOR for a nitroxide spin label (MTSSL) and a Gd(III) label (Gd·C1, a Gd(III) complex with a DOTAM-derived ligand) for a GB1 construct.²⁷ They reported a 2.7-fold gain in signal-to-noise ratio for the Gd(III) over the nitroxide label for the same concentration, even though the Gd–F distance was longer (∼10 Å for Gd vs. ∼8 Å for nitroxide).

Cu(II)–NTA label

We expected better resolution for this label since it is a rigid moiety. However, the resolution was similar to the other labels. One possible reason for this may be the power broadening due to the RF pulse lengths used. The influence of that could not be checked because of the poor SNR at the W-band. Further studies are needed to clarify whether it is a general phenomenon or specific to the system studied. As in the case of nitroxides, additional geometric information can be extracted from the orientation selection behavior of the spectra. Unfortunately, poor SNR is seen at the W-band due to the broad EPR spectrum.

At this juncture, it is worth pointing out that all measurements were carried out at W-band, where the ¹⁹F signals are well separated from the ¹H signals, and orientation selection is more pronounced, especially for nitroxide radicals. At the Q-band, the sensitivity of an individual ENDOR spectrum is expected to be higher for S = 1/2 systems with g-anisotropy, as the apparent spectral width grows proportionally with the microwave frequency. However, at Q-band ¹⁹F and ¹H ENDOR spectra overlap. To overcome this, either ¹H ENDOR spectra need to be recorded separately from samples without the ¹⁹F label and subtracted³⁰ or deuterated spin labels can be used,³⁹ however these may not be readily available. For high-spin labels, such as Gd(III) or Mn(II), for which the width of the |–1/2〉 → |+1/2〉 EPR transition decreases linearly with the inverse microwave frequency, high-field measurements are advantageous.

Finally, predicting distance distribution based on available atomic structures is not always satisfactory, and significant discrepancies were observed for all spin-labeled Ub M1C variants. This suggests that the N-terminus is not a desirable position for spin labeling for this particular protein. For other proteins, the in silico predicted distances demonstrated decent agreement with the experimental distances, obtained either from a single distance or Gaussian distance distribution fit of the experimental ENDOR spectra (except for trityl labeled GB1 K31C). In the case of Gd(III), a good agreement was reported earlier between the ENDOR-derived distances and those reported by PRE measurements.²⁸ Therefore, we attribute the discrepancies to the limitations of the methods used for predicting the distance distribution to an accuracy below 2 Å.

Conclusions

We presented a comparative W-band ¹⁹F ENDOR study for three different types of spin labels, namely, nitroxides, trityls, and Gd(III). These tags were attached at two different sites in two proteins with a single ¹⁹F labeled amino acid. For one of the proteins, ¹⁹F ENDOR spectra were also recorded for a Cu(II)–NTA label situated close to the positions of the other spin labels. In all cases, the ¹⁹F ENDOR signals were well separated from the ¹H signals. For resolved ENDOR spectra, all labels resulted in comparable line widths and, hence, a comparable range of accessible distances. However, those with longer tethers, e.g., CT02MA and OXMA, that produce more significant deviations of the measured e–n distances from the ¹⁹F–C distances are less effective regarding the structural information they can provide. They did not provide resolved ¹⁹F doublets in half of the cases, while those with the shorter tethers did. For sensitivity, Gd(III) performed best at the W-band, and nitroxides and Cu(II) provided additional structural information, namely, the e–n vector orientation derived from orientation selection measurements. Our data suggest that it is necessary to push the accuracy of spin labels rotamer prediction to calculate distance distributions based on available atomic structures. For the unusual case of Ub M1C, all spin label-derived distances consistently deviated from the predicted distance, indicating that the label at position 1 in the amino acid sequence results in an altered protein structure induced by the attachment of the tag.

Data availability

Programs used for spectral simulations along with the data and simulation results for this manuscript can be accessed at https://sourceforge.net/projects/mimsgd/.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was funded by the National Science Foundation USA-Israel Science Foundation program through BSF 2021617 (to DG), and NSF-MCB 2116534 (to AMG), NSF grant CHE 1708773 (to AMG), the NSFC-ISF China-Israel 3559/21 Research Grant Program (to DG) as well as the National Natural Science Foundation of China 22174099 and 21871210 to (to YPL) and made possible, in part, by support from the Helen and Martin Kimmel Institute for Magnetic Resonance Research and the historic generosity of the Harold Perlman Family (DG). We are indebted to Dr Maxx Tessmer and Prof. Stefan Stoll for discussions and help with ChiLife software.

References

1. I. García-Rubio, Arch. Biochem. Biophys., 2020, 684, 108323.
2. K. Möbius and A. Savitsky, Appl. Magn. Reson., 2023, 54, 207–287.
3. A. Bogdanov and D. Goldfarb, in Integrated Structural Biology, ed. T. Polenova and A. Gronenborn, Royal Society of Chemistry, 2023, pp. 77–130.
4. D. Abdullin and O. Schiemann, ChemPlusChem, 2020, 85, 353–372.
5. L. Galazzo, M. Teucher and E. Bordignon, Methods Enzymol., 2022, 666, 79–119.
6. P. P. Borbat, E. R. Georgieva and J. H. Freed, J. Phys. Chem. Lett., 2013, 4, 170–175.
7. P. E. Spindler, I. Waclawska, B. Endeward, J. Plackmeyer, C. Ziegler and T. F. Prisner, J. Phys. Chem. Lett., 2015, 6, 4331–4335.
8. T. Schmidt, M. A. Wälti, J. L. Barber, E. J. Hustedt and G. M. Clore, Long Distance Measurements up to 160 Å in the GroEL Tetradecamer Using Q-Band DEER EPR Spectroscopy, Angew. Chem., Int. Ed., 2016, 55, 15905–15909,  DOI:10.1002/anie.201609617.
9. R. Ward, A. Bowman, E. Sozudogru, H. El-Mkami, T. Owen-Hughes and D. G. Norman, J. Magn. Reson., 2010, 207, 164–167.
10. L. Liu, D. J. Mayo, I. D. Sahu, A. Zhou, R. Zhang, R. M. McCarrick and G. A. Lorigan, in Methods in Enzymology, ed. P. Z. Qin and K. Warncke, Academic Press, 2015, vol. 564, pp. 289–313.
11. N. Cox, A. Nalepa, W. Lubitz and A. Savitsky, J. Magn. Reson., 2017, 280, 63–78.
12. F. Hecker, J. Stubbe and M. Bennati, J. Am. Chem. Soc., 2021, 143, 7237–7241.
13. M. Horitani, A. R. Offenbacher, C. A. M. Carr, T. Yu, V. Hoeke, G. E. Cutsail, III, S. Hammes-Schiffer, J. P. Klinman and B. M. Hoffman, J. Am. Chem. Soc., 2017, 139, 1984–1997.
14. B. M. Hoffman, Acc. Chem. Res., 2003, 36, 522–529.
15. L. C. Seefeldt, Z.-Y. Yang, D. A. Lukoyanov, D. F. Harris, D. R. Dean, S. Raugei and B. M. Hoffman, Chem. Rev., 2020, 120, 5082–5106.
16. C. de Lichtenberg, L. Rapatskiy, M. Reus, E. Heyno, A. Schnegg, M. M. Nowaczyk, W. Lubitz, J. Messinger and N. Cox, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2319374121.
17. A. Schnegg, A. A. Dubinskii, M. R. Fuchs, Y. A. Grishin, E. P. Kirilina, W. Lubitz, M. Plato, A. Savitsky and K. Möbius, Appl. Magn. Reson., 2007, 31, 59–98.
18. P.-P. Zänker, G. Jeschke and D. Goldfarb, J. Chem. Phys., 2005, 122, 024515.
19. A. Meyer, S. Dechert, S. Dey, C. Höbartner and M. Bennati, Angew. Chem., Int. Ed., 2020, 59, 373–379.
20. F. J. Tucci, R. J. Jodts, B. M. Hoffman and A. C. Rosenzweig, Nat. Catal., 2023, 6, 1194–1204.
21. A. Kehl, M. Hiller, F. Hecker, I. Tkach, S. Dechert, M. Bennati and A. Meyer, J. Magn. Reson., 2021, 333, 107091.
22. H. Wiechers, A. Kehl, M. Hiller, B. Eltzner, S. F. Huckemann, A. Meyer, I. Tkach, M. Bennati and Y. Pokern, J. Magn. Reson., 2023, 353, 107491.
23. M. Gauger, M. Heinz, A.-L. J. Halbritter, L. S. Stelzl, N. Erlenbach, G. Hummer, S. T. Sigurdsson and T. F. Prisner, Angew. Chem., Int. Ed., 2024, e202402498.
24. N. B. Asanbaeva, A. A. Sukhanov, A. A. Diveikina, O. Y. Rogozhnikova, D. V. Trukhin, V. M. Tormyshev, A. S. Chubarov, A. G. Maryasov, A. M. Genaev, A. V. Shernyukov, G. E. Salnikov, A. A. Lomzov, D. V. Pyshnyi and E. G. Bagryanskaya, Phys. Chem. Chem. Phys., 2022, 24, 5982–6001.
25. N. B. Asanbaeva, D. S. Novopashina, O. Y. Rogozhnikova, V. M. Tormyshev, A. Kehl, A. A. Sukhanov, A. V. Shernyukov, A. M. Genaev, A. A. Lomzov, M. Bennati, A. Meyer and E. G. Bagryanskaya, Phys. Chem. Chem. Phys., 2023, 25, 23454–23466.
26. A. Meyer, A. Kehl, C. Cui, F. A. K. Reichardt, F. Hecker, L.-M. Funk, M. K. Ghosh, K.-T. Pan, H. Urlaub, K. Tittmann, J. Stubbe and M. Bennati, J. Am. Chem. Soc., 2022, 144, 11270–11282.
27. M. Judd, E. H. Abdelkader, M. Qi, J. R. Harmer, T. Huber, A. Godt, A. Savitsky, G. Otting and N. Cox, Phys. Chem. Chem. Phys., 2022, 24, 25214–25226.
28. M. Seal, W. Zhu, A. Dalaloyan, A. Feintuch, A. Bogdanov, V. Frydman, X.-C. Su, A. M. Gronenborn and D. Goldfarb, Angew. Chem., Int. Ed., 2023, 62, e202218780.
29. A. Bogdanov, V. Frydman, M. Seal, L. Rapatskiy, A. Schnegg, W. Zhu, M. Iron, A. M. Gronenborn and D. Goldfarb, J. Am. Chem. Soc., 2024, 146, 6157–6167.
30. S. L. Schumann, S. Kotnig, Y. Kutin, M. Drosou, L. Stratmann, Y. Streltsova, A. Schnegg, D. Pantazis, G. Clever and M. Kasanmascheff, Chem. – Eur. J., 2023, e202302527.
31. D. Klose, J. P. Klare, D. Grohmann, C. W. Kay, F. Werner and H. J. Steinhoff, PLoS One, 2012, 7, e39492.
32. G. Hagelueken, R. Ward, J. H. Naismith and O. Schiemann, Appl. Magn. Reson., 2012, 42, 377–391.
33. M. H. Tessmer, E. R. Canarie and S. Stoll, Biophys. J., 2022, 121, 3508–3519.
34. Y. Yang, F. Yang, Y.-J. Gong, T. Bahrenberg, A. Feintuch, X.-C. Su and D. Goldfarb, J. Phys. Chem. Lett., 2018, 9, 6119–6123.
35. A. Giannoulis, Y. Yang, Y. J. Gong, X. Tan, A. Feintuch, R. Carmieli, T. Bahrenberg, Y. Liu, X. C. Su and D. Goldfarb, Phys. Chem. Chem. Phys., 2019, 21, 10217–10227.
36. W. L. Hubbell, H. S. McHaourab, C. Altenbach and M. A. Lietzow, Structure, 1996, 4, 779–783.
37. O. H. Griffith and H. M. McConnell, Proc. Natl. Acad. Sci. U. S. A., 1966, 55, 8–11.
38. S. Ghosh, M. J. Lawless, G. S. Rule and S. Saxena, J. Magn. Reson., 2018, 286, 163–171.
39. L. Remmel, A. Meyer, K. Ackermann, G. Hagelueken, M. Bennati and B. E. Bode, Angew. Chem., Int. Ed., 2024, e202411241.
40. S. Vijay-Kumar, C. E. Bugg and W. J. Cook, J. Mol. Biol., 1987, 194, 531–544.
41. A. M. Gronenborn, D. R. Filpula, N. Z. Essig, A. Achari, M. Whitlow, P. T. Wingfield and G. M. Clore, Science, 1991, 253, 657–661.
42. M. Poncelet, T. Ngendahimana, T. D. Gluth, E. H. Hoblitzell, T. D. Eubank, G. R. Eaton, S. S. Eaton and B. Driesschaert, Analyst, 2022, 147, 5643–5648.
43. M. Poncelet, J. L. Huffman, V. V. Khramtsov, I. Dhimitruka and B. Driesschaert, RSC Adv., 2019, 9, 35073–35076.
44. T. J. Reddy, T. Iwama, H. J. Halpern and V. H. Rawal, J. Org. Chem., 2002, 67, 4635–4639.
45. I. Dhimitruka, M. Velayutham, A. A. Bobko, V. V. Khramtsov, F. A. Villamena, C. M. Hadad and J. L. Zweier, Bioorg. Med. Chem. Lett., 2007, 17, 6801–6805.
46. H. Hintz, A. Vanas, D. Klose, G. Jeschke and A. Godt, J. Org. Chem., 2019, 84, 3304–3320.
47. O. Y. Rogozhnikova, V. G. Vasiliev, T. I. Troitskaya, D. V. Trukhin, T. V. Mikhalina, H. J. Halpern and V. M. Tormyshev, Eur. J. Org. Chem., 2013, 3347–3355.
48. Z. Hasanbasri, K. Singewald, T. D. Gluth, B. Driesschaert and S. Saxena, J. Phys. Chem. B, 2021, 125, 5265–5274.
49. Z. Hasanbasri, M. Poncelet, H. Hunter, B. Driesschaert and S. Saxena, J. Magn. Reson., 2023, 347, 107363.
50. W. Zhu, D. T. Yang and A. M. Gronenborn, J. Am. Chem. Soc., 2023, 145, 4564–4569.
51. L. J. Berliner, J. Grunwald, H. O. Hankovszky and K. Hideg, Anal. Biochem., 1982, 119, 450–455.
52. K. Singewald, J. A. Wilkinson and S. Saxena, Bio-Protoc., 2021, 11, e4258.
53. O. Schiemann, C. A. Heubach, D. Abdullin, K. Ackermann, M. Azarkh, E. G. Bagryanskaya, M. Drescher, B. Endeward, J. H. Freed, L. Galazzo, D. Goldfarb, T. Hett, L. Esteban Hofer, L. Fábregas Ibáñez, E. J. Hustedt, S. Kucher, I. Kuprov, J. E. Lovett, A. Meyer, S. Ruthstein, S. Saxena, S. Stoll, C. R. Timmel, M. Di Valentin, H. S. McHaourab, T. F. Prisner, B. E. Bode, E. Bordignon, M. Bennati and G. Jeschke, J. Am. Chem. Soc., 2021, 143, 17875–17890.
54. G. Jeschke and Y. Polyhach, Phys. Chem. Chem. Phys., 2007, 9, 1895–1910.
55. I. Gromov, V. Krymov, P. Manikandan, D. Arieli and D. Goldfarb, J. Magn. Reson., 1999, 139, 8–17.
56. A. Feintuch, D. Shimon, Y. Hovav, D. Banerjee, I. Kaminker, Y. Lipkin, K. Zibzener, B. Epel, S. Vega and D. Goldfarb, J. Magn. Reson., 2011, 209, 136–141.
57. F. Mentink-Vigier, A. Collauto, A. Feintuch, I. Kaminker, V. Tarle and D. Goldfarb, J. Magn. Reson., 2013, 236, 117–125.
58. B. Epel, D. Arieli, D. Baute and D. Goldfarb, J. Magn. Reson., 2003, 164, 78–83.
59. A. N. A. Zecevic, G. R. Eaton, S. S. Eaton and M. Lindgren, Mol. Phys., 1998, 95, 1255–1263.
60. M. H. Tessmer and S. Stoll, PLoS Comput. Biol., 2023, 19, e1010834.
61. E. J. Hustedt, R. A. Stein, L. Sethaphong, S. Brandon, Z. Zhou and S. C. DeSensi, Biophys. J., 2006, 90, 340–356.
62. M. R. Fleissner, D. Cascio and W. L. Hubbell, Protein Sci., 2009, 18, 893–908.
63. C. Beier and H.-J. Steinhoff, Biophys. J., 2006, 91, 2647–2664.
64. Y. Polyhach, E. Bordignon and G. Jeschke, Phys. Chem. Chem. Phys., 2011, 13, 2356–2366.
65. A. E. Stillman and R. N. Schwartz, Mol. Phys., 1978, 35, 301–313.
66. M. Lu, S. Sarkar, M. Wang, J. Kraus, M. Fritz, C. M. Quinn, S. Bai, S. T. Holmes, C. Dybowski, G. P. A. Yap, J. Struppe, I. V. Sergeyev, W. Maas, A. M. Gronenborn and T. Polenova, J. Phys. Chem. B, 2018, 122, 6148–6155.
67. U. H. N. Dürr, S. L. Grage, R. Witter and A. S. Ulrich, J. Magn. Reson., 2008, 191, 7–15.
68. S. L. Grage, U. H. N. Dürr, S. Afonin, P. K. Mikhailiuk, I. V. Komarov and A. S. Ulrich, J. Magn. Reson., 2008, 191, 16–23.
69. C. Gemperle and A. Schweiger, Chem. Rev., 1991, 91, 1481–1505.
70. W. B. Mims, Phys. Rev., 1968, 168, 370–389.
71. K. M. Salikhov, S. A. Dzuba and A. M. Raitsimring, J. Magn. Reson., 1981, 42, 255–276.
72. N. Fleck, C. Heubach, T. Hett, S. Spicher, S. Grimme and O. Schiemann, Chem. – Eur. J., 2021, 27, 5292–5297.

---

Footnote

† Electronic supplementary information (ESI) available: Additional details on experiments and simulations, spin relaxation properties of the labels, individual ENDOR spectra of nitroxides at different magnetic fields, results of in silico calculations of distance distributions with different computational approaches, and signal-to-noise ratios of the recorded spectra are provided. See DOI: https://doi.org/10.1039/d4cp02996h

---