Theoretical investigation of Cu₅/silicates deposited on rutile TiO₂ as a photocatalyst

Abstract

Titanium dioxide (TiO₂) is an exceptional compound with unique optical properties, which have been intensively used for applications in photocatalysis. Recent studies show that Cu₅ atomic quantum clusters (AQCs) could facilitate visible light absorption and enhance the photocatalytic properties of rutile TiO₂ by creating mid-gap states. In this work, to move the theory of these catalysts closer to the experiment, we investigate the electronic structures of Cu₅ adsorbed on a perfect and reduced rutile TiO₂ surface in the absence and presence of silicate SiO₃²⁻ ions, which are introduced for the purification of Cu₅ AQCs. Encouragingly, our DFT simulations predict that the presence of SiO₃²⁻ does not reduce the gap states of the Cu₅@TiO₂ composite and could even enhance them by shifting more states into the band gap. Our results also demonstrate that the polarons created by oxygen vacancies (O_v) and Cu₅ coexist within the band gap of TiO₂. Indeed an O_v behaves like a negative gate on the electronic states located on the AQCs, thereby shifting states out of the valence band into the band gap, which could lead to enhanced photocatalytic performance.

---

1. Introduction

The continuous use of non-renewable fossil fuels to fulfil energy demands has released a huge amount of carbon dioxide into the atmosphere resulting in increased global warming and air pollution.¹ To address this issue, the production of hydrogen gas (H₂) is necessary as it is sustainable, energy-dense, and eco-friendly.² Hydrogen is used in various fields such as gas welding, petroleum refinery, electricity production, automobile, rocket fuel,³ and transportation fuel.⁴ Therefore, it is important to find a cost-effective method of hydrogen manufacture. Current state-of-the-art technologies using water electrolysis to produce pure H₂ have low overall conversion efficiencies (below 20%) because they first require conversion from other forms of energy to electricity.⁵ Hence, photocatalytic water splitting to produce hydrogen from water is particularly attractive due to the abundance, availability, and low cost of the water feedstock for a renewable energy source.

Titanium dioxide (titania; TiO₂) is an exceptional compound with unique optical properties that facilitate photocatalytic activity.⁶ It has been intensively utilized in photocatalysis as it is highly stable, non-toxic, eco-friendly, and not costly.⁷ However, TiO₂ has a low photoreaction efficiency partially due to its large intrinsic band gap,⁸ which limits its ability to absorb light, especially in the visible region. Additionally, it exhibits a high rate of charge recombination between photogenerated holes in the valence band (VB) and photogenerated electrons in the conduction band (CB).⁹ Many strategies have been developed to modify TiO₂ so that its bandgap is reduced and conductivity is increased. For instance, the bandgap of TiO₂ is reduced if titanium or oxygen atoms in TiO₂ lattice are replaced with metal and non-metal dopants.¹⁰ Another method to promote the photocatalysis of TiO₂ is by combining TiO₂ and advanced materials such as carbon-based materials, transition metal dichalcogenides, metal oxides, metal clusters, and metal–organic frameworks,¹¹ which could facilitate charge separation and diffusion of light-induced electrons and holes. In addition, charge separation and catalytic properties are dependent on the size and shape of adsorbed metal particles. For ground-state reactions, the increased catalytic activity is due to the formation of new active sites at the interfaces between metal particles and the surface or in the support overlayer.¹²

Metal clusters such as Cu₅ possess a sub-nanometre size and molecule-like electronic structures. They do not sustain their metallicity, lack plasmonic behavior, and have a HOMO–LUMO energy gap like a molecule, which enhances their chemical and physical properties for innovative applications.^13,14 Cu₅ clusters have a low reactivity to oxygen dissociation, making them resistant to oxidation. As a result, Cu₅ clusters are particularly interesting candidates for catalytic applications compared to larger systems such as Cu₈ or Cu₂₀.^15,16 When these copper clusters are deposited on the surface of TiO₂, they can shift the adsorption from the high energy range of the solar spectrum (UV spectrum) to the visible range (corresponding to the highest intensity region of the spectrum of sunlight). Therefore, much more energy can be harvested from sunlight, and the coated TiO₂ can store this energy in the form of charge pairs, electrons, and holes for later use.^17,18 Kinetic control through electrochemical methods is used to synthesize Cu₅ clusters exhibiting outstanding chemical and thermodynamical stability in solution throughout the pH range.¹⁹ Nevertheless, the AQCs need to be purified and separated from several contaminants such as Cu²⁺ ions, nitrates, and isopropyl alcohol (IPA). In order to obtain the catalysts with high photocatalytic performance and achieve scaling up, it is urgent and challenging to improve the purity of Cu₅ clusters, especially by removing the Cu²⁺ ions which could poison the catalysts. Silicates can be expected to be used as precipitants to extract those Cu₅ clusters and the possibly contaminants such as Cu²⁺ ions as well, where those inorganic groups are predicted to bind to the copper clusters, but not be reduced by them.^20–24 Due to the presence of silicates, AQCs could be lyophilized and redispersed in pure water, with no loss. This can then be followed by a series of complicated purification processes to remove other contaminants, but the presence of AQC/silicate composites is inevitable. For this reason, it is of interest to examine the properties of such composites when adsorbed onto the surface of titania, to determine if their catalytic properties are hindered or not.

Therefore, in this paper, we explored the interaction between Cu₅ AQCs and silicates and the effect of silicates binding to Cu₅ AQCs on the structural and electronic properties. More specifically, the adsorption properties of Cu₅/silicate on the perfect and reduced TiO₂ are investigated to obtain an in-depth understanding of their electronic properties. Importantly, it is found that the presence of silicates does not hinder the emergence of mid-gap states including the polaronic states, and even increases the number of gap states by behaving like a negative gate on the AQC, which shifts states into the gap from the TiO₂ valence band. In addition, the polaron states due to oxygen vacancies, which coexist with those originating from Cu₅, are not impacted by the presence of silicates.

2. Computational methods

By using the method of periodic boundary condition in Vienna Ab initio Simulation Package (VASP),^25–27 the electronic properties, as well as the geometrical properties, are determined for rutile TiO₂ and Cu₅@TiO₂ in the absence and presence of silicates and oxygen vacancies. Interactions between valence electrons and the ion core of copper, oxygen, silicon, and titanium are described through the projector augmented wave (PAW method) method^28,29 using the spin-polarized density functional theory approach. Specifically, potpaw.54 PBE potentials are adopted in the link. https://www.vasp.at/wiki/index.php/Available_pseudopotentials. The 3d¹⁰ 4s¹ orbitals of Cu, 2s² 2p⁴ of O, 3s² 3p² of Si, 3s¹ of Na, and 3s² 3p⁶ 4s² 3d² of Ti are referred to as valence electrons. The generalized gradient approximation (GGA) functional alone is unsuitable for electronic structure calculations, as it introduces more than a 50 percent error in the bandgap calculation for some materials.³⁰ Since such inaccuracies render it much more challenging to locate the conduction and valence bands, we introduce some corrections to bring the value closer to the experimental one.³⁰ Here the electronic exchange–correlation effect was described by a GGA with Perdew–Burke–Ernzerhof (PBE) functional along with the correction term, the Hubbard U, as GGA in its original form cannot predict the polaronic states, i.e., the SOMO that arises in Ti³⁺ of TiO₂ and that of Ce³⁺ in CeO₂.^31,32 In accordance with the literature, the value of U for titanium and copper is taken as 4.2 eV and 5.2 eV, respectively.¹⁷ Using the basis set of plane wave types, with a cut-off energy of 500 eV, the wavefunctions of Kohn–Sham were further extended. As for the calculations with TiO₂ substrates, the Brillouin zone is sampled at the Γ point due to the large unit cell (13.12 Å × 12.04 Å) in the two directions with periodic boundary conditions (x and y directions). The DFT-D3 technique of Grimme along with Becke–Jonson damping function³³ is adopted to describe properly the van der Waals interactions which could result in precise binding or adsorption energies along with the geometrical optimizations.¹³ Assuming similar corrections for entropy and enthalphy in the various adsorption scenarios, electronic energies should suffice for an energetic comparison also at temperatures larger than 0 K. Therefore, the electronic energy without thermal corrections is adopted for the whole work.

The hybrid functional HSE06³⁴ is also reported to yield correct electronic structures including the polaronic states and band gaps.^35–37 This is used here in the DOS calculation based on the geometries relaxed by the DFT+U approach mentioned above. In principle, the hybrid functional HSE06 shall be used for the geometrical optimization and continuously for the electronic structure calculations. However, HSE06 is really time-consuming. An alternative way is to carry out the geometrical relaxation by using DFT+U which is well demonstrated by literatures to be capable to describe the localized d orbitals and further to predict the polarons and accurate band gaps compared to experimental data.^18,38

The Bader analysis³⁹ for studying the distribution of atomic charge is adopted based on the calculations through spin-polarized hybrid functional HSE06.^13,34,39,40 As for some nanoclusters such as Au₂₅, nanodiamonds, different competitive approaches^41–46 are adopted to investigate quasiparticle and optical properties in quantum confined systems.”

The rutile TiO₂(110) surface containing 64 Ti atoms and 128 oxygen atoms is modelled by 12.04 Å × 13.12 Å unit cells in four O–Ti–O trilayers periodic slab. To ensure that the supercell itself and the periodic images in the z-direction will not interact, a 20 Å vacuum is employed in the z-direction. The active sites on the rutile TiO₂(110) surface, are under-coordinated atoms, containing two-fold coordinated oxygen atoms (O_2c) at bridge sites and five-fold coordinated titanium atoms (Ti_5c), whereas the inactive saturated atoms are three-fold coordinated oxygen atoms (O_3c) and x-fold coordinated titanium atoms (Ti_6c) shown in Fig. S1 (ESI†). VESTA software⁴⁷ is used to build and visualize all of the structures shown.

3. Results and discussion

3.1 The adsorption of SiO₃²⁻ on Cu₅

First, as a benchmark calculation, we investigated the gas-phase stability of Cu₅ AQCs. Fig. 1a and c illustrate the geometries of Cu₅ AQCs. These simulations reveal that the 2-dimensional (2d) planar configuration in Fig. 1c is more energetically preferable by 0.26 eV than the 3-dimensional (3d) bipyramidal configuration shown in Fig. 1a in the gas phase. As seen in Fig. 1, the bipyramidal Cu₅ cluster lacks precise D_3h symmetry and consists of a trigonal ring (equatorial Cu atoms) with capping atoms (axial Cu atoms) above and below the ring. Those results are consistent with our previous publication.¹³ Next, the effect of a silicate ion SiO₃²⁻ on structural and electronic properties is investigated, because silicates are introduced as a by-product during the Cu₅ purification process. In order to simulate the silicate ion SiO₃²⁻ using DFT, we examined a neutral system consisting of two sodium Na⁺ ions adsorbed on one silicate ion SiO₃²⁻. From Bader charge analysis, it is found that two Na atoms donate 2 electrons to silicon oxide moiety and SiO₃²⁻ is formed, which indicates that the correct silicate model with 2− a valence charge is adopted. The model for a neutral system with a Cu atom as the cation fails to give a divalent silicate ion, and was therefore abandoned (see more details in Fig. S2 of ESI†). More importantly, the sodium atoms make no contributions to the gap states, which further demonstrates the neutral system Na₂SiO₃ is an appropriate model molecule for understanding the effect of silicate ions.

Fig. 1 Configurations and net charges of pyramidal Cu₅ (a) and pyramidal Cu₅/SiO₃²⁻ (b), trapezoidal Cu₅ (c) and trapezoidal Cu₅/SiO₃²⁻ (d). The green number displays the net (excess) charges on each atom and the black number orders each atom. The blue balls represent Cu atoms, the red ones are for O atoms, the yellow for Na atoms, and the green for Si atoms.

To gain a better understanding of the impact of silicate, we first studied the adsorption of SiO₃²⁻ on the gas phase Cu₅ AQCs as shown in Fig. 1b and d which are the most stable pyramidal and trapezoidal Cu₅/SiO₃²⁻. Silicate ions were brought to different positions around Cu₅ respectively and geometrical optimization was performed. The metastable configurations were shown in Fig. S4 of ESI.† It is found that the SiO₃²⁻ binds more strongly to a Cu₅ AQC than oxygen (see Fig. S3, ESI†) for both pyramidal and trapezoidal shapes with a large adsorption energy E_a = −2.92 eV (pyramidal) and E_a = −2.45 eV (trapezoidal) respectively, while for O₂, E_a = −2.1 eV and −1.75 eV. This means that in the presence of O₂ and SiO₃²⁻, the SiO₃²⁻ will bind first to the Cu₅ AQCs. The adsorption energies E_a of SiO₃²⁻ were estimated to examine the stability of the complex using the equation

E_a = E_Cu5SiO3²⁻ − (E_Cu5 + E_SiO3²⁻)

In this equation, E_Cu5SiO3²⁻ is the total energy of Cu₅ with the silicate SiO₃²⁻ adsorbed, E_Cu5 is the total energy of Cu₅ without SiO₃²⁻, and E_SiO3²⁻ is the total energy of SiO₃²⁻ (note: silicate ion is accompanied by two Na cations). Net charges from Bader charge analysis are displayed by the green numbers around each atom. As expected, each of the sodium atoms loses roughly 0.9 electrons to create the silicate ion of interest. Additionally, the pyramidal Cu₅ gains about 0.18 electrons from the bonded silicate. While the trapezoidal loss is around 0.1 electrons. A metastable binding configuration (right panel) alongside the most stable (left panel) one for both pyramidal and trapezoidal is presented in Fig. S4 and S5 (ESI†) respectively. Table 1 illustrates the bond lengths for both pyramidal and trapezoidal with and without SiO₃²⁻. It is clear that after adding SiO₃²⁻. Most of the bonds have been changed; for example, the bond between 4 and 5 atoms has been elongated in both pyramidal and trapezoidal, while the bond length between 2–5 and 4–2 has been shortened.

Table 1 Bond lengths comparison for pyramidal and trapezoidal Cu₅ isomers

Bond length	Pyramidal (Å)	Pyramidal/SiO3^2− (Å)	Trapezoidal (Å)	Trapezoidal/SiO3^2− (Å)
1–3	2.40	2.40	—	—
1–5	2.40	2.42	2.35	2.36
4–3	2.42	2.35	2.35	2.36
4–5	2.42	2.62	2.37	2.68
2–3	2.42	2.55	2.33	2.33
2–5	2.42	2.36	2.38	2.36
1–2	2.33	2.42	2.33	2.33
1–4	2.33	2.47	—	—
4–2	2.53	2.35	2.38	2.36

---

3.2 The deposition of Cu₅ on a pristine and reduced rutile TiO₂(110)

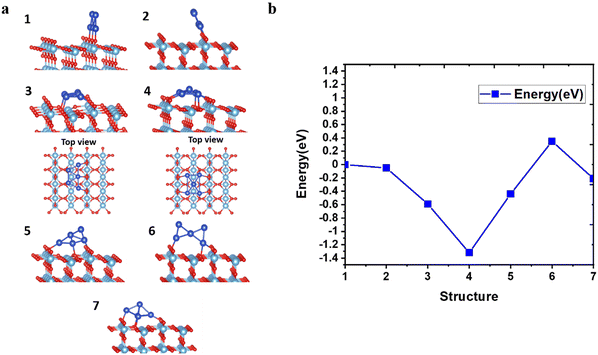
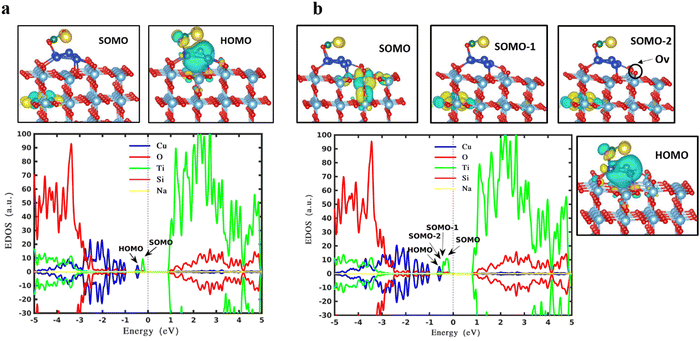
To investigate the geometrical stability of AQCs on the pristine rutile TiO₂(110) substrate, we deposited the optimized trapezoidal and pyramidal clusters on the surface of TiO₂ at different angles and positions, as shown in Fig. 2a. Furthermore, we calculated the total energies with respect to the different configurations created by tilting and displacing the Cu₅ AQCs on supports, as depicted in Fig. 2b. Based on a series of manually arranged initial guesses for the placement of Cu₅ along the trough, minimum energy structures have been obtained from a follow-up geometry optimization. The results exhibit that structure 4 is the most stable configuration, which deforms to a new pyramid-shaped structure with the adsorption energy up to −2.26 eV. In contrast, structures 3 and 7 are found to be the metastable structures which are shed light on in the following text and the remaining are presented in ESI† (see Fig. S6 and S7).

Fig. 2 Configurations and energetics of Cu₅ cluster deposited on rutile TiO₂(110) surface. Geometrically optimized configurations based on different positions (a), and energy evolution as the function of different positions of Cu₅ cluster (b).

The hybrid HF/DFT HSE06 functional provides a direct band gap of 3.26 eV for the (rutile) TiO₂(110) surface in this work (see Fig. S1, ESI†). Moreover, this approach likewise considers restricted gap states in various modifications of TiO₂, such as introducing localized Ti³⁺ 3d states below the conduction band. Bader analysis reveals that a Cu₅ cluster transfers 1.1 electrons to the pristine TiO₂; as can be observed in Fig. 3a, the donated electron becomes localized in one specific 3d orbital lying at the surface plane and cantered at the titanium (5f) atom right below the Cu₅ cluster, resulting in a localized polaron at 1.0 eV below the conduction band. This polaronic state is depicted by the green peak in the vicinity of 0 eV in the density of states (DoS) plot, and by the yellow and green electronic clouds in SOMO (the singly occupied molecular orbital) at the top of the graph. The HOMO (the highest occupied molecular orbital) situated on the Cu₅ clusters, is represented by a blue peak near −0.5 eV. It is also noted that many gap states are observed resulting from the copper cluster, which improves the absorption of visible photons and enables photocatalytic activities.

Fig. 3 Frontier molecular orbitals and spin density of states of the most stable structure originating from the trapezoidal Cu₅ on a pristine rutile TiO₂(110) surface (a) and a reduced rutile TiO₂(110) (b). The SOMOs and HOMO are presented (SOMO: the singly occupied molecular orbital; HOMO: the highest occupied molecular orbital). The green, red, and blue curves represent the states located on titanium, oxygen, and copper atoms respectively. Bader charge analysis reveals that 1.1 electrons (a) and 0.99 electrons (b) are transferred from Cu₅ to the support. The dashed line at 0 eV indicates the Fermi energy level.

The DOS plotting combined with molecular orbital and Bader charge analysis demonstrates that excess electrons transferred from AQC locate on Ti_3d orbitals in the rutile TiO₂(110) system. These excess electrons have some similarities with the excess electrons originating from oxygen vacancies and interstitial titanium atom in rutile TiO₂(110) reported in literatures.^36,48 They are all bandgap states, which are located at ∼1 eV below the conduction band sitting on Ti_3d orbitals on the surface or subsurface. Importantly, they are all accompanied by the lattice structural distortions or deformations shown in the Fig. S18 (ESI†).

Those bandgap states are called polaronic states by many papers, which are detectable at ∼1.0 eV binding energy in UV photoelectron spectroscopy (UPS).^49,50 It has been reported that³⁷ a water-adsorbed TiO₂(110) surface was imaged by using a STM, with the sample bias set at −1 V and found that the filled state image exhibits lobe-like features along the Ti_5c rows, which correspond to the band-gap-state electrons (or excess electrons) in TiO₂(110) created as a result of bridging-O (O_b-vac) formation. Furthermore, the paper also states that their experiments and ground-state calculations based on DFT indicate that the excess electrons in TiO₂ are attracted to the top surface layer by water, as a result of strong adsorbate–polaron coupling. Later the same group used time-resolved pump–probe photoemission spectroscopy to study the dynamics of charge-carrier recombination and trapping on hydroxylated rutile TiO₂(110), where the electrons associated with defects are excited into the bottom of the conduction band from the polaronic states within the band gap, which are retrapped within around 45 fs with the infrared excitation.⁵¹ They also took UV photoemission spectroscopy (UPS), two-photon photoemission spectroscopy (2PPE), and density functional theory (DFT) to show the adsorbates have profound, yet different effects on the photoexcitation of the polarons in rutile TiO₂(110).³⁵ All above experimental and theoretical research demonstrates the existence of polarons originating from defects and vacancies.

Creating oxygen vacancies in TiO₂ can introduce variations in electronic, optical, and structural properties. This can result in enhanced applications of TiO₂ such as improved photocatalytic and magnetic properties.⁵² Furthermore, they can also serve as active sites for water splitting. The oxygen vacancies cause the distortion of the TiO₂ lattice, which results in the formation of polaronic states.⁵³ These oxygen defects give rise to Ti³⁺ 3d states, the presence of which can be confirmed by observing the peaks of the photoemission spectrum.⁵⁴ Through the spectrum obtained by optical absorption spectroscopy, it can be demonstrated that oxygen vacancy allows absorption in the visible region of electromagnetic radiation.⁵⁵ In our current studies, we have investigated the effects of depositing those trapezoidal and pyramidal Cu₅ clusters on a reduced rutile TiO₂(110) in order to understand the interactions between adsorbates and oxygen vacancies to gain more sights into the more practical issues. As benchmark calculations, one bridging oxygen vacancy on the rutile TiO₂(110) surface is created, and a defective substrate⁵³ is formed, where two excess electrons are generated resulting in two polarons as shown in Fig. S8 (ESI†). The polaronic states represented by the green peeks below the bottom of the conduction band can be observed. Similar results were obtained for various oxygen vacancy positions (see Fig. S8, ESI†), where the energies of these gap states are in very good agreement with EELS observations.⁵⁶

Fig. 3b represents gap states when the trapezoidal Cu₅ cluster is deposited onto the surface of reduced rutile TiO₂. Overall, the gap states due to the copper (blue curves) decrease a little, which might originate from the shape change of the cluster in the absence and presence of the oxygen vacancy. However, the polaron state increases from one (SOMO peak of Fig. 3a) to three (green peaks below the Fermi level: SOMO−2, SOMO−1, SOMO peaks of Fig. 3b). As previously mentioned, the oxygen vacancy in rutile TiO₂ leads to two excessive electrons resulting in two polaronic states, which get concentrated on the oxygen atoms in the neighborhood. An additional alteration of the surface by placing AQC on TiO₂ induces the formation of the third polaronic state owing to the one-electron transferred from AQC to the substrate which gets trapped into the empty 3d state of the titanium atom.^57–59 It is concluded that the polarons originating from oxygen vacancy and deposited cluster coexist with each other and no suppression is observed.

The undeformed planar Cu₅ is further investigated, which is the metastable structure shown in Fig. S6a (ESI†). This trapezoidal Cu₅ transfers 1.03 electrons to the titania support, which induces one polaronic state to sit at around −0.3 eV. The overall gap states due to copper atoms (blue curves) decrease a little compared with the most stable structure shown in Fig. 3a. By contrast, on the reduced surface presented in Fig. S6b (ESI†), the cluster donates 0.77 electrons to the support, which is 0.26 electron less than the stoichiometric surface. This may be explained by the fact that the oxygen vacancy induces a less evenly distributed charge on the reduced TiO₂ surface.⁵³

In contrast, the decoration of bipyramidal AQC is shown in Fig. 4 on a pristine and reduced TiO₂ surface. On a pristine surface, two polaronic states (green peaks in the vicinity of the Fermi level) are obtained which stem from the charge transfer of 1.4 electrons, and fewer gap states originating from the Cu₅ cluster are observed compared to the more planar structures shown in Fig. 3 and 4. These benchmark calculations are consistent with a previous publication.¹³ When this bipyramidal Cu₅ is deposited on the reduced surface, very interesting results are obtained. First, the blue curves shift out from the valence band leading to more gap states, which can promote the absorption of light in the visible range. This suggests that the reduced surface imposes a negative gating effect on the Cu₅ cluster, which causes an upward shift for the electronic states sitting on the cluster. Second, three polarons (SOMO−2, SOMO−1, and SOMO) are created instead of four. From the Bader charge analysis, 1 electron is transferred to the substrate, which is 0.4 less than the case of the pristine substrate, indicating that the reduced surface with unevenly dispersed charges also prevents the charge transfer from Cu₅. Actually, the above negative gating effect and the prevention of the charge transfer are both reflections of the strong interaction between the reduced surface and the bipyramidal Cu₅. However, it still can be concluded that the polarons created by charge transfer of AQC and oxygen vacancy coexist. This phenomenon is not observed for the new pyramidal Cu₅ in Fig. 3. Last but not least, a high-energy HOMO (the little blue peak in the vicinity of the Fermi level) is obtained, where the states are located on the Cu₅ cluster. This high energy level indicates the presence of active sites on the Cu₅ cluster, which can easily donate electrons to the proton to promote the hydrogen evolution reaction (HER). It is noted that one Cu–Cu bond is elongated due to the nearby oxygen vacancy on the surface. Finally, we suggest that the high-energy level is associated with specific bond elongation, which is verified by constructing a similar metastable structure on the pristine surface (see Fig. S9, ESI†).

Fig. 4 Frontier molecular orbitals and spin density of states of bipyramidal Cu₅ deposited on a pristine (a) and reduced (b) rutile TiO₂(110). The green, red, and blue curves represent the states located on titanium, oxygen, and copper atoms. Bader charge analysis reveals that 1.4 electrons (a) and 1.0 electrons (b) are transferred from Cu₅ to the support. The dashed line indicates the Fermi energy level of 0 eV.

3.3 The deposition of Cu₅/SiO₃²⁻ on a pristine and reduced rutile TiO₂(110)

As one of the key issues of this work, we aim to study and understand the influence of silicates, which are introduced experimentally during the purification process. Therefore, further calculations are carried out in terms of the geometric and electronic properties of Cu₅/SiO₃²⁻ deposited on TiO₂, based on the optimal adsorption configuration of Cu₅ on TiO₂ shown in Fig. 2 and the most stable trapezoidal Cu₅/SiO₃²⁻ in Fig. 1d. From Fig. 5, it is clear that there is no contribution from sodium atoms to the gap states. As for the gap states, no decrease is observed compared to the bare AQC shown in Fig. 3, which shows that the adsorption of silicate does not affect the electronic structures of AQCs and therefore photo absorption will not be impacted. Bader charge analysis demonstrates that the Cu₅/SiO₃²⁻ complex transfers around 1.04 electrons to the TiO₂, creating a polaronic state at 1.1 eV below the bottom of the conduction band (see the green peak at ∼−0.2 eV). This polaron is located at the sublayer of the TiO₂(110) slab as seen from the molecular orbital plotting in the top panel of Fig. 5a. By contrast, on the reduced surface shown in Fig. 5b, two polarons are observed which stem from the 0.94 electron transfer from the AQC complex and the one oxygen vacancy (SOMO and SOMO−1) as seen in the top panel of Fig. 5b. While the second green peak at around −0.3 eV corresponds to the SOMO−2 which is created by the transferred electron from the cluster to the second layer of the substrate.

Fig. 5 Molecular orbitals of trapezoidal Cu₅ cluster in the presence of SiO₃²⁻ deposited on a pristine rutile TiO₂(110) surface (a), and on a reduced rutile TiO₂(110) surface (b), and their corresponding spin densities of states. The green, red, and blue curves represent the states located on titanium, oxygen, and copper atoms respectively. Bader charge analysis reveals that 1.02 electrons (a) and 0.94 electrons (b) are transferred from Cu₅ to the support. The dashed line indicates the Fermi energy level of 0 eV.

In order to further investigate how the influence of a Na ion depends on its distance from the silicate, and to show that its +1 valence of Na persists in the simulation, the distance between one of the two Na ions and one of the three oxygens was increasing from 2.33 Å (Fig. S19a, ESI†) to 3.1 Å (Fig. S19e, ESI†). As expected, the silicate receives two electrons by the two ions in the model. As we moved the two Na ions away step by step (Fig. S19c and e, ESI†) it can be seen that the density of states survives and polaronic state persists in the same position in energy, and only slight shifting of the blue peaks originating from Cu atoms is observed. Overall, this shows that increasing the distance of Na ions from the silicate has negligible impact and that the +1 valence of Na ions persists.

In addition, the catalysts composing of TiO₂ and Cu₅ are utilised, after deposition of a concentrated water dispersion of Cu₅-silicates and dried, in the state of powder in the reactor which means the cations are around the anions. That is to say, the close distance between Na ions and silicate is acceptable in simulation.

Fig. 6 shows the adsorption of SiO₃²⁻ onto the pyramidal AQC adsorbed on rutile TiO₂(110). In comparison to the bare pyramidal Cu₅ on support presented in Fig. 4, several differences are observed. First, whatever the stoichiometric or the reduced nature of the surface, the gap states increase, as indicated by the upward shifting of the blue curves, which will promote the absorption of light in the visible range. This suggests that the silicate ions apply a negative gating effect on those 3-dimensional Cu₅ cluster, which causes the upward displacement of the electronic states sitting on the cluster. Second, one polaron (SOMO) is formed for the stoichiometric surface shown in Fig. 6a. From the Bader charge analysis, 1 electron is transferred to the substrate, which is 0.4 less than the case of the bare cluster shown in Fig. 4a. However, the results shown in Fig. 6b demonstrate that the polarons created by charge transfer of AQC and oxygen vacancy coexist. Third, the high-energy HOMO is not obtained with silicate adsorption, which might be understood by the fact the AQC deforms a lot and many elongations in bond length occur. In addition, different positions of oxygen vacancies have been investigated for both pyramidal and trapezoidal (see Fig. S10, ESI†).

Fig. 6 Molecular orbitals of pyramidal Cu₅ cluster in the presence of SiO₃²⁻ deposited on a pristine rutile TiO₂(110) surface (a), and on a reduced rutile TiO₂(110) surface (b), and their corresponding spin densities of states. The green, red, and blue curves represent the states located on titanium, oxygen, and copper atoms respectively. Bader charge analysis reveals that 1.0 electrons (a) and 1.0 electrons (b) are transferred from Cu₅ to the support. The dashed line indicates the Fermi energy level of 0 eV.

For more detailed investigations, we also considered different deposition positions of the metastable trapezoidal and pyramidal of Cu₅/SiO₃²⁻ on rutile TiO₂(110) surface (see Fig. S11, and S12, ESI†). Experimentally, we introduce a Cu₅/SiO₃²⁻ molar ratio = 1. The reason for this is to avoid the aggregation of clusters when they are freeze dried. This is needed to have a dispersion of clusters with enough concentration to deposit the desired amount (loading) on the TiO₂ substrates. This means that we would expect to have one silicate ion per Cu₅, but this is an average value. Some Cu₅ clusters may also have 0, 2 or even 3 silicates bind to them and therefore we also considered more silicate adsorption such as two and three SiO₃²⁻ on a perfect and reduced TiO₂(110) (see more details in Fig. S13–S17 of ESI†). To conclude, during the purification process of the Cu₅ AQCs in a water solution, the doping of Cu₅/SiO₃²⁻ does not reduce and even, in some cases, enhances the gap states of TiO₂(110). It should be noted that the present of water might not be inevitable, their impact will be investigated in our future work.

To further understand the impact of silicate alone, the most energetically stable adsorption of silicates is obtained shown in Fig. S20 (ESI†) where two distances between Na ions and silicate were tested. It is demonstrated that changing the distance has a negligible influence on the density of states and band gap. Overall, the silicate ion alone will not affect the electronic structures of the pristine TiO₂ substrate.

4. Conclusion

In this study, we have carried out DFT calculations to understand the effects of adsorbing AQCs on perfect and reduced rutile TiO₂ in the presence and absence of SiO₃²⁻. The geometric properties, orbitals, and their corresponding spin density of states of each relaxed structure were calculated. It is concluded that the adsorbed AQCs serve to reduce the bandgap in the stoichiometric as well as reduced TiO₂ substrates by introducing polaronic states in the band gap and those gap states sitting on Cu cluster can shift the solar absorption from ultraviolet to the visible region. Both pyramidal and trapezoidal Cu AQCs are oxidized by donating one or two electrons to the substrate. The polarons induced by charge transfer from AQCs to the substrate can persist in the presence of oxygen vacancies and even coexist with those created by the O_v. It is also found that the reduced surfaces behave like a negative gate to the AQC and the states sitting on the Cu are gated out of the valence band and into the band gap. This means the enhancement of the photocatalysis due to oxygen vacancies can be interpretated from at least three aspects: one is the polaron states created by O_vs; second, O_vs behave like a negative gate to the states located on the AQCs; third, O_vs enhance the adsorption of adsorbates. Furthermore, a high-energy HOMO in the vicinity of the conduction band is obtained, indicating the presence of active sites on the Cu₅ cluster, which will easily donate electrons to a proton to promote the hydrogen evolution reaction (HER). It has been discussed that the improved catalytic properties of Cu₅/TiO₂ in terms of reducing CO₂ decomposition barrier compared to bare Cu₅ and demonstrated that an electron “jump” from the HOMO triggered by solar photos is responsible for the generation of the CO₂˙⁻ radical attached to the Cu₅-modified TiO₂ surface.¹⁸ Based on the fact that many gap states directly and indirectly (the polaronic state) originating from the deposited Cu₅ are produced no matter the shapes or the deposition orientations of Cu₅, the electrons located on copper atoms with higher densities activated by solar photos in the infrared or visible regions are expected to be able to be transferred to the orbitals bearing the higher densities localized on CO₂. Furthermore, our results also demonstrate that the presence of SiO₃²⁻ will not decrease and even increase the gap states for some geometric structures by providing a negative gating to the AQCs. This demonstrates that the presence of silicate ions, an inevitable consequence of the current metal cluster purification process, does not hamper the photo absorption ability of the Cu₅-modified TiO₂ support but might even enhance it.

Data availability

Data are available upon request from the authors.

Conflicts of interest

There are no conflicts to declare.

References

1. H.-T. Pao and C.-M. Tsai, CO₂ emissions, energy consumption and economic growth in BRIC countries, Energy Policy, 2010, 38(12), 7850–7860.
2. S. Z. Baykara, Hydrogen: A brief overview on its sources, production and environmental impact, Int. J. Hydrogen Energy, 2018, 43(23), 10605–10614.
3. I. Staffell, et al., The role of hydrogen and fuel cells in the global energy system, Energy Environ. Sci., 2019, 12(2), 463–491.
4. B. Zhu, R. Zou and Q. Xu, Metal–organic framework based catalysts for hydrogen evolution, Adv. Energy Mater., 2018, 8(24), 1801193.
5. S. Abanades, Metal oxides applied to thermochemical water-splitting for hydrogen production using concentrated solar energy, ChemEngineering, 2019, 3(3), 63.
6. A. S. Mazheika, et al., Theoretical study of adsorption of Ag clusters on the anatase TiO₂(100) surface, J. Phys. Chem. C, 2011, 115(35), 17368–17377.
7. S.-P. Hong, et al., Comprehensive study on the morphology control of TiO₂ nanorods on foreign substrates by the hydrothermal method, Cryst. Growth Des., 2018, 18(11), 6504–6512.
8. J. Wang, et al., Band structure tuning of TiO₂ for enhanced photoelectrochemical water splitting, J. Phys. Chem. C, 2014, 118(14), 7451–7457.
9. St Neaţu, et al., Gold–copper nanoalloys supported on TiO₂ as photocatalysts for CO₂ reduction by water, J. Am. Chem. Soc., 2014, 136(45), 15969–15976.
10. C. McManamon, et al., A facile route to synthesis of S-doped TiO₂ nanoparticles for photocatalytic activity, J. Mol. Catal. A: Chem., 2015, 406, 51–57.
11. I. Majeed, et al., Titania supported MOF-199 derived Cu–Cu₂O nanoparticles: highly efficient non-noble metal photocatalysts for hydrogen production from alcohol–water mixtures, Catal. Sci. Technol., 2017, 7(3), 677–686.
12. A. Sclafani and J.-M. Herrmann, Influence of metallic silver and of platinum-silver bimetallic deposits on the photocatalytic activity of titania (anatase and rutile) in organic and aqueous media, J. Photochem. Photobiol., A, 1998, 113(2), 181–188.
13. Q. Wu, et al., Tuning the surface states of TiO₂ using Cu₅ atomic clusters, Appl. Surf. Sci., 2022, 594, 153455.
14. D. Buceta, et al., Stability and Reversible Oxidation of Sub-Nanometric Cu₅ Metal Clusters: Integrated Experimental Study and Theoretical Modeling, Chem. – Eur. J., 2023, e202301517.
15. E. Fernandez, M. Boronat and A. Corma, Trends in the reactivity of molecular O₂ with copper clusters: influence of size and shape, J. Phys. Chem. C, 2015, 119(34), 19832–19846.
16. P. Concepción, et al., Enhanced stability of Cu clusters of low atomicity against oxidation. Effect on the catalytic redox process, ACS Catal., 2017, 7(5), 3560–3568.
17. M. P. de Lara-Castells, et al., Increasing the optical response of TiO₂ and extending it into the visible region through surface activation with highly stable Cu₅ clusters, J. Mater. Chem. A, 2019, 7(13), 7489–7500.
18. P. López-Caballero, A. W. Hauser and M. Pilar de Lara-Castells, Exploring the catalytic properties of unsupported and TiO₂-supported Cu₅ clusters: CO₂ decomposition to CO and CO₂ photoactivation, J. Phys. Chem. C, 2019, 123(37), 23064–23074.
19. S. Huseyinova, et al., Synthesis of highly stable surfactant-free Cu₅ clusters in water, J. Phys. Chem. C, 2016, 120(29), 15902–15908.
20. M. A. López Quintela, D. B., Process for producing Atomic Quantum Clusters Derivatives, EU Pat., PCT/EP2023/075494, 2022.
21. J. Lee and E. Chung, Lithium recovery from a simulated geothermal fluid by a combined selective precipitation and solvent extraction method, Geothermics, 2022, 102, 102388.
22. I. M. Ali, Y. H. Kotp and I. M. El-Naggar, Thermal stability, structural modifications and ion exchange properties of magnesium silicate, Desalination, 2010, 259(1–3), 228–234.
23. J. H. Johnston, et al., Nano-structured composite calcium silicate and some novel applications, Curr. Appl. Phys., 2008, 8(3–4), 504–507.
24. Z.-f Cao, et al., Transforming structure of dolomite to enhance its ion-exchange capacity for copper (II), Colloids Surf., A, 2018, 539, 201–208.
25. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50.
26. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558.
27. G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251.
28. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758.
29. P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(23), 16223.
30. A. Janotti and C. G. Van de Walle, LDA+U and hybrid functional calculations for defects in ZnO, SnO₂, and TiO₂, Phys. Status Solidi B, 2011, 248(4), 799–804.
31. Q. Wan, et al., Single atom detachment from Cu clusters, and diffusion and trapping on CeO₂(111): Implications in Ostwald ripening and atomic redispersion, Nanoscale, 2018, 10(37), 17893–17901.
32. R. K. Singha, et al., Methane activation at the metal–support interface of Ni₄–CeO₂(111) catalyst: a theoretical study, J. Phys. Chem. C, 2019, 123(15), 9788–9798.
33. S. Grimme, et al., A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104.
34. A. Janotti, et al., Hybrid functional studies of the oxygen vacancy in TiO₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(8), 085212.
35. A. J. Tanner, et al., Polaron-adsorbate coupling at the TiO₂(110)-carboxylate interface, J. Phys. Chem. Lett., 2021, 12(14), 3571–3576.
36. B. Wen, et al., Defects, adsorbates, and photoactivity of rutile TiO₂(110): insight by first-principles calculations, J. Phys. Chem. Lett., 2018, 9(18), 5281–5287.
37. C. M. Yim, et al., Visualization of water-induced surface segregation of polarons on rutile TiO₂(110), J. Phys. Chem. Lett., 2018, 9(17), 4865–4871.
38. S. Dong, et al., Photoresponses of supported Au single atoms on TiO₂(110) through the metal-induced gap states, J. Phys. Chem. Lett., 2019, 10(16), 4683–4691.
39. R. F. Bader, Atoms in molecules, Acc. Chem. Res., 1985, 18(1), 9–15.
40. A. V. Krukau, et al., Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106.
41. G. Donati, et al., Molecular vibration induced plasmon decay, J. Phys. Chem. C, 2017, 121(28), 15368–15374.
42. M. Monti, et al., What Contributes to the Measured Chiral Optical Response of the Glutathione-Protected Au25 Nanocluster?, ACS Nano, 2023, 17(12), 11481–11491.
43. R. A. Beck, et al., Electronic Structures and Spectroscopic Signatures of Noble-Gas-Doped Nanodiamonds, ACS Phys. Chem. Au, 2023, 3(3), 299–310.
44. M. Medves, et al., Predictive optical photoabsorption of Ag24Au (DMBT) 18− via efficient TDDFT simulations, J. Chem. Phys., 2021, 155(8), 084103.
45. R. A. Beck, et al., Spectroscopic Signatures of the B and H4 Polyatomic Nitrogen Aggregates in Nanodiamond, J. Phys. Chem. C, 2020, 124(33), 18275–18283.
46. A. Petrone, et al., Electronic structures and spectroscopic signatures of silicon-vacancy containing nanodiamonds, Phys. Rev. B, 2018, 98(20), 205405.
47. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276.
48. P. Moses, et al., Donor defects and small polarons on the TiO₂(110) surface, J. Appl. Phys., 2016, 119(18), 181503.
49. S. Wendt, et al., The role of interstitial sites in the Ti 3d defect state in the band gap of titania, Science, 2008, 320(5884), 1755–1759.
50. C. Yim, C. Pang and G. Thornton, Oxygen vacancy origin of the surface band-gap state of TiO₂(110), Phys. Rev. Lett., 2010, 104(3), 036806.
51. Y. Zhang, et al., State-selective dynamics of TiO₂ charge-carrier trapping and recombination, J. Phys. Chem. Lett., 2019, 10(17), 5265–5270.
52. C. Lin, D. Shin and A. A. Demkov, Localized states induced by an oxygen vacancy in rutile TiO₂, J. Appl. Phys., 2015, 117(22), 225703.
53. P. López-Caballero, et al., Ag5-induced stabilization of multiple surface polarons on perfect and reduced TiO₂ rutile (110), J. Chem. Phys., 2020, 153(16), 164702.
54. F. De Angelis, et al., Theoretical studies on anatase and less common TiO₂ phases: bulk, surfaces, and nanomaterials, Chem. Rev., 2014, 114(19), 9708–9753.
55. X. Yu, et al., Effects of oxygen defects on electronic band structures and dopant migration in Sn-doped TiO₂ by density functional studies, Chem. Phys. Lett., 2020, 754, 137732.
56. M. A. Henderson, et al., Insights into photoexcited electron scavenging processes on TiO₂ obtained from studies of the reaction of O2 with OH groups adsorbed at electronic defects on TiO₂(110), J. Phys. Chem. B, 2003, 107(2), 534–545.
57. W. Mackrodt, E.-A. Simson and N. Harrison, An ab initio Hartree-Fock study of the electron-excess gap states in oxygen-deficient rutile TiO₂, Surf. Sci., 1997, 384(1–3), 192–200.
58. M. Ramamoorthy, R. King-Smith and D. Vanderbilt, Defects on TiO₂(110) surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(11), 7709.
59. P. Lindan, et al., First-principles spin-polarized calculations on the reduced and reconstructed TiO₂(110) surface, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55(23), 15919.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02903h

---