Cold reactions of He⁺ with OCS and CO₂: competitive kinetics and the effects of the molecular multipole moments

Abstract

The reactions of He⁺ with OCS and CO₂ have been studied at collision energies between ∼k_B ⋅ 200 mK and ∼k_B ⋅ 30 K by merging a beam of Rydberg He atoms with rotationally cold (∼3.5 K) seeded supersonic expansions containing either OCS or ¹³CO₂ or a mixture of OCS (mole fraction 23.2%) and ¹³CO₂ (76.8%). The observed product ions of the He⁺ + ¹³CO₂ and He⁺ + OCS reactions are ¹³CO⁺, and CS⁺ and CO⁺, respectively. The He⁺ + OCS capture rate coefficient increases by ∼75% with decreasing collision energy over the investigated range, whereas that of He⁺ + ¹³CO₂ decreases by ∼40%. The analysis of the experimental results using an adiabatic-channel capture model indicates that these opposite collision-energy dependences of the rate coefficients arise from the interaction between the charge of the ion and the electric multipole moments of OCS and ¹³CO₂. From the relative product-ion yields observed when using the mixture of OCS and ¹³CO₂, the He⁺ + OCS collisions are inferred to be ∼20% more reactive than those between He⁺ and ¹³CO₂. The comparison of the calculated thermal rate coefficients with earlier experiments suggests that about half of the He⁺ + ¹³CO₂ collisions are reactive.

---

1 Introduction

For over fifty years, cold ion–molecule reactions have been an object of interest in chemical physics and astrophysics.^1–15 Their rate coefficients have been predicted to display a characteristic and sometimes strong collision-energy (E_coll) dependence at near-zero E_coll resulting from the interaction between the charge of the ion and the electric dipole and quadrupole moments of the neutral molecule.^5–13 The effect of these charge–multipole-moment interactions makes the commonly used temperature- and E_coll-independent Langevin rate coefficients k_L¹⁶ unsuitable to describe many chemical processes occurring in the interstellar medium.⁶ Measuring and modeling the reaction rate coefficients of ion–molecule reactions at low temperatures and low collision energies offers insight into the fundamental aspects of cold chemistry.^17–21

Ion–molecule reactions have been studied from room temperature down to ∼10 K using ion guides and traps,^22–24 supersonic flows,^25,26 and, more recently, laser-cooled and sympathetically cooled ions in ion traps and Coulomb crystals.^{17,19,20,27–29} Even lower temperatures have been reached in ion–atom reactions in hybrid traps.^30–32 Probing the sub-10 K region is experimentally challenging because stray electric fields and space-charge effects easily accelerate and heat up the ions. In the last decade, experimental investigations of cold ion–molecule reactions in a range of collision energies tunable from ∼k_B ⋅ 60 K down to ∼k_B ⋅ 200 mK have become possible through the development of a merged-beam technique in which the ion is substituted by the ion core of Rydberg atoms or molecules.^33–36 The highly excited Rydberg electron ensures charge neutrality and shields the reactions taking place within its orbit from stray electric fields without otherwise influencing them.^34,37–40

In recent studies of cold ion–molecule reactions, it was experimentally demonstrated that the partial-charge distribution in the neutral molecule dictates how the reaction rate coefficient varies with the collision energy near zero, confirming theoretical predictions made almost forty years ago.^5–9 For polar molecules,^36,41–43 the rotational-state-averaged rate coefficients k(E_coll) increase as E_coll approaches zero. For quadrupolar molecules, k(E_coll) typically increases as E_coll approaches zero for molecules with a positive zz component of the quadrupole-moment tensor (Q_zz)^35,44,45 and decreases if the molecular reactant has a negative Q_zz.^45,46 For molecules with neither a dipole moment nor a quadrupole moment, such as CH₄, k(E_coll) stays constant within the experimentally attainable E_coll range and sensitivity.⁴⁷

The work reported in this article was carried out as part of a series of systematic investigations of ion–molecule reactions at low collision energies and temperatures.^{34–36,40–43,45–48} It presents a comparative investigation of the He⁺ + OCS and the He⁺ + CO₂ reactions in the E_coll range from ∼k_B ⋅ 30 K down to ∼k_B ⋅ 200 mK. OCS and CO₂ are both linear triatomic molecules with electronic ground state of ¹Σ⁺ symmetry. Their relevant physical properties are presented in Table 1. OCS, unlike CO₂, is not centrosymmetric and thus has a permanent electric dipole moment. CO₂ is nonpolar but has a large (negative) quadrupole moment. We present experimental and theoretical studies of the effects of such different partial-charge distributions on the reaction rate coefficients of each reaction individually and also directly compare their rate coefficients by simultaneously measuring both reactions using an (OCS:¹³CO₂) gas mixture of well-defined composition.

Table 1 Comparison of the properties and physical constants of OCS and CO₂ relevant for the prediction of the capture rate coefficients of ion–molecule reactions

Molecule	OCS	CO2
a Value for ^16O^12C^32S. b Value for ^13C^16O2.
Electronic ground state	^1Σ^+	^1Σ^+g
Mass m (u)	60.07^a	45.00^b
Dipole moment |μel| (D)	0.715^49	0
Quadrupole moment Qzz (D Å)	−0.295^50	−4.278^51
Polarizability volume α′ (Å^3)	5.090^52	2.507^53
Polarizability anisotropy Δα′ (Å^3)	4.16^54	2.14^54
Rotational constant B0 (cm^−1)	0.20286^55^a	0.3902374^56^b
Langevin rate kL (10^−15 m^3 s^−1)	2.7276^a	1.9360^b

---

Several investigations of the thermal reactions between He⁺ and carbonyl sulfide (OCS) and carbon dioxide (CO₂) have been carried out since the 1960s. The He⁺ + OCS reaction was studied by monitoring the emission spectrum of OCS in helium flowing-afterglow experiments, and CO^+57–59 and CS^+57,58 were identified as the ionic products, but no branching ratios were reported. The He⁺ + CO₂ reaction has been studied extensively at 300 K and above in drift-tube,⁶⁰ ion-cyclotron resonance,^61,62 selected-ion-flow-tube,^63,64 flow-drift-tube,⁶⁵ flowing-afterglow,^66,67 and crossed-beam velocity-map-imaging⁶⁸ experiments. The following reaction channels and branching ratios have been reported:

Thermal rate constants k(T ≈ 300 K) between 0.85 (±20%) × 10⁻¹⁵ m³ s⁻¹ (ref. 66) and 1.2 (±50%) × 10⁻¹⁵ m³ s⁻¹ (ref. 67) have been reported. Rowe et al.⁶⁹ conducted the lowest temperature experiment to date involving the He⁺ + CO₂ reaction, and obtained k(70 K) = 1.6 (±30%) × 10⁻¹⁵ m³ s⁻¹, which is only slightly lower than the Langevin rate constant k_L^CO₂ of the He⁺ + CO₂ reaction (see Table 1).

This article is structured as follows: in Section 2 we describe the experimental setup and procedure. Section 3 presents the experimental results and Section 4 the theoretical analysis. The competitive kinetics study of the reaction between He⁺ and a mixture of OCS and ¹³CO₂ is discussed in Section 5. The conclusions are presented in Section 6.

2 Experiment

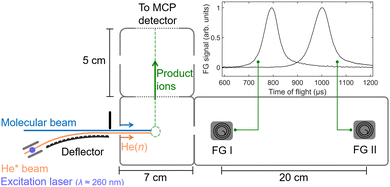
We study ion–molecule reactions near zero collision energy using the merged-beam apparatus⁴¹ depicted in Fig. 1. A supersonic expansion of He atoms is generated using a cryogenic home-built valve delivering short gas pulses with a duration of ∼20 μs at a repetition rate of 25 Hz. An electric discharge populates the He* (1s)¹(2s)^{1 3}S₁ metastable state near the valve orifice. The beam of He* atoms propagates with a velocity of ∼1000 m s⁻¹ and is crossed at right angles by laser light (wavelength of ∼260 nm, pulse energy of ~400 μJ) in the presence of an electric field just before a curved Rydberg–Stark deflector. After photoexcitation of the He* atoms to a selected Rydberg–Stark state of principal quantum number n in the range between 25 and 50 (n = 35 was used to obtain the results presented in this article), the He(n) Rydberg atoms are trapped, deflected and accelerated to higher or lower velocities by applying the appropriate time-dependent potentials to the electrodes of the surface deflector.^33,36,70 This deflector is used to merge the He(n) beam with a beam of ground-state (GS) neutral molecules (¹³CO₂ or OCS) and set the forward velocity v_He(n) of the He(n) beam. The collision between the ground-state molecules and the He(n) atoms takes place in a reaction region embedded in a time-of-flight (TOF) mass spectrometer.

Fig. 1 Schematic representation of the merged-beam setup used to study the reactions between He⁺ and small molecules (here OCS and ¹³CO₂) at low collision energies, consisting of the surface-electrode deflector and decelerator, the time-of-flight mass spectrometer, and a free-flight region used to measure the velocity distributions of the supersonic beams containing OCS and ¹³CO₂ with two fast-ionization gauges (FG).

The collision energy E_coll = μ_He(n)–GS(v_He(n) − v_GS)²/2 is tuned by changing v_He(n) while keeping the velocity v_GS of the ground-state beam constant (μ_He(n)–GS is the reduced mass of the reactants). This beam is generated by a second home-built valve, which also delivers short (∼20 μs) gas pulses. The ∼0.6-m-long propagation distance of the short gas pulses ensures a large spatial dispersion, so that the small cloud of He(n) atoms overlaps with neutral reactants in a narrow velocity class. As a result, we achieve a collision-energy resolution of ∼k_B ⋅ 200 mK near E_coll = 0, which arises mainly from the velocity-distribution width of the deflected He(n)-atom beam.^33,36

To study the He⁺ + OCS and He⁺ + CO₂ reactions, we use seeded supersonic beams containing either OCS or ¹³CO₂ or a (23.2 : 76.8) OCS : ¹³CO₂ mixture (mole ratio) prepared by weighing the gas samples. The simultaneous measurement of the two reactions in a single set of measurements using a mixture containing both OCS and ¹³CO₂ serves three purposes: first, it enables us to verify that the measurements are not significantly affected by possible differences in the expansions of the different gas mixtures; second, the ∼3–5% seeding ratio ensures the same velocity for OCS and ¹³CO₂; and third, it offers the prospect of directly comparing the rate coefficients of the two reaction systems. ¹³CO₂ was chosen instead of ¹²CO₂ to distinguish between the CO⁺ products from the two reaction systems, which made a competitive-kinetics investigation possible. Seeding the neutral molecules (∼3–5%) in a mixture⁷¹ of He and Ne allows one to efficiently cool the rotational degrees of freedom and avoid the formation of OCS clusters while imposing a similar velocity to the neutral reactants in all three different experiments. With this approach, we could also select a v_GS value within the range of velocities v_He(n) that can be generated with the surface-deflector and thus vary v_rel = v_He(n) − v_GS through zero.

An electric-field pulse is used to extract the product ions of the reactions toward a microchannel-plate (MCP) detector along a time-of-flight tube and to detect them mass selectively as E_coll is varied. Examples of TOF mass spectra are displayed in Fig. 2. The spectra plotted in black were recorded near E_coll = 0 for the reactions between He(n = 35) atoms travelling at v_He(n) = 1050 m s⁻¹ and OCS (a), ¹³CO₂ (b), and a mixture of OCS and ¹³CO₂ (c). The corresponding background spectra in red were recorded with the Rydberg-excitation laser turned off, i.e., in the absence of He(n) atoms. The ions which appear in these spectra correspond to products of the Penning-ionization reactions between He* and the background molecules in the chamber, i.e., H₂O (O⁺, OH⁺ and H₂O⁺), and either OCS (S⁺ and OCS⁺) or ¹³CO₂ (¹³CO₂⁺). The peaks which are only present in the spectra plotted in black, namely CO⁺ and CS⁺ in panels (a) and (c) and ¹³CO⁺ in panels (b) and (c), are from the products of the studied ion–molecule reactions. Two different ion products (CO⁺ and CS⁺) are observed in the He⁺ + OCS reaction system [panel (a)], corresponding to the two reaction channels He⁺ + OCS → He + S + CO⁺ and He⁺ + OCS → He + O + CS⁺. A single reaction channel, He⁺ + ¹³CO₂ → He + O + ¹³CO⁺, is detected for the He⁺ + ¹³CO₂ reaction system [see panel (b)]. The product ions resulting from the other reactive channels of He⁺ + ¹³CO₂ shown in eqn (1) and from He⁺ + OC³⁴S are not observed. However, the sensitivity of our experiment does not allow for the detection of ions that are formed in reaction channels with branching ratios below ∼10%.

Fig. 2 Time-of-flight mass spectra of the ion signals recorded after the reaction between He Rydberg atoms (n = 35) and (a) OCS, (b) ¹³CO₂, and (c) a mixture of OCS and ¹³CO₂. The spectra in red correspond to background measurements obtained with the Rydberg-excitation laser turned off. The reaction products are labeled in black bold font. See text for details.

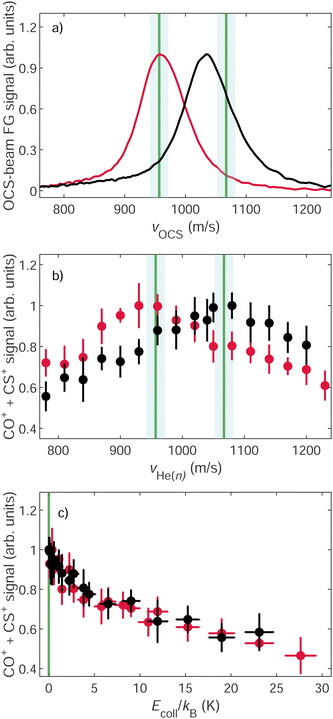
The velocity distribution of the ground-state beam was measured using two fast-ionization gauges (FG I and II in Fig. 1) as explained in detail in ref. 43. The effects of changing the ratio of He and Ne in the ground-state-beam expansion are illustrated in panel (a) of Fig. 3, which displays the velocity distributions obtained from measurements of the flight times using a fast-ionization gauge (FG I in Fig. 1). The distribution displayed in red corresponds to a beam containing ∼3% OCS seeded in a mixture of He : Ne (2 : 3), which resulted in a mean velocity of ∼960 m s⁻¹. Seeding ∼3% OCS in a (1 : 1) mixture of He and Ne yielded a faster beam with a mean velocity of ∼1035 m s⁻¹ (black trace). The vertical green lines correspond to the mean velocity of the OCS-molecule cloud overlapping with the He(n) atoms in the reaction region. These velocities were selected by applying appropriate time delays between the OCS and the He* gas-pulse triggers. The green shaded regions represent the estimated uncertainty of ±15 m s⁻¹ in the velocity measurements using the fast-ionization gauges. To avoid turbulent parts of the beams and the formation of clusters, we typically targeted velocity classes which either corresponded to the mean velocity of the ground-state beam (960 m s⁻¹), as in the distribution displayed in red, or to a faster velocity, as in the distribution displayed in black, for which v_OCS ≈ 1070 m s⁻¹. The experiments are carried out under conditions where the densities of the GS molecules by far exceed those of He(n) and the reaction probability of He(n) is less than 1%. Consequently, the product-ion signals follow pseudo-zero-order kinetics and directly correspond to the relative rate coefficients.

Fig. 3 (a) Velocity distributions, measured with the fast-ionization gauges, of supersonic beams consisting of ∼3% OCS seeded in He : Ne mixtures of 1 : 1 (black) and 2 : 3 (red) pressure ratios. (b) and (c) Corresponding total integrated product-ion signal (CO⁺ and CS⁺) of the He⁺ + OCS reaction as a function of (b) the He(n)-beam velocity and (c) the collision energy. The vertical green lines in panels (a) and (b) indicate the targeted OCS velocities in each beam (∼960 m s⁻¹ and ∼1070 m s⁻¹, respectively), which correspond to E_coll = 0 in panel (c). The areas shaded in light green in panels (a) and (b) correspond to the experimental uncertainty of ±15 m s⁻¹ in the targeted OCS beam velocities. The vertical error bars in panels (b) and (c) represent ±1σ and the horizontal bars in panel (c) the collision-energy resolution.

3 Results

Panel (b) of Fig. 3 depicts the relative total product-ion yields of the He⁺ + OCS reaction as a function of v_He(n). The yield corresponding to the OCS beam with v_OCS ≈ 960 m s⁻¹ is depicted in red and that of the beam with v_OCS ≈ 1070 m s⁻¹ in black [see panel (a) of Fig. 3]. These product yields, corresponding to the sum of the integrated CO⁺ and CS⁺ signals, were obtained by recording TOF mass spectra such as those displayed in Fig. 2 as a function of the velocity of the He(n) beam. The integrated signals were normalized by the density of He(n) atoms in the reaction zone, as determined in a separate measurement using pulsed-field ionization.^40,41 The data were further corrected for the different densities of the decelerated and accelerated He(n) beams, as explained in ref. 41. The green lines in panels (a) and (b) illustrate that changing the target velocity of the OCS beam from 960 m s⁻¹ to 1070 m s⁻¹ results in a shift of the He(n) mean velocity at which the reaction yield reaches a maximal value, which in both cases occurs when v_OCS = v_He(n), i.e., at zero relative velocity. The same data are displayed in panel (c) as a function of the collision energy. The increase in product-ion yield as the relative velocity between the reactants approaches zero, observed in both data sets, is a typical signature of ion–molecule reactions involving polar molecules, as previously observed for CH₃F,³⁶ NH₃,^41,43 and NO.⁴²

Fig. 4 presents a comparison of the dependence on v_rel of the product yields obtained in the measurements of the reactions of He⁺ with OCS [panel (a)], ¹³CO₂ (b), and the OCS:¹³CO₂ mixture (c). The integrated product-ion signal obtained in individual measurements is shown as as pale-color circles as a function of v_He(n) in the range between 800 m s⁻¹ and 1200 m s⁻¹. The corresponding averages of the product-ion signal are shown with dark-color circles. The vertical error bars correspond to one standard deviation.

Fig. 4 Integrated product-ion signals of the reactions between He⁺ and OCS [(a) and (d)], ¹³CO₂ [(b) and (e)], and a mixture of OCS and ¹³CO₂ [(c) and (f)] as a function of the He(n)-beam velocity [(a)–(c)] and the collision energy [(d)–(f)] for fixed velocities of the ground-state molecular beams (v_OCS ≈ 960 m s⁻¹, v_13CO2 ≈ 1000 m s⁻¹, v_mix ≈ 990 m s⁻¹). The data points plotted in pale and dark colors represent individual measurements and their weighted averages, respectively. The vertical error bars represent ±1σ and the horizontal bars in panels (d)–(f) the E_coll resolution. The pale red and blue lines in panels (d)–(f) correspond to the calculated state-averaged capture rate coefficients. The maxima (minima) in product formation for the He⁺ + OCS (He⁺ + ¹³CO₂) reaction occur when v_He(n) = v_GS (i.e., for E_coll = 0), as indicated by the green vertical lines in panels (a)–(c).

Panels (d)–(f) present the same data as a function of E_coll. In these panels, the vertical error bars correspond to one standard deviation and the horizontal bars to the experimental collision-energy resolution ΔE_coll [see eqn (1) in ref. 36]. The data were binned according to E_coll, with bin sizes proportional to ΔE_coll. The colored lines represent the rotational-state-averaged reaction rate coefficient calculated using the capture-rate-coefficient model presented in Section 4. In our experiment, relative (as opposed to absolute) rate coefficients are measured, and therefore, for the comparison, the experimental data are scaled by a global factor to yield the best agreement with the calculated reaction rate coefficients.

Panel (a) of Fig. 4 corresponds to the results obtained for the He⁺ + OCS reaction for an OCS beam with v_OCS = 960 m s⁻¹ and already displayed in panels (b) and (c) of Fig. 3 but showing, in addition, the yields of the CO⁺ and CS⁺ products as pink and orange circles, respectively. Both product yields reveal the same dependence on the relative velocity between the reactants within the experimental uncertainties, which indicates that the branching ratio of the two product channels is independent of the collision energy. The observed CO⁺ branching ratio is (70 ± 8.5)%. We observe an increase of about 75% in the total He⁺ + OCS product yield as v_He(n) is varied from 800 m s⁻¹ (1200 m s⁻¹) up (down) to 960 m s⁻¹, which is the mean velocity of the reacting OCS molecules in this experiment. The red circles in panel (d) show that the sum of the CO⁺ and the CS⁺ product yields increases by 75% as the collision energy is reduced from ∼k_B ⋅ 30 K down to zero.

The product yield of the He⁺ + ¹³CO₂ reaction [panel (b)] exhibits the opposite behavior, i.e., a decrease in the ¹³CO⁺ product formation (blue circles) by 40% as v_He(n) is scanned toward v_13CO2, i.e., toward E_coll = 0 [see panel (e)]. The trends of increasing (decreasing) rate coefficients for the He⁺ + OCS (He⁺ + ¹³CO₂) reactions as v_rel approaches zero are also observed in the experiments carried out with the OCS:¹³CO₂ mixture, as shown in panels (c) and (f). This observation demonstrates that these trends are not influenced by the different gas-expansion conditions in these measurements, as expected, and that the main systematic sources of error are accounted for by the procedure used to normalize the product signal using the measured relative densities of the He(n) and the ¹³CO₂/OCS reactants.

4 Analysis of the capture rate coefficients

To analyze the experimental results presented in Section 3, we use a capture model originally developed by Clary and coworkers^5,6,9 and Troe and coworkers,^7,8,10–13 as detailed in ref. 41,45,47. The rate-coefficient calculations rely on the use of potentials that include the interaction between the charge of the ion and the electric multipole moments of the neutral molecules. Descriptions of this model along with the relevant equations can be found, e.g., in ref. 41,42. Here, we only summarize the main aspects.

We determine adiabatic long-range electrostatic interaction potentials between the ion (here He⁺) and the neutral molecule (here OCS or ¹³CO₂) for each individual molecular rotational level i that is significantly populated at the rotational temperature T_rot of the supersonic expansion. These potentials are given by

V_i^(L)(R) = V_L(R) + ΔE_i(R), (2)

where V_L = L²/(2μR²) − α′q²/(8πε₀R⁴) is the pure Langevin potential consisting of a centrifugal-potential term and a charge–induced-dipole attraction term¹⁶ and ΔE_i(R) represents the Stark shifts of the rotational levels of the neutral molecule induced by the field of the ion. Without considering ΔE_i, the Langevin potential V_L(R) gives rise to a rate constant k_L which is independent of the temperature and the collision energy, whereas the ΔE_i terms introduce a collision-energy dependence of the reaction rate coefficients. The Stark shifts ΔE_i of the rotational levels of OCS and ¹³CO₂ result from the charge–dipole (∝μ_elR⁻²) and charge–quadrupole (∝Q_zzR⁻³) interactions and are calculated by diagonalizing the Hamiltonian matrix [see eqn (9)–(11) in ref. 41] in the appropriate rigid-rotor basis using the known values of the molecular dipole and quadrupole moments, as listed in Table 1. The ΔE_i terms initially increase in magnitude at low fields as the distance between the ion and the molecule decreases and the molecule is exposed to the increasing (inhomogeneous) electric field of the ion.

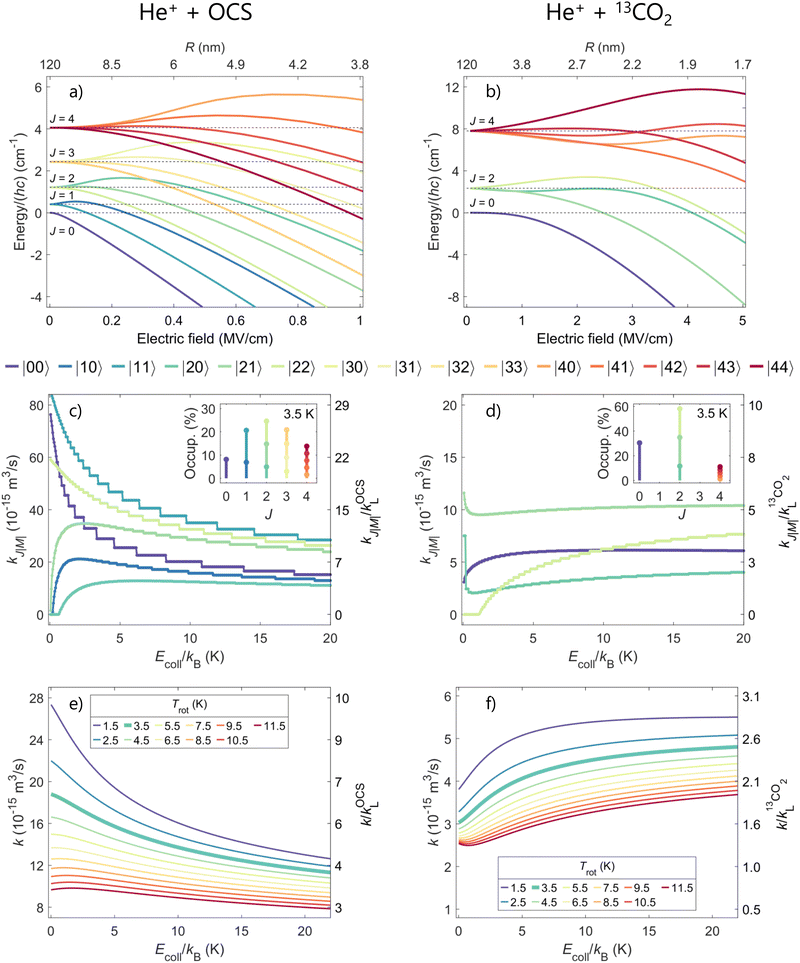
Panels (a) and (b) of Fig. 5 display the converged calculated Stark shifts of OCS and ¹³CO₂, respectively, in the field of the approaching He⁺ ion. The results are depicted as a function of the electric field [e/(4πε₀R²)] (bottom axis) and of the ion–molecule distance R (top axis) for all rotational levels with J ≤ 4, which are the ones significantly populated at T_rot = 3.5 K. The rotational state density of OCS is higher than that of ¹³CO₂ because B₀^OCS < B₀^13CO₂ and because, unlike in OCS [panel (a)], only even-J states are populated in ¹³CO₂ [panel (b)] as a result of nuclear-spin statistics. Moreover, OCS has a permanent electric dipole moment. Consequently, its rotational levels are subject to larger Stark shifts than those of ¹³CO₂. For example, the |00〉 state of OCS is shifted by −4 cm⁻¹ at a field of ∼0.4 MV cm⁻¹, whereas a field of ∼2.3 MV cm⁻¹ is needed to produce the same shift in ¹³CO₂.

Fig. 5 (a) and (b) Stark shifts of the rotational levels of OCS (a) and ¹³CO₂ (b) with J ≤ 4 in the field of the He⁺ ion. (c) and (d) Rotational-state-specific rate coefficients calculated for the reactions of He⁺ with OCS (c) and ¹³CO₂ (d) for J ≤ 2. State-averaged rate coefficients for the He⁺ + OCS (e) and the He⁺ + ¹³CO₂ (f) reactions corresponding to the sum of the state-specific rate coefficients weighted by the probabilities of occupation of the rotational states for rotational temperatures T_rot between 1.5 and 11.5 K and considering the collision-energy resolution. The bold green lines in panels (e) and (f) correspond to T_rot = 3.5 K and the corresponding occupation probability of the rotational levels is given in the insets of panels (c) and (d).

Negative (positive) Stark shifts lead to attractive (repulsive) potential terms which increase (decrease) the values of the rate coefficients. The state-specific reaction rate coefficients k_i resulting from the modified He⁺ + OCS and He⁺ + ¹³CO₂ interaction potentials are depicted in panels (c) and (d) of Fig. 5. They are displayed on an absolute scale (left axis) and normalized to their corresponding Langevin rates k_L (right axis) as a function of the collision energy. The rate coefficients of OCS are typically several times larger than those of ¹³CO₂, both on the absolute and on the k_L-normalized scale. The rate coefficients of the |00〉 and |11〉 rotational states in OCS [panel (c)], for example, exhibit a strong E_coll dependence and increase by factors of approximately 5 and 3, respectively, as the collision energy decreases from ~k_B ⋅ 20 K down to zero. This behavior is the consequence of the strong high-field-seeking character of these rotational states, as seen in panel (a).

The E_coll dependence of the state-specific rate coefficients of the He⁺ + ¹³CO₂ reaction is less pronounced because the charge-quadrupole interaction is weaker than the charge-dipole interaction and the zero-field spacings of the rotational levels are larger than in OCS [see panel (b)]. For both molecules, states exhibiting a low-field-seeking behavior such as the |22〉 state of ¹³CO₂ and the |20〉 state of OCS have vanishing rate coefficients at low collision energies [see panels (c) and (d) of Fig. 5].

The insets in panels (c) and (d) show the probabilities of occupation of the relevant states of OCS and ¹³CO₂ at the rotational temperature of the supersonic beam, which we estimate to be 3.5 K on the basis of the comparison with the calculated rotational-state-averaged rate coefficients and of similar experiments carried out with molecules such as N₂, NO, and CO for which the rotational temperature could be determined spectroscopically. These insets illustrate that more J levels are populated and contribute to the averaged He⁺ + OCS rate coefficient compared to the He⁺ + ¹³CO₂ reaction. To obtain the E_coll-dependent state-averaged reaction rate coefficients of the He⁺ + OCS [He⁺ + ¹³CO₂] reaction shown in panel (e) [(f)], we weighted the state-specific rate coefficients by the corresponding probabilities of occupation considering rotational temperatures between 1.5 K and 11.5 K. In both reactions, the calculations indicate that lowering the rotational temperature leads to an increase of the state-averaged rate coefficients, unlike in the He⁺ + NH₃ (ND₃)⁴¹ and D₂⁺ + NH₃ (ND₃)⁴³ reactions, and to a stronger E_coll dependence of the reaction rate coefficient. This effect is explained by the fact that, for both OCS and ¹³CO₂, the most strongly high-field-seeking states are the lower rotational levels, which have a higher probability of occupation at the lowest rotational temperatures.

The state-averaged rate coefficients of both reactions at the estimated rotational temperature of the neutral molecules (T_rot = 3.5 K) are displayed with a thick green line in panels (e) and (f) of Fig. 5, and are compared with experimental data in panels (d)–(f) of Fig. 4. The results of the experiments and calculations are in agreement for the three sets of experimental data depicted in Fig. 4 and for both the He⁺ + OCS and the He⁺ + ¹³CO₂ reactions. We attribute the very different dependences on E_coll and magnitudes of the rate coefficients of the He⁺ + OCS and He⁺ + ¹³CO₂ reactions to the fact that OCS—unlike ¹³CO₂—is a polar molecule with closely spaced rotational levels that are much more easily mixed by the inhomogeneous electric field of the approaching He⁺ ion.

At high electric fields, or, equivalently, at small ion–molecule distances, the quadratic Stark effect orients the dipole in OCS, which contributes to enhance the reaction rates, particularly at low collision energies. In contrast, the Stark shifts of ¹³CO₂, which has a negative quadrupole moment, reduce the state-averaged rate coefficient as E_coll approaches zero.⁴⁵¹³CO₂ thus displays the same behavior as N₂⁴⁵ and CO,⁴⁶ which also have negative quadrupole moments. Based on the calculations [see panel (d) of Fig. 5], one might be able to observe an increase of the rate coefficient in the He⁺ + ¹³CO₂ reactions at collision energies E_coll/k_B ≪ 1 K, below the E_coll/k_B > 200 mK accessible in the present experiments.

Fig. 6 compares the He⁺ + ¹³CO₂ thermal capture rate coefficients calculated as described in ref. 41 (blue line and dots) with earlier experimental thermal rate coefficients corresponding to the sum of the rates of the different product channels.^{61,63,65–67,69} Most of the experimental rate constants were measured at 300 K and only one at 70 K.⁶⁹ All experimental values are significantly smaller than the calculated capture rates. Agreement of the calculated rates with the experimental ones can be reached by scaling the former by a factor of ∼0.45, corresponding to the black curve. These results would suggest that only about half of the capture processes are reactive in this system, which is surprising for a barrier-free exothermic reaction. Theoretical calculations including the short-range interactions would be needed to fully account for the observed rate coefficients and branching ratios.

Fig. 6 Comparison of the calculated thermal rate coefficients of the He⁺ + ¹³CO₂ reaction (blue line and dots) and the experimental values of k(T) obtained in ref. 61,63,65–67,69 for He⁺ + CO₂. The black line and dots correspond to the calculated k(T) scaled by a factor of 0.45. The inset shows k(T) for temperatures between ∼0 and 10 K.

5 Competitive kinetics

As explained in Section 2, the use of an OCS:¹³CO₂ mixture with precise composition offers the possibility of measuring the dependence of their relative rate coefficients on the collision energy. We can relate the experimentally determined and the calculated rate-coefficient ratios using the equationwhere x^OCS and x^13CO₂ are the mole fractions of the two species (x^13CO₂/x^OCS = 3.305 in our experiments), and η^OCS and η^13CO₂ are the probabilities of reactive collision of the He⁺ + OCS and the He⁺ + ¹³CO₂ reactions, which need not be equal to 1 or to each other.

The calculations presented in Section 4 focus on the capture rate coefficients, and do not distinguish between capture processes leading to reaction products or (in)elastic collisions. Moreover, our experiment only monitors reactive channels and does not yield absolute rate coefficients because we do not measure the absolute concentrations of the reactants, only the relative ones. Using a mixture of molecular reactants with well-known concentrations, however, allows us to determine the ratio of the corresponding rate coefficients and its dependence on E_coll and, viaeqn (3), to extract the ratio of reactivities η⁽ⁱ⁾/η⁽ⁱⁱ⁾ assuming the validity of the capture model (see also ref. 72). This comparison relies on the assumptions that the detection efficiency is the same for all products, and that the density ratio of the reactants within the supersonic expansion is the same as in the prepared gas sample, which is equivalent to neglecting possible different expansion velocities and forward-velocity slips resulting from the different masses of the two species.

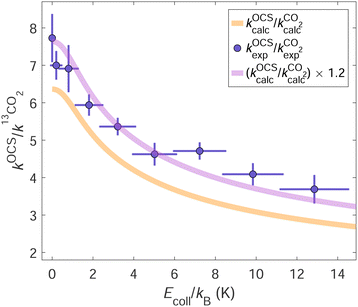
In Fig. 7, we show the ratio of the total product-ion yields of the He⁺ + OCS and the He⁺ + ¹³CO₂ reactions measured using the seeded (23.2 : 76.8) OCS:¹³CO₂ mixture (mole ratio) as a function of E_coll. The purple dots correspond to the experimentally measured sum of the CO⁺ and the CS⁺ product signals from the He⁺ + OCS reaction divided by the ¹³CO⁺ product signal from the He⁺ + ¹³CO₂ reaction and scaled by x^13CO₂/x^OCS. These product-ion signals are individually shown in panel (f) of Fig. 4.

Fig. 7 Rate-constant ratios of the He⁺ + OCS and the He⁺ + ¹³CO₂ reactions obtained experimentally using a OCS:¹³CO₂ gas mixture (purple dots) and predicted using adiabatic capture theory (orange line). The purple line is obtained by assuming that the collisions of He⁺ with OCS are 1.2 times as reactive as those with ¹³CO₂. The vertical error bars represent ±1σ and the horizontal bars the E_coll resolution.

The ratio of the calculated total capture rate coefficients of the two reactions (orange line) is smaller by about 20% than the experimentally measured ratio, but otherwise displays the same dependence on E_coll. This observation suggests that the He⁺ + OCS and the He⁺ + CO₂ collisions do not have the same probabilities of yielding products upon capture. Scaling the calculated rate-coefficient ratio by η^OCS/η^13CO₂ = 1.2 (purple line) leads to almost perfect agreement between calculations and experiment, which indicates that He⁺ + OCS capture processes are ∼20% more reactive than He⁺ + CO₂ capture processes. This result is obtained by considering T_rot = 3.5 K for both OCS and CO₂, which leads to the best agreement for the data presented in panel (f) of Fig. 4. If we allow T_rot to vary by ±1 K for each reactant, η^OCS/η^13CO₂ can vary from ∼1.05 to ∼1.3 while yielding reasonable agreement between the experimental and calculated results.

6 Conclusions

In this article, we have studied the reactions between He⁺ and CO₂ and OCS at low collision energies using the Rydberg-merged-beam approach.^34,36 The experiments were carried out using He:Ne-seeded supersonic beams of pure OCS and ¹³CO₂, as well as a (23.2 : 76.8) mixture of OCS and ¹³CO₂, to assess the roles of the dipole and quadrupole moments in these systems and to examine the relative rate constants under conditions of competitive kinetics. The studies of He⁺ + OCS and He⁺ + ¹³CO₂ using a single expansion containing both OCS and ¹³CO₂ further allowed us to verify that the observed kinetics do not depend on the composition of the supersonic expansions.

Two reaction channels with an E_coll-independent branching ratio were observed in the He⁺ + OCS reaction, leading to the formation of CO⁺ (∼70%) and CS⁺ (∼30%), but only one product ion (¹³CO⁺) was observed in the He⁺ + ¹³CO₂ reaction. Whereas the rate coefficient of the He⁺ + ¹³CO₂ → He + ¹³CO⁺ + O reaction decreases by ∼40% between ∼k_B ⋅ 30 K and zero, the overall rate coefficient of the He⁺ + OCS reaction increases by ∼75% over the same E_coll range. The reaction probabilities upon capture were estimated to be ∼20% larger in the He⁺ + OCS system. Comparing calculated thermal rate coefficients of the He⁺ + CO₂ reaction system with thermal rates at 70 K and 300 K determined in earlier studies suggests that only about half of the collisions are reactive in this system. Theoretical calculations including the short-range interactions would be needed for the full interpretation of the observed branching ratios and reaction probabilities.

Data availability

All essential data are included in the article. Further data may be obtained from the authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Daniel Zindel for the preparation of the gas mixtures, Josef A. Agner and Hansjürg Schmutz for the technical assistance, and Dr. Raphaël Hahn and David Schlander for fruitful discussions. This work was supported by the Swiss National Science Foundation (Grant No. 200020B 200478).

References

1. E. Herbst and W. Klemperer, Astrophys. J., 1973, 185, 505–533.
2. E. Roueff, Phys. Scr., 1987, 36, 319–322.
3. D. Smith, Chem. Rev., 1992, 92, 1473–1485.
4. T. P. Snow and V. M. Bierbaum, Ann. Rev. Anal. Chem., 2008, 1, 229–259.
5. D. C. Clary, D. Smith and N. G. Adams, Chem. Phys. Lett., 1985, 119, 320–326.
6. D. C. Clary, Ann. Rev. Phys. Chem., 1990, 41, 61–90.
7. J. Troe, J. Chem. Phys., 1987, 87, 2773–2780.
8. J. Troe, J. Chem. Phys., 1996, 105, 6249–6262.
9. T. Stoecklin, D. C. Clary and A. Palma, J. Chem. Soc., Faraday Trans., 1992, 88, 901–908.
10. E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2005, 122, 184311.
11. M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 084311.
12. M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 144315.
13. E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2016, 145, 244315.
14. V. G. Anicich and W. T. Huntress, Jr., Astrophys. J., Suppl. Ser., 1986, 62, 553–672.
15. V. Wakelam, I. W. M. Smith, E. Herbst, J. Troe, W. Geppert, H. Linnartz, K. Öberg, E. Roueff, M. Agúndez, P. Pernot, H. M. Cuppen, J. C. Loison and D. Talbi, Space Sci. Rev., 2010, 156, 13–72.
16. P. Langevin, Ann. Chim. Phys., 1905, T5, 245–288.
17. S. Willitsch, Chemistry with controlled ions, Advances in Chemical Physics, John Wiley & Sons, Inc., 2017, vol. 162, pp. 307–340.
18. Cold Chemistry: Molecular Scattering and Reactivity Near Absolute Zero, ed. O. Dulieu and A. Osterwalder, The Royal Society of Chemistry, 2017.
19. L. S. Petralia, A. Tsikritea, J. Loreau, T. P. Softley and B. R. Heazlewood, Nat. Commun., 2020, 11, 173.
20. J. Toscano, H. J. Lewandowski and B. R. Heazlewood, Phys. Chem. Chem. Phys., 2020, 22, 9180–9194.
21. A. Tsikritea, J. A. Diprose, T. P. Softley and B. R. Heazlewood, J. Chem. Phys., 2022, 157, 060901.
22. D. Gerlich, Low Temperatures and Cold Molecules, Imperial College Press, London, 2008, ch. 3, pp. 121–174.
23. R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001.
24. C. R. Markus, O. Asvany, T. Salomon, P. C. Schmid, S. Brünken, F. Lipparini, J. Gauss and S. Schlemmer, Phys. Rev. Lett., 2020, 124, 233401.
25. J. B. Marquette, B. R. Rowe, G. Dupeyrat, G. Poissant and C. Rebrion, Chem. Phys. Lett., 1985, 122, 431–435.
26. B. R. Rowe, A. Canosa and V. Le Page, Int. J. Mass Spectrom. Ion Processes, 1995, 149–150, 573–596.
27. S. Willitsch, M. T. Bell, A. D. Gingell and T. P. Softley, Phys. Chem. Chem. Phys., 2008, 10, 7200–7210.
28. O. A. Krohn, K. J. Catani, S. P. Sundar, J. Greenberg, G. da Silva and H. J. Lewandowski, J. Phys. Chem. A, 2023, 127, 5120–5128.
29. O. A. Krohn and H. J. Lewandowski, J. Phys. Chem. A, 2024, 128, 1737–1752.
30. P. Puri, M. Mills, C. Schneider, I. Simbotin, J. A. Montgomery Jr., R. Côté, A. G. Suits and E. R. Hudson, Science, 2017, 357, 1370–1375.
31. P. Puri, M. Mills, I. Simbotin, J. A. Montgomery Jr., R. Côté, C. Schneider, A. G. Suits and E. R. Hudson, Nat. Chem., 2019, 11, 615–621.
32. A. Voute, A. Dörfler, L. Wiesenfeld, O. Dulieu, F. Gatti, D. Peláez and S. Willitsch, Phys. Rev. Res., 2023, 5, L032021.
33. P. Allmendinger, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 043403.
34. P. Allmendinger, J. Deiglmayr, O. Schullian, K. Höveler, J. A. Agner, H. Schmutz and F. Merkt, Chem. Phys. Chem., 2016, 17, 3596–3608.
35. P. Allmendinger, J. Deiglmayr, K. Höveler, O. Schullian and F. Merkt, J. Chem. Phys., 2016, 145, 244316.
36. V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 125, 263401.
37. S. T. Pratt, J. L. Dehmer, P. M. Dehmer and W. A. Chupka, J. Chem. Phys., 1994, 101, 882–890.
38. E. Wrede, L. Schnieder, K. Seekamp-Schnieder, B. Niederjohann and K. H. Welge, Phys. Chem. Chem. Phys., 2005, 7, 1577–1582.
39. M. Matsuzawa, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 054701.
40. F. B. V. Martins, V. Zhelyazkova, Ch. Seiler and F. Merkt, New J. Phys., 2021, 23, 095011.
41. V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 21606–21622.
42. V. Zhelyazkova, F. B. V. Martins, S. Schilling and F. Merkt, J. Phys. Chem. A, 2023, 127, 1458–1468.
43. R. Hahn, D. Schlander, V. Zhelyazkova and F. Merkt, Phys. Rev. X, 2024, 14, 011034.
44. K. Höveler, J. Deiglmayr and F. Merkt, Mol. Phys., 2021, 119, e1954708.
45. V. Zhelyazkova, F. B. V. Martins, M. Žeško and F. Merkt, Phys. Chem. Chem. Phys., 2022, 24, 2843–2858.
46. F. B. V. Martins, V. Zhelyazkova and F. Merkt, New J. Phys., 2022, 24, 113003.
47. V. Zhelyazkova, F. B. V. Martins and F. Merkt, Phys. Chem. Chem. Phys., 2022, 24, 16360–16373.
48. K. Höveler, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 2676–2685.
49. F. J. Lovas, J. S. Coursey, S. A. Kotochigova, J. Chang, K. Olsen and R. A. Dragoset, NIST Standard Reference Database 117, 2003.
50. N. Chetty and V. W. Couling, Mol. Phys., 2011, 109, 655–666.
51. C. Graham, D. A. Imrie and R. E. Raab, Mol. Phys., 1998, 93, 49–56.
52. M. Gussoni, R. Rui and G. Zerbi, J. Mol. Struct., 1998, 447, 163–215.
53. T. N. Olney, N. M. Cann, G. Cooper and C. E. Brion, Chem. Phys., 1997, 223, 59–98.
54. M. P. Bogaard, A. D. Buckingham, R. K. Pierens and A. H. White, J. Chem. Soc., Faraday Trans., 1978, 74, 3008–3015.
55. G. Herzberg, Molecular Spectra and Molecular Structure, Volume III, Electronic Spectra and Electronic Structure of Polyatomic Molecules, Van Nostrand Reinhold Company, New York, 2nd edn, 1966.
56. D. Bailly and C. Rossetti, J. Mol. Spectrosc., 1984, 105, 229–245.
57. M. Tsuji, M. Matsuo and Y. Nishimura, Int. J. Mass Spectrom. Ion Phys., 1980, 34, 273–286.
58. H. Sekiya, M. Tsuji and Y. Nishimura, Chem. Phys. Lett., 1983, 100, 494–498.
59. H. Sekiya, M. Tsuji and Y. Nishimura, Bull. Chem. Soc. Jpn., 1984, 57, 3329–3330.
60. H. Chatham, D. Hils, R. Robertson and A. C. Gallagher, J. Chem. Phys., 1983, 79, 1301–1311.
61. V. G. Anicich, J. B. Laudenslager, W. T. Huntress, Jr. and J. H. Futrell, J. Chem. Phys., 1977, 67, 4340–4350.
62. J. B. Laudenslager, W. T. Huntress, Jr. and M. T. Bowers, J. Chem. Phys., 1974, 61, 4600–4617.
63. N. G. Adams and D. Smith, J. Phys. B: At. Mol. Phys., 1976, 9, 1439–1451.
64. N. G. Adams and D. Smith, Int. J. Mass Spectrom. Ion Phys., 1976, 21, 349–359.
65. W. Lindinger, D. L. Albritton and F. C. Fehsenfeld, J. Chem. Phys., 1975, 62, 4957–4958.
66. R. C. Bolden, R. S. Hemsworth, M. J. Shaw and N. D. Twiddy, J. Phys. B: At., Mol. Opt. Phys., 1970, 3, 45–60.
67. F. C. Fehsenfeld, A. L. Schmeltekopf, P. D. Goldan, H. I. Schiff and E. E. Ferguson, J. Chem. Phys., 1966, 44, 4087–4094.
68. Q. Guo, Y. Zhi, J. Hu and S. X. Tian, J. Phys. Chem. A, 2024, 128, 3821–3829.
69. B. R. Rowe, J. B. Marquette and C. Rebrion, J. Chem. Soc., Faraday Trans., 1989, 85, 1631.
70. V. Zhelyazkova, M. Žeško, H. Schmutz, J. A. Agner and F. Merkt, Mol. Phys., 2019, 117, 2980–2989.
71. C.-H. Chang and D. J. Nesbitt, J. Chem. Phys., 2015, 142, 244313.
72. F. B. V. Martins, V. Zhelyazkova, A. Osterwalder and F. Merkt, Chimia, 2023, 77, 221–224.

---

Footnote

† These authors contributed equally to this work.

---