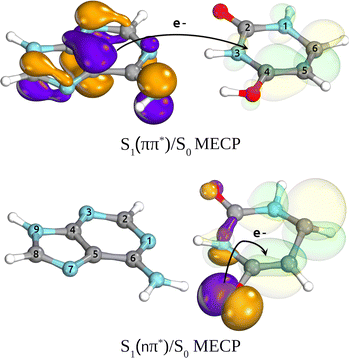Theoretical insight into photodeactivation mechanisms of adenine–uracil and adenine–thymine nucleobase pairs

Abstract

In this work, several plausible intra- and intermolecular photoinduced processes of the Watson–Crick base pairs of adenine with uracil (A–U) or thymine (A–T) according to the results of spin component scaling variant of algebraic diagrammatic construction up to the second order [SCS-ADC(2)] calculations are discussed. Although widely explored, these systems lack complete characterization of possible intramolecular relaxation channels perturbed by intermolecular interactions. In particular, we address the still open debate on photodeactivation via purine-ring puckering at the C2 or C6-atom position of adenine. We also show that the presence of low-lying, long-lived ¹nπ* states can be a significant factor in hindering relaxation via an electron-driven proton transfer process, as the population of these states can lead to an efficient intersystem crossing to a triplet manifold, the estimated rate of which is 1.6 × 10¹⁰ s⁻¹ which exceeds the corresponding internal conversion to the ground state by an order of magnitude. Additionally, the SCS variant of the ADC(2) method is shown to provide a more balanced description of valence and charge-transfer excited states.

---

1 Introduction

The photochemical and photophysical properties of nucleobases have been studied for decades.^1–8 Although widely explored, these systems continue to be an important subject of scientific curiosity due to the wide range of photodeactivation mechanisms under UV exposure and discrepancies regarding their mechanistic details.^5–7 The situation becomes much more complex in nucleic acids, where additional processes may occur, including the formation of delocalized excitonic and excimeric states, excitation energy transfer, intrastrand and interstrand electron and proton transfer processes, among others.^7,8 In general, in aggregates of nucleobases, the local intramolecular nonradiative decay processes compete with intermolecular processes, and the simplest model systems to study these processes are hydrogen-bonded or stacked nucleobase dimers.^9–29

Surprisingly, studies of these processes on an equal footing are scarce, even for canonical base pairs. Theoretical studies of base pairs generally focus on plausible intermolecular processes, in particular electron-driven proton transfer (EDPT),^9,30 which is agreed to be the main deactivation channel of the photoexcited gas-phase Watson–Crick (WC) guanine–cytosine (G–C) base pair. It is firmly established that in this system, the population of the dark charge-transfer (CT) state, associated with a significant electron density transfer from the purine to the pyrimidine, leads to a very efficient photoexcitation decay within ∼100 fs,^9,11,31,32 which causes a characteristic broad UV absorption band in the gas phase.³¹ The most likely mechanistic explanation of this process is the transfer of a proton from the N1 atom of guanine to the N3 atom of cytosine, which stabilizes the CT state and eventually leads to a crossing with the ground state in a barrierless manner.^7,9,23,33

Although a direct photoinduced EDPT process appears unlikely in DNA,²⁰ there are spectroscopic indications that it could be possible within the A–U pair in the A-form RNA double helix.³⁴ The photochemistry of adenine complexes with uracil (A–U) or thymine (A–T) has received less attention than G–C,^{10,13,15,16,27,35} and these have been studied mainly in the context of the plausibility of the spurious EDPT deactivation mechanism. Given the apparent similarities of uracil and thymine^34,36–38 and according to ab initio calculations, this mechanism should be possible in the WC base pair of A–T.^10,16,23,39 However, its experimental verification was hindered due to a different equilibrium geometry assumed in the gas phase.^40,41 Also, recent computational results of Jouybari et al.²⁷ did not yield the population of the CT state in nonadiabatic dynamics, which in this system is too far apart from the optically accessible locally excited (LE) state in the Franck–Condon region. Instead, the authors suggest that the main decay path of A–T involves a LE ¹ππ* transition on the thymine, which is consistent with the experimental findings. Femtosecond pump–probe ionization spectroscopy of A–T vapors indicates that after excitation to the lowest ¹ππ* state, internal conversion leads to the population of the ¹nπ* state having a lower energy, with a lifetime of 2.4 ps.⁴² In a subsequent study of Samoylova et al.¹³ an additional decay channel was observed with a lifetime of approximately 40 ps that was tentatively assigned to an intermolecular relaxation process.

In this work, we attempt to provide credible insight into plausible intra- and intermolecular photoinduced processes in the A–U and A–T WC base pairs. Although the photodynamics of isolated nucleobases is well known and there have been earlier attempts to describe the mechanism of photoinduced hydrogen transfer in canonical nucleobase pairs, the deactivation of the A–U and A–T base pairs through intramolecular channels has not been thoroughly studied.

2 Methods

The equilibrium geometries of the ground state were located using the second-order Møller–Plesset perturbation theory (MP2).⁴³ The relevant stationary points on the excited-state potential energy (PE) surfaces and the minimum energy crossing points (MECPs) of the adiabatic PE surfaces were found using the spin component scaling variants⁴⁴ of algebraic diagrammatic construction up to the second order (SCS-ADC(2))^45,46 or SCS-MP2 methods for the excited and ground electronic states, respectively. The vertical excitation energies and other excited-state properties were obtained using the SCS-ADC(2) method. In general, no symmetry constraints were imposed during geometry optimization. All of the above calculations were performed using the TURBOMOLE 7.3 package⁴⁷ and assuming the cc-pVTZ correlation-consistent basis set.⁴⁸

The relevant MECPs were located using the sequential penalty-constrained optimization proposed by Levine, Martinez, and Coe and implemented in the CIOpt package.⁴⁹ Potential energy profiles were calculated by linear interpolation in internal coordinates (LIIC) between stationary points using the same electronic structure calculation methods, i.e., the SCS-MP2 and SCS-ADC(2) methods and the cc-pVTZ basis set. The reliability of the SCS-MP2/SCS-ADC(2) PE profiles was tested against the multiconfigurational second-order n-electron valence state perturbation theory (NEVPT2) results obtained assuming the state-averaged (SA) complete active space self-consistent field (CASSCF) reference wavefunction and the cc-pVTZ basis set using the ORCA 4.2.1 package.⁵⁰ The active space in the NEVPT2 calculations included 10 electrons correlated in 8 orbitals. In the case of A–U the active space consisted of 3 occupied π, 2 occupied n and 3 virtual π* orbitals and was averaged over the two lowest-lying states; while in the case of A–T the active space consisted of 4 occupied π, 1 occupied n, 2 virtual π* and 1 virtual σ* orbital and was averaged over the four lowest-lying states. The orbitals included in the active spaces are plotted in the ESI.†

The intermolecular charge transfer character of the electronic states was assigned on the basis of the transition density matrix analysis proposed by Plasser et al.⁵¹ The charge transfer numbers defined as partial summations over squared transition density matrix elements of molecular fragments were calculated using the TheoDore 1.5.1 package.^51–53 These numbers were calculated based on Mulliken-type analysis⁵⁴ and were used to determine the weight of charge transfer configurations for a given state (denoted as Ω_CT). This quantity vanishes for localized or delocalized Frenkel excitonic states and approaches unity for charge transfer or charge resonance states.

The transition rates of radiative and nonradiative processes were calculated using the thermal vibration correlation function (TVCF) formalism for excited state decay, developed by Shuai et al.^55–57 and implemented in MOMAP 2020.B package.⁵⁸ The TVCF approach is based on the Fermi golden rule approximation reformulated into a time-dependent framework using a fast Fourier transformation of the Dirac delta function for vibrational states in the harmonic approximation, eliminating the need for the time-consuming exponential scaling summation over vibrational states. The manifolds of vibrational states for initial and final states were obtained in the harmonic approximation taking into account Duschinsky rotation effects. Due to the availability of non-adiabatic coupling terms, these calculations were performed using the TD-DFT approach, assuming ωB97X-D3 exchange–correlation functional and def2-SVP basis set available in the QChem 6.1 package.⁵⁹ Further details of these calculations are reported in the ESI.†

The conductor-like screening model (COSMO)⁶⁰ combined with the SCS-ADC(2) method was used to estimate the effects of solvation on the potential energy profiles. The vertical excitation energies in the FC region were calculated assuming nonequilibrium solvation with a slow part of the apparent surface charges equilibrated for the ground state and the fast part, depending on the refraction index, for the excited state, according to the iterative PTED scheme implemented in the TURBOMOLE package.

3 Results and discussion

3.1 Electronic states in the Franck–Condon region

The equilibrium geometries of the canonical WC base pairs A–U and A–T are presented in Fig. 1 with the corresponding bond lengths. Geometry optimization without symmetry constraints generally yields planar or quasiplanar structures of heterocyclic rings with minor deviations owing to the pyramidalization of amino groups or the presence of a methyl group. In the ESI† we also report other local minima of the A–U complexes located and the corresponding selected vertical excitation energies.

Fig. 1 Geometries of canonical nucleobases paired in the Watson–Crick scheme, optimized at the MP2/cc-pVTZ level of theory.

The located equilibrium geometries were assumed in consecutive single-point calculations of vertical excitation energies for 15 lowest-lying excited states. Table 1 presents vertical excitation energies for selected low-lying electronic states with corresponding oscillator strengths and assigned transition characters (the lower indices indicate the localization of a given orbital). The vertical spectra in the FC region are similar for both systems, with seemingly minor changes in the ordering of the corresponding excited states. In particular, in A–T the lowest-lying excited state of a character is located at 5.30 eV and is the S₃ excited state, whereas the is the S₄ excited state lying at 5.46 eV. This change may be relevant considering the subsequent population of the lower-lying LE state of ¹nπ* character and further relaxation on its hypersurface. The lowest ¹nπ* state is located at about 5.1 eV in both systems and is associated with the electronic transition from the carbonyl oxygen lone electron pair to the π* orbital localized on the aromatic ring of the respective pyrimidine.

Table 1 Properties of selected low-lying electronic states of canonical base pairs A–T and A–U, calculated using SCS-ADC(2)/cc-pVTZ method assuming the ground-state equilibrium geometries optimized using MP2/cc-pVTZ method. The oscillator strengths (f_osc), vertical excitation energies in eV (E_exc) and the weights of the CT configurations (Ω_CT) are reported. The last column shows the reference values of excitation energies calculated at the EOM-CC level^a

Base	State/transition	f osc	E exc	Ω CT	E ^EOM-CCexc
a EOM-CCSD/cc-pVDZ results adopted from Benda et al.^21 for A–T in the arrangement denoted WW1.
A–T		5.334 × 10^−5	5.11	0.050	5.24
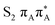
		0.015	5.19	0.008	5.34
		0.284	5.30	0.012	5.52
		0.239	5.39	0.009	5.60
		3.558 × 10^−4	5.64	0.044	5.65
		0.292	6.60	0.428
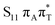
		0.238	6.66	0.505
		1.569 × 10^−4	6.90	0.102
A–U		9.254 × 10^−5	5.09	0.049
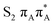
		0.017	5.19	0.007
		0.338	5.33	0.008
		0.178	5.46	0.009
		3.288 × 10^−4	5.65	0.041
		0.152	6.57	0.659
		0.373	6.65	0.260
		1.638 × 10^−4	6.93	0.137

---

It is interesting to note that the experimental results⁴² regarding the A–T dimer indicate that after excitation to the lowest ¹ππ* state, internal conversion leads to the population of the ¹nπ* state having a lower energy, with a lifetime of 2.4 ps. The same study shows that the nonradiative transition from the ¹ππ* to the ¹nπ* state through a conical intersection occurs at an ultrafast pace <100 fs (that assignment was based on Koopmans’ ionization correlations calculated at the TD-B3LYP/6-31++G(d,p) level). The ordering of states and the position of nπ* states in the singlet manifold are particularly important because they lie below both the CT and the lowest bright state in the FC region, increasing the probability of their population in the photodynamics of A–T/A–U.

Recently, we discussed an alternative EDPT process that occurs on the hypersurface of the guanine–cytosine (G–C) base pair.²⁵ However, analysis of natural transition orbitals revealed a minor weight of charge transfer configurations for the lowest-lying ¹nπ* states of A–U/A–T (denoted as Ω_CT in Table 1). The partial CT character of ¹nπ* excited states is observed only for higher-lying states (at about 6.9 eV). Therefore, we conclude that an analogous mechanism is not available from the FC region in the case of A–T and A–U base pairs. This may be one of the reasons why both thymine and uracil are more vulnerable to photodamage than cytosine in the nucleic acid duplex.⁶¹

Although ¹nπ* states usually have very weak spectral features due to negligible oscillator strength, trapping a molecule in such a dark reactive state could have significant consequences. Particularly interesting in this context is that ¹nπ* states can contribute to both photostability and photodamage of nucleic acids due to their long-lived character and the possibility of a population of triplet states in pyrimidines through efficient ISC.^62–65

As indicated in earlier studies, the charge transfer state of the ¹ππ* character lies substantially higher than the bright state. According to our SCS-ADC(2) calculations, the S₉ state is the lowest CT state located at 6.66 and 6.57 eV in the FC region, respectively, for A–T and A–U. This is more than 1.1 eV above the bright state (cf.Table 1) and significantly higher than previous CC2 estimates reported by Perun et al. (6.26 eV)¹⁰ and Benda et al. (6.29 eV).²¹ We refer to the latter article for an extensive discussion of the earlier computational results. In general, CC2 calculations estimate the CT state at about 0.6–0.8 eV above the bright state in the FC region,²¹ which compares well with the ADC(2) results (0.84 and 0.80 eV for A–T and A–U, respectively). However, the SCS scheme significantly destabilizes CT states,⁶⁶ thus bringing the SCS-ADC(2) results closer to the reference NEVPT2 values (see Fig. 2).

Fig. 2 LIIC between the FC region and MECP for WC A–U and A–T. The SCS-MP2/SCS-ADC2 results are plotted as solid (A–T) or dashed (A–U) lines. The corresponding NEVPT2 energies are shown as triangles (A–T) or circles (A–U).

Given that the population of the CT state can be challenging,^7,27 the excited-state dynamics of the studied base pairs is likely dominated by intramolecular processes. This conclusion is supported by transient electronic and vibrational absorption spectroscopies of the substituted A–T base pair.⁴⁰ It is also interesting to note that unlike in A–U the NEVPT2 PE profile for the EDPT process in A–T indicates a sloped topography of the MECP with the ground state (Fig. 2). Therefore, A–T can decay through a local ¹ππ* transition associated with purine puckering at the C2- or C6-atom position⁶⁷ or through processes involving ¹ππ* (ref. 27) and ¹nπ* transitions on pyrimidine.

Excitation decay through the EDPT channel in A–T/A–U WC base pairs appears unlikely or of secondary importance.^27,40,68,69 However, evidence of the EDPT decay channel involving H-bonded A–U base pairs, which has a relatively short timescale of 2.9 ps,³⁴ which is virtually identical to that reported by Röttger et al.⁷⁰ for the WC base pair of G–C, calls for a thorough theoretical investigation. These findings are rather unexpected considering also that a corresponding channel seems inaccessible in both the gas phase A–T and the double-stranded d(A)_n·d(T)_n duplex.²⁰ Given the apparent similarities of uracil and thymine, the same obstacles to detect EDPT should be assumed in the base pair A–U. Specifically, a negligible population of WC conformers in the gas phase (see ESI†) and the influence of the RNA environment that was discussed in several studies.^34,36–38 Consequently, investigation of the EDPT process in comparison to intramolecular excitation decay channels remains interesting, particularly in WC A–U.

Comparison of intra- and intermolecular deactivation mechanisms. The calculations started with optimization of the minima on the S₁ PE surfaces for A–T and A–U using the SCS-ADC(2)/cc-pVTZ method, initiated by forcing the transfer of a proton from adenine to thymine or uracil. The S₁/S₀ energy gaps dropped below 1 eV at the located S₁ minima; therefore, these geometries provided an excellent starting point to determine the MECPs between the S₁ and S₀ PE surfaces. Considering that the ¹nπ* dark LE state located on the pyrimidine moiety is the lowest lying singlet state for the A–U and A–T systems, a subsequent MECP optimization was performed in search of the photorelaxation channel on the ¹nπ* hypersurface.

A comparison of and 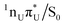MECPs found on the S₁ PE surface of the base pair A–U is presented in Fig. 3. The former, shown in the top panel, corresponds to the EDPT channel. The amino hydrogen transfer that follows the CT transition stabilizes the structure, and the most noticeable geometric changes are the elongation of the C4–O bond of U by 0.14 Å due to keto–enol tautomerization and the change in dihedral angle δ(H₅C₅C₆H₆) by almost 20°. In the latter intramolecular 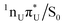conical intersection depicted in the lower panel, the WC A–U base pair undergoes local structural changes within the uracil molecule similar to those reported for S₁/S₀ of isolated uracil by Matsika⁷¹ or CI₁ and CI₃ conical intersections of isolated thymine reported by Perun et al.⁷² Compared to the equilibrium geometry of the ground state (cf.Fig. 1), this MECP shows out-of-plane (oop) pyramidalization of the pyrimidine ring atoms N3 and C6 (mostly the latter, hence denoted C6-oop(U)). Despite some similarities, the observed structural changes in the base pair are not as pronounced as in bare nucleobases, presumably due to the stabilization provided by the complementary base.

Fig. 3 Structures of the and minimum energy crossing points located using SCS-MP2/SCS-ADC(2)/cc-pVTZ method for A–U. Occupied (solid purple and orange) and virtual (translucent green and yellow) molecular orbitals for the leading amplitudes are shown indicating the orbital character of the corresponding S₁ state.

Further investigation included linear interpolation in internal coordinates (LIIC) between three stationary points: S₀ and S₁ minimum energy structures, and the corresponding S₁/S₀ MECPs. The potential energy profiles of the low-lying electronic state for the canonical A–U are shown in Fig. 4. There are three competing mechanisms that can lead to internal conversion to the ground state.

Fig. 4 Selected mechanisms of nonradiative deactivation of photoexcited A–U. The right PE cut along the amino N–H transfer shows EDPT through LE/CT and CT/S₀ MECPs, while the left plot presents relaxation through U puckering on the ¹nπ* or the ¹ππ* PE surface with respect to the interpolated ring-puckering coordinate plotted in mass-weighted Cartesian coordinates in .

On the right side of the plot, the potential energy cuts along the amino N–H distance indicate a decay path through LE/CT and CT/S₀ crossings via EDPT process. Although the barrier for this process exceeding 1 eV is most likely exaggerated due to interpolation, the CT state is apparently inaccessible from the lowest bright states. However, considering the substantial oscillator strengths of the S₉ and S₁₁ states that have a leading CT ¹ππ* contribution with the admixture of LE ¹ππ* configurations in the FC region, these could be directly populated by a UV-C pulse well below the ionization potential of the nucleobases.^73,74 This possibility of a direct population of the repulsive CT state could be interesting in the context of the prebiotic chemistry of nucleotides and further experimental investigations.

On the other hand, the two lowest LE states, namely the dark ¹nπ* and bright ¹ππ* are nearly degenerate along the first few steps of interpolation at the SCS-ADC(2) level, increasing the chance of internal conversion from the bright to the dark excited state of the ¹nπ* character. Although it is generally known that the population of the ¹nπ* state of thymine is strongly reduced in the polar solvent⁷⁵ and base pairing also destabilizes these transitions,^76,77 the presence of these low-lying and long-living states can be a significant factor in the observed relaxation impediment due to EDPT⁴² because their population can lead to other internal conversion processes and intersystem crossing to triplet states in pyrimidines.^62,64 Presumably, these channels may compete or even dominate in non-radiative deactivation processes of A–T or A–U. Taking into account experimental evidence of photorelaxation through the EDPT channel in the adenine homodimer,⁶⁸ it is worth considering that the processes involving pyrimidines are indeed an obstacle to effective relaxation through the exchange of protons along hydrogen bonds.

The locally excited 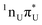state lies 0.24 eV below the S₃ bright state of a partial 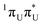character in the FC region. Thus, after photoexcitation to the bright state, there is an opportunity to cross with the lower lying ¹nπ* state in a barrierless manner and trigger the competing deactivation mechanism presented on the left side of Fig. 4. In this scenario, the excitation occurs on the surface of the S₁¹nπ* state toward the S₁ PE minimum along the deformation coordinate of the pyrimidine ring and then to the S₁/S₀ MECP. The latter lies 0.86 eV above the S₁ minimum and has a sloped topography. Nevertheless, considering that the energy of the bright state in the FC region lies above this MECP, internal conversion through this channel could be possible. However, it is more likely that population trapping occurs in the ¹nπ* state, possibly followed by an intersystem crossing (ISC) to a triplet manifold.

The credibility of S₁ → T₂ ISC is supported by the change in the molecular orbital character of the initial and final states and a substantial spin–orbit coupling between them. According to the SCS-ADC(2) calculations, the S₁ and T₂ states at the minimum of S₁ PE surface are nearly degenerate (cf.Table 2) and the mean SOC between them amounts to 58.3 cm⁻¹ (SA-2-CASPT2(12,10)/cc-pVTZ-DK results). Geometry optimization using the SCS-ADC(2) method on the T₂ PE surface leads to the S₁/T₂/T₁ states crossing at 4.12 eV. Therefore, considering the steeply sloped character of the corresponding S₁/S₀ MECP, the population of the S₁ state could decay through the ISC to the T₂ state and subsequent T₂/T₁ crossing.

Table 2 Selected excitation energies calculated at the minimum-energy geometry of the first excited state of A–U dimer using the SCS-ADC(2)/cc-pVTZ method. Subscripts A and U indicate the localization of a given molecular orbital on a particular nucleobase determined employing the NTO analysis

State/transition		E exc [eV]	f	Ω CT
T1		2.77	0.000	0.020
S1		2.83	1.47 × 10^−4	0.030
T2		2.90	0.000	0.014
S2		3.79	0.179	0.013
T3		4.14	0.000	0.010
T4		4.19	0.000	0.003

---

Indeed, the ISC transition rate between the and states calculated using the TVCF approach combined with ωB97X-D3/def2-SVP method amounts to 1.60 × 10¹⁰ s⁻¹, which is consistent with the k_ISC rate calculated for isolated uracil by Etinski et al. (2.60 × 10¹⁰ s⁻¹)⁷⁸ and Karak et al. (1.37 × 10¹¹ s⁻¹).⁷⁹ The calculated reverse ISC rate k_RISC of 3.99 × 10⁻³ s⁻¹ is negligible. Interestingly, the corresponding S₁–S₀ internal conversion k_IC rate is an order of magnitude smaller (1.29 × 10⁹ s⁻¹) while the radiative rate of this transition is a few orders of magnitude smaller (see ESI† for details). These results imply that the intersystem crossing to a triplet manifold may be of great importance in the WC A–U.

The suggested process occurring on the ¹nπ* state hypersurface is similar to that discussed by Böhnke et al.⁸⁰ in the WC 2-aminopurine–thymine dimer. In their findings based on time-resolved fluorescence and transient vibrational absorption spectroscopy supplemented with CC2 calculations, the authors conclude that one of the decay paths after excitation to ¹ππ* proceeds to a short-lived (<100 fs) intermediate state of ¹nπ* character, the population of which is partially recovered to the electronic ground state and partially transferred via ISC to the ³ππ* state.⁸⁰

According to the findings of Jouybari et al.²⁷ we also attempted to find the photorelaxation mechanisms that may occur on the ¹ππ* PE hypersurfaces of T and U. Indeed, the geometry optimization on the surface of the S₂ state proceeds to the crossing point with the ground state. We located the corresponding MECP of ¹ππ* LE state on U/T with S₀ that is associated with a twist of the C5–C6 bond and distortion of the C5 atom out of plane. It is located at 3.95 eV (4.03 eV) for A–U (A–T) and according to the performed LIIC (shown with gray dashed lines in Fig. 4) it corresponds to a barrierless deactivation from the FC region to a peaked conical intersection with the ground state.

Next, we discuss intramolecular processes involving adenine. It was previously reported that the population of the ¹ππ* state of 9H-adenine leads to a minimum on the S₁ PE surface, which is located near a crossing point with the ground state and the corresponding ¹ππ*/S₀ conical intersection associated with puckering of the C2 atom can be reached without an energy barrier.^81–85 The most accurate nonadiabatic dynamics simulations using the MRCIS and XMS-CASPT2 Hamiltonians^85–88 also indicated a second deactivation funnel responsible for ultrafast relaxation of adenine, which is the C6 ring-puckered channel. Although the latter is considered of secondary importance in the ab initio MRCI dynamics,^85,87 the results of surface hopping ADC(2) dynamics⁸⁹ find it to be equally contributing to the photodynamics of isolated adenine. Furthermore, for solvated adenine and polymeric (dA)₁₀ molecule, the C6 puckering process prevails over the C2 folding channel in the semiempirical MRCI dynamics.⁹⁰ The hydrogen bonding introduced by the complementary pyrimidine can, however, completely suppress this channel.⁶⁷ Therefore, to address this open question,⁴ it is relevant to investigate whether deactivation by puckering of the purine ring on the ¹ππ* PE surface is plausible in A–U and A–T WC base pairs.

A total of three MECP structures were located on the S₁ PE surface, corresponding to the LE transitions of adenine. All these structures correspond to puckering of the adenine ring, resulting in atoms C2 or C6 distorted out of the heterocyclic plane (denoted further as C6-oop(A) or C2-oop(A)).

The first two MECPs shown in the right part of Fig. 5 correspond to different modes of C2 atom distortion, either above or below the plane of the purine ring. The corresponding MECPs have been located and are shown along with the interpolated PE cuts from the FC region with respect to the mass-weighted displacement of the Cartesian coordinates. Both MECPs are easily accessible from the FC region, even though the LIIC path plotted with a dashed line shows a negligible PE barrier of 0.04 eV. The latter is likely an artifact of the interpolation procedure. The corresponding LE/S₀ MECP is shown as the bottom right structure in Fig. 5. It is characterized by an out-of-plane distortion of the C2 atom with a slight elongation of the adenine C2–N3 and C2–N1 bonds by 0.09 Å and 0.08 Å, respectively. The dihedral angle δ(N₁C₂N₃C₄) of adenine changes from 0° to 63.4° with respect to the ground state structure. This MECP is located 4.33 eV above the ground state, which is 0.49 eV lower than the other C2-puckered MECP and is easily accessible from the FC region.

Fig. 5 Potential energy cuts presenting radiationless deactivation mechanisms associated with the ring-puckering of adenine in the A–U base pair. The relative energies in eV are plotted against the respective interpolated ring-puckering mass-weighted coordinates in .

The alternative higher-lying C2-puckered MECP is presented to the top right of Fig. 5. It shows a significant displacement along the C2–N3 bond of adenine (elongated by 0.17 Å) and the dihedral angle δ(N₁C₂N₃C₄) that changed from 0° to −81.6°, with respect to the equilibrium geometry. This MECP features a slightly sloped topography; however, the energy barrier from the corresponding S₁ PE minimum to S₁/S₀ MECP amounts only to 0.28 eV, which is roughly a third of that found for ¹nπ*/S₀.

We also located the C6-puckered MECP in the A–T and A–U base pairs. The corresponding structure and interpolated PE profile for A–U are shown in the left part of Fig. 5. This MECP is characterized by the elongation of the adenine N1–C6 bond by 0.13 Å and the change in the dihedral angle δ(C₂N₁C₆C₅) from 0° to −42.2°. This MECP also features an out-of-plane distortion of the –NH₂ group and is the most distorted of all puckered structures, as indicated by the mass-weighted displacement of the Cartesian coordinates. The dihedral angle between the N9–C8 bond of adenine and the N1–C2 bond of uracil, δ([A]N₉C₈–N₁C₂[U]), changes from 0° to 88.8°. As with the previously discussed C2-puckering paths, the C6-puckering mechanism appears to be easily accessible from the FC region, although the corresponding MECP has a slightly sloped topography.

Geometry optimization on the excited state PE surface for A–U and A–T leads to the minimum, even though we were able to locate the corresponding minimum energy structure of isolated adenine. This may be a consequence of the formation of hydrogen bonds involving the N1 lone electron pair, which results in an increased energy of nπ* transitions.²¹

The mechanisms discussed so far are mainly related to the isolated WC A–U/A–T base pairs, and these are plotted schematically in Fig. 6 for A–U. The analogous scheme for the WC A–T is very similar and is shown in Fig. S7 of the ESI.† The relative energies of the excited-state minima and MECPs are within 0.01–0.05 eV. The major difference is in the ordering of LE ¹ππ* states located on different nucleobases, which should not affect the mechanisms discussed.

Fig. 6 Schematic representation of the investigated radiationless deactivation mechanisms in the A–U base pair. The values show energies relative to the ground state in eV. Ring-puckering paths are labeled with puckered base and the most distorted ring atom, e.g. C6-oop(U) indicates uracil atom C6 distorted out of plane.

The photochemistry of nucleosides is obviously much more complex, since it involves quite a few isomers and the possibility of formation of intramolecular hydrogen bonds and additional deactivation channels. Interesting case studies can be found, for example, in papers by Tuna et al.,⁹¹ Janicki et al.⁹² or Mansour et al.⁹³ Nonetheless, to gain some insight into the effects of glycosidic bond formation, we investigated the key stationary points for methylated base pairs. We located minimum energy structures of the ground state, first excited state, and MECPs after introducing the methyl groups at the N1 atom of uracil and N9 of adenine. The results presented in Table S3 of the ESI† show minor relative energy differences (below 0.05 eV) between the optimized S₁ excited states minima and the respective MECPs associated with the selected deactivation mechanisms.

We also attempted to investigate the effects of the environment on the vertical excitation energies of key excited states in the FC region of the A–U base pair using the SCS-ADC(2)/COSMO approach. Vertical excitation energies were calculated within the nonequilibrium model. We selected dielectric constants characteristic for water (ε = 78.34), as the most relevant polar solvent, and for chloroform (ε = 4.8). The results presented in Table S2 of ESI† indicate relatively minor solvatochromic shifts of the relevant states that are usually below 0.1 eV. Although the order of LE states in the complex is slightly changed, the order of low-lying states located at a given nucleobase stays the same as in vacuum. Thus, the solvation effects should not affect the qualitative conclusions. The vertical excitation energies of the lowest ¹nπ* states are generally blueshifted by roughly 0.1 eV in either chloroform or water but these dark states are still found below the lowest-lying bright state. Interestingly, the CT state is red-shifted by nearly 0.2 eV in the chloroform but not in water. This solvent was previously suggested to be a good representative of the dielectric environment within a DNA double helix.^70,94,95 Therefore, the general discussion of the potential deactivation mechanisms in the A–U is virtually unaffected by solvation and, in fact, may strengthen our conclusions.

It is worth emphasizing that the distortion of all the discussed intramolecular MECPs from the quasi-planar structure, especially the MECPs associated with puckering of C2 and C6 atoms of adenine, question the plausibility of these paths in DNA and RNA structures. However, a comparison of selected structural parameters with data derived from crystallographic and molecular dynamics databases indicates that only the C6-puckered(A) MECP geometry does not fit the determined ranges of parameters and may be unattainable in the nucleic acids. This discussion continues in Section 7 of the ESI.†

3.2 Validation of the computational protocol

It should be noted that initially the PE profiles were computed using the MP2 method for the ground state and the ADC(2) method for the excited states. These were further compared with the results of the spin component scaling variants⁹⁶ of these methods (that is, SCS-MP2 and SCS-ADC(2)), assuming the same interpolated geometries. Recent studies indicated that the SCS variant of the CC2 method essentially alleviates the underestimation of excitation energies (i.e. excessive stabilization) of CT, Rydberg and nπ* states.⁶⁶ Since the ADC(2) method suffers from similar problems, considering the formal similarities between the ADC(2) and CC2 methods, the SCS variant should produce a more balanced description of the valence and CT states.

The accuracy of the chosen methodology was tested against the results obtained using the state-averaged strongly-contracted n-electron valence perturbation method (SC-NEVPT2) assuming the same interpolated geometries. The complete active space in NEVPT2 calculations included 10 electrons correlated in 8 orbitals (3 occupied π, 2 occupied n and 3 virtual π*). Such active space was reported to be correct for an appropriate description of the CT states.⁹⁷ It can be concluded from Fig. 7 that the SCS-ADC(2) method returns reliable energies of the ¹ππ* states that agree well with the NEVPT2 results, in stark contrast to the ADC(2) approach, which systematically underestimates the energies of the CT and ¹nπ* states. The excitation energies obtained using the SCS-ADC(2) method are slightly underestimated for the ¹nπ* states. It is also well documented that hydrogen bonding destabilizes the ¹nπ* states in WC base pairs,^21,80 and their description is more demanding than the ¹ππ* states.

Fig. 7 Selected mechanism of nonradiative deactivation of photoexcited A–U. On the right PE cut along the amino N–H transfer shows EDPT via LE/CT and CT/S₀ and on the left relaxation through U puckering on the ¹nπ* surface is schematically presented with respect to the interpolated ring-puckering plotted in mass-weighted Cartesian coordinates in .

Note that the interpolated PE profiles of the S₀ state calculated using different variants of the ADC(2) method (shown with solid and dashed green lines) are virtually identical. However, there is a substantial difference between the SCS-ADC(2) or NEVPT2 results and the ADC(2) results for the CT state (black lines or triangles) and the ¹nπ* state (red lines), particularly in the close proximity of the conical intersection region. It shows that although the choice of the theoretical approach does not affect the description of the PE surface in the ground state, it is essential to determine the PE surfaces of the CT and ¹nπ* states, and hence the MECPs with these surfaces. The SCS approach is also advantageous in the context of intermolecular interaction among nucleobases. The dispersion interaction in base pairs has been indicated to be substantially overestimated by MP2 method^98,99 which is to some extent corrected when the SCS-MP2 variant is used. Therefore, in the discussion, we focus on the results of SCS-MP2/SCS-ADC(2) calculations.

4 Conclusions

To sum up, our calculations indicate that all intramolecular channels involving either pyrimidine or purine ring distortion should be accessible from the FC region. Thus, we infer that multiple alternative relaxation pathways for A–U and A–T coexist, possibly making detection of the EDPT process more difficult in the examined systems. The latter process, even though apparently inaccessible from the lowest-lying bright state, could in principle occur after direct population of the CT state by the UV-C pulse.

The C6 and C2-puckered adenine MECPs (C6-oop(A) and C2-oop(A)) with peaked topography appear to be slightly more plausible than the C2-puckered adenine (with different ring-distortion) and the N3/C6 puckered uracil or thymine ¹nπ*/S₀ MECPs (C6-oop(U/T)) with a sloped topography. The close proximity of two bright states (shown in blue and gray lines in Fig. 5) strengthens the possibility of non-radiative deactivation by puckering of adenine. Furthermore, geometric constraints within nucleic acids appear to diminish the probability of photorelaxation on the 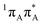hypersurface associated with the C6-atom puckering of adenine in the base pairs A–U and A–T in favor of the puckering of the C2 atom.

It should be underlined that experimental studies of A–T photodynamics conclude that it is dominated by intramonomer processes, involving a population of ¹nπ* states.^42,100 Indeed, according to our calculations, there is no barrier on ¹nπ* A–U/A–T PE surfaces between the FC region and the S₁ minimum of the ¹nπ* character. The corresponding LE/S₀ MECPs have a strongly sloped topography with a substantial barrier of 0.86–0.87 eV. However, the near-degeneracy of the S₁ and T₂ states and the fact that they are strongly coupled through spin–orbit interaction indicate an efficient intersystem crossing, whose estimated rate of 1.6 × 10¹⁰ s⁻¹, exceeds by an order of magnitude the corresponding internal conversion to the ground state.

Author contributions

K. S. performed most of the calculations, analyzed the data with R. W. G. and wrote the first draft of the manuscript, which was edited by R. W. G. All authors participated in conceptualization of the research which was supervised by R. W. G.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by a grant no. 2021/41/N/ST4/04532 from the National Science Centre Poland. The authors acknowledge the resources provided by the Wrocław Centre of Networking and Supercomputing (WCSS). K. S. acknowledges the assistance of Dr. Rafał Szabla and thanks for the discussions.

References

1. C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2020.
2. C. T. Middleton, K. d L. Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernández and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239.
3. K. Kleinermanns, D. Nachtigallová and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342.
4. M. Barbatti, A. C. Borin and S. Ullrich, Photoinduced Phenomena in Nucleic Acids I, Springer International Publishing, Cham, 2014, vol. 355, pp. 1–32.
5. A. Giussani, J. Segarra-Martí, D. Roca-Sanjuán and M. Merchán, Photoinduced Phenomena in Nucleic Acids I: Nucleobases in the Gas Phase and in Solvents, Springer International Publishing, Cham, 2015, pp. 57–97.
6. S. Mai, M. Richter, P. Marquetand and L. González, Photoinduced Phenomena in Nucleic Acids I: Nucleobases in the Gas Phase and in Solvents, Springer International Publishing, Cham, 2015, pp. 99–153.
7. R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593.
8. L. Martinez Fernandez, F. Santoro and R. Improta, Acc. Chem. Res., 2022, 55, 2077–2087.
9. A. L. Sobolewski, W. Domcke and C. Hattig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906.
10. S. Perun, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2006, 110, 9031–9038.
11. G. Groenhof, L. V. Schäfer, M. Boggio-Pasqua, M. Goette, H. Grubmüller and M. A. Robb, J. Am. Chem. Soc., 2007, 129, 6812–6819.
12. P. R. Markwick, N. L. Doltsinis and J. Schlitter, J. Chem. Phys., 2007, 126, 01B623.
13. E. Samoylova, T. Schultz, I. Hertel and W. Radloff, Chem. Phys., 2008, 347, 376–382.
14. K. B. Bravaya, O. Kostko, M. Ahmed and A. I. Krylov, Phys. Chem. Chem. Phys., 2010, 12, 2292–2307.
15. Y.-J. Ai, F. Zhang, G.-L. Cui, Y. Luo and W.-H. Fang, J. Chem. Phys., 2010, 133, 064302.
16. J. P. Gobbo, V. Sauri, D. Roca-Sanjuan, L. Serrano-Andres, M. Merchan and A. C. Borin, J. Phys. Chem. B, 2012, 116, 4089–4097.
17. P. G. Szalay, T. Watson, A. Perera, V. Lotrich and R. J. Bartlett, J. Phys. Chem. A, 2013, 117, 3149–3157.
18. M. K. Shukla and J. Leszczynski, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 637–649.
19. L. Blancafort and A. A. Voityuk, J. Chem. Phys., 2014, 140, 095102.
20. Y. Zhang, K. de La Harpe, A. A. Beckstead, R. Improta and B. Kohler, J. Am. Chem. Soc., 2015, 137, 7059–7062.
21. Z. Benda and P. G. Szalay, Phys. Chem. Chem. Phys., 2016, 18, 23596–23606.
22. V. A. Spata, W. Lee and S. Matsika, J. Phys. Chem. Lett., 2016, 7, 976–984.
23. B. Marchetti, T. N. V. Karsili, M. N. R. Ashfold and W. Domcke, Phys. Chem. Chem. Phys., 2016, 18, 20007–20027.
24. I. Conti and M. Garavelli, J. Phys. Chem. Lett., 2018, 9, 2373–2379.
25. K. E. Szkaradek, P. Stadlbauer, J. Šponer, R. W. Góra and R. Szabla, Chem. Commun., 2020, 56, 201–204.
26. L. J. Karas, C.-H. Wu, H. Ottosson and J. I. Wu, Chem. Sci., 2020, 11, 10071–10077.
27. M. Y. Jouybari, J. A. Green, R. Improta and F. Santoro, J. Phys. Chem. A, 2021, 125, 8912–8924.
28. J. A. Green, M. Yaghoubi Jouybari, H. Asha, F. Santoro and R. Improta, J. Chem. Theory Comput., 2021, 17, 4660–4674.
29. S. Hartweg, M. Hochlaf, G. A. Garcia and L. Nahon, J. Phys. Chem. Lett., 2023, 14, 3698–3705.
30. T. Schultz, E. Samoylova, W. Radloff, I. V. Hertel, A. L. Sobolewski and W. Domcke, Science, 2004, 306, 1765–1768.
31. A. Abo-Riziq, L. Grace, E. Nir, M. Kabelac, P. Hobza and M. S. De Vries, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 20–23.
32. P. R. Markwick and N. L. Doltsinis, J. Chem. Phys., 2007, 126, 05B603.
33. A. L. Sobolewski and W. Domcke, Europhys. News, 2006, 37, 20–23.
34. R. C.-T. Chan, C. Ma, A. K.-W. Wong, C. T.-L. Chan, J. C.-L. Chow and W.-M. Kwok, J. Phys. Chem. Lett., 2022, 13, 302–311.
35. M. Dargiewicz, M. Biczysko, R. Improta and V. Barone, Phys. Chem. Chem. Phys., 2012, 14, 8981–8989.
36. K. H. Johnson, D. M. Gray and J. C. Sutherland, Nucleic Acids Res., 1991, 19, 2275–2280.
37. M. Pollum, L. Martinez-Fernandez and C. E. Crespo-Hernandez, Photoinduced Phenomena in Nucleic Acids I: Nucleobases in the Gas Phase and in Solvents, 2015, pp. 245–327.
38. S. Reiter, D. Keefer and R. de Vivie-Riedle, J. Am. Chem. Soc., 2018, 140, 8714–8720.
39. G. Villani, Chem. Phys., 2005, 316, 1–8.
40. K. Röttger, H. J. Marroux, A. F. Chemin, E. Elsdon, T. A. Oliver, S. T. Street, A. S. Henderson, M. C. Galan, A. J. Orr-Ewing and G. M. Roberts, J. Phys. Chem. B, 2017, 121, 4448–4455.
41. M. Kratochvíl, J. Šponer and P. Hobza, J. Am. Chem. Soc., 2000, 122, 3495–3499.
42. E. Samoylova, H. Lippert, S. Ullrich, I. V. Hertel, W. Radloff and T. Schultz, J. Am. Chem. Soc., 2005, 127, 1782–1786.
43. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
44. S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102.
45. A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299.
46. A. Dreuw, A. Papapostolou and A. L. Dempwolff, J. Phys. Chem. A, 2023, 127(32), 6635–6646.
47. TURBOMOLE v7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.com.
48. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
49. B. G. Levine, J. D. Coe and T. J. Martinez, J. Phys. Chem. B, 2008, 112, 405–413.
50. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
51. F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106.
52. F. Plasser, S. A. Bäppler, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024107.
53. F. Plasser, J. Chem. Phys., 2020, 152, 084108.
54. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
55. Q. Peng, Y. Yi, Z. Shuai and J. Shao, J. Chem. Phys., 2007, 126, 114302.
56. Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, J. Phys. Chem. A, 2010, 114, 7817–7831.
57. Z. Shuai, Chin. J. Chem., 2020, 38, 1223–1232.
58. Y. Niu, W. Li, Q. Peng, H. Geng, Y. Yi, L. Wang, G. Nan, D. Wang and Z. Shuai, Mol. Phys., 2018, 116, 1078–1090.
59. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184–215.
60. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799.
61. S. Mouret, C. Baudouin, M. Charveron, A. Favier, J. Cadet and T. Douki, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13765–13770.
62. P. M. Hare, C. E. Crespo-Hernández and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 435–440.
63. R. Szabla, H. Kruse, J. Šponer and R. W. Góra, Phys. Chem. Chem. Phys., 2017, 19, 17531–17537.
64. A. J. Pepino, J. Segarra-Martí, A. Nenov, I. Rivalta, R. Improta and M. Garavelli, Phys. Chem. Chem. Phys., 2018, 20, 6877–6890.
65. J. Dezalay, M. Broquier, S. Soorkia and G. Grégoire, Eur. Phys. J. D, 2021, 75, 1–11.
66. A. Tajti and P. G. Szalay, J. Chem. Theory Comput., 2019, 15, 5523–5531.
67. Y. Lu, Z. Lan and W. Thiel, Angew. Chem., 2011, 123, 6996–6999.
68. I. Hünig, C. Plützer, K. A. Seefeld, D. Löwenich, M. Nispel and K. Kleinermanns, ChemPhysChem, 2004, 5, 1427–1431.
69. C. E. Crespo-Hernández, B. Cohen and B. Kohler, Nature, 2005, 436, 1141–1144.
70. K. Röttger, H. J. B. Marroux, M. P. Grubb, P. M. Coulter, H. Böhnke, A. S. Henderson, M. C. Galan, F. Temps, A. J. Orr-Ewing and G. M. Roberts, Angew. Chem., Int. Ed., 2015, 54, 14719–14722.
71. S. Matsika, J. Phys. Chem. A, 2004, 108, 7584–7590.
72. S. Perun, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2006, 110, 13238–13244.
73. D. Roca-Sanjuán, M. Rubio, M. Merchán and L. Serrano-Andrés, J. Chem. Phys., 2006, 125, 084302.
74. K. Lewis, K. Copeland and G. Hill, Int. J. Quantum Chem., 2014, 114, 1678–1684.
75. J. Cerezo, Y. Liu, N. Lin, X. Zhao, R. Improta and F. Santoro, J. Chem. Theory Comput., 2018, 14, 820–832.
76. F. Santoro, V. Barone and R. Improta, ChemPhysChem, 2008, 9, 2531–2537.
77. F. Santoro, V. Barone and R. Improta, J. Am. Chem. Soc., 2009, 131, 15232–15245.
78. M. Etinski, J. Serb. Chem. Soc., 2011, 76, 1649–1660.
79. P. Karak, T. Moitra, K. Ruud and S. Chakrabarti, Phys. Chem. Chem. Phys., 2023, 25, 8209–8219.
80. H. Böhnke, K. Röttger, R. A. Ingle, H. J. Marroux, M. Bohnsack, N. K. Schwalb, A. J. Orr-Ewing and F. Temps, J. Phys. Chem. B, 2019, 123, 2904–2914.
81. S. Perun, A. L. Sobolewski and W. Domcke, J. Am. Chem. Soc., 2005, 127, 6257–6265.
82. L. Blancafort, J. Am. Chem. Soc., 2006, 128, 210–219.
83. L. Serrano-Andres, M. Merchan and A. C. Borin, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8691–8696.
84. L. Serrano-Andrés, M. Merchán and A. C. Borin, J. Am. Chem. Soc., 2008, 130, 2473–2484.
85. M. Barbatti, Z. Lan, R. Crespo-Otero, J. J. Szymczak, H. Lischka and W. Thiel, J. Chem. Phys., 2012, 137, 22A503.
86. M. Barbatti and H. Lischka, J. Am. Chem. Soc., 2008, 130, 6831–6839.
87. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458.
88. J. W. Park and T. Shiozaki, J. Chem. Theory Comput., 2017, 13, 3676–3683.
89. F. Plasser, R. Crespo-Otero, M. Pederzoli, J. Pittner, H. Lischka and M. Barbatti, J. Chem. Theory Comput., 2014, 10, 1395–1405.
90. Y. Lu, Z. Lan and W. Thiel, J. Comput. Chem., 2012, 33, 1225–1235.
91. D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 122–127.
92. M. J. Janicki, C. L. Kufner, Z. R. Todd, S. C. Kim, D. K. O'Flaherty, J. W. Szostak, J. Šponer, R. W. Góra, D. D. Sasselov and R. Szabla, J. Phys. Chem. Lett., 2021, 6707–6713.
93. R. Mansour, J. M. Toldo and M. Barbatti, J. Phys. Chem. Lett., 2022, 13, 6194–6199.
94. K. Siriwong, A. A. Voityuk, M. D. Newton and N. Rösch, J. Phys. Chem. B, 2003, 107, 2595–2601.
95. J. Mazur and R. L. Jernigan, Biopolymers, 1991, 31, 1615–1629.
96. A. Hellweg, S. A. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 4119–4127.
97. C. Zuluaga, V. A. Spata and S. Matsika, J. Chem. Theory Comput., 2020, 17, 376–387.
98. S. M. Cybulski and M. L. Lytle, J. Chem. Phys., 2007, 127, 141102–141102-4.
99. P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
100. C. Canuel, M. Mons, F. Piuzzi, B. Tardivel, I. Dimicoli and M. Elhanine, J. Chem. Phys., 2005, 122, 074316.

---

Footnote

† Electronic supplementary information (ESI) available: Conformational analysis, selected excitation energies, spin–orbit couplings, results of transition rate calculations and a scheme of deactivation mechanisms for the A–T WC base pair. See DOI: https://doi.org/10.1039/d4cp02817a

---