The effect of heavy atoms on the deactivation of electronic excited states of dye molecules near the surface of metal nanoparticles

Abstract

The influence of a heavy atom and the plasmon field on the efficiency of populating the lowest triplet state (T₁) and on the phosphorescence intensity has been studied for fluorescein, 2Br-fluorescein, eosin and erythrosine, which have an increasing number of substituted heavy atoms. We show that the heavy atoms affect not only the rate constant of intersystem crossing (k_ISC) but also the rate constant of internal conversion (k_IC). The calculations show that the C–H bonds in the meso position are the primary acceptors of the excitation energy of the lowest excited electronic singlet state (S₁). Substitution of the meso hydrogen atoms with I or Br leads to a smaller k_IC rate constant of 1 × 10⁸ s⁻¹ for fluorescein to 8 × 10⁶ s⁻¹ for eosin. Substitution with heavy atoms also leads to a larger ISC rate constant (k_ISC) between the T₂ and S₁ states because the spin–orbit coupling matrix element 〈S₁|H_SO|T₂〉 increases by two orders of magnitude from 0.36 cm⁻¹ for fluorescein to 35.0 cm⁻¹ for erythrosine. The phosphorescence rate constant increases by three orders of magnitude from 4.8 × 10 s⁻¹ for fluorescein to 3.3 × 10⁴ s⁻¹ for erythrosine, which is supported by experimental data. The plasmon effect increases the intensity of the xanthene dye emissions. The intensity and the quantum yield of fluorescence increase in the series fluorescein < 2Br-fluorescein < eosin < erythrosine. The intensity of the delayed fluorescence and phosphorescence grows in the same way. The enhancement factor of the phosphorescence intensity increases from 1.8 to 5.6 in the series from fluorescein to erythrosine. The differences in the plasmon effect originate from intensity borrowing to the radiative triplet–singlet transition (T₁ → S₀) from the singlet–singlet transitions (S_n → S₀), which is more efficient when molecules have heavy atoms in the meso position.

---

1. Introduction

Triplet states of organic dyes play a decisive role in many photophysical and photochemical processes. The population of the triplet states depends on the size of the spin–orbit coupling (SOC), which can be enhanced by substituting heavy atoms to the molecule.¹ Thus, introducing a heavy atom into a luminophore molecule increases the rate constant of intersystem crossing (k_ISC) that is responsible for populating triplet states from the singlet manifold. The intersystem crossing (ISC) rate constant between singlet and triplet states is proportional to the square of the SOC matrix element.² The presence of a heavy atom leads to an increased phosphorescence intensity.

Due to the sensitivity of the phosphorescence to temperature, molecular aggregation, and quenching by molecular oxygen, it is also utilized in other contexts. Due to the long phosphorescence lifetime, it is also used in biomedical applications and bioimaging.^3,4 Phosphorescence plays a crucial role in studies of the electronic structure of organic molecules.^2,5 Intense phosphorescence emission is necessary when constructing materials for chemiluminescent and luminescent sensors, OLED and PHOLED systems, up-conversion devices, and anti-counterfeiting and data-encryption materials.^6–9

A modern method to enhance phosphorescence is to utilize the plasmon effect of metal nanoparticles (NPs). The impact of the plasmon effect of metal NPs on the phosphorescence of organic dyes was considered in ref. 10–16. We recently developed a quantum chemical method for calculating the phosphorescence quantum yield of molecules in the vicinity of plasmonic NPs.¹⁷ The calculations showed that the maximum quantum yield of phosphorescence is obtained when the molecule is 4–6 nm from the NP surface.¹⁷

Heavy atoms and the plasmon effect of metal NPs enhance the phosphorescence efficiency, which is observed as a decrease in the quantum yield of fluorescence, accompanied by an increase in the phosphorescence intensity. We investigate here the two effects separately and together for xanthene molecules by systematically increasing the number of heavy atoms. The studied molecules are fluorescein, 2Br-fluorescein, 4Br-fluorescein (eosin Y, 2′,4′,5′,7′-tetrabromofluorescein), and 4I-fluorescein (2′,4′,5′,7′-tetraiodofluorescein, erythrosine B), which are often used for labeling and probing biomolecules in biomedical research.^18–21 Fluorescein and its derivatives have large absorption cross-sections, high fluorescence quantum yield, and the ability to attach to biomolecules, especially to amide groups.²² Since their lifetime and quantum yield of phosphorescence are sensitive to the surrounding medium, they can be used as detectors or media sensors in microenvironmental studies.^23,24 The phosphorescence of erythrosine and the rose bengal dye is often used for determining the oxygen content in samples.²⁵ The lowest excited triplet state of the xanthene dyes is used in photosensor reactions for generating reactive singlet oxygen species.^26–28

Internal conversion (IC) between the S₁ and S₀ states competes with the ISC from S₁ to T_n and affecting thereby the population of the lowest excited states. The IC rate constant (k_IC) can be made smaller by replacing C–H bonds with C–D or C–X, where X is a heavier atom.^29,30 The competition between the IC and ISC processes of the studied molecules has not been previously examined. In this work, we have also performed quantum chemical calculations of k_IC for the xanthene dyes and studied how it changes when substituting fluorescein with heavy atoms.

2. Experimental and computational details

2.1. Materials and methods

The molecular structures of the studied xanthene dyes are shown in Fig. 1. They were purchased from Sigma Aldrich. Fluorescein was of BioReagent HPLC grade, while the other xanthene dyes had a purity of at least 95%.

Fig. 1 The molecular structures of the studied xanthene dyes.

Silver island films (SIFs) were synthesized using silver nitrate (AgNO₃), sodium hydroxide (NaOH), ammonium hydroxide (NH₄OH), D-glucose, and polyvinyl alcohol (PVA) for the polymer films. All reagents were of analytical grade purity from Sigma Aldrich. Ultrapure water obtained from the Smart S15 UVF system (Drawell) was used in the sample preparations.

Films of the dyes in PVA were spin-coated at 3000 rpm either on the SIFs or on clean glass substrates, which were used as reference samples. The dye concentration in the 5 wt% polymer was 5 × 10⁻⁴ mol L⁻¹. Microweighing was used to control the thickness of the films on the different substrates. The mass of the dye films on the glass surfaces and on the SIFs was almost identical.

The silver island films were prepared as described in ref. 31 and 32. The synthesized SIFs consisted of particles with an average diameter of 95 ± 31 nm,^17,31 which was determined by scanning electron microscopy using a Mira 3LMU (Tescan). The absorption spectrum of the SIFs exhibits a broad band in the visible range of the spectrum.

2.2. Spectroscopical methods

The absorption and fluorescence spectra were measured using a Cary-300 and an Eclipse spectrometer (Agilent), respectively. Fluorescence decay kinetics were recorded in time-correlated single photon counting (TCSPC) mode using a TCSPC system (Becker&Hickl) with excitations by a diode laser at λ_gen = 488 nm and τ = 120 ps (Becker&Hickl). The lifetimes were estimated using the SPC Image software (Becker&Hickl). The quality of the fit was assessed by the χ² test.

Delayed fluorescence (DF) and phosphorescence spectra were measured after the Xe lamp flash (300 μs) using the Eclipse spectrometer (Agilent). The decay kinetics of the DF and the phosphorescence of the dye films were recorded using an FLS1000 spectrometer (Edinburgh Instr.). The samples were photoexcited at λ_gen = 532 nm using an Nd:YAG laser (SolarLS). The quantum yield of fluorescence (φ_fl) of the investigated samples was estimated by the absolute method^31,33 using an integrating sphere AvaSphere 30-REFL coupled to an AvaSpec-ULS2048 spectrometer (Avantes), with the Nd:YAG laser and the OPO system (SolarLS) as a monochromatic light source.

2.3. Computational methods

Fluorescein, 2Br-fluorescein, eosin, and erythrosin in solution can exist in various charged forms across a wide pH range.^18,34–36 However, as demonstrated in ref. 18, 36 and 37, the most intense transition between the singlet ground state (S₀) and the first excited singlet state (S₁) occurs for molecules in the dianionic form. The dianionic form of xanthene dyes was therefore chosen in the present study. Optimization of the molecular geometry in the S₁ and T₁ states was performed using the density functional theory (DFT) and time-dependent DFT (TD DFT) methods with the B3LYP functional,³⁸ 6-31++G(d,p) basis set and polarizable continuum model (PCM)³⁹ with ethanol as solvent. The calculations were carried out with Gaussian 16.⁴⁰ The B3LYP functional was chosen since it reproduced experimental data very well,^37,41 and the 6-31++G(d,p) basis set with diffuse functions is appropriate for the present electronic structure calculations.

The rate constants for IC (k_IC), ISC (k_ISC), and for radiative (k_r) electronic transitions were calculated using a computational approach developed by Valiev et al. as described in ref. 17,42–45. Estimating rate constants requires calculations of nonadiabatic coupling matrix elements (NACME) and spin–orbit coupling matrix elements (SOCME), which were calculated using Gaussian 16 and the MOLSOC code.⁴⁶ The phosphorescence rate constants (k_phos) were computed using the Dalton code.^2,47

3. Results and discussion

3.1. The heavy atom effect on the deactivation of excited states of the xanthene dyes

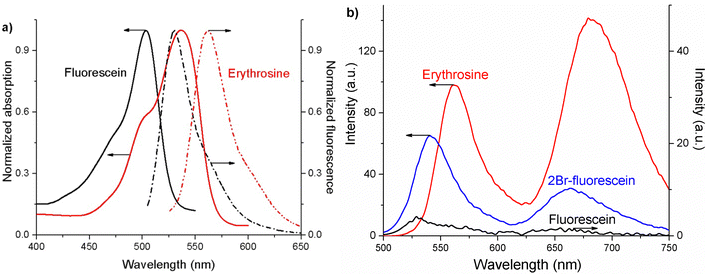
The xanthene dyes absorb in the range of 400–600 nm, while they fluoresce in the range of 500–650 nm. Experimental studies (Fig. 2(a)) show that a bathochromic shift is observed in the absorption and the fluorescence spectra of the xanthene dyes when increasing the number and mass of the substituted heavy atoms (Table 1). Their fluorescence lifetime (τ_fl) also decreases when substituting heavy atoms to the meso positions (Table 1). The experimental fluorescence lifetime of fluorescein is 4.5 ± 0.15 ns, whereas for erythrosine, it is 0.6 ± 0.15 ns.

Fig. 2 (a) Normalized absorption (solid lines) and fluorescence (dashed lines) spectra of fluorescein and erythrosine in PVA. (b) The delayed fluorescence and phosphorescence spectra of fluorescein, 2Br-fluorescein and erythrosine in PVA.

Table 1 The wavelength of the maximum of the absorption spectra (λ^abs_max in nm), the wavelength of the maximum of the fluorescence spectra (λ^fl_max in nm), and the fluorescence lifetime (τ_fl ± 0.15 in ns) of fluorescein and its derivatives in PVA. The quantum yield of fluorescence (φ_fl) in ethanol is compared to literature values reported in ref. 18

Dye	λ ^absmax	λ ^flmax	τ fl ± 0.15	φ fl ± 0.03
a Reported in ref. 18.
Fluorescein	502	530	4.5	0.97 [0.97]^a
2Br-fluorescein	514	545	4.1	0.60 [0.62]^a
Eosin	525	551	1.8	0.67 [0.69]^a
Erythrosine	535	560	0.6	0.11 [0.08]^a

---

The measured quantum yields of fluorescence in ethanol solutions correlate well with data published in ref. 18 and 48. The quantum yield of luminescence decreases with increasing number and mass of halogen atoms in the xanthene dyes. The observed decrease in the fluorescence lifetime and the quantum yield can be attributed to the heavy atom effect.¹ For Br- or I-substituted fluorescein dyes, the decay from the S₁ state is faster than for unsubstituted fluorescein. The S₁ state decays both to the ground state S₀ and to the lower-lying triplet states due to the large SOC leading to faster ISC transitions and a higher concentration of molecules in the triplet state, which results in a stronger delayed fluorescence (DF) and phosphorescence (Fig. 2(b)).

The long-lived luminescence spectra exhibit two bands corresponding to DF and phosphorescence, which are bathochromically shifted to longer wavelengths in the series fluorescein < 2Br-fluorescein < eosin < erythrosine (Table 2). The DF of the investigated dyes has a thermally activated nature, which is well-known for the studied xanthene dyes.^49,50 The DF is due to the thermally activated reverse ISC from T₁ to the S₁ state. The phosphorescence is stronger for erythrosine and eosin as compared to that of fluorescein and 2Br-fluorescein.

Table 2 The wavelength of the maximum (λ_max in nm) of spectra, the power-law exponent n (dimensionless)^a and part of contribution (A₁ in %) of a this part of decay kinetics into total luminescence decay curve, the lifetimes (τ in ms)^b and part of contribution (A₂ in %) of exponential part of decay kinetics into total luminescence decay curve for delayed fluorescence (upper part of the table) and phosphorescence (lower part of the table) of the xanthene dyes

Dye	λ max	I∼t^−n	A 1	τ ± 0.2	A 2
a Power-law exponent n was estimated when the decay curve of luminescence was approximated by a power law I∼t^−n in the time range of t = 0–0.5 ms. b The lifetime τ was estimated when the decay curve of luminescence was approximated with mono-exponent law.
Delayed fluorescence
Fluorescein	535	0.20 ± 0.01	16	3.80	84
2Br-fluorescein	545	0.16 ± 0.01	12	3.70	88
Eosin	550	0.25 ± 0.01	6	3.20	94
Erythrosine	560	—	—	0.68	—
Phosphorescence
Fluorescein	645	0.17 ± 0.01	12	3.30	88
2Br-fluorescein	660	—	—	3.20	—
Eosin	680	—	—	3.00	—
Erythrosine	685	—	—	0.70	—

---

The decay kinetics of the DF of the fluorescein, 2Br-fluorescein and eosin films do not follow the mono-exponent decay law (Fig. 3). The DF lifetime (τ) decreases with increasing number and mass of halogen atoms. The shorter lifetimes of the DF and phosphorescence of erythrosine are due to an increasing deactivation channel from the T₁ state to both the S₀ and the S₁ states because the molecules containing heavy atoms have a stronger SOC than fluorescein.

Fig. 3 The decay kinetics of the intensity of the delayed fluorescence of fluorescein and its derivatives in PVA.

In condensed media, the decay of triplet states can occur via both monomolecular (1) and (2) and bimolecular (3) processes:

T₁ → S₀ + hν_phos phosphorescence; (1)

T₁ [long arrow, wavy then straight] S₁ → S₀ + hν_DF thermally activated DF; (2)

T + T → [T⋯T] → S₁ + S₀ → 2S₀ + hν_ADF triplet–triplet annihilation (TTA). (3)

The decay kinetics of the phosphorescence and the thermally activated DF is described by a mono-exponent decay. In homogeneous media, the TTA rate constant is time independent and the annihilation DF (ADF) decays exponentially with a lifetime given by τ_ADF = τ_Phos/2, where τ_ADF is the ADF lifetime and τ_Phos is the phosphorescence lifetime.^51,52

In solid heterogeneous structures, the TTA process annihilates closely spaced triplet pairs. The luminescence intensity is then determined by the number of these pairs. Due to the different distance between the pairs, the TTA rate constant is time dependent implying that the intensity of the ADF decay becomes non-exponential. In the early stage of the decay, the intensity of the ADF can be approximated by a power law (I∼t⁻ⁿ).^53,54

The DF intensity of fluorescein, 2Br-fluorescein, and eosin was approximated by a power law (I∼t⁻ⁿ) in the beginning of the emission (at t = 0–0.5 ms), while the shape of the later part of the DF decay is exponential. The power-law exponent (n) contribution (A₁) of 16% is larger for fluorescein than for 2Br-fluorescein. For eosine, the A₁ contribution is only 6% of the entire DF suggesting that the TTA process is more important in fluorescein films immediately after sample excitation than for eosin. This is also supported by the decay of the phosphorescence intensity of fluorescein that is well described by a power law in the initial part of the decay curve and by a mono-exponential decay law for longer times of the decay curve. The later part (t > 0.5 ms) of the DF intensity decay is due to reverse ISC from the T₁ to the S₁ state, since the lifetimes of the DF and the phosphorescence are similar. The triplet annihilation of the DF is more efficient in fluorescein than for other dyes because the SOC is weaker. This leads to slower transitions of the T₁ states to the S₀ and S₁ states via phosphorescence or ISC. The almost absent TTA process in the eosin and erythrosine films can be explained by the heavy atom effect that causes a fast transition to the triplet state, which then rapidly undergoes the radiative T₁ → S₀ transition and reverse ISC T₁ [long arrow, wavy then straight] S₁. This mechanism is supported by the short phosphorescence lifetimes of eosin and erythrosine (Table 2).

Quantum chemical calculations of the radiative and non-radiative rate constants of electronic transitions and of the energy levels were performed to understand the experimental data. The results of the calculations are summarized in Table 3. The calculated energies of the S₁ state of the investigated molecules agree within 0.2 eV with the experimental data. The T₁ state is the only excited state located below S₁. The energy gap of 0.7–0.8 eV between the S₁ and T₁ states of the xanthene dyes is large.

Table 3 Calculated and experimental (in parenthesis) ground-state excitation energies (in eV) of the S₁, T₁ and T₂ states, the spin–orbit coupling matrix elements (〈S₁|H_SO|T₁〉 and 〈S₁|H_SO|T₂〉 in cm⁻¹), rate constants (k in s⁻¹) of photophysical processes of the xanthene dyes, and phosphorescence lifetimes (τ^calc_phos in ms) are reported

	Fluorescein	2Br-fluorescein	Eosin	Erythrosine
S1	2.43 (2.34)	2.42 (2.27)	2.44 (2.25)	2.39 (2.23)
T1	1.64 (1.92)	1.67 (1.88)	1.72 (1.82)	1.67 (1.81)
T2	2.56	2.50	2.49	2.49
〈S1|HSO|T1〉	0.17	3.95	1.14	0.9
〈S1|HSO|T2〉	0.36	12.6	26.8	35.0
k ISC(S1 → T1)	2.5 × 10^3	3.0 × 10^6	3.5 × 10^5	2.0 × 10^5
k IC(S1 → S0)	1 × 10^8	1 × 10^8	8 × 10^6	6 × 10^7
k r (S1 → S0)	3.6 × 10^8	3.5 × 10^8	3.5 × 10^8	8 × 10^7
k phos(T1 → S0)	4.8 × 10^1	4.0 × 10^2	2.1 × 10^3	3.3 × 10^4
τ ^calcphos	21.00	2.50	0.47	0.03

---

The ISC rate constant between the S₁ and T₁ states (k_ISC(S₁ → T₁)) is small since it is proportional to the square of the small 〈S₁|H_SO|T₁〉 matrix element.^17,55 The ISC process cannot compete with IC and the radiative decay process of the S₁ state. The 〈S₁|H_SO|T₁〉 matrix element for fluorescein is also much smaller than for 2Br-fluorescein, eosin and erythrosine, whose k_ISC(S₁ → T₁) is significantly larger due to the presence of the heavy atoms (Fig. 4). The experimentally observed decrease in the quantum yield of fluorescence φ_fl in the series from fluorescein to erythrosine cannot be explained by considering only the transition channel between S₁ and T₁.

Fig. 4 The Jablonsky diagram for fluorescein and erythrosine. The rate constants are given in s⁻¹.

The calculations show that there is another triplet state (T₂) slightly above S₁. The energy gap ΔE_S1T2 between T₂ and S₁ is only 0.1 eV implying that the T₂ state is populated through the thermally activated process, whose efficiency depends strongly on the Boltzmann factor.¹⁷ We did not consider the rate constant of the reversed ISC process from the T₂ to the S₁ state in the calculation of the fluorescence quantum yield φ_fl because the accuracy of the quantum chemical calculation of the excitation energies is ∼0.2 eV, which is not accurate enough to estimate a reliable Boltzmann factor. Calculations in ref. 37 showed that the excitation energy of the T₂ state is very sensitive to environmental effects and in some cases, T₂ may even be below the S₁ state. The calculated 〈S₁|H_SO|T₂〉 matrix element increases from 0.36 to 35.0 cm⁻¹ in the series from fluorescein to erythrosine. The calculated phosphorescence rate constants (k_phos(T₁ → S₀)) in Table 3 correlate well with the number and mass of the heavy atoms. The k_phos(T₁ → S₀) rate constants increase in the series from fluorescein to erythrosine. The calculated phosphorescence lifetimes (τ^calc_phos) also correlate well with experimentally measured total lifetimes of phosphorescence τ_Phos, which are 3.3 ms for fluorescein and 0.7 ms for erythrosine. The total phosphorescence lifetime is not caused only by the phosphorescence radiative process but also through non-radiative channels.¹⁷

The k_IC(S₁ → S₀) rate constants for eosin and erythrosine in Table 3 are significantly smaller than for fluorescein and 2Br-fluorescein. The k_IC(S₁ → S₀) rate constants were obtained by using an approximate computational method that accounts only for contributions from the C–H bonds, which has been previously shown to be the dominating contribution to the IC rate constant.⁵⁶ The main contribution to k_IC(S₁ → S₀) originates from the C–H bonds in the meso-positions (Fig. 5).

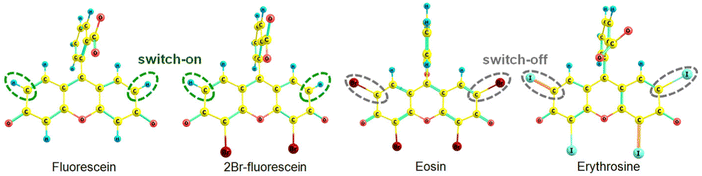Fig. 5 The most important accepting bonds in the internal conversion process are surrounded by the dashed lines.

When hydrogen atoms in the meso positions are replaced by iodine or bromine atoms, the bonds to the meso carbon atoms do not contribute significantly to the IC rate constant, leading to a smaller k_IC(S₁ → S₀) rate constant. The calculations show how the heavy atoms affect the IC rate constant of the studied xanthene dyes.

3.2. The plasmon effect

There were no noticeable changes in the position of the absorption and emission bands when the dye films were deposited on a SIF surface instead of on a glass surface. The measurements showed that the plasmon effect of the SIF significantly increases the absorbance of the studied dyes (Table 4), leading to an increase in the optical density (D) at the maximum of the absorption band.

Table 4 Changes due to the plasmon effect in the optical density (D), the integral intensity of fluorescence (I_fl), the fluorescence quantum yield (φ_fl), the delayed fluorescence (I_DF) and the phosphorescence (I_Phos) intensity as well as their lifetimes (τ_fl, τ_DF, τ_Phos) for the xanthene dyes were measured in PVA

Molecule	D ^SIF/D^glass	I ^SIFfl/I^glassfl	ϕ ^SIFfl/ϕ^glassfl	I ^SIFDF/I^glassDF	ϕ ^SIFPhos/ϕ^glassPhos
Optical density, intensities, quantum yield
Fluorescein	1.1	1.8	1.83	1.7	1.8
2Br-fluorescein	2.1	2.0	1.87	2.5	2.6
Eosin	2.5	4.1	3.73	4.1	4.0
Erythrosine	3.2	7.6	5.60	5.5	5.6

---

	τ ^SIFfl/τ^glassfl	τ ^SIFDF/τ^glassDF	τ ^SIFPhos/τ^glassPhos
Lifetimes
Fluorescein	0.96	0.59	0.92
2Br-fluorescein	0.93	0.77	0.90
Eosin	0.86	0.98	0.97
Erythrosine	0.83	0.98	0.99

---

The larger D value is due to the presence of the silver particles and because the films have different thicknesses. To eliminate the influence of the thickness of the film, the absorption spectrum of the SIF with the dye films was measured and corrected for the absorption spectrum recorded for the same SIF before the dye film was deposited on it. The substrate with a pure dye film and with the SIF and the dye sample were weighted showing that their masses were almost identical. Thus, the observed change in the optical density is due to the plasmon effect of the SIF. The larger optical density leads to a significant increase in the fluorescence intensity.

The observed increase in the fluorescence intensity (I_fl) is not only due to the changes in D but also due to an increase in the quantum yield of fluorescence (φ_fl) and the decrease in the fluorescence lifetime (τ_fl). Thus, the stronger intensity is due to the plasmon enhancement of the radiative emission from the S₁ state to the S₀ state.^31,57–59 The increase in I_fl and φ_fl grows in the series from fluorescein to erythrosine because the plasmon effect is larger for photo processes of lower efficiency.^58,59

The enhancement of the DF and phosphorescence is larger for the xanthene dyes having heavy atoms. The amplification coefficients of the DF and the phosphorescence are between 1.7 and 5.6 for the studied dyes. The observed differences in the plasmon effect on the long-lived luminescence of the xanthene dyes are due to a larger intensity borrowing of the T₁ → S₀ transition from the S₁ → S₀ transition in the molecules with heavy atoms, which was also verified by calculating SOC values (Table 3).

4. Conclusion

The synergy of the effects of heavy atoms and plasmons on the luminescence properties of xanthene dyes was investigated. Experimental data showed that the presence of heavy atoms leads to a decrease in the lifetime of the excited singlet state and the fluorescence quantum yield. Substituting heavy atoms to the molecules results in a faster ISC transfer to the triplet state, as evidenced by the enhanced intensity and reduced lifetimes of the phosphorescence and the DF. Analysis of the decay of the phosphorescence and the DF shows that for unsubstituted fluorescein, the initial part of the decay is due to the TTA process. With increasing the number and mass of the heavy atoms, the contribution from TTA to the decay of the T₁ state decreases because the phosphorescence and the DF are faster.

The heavy atom effect was also studied using quantum chemical calculations. The influence on the rate constants of IC (k_IC(S₁ → S₀)), phosphorescence (k_phos(T₁ → S₀)), and ISC (k_ISC(S₁ → T₁)) was investigated. The calculations showed that substitution of a heavy atom in specific positions leads to a decrease in k_IC(S₁ → S₀), from 1 × 10⁸ s⁻¹ for fluorescein to 6 × 10⁷ s⁻¹ for erythrosine and 8 × 10⁶ s⁻¹ for eosin. The slower IC process is due to fewer good acceptor modes of the electronic excitation energy for the non-radiative transition between the S₁ and S₀ states.

The rate constant of phosphorescence increases by an order of magnitude in the series from fluorescein to erythrosine because the number and mass of heavy atoms increase in that series. The 〈S₁|H_SO|T₂〉 matrix element increases with the number and mass of the heavy atoms. The present study suggests that the lowest triplet state T₁ is populated via two channels: through the ISC between the S₁ and T₁ states and through the IC between the T₂ and T₁ states. The calculated IC rate constant for the T₂ [long arrow, wavy then straight] T₁ transition is about 10¹¹ s⁻¹.

The plasmon effect significantly enhances the absorbance, which is reflected in the increased optical density at the maximum of the absorption band. The increase in the intensity and the quantum yield of fluorescence grows in the series of fluorescein < 2Br-fluorescein < eosin < erythrosine. The enhancement of the DF and the phosphorescence is larger for the halogenated molecules. The phosphorescence of fluorescein is enhanced by a factor of 1.8, and for erythrosine, it is 5.6 times stronger. The differences in the plasmon effect can be attributed to the intensity borrowing of the intensity of the radiative triplet–singlet transition (T₁ → S₀) from singlet–singlet transitions (S_n → S₀), which is larger for molecules with heavy atoms.

The obtained results show that the phosphorescence efficiency of organic dyes can be significantly enhanced by taking advantage of both the heavy-atom effect of substituents and the plasmonic effect of metal NPs. Strongly phosphorescent dyes are useful in biomedical research and in the development of sensor devices, OLED and PHOLED systems, anti-counterfeiting and data encryption materials.

Author contributions

N. I.: conceptualization, methodology, resources, project administration, writing – review and editing; E. S.: investigation, data curation, validation and visualization, writing – original draft, writing – review and editing; R. V.: methodology, conceptualization, calculations; modelling, software, writing – original draft, writing – review and editing; A. A.: investigation, formal analysis; D. S.: conceptualization, data validation, writing – review and editing. The authors have discussed the obtained results and contributed equally to the final version of the manuscript.

Data availability

Quantum chemical software utilized: (1) The optimized molecular structures, excitation energies, and matrix elements of spin-orbital coupled interaction operators were computed using GAUSSIAN 16 [https://gaussian.com/gaussian16/] and MOLSOC [https://github.com/gaox-qd/pysoc]. The results of these calculations are compiled and discussed in detail in the main text of the article. (2) The intramolecular rate constants were determined using proprietary code developed by Valiev and colleagues: [https://pubs.rsc.org/en/content/articlelanding/2020/cp/d0cp03231j]. (3) The working expressions for intermolecular rate constants, along with the initial parameters, are provided and discussed within the main text. (4) All measured photophysical values are reported in the main text of the article, with detailed measurement procedures described.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP14870117). This work has been supported by the Academy of Finland through projects 340582 (RRV) and 340583 (DS). We thank CSC – IT Center for Science, Finland for computer time.

References

1. S. P. McGlynn, T. Azumi and M. Kinoshita, Molecular Spectroscopy of the Triplet State, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1969.
2. G. Baryshnikov, B. F. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500–6537.
3. B. Chang, J. Chen, J. Bao, T. Sun and Z. Cheng, Chem. Rev., 2023, 123(24), 13966–14037.
4. R. Knoblauch, B. Bui, A. Raza and Chris D. Geddes, Phys. Chem. Chem. Phys., 2018, 20, 15518–15527.
5. M. Stanitska, D. Volyniuk, B. Minaev, H. Agren and J. V. Grazulevicius, J. Mater. Chem. C, 2024, 12, 2662–2698.
6. R. E. Bangle, H. Li and M. H. Mikkelsen, ACS Nano, 2023, 17, 24022–24032.
7. M. S. Weaver, M. A. Fusella, R. Saramak, R. Bushati, H. Mundoor, V. M. Menon, N. J. Thompson and J. J. Brown, J. Mater. Chem. C, 2022, 10, 4182–4186.
8. Z. Zhou, X. Xie, Z. Sun, X. Wang, Z. An and W. Huang, J. Mater. Chem. C, 2023, 11, 3143–3161.
9. M. Ji and X. Ma, Ind. Chem. Mater., 2023, 1, 582–594.
10. T. M. Chmereva, M. G. Kucherenko, F. Yu Mushin and A. P. Rusinov, J. Appl. Spectrosc., 2024, 91, 1–9.
11. H. Mishra, B. L. Mali, J. Karolin, A. I. Dragan and C. D. Geddes, Phys. Chem. Chem. Phys., 2013, 15, 19538–19544.
12. Y. Zhang, K. Aslan, M. J. R. Previte, S. N. Malyn and C. D. Geddes, J. Chem. Phys. B, 2006, 110, 25108–25114.
13. M. Meng, F.-L. Zhang, J. Yi, L.-H. Lin, C.-L. Zhang, N. Bodappa, C.-Y. Li, S.-J. Zhang, R. F. Aroca, Z.-Q. Tian and J.-F. Li, Anal. Chem., 2018, 90, 10837–10842.
14. S. Bidault, A. Devilez, V. Maillard, L. Lermusiaux, J.-M. Guigner, N. Bonod and J. Wenger, ACS Nano, 2016, 10, 4806–4815.
15. H. Wang, J. Jung, K. Chung, J. W. Lim, Y. You, J. Kim and D. H. Kim, J. Appl. Phys., 2017, 122, 153103.
16. R. Lakshmanan, N. C. Shivaprakash and S. Sindhu, J. Lumin., 2018, 196, 136–145.
17. N. K. Ibrayev, R. R. Valiev, E. V. Seliverstova, E. P. Menshova, R. T. Nasibullin and D. Sundholm, Phys. Chem. Chem. Phys., 2024, 26, 14624–14636.
18. E. Slyusareva, A. Sizykh, A. Tyagi and A. Penzkofer, J. Photochem. Photobiol., A, 2009, 208, 131–140.
19. Y. Kushida, T. Nagano and K. Hanaoka, Analyst, 2015, 140, 685–695.
20. S. M. Derayea and D. M. Nagy, Rev. Anal. Chem., 2018, 37, 20170020.
21. M. Kabeláč, F. Zimandl, T. Fessl, Z. Chval and F. Lankaš, Phys. Chem. Chem. Phys., 2010, 12, 9677–9684.
22. K. N. Patterson, M. A. Romero-Reyes and J. M. Heemstra, ACS Omega, 2022, 7, 33046–33053.
23. V. S. Maryakhina, Laser Phys., 2016, 26, 105603.
24. V.-N. Nguyen, A. Kumar, M. H. Lee and J. Yoon, Coord. Chem. Rev., 2020, 425, 213545.
25. S. K. Lam, M. A. Chan and D. Lo, Sens. Actuators, B, 2001, 73, 135–141.
26. Y. Zhang, K. Aslan, M. J. Previte and C. D. Geddes, J. Fluoresc., 2007, 17, 345–349.
27. E. Gandin, Y. Lion and A. Van de Vorst, J. Photochem. Photobiol., 1983, 37, 271–278.
28. N. Macia, R. Bresoli-Obach, S. Nonell and B. Heyne, J. Am. Chem. Soc., 2019, 141, 684–692.
29. V. L. Ermolaev, Opt. Spectrosc., 2016, 121, 567–584.
30. R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, G. V. Baryshnikov, D. Sundholm, H. Ågren, B. F. Minaev and T. Kurtén, Phys. Chem. Chem. Phys., 2020, 22, 22314–22323.
31. N. K. Ibrayev, E. V. Seliverstova, R. R. Valiev, A. E. Kanapina, A. A. Ishchenko, A. V. Kulinich, T. Kurten and D. Sundholm, Phys. Chem. Chem. Phys., 2023, 25, 22851–22861.
32. K. Aslan, Z. Leonenko, J. R. Lakowicz and C. D. Geddes, J. Fluoresc., 2005, 15, 643–654.
33. C. Würth, M. G. González, R. Niessner, U. Panne, C. Haisch and U. R. Genger, Talanta, 2012, 90, 30–37.
34. D. C. Neckers and O. M. Valdes-Aguilera, Adv. Photochem., 1993, 18, 315–394.
35. J. Paczkowski, J. J. Lamberts, B. Paczowska and D. C. Neckers, J. Free Radicals Biol. Med., 1985, 1, 341–351.
36. A. V. Rogova, F. N. Tomilin, M. A. Gerasimova and E. A. Slyusareva, Russ. Phys. J., 2020, 63, 1417–1423.
37. B. Demirbay, G. Baryshnikov, M. Haraldsson, J. Piguet, H. Ågren and J. Widengren, Methods Appl. Fluoresc., 2023, 11, 045011.
38. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
39. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
41. M. A. Gerasimova, F. N. Tomilin, E. Yu Malyar, S. A. Varganov, D. G. Fedorov, S. G. Ovchinnikov and E. A. Slyusareva, Dyes Pigm., 2020, 173, 107851.
42. R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, A. Kurtsevich, D. Sundholm and T. Kurten, Phys. Chem. Chem. Phys., 2021, 23, 6344–6348.
43. R. R. Valiev, V. N. Cherepanov, R. T. Nasibullin, D. Sundholm and T. Kurten, Phys. Chem. Chem. Phys., 2019, 21, 18495–18500.
44. R. R. Valiev, V. N. Cherepanov, V. Y. Artyukhov and D. Sundholm, Phys. Chem. Chem. Phys., 2012, 14, 11508–115017.
45. R. R. Valiev, V. N. Cherepanov, G. V. Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 6121–6133.
46. S. G. Chiodo and M. Leopoldini, Comput. Phys. Commun., 2014, 185, 676–683.
47. H. Ågren, B. F. Minaev and S. Knuts, J. Phys. Chem., 1994, 98, 3943–3949.
48. G. R. Fleming, A. W. E. Knight, J. M. Morris, R. J. S. Morrison and G. W. Robinson, J. Am. Chem. Soc., 1977, 99, 4306–4311.
49. D. M. Hedstrand, W. H. Kruizinga and R. M. Kellogg, Tetrahedron Lett., 1978, 19, 1255–1258.
50. C. A. Parker and C. G. Hatchard, Trans. Faraday Soc., 1961, 57, 1894–1904.
51. C. A. Parker, Photoluminescence of Solutions, Elsevier Publishing Co., Amsterdam, 1968.
52. M. Pope and Ch. E. Swenberg, Electronic Processes in Organic Crystals and Polymers, Oxford University Press, Oxford, 1999.
53. N. A. Efremov, S. G. Kulikov, R. I. Personov and Yu. V. Romanovskii, Chem. Phys. Lett., 1988, 128, 9–21.
54. N. A. Efremov, S. G. Kulikov, R. I. Personov and Yu. V. Romanovskii, Phys. Solid State, 1989, 3, 103–111.
55. H. Yersin, R. Czerwieniec, U. Monkowius, R. Ramazanov, R. Valiev, M. Z. Shafikov, W. M. Kwok and C. Ma, Coord. Chem. Rev., 2023, 478, 214975.
56. R. R. Valiev, B. S. Merzlikin, R. T. Nasibullin, A. Kurtzevitch, V. N. Cherepanov, R. R. Ramazanov, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2023, 25, 6406–6415.
57. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002.
58. E. Seliverstova, N. K. Ibrayev, G. Omarova, A. Ishchenko and M. Kucherenko, J. Lumin., 2021, 235, 118000.
59. C. D. Geddes and J. R. Lakowicz, J. Fluoresc., 2002, 12, 121–129.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02621g

---