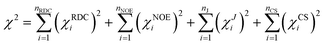Extending molecular dynamics with dipolar NMR tensors as constraints to chiral phosphorus compounds

Abstract

Molecular dynamics with orientational constraints (MDOC) simulations use NMR parameters as tensorial constraints in the stereochemical analysis of small molecules. ¹³C–³¹P Residual dipolar couplings-aided MDOC simulations of small phosphorus molecules determined the relative configurations of rigid molecules after including ³J_H–H-couplings as additional constraints. However, flexible molecules remain a problem.

---

Introduction

Compounds with the stereogenic centre on a phosphorus atom (e.g., Josiphos ligands¹) are essential in coordination chemistry and stereoselective catalysis. However, P-chiral compounds are often difficult to synthesize stereoselectively, and classical synthesis yields a mixture of isomers which may be difficult to separate.^2,3 To determine phosphorus stereochemistry (configuration and conformation), several advanced NMR methods can be used, such as residual dipolar coupling (RDC) analysis.^4–8

The RDC analysis enables to assign the relative configuration of small to medium sized molecules,^7–11 but some problems arise upon high molecular flexibility^12–15 or lack of ¹H–¹³C RDC values.

Previously,¹⁶ we have studied model phosphorus-based compounds by ¹³C–³¹P RDC analysis, with the phosphorus atom incorporated into a cycle to suppress molecular flexibility. However, we were unable to unambiguously determine the relative configuration using the P-based RDC analysis of low-energy conformers. These low-energy structures probably do not reflect the actual structures present in the anisotropic environment of RDC experiments. To create a new population of conformers in the alignment medium needed for RDC analysis, we applied molecular docking.^17,18

Molecular docking ultimately improved our ability to determine the relative configuration of mildly flexible molecules, but not highly flexible molecules.¹⁹ Nevertheless, this issue may be solved using a recently developed method: molecular dynamics with orientational constraints (MDOC).^20–22

MDOC generates trajectories comprising a multitude of conformers using dipolar-coupling tensors (or other NMR interaction tensors) for each ¹H–¹³C or ¹³C–³¹P coupling. To reach the time scale of NMR experiments in molecular dynamics simulations, MDOC applies tensorial constraints that rotate molecules and their mobile groups, thus making it possible to heat up the rotational degrees of freedom. Moreover, we can adjust equilibria between rotamers using scalar constraints, such as J-couplings and NOE distances.

MDOC has been recently applied to the structural elucidation and diastereomer discrimination of several small and flexible molecules, such as cellobiose²² and oidiolactone B,²¹ and of molecules with multiple rotamers, such as sagittamide A.²³ However, a recent MDOC study²⁴ has highlighted two major issues that must be considered in stereochemical analysis: (i) stiff molecules, e.g., strychnine, actually have several conformers in solution, and (ii) transient structures, mainly controlled by the entropy term TΔS of free energy, also contribute to conformer distribution.

In this study, we applied MDOC to model phosphorus-containing compounds (Fig. 1) with various degrees of molecular flexibility, as indicated by the nConf₂₀ parameter. This parameter can be used for quantification of molecular flexibility²⁵ (calculation details are provided in the ESI†). The descriptor is the count of conformers of a molecule with energies between the lowest energy conformer and the selected relative energy threshold and presents consequently the number of energetically accessible conformations.

Fig. 1 Structures of the studied compounds and their flexibility parameters.

In this work, we implemented ³¹P NMR parameters (RDCs and J-couplings) in MDOC analysis, showing that these data may facilitate stereochemical analysis of phosphorus compounds.

Computational methods

MDOC simulations

To perform MDOC simulation, pseudo-energy terms are added to the energy expression of the COSMOS-NMR force field E^FF.²⁶ The pseudo-energies contain expressions depending on the differences between calculated and experimental dipolar tensors D or other scalar NMR parameters such as NOE distances (denoted by R) and vicinal ³J couplings (the different values are denoted by the indices k, l, m).
The first pseudo-energy term is the tensorial pseudo-energy that sums up all 9 components of the dipolar tensors (α, β run from 1 to 3). The other two terms are scalar terms that influence structures and equilibria of conformers. The force constants k or weights of the different terms are given in Table S11 (ESI†). From the force-field energies, we have to calculate derivatives with respect to the coordinates of the atoms and from these forces the velocities of the equations of motion are calculated. The forces derived of the scalar terms, as distance and ³J terms, act on inner coordinates like distances and torsion angles. But not the forces of the tensorial dipolar terms.

The equation above represents the derivatives of the calculated dipolar tensor D of atom A with respect to the Cartesian coordinates x_γ. Since the NMR tensors depend on the orientation of the molecules within the external magnetic field transformation matrices T are introduced that transform the tensors from their local molecular coordinate system to the global laboratory system. The forces calculated from the transformation matrices T induce motions and reorientations of the molecule and parts of them (for more details and the scaling factor s(ΔD) see Sternberg et al.).²³

What happens if no tensorial constraints from RDCs are available and only scalar constraints such as ³J couplings are extracted? The score for the ³J couplings will be only slightly worse than in the simulation with RDC tensors (n/χ² = 1.0 < 1.4) but all RDC values are far away from the error bounds (n/χ² = 1.3 × 10⁻⁶). The motional average in the molecular dynamics does not take place without tensorial forces but the measured RDC values are motional mean values. On the other hand, it is possible to predict ³J couplings from MDOC simulations with only RDC constraints as it was used for assignment of prochiral hydrogen atoms H1A and H1B (Fig. 6).

As in traditional MD simulations, the temperature is controlled by a thermostat program (see Table S10, ESI†). This is always necessary in MDOC simulations because the tensorial pseudo-forces produce heat. All dipolar tensors and other NMR parameters have to be averaged with proceeding MD simulation. The tensorial pseudo-forces are at the begin of the simulation very large since no motional average was reached. Therefore, these pseudo-forces are gradually switched on so that their full action is reached after approximately 1 ns. Therefore, the total duration of the MDOC simulation should be much longer than 1 ns. Most parameters of the simulation were tested in former investigations, but the weight and width parameters k of the pseudo forces should be adjusted in preliminary simulations (see Table S11, ESI†).

The calculation of the dipolar tensors and NOE distances is straightforward²³ but for the ³J, the Altona equations²⁷ were used.

Scoring calculations against experiments

The final result of an MDOC simulation was obtained by an average of the calculated RDC or ³J couplings over the trajectory represented by 2000 (or more) data and coordinate snapshots. The values were far from an equilibrium state since in the beginning of the simulation and thus the first nano second of the simulation was skipped.

The quality of MDOC simulations can be deduced using the n/χ² parameter:

In this equation, the e^q denotes the errors of the experimental properties, and a quality parameter n/χ² higher than one means that the calculated quantities q^calc are on average within the experimental error ranges e^q. When calculating the χ² parameter, we considered two types of data - RDC and ³J couplings. For a good simulation, all, or at least most, summands in eqn 1 should be lower than 1.0. Under these conditions, the calculated values are within the experimental error limits, and n/χ² is higher than one.

The n/χ² value is an absolute measure of how accurately a set of calculated values represents an experiment. For comparing several datasets, a probability has been developed based on the product probabilities of deviations between calculated and experimental values. The χ-probability has been recently developed to incorporate several types of data (RDCs and ³J couplings in this study) into a consistent tool.²⁸ The formalism of the χ-probability was developed on the same basis as the well established Bayesian measure DP4 developed by Smith and Goodman²⁹ as stereochemical score using chemical shifts. The χ-probability differs from DP4 in the following points: (i) instead of chemical shift differences, absolute χ-values are used, and (ii) the normal distribution is used for defining the probability that a calculated value differs from the experiment under consideration of the individual error. The χ-probability is more useful than DP4 because the error is considered, and different properties can be contracted into one score.

Conformational analysis of pyrrolidine ring

The conformers of the five-membered rings were investigated using the phase angle P, as introduced by Altona and Sundaralingam.³⁰ The torsion angles ϕ₀ to ϕ₄ are defined as follows. The phase angle P was calculated for all snapshots of an MDOC simulation omitting the first nano second.

Results and discussion

MDOC analysis of 1

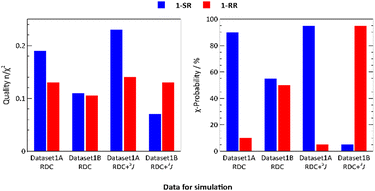
Diastereomers of 1 were prepared as described in our previous study and the absolute configuration was determined by X-ray diffraction.¹⁶ In the present investigation, a 40 ns MDOC simulation was performed for both stereoisomers with the data sets 1A and 1B (for the parameters of the simulation see the ESI†).

For both datasets, 1A and 1B, the quality factors²⁸n/χ² (details in the section “Computational methods”) were low, reaching 0.1 and 0.2, respectively, due to the relatively small ¹³C–³¹P couplings and narrow error ranges. Because these quality factor values prevented us from assigning the relative configuration, we calculated the χ-probability²⁸ (Table S10, ESI†) and assigned dataset 1A as 1-SR by 90%, in line with X-ray data.¹⁶ However, the 1-RR configuration was still unclear. As in our previous studies,^16,19 we were unable to identify the relative configuration using only RDC data (Table S10, ESI†). For this reason, we included J-couplings in MDOC simulations. J-Couplings are valuable parameters, especially for stereogenic centres, but we failed to experimentally assign the ³J_H–H-couplings of the diastereotopic hydrogens H1A (pro-S) and H1B (pro-R) to H2 (see Fig. 6). Therefore, we performed preliminary MDOC simulations, but instead of using the ³J_H–H-couplings as additional constraints, we calculated them as the mean value of 2000 snapshots of the MDOC trajectory. With these computed values, we assigned ³J_H–H-couplings (Table S13, ESI†).

In the final MDOC simulation, using ³J_H–H-couplings as additional scalar constraints, we reached 96 and 97% χ-probability of assigning 1-SR and 1-RR to datasets 1A and 1B, respectively (Fig. 2).

Fig. 2 Statistical analysis of NMR data calculated from MDOC trajectories of 1.

Encouraged by these results, we investigated conformational equilibria from the 2000 snapshots of the trajectories. From MDOC trajectories of the torsion angles of 1-SR, we derived the populations of individual conformers. The conformations of the five-membered rings were investigated using the phase angle P, as introduced by Altona and Sundaralingam.³⁰ The maximum of the distribution was at P = 208°, and most (98.4%) P values belonged to the South conformation. In this simulation, we identified another five-membered ring conformation separated from the major conformations by a minimum. However, this North conformation accounted for only 1.6% of occurrences (see Fig. 3). Inspecting the torsion of the (O2–C1–C2–N) angle of the adjacent five-membered ring (see Fig. 3) we observe a small −gauche contribution of about 6% additionally to the major +gauche conformation, with a maximum P at 28° (Fig. 3). The two adjacent ring systems preform a coupled motion.

Fig. 3 Distribution of torsion angles of 1-SR as derived from a MDOC trajectory. The conformation of the adjacent five-membered ring is analysed using the pseudo-rotation cycle (panel A). The conformers of the five-membered rings containing the phosphorous atom are displayed using the rotation about the C1–C2 bond (torsion (O2–C1–C2–N), panel B). The (N–P–C1′–C2′) torsion (panel C) indicates that the rotation of the phenyl group is not restricted (for details, see Table 1).

The dihedral distributions of 1-RR were like those of 1-SR (Fig. 3), but the maximum of the (O2–C1–C2–N) distribution was at 20° (+gauche in 96%). And while we also observed two conformers of the five-membered rings, the contribution of the second conformer was minimal (for details see Table 1). The maximum of the pseudo-rotational angle of the more populated conformation (98.2%) was at P = 168°. As with 1-SR, the phenyl rotation was not restricted.

Table 1 Data assignment to the relative configuration and conformer analysis of compounds 1 to 3

Comp. (Fig. 1)	Data	χ-Probab. [%]	Five-membered ring pseudo-rot. angle
			Major contrib.		Minor contrib.
			Max [°]	Area [%]	Max [°]	Area [%]
1-SR	1A	96	208	98	68	2
1-RR	1B	97	168	95	36	5
2-RR	2A	72	168	95	36	5
2-RS	2B	85	50	92	178	8
3-RR	3A	46	—	—	—	—
3-SR	3B	89	—	—	—	—

---

MDOC analysis of 2

Diastereomers of 2 were prepared as described in our previous study.¹⁶ However, crystallization always caused ring opening leading to loss of the stereogenic centre on the phosphorus atom, therefore, absolute configuration was not determined. For this reason, we worked with both NMR datasets 2A and 2B. The MDOC analysis of 2 showed that the quality n/χ² of the RDC data was as low as in the analysis of 1, so we calculated ³J_H–H-couplings based on a preliminary MDOC simulation to assign the measured couplings to the pro-chiral hydrogens on carbon C1–H1A (pro-S) and H1B (pro-R) (see Fig. 6). These ³J_H–H proved to be essential for the chiral assignment since they connect the chiral centre C2 (R or S) to the prochiral hydrogen atoms. In this process, ³J_H–H-couplings proved essential for dataset assignment from the final MDOC simulation (Table S17, ESI†). The χ-probability indicated an 85 and 72% probability of assigning 2-RS and 2-RR to datasets 2B (Fig. 4, red bars) and 2A (Fig. 4, blue bars), respectively, improving our previous low-energy-conformer¹⁶ and molecular-docking¹⁹ results, with only unilateral diastereomeric discrimination for 2-SR. Once again, we derived conformer occurrence and populations from MDOC trajectories of the torsion angles. In 2-RR, we observed two conformers of the five-membered ring: one major component (94.7%) with a maximum of 168° and one minor component (5.3%, Fig. 5A in red) with a maximum of 36°. The torsion of the (O2–C1–C2–N) angle was 90% in (−) gauche conformation with a maximum at −22° (Fig. 5). As in the case of compound 1 the pseudo-rotations of the two adjacent five-membered ring systems were coordinated. The most dynamic region of both isomers of 2 was the (P–O1–C1′) bridge. The rotation around the P–O1 bond was not restricted, but the rotation around the O1–C1′ bond displayed two broad maxima at approximately +100° and −100°. The angles around 0° were strongly avoided (Fig. 5).

Fig. 4 Statistical analysis of NMR data calculated from MDOC trajectories of 2.

Fig. 5 Distribution of torsion angles of 2-RR calculated from the MDOC trajectory. The conformation of the adjacent five-membered ring is analysed using the pseudo-rotation cycle (panel A) (for details, see Table 1). The conformers of the P-containing five-membered rings is displayed using the rotation about the C1–C2 bond (torsion (O2–C1–C2–N), panel B) and the chlorophenyl residue is linked to the phosphorous over an oxygen bridge. The (N–P–O1–C1′) torsion (panel C) indicates that the rotation is not restricted but the rotation about the (P–O1–C1′–C2′) bond displays two minima (panel D).

The distribution of P of 2-RS had two components: a major component (92.3%) with a maximum at 50° and a minor component (7.7%) with a maximum at 178°. The dihedral distributions of the 2-RS structure mirrored those of 2-RR (Table 1), but the torsion of the (O2–C1–C2–N) angle peaked at 30° ((+)gauche in 96%). When comparing 1-RR and 2-RR (see Table 1), we observed that different substituents on the phosphorus had a negligible influence on the ring conformations, but the change in configuration from 2-RR to 2-RS considerably affected the five-membered ring conformation.

MDOC analysis of 3

Menthol derivative 3 was prepared and separated as described in ESI.† The structure was determined by NMR spectroscopy, the NMR signal assignment of two datasets 3A and 3B is in ESI.† However, the absolute configuration was not assigned by XRD because compound 3 did not crystallize. For compounds 3-SR and 3-RR, we performed MDOC simulations using three datasets, namely 3A, 3B and 3A-ex. Dataset 3A-ex was introduced to solve the uncertainty in the assignment of the ³J_H–H-couplings. In dataset 3A-ex, the ³J_H–H-couplings of the CH₃ protons of the groups C7-CH₃ to H7 were interchanged in relation to dataset 3A. The data quality of MDOC simulations of compounds 3 (Fig. 7) was nearly perfect. All RDCs were calculated within the experimental error limit, except P–C1 RDC (Tables S19 and S20, ESI†). This P–C1 RDC is essential to determine the configuration on the phosphorus atom because it reflects the interaction of the chiral phosphorus centre (R or S) with C1(R) of the menthol residue.

Fig. 6 Typical conformers of the compounds 1-SR (A) and 2-RR (B). The most abundant conformers are selected according to the maxima of the phase angle P and maxima of the torsion distributions in the Fig. 3 and 5.

Fig. 7 Statistical analysis of NMR data calculated from MDOC trajectories of 3.

Fig. 7 displays the χ-probability of the two structures 3-RR (blue) and 3-SR (red) with the three datasets (3A, 3B and 3A-ex). With a 79.6% probability, we can assign dataset 3B to configuration 3-SR. However, the assignment to the other datasets, 3A and 3A-ex, is inconclusive, mainly due to the outlier of the P–C1 RDCs (Tables S19 and S20, ESI†). The χ-probability did not allow a final assignment. Only a preliminary assignment was performed due to the P–C1 RDC outlier: dataset 3B was assigned to the structure 3-SR, but dataset 3A was not assigned. The highest score of 3-RR was derived from 3A-ex data set. Inspecting the P–C1 RDC, we observed that in dataset 3B the value is lower (−0.72 Hz) than the value of dataset 3A or 3A-ex (−0.55 Hz). The assignment to the other datasets 3A and 3A-ex is inconclusive mainly because of the P–C1 RDC outlier. If we preliminarily assign 3-SR to dataset 3B and 3-RR to 3A or 3A-ex (3A-ex was selected because of the larger χ-probability), we get the same sequence in the simulated RDC values (−0.552 < −0.469).

To eliminate the P–C1 RDC outlier, we performed simulations using larger weight for RDC pseudo-forces (see Table S11, ESI†), albeit to no avail. Therefore, we used the same simulation parameters as in compounds 1 and 2. The problem was mainly caused by the rapid rotations of the menthol ring around the two bonds of the P–O1–C1 bridge (Fig. S7, ESI† like those of the P–O1–C6–C7 dihedral distribution in Fig. 5). This motion is only weakly hindered by steric effects, resulting in an averaging of the essential P–C1 RDC value due to the fast molecular motion.⁶ This problem may only be solved by adding more constraints characterizing the motion of the menthol residue. Nevertheless, the MDOC results of 3 show significant improvement over the low-energy analysis which was inconclusive (Section 1.5 of the ESI†).

Conclusions

To conclude, in MDOC analysis, RDC tensors can be used as constraints to simulate most features of molecular motion and to reproduce oriented NMR experiments. Discriminating relative configurations often requires introducing additional long-range constraints, such as ³J-couplings. Using these NMR data, we can determine the relative configuration of phosphorus-containing diastereomers of rigid molecules, such as 1 and 2. For 3, this procedure is only partly conclusive because the rapid motion of the menthol residue leads to an outlier of the essential P–C1 RDC value. Therefore, we cannot determine the configuration of a stereogenic centre on phosphorus atom directly from the P–C1 RDC only, but using other stereogenic centres. Nevertheless, using the χ-probability, we can reach values above 85% probability of correct assignment (see Table 1) in most cases. These RDC-aided MDOC simulations enable us to not only identify relative configurations but also study conformational equilibria. In reactions that proceed only with selected conformers, the MDOC analysis may be used to elucidate reaction mechanisms. However, molecular flexibility still remains a challenge in RDC analysis and, therefore, new methods and improvements are highly desirable.

Author contributions

U. S. investigation, software, validation, visualization, writing, M. C. T. investigation, writing, L. T. formal analysis, A. E. synthesis, J. H. chiral separation, O. B. synthesis, and E. P. conceptualization, project administration, supervision, writing, funding acquisition.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Czech Science Foundation (21-23014S, E. P.). We thank Kvetoslava Kertisová for the HR-MS analysis and Dr Carlos V. Melo for editing the manuscript.

Notes and references

1. H. U. Blaser, B. Pugin and F. Spindler, Helv. Chim. Acta, 2021, 104, e2000192.
2. M. Dutartre, J. Bayardon and S. Jugé, Chem. Soc. Rev., 2016, 45, 5771–5794.
3. A. Mondal, N. O. Thiel, R. Dorel and B. L. Feringa, Nat. Catal., 2022, 5, 10–19.
4. A. Mangoni, V. Esposito and A. Randazzo, Chem. Commun., 2003, 154–155.
5. B. Luy, K. Kobzar and H. Kessler, Angew. Chem., Int. Ed., 2004, 43, 1092–1094.
6. C. M. Thiele, Eur. J. Org. Chem., 2008, 5673–5685.
7. G. Kummerlöwe and B. Luy, TrAC, Trends Anal. Chem., 2009, 28, 483–493.
8. G. Kummerlöwe and B. Luy, Annu. Rep. NMR Spectrosc., 2009, 68, 193–230.
9. R. M. Gschwind, Angew. Chem., Int. Ed., 2005, 44, 4666–4668.
10. J. L. Yan and E. R. Zartler, Magn. Reson. Chem., 2005, 43, 53–64.
11. C. M. Thiele, Concepts Magn. Reson. A, 2007, 30A, 65–80.
12. B. Böttcher and C. M. Thiele, eMagRes, John Wiley & Sons, Ltd., 2012 DOI:10.1002/9780470034590.emrstm1194.
13. R. Berger, J. Courtieu, R. R. Gil, C. Griesinger, M. Köck, P. Lesot, B. Luy, D. Merlet, A. Navarro-Vazquez, M. Reggelin, U. M. Reinscheid, C. M. Thiele and M. Zweckstetter, Angew. Chem., Int. Ed., 2012, 51, 8388–8391.
14. L. Y. Liu, H. Sun, C. Griesinger and J. K. Liu, Nat. Prod. Bioprospect., 2016, 6, 41–48.
15. C. M. Thiele, V. Schmidts, B. Böttcher, I. Louzao, R. Berger, A. Maliniak and B. Stevensson, Angew. Chem., Int. Ed., 2009, 48, 6708–6712.
16. M. Tichotová, A. Ešnerová, L. Tučková, L. Bednárová, I. Císařová, O. Baszczyňski and E. Procházková, J. Magn. Reson., 2022, 336, 107149.
17. F. Stanzione, I. Giangreco and J. C. Cole, Prog. Med. Chem., 2021, 60, 273–343.
18. K. A. Peele, C. Potla Durthi, T. Srihansa, S. Krupanidhi, V. S. Ayyagari, D. J. Babu, M. Indira, A. R. Reddy and T. C. Venkateswarulu, Inform. Med. Unlocked, 2020, 19, 100345.
19. M. C. Tichotová, L. Tučková, H. Kocek, A. Růžička, M. Straka and E. Procházková, Phys. Chem. Chem. Phys., 2024, 26, 2016–2024.
20. M. Di Pietro, P. Tzvetkova, T. Gloge, U. Sternberg and B. Luy, Liq. Cryst., 2020, 47, 1–15.
21. P. Tzvetkova, U. Sternberg, T. Gloge, A. Vazquez and B. Luy, Chem. Sci., 2019, 10, 8774–8791.
22. M. Di Pietro, U. Sternberg and B. Luy, J. Phys. Chem. B, 2019, 123, 8480–8491.
23. U. Sternberg, P. Tzvetkova and C. Muhle-Goll, Phys. Chem. Chem. Phys., 2020, 22, 17375–17384.
24. U. Sternberg and R. Witter, Molecules, 2022, 27, 7987.
25. J. G. P. Wicker and R. I. Cooper, J. Chem. Inf. Model., 2016, 56, 2347–2352.
26. M. Möllhoff and U. Sternberg, J. Mol. Model., 2001, 7, 90–102.
27. C. A. G. Haasnoot, F. A. A. M. De Leeuw, H. P. M. De Leeuw and C. Altona, Biopolymers, 1981, 20, 1211–1245.
28. U. Sternberg and C. Farès, Phys. Chem. Chem. Phys., 2022, 24, 9608–9618.
29. S. G. Smith and J. M. Goodman, J. Am. Chem. Soc., 2010, 132, 12946–12959.
30. C. Altona and M. Sundaralingam, J. Am. Chem. Soc., 1972, 94, 8205–8212.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02401j

---