 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Acceleration of xenon kick-out exchange in a cryptophane host explained by ab initio simulation†
Rodolphe
Pollet
 *,
Jean-Pierre
Dognon
*,
Jean-Pierre
Dognon
 and
Patrick
Berthault
and
Patrick
Berthault

Université Paris-Saclay, CEA, CNRS, NIMBE, 91191, Gif-sur-Yvette, France. E-mail: rodolphe.pollet@cea.fr
First published on 28th August 2024
Abstract
The degenerate exchange involving xenon and anti-cryptophane-222-(OCH2COOH)6 in basic water is studied. The reaction consists of the intrusion of a xenon atom into a cavity hosting another xenon and the escape of the latter from the cage to reach the aqueous solution. A series of constrained ab initio molecular dynamics simulations were performed according to the Blue Moon ensemble method to reconstruct the free-energy profile for the degenerate exchange reaction at ambient temperature. In addition to the estimation of the free-energy barrier height of the reaction, analysis of the trajectories provides details on its mechanism as well as on the nature of its transition state, where both Xe atoms interact through strong dispersion forces owing to moderate confinement effects.
Introduction
A highly promising molecular imaging approach uses 129Xe NMR-based biosensors. Pioneered by the group of Pines,1 it counteracts the low sensitivity of NMR by using hyperpolarized xenon hosted in dedicated molecular systems that give it a specific spectral signature.2 These host systems decorated with ligands are designed to reach the biological receptors of interest and specifically reveal them.The most powerful method for detecting small quantities of bioprobes via129Xe NMR is based on an indirect CEST (chemical exchange saturation transfer) approach3 denoted HYPERCEST,4 where the main (free) xenon signal is detected after saturation of the bound xenon frequency. The xenon exchange acts as a pipeline to translate the information on the presence of the bound xenon as a depletion of the main xenon signal. Spatio-temporal encoding methods further increase the sensitivity of the approach.5
Among the most effective xenon host molecules (offering high selectivity for the noble gas, high-frequency separation between the free and bound states, and adequate in-out xenon exchange), cryptophanes have a place of choice. But whatever the host system used, it has been shown that the effectiveness of the approach strongly depends on the xenon in-out exchange rate.6,7
We recently compared the interaction of xenon with two cryptophane congeners, the syn- and anti-cryptophane-222-(OCH2COOH)6. While hyperpolarized 129Xe NMR studies found that the former exhibits a faster xenon in-out exchange,8ab initio molecular dynamics explained these differences.9 Among other structural characteristics, a water molecule blocking the portal of anti-cryptophane was shown to slow down the xenon exchange.
In recent years, however, it has been shown that the simple (dissociative) exchange characterized by equilibrium
| Xe* + Cr ⇌ Xe*@Cr | (1) |
The dynamics of this host–guest system is governed by dissociative and degenerate exchange reactions, whose specific mechanisms and rates directly affect the sensitivity of the HYPERCEST method. Specifically, the latter reaction depends on the free xenon concentration because
 | (2) |
In this work, the expected faster degenerate exchange involving xenon and anti-cryptophane-222-(OCH2 COOH)6 is studied. We remodeled the theoretical approach adopted for the study of the dissociative exchange, namely the Blue Moon ensemble method,14 to reconstruct the free-energy profile for degenerate exchange at ambient temperature.9 Here the reaction path combined the intrusion of a free xenon atom into a cavity hosting another Xe and the escape of the latter, which was kicked out from the cage to reach the aqueous solution. The whole method consists in a series of constrained ab initio molecular dynamics (AIMD)15 simulations where the difference between the distances of both Xe atoms to the center of mass of the cryptophane, rXe*-CM–rXe-CM, varies from largely positive (i.e., bound Xe and free Xe*) to negative (i.e., bound Xe* and free Xe) values (see eqn 3–7). In addition to the estimation of the barrier height of the degenerate exchange reaction, analysis of the trajectories provides details about its mechanism as well as the nature of its transition state, where both Xe atoms strongly interact under confined conditions.
From a configuration extracted from our previous ab initio trajectory,9 we prepared the system by adding a new xenon atom in the center of an empty anti-cryptophane-222-(OCH2COO−)6 cage with another xenon atom at approximately 4 Å from its closest carboxylate arm. The simulation of the anionic form is justified by the fact that the molecule is soluble in water at pH ≥7, i.e. above its pKa value.16,17 The system also includes 153 water molecules together with six Na+ counterions, in an orthorhombic box of 20.9 × 22.3 × 17.5 Å3 (see Fig. 1). The choice of an explicit description of the solvent instead of a simple dielectric continuum model is justified by the active role of water molecules which coordinate to carboxylate groups fixing their orientations, solvate the free xenon atom, and can block portals by forming hydrogen bonds with the host molecule. With the enhanced implementation of the CPMD code with four OpenMP threads per MPI task at 512 AMD EPYC cores, a trajectory of 9 ps per day can be performed on such complex system.
 | ||
| Fig. 1 Typical configuration of the Xe* + Xe@Cr system (in CPK representation) including 153 water molecules (in transparent licorice representation) and six Na+ (in blue) counterions. | ||
In order to provide a more balanced description of the interactions between the two Xe atoms, the cryptophane, and water, we improved our previous Xe ultrasoft pseudopotential by adjusting the cutoff radii for the s, p, and d channels to 2.0, 2.0, and 2.1a0, and the f local potential to 2.1a0, the inner radius to 1.05a0, the partial core radius to 0.6a0. This new pseudopotential was validated by checking the optimized geometries of the isolated Xe2, Xe–CH4, and Xe–H2O complexes (see ESI†).
The Car–Parrinello (CP)18 simulations were performed at 300 K with an enhanced version of the CPMD code.19 The calculation relied on the PBE exchange–correlation approximation20 corrected for dispersion effects according to the D3 with zero-damping method.21 The fictitious electron mass was set to 700 a.u. and the time step to 6 a.u. The use of deuterium atoms and massive Nosé–Hoover chains (i.e., one for each degree of freedom)22 for the nuclei and electrons helped to maintain the adiabaticity during the CP simulation. The atomic mass of Xe was set at its standard atomic weight of 131.293 a.m.u. The time length of the unconstrained CP trajectory was 9.4 ps.
A series of 22 constrained molecular dynamics simulations were performed according to the Blue Moon prescription14 to calculate the free-energy profile for the degenerate exchange reaction (2). The reaction coordinate ξ was the difference between the distances from each of the two xenon atoms and the center of mass (CM) of the cavity, namely rXe*-CM–rXe-CM. The length of each constrained trajectory was 9.4 ps, which included a 3 ps period of relaxation, in order to obtain well-converged average Lagrange multipliers. The change in free energy along ξ was eventually obtained by numerically integrating the time-averaged force of constraint along the reaction path according to
 | (3) |
 | (4) |
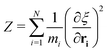 | (5) |
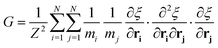 | (6) |
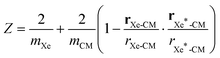 | (7) |
Results and discussion
First the structure of the Xe* + Xe@Cr system is briefly described, then the degenerate exchange reaction is analyzed. In the initial CP trajectory of 9.4 ps, the free Xe* atom was surrounded by approximately 20 water molecules (between 2.85 and 5.45 Å with a maximum at 4.05 Å, see Fig. S1, ESI†), at 3.6 Å from a carboxylate group and 10.3 Å from the encapsulated Xe. The geometry of the filled cryptophane was barely affected by the presence of this external xenon atom, with OCCO dihedral angles (179, 72 and 62°) and diameters (8.7, 9.3 and 9.6 Å), defined as distances between corresponding CH2 carbon atoms of the cyclotriveratrylene bowls, close to the values reported in our study of the simple – dissociative – Xe@Cr exchange (1).9 Prior to the exchange, the three ethylenedioxy bridges therefore exhibited a tgg conformation.Free-energy profile for the xenon degenerate exchange as obtained from eqn 3 is shown in Fig. 2, and free-energy differences between A–E configurations (see Fig. S2 (ESI†) for representative pictures) are reported in Table 1 (A is the initial and E the final states). The local minimum B where Xe* is near the portal is approximately 8 kJ mol−1 higher than when the atom is farther in bulk water (A). The free-energy barrier, between A and C, is estimated to approximately 51 kJ mol−1. For comparison, the free energy difference corresponding to the dissociative escape of a xenon atom from the center of this cage was estimated to 68 kJ mol−1,9 namely 26 kJ mol−1 greater than ΔFB–C. Configurations D and B, where one xenon atom is located outside a portal and the other is inside the cage are close in free energy, with a difference of only 1 kJ mol−1. The final state (that is, bound Xe* and free Xe) is, however, approximately 30 kJ mol−1 higher in free-energy than the initial state (that is, bound Xe and free Xe*). Although the statistical errors are larger for this final state owing to the Blue Moon protocol, this difference can be caused by a conformational change in the cryptophane, as explained in the detailed analysis that follows.
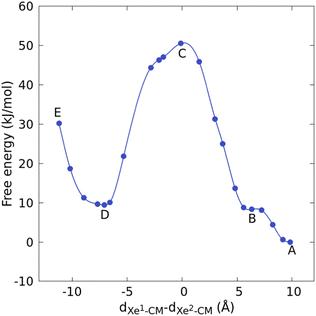 | ||
| Fig. 2 Free-energy profile for the xenon degenerate exchange as obtained by the Blue Moon method. Natural cubic splines was used for interpolation. | ||
| A–B | B–C | C–D | D–E | |
|---|---|---|---|---|
| ΔF | 08.31 | 42.21 | 41.12 | 20.84 |
Degenerate exchange begins with the intrusion of Xe* into the cage. The atom crossed an available portal between a gauche and a trans conformations of ethylenedioxy bridges despite the presence of a blocking water molecule that formed hydrogen bonds between its hydrogen atoms and oxygen atoms of two OCH2COO− arms. These features were also observed during the escape of xenon in the case of the dissociative exchange (1) and are responsible for the higher free-energy barrier of the present anti isomer compared to the syn isomer, which experimentally exhibits a faster xenon in-out rate.9 The second event of the degenerate exchange was the escape of Xe, which was kicked out by the intruder. The available reaction path crossed a portal between two gauche conformations, which was not favorable, so that the approach of Xe caused one conformational change from g to t. This gt configuration seems therefore required for any xenon atom to enter or leave the cage although the gauche ethylenedioxy bridges provide a more stable complex. In other words, “breathing” of the cage is required for in-out motions of xenon. Interestingly, such self-organization in response to a stimulus (i.e., the degenerate exchange) is an example of adaptive chemistry.23 During the escape of Xe, the portal also opened, as shown by the 2 Å increase of the separation between two carboxylate arms. The resulting “gating” phenomenon is therefore a combination of the sliding and French door mechanisms.24 To get an indication of how long this new conformation can last with Xe outside of the cage, one of the Blue moon trajectory (approximately 12 kJ mol−1 below E and with a xenon–xenon separation of 10.6 Å) was extended up to 19 ps and the cryptophane remained in this gtt conformation.
Between these two events, namely intrusion and escape, in the transition state (C), the two xenon atoms formed a dimer located in the center of the cage, which preserved its conformation ggt and whose dimensions only increased weakly (by a few percent). Both atoms were equidistant from the center of mass of the cryptophane, facing two portals, so the average angle of Xe-CM-Xe* was 142°. The average Xe–Xe* distance was 3.87 Å, which is 0.61 Å shorter than our estimate in vacuo (see ESI†). Such confinement effects have been observed for noble gases in fullerenes.25–27 Especially for Xe2@C60, a genuine chemical bond has been found with a length of 2.49 Å.28 In the Cr222(OCH2COO−)6 cryptophane, the electron localization function (ELF)29–31 did not show any sign of such a shared electron bond (see Fig. 3). Recently, ELF analysis has been conducted not only for chemical bonding but also for physical binding, such as ionic binding, hydrogen binding, or van der Waals binding.32 Here, the apparent contraction of the ELF basins, the nonzero ELF value (0.064) between the two nuclei (see Fig. 4), and the distance which is shorter than the sum of van der Waals radii denoted a strong dispersion interaction. We infer that the confinement effects are therefore moderate for Xe2@Cr.
 | ||
| Fig. 4 Electron localization function (ELF) profile along the Xe–Xe* axis calculated at the transition state geometry with a Goedecker pseudopotential for Xe and a plane-wave cutoff energy of 120 Ry. | ||
Conclusions
The degenerate exchange exhibits a much shorter reaction time (approximately a tenth of milliseconds at the studied concentration in free xenon according to Eyring equation) than the dissociative mechanism. The reaction crosses a transition state where both xenon atoms interact through strong dispersion forces because of moderate confinement effects. When the first xenon atom is kicked out by the second one, the gate of the cryptophane cage simultaneously undergoes an opening and a deformation, namely a conformational change of an ethylenedioxy linker from gauche to trans with a higher free energy.According to this simulation, the xenon in-out exchange rate could depend on the relative proportion of gtt and ggt conformations for the ethylenedioxy linkers of the cryptophanes. The limiting step being the passage from one conformation to the other one, with increasing xenon density, a more important number of cryptophanes should remain in gtt (or ttt) conformation, facilitating the xenon exchange. This spectacular case of molecular adaptation has important consequences on the efficacy of the 129Xe NMR bioprobes based on anti-cryptophanes.
Data availability
The data that support the findings of this study are available in the ESI,† of this article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was granted access to the HPC resources of TGCC under the AD010811468R1 and AD010811468R2 allocations made by GENCI. The authors warmly thank Thierry Brotin and his team at ENS Lyon for giving them access to these water-soluble crytophanes.References
- M. M. Spence, S. M. Rubin, I. E. Dimitrov, E. J. Ruiz, D. E. Wemmer, A. Pines, S. Q. Yao, F. Tian and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10654–10657 CrossRef CAS PubMed.
- P. Berthault, G. Huber and H. Desvaux, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 55, 35–60 CrossRef CAS.
- S. Forsén and R. A. Hoffman, J. Chem. Phys., 1963, 39, 2892–2901 CrossRef.
- L. Schröder, T. J. Lowery, C. Hilty, D. E. Wemmer and A. Pines, Science, 2006, 314, 446–449 CrossRef PubMed.
- C. Boutin, E. Léonce, T. Brotin, A. Jerschow and P. Berthault, J. Phys. Chem. Lett., 2013, 4, 4172–4176 CrossRef CAS PubMed.
- M. Zaiss, M. Schnurr and P. Bachert, J. Chem. Phys., 2012, 136, 144106 CrossRef PubMed.
- M. Kunth, C. Witte, A. Hennig and L. Schröder, Chem. Sci., 2015, 6, 6069–6075 RSC.
- E. Léonce, T. Brotin and P. Berthault, Phys. Chem. Chem. Phys., 2022, 24, 24793–24799 RSC.
- R. Pollet, J.-P. Dognon and P. Berthault, Chem. Phys. Chem., 2023, 25, e202300509 CrossRef PubMed.
- K. Bartik, M. Luhmer, J.-P. Dutasta, A. Collet and J. Reisse, J. Am. Chem. Soc., 1998, 120, 784–791 CrossRef CAS.
- G. Huber, L. Beguin, H. Desvaux, T. Brotin, H. A. Fogarty, J.-P. Dutasta and P. Berthault, J. Phys. Chem. A, 2008, 112, 11363–11372 CrossRef CAS PubMed.
- S. Korchak, W. Kilian and L. Mitschang, Chem. Commun., 2015, 51, 1721–1724 RSC.
- M. Kunth, C. Witte and L. Schröder, J. Chem. Phys., 2014, 141, 194202 CrossRef CAS PubMed.
- M. Sprik and G. Ciccotti, J. Chem. Phys., 1998, 109, 7737–7744 CrossRef CAS.
- D. Marx and J. Hutter, Ab initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, Cambridge, 2009 Search PubMed.
- G. Huber, T. Brotin, L. Dubois, H. Desvaux, J.-P. Dutasta and P. Berthault, J. Am. Chem. Soc., 2006, 128, 6239–6246 CrossRef CAS PubMed.
- E. Léonce, J.-P. Dognon, D. Pitrat, J.-C. Mulatier, T. Brotin and P. Berthault, Chem. – Eur. J., 2018, 24, 6534–6537 CrossRef PubMed.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- T. Klöffel, G. Mathias and B. Meyer, Comput. Phys. Commun., 2021, 260, 107745 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- J.-M. Lehn, Angew. Chem., Int. Ed., 2013, 52, 2836–2850 CrossRef CAS PubMed.
- K. Houk, K. Nakamura, C. Sheu and A. E. Keating, Science, 1996, 273, 627–629 CrossRef CAS PubMed.
- D. Paul, H. Dua and U. Sarkar, Front. Chem., 2020, 8, 621 CrossRef CAS PubMed.
- I. Fernández, M. Solà and F. M. Bickelhaupt, J. Chem. Theory Comput., 2014, 10, 3863–3870 CrossRef PubMed.
- M. Khatua, S. Pan and P. K. Chattaraj, J. Chem. Phys., 2014, 140, 164306 CrossRef PubMed.
- A. Krapp and G. Frenking, Chem. – Eur. J., 2007, 13, 8256–8270 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- D. Marx and A. Savin, Angew. Chem., Int. Ed. Engl., 1997, 36, 2077–2080 CrossRef CAS.
- K. Koumpouras and J. A. Larsson, J. Phys.: Condens. Matter, 2020, 32, 315502 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tests of the new Xe pseudopotential, radial distribution function of water molecules, configurations along the degenerate exchange reaction. See DOI: https://doi.org/10.1039/d4cp02378a |
| This journal is © the Owner Societies 2024 |

