CO₂ ultrathin film growth on a monolayer of CO₂ adsorbed on the NaCl(100) surface: sticking coefficient and IR-optical signatures in the ν₃ region

Abstract

CO₂ ultrathin molecular films were grown onto a preadsorbed monolayer NaCl(100)/p(2 × 1)-CO₂ at 40 K. Polarization infrared spectroscopy (PIRS) reveals that so-prepared films have better quality than directly grown films. A sticking probability of 0.74 ± 0.1 was deduced from the integrated IR absorption. The presence of the monolayer doublet in the film spectra suggests a Stranski–Krastanov film growth with locally varying film thicknesses on the surface. In the region of the ν₃(¹²C¹⁶O₂) band, fine structure was observed between the well-known transverse-optical (TO) and longitudinal optical (LO) bands. Two independent computational models were applied to analyze the nature of the observed fine structure. Both pair potential calculations in combination with a vibrational exciton model as well as plane-wave density functional theory (DFT) in combination with phonon calculations of IR intensities at the Γ-point reveal that a weak mode visible in s-polarization and p-polarization originates from a vibrational film excitation located near the substrate interface. A series of p-polarized weak bands appearing and partly disappearing upon film-growth is assigned to film stacks of unique local thickness.

---

1 Introduction

Thin films of CO and CO₂ grown on ionic single crystal surfaces like NaCl or KBr have attracted interest in a variety of applications. In the astrophysical context, they have been used to study the infrared-optical properties of mixed, amorphous, and crystalline ice in laboratory experiments, in comparison with IR spectra from planetary or interstellar origins.^1–5 Recently, the significance of vibrational pooling for isomerization processes in such films was demonstrated.⁶ In CO₂ thin films, vibrational coupling is thought to play a crucial role in the photodesorption of CO₂ from CO₂ ice,⁷ since the excitation energy of the ν₃ asymmetric stretch mode (28 kJ mol⁻¹) comes close to the desorption energy of physisorbed CO₂.

The surface science approach to investigate such phenomena is based on structurally well-defined model systems, if they are available. The very similar lattice parameters of NaCl (5.64 Å at room temperature⁸) and cubic CO₂ ice (5.62 Å at 150 K (ref. 9)) suggest that the NaCl(100) surface should be a prefered substrate to prepare and study well-defined films of CO₂.

In fact, on the NaCl(100) surface below about 80 K, the first layer of carbon dioxide is a well-ordered herring-bone structure with p(2 × 1) translational symmetry.^10–12 The observed characteristic doublet in the ν₃ region was assigned to dipole–dipole coupling of the two translationally inequivalent molecules in this p(2 × 1) unit cell.^13,14 While the surface geometry of the first layer of these is well-known from quantitative low-energy electron diffraction experiments¹⁰ (LEED), experimental information on the structure of CO₂ ultrathin films of several layers thickness has been provided mainly by helium atom scattering (HAS) experiments.¹¹ A c(2 × 2) translational symmetry was deduced for multilayer CO₂ films grown on a preadsorbed monolayer on the NaCl(100) at 40 K, resembling the low-temperature crystalline structure of α-CO₂ ice.^9,15 Using spot analysis-LEED (SPALEED), the c(2 × 2) symmetry of CO₂ multilayers has also been detected on NaCl(100) films grown epitaxially on Ge(100)¹² between 78 K and 83 K. Transmission infrared spectroscopy experiments on multilayer CO₂ films grown on NaCl(100) have been conducted by Berg et al.,^16,17 and an elaborate analysis of the relation between IR spectrum profiles and film structure based on vibrational exciton theory has been given by these authors.¹⁷ In the region of the ν₃ asymmetric stretch mode, the spectrum profiles were dominated by massive absorptions at 2344 cm⁻¹ and 2382 cm⁻¹, the latter being interpreted as the longitudinal optical (LO) mode of α-CO₂.¹⁶ Early works by Fox and Hexter¹⁸ and Zumofen¹⁹ showed that vibrational dipole–dipole interaction in slabs of molecular crystals of α-CO or α-CO₂ should show a splitting of their fundamental stretch modes into a doubly-degenerated transverse-optical (TO) and a LO mode.

It should be noted that at substrate temperatures below 35 K, CO₂ grows in its amorphous phase, while above 35 K, the film structure irreversibly transforms into the cubic structure.² In the present work, ultrathin films less than 10 monolayers thick were grown at 40 K on a preadsorbed well-defined monolayer of CO₂ on the NaCl(100) surface. Polarization infrared spectroscopy (PIRS) in the ν₃-region reveals that layers grown in this way have additional weak infrared features between the TO and LO bands. To the best of my knowledge, these additional peaks haven't been described in literature so far. The aim of this article is to give an interpretation of these additional features. Therefore spectrum simulations using two different computational methods are applied and support is given that the presence of these weak features correlates with the high long-range order of the so-prepared films.

The article is organized as follows: in Section 2 the experimental methods and results are described. The modeling of the thin films and the related IR spectra is presented in Section 3. In Section 4 the experimental and computational results are discussed and an interpretation of the observed spectrum profiles is given.

2 Experiment

The apparatus for surface science experiments with insulator single crystal surfaces was described in detail in previous papers.^20–22 It consists of an ultrahigh vacuum chamber (UHV) coupled to a Michelson type Bruker IFS 120 HR infrared spectrometer. The design of the sample holder allows PIRS experiments in transmission geometry at off-normal incidence. The spectra were recorded using an liquid N₂ cooled InSb detector at a resolution of 0.2 cm⁻¹. The IR beam struck the sample under an angle of incidence of β = 45° with respect to the surface normal. A NaCl single crystal (Korth Kristalle, Kiel, Germany) sized 20 mm × 20 mm was cleaved in dry nitrogen atmosphere twice to obtain a slice of 3 mm thickness with two freshly prepared (100) surfaces. The sample was transferred into the UHV chamber within about 30 minutes. Under measurement conditions, the residual gas pressure was below 1 × 10⁻¹⁰ mbar. Residual gas analysis was possible using a quadrupole mass spectrometer. The pressure was measured using an ionization gauge. All reported pressure values are corrected for the ionization cross section of CO₂. The surface quality of the bare NaCl(100) surface was checked in low-energy electron diffraction (LEED) experiments using a multichannelplate LEED optics (MCPLEED, Omicron).

Carbon dioxide ultrathin films were prepared by integral dosage of CO₂ (purity 99.995%) using a leak valve. In the first step a saturated monolayer CO₂ was grown by exposing the NaCl(100) surface at a sample temperature of 75 K to CO₂ at a partial pressure of 7 × 10⁻⁹ mbar. The formation of the saturated monolayer was checked by recording PIRS spectra in s- and in p-polarization. The topmost spectrum (black color) in Fig. 1 shows the characteristic doublet^23,24 of an in-phase (ML+, 2338.6 cm⁻¹) and an out-of-phase (ML−, 2349.1 cm⁻¹) vibrational mode of the herringbone NaCl(100)/p(2 × 1)-CO₂ monolayer phase which is stable at 75 K and p_CO2 = 7 × 10⁻⁹ mbar. From these spectra, the total integrated absorbance of the saturated monolayer in the region of the doublet was determined to be A_s = 0.18 cm⁻¹ in s-polarization and A_p = 0.16 cm⁻¹ in p-polarization. These values are close to values reported for the saturated monolayer in ref. 24.

Fig. 1 PIRS spectra of carbon dioxide ultrathin films grown on the NaCl(100) surface with average thickness between 1 and 3 monolayers. For the purpose of clarity the spectra are shifted vertically. For line positions and further characterization of observed infrared modes see Table 1.

In order to grow additional layers of CO₂, the sample was further cooled down to a temperature of 40 K while the leak-valve was closed. Then the sample was repeatedly exposed to gas-phase CO₂ at a partial pressure of 7 × 10⁻⁹ mbar and defined times of exposure. Between each of such additional dosages, pairs of PIRS spectra were recorded at stopped exposure. No signs of desorption were observed under these conditions. Some of these film spectra are shown in Fig. 1 at lower coverage and, for higher coverage, in Fig. 2. For the determination of the average coverage of the CO₂ film, the total integrated absorbance in the region of the ν₃ asymmetric stretch mode was analyzed. The resulting total absorbances for the whole sequence of spectra are shown in Fig. 3. Apparently, a linear relation between time of exposure and integrated absorbance is observed. This justifies the calibration of the measured absorbances with the absorbances of the monolayer in order to assign an average coverage to the various film spectra and, moreover, to determine the sticking probability S of carbon dioxide molecules under the given conditions. Both sets of spectra analyzed independently are consistent with a film growth rate of r = 1.9 × 10⁻³ ML s⁻¹ (1 ML = 1 monolayer = 6.28 × 10¹⁸ molecules per m²). From the comparison with the growth rate from the well-known Hertz–Knudsen equation

resulting from kinetic gas theory (T_gas = 300 K), a sticking probability of S = 0.74 ± 0.1 for the given conditions is deduced. The assumed error is mainly due to a possible systematic uncertainty of the pressure measurement. Thus, the spectra shown in Fig. 1 can be assigned to average film thicknesses between 1 ML and 3 ML, while the series depicted in Fig. 2 corresponds to average film thicknesses between 3 ML and 7 ML. The total exposure during this experiment was 15.8 L (1 Langmuir L = 1.33 × 10⁻⁴ Pa s), and the deposition rate was about 0.005 L s⁻¹ and thus smaller than the deposition rates between 0.01 and 0.1 L s⁻¹ reported by Lange et al.¹¹

Fig. 2 PIRS spectra of carbon dioxide ultrathin films grown on the NaCl(100) surface with average thickness between 3 and 7 monolayers. For the purpose of clarity the spectra are shifted vertically. For line positions and further characterization of observed infrared modes see Table 1.

Fig. 3 Integrated absorbance of the sequence of film spectra grown on the saturated monolayer CO₂p(2 × 1)/NaCl(100) as a function of time of exposure. The lines are best-fit straight lines from a linear fit of the data for s-polarization (blue balls), and p-polarization (red balls). Values for the integrated absorbance were obtained by means of integration of the spectra over the whole ν₃ region.

In the following the various observed IR absorptions shall be discussed. A list of observed peaks can be found in Table 1. A detailed inspection of the film spectra in the low-coverage regime, Fig. 1, can be summarized as follows: upon further exposure of the first layer CO₂ to gas-phase CO₂, there is a weakening of the doublet ML+ and ML−, while additional bands become apparent. At 2344 cm⁻¹ a doublet develops which merges into the transverse optical modes TO-sh and TO at 2342.8 cm⁻¹ and 2345.1 cm⁻¹ (green spectrum in Fig. 1). In addition, the LO mode becomes visible in p-polarization.

Table 1 Compilation of observed infrared modes in the region of the asymmetric stretch mode ν₃ of ¹²C¹⁶O₂, in comparison with results proposed from the vibrational exciton model and pw-DFT-D. All values are given in cm⁻¹. The third column indicates the behaviour of mode intensity with growing film thickness

Mode	Experiment	Tendency	VE model	pw-DFT-D	Assignment
ML+	2338.6	Weakening	2339.4	2349.4	First layer in-phase vibration
ML−	2349.1	Weakening	2347.4	2356.5	First layer out-of-phase vibration
TO	2344.6	Constantly strengthening	2343.1	2357.0	Transverse optical mode (at highest coverage)
TO-sh	2342.8	Constantly strengthening	2344.7	2357.4	Shoulder of TO mode (at highest coverage)
LO	2380.2	Constantly strengthening	2379.8	2389.1	Longitudinal optical mode (at highest coverage)
BL	2335.9	Weakening after formation	—	—	Bilayer film mode
SP1	2353.7	Unaffected after formation	2349.0	2365.9	Film mode visible in s- and p-polarization
P1(5)	2359.1	Weakening after formation	2357.8	2367.9	Film mode (p-polarization), 5 layers
P1(6)	2363.7	Weakening after formation	2362.6	2372.6	Film mode (p-polarization), 6 layers
P1(7)	2367.2	Moderately strengthening	2366.2	2376.9	Film mode (p-polarization), 7 layers
P1(8)	2369.9	Moderately strengthening	2369.0	2379.3	Film mode (p-polarization), 8 layers
P1(9)	2372.0	—	—	—	Film mode (p-polarization), 9 layers
P2(8)	2357.2	—	2355.9	2367.0	Film mode (p-polarization), 8 layers

---

Furthermore, at 2335.7 cm⁻¹ a band denoted BL appears after additional exposure of only 2 to 4 minutes (blue spectrum), and becomes weaker again at further dosage, as the film thickness increases. This band is thus assigned to the bilayer CO₂/NaCl(100), which is not further discussed in this paper, but shall be addressed in detail in further studies.

Moreover, an additional weak feature denoted SP1 is observed at 2353.7 cm⁻¹ both in s-polarization and p-polarization. The feature does not shift in position at higher coverage (Fig. 2). Further weak absorptions are seen predominantly in p-polarisation in the high-coverage regime in Fig. 2. These absorptions are tabulated in Table 1, and are reproduced on an enlarged scale in Fig. 4 where they are denoted as peaks P1(5), P1(6), P1(7), P1(8), and P2(8). The significance of the labeling of the various peaks will become clear in the next section. Inspection of Fig. 4 reveals the following qualitative result: the peaks P1(i), i = 5, 6, 7, 8 are present in the various spectra with different strength. At the same time, the peak centers of P1(6), P1(7), and P1(8) are at the same position in the three differerent spectra, i.e. these peaks do not shift with layer thickness. While P1(5) is pronounced in the red spectrum with lowest coverage, the peak nearly disappears in the higher coverage spectra. In contrast, the feature P1(7) and P1(8) are weaker in the red spectrum and become more pronounced as coverage increases. A first interpretation of these peaks is based on their assignment to film domains with a unique number of layers coexisting on the surface. As the surface is exposed to gas-phase CO₂, the abundance of a film domain with a certain number of layers first increases, and is then again expected to decrease due to the stacking of additional layers of CO₂ molecules on top of it. By consequence, the peaks associated to domains with this certain number of layers will be weakened. It is the task of spectra simulations to show that a series of modes with the observed behaviour can indeed be explained in this way.

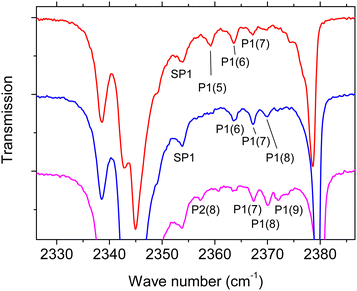Fig. 4 Enlarged representation of p-polarized IR spectra in the high coverage regime (Fig. 2) with fine structure features labeled SP1, P1, P2 (see also Table 1). For the purpose of clarity the spectra are shifted vertically. For line positions and further characterization of observed infrared modes see Table 1.

The following observations were made in additional experiments: (A) cautious tempering of the once prepared layers at temperatures of about 60 K did not significantly change the spectra profiles. (B) At further exposure of the once prepared layers to CO₂ the additional spectral features gradually become weaker.

3 Model calculations

In order to substantiate the interpretation of the observed IR absorptions, two different methods were used for the modeling of CO₂ thin film spectra. Both models are based on film geometries resulting from energy minimizations at 0 K. No temperature effects are thus included. The first method is the vibrational exciton (VE) model, which is simple but intuitive. It was previously applied by Berg et al. to monolayer and multilayer CO₂ thin films on the NaCl(100) surface.¹⁷ The second approach is based on state of the art phonon calculations within the framework of dispersion-corrected plane-wave density functional theory (pw-DFT-D).

Matching the experimental situation, the IR absorption of polarized light in transmission geometry is considered, with ultrathin CO₂ films being adsorbed both at the front side and at the back side of the NaCl single crystal. The latter is considered as a non-absorbing transparent substrate. For the index of refraction at 2350 cm⁻¹, a value of n = 1.52 was taken from ref. 25. The IR beam strikes the front side at an angle β = 45° measured against the surface normal. It is partially reflected and transmitted through the substrate. The direction vector of the electric field, [small epsilon, Greek, vector], is different at the front side and at the back side, and is calculated using Fresnel's equations.²⁶ Explicit formulae are given in ESI† (S1), where also a sketch of the optical path of the IR beam through the substrate interfaces is given. Thus, following the treatment of Berg and Ewing,¹⁷ the model assumes a single two-layer model in which the ultrathin adsorbate films do not influence the effective electric fields at the interfaces. This approximation has been discussed in ref. 17 and analyzed in more detail in ref. 27.

In general, an ordered adsorbate exhibits lower point symmetry than the NaCl(100) surface unit cell, and will thus be present in four different domain orientations with equal weights. In order to facilitate the domain averaging, it is convenient to rotate the electric field vectors accordingly instead of rotating the simulated film geometries.

3.1 Vibrational exciton model

The strength of the VE model is its conceptual simplicity, which nevertheless contains the necessary physics^17,18 to understand the splittings of vibrational modes in a film of translationally inequivalent molecules coupled by dynamic dipole–dipole interaction. The implementation used in this study is essentially identical to that described in ref. 22. The approach adopts the exciton model described in ref. 17 with the special assumption of strict twodimensional periodicity.

The basis of the model are the geometries of the monolayer with p(2 × 1) translational symmetry, and the multilayer films with c(2 × 2) translational symmetry. These were optimized by means of minimizing the film cohesive energy

involving intermolecular interaction potentials V_ij between N carbon dioxide molecules distributed over a sufficiently large number of 2D unit cells. V_ij was calculated from the high quality SAPT-s parameter set from symmetry adapted perturbation theory by Bukowski et al.²⁸ The molecule surface interaction potential V_MS,i considers electrostatic interaction taking the CO₂ site charges from the SAPT-s potential and the NaCl(100) electrostatic surface potential from Lennard-Jones and Dent.²⁹ Moreover, V_MS,i includes a short-range contribution described by atomic site Lennard-Jones parameters^30,31 using the Berthelot combination rules. Further details of the potential calculations can be found in the ESI† (S2).

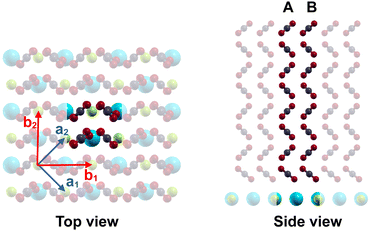
The optimized geometry of a ultrathin film comprising 8 layers and c(2 × 2) symmetry is shown in Fig. 5. Each layer contains two translationally inequivalent molecules A and B. At the interfaces, the orientation and the tilt angle of the molecules with respect to the surface normal differ somewhat from the structure in the middle of the film, where the interlayer distance is 2.67 Å. This value is slightly smaller than the bulk value of 2.79 Å for α-CO₂ at 80 K, obtained by Mangan et al.¹⁵

Fig. 5 Structure of a CO₂ film with 8 layers on the NaCl(100) surface, as obtained from potential calculations. The vectors a⃑_i, i = 1, 2 are the substrate 2D lattice vectors, b⃑_i are the 2D lattice vectors of the c(2 × 2) superlattice. The highlighted areas show the basis comprising two translationally inequivalent CO₂ molecules A and B per layer. Na⁺ and Cl⁻ are represented by cyan and green balls, respectively, oxygen and carbon by red and black balls.

Using the intermolecular distance

r_s,s′,n,m = |r⃑_s − r_s′ − nb⃑₁ − mb⃑₂| (3)

between a molecule s in the unit cell at g⃑₀₀ = 0 and a molecule s′ in the unit cell at g⃑_nm indexed by the integers n and m, and the unit vector v⃑_s,s′,n,m connecting their center of masses, a dipole–dipole interaction tensor¹⁸U is calculated by summation over the c(2 × 2) lattice vectors:

The prime symbol in the sum denotes that s′ ≠ s for n = m = 0, and e⃑_s,n,m is the unit vector pointing along the direction of the induced electric dipole moment of a molecule s in unit cell indexed by n and m, respectively. For the ν₃ asymmetric stretch mode of the linear triatomic CO₂, the induced dipole moment and thus e⃑_s,n,m is parallel to the molecule's axis.

Given a film with S inequivalent molecules with singleton wave number [small nu, Greek, tilde]₀ and vibrational polarizability α_vib related to a fundamental vibrational mode, the eigenvalue problem

determines the eigenvectors c_s′k and wave numbers [small nu, Greek, tilde]_k for the S exciton solutions, which are characterized by a vibrational exciton state¹⁸a linear combination of products in which all but the sth molecule are in their vibrational ground state, while molecule s is singly excited. Optimized values for α_vib and [small nu, Greek, tilde]₀ are given in Table 3. After solution of eqn (5) using standard linear algebra methods, the absorption stick spectrum for s-polarization and p-polarization is obtained by means of

F is the area of the surface unit cell. Eqn (7) sums up the contribution from the front side (i = 1) and the back side (i = 2) and performs a domain averaging using appropriate direction vectors of the electric field at the front side and at the back side, as introduced above. Eqn (7) is obtained from a textbook time-dependent perturbation theory treatment of the transition probability in analogy to gas-phase IR spectroscopy with the exception that the molecules are regularly oriented. Moreover, the factor F cos β in the denominator of the prefactor accounts for the surface area irradiated by the IR beam under oblique incidence. Note also that α_vib is related to the square of the dipole-moment derivative via³²

with c being the vacuum speed of light. The calculated stick spectra for the monolayer with p(2 × 1) geometry and films between 4 layers and 8 layers are reproduced in Fig. 6. The monolayer spectrum reproduces the doublet of in-phase (ML+) and out-of-phase (ML−) vibrations of the two inequivalent molecules (cf.Fig. 1 and Table 1). The most intense peaks in the film spectra are the modes denoted TO, TO-sh, and LO, the latter being visible only in p-polarization, consistent with an induced vibrational dipole-moment normal to the surface plane. Besides these peaks, the most intense of the weak modes visible both in s-polarisation and p-polarisation is denoted SP1. Accordingly, the second most intense of the weaker peaks visible both in s-polarisation and p-polarisation is named SP2. The most intense mode visible almost exclusively in p-polarisation is denoted P1(i), where the index i stands for the number of layers in the film.‡ A special situation is observed in the simulated spectra for a film of 5 layers thickness. Here, the peaks SP2 and P1(5) seem to coincide. The wave numbers of the most intense modes for films with varying number of layers are shown in Fig. 7. While the intense TO mode, its shoulder TO-sh, and the weaker feature SP1 do not change their wave number with film thickness substantially, the LO mode's wave number increases moderately, which is also observed in the experiment (cf.Fig. 1 and 2). A marked shift to higher wave numbers as the number of layers increases, however, is observed for the feature P1 in p-polarization. Visible both in s-polarization and p-polarization, a weak feature SP2 shifts to lower wave numbers.

Fig. 6 Stick spectra obtained with the vibrational exciton model for a monolayer CO₂, and films between four and eight layers. For comparison with experimental spectra a superposition of stick spectra should be assumed, reflecting the coexistence of domains with different numbers of layers.

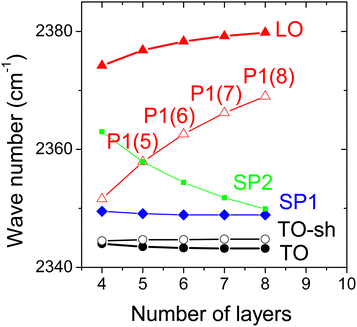Fig. 7 Results of vibrational exciton model for multilayer CO₂ films on NaCl(100): wave numbers of the most intense modes modes dependent on film thickness.

Concerning the nature of the various exciton modes, it is instructive to look at their eigenvectors, which are reproduced for some modes of an eight layer film in Table 2. For each of the 8 layers, the coefficients c_s,k are tabulated for its two inequivalent molecules A and B (see also Fig. 5). Higher absolute values of c_s,k correspond to a higher localization of the vibrational exciton at a certain molecule, or, accordingly, a higher vibrational displacement amplitude. While the most intense modes TO and LO have similar absolute c_s,k values across the whole film, the situation is different especially for the mode SP1, which has higher absolute values in the first three layers at the bottom near the substrate interface. Similarly, the mode TO-sh appears to be located in the topmost three layers near the interface to the vacuum. Moreover, the sign of these coefficients provides information about the relative phase of the molecule's vibration. Equal phases indicate in-phase motion, while opposite signs indicate out-of-phase motion, respectively. Thus, within the vibrational exciton model, the mode TO appears to be a collective in-phase mode of all molecules within the film, while in the mode TO-sh, the two inequivalent molecules A and B within a layer are out-of-phase with each other. Similarly, molecule A and B vibrate out-of-phase also in mode SP1, while in modes P1(8) and LO, the molecules within a layer vibrate in-phase.

Table 2 Modeling of CO₂ film spectra using the vibrational exciton approach: eigenvectors c_s,k of selected modes in a film with 8 layers. For the definition of c_s,k see eqn (6). Each layer contains two translationally inequivalent molecules A and B (see Fig. 5)

Layer	TO		TO-sh		SP1		P1(8)		LO
	Mol. A	Mol. B	Mol. A	Mol. B	Mol. A	Mol. B	Mol. A	Mol. B	Mol. A	Mol. B
1	−0.207	−0.207	0.027	−0.026	−0.553	0.552	−0.240	−0.240	−0.066	−0.066
2	−0.284	−0.284	0.009	−0.008	−0.421	0.421	0.336	0.336	0.175	0.175
3	−0.309	−0.309	−0.026	0.026	−0.126	0.126	−0.074	−0.074	−0.290	−0.290
4	−0.310	−0.311	−0.060	0.060	−0.032	0.032	−0.266	−0.266	0.360	0.360
5	−0.288	−0.289	−0.112	0.112	−0.012	0.012	0.268	0.268	−0.360	−0.360
6	−0.243	−0.243	−0.244	0.244	−0.009	0.009	0.068	0.068	0.291	0.291
7	−0.180	−0.180	−0.432	0.432	−0.010	0.010	−0.331	−0.331	−0.178	−0.178
8	−0.098	−0.097	−0.485	0.484	−0.010	0.010	0.258	0.258	0.069	0.069

---

The results obtained from the VE model will be further discussed below in Section 4.

3.2 Plane-wave DFT-D

The geometries of the monolayer as well as films with c(2 × 2) symmetry and thicknesses between four and eight layers were optimized using the quantum espresso (QE) package^33,34 (version 7.1). The molecular film was stacked on a four-layer slab of NaCl(100) with a pre-optimized lattice parameter of 5.7 Å. The pseudo-potentials using Perdew–Burke–Ernzerhof-funtionals³⁵ (PBE) and the projector augmented wave formalism³⁶ were taken from Dal Corso's pseudopotential library.³⁷ A cut-off energy of 41 Ry for the wavefunction and 246 Ry for the density was used in combination with a 3 × 3 × 1 Monkhorst–Pack grid. Grimme's DFT-D2 parameters³⁸ for dispersion interaction were used.

Details of the optimized geometries are given in the ESI† (S3). It is worth to mention that the interlayer distance in the middle of the film is 2.86 Å and thus somewhat larger than the experimental bulk value of 2.79 Å given above. For the optimized geometries, a phonon calculation at the Γ-point was made to determine the infrared intensities. In order to generate polarization infrared stick spectra, the QE postprocessing code for the evaluation of IR intensities from the dynamical matrix was slightly modified to print out the polarization vector p⃑_k involved with a certain infrared mode k.§ Normally, the “infrared intensity” or infrared cross-section³⁹ in units of Debye² Å⁻² amu⁻¹ of a single mode k is computed by means of

I(k) = I_c(p⃑_k)² (9)

where I_c is a proper conversion factor. For the special experimental situation described at the beginning of this section, domain averaged PIRS intensities for mode k were recalculated introducingwhere [small epsilon, Greek, vector]_i,d is the direction vector of the electric field associated with domain d for either s-polarization or p-polarization at the front side i (i = 1) or at the back side (i = 2). For explicit values of [small epsilon, Greek, vector]_i,d see ESI† (S1).

The PIRS stick spectra for the monolayer and films of various thickness are shown in Fig. 8. Explicit data of the calculated modes are tabulated in the ESI† (S3). Table S6 (ESI†) also compares calculated intensities for the monolayer modes with experimental integrated absorbances. The wave numbers of some modes are also listed in Table 1. The modes ML+, ML−, TO, and LO are blue-shifted in comparison with experimental values, mainly due to the harmonic approximation without the use of a scaling factor. However, as further discussed below, the simulated LO–TO splitting of 32.1 cm⁻¹ for a film with 8 layers is quite close to the experimental value of 35.6 cm⁻¹. Apart from the shoulder of the TO mode denoted TO-sh, a weak feature SP1 both in s-polarization and p-polarization changes only little between 2367 cm⁻¹ and 2365 cm⁻¹, as the number of layers increases. In p-polarised spectra, the wave number of feature P1 moves from 2362 cm⁻¹ for a film with four layers up to 2379 cm⁻¹ for a film with 8 layers. For films with 7 and 8 layers thickness, a weaker feature P2 appears in p-polarization (see Fig. 8). The vibrational displacements involved with some modes of a filme with 8 layers are shown in Fig. 9 where the scaled amplitude and direction of the displacements is indicated by green arrows. Most striking is the behaviour of mode SP1 with the largest vibrational displacements essentially in the first two layers at the interface to the NaCl substrate, in accordance to the characterization of this mode by the VE model. In the following, these results will be further discussed and compared to the experimental findings.

Fig. 8 Stick spectra obtained with plane wave DFT-D for a monolayer CO₂, and films between four and eight layers. Infrared intensities are given in Debye² Å⁻² amu⁻¹. For comparison with experimental spectra a superposition of stick spectra should be assumed, reflecting the coexistence of domains with different numbers of layers.

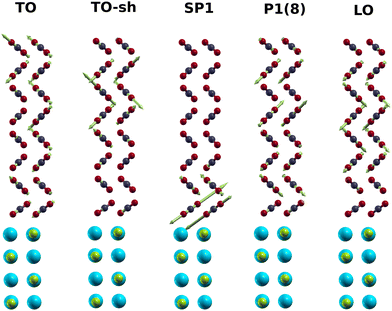Fig. 9 Displacement patterns of selected normal modes obtained from pw-DFT-D simulation for a CO₂ film with 8 layers. Cyan and green balls represent the substrate Na⁺ and Cl⁻, respectively. Green arrows indicate the vibrational forces on atoms in a normal mode.⁴⁰ The mode TO-sh is the shoulder of the TO.

4 Discussion

In the HAS experiments by Lange et al.¹¹ diffraction spots of the first layer NaCl(100)/p(2 × 1)-CO₂ were visible up to an exposure of 170 L, suggesting a coexistence of the first layer with multilayer CO₂ at 40 K. This excludes a layer-by-layer growth mode of CO₂ despite the quite small lattice mismatch with the NaCl substrate. The present results from IR spectroscopy are consistent with this picture. As can be seen in Fig. 1, the mode ML+ assigned to the preadsorbed monolayer is still visible in the multilayer spectra, and the mode ML− stays visible as a shoulder at the high frequency side of the TO mode. In the absence of layer-by-layer growth, the coexistence of domains with different film thickness is conceivable. By consequence, the IR spectra shown in Fig. 1 should be interpreted as a superposition of spectra resulting from coexisting domains with varying number of layers. The evaluation of integrated absorbance data (Fig. 3) provides an average number between one and seven monolayers for the presented spectra. Moreover, a sticking coefficient of S = 0.74 ± 0.1 is deduced, which is a reasonable value. In a previous study a sticking probability of one was ad hoc assumed⁴ for CO₂ ice at 80 K and below. Moreover, the present value is somewhat smaller and scarcely in line with the value of 1.0 ± 0.2 found by Weida et al.,⁴¹ and, moreover, with a value of 0.9 obtained recently from state-resolved experiments by Jansen and Juurlink.⁴²

The preparation method to grow the thin films onto a preadsorbed monolayer leads to the appearance of additional spectral features between the intense TO and LO modes. Basically two kinds of features in the ν₃ spectrum in Fig. 1 and 2 are observed. Firstly, a band visible both in s-polarized and p-polarized spectra, thus denoted SP1. Secondly, a series of weak peaks only visible in p-polarized spectra. Inspection of the enlarged representation in Fig. 4 shows that the peaks P1(5) and P1(6) become weaker as the coverage increases (spectrum colored magenta), while P1(7) and P1(8) become stronger. From the Stransky–Krastanov growth mode and these findings it was concluded at the end of Section 2 that the peaks P1(i) should be assigned to film domains of a characteristic number of layers. This assumption is supported by two different computational models to simulate PIRS spectra introduced in Section 3.

The computational models yield similar results for the film modes in the ν₃ region, although there are differences in the absolute position of the IR bands. With the vibrational polarizabilities and singleton-frequencies given in Table 3, the vibrational exciton approach reproduces quite well the Davydov-splitting in the p(2 × 1) monolayer phase, and the TO–LO-splittings of the film modes (35.6 cm⁻¹ experimentally versus 36.1 cm⁻¹ calculated, see Table 1). The DFT approach has no extra optical parameters and no scaling factor was applied to compensate for the missing anharmonicity in the model. Thus the calculated band positions appear basically blue-shifted by about 10 cm⁻¹. Nevertheless, the calculated TO–LO-splitting of 32.1 cm⁻¹ is close to the experiment. It can thus be noted that both computational models reproduce the observed characteristic splittings of the films in a satisfactory manner. It is worth to mention that both models reproduce the slight blue shift of the LO peak with increasing thickness seen in Fig. 2. In the following, the discussion focuses on the most intense of these additional spectral features seen in the experiment. The peak labeled SP1 is visible both in s-polarized and p-polarized film spectra, and its wavenumber near 2354 cm⁻¹ (see Table 1, Fig. 1 and 2) does not change substantially as the film thickness increases. The counterpart in the simulated spectra are film modes at 2349 cm⁻¹ (VE approach) and between 2366 cm⁻¹ and 2369 cm⁻¹ (DFT-model). In both simulations, SP1 is the strongest feature visible both in s-polarization and p-polarization. And, moreover, within both models the feature does not change substantially its position as the number of layers increases (see Fig. 6–8 and 10). As described above, further analysis of the simulation results suggest that this mode is a vibrational excitation of the molecules in the layers close to the NaCl substrate, and this might in part explain the only minor change in wave number with increasing coverage. Indeed, in terminology of surface phonon lattice dynamics, one could characterize SP1 as a optical localized mode⁴³ at the interface.

Table 3 Singleton wave numbers and vibrational polarizabilities of CO₂ molecules for the VE model

	[small nu, Greek, tilde] 0 (cm^−1)	α vib (Å^3)
CO2-p(2 × 1)/NaCl(100)	2344.8	0.48
CO2 multilayers	2349.8	0.30

---

Fig. 10 Results of pw-DFT-D for multilayer CO₂ films on NaCl(100): wave numbers of the most intense modes modes.

In both models, the strongest peak P1 largely visible in p-polarization has a considerable increase in wave number as the thickness of the film increases between 4 and 8 layers (see Fig. 7 and 10). This indeed justifies the assignment to the series of peaks denoted P1(i) in the experiments (see Table 1). Visibility in p-polarization is related to an induced total vibrational dipole moment nearly perpendicular to the surface plane. The displacement pattern for the pw-DFT-D model depicted for this mode in Fig. 9 and the eigenvector coefficients c_s,k from vibrational exciton theory in Table 2 reveal an in-phase vibration of the molecules within a layer, and strongly alternating vibrational amplitudes of the molecules in different layers. This behaviour resembles to some extent to a nodal pattern of excitation of the entire film stack. In spite of the similarities in the two models, however, there are also some differences concerning the amplitude and phase of the molecules across the film stack. So, unlike in the case of mode SP1, a further more concrete interpretation of the nature of the mode P1 seems not possible.

There are also some differences between the two models concerning the very weak modes. While the vibrational exciton ansatz predicts a further series of peaks SP2 visible in s-polarization and p-polarization (cf.Fig. 6), this feature was not observed in the experiment (cf.Fig. 2), and is also not markedly present in the pw-DFT-D stick spectra. It is conceivable, that within the vibrational exciton approach, dynamic dipole–dipole coupling is to some extent overestimated, since the interlayer distance from the cohesive energy minimization was about 0.1 Å smaller than the respective bulk value, while the interlayer distances from pw-DFT-D exceed the bulk value by about 0.1 Å. Note that in the VE model, this structural property affects the dipole–dipole sum U in eqn (4)via the intermolecular distance r between two molecules. Within the pw-DFT-D model, on the other hand, an extra feature P2 visible in p-polarization is predicted for film thicknesses of 7 and 8 layers, respectively (see Fig. 8). In the enlarged version of p-polarized experimental spectra shown in Fig. 4, an albeit weak peak at 2357.2 cm⁻¹ was tentatively assigned as P2(8).

Next, the conditions for the appearance of the additional weak peaks in experimental spectra shall be discussed. Both computational models assume strict two-dimensional periodicity of a slab of CO₂ molecules, which on a real surface, is only met in an approximate fashion, due to truncation effects, and various forms of static and dynamical disorder. It seems that long-range order within a film domain within a sufficiently large number of 2D unit cells is a precondition for the appearance of the observed additional spectral features. From the widths of diffraction peaks observed in the HAS experiments,¹¹ Lange et al. estimated an extension of ordered CO₂ film domains of about 250 Å, corresponding to about 2000 c(2 × 2) unit cells. In the present study, CO₂ films were grown under similar conditions on a preadsorbed monolayer at the same temperature and similar growth rates. If a similar film quality would thus be presumed for the films prepared in the present work, an eight layer film with this extension would contain about 30 000 CO₂ molecules. In the detailed IR spectroscopic study by Berg et al.,¹⁷ multilayer films with an estimated thickness of about 4 monolayers were prepared at 65 K at a ten times larger growth rate.¶ The spectrum of the so prepared films only shows the monolayer doublet and the TO and LO peaks. Moreover, Berg et al. conducted a vibrational exciton spectrum simulation in this study.¹⁷ It involved a four layer finite film cluster of 1800 molecules, thus extending over 225 unit cells. Their simulated spectrum did not exhibit additional pronounced spectral features. From gas-phase clusters it is well-known that shape and size can crucially affect the vibrational spectrum.⁴⁴ A further hint is the observation mentioned at the end of Section 2 that the additional peaks gradually become weaker with increasing exposure. It is conceivable that film domains become more fragmented and domain sizes have the tendency to decrease if the film thickness increases. So it seems that the presence of additional spectral features as those observed in this work is related to large film domains with long-range order, and ultrathin films with coverages up to about 10 monolayers. It is also worth to mention that in experiments with multilayer adsorption on other substrates (CaF₂(111), KBr(100), KCl(100)) this kind of size-dependent fine structure was not observed so far.

Finally, possible alternative mechansim causing line splittings in the CO₂ films shall be briefly discussed. Mode interactions due to Fermi resonances in carbon dioxide do not fall in the region of the ν₃ assymmetric stretch mode,⁴⁵ why these can be ruled out. Moreover, combination bands of internal modes and external modes have been ruled out previously¹⁷ as a source of splittings, since for physisorbed molecules like CO₂ such combination bands are expected to be weak and diffuse.¹⁷ Finally, the presence of molecules in different energetically inequivalent sites could lead to splittings. While in systems like CO chemisorbed on Cu(211) or Cu(111) the IR spectra of CO show distinct splittings due to different red-shifts,⁴⁶ such effects are much less pronounced in the case of weakly interacting physisorbed molecules, and are thus unlikely to explain the oberved splittings. Vibrational dipole–dipole coupling thus appears to be the dominant mechanism explaining the film spectra of CO₂ in the physisorbed state.

Possible applications of the observed spectral features between the TO and LO modes might involve experiments with the possibility to vibrationally excite an ultrathin film e.g. specifically at its interfaces. Vibrational energy transfer in a CO₂ molecular crystal has been considered by Falk.² Only recently, Ioppolo et al. studied the possibility of reorientation and desorption from amorphous and crystalline CO₂ ice by tunable free-electron laser irradiation at various energies near the ν₃ mode.⁴⁷ While a frequency dependent restructuring was not clearly observed in crystalline ice,⁴⁷ such experiments could show quite different results with ultrathin films on NaCl(100) if the excitation energy would match the various additional modes found in this study.

Moreover, the observed fine structure related to long range ordered film structure is an argument to use NaCl as a preferred substrate to grow high quality CO₂ films. The only slightly higher effort to grow CO₂ on a preadsorbed monolayer has the benefit to prepare well-defined films, and the presence of the weak features between the TO and LO modes is a verification of their quality.

As noted in Section 2, future work shall investigate in detail the formation of the bilayer and the possible reorientation effects involved if the second and the third layer starts to form.

5 Conclusions

Multilayer CO₂ films were grown at low adsorption rates on a preadsorbed monolayer NaCl(100)/p(2 × 1)-CO₂ at 40 K. Polarization IR spectroscopy experiments revealed a size-dependent fine structure in the ν₃ asymmetric stretch region. In agreement with a previous helium diffraction study,¹¹ a Stranski–Krastanov growth of CO₂ is deduced, and a sticking coefficient of 0.74 ± 0.1 was determined based on the integrated absorbance of the IR spectra. Between the TO and LO peaks an additional absorption at 2354 cm⁻¹ was detected independent of coverage both in s-polarization and p-polarization. Moreover, a series of weak peaks appearing exclusively in p-polarized spectra were assigned to film domains with a unique number of layers. Two kinds of spectra simulations based on the vibrational exciton approach and on plane-wave density functional theory were used to calculate stick spectra of the monolayer and films between 4 and 8 monolayers. According to these models, the additional feature in s-polarization and p-polarization can be assigned to a vibrational excitation of the molecules in the layers located near the interface to the NaCl substrate. Moreover, both models support an additional mode visible in p-polarization with a marked increase of wave number with the number of layers. Assuming the coexistence of film domains with varying number of layers in the experiment, this mode explains the series of features occurring in p-polarized spectra.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

I am grateful to the University of Magdeburg and its facilities for financial and technical support of the ongoing projects.

Notes and references

1. I. R. Cooke, E. C. Fayolle and K. I. Öberg, Astrophys. J., 2016, 832, 5.
2. M. Falk, J. Chem. Phys., 1987, 86, 560–564.
3. R. M. Escribano, G. M. M. Caro, G. A. Cruz-Diaz, Y. Rodríguez-Lazcano and B. Maté, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12899–12904.
4. K. Isokoski, C. A. Poteet and H. Linnartz, Astron. Astrophys., 2013, 555, A85.
5. S. A. Sandford and L. J. Allamandola, Astrophys. J., 1990, 355, 357.
6. J. A. Lau, A. Choudhury, C. Li, D. Schwarzer, V. B. Verma and A. M. Wodtke, Science, 2020, 367, 175–178.
7. C. Yuan, J. Yates and T. John, J. Chem. Phys., 2013, 138, 154303.
8. Y. Li, Y. Li, C. Li, X. Zhang, F. Zeng, H. Lin, Z. Su and C. Mahadevan, J. Alloys Compd., 2020, 849, 156592.
9. A. Simon and K. Peters, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2750–2751.
10. J. Vogt and H. Weiss, J. Chem. Phys., 2003, 119, 1105–1114.
11. G. Lange, D. Schmicker, J. P. Toennies, R. Vollmer and H. Weiss, J. Chem. Phys., 1995, 103, 2308–2319.
12. J. Schimmelpfennig, S. Fölsch and M. Henzler, Surf. Sci., 1991, 250, 198–206.
13. J. Heidberg, E. Kampshoff, O. Schönekäs, H. Stein and H. Weiss, Ber. Bunsenges. Phys. Chem., 1990, 94, 112–118.
14. J. Heidberg, E. Kampshoff, R. Kühnemuth and O. Schönekäs, Surf. Sci., 1992, 269–270, 120–127.
15. T. Mangan, C. Salzmann, J. Plane and B. Murray, Icarus, 2017, 294, 201–208.
16. O. Berg and G. E. Ewing, Surf. Sci., 1989, 220, 207–229.
17. O. Berg, R. Disselkamp and G. E. Ewing, Surf. Sci., 1992, 277, 8–20.
18. D. Fox and R. M. Hexter, J. Chem. Phys., 1964, 41, 1125–1139.
19. G. Zumofen, J. Chem. Phys., 1978, 68, 3747–3759.
20. A. G. Cabello-Cartagena, J. Vogt and H. Weiss, J. Chem. Phys., 2010, 132, 074706.
21. J. Vogt and H. Weiss, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125415.
22. F. Traeger, M. Hadnadjev, J. Vogt and H. Weiss, J. Phys. Chem. A, 2011, 115, 6986–6996.
23. J. Heidberg, M. Hustedt, E. Kampshoff and V. Rozenbaum, Surf. Sci., 1999, 427–428, 431–438.
24. J. Heidberg, E. Kampshoff, R. Kühnemuth, O. Schönekäs, H. Stein and H. Weiss, Surf. Sci., 1990, 226, L43–L47.
25. E. D. Palik, Handbook of Optical Constants of Solids, Academic Press, Orlando, Florida, 1985.
26. V. Tolstoy, I. Chernishova and V. Skryshevsky, Handbook of Infrared Spectroscopy of Ultrathin Films, Wiley, Hoboken, New Jersey, 2003.
27. H. H. Richardson, H.-C. Chang, C. Noda and G. E. Ewing, Surf. Sci., 1989, 216, 93–104.
28. R. Bukowski, J. Sadlej, B. Jeziorski, P. Jankowski, K. Szalewicz, S. A. Kucharski, H. L. Williams and B. M. Rice, J. Chem. Phys., 1999, 110, 3785–3803.
29. J. E. Lennard-Jones and B. M. Dent, Trans. Faraday Soc., 1928, 24, 92–108.
30. Z. Zhang and Z. Duan, J. Chem. Phys., 2005, 122, 214507.
31. D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757–3766.
32. D. Rinaldi, M. Ruiz-Lopez, M. Costa and J. Rivail, Chem. Phys. Lett., 1986, 128, 177–181.
33. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
34. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
37. A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350.
38. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
39. P. Giannozzi and S. Baroni, in Density-Functional Perturbation Theory, Handbook of Materials Modeling: Methods, ed. S. Yip, Springer, Netherlands, Dordrecht, 2005, pp. 195–214.
40. A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 176–179.
41. M. J. Weida, J. M. Sperhac and D. J. Nesbitt, J. Chem. Phys., 1996, 105, 749–766.
42. C. Jansen and L. B. F. Juurlink, Front. Chem., 2023, 11 DOI:10.3389/fchem.2023.1250711.
43. G. Benedek, M. Bernasconi, D. Campi, J. P. Toennies and M. J. Verstraete, in Surface Phonons: Theoretical Methods and Results, ed. M. Rocca, T. S. Rahman and L. Vattuone, Springer International Publishing, Cham, 2020, pp. 737–782.
44. R. Signorell, J. Chem. Phys., 2003, 118, 2707–2715.
45. C. W. McCluskey and D. S. Stoker, Raman observations of quantum interference in the ν₁/2ν₂Fermi dyad region of carbon dioxide, 2006, https://arxiv.org/abs/physics/0601182.
46. D. Zhang, V. Virchenko, C. Jansen, J. M. Bakker, J. Meyer, A. W. Kleyn, I. M. N. Groot, O. T. Berg and L. B. F. Juurlink, J. Phys. Chem. C, 2023, 127, 24158–24167.
47. S. Ioppolo, J. A. Noble, A. Traspas Muiña, H. M. Cuppen, S. Coussan and B. Redlich, J. Mol. Spectrosc., 2022, 385, 111601.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02311k

‡ Accordingly, the second most intense of the weaker peaks visible only in p-polarisation would be denoted P2(i) and so on.

§ The vector p⃑ is obtained by matrix multiplication of the effective charge tensor and the eigen displacements involved with a certain mode.

¶ This is estimated from the CO₂ partial pressure of 8 × 10⁻⁸ mbar reported in ref. 17.

---