 Open Access Article
Open Access ArticleSeparation of oxygen from nitrogen using a graphdiyne membrane: a quantum-mechanical study
Maryam A.
Rafiei
 *ab,
José
Campos-Martínez
*ab,
José
Campos-Martínez
 a,
Massimiliano
Bartolomei
a,
Massimiliano
Bartolomei
 a,
Fernando
Pirani
a,
Fernando
Pirani
 c,
Ali
Maghari
c,
Ali
Maghari
 b and
Marta I.
Hernández
b and
Marta I.
Hernández
 *a
*a
aInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas (IFF-CSIC), Serrano 123, 28006 Madrid, Spain. E-mail: maryam.rafiei@ut.ac.ir; marta@iff.csic.es
bDepartment of Physical Chemistry, School of Chemistry, College of Science, University of Tehran, Tehran, Iran
cDepartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, via Elce di Sotto 8, Perugia, 06123, Italy
First published on 2nd September 2024
Abstract
Efficient separation of oxygen and nitrogen from air is a process of great importance for many industrial and medical applications. Two-dimensional (2D) membranes are very promising materials for separation of gases, as they offer enhanced mass transport due to their smallest atomic thickness. In this work, we examine the capacity of graphdiyne (GDY), a new 2D carbon allotrope with regular subnanometric pores, for separating oxygen (16O2) from nitrogen (14N2). A quantum-mechanical model has been applied to the calculation of the transmission probabilities and permeances of these molecules through GDY using force fields based on accurate electronic structure computations. It is found that the 16O2/14N2 selectivity (ratio of permeances) is quite high (e.g., about 106 and 102 at 100 and 300 K, respectively), indicating that GDY can be useful for separation of these species, even at room temperature. This is mainly due to the N2 transmission barrier (∼0.37 eV) which is considerably higher than the O2 one (∼0.25 eV). It is also found that molecular motions are quite confined inside the GDY pores and that, as a consequence, quantum effects (zero-point energy) are significant in the studied processes. Finally, we explore the possibility of 18O2/16O2 isotopologue separation due to these mass-dependent quantum effects, but it is found that the process is not practical since reasonable selectivities are concomitant with extremely small permeances.
1 Introduction
Molecular oxygen (O2) and nitrogen (N2) are the major components of the atmosphere and, at the same time, are the two most demanded gases after hydrogen.1–4 Nitrogen is used as a feedstock, as an inert atmosphere or as a cryogenic agent in many industrial and scientific applications. Oxygen is a key ingredient in industry (chemical, petrochemical, etc.) and an essential element in medical treatments. Extracting high purity oxygen from air is conventionally carried out using techniques such as cryogenic distillation and pressure swing adsorption; however, these techniques require large capital costs and high energy consumption. An interesting alternative is the utilization of separation membranes, and in fact there has been intense research on a large set of membranes for O2/N2 separation.1,3–7 Besides good mechanical and chemical stability, an important requirement for membranes is a satisfactory trade-off between permeability (flow of the desired species) and selectivity (rejection of undesired species), as it is known that high selectivities are often accompanied by low permeances, and vice versa.7,8 Since decreasing the thickness of the membrane increases the permeability, new two-dimensional (2D) materials are viewed as very promising candidates for achieving large transport fluxes together with acceptable selectivities.9–13Among new 2D membranes, graphdiyne (GDY) stands out as an ideal material for gas separation applications. GDY is a planar carbon allotrope characterized by diacetylenic linkages joining graphene-like hexagons,14 thus leading to an uniform web of triangular pores of subnanometric size. This membrane was first synthesized15 in 2010 and, since then, there has been a burst of experimental and theoretical studies on its properties and applications,16–21 including gas and isotopic separation.22–25 The main separation mechanism in GDY is known as size sieving,11,26 where molecules smaller than the pore size are able to permeate, while larger molecules are rejected, the sizes being correlated with kinetic diameters.27 In this way, various studies have predicted high selectivities for the separation of H2 and He from larger molecules.28–31 It is worth pointing out that, due to the small size of the pores, the transport involves surmounting potential barriers, i.e., the molecule–membrane interaction is repulsive at the pore center. Moreover, the molecular motion along directions transverse to the transmission path becomes confined and, as described by Beenakker et al.,32 this feature can lead to an increase of the transmission barrier due to the zero-point energy (ZPE) associated to these transversal degrees of freedom, a quantum effect that is mass-dependent. Therefore, different isotopes would experience different effective barriers, allowing their separation (quantum sieving), as has been indeed found33,34 for the separation by GDY of 4He/3He and D2/H2.
Separation processes of larger molecules by GDY have been also reported, for instance, CO2/N235 and CO2/CH436 separation, or the separation of O2 from a mixture of harmful gases (Cl2, HCl, etc.).37 Selectivity can be enhanced by means of pore functionalization, as in the CO2/(N2, CH4) separation in oxygen-doped GDY38 or NO/(O2, CO) in boron-doped GDY.39 As far as we are aware, there are no previous studies in which the transport properties of O2 and N2 through GDY are compared on an equal footing. This is the main goal of the present work.
In this paper, accurate electronic structure calculations are employed to obtain reliable estimations of the N2–GDY and O2–GDY interaction potentials. It is found that the transmission barriers are rather high (about 250 and 370 meV for O2 and N2, respectively) and that the interaction potential rapidly increases for molecular displacements perpendicular to the transmission path; in other words, the diatoms are confined at the pore center. Confinement associated to the rotational degrees of freedom also occurs. In this situation, significant quantum effects can appear despite the relatively large masses of these molecules.32,40 Thus, a quantum approach has been here chosen to calculate transmission probabilities and permeances through GDY of the most abundant isotopologues of oxygen and nitrogen, 16O2 and 14N2, as well as their selectivity as a function of the temperature. In addition, we have also obtained the permeances of the very scarce 18O2 isotopologue, with the aim to explore the extent of mass-dependent quantum effects and hence the possibility of 18O2/16O2 separation, a process that is of great interest for several applications.41
The paper is organized as follows. The theoretical approach is presented is Section 2. In Section 3, results are reported and discussed with regard to interaction potential features, transmission probabilities, permeances, selectivities and the role of quantum effects. We end with some conclusions in Section 4.
2 Theoretical approach
We have investigated the transport of 14N2, 16O2 and 18O2 through a periodic single GDY membrane. In this study, the molecules are considered as rigid rotors. Unlike H2 molecules, heavier species like O2 and N2 are not expected to be well described as point-like particles (pseudoatoms) since the orientational anisotropy of the molecules is large.40 Below we firstly present the electronic structure calculations and the force field used for the molecule–GDY interaction potential. Then, we describe the quantum mechanical model adopted for the calculation of the transmission probabilities, from which the permeances and selectivities can be obtained.2.1 Interaction potential
Electronic structure calculations were performed to obtain interaction energies at the “coupled” supermolecular second-order Møller–Plesset perturbation (MP2C)42 theory and density functional theory (DFT) levels by using Molpro43 and ORCA 4.2.144 program packages, respectively. The (MP2C or DFT) interaction energies between a molecular prototype of GDY and the studied gases were obtained using| Einteraction = EGDY+gas − (EGDY + Egas) | (1) |
Accurate MP2C calculations were performed to obtain benchmark electronic structure estimations of the interaction in the N2–GDY system. In particular, distinct approach directions of the diatomic molecule as well as different (perpendicular and parallel) orientations of the latter with respect to the pore plane have been probed and the corresponding interaction energies were obtained by using the aug-cc-VQZ and aug-cc-VTZ basis sets47 for N2 and the GDY prototype, respectively. In addition, several DFT approaches were examined to assess their performances over the reference MP2C results. Among the DFT levels tested, the best results were obtained with the BP8648 (a generalized gradient approximation (GGA) functional that depends on both the electron density and its gradient) and B3LYP49 (a hybrid functional combining GGA and Hartree–Fock exchange) functionals. In these DFT calculations, a quadruple-zeta valence basis set with two sets of polarization functions (def2-QZVPP)50 was used and the D3 dispersion correction51 was applied. The primitive cut-off and integral threshold for the electron integral calculations were set to 2.5 × 10−12 and 2.5 × 10−11Eh, respectively, and the tolerance energy for convergence between two self-consistent field cycles was set to 10−8Eh. These choices provided the best agreement with the MP2C data. We have considered that these DFT levels, once validated for the N2–GDY prototype, can be safely used to obtain reliable estimations of the O2–GDY interaction, for which the MP2C approach is not suitable due to the O2 open shell character.
Global interaction potentials for the interactions between O2/N2 and the GDY molecular prototype are analytically represented by the sum of pairwise contributions between the O or N atoms in the diatom and the carbon and hydrogen atoms of the prototype. The improved Lennard-Jones (ILJ)52 formula is used to represent each of these atom–atom contributions, depending on R, the distance between O (or N) and the C or H atoms, and given by
 | (2) |
| O2/N2–GDY | R m | ε | β |
|---|---|---|---|
| O–C | 3.741 | 4.001 | 6.5 |
| N–C | 3.801 | 4.140 | 6.5 |
| O–H/N–H | 3.490 | 2.076 | 8.0 |
In Fig. 1 and 2, we present the profiles of the interaction potentials between the GDY prototype and N2 and O2, respectively, obtained from the different levels of theory employed and the ILJ parametrization, for different approach directions and molecular orientations. From these figures, it can be concluded that there is a rather good agreement among the different levels of calculation considered as well as with the ILJ force field.
 | ||
| Fig. 2 Same as Fig. 1 for the O2–GDY prototype energy interaction profiles obtained from B3LYP and BP86 calculations (points) as well as the ILJ analytical representation (solid lines). | ||
Finally, V, the interaction potential between O2/N2 and the extended GDY lattice (Fig. 3), is obtained by adding up all the pairwise ILJ contributions between the atoms of the molecule and the carbon atoms of the membrane for as many atoms in the lattice until a desired convergence in V is reached. The estimated errors in the determination of V are of about 0.02% for distances close to the membrane (z < 4 Å), increasing up to about 0.2% for larger distances (z ≈ 20 Å).
Table 2 presents the molecule–GDY potential barriers as obtained for the different electronic structure methods and force field employed, corresponding to the centers of mass of the molecules placed at the center of the pore and perpendicularly oriented with respect to the GDY plane (for the GDY prototype, they correspond to the tops of the barriers depicted in Fig. 1 and 2). Notice that, within the ILJ representation, the barriers for the extended GDY are slightly lower than those corresponding to the GDY prototype. This is because the interaction with the extended layer involves a large number of carbon atoms quite distant from the molecule but anyway contributing with a weak but attractive interaction.
| N2 | O2 | ||
|---|---|---|---|
| GDY prototype | MP2C | 367.5 | — |
| B3LYP-QZVPP+D3 | 425.2 | 251.9 | |
| BP86-QZVPP+D3 | 386.4 | 255.4 | |
| ILJ | 375.8 | 254.4 | |
| GDY | ILJ | 368.4 | 247.3 |
Apart from the technical details reported here, the general features of the O2–GDY and N2–GDY interactions are discussed in detail in Section 3.
2.2 Quantum transmission probabilities, permeances and selectivities
The Hamiltonian for the interaction of a rigid diatomic molecule of mass m and bond length r0 with a rigid membrane can be written as | (3) |
 | (4) |
Masses used in the calculations are 28.0134, 31.9898 and 35.9983 Da, while rotational constants are 0.2477, 0.1782 and 0.1585 meV for 14N2, 16O2 and 18O2, respectively.
In this work, we apply an adiabatic separation between z, the coordinate representing the molecular incidence towards the membrane, and the remaining variables, (θ,ϕ,x,y), collectively denoted as Q. This approach is related to reaction path theories in molecular reactive scattering,54,55 and treatments similar to the present one have been recently reported in simulations of the transmission of molecules through membranes.34,56,57 In a first step, the Schrödinger equation for coordinates Q is solved for a set of fixed values of z, ranging from zero to the asymptotic region:
 | (5) |
The eigenvalues Wn(z) become effective interaction potentials only depending on the molecule–membrane distance. They are obtained from diagonalization of the associated Hamiltonian. Details on these calculations are given in the Appendix.
The lowest eigenvalue of eqn (5), W0(z), corresponds to the ZPE-corrected potential along the incidence direction. In this work, we will only consider this lowest effective potential, which is a reasonable approximation for the study of the transmission at low energies/temperatures, as discussed in more detail in the next section.
In a subsequent step, transmission probabilities as functions of the translational energy, P(E), are computed by solving the scattering problem with a Hamiltonian only depending on the z coordinate:
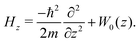 | (6) |
This equation is solved by means of a time-dependent wave-packet approach, as carried out in related works.31,34,58 An approach for solving the corresponding time-independent Schrödinger equation59 was also employed for translational energies well below the potential barrier (deep tunneling regime). Details about these calculations are also provided in the Appendix.
As discussed in earlier works,33,34 the probabilities P(E) must be scaled by a factor γ that takes into account the fraction of the membrane area that is effective for the transmission
| P*(E) = γP(E), | (7) |
Permeances as functions of temperatures are then obtained from the transmission probabilities, expressed as functions of the velocity, vz = (2E/m)1/2, as34
 | (8) |
with kB being the Boltzmann constant and f(vz,T) the Maxwell–Boltzmann velocity distribution given by
 | (9) |
Finally, to compare the permeation efficiency of two species A and B, an A/B selectivity or separation factor is defined as
 | (10) |
3 Results and discussion
We start this section with a discussion of the features of the N2–GDY and O2–GDY interaction potentials. Table 2 gives the energy barriers for the transmission of N2 and O2 through GDY (prototype and extended lattice) within different treatments. These barriers correspond to the saddle point in the transmission path of the molecules through the membrane, where the molecules are located at the center of the pore with their axes perpendicularly oriented with respect to the pore plane. The fact that the barrier for N2 is higher than that for O2 is an expected result since the N2 kinetic diameter (3.64 Å) is larger than the O2 one (3.46 Å).27 These diameters are correlated with the widths of the “electron clouds” along the axes of the diatoms27 or, similarly, with the perpendicular static dipole polarizabilities (10.24 and 8.23 a.u. for N2 and O2, respectively60). However, the large difference between the two barrier heights (the N2 barrier is ∼50% higher than the O2 one) could seem somewhat surprising, considering the relatively small difference in the molecular parameters. This feature can be understood from the repulsive character of the interactions around the pore region since, in this situation, slight variations in the molecular properties imply exponentially large differences in the resulting interaction energies.Another characteristic of the molecule–GDY interactions is the large confinement of the molecules in the pore region. This feature can be easily noticed from the inspection of Fig. 1 and 2, which show scans of the interaction energies between the GDY prototype and N2 and O2, respectively, for various molecular orientations and approach directions. Firstly, panels (a) and (b) of these figures show the interaction energies for the diatoms approaching the pore center along the z direction, for perpendicular and parallel orientations, respectively. It can be seen that the barrier drastically increases for the parallel orientation of the molecules, i.e., the rotational motion is hindered inside the GDY pore. On the other hand, panels (c) and (d) of the same figures depict the interaction potential for displacements around the pore center of the (perpendicularly oriented) molecules along the x and y directions, respectively. It is observed that the translational motion of the molecules is also affected by confinement.
Moving to the ZPE-corrected effective potentials, W0(z), obtained from solving eqn (5), they are shown using solid lines in Fig. 4 for 14N2 and 16O2/18O2, in the upper and lower panels, respectively. Dashed lines in these plots correspond to optimized molecule–GDY potentials, Vm(z), which are obtained by selecting the values of (θ,ϕ,x,y) minimizing V(θ,ϕ,x,y;z) at each z, i.e., Vm(z) = (θm,ϕm,xm,ym;z). The extent of ZPE in these systems can be estimated by the difference between W0(z) and Vm(z). It can be noticed that the ZPE is quite significant near the membrane pore: at z = 0, its contribution to the barrier height of W0 amounts to about 12–15%. This is due to the confinement of the molecules in this region, discussed in the previous paragraph. Neglecting the ZPE contribution can lead to a considerable overestimation of the permeances. Indeed, if this quantum effect were neglected, it is estimated that 16O2 and 14N2 permeances would be about four orders of magnitude larger at a temperature of 50 K, the factor being reduced to one order of magnitude at 200 K. Concerning the oxygen isotopologues (inset in the lower panel of Fig. 4), it is noted that there is a small but clear difference between their ZPE-corrected potential barriers (286.9 and 289.2 meV for 18O2 and 16O2, respectively). The effect of this difference on the permeances is discussed below.
Regarding the behavior of the ZPE at larger distances to the GDY layer, it is observed from Fig. 4 that the ZPE monotonously decreases with z and that at the minimum of both W0 and Vm potentials, at z ≈ 2.5 Å, it becomes almost negligible. It can be also noticed that both Vm(z) and W0(z) reach a further (local) minimum at z ≈ 3.5 Å. This feature is due to the topography of the O2–membrane and N2–membrane interaction potentials: the absolute minima at z ≈ 2.5 Å correspond to the molecules placed on top of the triangular-like pores, while, in the secondary minima, they sit on top of the hexagonal pores of GDY (Fig. 3), at a larger z distance.
The transmission probabilities of 16O2, 18O2 and 14N2 through GDY are reported in Fig. 5. It can be seen that these probabilities rise up at translational energies close to the barriers of the corresponding ZPE-corrected potentials (Fig. 4). In particular, it is seen that the 16O2 probability emerges at slightly larger energies than the 18O2 one, in correspondence with its higher ZPE (inset of Fig. 4). After their thresholds, the probabilities reach nearly similar plateaus (0.0046–0.0048) which are associated to γ, the effective size of the pore for each species. Comparing the two oxygen isotopologues, the effective pore size for 16O2 is larger than that of 18O2 because, being W0(z = 0) higher for the lighter molecule, the corresponding wavefunction extends over a larger region of the coordinate space. The behavior of the probabilities at energies lower than the effective barriers is shown in the insets of Fig. 5, where it can be seen that, in this tunneling regime, the probabilities decrease exponentially as the energy decreases. It can be noticed that the 16O2 probabilities decrease less rapidly than the 18O2 ones and eventually, for energies below ∼252 meV (close to the barrier of the “bare” O2–GDY potential), the 16O2 probabilities become larger than the 18O2 ones. This behavior is due to the tunneling effect, which is more favourable for the lighter species. In conclusion, these moderately heavy molecules exhibit sizable quantum effects (ZPE, tunneling) in their passage through GDY. It is worth mentioning that this behavior of the probabilities is very similar to that found for lighter species (He33,58,61 and H234) and their isotopologues.
The permeances of GDY for the transport of nitrogen and oxygen isotopologues are reported in the upper panel of Fig. 6 for temperatures between 20 and 300 K. In this temperature range, the 14N2 (16O2) de Broglie wavelength approximately varies from 0.28(0.26) Å, at 300 K, to 1.07(1.00) Å, at 20 K. It can be seen that all permeances are extremely small at the lowest temperatures; however, they rapidly raise with temperature up to about 100 K, where there is a more moderate increasing rate. This is the typical behavior of activated processes. Due to the fact that the transmission barrier of 16O2 is considerably lower than that of 14N2, the 16O2 permeation is much larger and, consequently, the 16O2/14N2 selectivity is very large, especially at low temperatures, as can be observed in the lower panel of Fig. 6.
At this point, it is worth recalling that the permeances of Fig. 6 correspond to the use of the lowest eigenvalue of eqn (5), W0(z), as the effective interaction potential. The subsequent effective potentials, Wn>0(z), should also contribute to the total transmission probabilities/permeances, but, since they involve somewhat higher transmission barriers, these contributions are unimportant at low energies/temperatures. Fig. 7 presents a diagram of the lowest eigenvalues of eqn (5) at z = 0 for 16O2 and 14N2 (transmission barriers of Wn(z), n = 0–20). We have estimated that the 16O2 and 14N2 permeances corresponding to the excited effective potentials Wn>0(z) are negligible below 100 K (less than 10% of the permeances from W0(z) in this temperature range). In other words, the permeances reported in Fig. 6 are accurate enough up to 100 K. Above this temperature, they are lower bounds of the total permeances because the contributions from the higher effective potentials are to be added. Nevertheless, we expect that the O2/N2 selectivity would keep similar values to those shown in Fig. 6. The reason for this assertion can be better understood looking at Fig. 7, where it can be seen that the density of energy levels in the O2 spectrum is pretty similar to that in the N2 spectrum. As a consequence, the contribution of the Wn>0 potentials to the total permeance should be of the same order of magnitude for both molecules, hence approximately preserving the selectivity. Finally, it is worth noting that the O2 permeance obtained at 300 K, of about 10 GPU, is close (considering that it is a lower bound, as discussed above) to the minimum accepted value of 20 GPU for industrial applications.62 At this temperature, the O2/N2 selectivity is ∼100, a value well above 6, the minimum acceptable value for separation applications.62 To put this result into context, O2/N2 selectivities in the range of 3–15 have been obtained using a variety of polymer-, perovskite- and carbon-based membranes.1 For thin films of graphene, in particular, a selectivity of 6 has been reported for five layers of graphene synthesized by chemical vapor deposition, supported on a permeable polymer.63 On the side of the theoretical simulations, we mention a molecular dynamics study of the O2/N2 separation using a bilayer nanoporous graphene where a selectivity factor of 26 and a permeance of 5 × 105 GPU were found for an optimum pore size of 3.45 Å.2 In summary, it is found that GDY could be an useful membrane for the separation of oxygen from air, even under room temperature conditions, a result that would be worth checking experimentally. Also, it would be important to investigate the effect of the interactions among the molecules and the initial O2/N2 concentration on the selectivity, a study that could be carried out by means of molecular dynamics simulations.
 | ||
| Fig. 7 Lowest eigenvalues of eqn (5), Wn (n = 0–20) at z = 0 for 16O2 and N2. See text for discussion. | ||
The permeances of the heavier oxygen isotopologue 18O2 are also shown in the upper panel of Fig. 6 (points). In the graph, it appears to be indistinguishable from the 16O2 permeance, as in fact both 18O2 and 16O2 permeances have very close values. Their difference can be better noticed by means of their ratio, i.e., the 18O2/16O2 selectivity, which is shown in the inset of the lower panel of Fig. 6. It is found that the selectivity is very small (∼1.5) for temperatures of 50 K and higher; however, it steadily increases as the temperature decreases, reaching a value of 3 at 20 K. This trend favouring the transport of the heavier molecule is due to the lower value of its ZPE-corrected potential barrier. Extending the calculation of the permeances to lower temperatures, it is found that the 18O2/16O2 selectivity reaches a maximum value of 4.5 at about 13.5 K, then rapidly decreases for lower temperatures. This behavior – also found for the transport of 4He/3He and D2/H2 through GDY33,34 – is due to the onset of tunneling which favors the transmission of the lighter species at sufficiently low temperatures. At any rate, the present results indicate that transmission through GDY is not a practical method for separating 18O2 from 16O2, primarily because the permeances are negligibly small at the temperatures of eventual interest.
4 Conclusion
Transport of oxygen and nitrogen molecules through GDY has been studied by means of quantum mechanical methods, with the primary aim of assessing the capability of this membrane to efficiently separate these two main components of air. Density functional theory calculations, benchmarked against accurate ab initio methods, have been applied to determine the interaction potential between O2 (and N2) and a molecular prototype of GDY and these data have served to build reliable analytical representations of these potentials, based on an improved Lennard-Jones formulation. It has been found that the barrier for transmission through GDY is higher for N2 than for O2, the result being rationalized from the sensitivity in the repulsive regime of the interaction potential to the molecular properties. Transmission probabilities and permeances were obtained from time-dependent wave-packet simulations using effective interaction potentials that include quantum corrections (ZPE). These quantum effects make a significant contribution to the height of the effective potential barriers due to the confinement of the molecular motions in the pore region. As a consequence of their different transmission barriers, the permeances for 16O2 transport are much larger than those for 14N2 over a large range of temperatures (20–300 K), predicting in this way that GDY is a very promising material for the separation and purification of oxygen from air. However, separation of the scarce 18O2 isotopologue from the abundant 16O2 one was found to be unfeasible.Given the good prospects for the oxygen–nitrogen separation by GDY, it would certainly be worth experimentally checking the present predictions. Recently, Zhou et al.25 have pioneered experiments on the permeation of gases of small molecules through multilayer GDY, so their set-up might be ideal to study a mixture of oxygen and nitrogen. In addition, it would be interesting to complement this study with other theoretical investigations, in particular molecular dynamics simulations,2,64 which would provide insights into the role of aspects not considered here, such as the molecule–molecule (self or mixed) interactions, the adsorption on the membrane, or membrane vibrations, into the O2/N2 transport dynamics.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Appendix: calculations of effective potentials and transmission probabilities
The ZPE-corrected interaction potentials, W0(z), are obtained from diagonalization of the Hamiltonian of eqn (5), represented using the basis setΦlm,i,j(Q) = ![[scr Y, script letter Y]](https://www.rsc.org/images/entities/char_e538.gif) lm(θ,ϕ)ψi(x)ψj(y), lm(θ,ϕ)ψi(x)ψj(y), | (11) |
![[scr Y, script letter Y]](https://www.rsc.org/images/entities/char_e538.gif) lm are tesseral (real) spherical harmonics65 and ψi(x) and ψj(y) are discrete variable representation (DVR) functions.66 It should be noted that the shape of the interaction potential, V(θ,ϕ,x,y;z), changes considerably as z increases from zero up to the asymptotic region. It is then necessary to adjust the properties of the basis set for the different molecule–membrane distances, in order to make the calculations affordable. Thus, for z = 0, where V quickly becomes very repulsive for (x,y) values away from the center of the pore (panels (c) and (d) of Fig. 1 and 2), we used a set of N = 15 “fixed-node” DVR basis functions:66
lm are tesseral (real) spherical harmonics65 and ψi(x) and ψj(y) are discrete variable representation (DVR) functions.66 It should be noted that the shape of the interaction potential, V(θ,ϕ,x,y;z), changes considerably as z increases from zero up to the asymptotic region. It is then necessary to adjust the properties of the basis set for the different molecule–membrane distances, in order to make the calculations affordable. Thus, for z = 0, where V quickly becomes very repulsive for (x,y) values away from the center of the pore (panels (c) and (d) of Fig. 1 and 2), we used a set of N = 15 “fixed-node” DVR basis functions:66 | (12) |
 | (13) |
The next step in our procedure concerns solving the quantum problem for the Hamiltonian Hz of eqn (6) to obtain the transmission probabilities. As in previous works,31,58 we apply the time-dependent wave packet method using the initial wave packet67
 | (14) |
Acknowledgements
Maryam A. Rafiei thanks the International and Research Councils of the University of Tehran for giving her the opportunity to spend a research trip at the Instituto de Fsica Fundamental (IFF-CSIC). We also thank Prof. M. Mella for useful discussions. The work has been funded through Spanish AEI grants PID2020-114957GB-I00/AEI/10.13039/501100011033 and PID2020-114654GB-I00/AEI/10.13039/501100011033. Allocation of computing time by CESGA (Spain) is also acknowledged.Notes and references
- N. F. Himma, A. K. Wardani, N. Prasetya, P. T. Aryanti and I. G. Wenten, Recent progress and challenges in membrane-based O2/N2 separation, Rev. Chem. Eng., 2019, 35, 591–625 CrossRef CAS.
- S. Wang, S. Dai and D.-E. Jiang, Entropic selectivity in air separation via a bilayer nanoporous graphene membrane, Phys. Chem. Chem. Phys., 2019, 21, 16310–16315 RSC.
- B. Adhikari, C. J. Orme, J. R. Klaehn and F. F. Stewart, Technoeconomic analysis of oxygen-nitrogen separation for oxygen enrichment using membranes, Sep. Purif. Technol., 2021, 268, 118703 CrossRef CAS.
- D. González-Revuelta, M. Fallanza, A. Ortiz and D. Gorri, Thin-film composite matrimid-based hollow fiber membranes for oxygen/nitrogen separation by gas permeation, Membranes, 2023, 13, 218 CrossRef PubMed.
- K. Chong, S. Lai, H. Thiam, H. Teoh and S. Heng, Recent progress of oxygen/nitrogen separation using membrane technology, J. Eng. Sci. Technol., 2016, 11, 1016–1030 Search PubMed.
- S. S. Karim, S. Farrukh, A. Hussain, T. Noor and M. Younas, A comprehensive overview of dual-layer composite membrane for air (O2/N2) separation, Polym. Polym. Compos., 2021, 29, S1630–S1640 CAS.
- Y. Liu, X. Chen, T. Han, C. Wang, H. Liu, Y. Sun, P. Zheng, H. Zhang and S. Luo, Rational macromolecular design and strategies to tune the microporosity for high-performance O2/N2 separation membranes, Sep. Purif. Technol., 2024, 334, 125978 CrossRef CAS.
- L. M. Robeson, The upper bound revisited, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Selective molecular sieving through porous graphene, Nat. Nanotechnol., 2012, 7, 728–732 CrossRef CAS PubMed.
- L. Huang, M. Zhang, C. Li and G. Shi, Graphene-based membranes for molecular separation, J. Phys. Chem. Lett., 2015, 6, 2806–2815 CrossRef CAS PubMed.
- L. Wang, M. S. Boutilier, P. R. Kidambi, D. Jang, N. G. Hadjiconstantinou and R. Karnik, Fundamental transport mechanisms, fabrication and potential applications of nanoporous atomically thin membranes, Nat. Nanotechnol., 2017, 12, 509–522 CrossRef CAS PubMed.
- L. F. Villalobos, D. J. Babu, K.-J. Hsu, C. Van Goethem and K. V. Agrawal, Gas separation membranes with atom-thick nanopores: The potential of nanoporous single-layer graphene, Acc. Mater. Res., 2022, 3, 1073–1087 CrossRef CAS PubMed.
- M.-C. Ferrari, Recent developments in 2D materials for gas separation membranes, Curr. Opin. Chem. Eng., 2023, 40, 100905 CrossRef.
- R. Baughman, H. Eckhardt and M. Kertesz, Structure-property predictions for new planar forms of carbon: Layered phases containing sp2 and sp atoms, J. Chem. Phys., 1987, 87, 6687–6699 CrossRef CAS.
- G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Architecture of graphdiyne nanoscale films, Chem. Commun., 2010, 46, 3256–3258 RSC.
- J. Zhou, X. Gao, R. Liu, Z. Xie, J. Yang, S. Zhang, G. Zhang, H. Liu, Y. Li, J. Zhang and Z. Liu, Synthesis of graphdiyne nanowalls using acetylenic coupling reaction, J. Am. Chem. Soc., 2015, 137, 7596–7599 CrossRef CAS PubMed.
- C. Huang, Y. Li, N. Wang, Y. Xue, Z. Zuo, H. Liu and Y. Li, Progress in research into 2D graphdiyne-based materials, Chem. Rev., 2018, 118, 7744–7803 CrossRef CAS PubMed.
- C. Owais, A. James, C. John, R. Dhali and R. S. Swathi, Selective permeation through one-atom-thick nanoporous carbon membranes: theory reveals excellent design strategies, J. Phys. Chem. B, 2018, 122, 5127–5146 CrossRef CAS PubMed.
- R. Sakamoto, N. Fukui, H. Maeda, R. Matsuoka, R. Toyoda and H. Nishihara, The accelerating world of graphdiynes, Adv. Mater., 2019, 31, 1804211 CrossRef CAS PubMed.
- X. Gao, H. Liu, D. Wang and J. Zhang, Graphdiyne: synthesis, properties, and applications, Chem. Soc. Rev., 2019, 48, 908–936 RSC.
- X. Yang, Z. Qu, S. Li, M. Peng, C. Li, R. Hua, H. Fan, J. Caro and H. Meng, Ultra-fast preparation of large-area graphdiyne-based membranes via alkynylated surface-modification for nanofiltration, Angew. Chem., 2023, 62, e202217378 CrossRef CAS PubMed.
- H. Qiu, M. Xue, C. Shen, Z. Zhang and W. Guo, Graphynes for water desalination and gas separation, Adv. Mater., 2019, 31, 1803772 CrossRef CAS PubMed.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez, F. Pirani, G. Giorgi and K. Yamashita, Penetration barrier of water through graphynes’ pores: first-principles predictions and force field optimization, J. Phys. Chem. Lett., 2014, 5, 751–755 CrossRef CAS PubMed.
- J. Xu and S. Meng, Molecular transport across a two-dimensional nanomesh membrane–graphdiyne, J. Phys. D: Appl. Phys., 2020, 53, 493003 CrossRef CAS.
- Z. Zhou, Y. Tan, Q. Yang, A. Bera, Z. Xiong, M. Yagmurcukardes, M. Kim, Y. Zou, G. Wang, A. Mishchenko, I. Timokhin, C. Wang, H. Wang, C. Yang, Y. Lu, R. Boya, H. Liao, S. Haigh, H. Liu, F. M. Peeters, Y. Li, A. K. Geim and S. Hu, Gas permeation through graphdiyne-based nanoporous membranes, Nat. Commun., 2022, 13, 4031 CrossRef CAS PubMed.
- Y. Jiao, A. Du, M. Hankel and S. C. Smith, Modelling carbon membranes for gas and isotope separation, Phys. Chem. Chem. Phys., 2013, 15, 4832–4843 RSC.
- N. Mehio, S. Dai and D.-E. Jiang, Quantum mechanical basis for kinetic diameters of small gaseous molecules, J. Phys. Chem. A, 2014, 118, 1150–1154 CrossRef CAS PubMed.
- Y. Jiao, A. Du, M. Hankel, Z. Zhu, V. Rudolph and S. C. Smith, Graphdiyne: a versatile nanomaterial for electronics and hydrogen purification, Chem. Commun., 2011, 47, 11843–11845 RSC.
- S. W. Cranford and M. J. Buehler, Selective hydrogen purification through graphdiyne under ambient temperature and pressure, Nanoscale, 2012, 4, 4587–4593 RSC.
- H. Zhang, X. He, M. Zhao, M. Zhang, L. Zhao, X. Feng and Y. Luo, Tunable hydrogen separation in sp-sp2 hybridized carbon membranes: A first-principles prediction, J. Phys. Chem. C, 2012, 116, 16634–16638 CrossRef CAS.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez, F. Pirani and G. Giorgi, Graphdiyne pores: “ad hoc” openings for helium separation applications, J. Phys. Chem. C, 2014, 118, 29966–29972 CrossRef CAS.
- J. J. M. Beenakker, V. D. Borman and S. Y. Krylov, Molecular transport in subnanometer pores: zero-point energy, reduced dimensionality and quantum sieving, Chem. Phys. Lett., 1995, 232, 379–382 CrossRef CAS.
- A. Gijón, J. Campos-Martínez and M. I. Hernández, Wave packet calculations of the quantum transport of atoms through nanoporous membranes, J. Phys. Chem. C, 2017, 121, 19751–19757 CrossRef.
- E. García-Arroyo, J. Campos-Martínez, M. Bartolomei, F. Pirani and M. I. Hernández, Molecular hydrogen isotope separation by a graphdiyne membrane: a quantum-mechanical study, Phys. Chem. Chem. Phys., 2022, 24, 15840–15850 RSC.
- Y. B. Apriliyanto, N. Faginas Lago, A. Lombardi, S. Evangelisti, M. Bartolomei, T. Leininger and F. Pirani, Nanostructure selectivity for molecular adsorption and separation: the case of graphyne layers, J. Phys. Chem. C, 2018, 122, 16195–16208 CrossRef CAS.
- S. Mahnaee, M. J. López and J. A. Alonso, Separation of CO2/CH4 gas mixtures using nanoporous graphdiyne and boron-graphdiyne membranes: influence of the pore size, Phys. Chem. Chem. Phys., 2024, 26, 15916–15926 RSC.
- Z. Meng, X. Zhang, Y. Zhang, H. Gao, Y. Wang, Q. Shi, D. Rao, Y. Liu, K. Deng and R. Lu, Graphdiyne as a high-efficiency membrane for separating oxygen from harmful gases: a first-principles study, ACS Appl. Mater. Interfaces, 2016, 8, 28166–28170 CrossRef CAS PubMed.
- L. Zhao, P. Sang, S. Guo, X. Liu, J. Li, H. Zhu and W. Guo, Promising monolayer membranes for CO2/N2/CH4 separation: Graphdiynes modified respectively with hydrogen, fluorine, and oxygen atoms, Appl. Surf. Sci., 2017, 405, 455–464 CrossRef CAS.
- M. A. Rafiei and A. Maghari, Theoretical study of NO/CO/O2 gas separation using graphdiyne and boron-doped graphdiyne membranes - A new corresponding state principle, Comput. Theor. Chem., 2024, 1235, 114534 CrossRef CAS.
- G. Garberoglio, Quantum states of rigid linear rotors confined in a slit pore: quantum sieving of hydrogen isotopes and extreme one dimensional confinement, Eur. Phys. J. D, 2009, 51, 185–191 CrossRef CAS.
- S. K. Ujjain, A. Bagusetty, Y. Matsuda, H. Tanaka, P. Ahuja, C. de Tomas, M. Sakai, F. Vallejos-Burgos, R. Futamura, I. Suarez-Martinez, M. Matsukata, A. Kodama, G. Garberoglio, Y. Gogotsi, J. Karl Johnson and K. Kaneko, Adsorption separation of heavier isotope gases in subnanometer carbon pores, Nat. Commun., 2021, 12, 2041 CrossRef PubMed.
- M. Pitonak and A. Heßelmann, Accurate intermolecular interaction energies from a combination of MP2 and TDDFT response theory, J. Chem. Theory Comput., 2010, 6, 168–178 CrossRef CAS PubMed.
- H. J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz and some others, MOLPRO, Version 2022.2, a Package of Ab Initio Programs, 2022, see https://www.molpro.net/ Search PubMed.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- Y. Pei, Mechanical properties of graphdiyne sheet, Phys. B, 2012, 407, 4436–4439 CrossRef CAS.
- R. A. Kendall, J. Dunning, H. Thom and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Pirani, S. Brizi, L. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Beyond the Lennard-Jones model: A simple and accurate potential function probed by high resolution scattering data useful for molecular dynamics simulations, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503 RSC.
- A. Gavezzotti, Calculation of intermolecular interaction energies by direct numerical integration over electron densities. 2. An improved polarization model and the evaluation of dispersion and repulsion energies, J. Phys. Chem. B, 2003, 107, 2344–2353 CrossRef CAS.
- W. H. Miller, N. C. Handy and J. E. Adams, Reaction path Hamiltonian for polyatomic molecules, J. Chem. Phys., 1980, 72, 99–112 CrossRef CAS.
- J. L. Bao and D. G. Truhlar, Variational transition state theory: theoretical framework and recent developments, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC.
- Y. Qu, F. Li and M. Zhao, Efficient hydrogen isotopologues separation through a tunable potential barrier: The case of a C2N membrane, Sci. Rep., 2017, 7, 1483 CrossRef PubMed.
- M. Li, L. Wang, H. Lei, Y. Yang, Y.-Q. Li, M. Zhao, J. Guan, W. Li and Y. Qu, Efficient helium and helium isotopes separation by phosphorus carbide P2C3 membrane, Adv. Theory Simul., 2022, 5, 2100327 CrossRef CAS.
- M. I. Hernández, M. Bartolomei and J. Campos-Martínez, Transmission of helium isotopes through graphdiyne pores: Tunneling versus zero point energy effects, J. Phys. Chem. A, 2015, 119, 10743–10749 CrossRef PubMed.
- A. Cedillo, Quantum mechanical tunneling through barriers: A spreadsheet approach, J. Chem. Educ., 2000, 77, 528 CrossRef CAS.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez and R. Hernández-Lamoneda, Long-range interaction for dimers of atmospheric interest: dispersion, induction and electrostatic contributions for O2–O2, N2–N2 and O2–N2, J. Comput. Chem., 2011, 32, 279–290 CrossRef CAS PubMed.
- M. S. Motallebiour, J. Karimi-Sabet and A. Maghari, 4 He/3 He separation using oxygen-functionalized nanoporous graphene, Phys. Chem. Chem. Phys., 2019, 21, 12414–12422 RSC.
- Z. Zhou, Permeance should be used to characterize the productivity of a polymeric gas separation membrane, J. Membr. Sci., 2006, 281, 754–756 CrossRef.
- H. W. Kim, H. W. Yoon, S.-M. Yoon, B. M. Yoo, B. K. Ahn, Y. H. Cho, H. J. Shin, H. Yang, U. Paik, S. Kwon, J.-Y. Choi and H. B. Park, Selective gas transport through few-layered graphene and graphene oxide membranes, Science, 2013, 342, 91–95 CrossRef CAS PubMed.
- C. Sun, M. S. H. Boutilier, H. Au, P. Poesio, B. Bai, R. Karnik and N. G. Hadjiconstantinou, Mechanisms of molecular permeation through nanoporous graphene membranes, Langmuir, 2014, 30, 675–682 CrossRef CAS PubMed.
- https://en.wikipedia.org/wiki/Spherical_harmonics#Real_form .
- J. T. Muckerman, Some useful discrete variable representations for problems in time-dependent and time-independent Quantum mechanics, Chem. Phys. Lett., 1990, 173, 200–205 CrossRef CAS.
- E. J. Heller, Time-dependent approach to semiclassical dynamics, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS.
- M. D. Feit, J. A. Fleck and A. Steiger, Solution of the Schrödinger equation by a spectral method, J. Comput. Phys., 1982, 47, 412–433 CrossRef CAS.
- D. Zhang and J. Z. H. Zhang, Full-dimensional time-Dependent treatment for diatom-diatom reactions: The H2 + OH reaction, J. Chem. Phys., 1991, 101, 1146–1156 CrossRef.
| This journal is © the Owner Societies 2024 |





