Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cyclohepta[def]fluorene as a bistable molecule: first principles studies on its electronic structure and the effects of benzo-extension, substitution and solvation†
Robert
Toews
 * and
Andreas
Köhn
* and
Andreas
Köhn

Institute for Theoretical Chemistry, University of Stuttgart, Pfaffenwaldring 55, D-70569 Stuttgart, Germany. E-mail: toews@theochem.uni-stuttgart.de; koehn@theochem.uni-stuttgart.de
First published on 12th July 2024
Abstract
Cyclohepta[def]fluorene 1 and its derivatives have received considerable attention due to possible technological applications as molecular devices. Despite efforts from both theory and experiment, the electronic structure of 1 has remained unclear. Herein, we report advanced first-principles calculations on 1 using a multireference and a coupled-cluster method. We confirm a bistability of 1 between a polar singlet state and a non-polar triplet state. We also study the effects of benzo-extension on the electronic structure and the influences of substitution and solvation on the ground state. Our results suggest that deliberate choice of substituents allows to toggle the multiplicity of the ground state. We also propose that due to its bistability, 1 represents an attractive building block for molecular devices.
1 Introduction
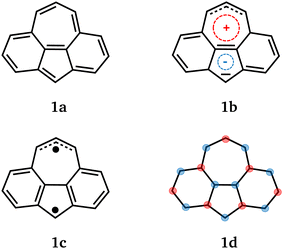
Non-alternant hydrocarbons are intensely studied due to possible technological applications such as in optical components1–3 or in quantum devices.4–6 In a quantum technological context, we want to note that unpaired electrons can be localized at certain carbon centres by engineering the molecular topology4 and that corresponding quantum devices are predicted to be suited for room temperature applications.5 Another useful property of some non-alternant hydrocarbons is bistability. This means that two electronic states with distinct properties compete for the ground state. Bistable molecules can serve as molecular memristors which are expected to be relevant for next-generation electronic devices.7,8Cyclohepta[def]fluorene 1 is obtained from azulene by adding benzene units between pentagon and heptagon at each side. It has 16 π-electrons and is thus an anti-aromatic compound by Hückel's rule. We can make several statements on the ground state of 1 using established concepts: a closed-shell singlet state of 1 is favored by the presence of two equivalent Kekulé structures, cf.1a in Fig. 1. Alternatively, we can represent the closed-shell singlet state by 1b to highlight the polarity of the azulene unit.
Clar's rule9,10 states that the resonance structure with most aromatic sextets dominates and suggests an open-shell ground state for 1, cf. the Clar structure 1c. Extending Ovchinikov's rule11 to non-alternant hydrocarbons suggests a triplet ground state for 1. If we consider that Ovchinikov's rule can be interpreted in terms of the Ising model, we can draw a spin alternation pattern as shown for 1d. This pattern qualitatively describes the spin distribution in the triplet state and has a spin frustration at the shared bond between pentagon and heptagon. The above statements on the ground state of 1 are in part contradictory and suggest a competition between closed-shell singlet and triplet state.
Several theoretical studies included 112–20 and most studies were based on semi-empirical methods such as a simplified Pariser Parr Pople method12 or the Hückel method.13 So far, the most precise treatment used the complete active space self-consistent field (CASSCF) method with a CAS(10,10) and a double zeta basis.18 The calculations confirmed an expected bistability of 1 and predicted a closed-shell singlet ground state. On the other hand, calculations with density functional theory (DFT) including zero point energies suggested a triplet ground state.19,20
As far as experimental investigations are concerned, the pristine compound 1 is synthetically inaccessible owing to its high reactivity. Successful synthesis and isolation of kinetically protected derivatives of 1 was accomplished by Horii et al. and the ground states were reported as singlet states in all cases that were examined.21,22 Benzo-extended derivatives of 1 were also reported23,24 with the work of Lombardi et al.23 showing that the considered derivatives have singlet ground states and very low-lying triplet states with singlet triplet gaps as small as 0.002 kcal mol−1.
Despite of theoretical and experimental efforts, the ground state of 1 as well as the effect of benzo-extension and substitution are so far in need of further characterization,21,22 which motivates a first principles study on the foregoing effects by advanced quantum chemical methods such as multireference and coupled-cluster methods. Next to benzo-extension and substitution, we will consider solvation effects using a continuum solvation model.
2 Computational details
2.1 Geometry optimizations
For all systems, equilibrium geometries of the closed-shell singlet and triplet state were determined using DFT and the B3LYP functional.25,26 For triplet geometries, the unrestricted formalism of DFT was applied. To study the effects of benzo-extension, we optimized geometries with a def2-TZVPP basis set, while for our study on substitution effects, we employed a def2-SVP basis set to keep computation times at an economic level. All geometry optimizations were performed with the TURBOMOLE program package27 using D3 dispersion correction with Becke–Johnson damping,28,29 density fitting and multipole acceleration.30 Optimized geometries were used for single-point calculations with more advanced methods and the treatment of solvation effects as stated below.2.2 Multireference calculations
Calculations were performed with the pair natural orbital multistate complete active space second order perturbation theory (PNO-MS-CASPT2) method,31,32 a CAS(10,10) and a def2-TZVPP basis set. Multireference calculations were performed on the B3LYP/def2-TZVPP geometries. All multireference calculations were performed with the MOLPRO quantum chemistry package.33–352.3 Coupled-cluster calculations
Calculations were performed using the PNO local coupled-cluster method with single and double excitations, a perturbative treatment of triple excitations and explicit correlation (PNO-LCCSD(T)-F12a)36 and a cc-pVDZ-F12 basis set.37 Coupled-cluster calculations were performed on the B3LYP/def2-SVP geometries. All coupled-cluster calculations were performed with the MOLPRO quantum chemistry package.33–352.4 Treatment of solvation effects
Single point calculations were performed with the conductor-like screening model (COSMO) as implemented in the TURBOMOLE program package38 using a B3LYP/def2-SVP level of theory. For each system, calculations were performed for a polar and non-polar environment. The polar environment was simulated with the dielectric constant ε → ∞ and the non-polar environment was simulated with ε = 2. All calculations were performed on a B3LYP/def2-SVP level of theory and on geometries that were optimized on the same level.3 Results and discussion
By this study we want to elucidate the relationship between molecular and electronic structure in 1 and related systems. We will first study the effects of benzo-extension by analyzing the resulting molecular geometries in Section 3.1 and the energy levels of low lying electronic states in Section 3.2. In Section 3.3, we will look at the influence of substituents on the ground state of 1. Moreover, we will consider the effects of solvation on the ground states. Finally, we will briefly motivate possible applications in molecular devices.The adiabatic singlet triplet splitting ΔEST is relevant for describing the ground state of diradicals. In our study, we use the definition
| ΔEST = ES − ET, | (1) |
3.1 Benzo-extension – geometries
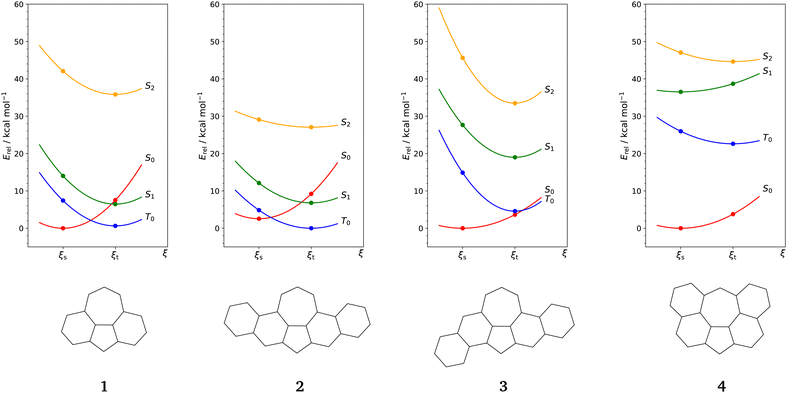
For our study, we consider 1 together with the benzo-extended derivatives 2–4 shown in Fig. 3. Derivatives 2 and 3 are isomers with 24 π-electrons and are, like 1, anti-aromatic compounds by Hückel's rule. We can also formulate Clar structures for 2 and 3 with unpaired electrons at the non-shared carbon centres of pentagon and heptagon. The key difference between 2 and 3 is in molecular symmetry. For symmetry reasons, the two Kekulé structures of 3 are not equivalent wand we show them separately as 3a and 3b. Using established concepts like Kekulé structures, Clar's rule and Ovchinikov's rule, we cannot make a decisive statement on the ground states of 2 and 3. | ||
| Fig. 3 Kekulé structures of benzo-extended derivatives 2 to 4. The structures 3a and 3b are not equivalent for symmetry reasons. | ||
Derivative 4 is an aromatic compound by Hückel's rule and does not have a Clar structure similar to 1c (cf.Fig. 1). The Kekulé structures and Ovchinikov's rule predict 4 to have a singlet ground state.
Bond lengths of 1 to 4 optimized on a B3LYP/def2-TZVPP level of theory are visualised in Fig. 2. The DFT dipole moments of singlet and triplet states are listed in Table 1.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| μ(S0)/D | 2.65 | 2.67 | 2.67 | 1.37 |
| μ(T0)/D | 0.32 | 0.15 | 0.37 | 0.21 |
For 1, the geometric properties of closed-shell singlet and triplet state were already put forward by Heilbronner et al.12 The closed-shell singlet geometry of 1 is characterized by a short central bond (1.38 Å) between pentagon and heptagon, which is in agreement with the two Kekulé structures that both have a double bond at this position. The shared bonds between benzene units and heptagon (1.44 Å) as well as benzene units and pentagon (1.47 Å) are elongated. The closed-shell singlet state has a high dipole moment of 2.65 D which can be linked to the azulene unit. In the triplet geometry, the benzene units of 1 tend to form separate aromatic systems as suggested by the Clar structure 1c in Fig. 1. The triplet state has a small dipole moment of 0.32 D which confirms its comparatively non-polar character.
We can observe similar trends in geometric properties and dipole moments for 2 and 3. Both derivatives have a polar singlet state and a non-polar triplet state. The triplet state of 2 tends to have the aromatic sextets at the terminal benzene units. For 3, the bond length alternation in the singlet state suggests that the Kekulé structure 3a is favored.
Singlet and triplet geometry of 4 show both a long central bond between pentagon and heptagon (approx. 1.46 Å). This is consistent with both Kekulé structures having a single bond at this position and the frustration according to Ovchinikov's rule (cf.1d in Fig. 1). A notable difference between both geometries is in the bond lengths of the benzene units which tend to be smaller in the triplet state. The closed-shell singlet state of 4 has a comparatively small dipole moment of 1.37 D which is in agreement with the aromatic character.
3.2 Benzo-extension – electronic states
Next, we look at the energy levels of low lying electronic states in 1–4. Fig. 4 illustrates these levels for closed-shell singlet and triplet geometries obtained on a CAS(10,10)-MS-CASPT2/def2-TZVPP level of theory. Using this method allows us to investigate the low-lying electronic manifold of the molecules and to detect a potential multideterminantal character of these states. Active orbitals for all considered systems are provided in Sections S1.1–S1.4 of the ESI.†We start our consideration with 1 and use the representations in Fig. 5 to illustrate the electronic states. The closed-shell singlet ground state S0 has a high CASSCF dipole moment of 2.38 D, consistent with the DFT value in Table 1. S0 can therefore be represented by the polar form in Fig. 1.
The triplet state T0 has a CASSCF dipole moment of 0.78 D which is somewhat higher than the DFT result but still small. The unpaired electrons in T0 are localized in agreement with the Clar structure, cf. ESI† Section S2.1. We can highlight that both unpaired electrons have the same spin orientation as shown in Fig. 5. Both S0 and T0 are ground states at their equilibrium geometries. The very small adiabatic splitting of ΔEST = −0.63 kcal mol−1 confirms the bistability of 1.
Despite the small energy gap, spin orbit coupling effects are negligibly small for this molecule and do not impact the singlet triplet splitting, see ESI.† This is expected for hydrocarbons. Spin–orbit coupling will of course impact dynamical processes like intersystem crossing between S0 and T0, which is beyond the scope of this study.
Configuration analysis shows that the singlet state S1 has open-shell character, cf. ESI† Section S2.1. The analysis also suggests that the unpaired electrons are distributed similar to T0 but with opposite spin orientations. The similarity between T0 and S1 is also supported by S1 having a small CASSCF dipole moment of 0.87 D. Changing from the singlet to the triplet geometry, the gap between S0 and S1 becomes inverted as shown in Fig. 4.
The singlet state S2 has a high energy and we include it into Fig. 4 because of strong coupling with S0, cf. ESI† Section S2.1. S2 has also open-shell character but the unpaired electrons are distributed over the entire π-system. Moreover, S2 has a notable CASSCF dipole moment of 1.65 D which is anti-parallel compared to S0. Therefore, we can represent S2 by the open-shell form in Fig. 5 with a positive partial charge at the pentagon and a negative one at the heptagon. The electronic states of 2 and 3 are analogous to 1, cf. ESI† Sections S2.2 and S2.3. For 2, this analogy is supported by the CASSCF dipole moments in Table 2. In contrast to 1, 2 has a triplet ground state with an adiabatic splitting of ΔEST = 2.56 kcal mol−1. Also, the gap between S1 and S0 at the triplet geometry is increased, and S2 has a lower energy, cf.Fig. 4. We can thus conclude that a symmetric benzo-extension of 1 stabilizes open-shell states such as T0, S1 and S2.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| μ(S0)/D | 2.38 | 2.19 | 1.52 | 0.85 |
| μ(T0)/D | 0.78 | 0.76 | 0.59 | 0.21 |
The asymmetric derivative 3 has a closed-shell singlet ground state S0 which remains also the lowest electronic state at the triplet geometry. S0 has a CASSCF dipole moment of 1.52 D which is smaller than the DFT value and T0 has also a comparatively small dipole moment of 0.37 D. The S0 dipole moment is also smaller than in 1 and 2 and we can link the decrease in polarity to the lowered symmetry. In fact, the configuration analysis in ESI† Section 2.3 shows significant mixing of S0 and S1. The reason is that due to the loss of the mirror plane going from 2 to 3, S0 and S1 fall into the same irreducible representation. Overall, we can state that asymmetric benzo-extension leads to a stabilization of S0 while symmetric extension maintains the symmetry protection of the S0 state.
4 has a closed-shell singlet ground state S0 with a large adiabatic splitting of ΔEST = −22.59 kcal mol−1. As shown in Fig. 4, the other open-shell states S1 and S2 are also elevated and this is consistent with 4 being a Hückel aromatic compound. S0 has a small CASSCF dipole moment of 0.85 D. This value is smaller than the DFT result in Table 1 and we can say that S0 is rather non-polar. Although the benzo-extension in the case of 4 maintains molecular symmetry, the electronic properties are significantly altered.
3.3 Substitution and solvation
Practical realization of molecules with 1 as a core requires protection by bulky side-groups. A successful substitution pattern is 3,8,10-tri-substitution as presented by Horii et al.21 These substituents could also be used to engineer the bistability of 1. In the following, we will compare 1 and the 3,8,10-tri-substituted derivatives shown in Fig. 6 and Table 3. Please note that for steric reasons, only inductive effects will be relevant. | ||
| Fig. 6 Substitution pattern of the 3,8,10-tri-substituted derivatives and chemical formulas for the non-trivial substituents 2,6-dichlorophenyl (Dcp) and 2,4,6-tris(iso-propyl) (Trip). | ||
| R1 | R2 | |
|---|---|---|
| 5 | Mes | Trip |
| 6 | Mes | Dcp |
| 7 | tBu | tBu |
| 8 | Dcp | tBu |
Triaryl-derivatives 5 and 6 are taken from an experimental work.21 With 7, we investigate the strong positive inductive effect of the tert-butyl (tBu) substituents. In 8, the 2,6-dichlorophenyl (Dcp) substituent at the pentagon has a negative inductive effect and the tBu groups at the heptagon have positive ones. In this section, we want to focus on the bistability phenomenon and will consider only adiabatic singlet triplet splittings ΔEST.
As established in Section 3.2, (see also Section S2.1 of the ESI†) both the S0 and the T0 state of 1 and related systems can be well represented by a single Slater determinant, and single-reference correlation methods like PNO-LCCSD(T)-F12a can be used to obtain an accurate estimate of ΔEST.
Table 4 shows best estimates of the adiabatic splitting ΔEgST for the gas phase, ΔEpST for a polar environment and ΔEnpST for a non-polar environment. The best estimates for the gas phase are the sum of ΔEccST and the zero point energy (ZPE) contribution ΔEzpeST calculated on a B3LYP/def2-SVP level of theory:
| ΔEgST = ΔEccST + ΔEzpeST. | (2) |
| ΔEpST = ΔEgST + ΔEs,pST, | (3) |
| ΔEnpST = ΔEgST + ΔEs,npST, | (4) |
| ΔEccST | ΔEgST | ΔEnpST | ΔEpST | |
|---|---|---|---|---|
| 1 | −0.68 | −0.21 | −0.66 | −1.77 |
| 5 | −0.42 | −0.20 | −0.44 | −0.92 |
| 6 | −2.66 | −2.09 | −2.46 | −3.16 |
| 7 | 1.54 | 2.35 | 1.86 | 0.71 |
| 8 | 2.43 | 2.34 | 2.26 | 2.04 |
For 1, the PNO-LCCSD(T)-F12a value of −0.68 kcal mol−1 confirms the MS-CASPT2 value of −0.63 kcal mol−1. Our gas phase estimate including ZPE effects ΔEST = −0.21 kcal mol−1 suggests that 1 has a closed-shell singlet ground state which is almost iso-energetic to the triplet state. We can therefore confirm the bistability of 1 which was put forward by Malrieu et al.18 The singlet state is stabilized by interactions with a polar and a non-polar environment, and this trend also applies to derivatives 5–8.
5 also shows bistability and the gas phase estimate of ΔEgST = −0.20 kcal mol−1 is very similar to 1. The Mes and Trip side-groups are both aromatic and electron-rich and we can explain our result by small inductive effects of these substituents. In a microcrystalline phase of 5, the environment will be rather non-polar due to the side-groups. We can therefore compare our estimate ΔEnpST = −0.44 kcal mol−1 with the experimental value ΔEexpST = −0.90 kcal mol−1 for a microcrystalline sample21 and assert good agreement.
For 6, the singlet state is more stable with a gas phase estimate of ΔEgST = −2.09 kcal mol−1. The Dcp substituent at the pentagon has a negative inductive effect. This effect reduces the charge separation at the azulene unit and stabilizes the singlet state in this way. Our estimate for a non-polar environment is ΔEnpST = −2.46 kcal mol−1 while the experimental value of ΔEexpST = −4.60 kcal mol−1 for a microcrystalline sample is significantly more negative. We have a better agreement for our estimate ΔEpST = −3.16 kcal mol−1 which suggests that the environment of 6 in the condensed phase has a polar character due to neighbouring Dcp groups.
7 has a triplet ground state with ΔEgST = 2.35 kcal mol−1. The tBu substituent at the pentagon increases the charge separation and destabilizes the singlet state. Our result for 7 illustrates, that ground states of a substituted derivatives can be engineered by inductive effects. We also predict a triplet ground state for 7 in a polar and non-polar environment.
In 8, the inductive effects increase the charge separation of the azulene unit, leading to a triplet ground state. Our gas phase estimate of ΔEgST = 2.34 kcal mol−1 is similar to that of 7. In contrast to 7, the adiabatic splitting remains relatively high in a polar and a non-polar environment. We can explain this result by all side-groups of 8 decreasing the polarity whereas in 7 only the tBu groups at the heptagon have this effect.
The ability to control electronic states in molecules is of high relevance for emerging technologies. We hold that derivatives of 1 are particularly attractive in this context and are already in part synthetically accessible. Here, we motivate possible applications in molecular devices.
One promising application is to induce switching between closed-shell singlet and an open-shell triplet state by an external stimulus. Considering that the two states differ in their dipole moments, we propose that using an electric field is convenient. A 3,8,10-tri-substituted derivative can be placed between two electrodes to obtain a single-molecule junction as shown in Fig. 7(a). Depending on the sign of the applied voltage, the closed-shell singlet state can be stabilized or destabilized. In order to ideally fine-tune electronic states, it will be desirable to have the electric field parallel to the C2 axis of 1. We therefore propose that 3,9-di-substituted derivatives as illustrated in Fig. 7(b) are more suitable for single-molecule junctions, although they have not yet been synthesized.
Due to the bistability, single-molecule junctions based on 1 could be used as molecular memristors.39 Moreover, these junctions are interesting for quantum applications, since closed-shell and open-shell state have different spin properties. By additional external stimuli such as magnetic fields, the spin state could be tuned, as was recently shown for a junction based on naphto-bis(thiadiazole).40
Molecular switches could be constructed by adsorbing 1 or a related system on a surface. Changing the adsorption site could induce the switching between closed-shell and open-shell state, as was recently demonstrated for an indenofluorene.41
4 Conclusion
We confirmed that cyclohepta[def]fluorene is a bistable molecule using state-of-the-art quantum-chemical methods, including multireference perturbation theory and coupled-cluster theory. In the gas phase, 1 has a closed-shell singlet ground state which is almost iso-energetic to a triplet state. In condensed phases, the singlet state will be stabilized additionally. Both states have distinct geometries and dipole moments.By considering benzo-extension, we showed that a symmetric extension can stabilize open-shell states in 1 whereas an asymmetric extension destabilizes these states. We also showed that 1 can be turned into an aromatic compound depending on the position at which the benzene units are placed. For the design of open-shell molecules we therefore suggest anti-aromatic derivatives of 1 that are symmetrically benzo-extended.
Our study on substitution effects suggested that the bistability of 1 can be engineered via inductive effects of the substituents. If these effects decrease the charge separation of the azulene unit, the singlet state is stabilized. Substituents that increase the charge separation destabilize the singlet state and can invert the singlet triplet splitting. The treatment of solvation effects showed that the singlet state is stabilized by interactions with a polar and a non-polar environment. For a polar environment, the stabilization is stronger.
We also discussed possible applications of derivatives of 1 in molecular devices. Due to the bistability, these derivatives are attractive candidates for molecular memristors, single-molecule junctions and molecular switches.
Data availability
The data that support the findings of this study are available on reasonable request from the corresponding author, RT.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster). A. K. also acknowledges support by the Stuttgart Center for Simulation Science (SimTech).References
- M. Nakano, K. Fukuda and B. Champagne, J. Phys. Chem. C, 2016, 120, 1193 CrossRef CAS
.
- J. Terence Blaskovits, M. H. Garner and C. Corminboeuf, Angew. Chem., Int. Ed., 2023, 62, e202218156 CrossRef CAS PubMed
.
- M. E. Sandoval-Salinas, G. Ricci, A. Pérez-Jiménez, D. Casanova, Y. Olivier and J.-C. Sancho-Garcia, Phys. Chem. Chem. Phys., 2023, 25, 26417 RSC
.
- F. Lombardi, A. Lodi, J. Ma, J. Liu, M. Slota, A. Narita, W. K. Myers, K. Müllen, X. Feng and L. Bogani, Science, 2019, 366, 1107 CrossRef CAS PubMed
.
- F. Lombardi, M.-Y. Tsang, M. Segantini, J. Ma, W. K. Myers, X. Feng, B. Naydenov and L. Bogani, Phys. Rev. B, 2022, 105, 094106 CrossRef CAS
.
- C. Li, Y. Liu, Y. Liu, F.-H. Xue, D. Guan, Y. Li, H. Zheng, C. Liu, J. Jia and P.-N. Liu,
et al.
, CCS Chem., 2023, 5, 695 CrossRef CAS
.
- M. J. Marinella and A. A. Talin, Nature, 2021, 597, 51 CrossRef PubMed
.
- X. Wen, W. Tang, Z. Lin, X. Peng, Z. Tang and L. Hou, Appl. Phys. Lett., 2023, 122, 173301 CrossRef CAS
.
-
E. Clar, Mobile Source Emissions Including Policyclic Organic Species, Springer, 1972, pp. 49–58 Search PubMed
.
- C. Glidewell and D. Lloyd, Tetrahedron, 1984, 40, 4455 CrossRef CAS
.
- A. A. Ovchinnikov, Theor. Chim. Acta, 1978, 47, 297 CrossRef CAS
.
- P. Baumgartner, E. Weltin, G. Wagnière and E. Heilbronner, Helv. Chim. Acta, 1965, 48, 751 CrossRef CAS
.
- R. Zahradnik, J. Michel and J. Pancir, Tetrahedron, 1966, 22, 1355 CrossRef CAS
.
- A. DasGupta and N. K. DasGupta, Can. J. Chem., 1974, 52, 155 CrossRef CAS
.
- A. DasGupta and N. DasGupta, Theor. Chim. Acta, 1974, 33, 177 CrossRef CAS
.
- H. Vogler, Int. J. Quantum Chem., 1986, 30, 97 CrossRef CAS
.
- Z. Zhou and R. G. Parr, J. Am. Chem. Soc., 1989, 111, 7371 CrossRef CAS
.
- N. Guihery, D. Maynau and J.-P. Malrieu, New J. Chem., 1998, 22, 281 RSC
.
- M. Nendel, B. Goldfuss, K. Houk, K. Hafner and U. Grieser, Theor. Chem. Acc., 1999, 102, 397 Search PubMed
.
- M. Nendel, B. Goldfuss, B. Beno, K. Houk, K. Hafner and H.-J. Lindner, Pure Appl. Chem., 1999, 71, 221 CrossRef CAS
.
- K. Horii, R. Kishi, M. Nakano, D. Shiomi, K. Sato, T. Takui, A. Konishi and M. Yasuda, J. Am. Chem. Soc., 2022, 144, 3370 CrossRef CAS PubMed
.
- A. Konishi, K. Horii and M. Yasuda, J. Phys. Org. Chem., 2023, 36, e4495 CrossRef CAS
.
- F. Wu, J. Ma, F. Lombardi, Y. Fu, F. Liu, Z. Huang, R. Liu, H. Komber, D. I. Alexandropoulos and E. Dmitrieva,
et al.
, Angew. Chem., 2022, 134, e202202170 CrossRef
.
- F. Wu, A. Barragán, A. Gallardo, L. Yang, K. Biswas, D. Écija, J. I. Mendieta-Moreno, J. I. Urgel, J. Ma and X. Feng, Chem. – Eur. J., 2023, 29, e202301739 CrossRef CAS PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS
.
- TURBOMOLE V7.7 2022, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, https://www.turbomole.com.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed
.
- M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136 CrossRef CAS
.
- F. Menezes, D. Kats and H.-J. Werner, J. Chem. Phys., 2016, 145, 124115 CrossRef PubMed
.
- D. Kats and H.-J. Werner, J. Chem. Phys., 2019, 150, 214107 CrossRef PubMed
.
- H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, J. Baker, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, P. Pulay, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version 2023.1, a package of ab initio programs, https://www.molpro.net.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS
.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin,
et al.
, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed
.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2018, 14, 198 CrossRef CAS PubMed
.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef
.
- A. Schäfer, A. Klamt, D. Sattel, J. C. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187–2193 RSC
.
- W. Si, J. Li, G. Li, C. Jia and X. Guo, J. Mater. Chem. C, 2024, 12, 751 RSC
.
- C. Yang, Z. Chen, C. Yu, J. Cao, G. Ke, W. Zhu, W. Liang, J. Huang, W. Cai and C. Saha,
et al.
, Nat. Nanotechnol., 2024, 1 Search PubMed
.
- S. Mishra, M. Vilas-Varela, L.-A. Lieske, R. Ortiz, S. Fatayer, I. Rončević, F. Albrecht, T. Frederiksen, D. Peña and L. Gross, Nat. Chem., 2024, 16, 755 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Active orbitals and configuration analysis for selected systems, and additional details on multireference and coupled-cluster calculations. See DOI: https://doi.org/10.1039/d4cp02247e |
| This journal is © the Owner Societies 2024 |