Open Access Article
Open Access ArticleWavefunction theory and density functional theory analysis of ground and excited electronic states of TaB and WB†
Isuru R.
Ariyarathna

Physics and Chemistry of Materials (T-1), Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: isuru@lanl.gov
First published on 25th July 2024
Abstract
Several low-lying electronic states of TaB and WB molecules were studied using ab initio multireference configuration interaction (MRCI), Davidson corrected MRCI (MRCI+Q), and coupled cluster singles doubles and perturbative triples [CCSD(T)] methods. Their full potential energy curves (PECs), equilibrium electron configurations, equilibrium bond distances (res), dissociation energies (Des), excitation energies (Tes), harmonic vibrational frequencies (ωes), and anharmonicities (ωexes) are reported. The MRCI dipole moment curves (DMCs) of the first 5 electronic states of both TaB and WB are also reported and the equilibrium dipole moment (μ) values are compared with the CCSD(T) μ values. The most stable 13Π (1σ22σ23σ11π3) and 15Δ (1σ22σ23σ11π21δ1) electronic states of TaB lie close in energy with ∼62 kcal mol−1De with respect to the Ta(4F) + B(2P) asymptote. However, spin–orbit coupling effects make the 15Δ0+ state the true ground state of TaB. The ground electronic state of WB (16Π) has the 1σ22σ13σ11π31δ2 electron configuration and is followed by the excited 16Σ+ and 14Δ states. Finally, the MRCI De, re, ωe, and ωexe values of the 13Π state of TaB and 16Π and 14Δ states of WB are used to assess the density functional theory (DFT) errors on a series of exchange–correlation functionals that span multiple-rungs of the Jacob's ladder of density functional approximations (DFA).
I. Introduction
A fundamental understanding of the electron distribution of atoms and small molecules provides us with valuable information on their properties that are vital for the progression of many disciplines of science such as catalysis, surface science, synthetic chemistry, astrophysics, and plasma science. For this topic, experimental spectroscopic studies and computational explorations have become quite indispensable avenues for gaining useful insight into electronic structures of molecules and for predicting their reactivities.1–8 Indeed, many experimental spectroscopic analyses are conjoined with theoretical predictions for resolving and understanding spectral features.1–4,6,7 However, it should be noted that both spectroscopic and high-level ab initio studies of small molecular species are highly challenging to perform and requires a great deal of experimental and theoretical expertise.1,2,9–13So far, many attempts have been made to understand the electronic spectra of diatomic molecular species. In particular, the main focus has been on transition metal (TM) monoxides and mononitrides due to their applications in catalysis and surface science (see ref. 9, 10, 14 and 15 and references therein). Interestingly, only a few such attempts have been made on 1st and 2nd row TM monoborides,16–31 and even less for 3rd row TM monoborides, likely due to their strong relativistic effects.12,24,25,31–37 Consequently, a high-level theoretical analysis of TaB has not yet been explored. Hence a part of the present work is devoted to analyzing ab initio electronic structures of the TaB molecule. Furthermore, a series of excited electronic states of its neighboring monoboride WB was also analyzed.
Recently, a resonant two-photon ionization spectroscopic analysis was performed by the Morse group to measure the bond dissociation energies of several early TM borides including TaB and WB.31 Their measured D0 values of TaB and WB are 2.700(3) and 2.730(4) eV, respectively. Importantly, this is the only experimental spectroscopic analysis reported so far for early TM monoborides. They further performed DFT/B97-1 (with the aug-cc-pVTZ-PP of Ta/W and cc-pVTZ of B basis set) analysis and predicted 5Δ and 6Σ+ ground states for TaB and WB with D0 values of 2.95 and 2.89 eV, respectively. Furthermore, for TaB they observed 3Π and 3Σ+ states lying 0.07 and 0.5 eV above the 5Δ of TaB. A DFT/B3LYP (with the LANL2DZ basis set) study reported prior to the work by the Morse group (by Kalamse et al.) has identified this 3Σ+ as the ground state of TaB with a binding energy of 2.49 eV.38 Furthermore, the same DFT study by Kalamse et al., predicted a 6Σ− ground electronic state for WB with a binding energy of 2.77 eV.38 The only high-level ab initio study available for WB is the work by Melo and Dixon, which predicted a 6Π ground state for the WB which is followed by the 6Σ+ and 4Δ excited electronic states.12 Of course, the spin–orbit effects are expected to be strong for heavy WB and the inclusion of spin–orbit coupling effects at the CASPT2 (complete active space second-order perturbation theory) level has produced a 6Π7/2 spin–orbit ground state for the molecule with a 2.67 eV D0 which is in harmony with the experimental value reported by the Morse group.12,31
Ab initio multireference methods provide accurate predictions for molecular systems with complicated electronic structures.39,40 In particular, the widely accepted MRCI is an ideal method of choice to analyze the excited states of highly correlated systems with dense electronic spectra.41–45 This is due to the fact that many excited electronic states of various molecular systems are multireference in nature and their wavefunctions prevail by more than one dominant electronic configuration. However, achieving appropriate convergence criteria for multireference calculations is challenging and hence they are markedly less popular. Furthermore, high-level multireference analysis requires a substantial amount of computing power and the calculations are only feasible for small molecular systems containing only a few atoms. On the other hand, approximate DFT is a popular method being used to gain insight into many chemical phenomena due to its favorable accuracy–efficiency compromise.46–50 Indeed, its user-friendly black box nature is rather alluring. Of course, DFT has become quite imperative for predicting properties of larger molecular complexes and solids, where the implementation of expensive wavefunction theories (WFT) is not yet possible. However, DFT predictions are susceptible to being influenced by the exchange–correlation functional utilized and are known to be system and property dependent.37,51,52 This complicates the application of DFT and its reliability. In principle we would expect better predictions from more expensive functionals that belong to higher rungs of the Jacob's ladder of DFA53 compared to the less expensive functionals at the lower rungs. However, climbing up the Jacob's ladder of DFA does not guarantee improvements to the accuracy of the predictions especially for highly correlated TM-based systems that are known to be affected by static correlation errors and delocalization errors.37,51 Hence, often the selection of an appropriate functional to represent a system and a property is followed by DFT benchmark studies.
The current work analyzes 10 and 14 low-lying electronic states of TaB and WB respectively. Their full PECs, electronic configurations, Des, res, Tes, ωes, ωexes, and μ values are reported by means of MRCI,54–56 MRCI+Q, and CCSD(T)57 levels of theory with correlation consistent basis sets. The Des, res, ωes, and ωexes values of three low energy single-reference electronic states of TaB and WB are also calculated with a set of exchange–correlation functionals that falls under multiple-rungs of the Jacob's ladder of DFA53 and the DFT errors were assessed with respect to the WFT findings.
II. Computational details
WFT and DFT calculations were performed utilizing MOLPRO 2023.258–60 and Gaussian 1661 quantum chemistry packages, respectively. First, full PECs of ground and several excited electronic states of TaB and WB were produced under the internally contracted MRCI method54–56 with the quadruple-ζ quality correlation consistent cc-pVQZ basis set of B and cc-pVQZ-PP set of Ta and W.62,63 The Stuttgart relativistic pseudopotentials that represent 1s22s22p63s23p64s23d104p64d104f14 electrons were used (ECP60) for Ta and W atoms.63 All MRCI calculations were performed on top of complete active space self-consistent field (CASSCF)64–67 reference wavefunctions (WFs). The CASSCF wavefunctions of TaB and WB were generated by allocating 8 and 9 electrons, respectively, to 13 orbitals [i.e., CAS(8,13) and CAS(9,13)]. At the dissociating limit, the 13 active orbitals are purely 6s, 6p, and 5d atomic orbitals of the metal atom (M = Ta/W) and 2s and 2p atomic orbitals of B. Under the utilized C2v Abelian sub point group, the active orbitals are 6a1 (6s, 5dz2, 5dx2−y2, and 6pz of M and 2s and 2pz of B), 3b1 (5dxz and 6px of M and 2px of B), 3b2 (5dyz and 6py of M and 2py of B), and 1a2 (5dxy of M). At the CASSCF level a series of PECs arising from Ta(4F) + B(2P), Ta(4P) + B(2P), and Ta(2G) + B(2P) combinations were studied. At the proceeding MRCI level, the PECs of the lowest 10 molecular electronic states of TaB were produced. For WB, at the CASSCF level, all PECs of W(7S) + B(2P), W(5D) + B(2P), and W(3P) + B(2P) and several PECs of W(3H) + B(2P) were investigated but only the PECs of the 14 lowest energy states of WB were investigated at the MRCI level. In all MRCI calculations, single and double electron promotions from active space to virtual space were allowed.To obtain more accurate energetics and spectroscopic parameters, another set of MRCI calculations were performed around the equilibrium bond distance region by including only 10 (of TaB) and 14 (of WB) states at the CASSCF and MRCI level. For these calculations the same quadruple-ζ quality basis set was used. Davidson correction (MRCI+Q) was applied as a size-extensivity correction. The numerical values of MRCI and MRCI+Q PECs were used to solve the ro-vibrational Schrödinger equation to calculate ωe and ωexe values. Similarly, the minima of the PECs were used to calculate Tes, res, and Des. Specifically, the Des of molecular electronic states were calculated with respect to Ta(4F) + B(2P) or W(7S) + B(2P) fragments that are separated by 200 Å. The reported spin–orbit coupling effects were calculated at the MRCI level by implementing the Breit–Pauli Hamiltonian (more information regarding the spin–orbit analysis is provided in the discussion section). Dipole moment curves (DMCs) of several low-lying electronic states of TaB and WB were also produced at the MRCI level under the same basis set.
Low-lying single-reference electronic states of TaB were further investigated by performing single-reference CCSD(T)57 calculations constructed on Hartree–Fock wavefunctions. Two types of CCSD(T) calculations were performed utilizing cc-pVQZ62 (B) cc-pVQZ-PP (Ta)63 and aug-cc-pV5Z68 (B) aug-cc-pV5Z-PP (Ta)63 basis sets. For simplicity, hereafter, the CCSD(T) calculations carried out with the latter basis set are denoted by A5Z-CCSD(T). Furthermore, another set of CCSD(T) calculations were executed by correlating 5s25p6 core electrons of Ta using the aug-cc-pV5Z68 (B) aug-cc-pwCV5Z-PP (Ta)63 basis set [hereafter called A5Z-C-CCSD(T)]. The dipole moment (μ) values of low-lying single-reference electronic states of both TaB and WB were studied at coupled cluster levels using the finite-field approach by applying a field (f) of 0.01 a.u. to the positive and negative directions of the M–B and using the resulting E(f) and E(−f) energies in the μ = [E(f) − E(−f)]/2f equation.
The single-reference 13Π state of TaB and 16Π and 14Δ states of WB were also studied under DFT with a series of exchange–correlation functionals that span several rungs of the Jacob's ladder of DFA.53 Specifically, semi-local generalized gradient approximation (GGA: BP86,69,70 BLYP,71,72 PBE73), meta-GGA (MGGA: TPSS,74 MN15-L75), global GGA hybrid (B3LYP,76,77 B3P86,69,76 B3PW91,76 PBE078,79), MGGA hybrid (TPSSh,74 M06,80 M06-2X,80 MN1581), and range-separated hybrid (RSH: LRC-ωPBE,82 CAM-B3LYP,83ωB97X84) functionals were applied. For all DFT calculations, default SCF (self-consistent field) convergence thresholds, grids, and frozen core settings implemented in Gaussian 16 were utilized. In each case, stable = opt Gaussian keyword was used to obtain stable wavefunctions. The cc-pVQZ (B) cc-pVQZ-PP (Ta) basis set was used for all DFT calculations.
III. Results and discussion
III.A. TaB
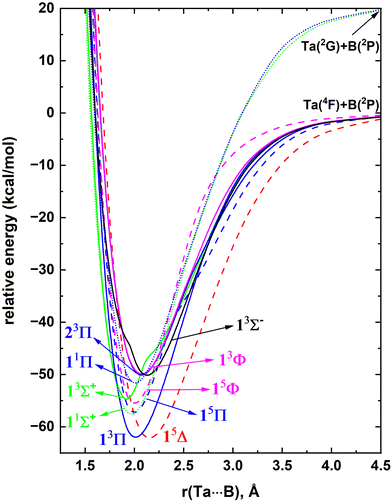
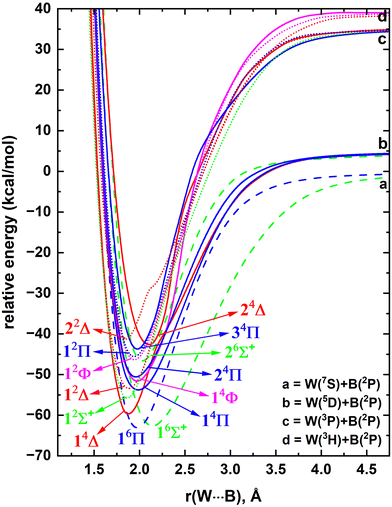
The MRCI constructed on top of CASSCF WFs accounts for a large fraction of the dynamic electron correlation and hence the results of this method are highly reliable. In particular, this technique is well known for producing accurate potential energy profiles of the ground and electronically excited states of highly correlated diatomic molecular species.10,37,41–43In the present work, first, we have analyzed the electronic states of Ta and B atoms to gain insight into the molecular electronic states that they form. Ta has a 4F ground electronic term with the 5d36s2 valence electronic configuration. Its first two electronically excited states (i.e., 4P and 2G) lying at 17.3–26.5 and 27.7–30.6 kcal mol−1 have the same electron arrangement as the ground states.85 The electronic spectrum of Ta is highly complicated beyond the 2G state due to a series of closely arranged states (see the experimental excitation energies listed in ref. 85). Hence, here we have selected the low-lying 4F, 4P, and 2G electronic states of Ta to investigate their reactions with a B atom. The ground state of the B atom is a 2P with the [He]2s22p1 electron configuration. Its first excited state (i.e., 4P; [He]2s12p2) lies ∼82 kcal mol−1 above.85 As B(4P) is comparatively high in energy, its interactions with Ta were not considered. The selected reactants in the present work are Ta(4F) + B(2P), Ta(4P) + B(2P), and Ta(2G) + B(2P). Specifically, we have investigated the 21(quintet + triplet) and 9(quintet + triplet) PECs originating from Ta(4F) + B(2P) and Ta(4P) + B(2P) respectively and the 27 singlet-spin PECs originating from the Ta(2G) + B(2P) asymptote (ESI,† Fig. S1). As shown in the ESI† Fig. S1, the electronic spectrum of TaB is dense and highly complicated, hence only the 10 lowest lying molecular electronic states of TaB were investigated at the MRCI level. The MRCI PECs of TaB are given in Fig. 1. The electronic states arising from the Ta(4P) + B(2P) asymptotes are not among the 10 most stable electronic states of TaB and hence they are not shown in Fig. 1. Note that only two singlet spin electronic states originating from Ta(2G) + B(2P) fall among the 10 reported states of TaB. The two most stable electronic states of TaB (i.e., 13Π and 15Δ) dissociate into Ta(4F) + B(2P) fragments, and have ∼62 kcal mol−1De. Similar to the Ta atom, the excited electronic spectrum of TaB is complicated with a set of closely arranged electronic states and specifically the 2nd to 10th excited states of TaB are assembled within 8 kcal mol−1 of energy.
The dominant electron configurations and configuration interaction coefficients collected at the corresponding equilibrium distances of the studied states of TaB are listed in Table 1. The contours of the state-average CASSCF active orbitals obtained at the re = 2.0 Å are plotted in Fig. 2. The 1σ molecular orbital consists of the dominant 2s of B and minor 5dz2 and 6s character of Ta. The 2σ is dominantly the 6s of Ta but bears a small contribution from the 2s of B. The hybridization of the 5dz2 of Ta with 2pz of B is shown in the 3σ molecular orbital. Similarly, the 5dxz(Ta) + 2px(B) and 5dyz(Ta) + 2py(B) combinations give rise to the perpendicular 1πx and 1πy bonding molecular orbitals. The 1πx* and 1πy* antibonding molecular orbitals resulting from 5dxz(Ta) – 2px(B) and 5dyz(Ta) – 2py(B) are also present in the active space but not given in Fig. 2 since they are not occupied by the reported states. Due to the symmetry effects, the 5dx2−y2 and 5dxy atomic orbitals of Ta do not hybridize with the active orbitals of B and hence directly correlate to the 1δx2−y2 and 1δxy orbitals of Fig. 2.
| Statea | Coefficientb | 1σ | 2σ | 3σ | 1πx | 1πy | 1δx2−y2 | 1δxy |
|---|---|---|---|---|---|---|---|---|
| a Only B1 components of Π and Φ states and A1 of the 15Δ under C2v symmetry are listed. b Only the configuration interaction coefficients that are equal or larger than 0.25 of the corresponding natural orbital representations are listed. | ||||||||
| 13Π | 0.90 | 2 | 2 | α | α | 2 | 0 | 0 |
| 15Δ | 0.88 | 2 | 2 | α | α | α | 0 | α |
| 11Σ+ | 0.88 | 2 | 2 | 0 | 2 | 2 | 0 | 0 |
| 15Π | −0.64 | 2 | α | α | α | 2 | α | 0 |
| 0.64 | 2 | α | α | 2 | α | 0 | α | |
| 15Φ | 0.65 | 2 | α | α | α | 2 | α | 0 |
| 0.65 | 2 | α | α | 2 | α | 0 | α | |
| 13Σ+ | 0.87 | 2 | α | α | 2 | 2 | 0 | 0 |
| 11Π | −0.57 | 2 | 2 | α | β | 2 | 0 | 0 |
| 0.57 | 2 | 2 | β | α | 2 | 0 | 0 | |
| 23Π | 0.47 | 2 | 2 | 0 | 2 | α | 0 | α |
| −0.46 | 2 | 2 | 0 | α | 2 | α | 0 | |
| 0.30 | 2 | α | β | 2 | α | 0 | α | |
| −0.30 | 2 | α | β | α | 2 | α | 0 | |
| 13Φ | 0.46 | 2 | 2 | 0 | 2 | α | 0 | α |
| 0.47 | 2 | 2 | 0 | α | 2 | α | 0 | |
| 0.25 | 2 | α | β | 2 | α | 0 | α | |
| 0.25 | 2 | α | β | α | 2 | α | 0 | |
| −0.27 | 2 | α | α | α | 2 | β | 0 | |
| −0.27 | 2 | α | α | 2 | α | 0 | β | |
| 13Σ− | 0.75 | 2 | 2 | 2 | α | α | 0 | 0 |
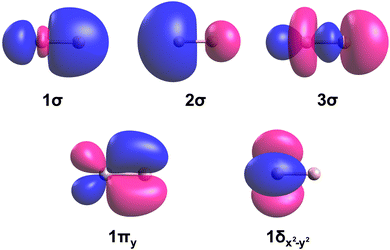 | ||
| Fig. 2 Select molecular orbitals of TaB. The Ta (left atom) and B (right atom) atoms of each orbital plot are shown in gray and soft-pink colors, respectively. The rotations of 1πy by 90° and 1δx2−y2 by 45° along the z-axis yield the 1πx and 1δxy molecular orbitals, respectively. Blue and pink colors correspond to the negative and positive phases of the molecular orbitals. The contours were produced using the Avogadro software.86,87 The molecular orbitals of WB have similar shapes. | ||
At the equilibrium distance, the 13Π state has the 1σ22σ23σ11π3 dominant electronic configuration (Table 1) which accounts for an approximate bond order of 2. Its effective bond order based on the dominant electron configuration is indeed 1.6. The electronic configuration of the 15Δ can be produced by transferring an electron from the 1πy of 13Π to an 1δ orbital (i.e., 1σ22σ23σ11π21δ1). Since the 1δ orbitals are non-bonding, the bond order of the 15Δ is ∼1.5. As expected, the lower bond order of the 15Δ compared to the 13Π translates to a longer re of the former compared to the latter (Fig. 1). The second excited state of the TaB is a 1Σ+ with a 1σ22σ21π4 electron arrangement with a bond order of 2. Note that the first three electronic states of TaB (i.e., 13Π, 15Δ, 11Σ+) are single-reference in nature and are followed by the multireference 15Π and 15Φ states. These two 15Π and 15Φ states possess similar electron arrangements that are separated by the (1πx)2(1πy)1 − (1πx)1(1πy)2 and (1πx)2(1πy)1 + (1πx)1(1πy)2 components, respectively (Table 1). An electron transfer from 2σ of 11Σ+ to the 3σ orbital produces the next electronic state of TaB (i.e., 13Σ+). The proceeding 11Π is the corresponding open-shell multireference singlet spin electronic state of the 13Π. The lower stability of the low-spin 11Π compared to the 13Π is an example of the preservation of the Hund's rule.
The CCSD(T) level of theory can represent single-reference electronic states of molecules with high accuracy and hence are adopted to analyze the three lowest energy electronic states of TaB (13Π, 15Δ, and 11Σ+). The coupled cluster, MRCI, and MRCI+Q De, re, Te, ωe, and ωexe values of the studied states of TaB are listed in Table 2. The CCSD(T) calculations require less computational resources compared to MRCI and therefore we were able improve the basis set from cc-pVQZ (B) cc-pVQZ-PP(Ta) to aug-cc-pV5Z (B) aug-cc-pV5Z-PP(Ta) to provide more accurate estimates for the properties of TaB. Importantly, at this level using the aug-cc-pV5Z (B) aug-cc-pwCV5Z-PP(Ta) basis set we were able to acquire the correlation of the inner 5s25p6 electrons of Ta which is expected to further improve the accuracy of the predictions. As shown in the potential energy profile (Fig. 1), the 13Π and 15Δ states of TaB lie very close in energy and at the MRCI and MRCI+Q levels the former is ∼0.2 kcal mol−1 more stable compared to the latter (Table 2). However, this relative stabilization of 13Π over 15Δ is within the margin of error of the methods and the basis set, and hence it is difficult to decisively assign the exact ground state for TaB. Indeed, this is true as demonstrated by the 0.7 kcal mol−1 stability of 15Δ compared to the 13Π at the CCSD(T). At the A5Z-CCSD(T) level the relative stabilization of 15Δ compared to the 13Π decreases to 0.2 kcal mol−1. However, the core electron correlated coupled cluster [i.e., A5Z-C-CCSD(T)] switched the ground state prediction to a 0.7 kcal mol−1 more stable 13Π compared to the 15Δ, which also agrees with the MRCI and MRCI+Q prediction. Under all utilized levels of theory, the De of 13Π and 15Δ are ∼60.5–63.5 kcal mol−1 (Table 2). For all states MRCI+Q predicted 1–2 kcal mol−1 higher Des compared to the MRCI Des (Table 2).
| State | Methoda | D e | r e | T e | ω e | ω e x e |
|---|---|---|---|---|---|---|
| a Davidson corrected MRCI is given as MRCI+Q. The cc-pVQZ-PP (60ECP) of Ta and cc-pVQZ of B basis set was applied for all MRCI, MRCI+Q, and CCSD(T) calculations. The aug-cc-pV5Z-PP (60ECP) of Ta and aug-cc-pV5Z of B basis set used coupled cluster calculations are labeled as A5Z-CCSD(T). The 5s25p6 (of Ta) core electrons correlated coupled cluster calculations performed with aug-cc-pwCV5Z-PP (60ECP) of Ta and aug-cc-pV5Z of B set are denoted by A5Z-C-CCSD(T). | ||||||
| 13Π | A5Z-C-CCSD(T) | 62.35 | 1.977 | 0 | 697 | 3.2 |
| A5Z-CCSD(T) | 61.82 | 1.994 | 67 | 684 | 3.5 | |
| CCSD(T) | 60.67 | 1.996 | 238 | 682 | 3.5 | |
| MRCI | 62.37 | 2.012 | 0 | 663 | 3.7 | |
| MRCI+Q | 63.49 | 2.014 | 0 | 658 | 3.8 | |
| 15Δ | A5Z-C-CCSD(T) | 61.65 | 2.120 | 242 | 582 | 2.4 |
| A5Z-CCSD(T) | 62.01 | 2.141 | 0 | 586 | 2.9 | |
| CCSD(T) | 61.35 | 2.142 | 0 | 585 | 2.9 | |
| MRCI | 62.17 | 2.155 | 68 | 576 | 1.9 | |
| MRCI+Q | 63.27 | 2.156 | 76 | 573 | 2.1 | |
| 11Σ+ | A5Z-C-CCSD(T) | 59.80 | 1.943 | 890 | 656 | 2.6 |
| A5Z-CCSD(T) | 59.41 | 1.959 | 911 | 662 | 2.9 | |
| CCSD(T) | 58.09 | 1.960 | 1141 | 662 | 3.0 | |
| MRCI | 57.88 | 1.966 | 1568 | 645 | 3.1 | |
| MRCI+Q | 59.35 | 1.968 | 1450 | 645 | 3.2 | |
| 15Π | MRCI | 57.42 | 1.998 | 1730 | 706 | 3.8 |
| MRCI+Q | 58.78 | 2.001 | 1648 | 707 | 4.6 | |
| 15Φ | MRCI | 55.68 | 1.999 | 2340 | 707 | 3.0 |
| MRCI+Q | 57.07 | 2.002 | 2247 | 709 | 3.9 | |
| 13Σ+ | MRCI | 55.40 | 1.904 | 2438 | 774 | 4.8 |
| MRCI+Q | 57.05 | 1.906 | 2254 | 764 | 4.5 | |
| 11Π | MRCI | 51.75 | 2.008 | 3713 | 655 | 5.3 |
| MRCI+Q | 53.11 | 2.009 | 3630 | 650 | 5.0 | |
| 23Π | MRCI | 50.35 | 2.072 | 4203 | 605 | 7.2 |
| MRCI+Q | 51.85 | 2.071 | 4072 | 606 | 6.8 | |
| 13Φ | MRCI | 50.09 | 2.076 | 4292 | 572 | −0.4 |
| MRCI+Q | 51.59 | 2.075 | 4164 | 575 | −0.3 | |
| 13Σ− | MRCI | 50.07 | 2.121 | 4300 | 592 | 3.3 |
| MRCI+Q | 51.77 | 2.123 | 4101 | 597 | 3.7 | |
The re values of the 13Π, 15Δ, and 11Σ+ states decreased moving from CCSD(T) to A5Z-CCSD(T) to A5Z-C-CCSD(T), and the observation that the core electron correlation tends to contract the res is consistent with our previous findings on diatomic species.37,41,88 The MRCI and MRCI+Q predicted slightly longer re values compared to CCSD(T) (by 0.01–0.02 Å) and the discrepancy between MRCI and MRCI+Q re predictions is less than 0.004 Å. Overall, at the MRCI level, the observed order of the electronic states of TaB is 13Π, 15Δ, 11Σ+, 15Π, 15Φ, 13Σ+, 11Π, 23Π, 13Φ, and 13Σ−. The MRCI+Q order is the same as MRCI except for the slightly stabilized 13Σ− over the 13Φ (by 63 cm−1) (Table 2).
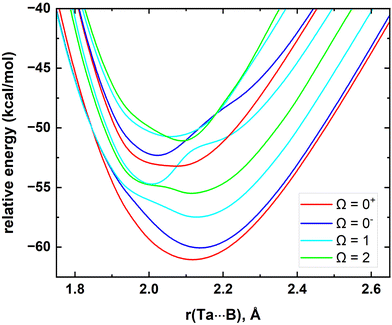
In the present work we have performed a spin–orbit analysis for the Ta atom to evaluate its splitting and to compare our results with the experimental literature values. Our calculated MRCI values and the experimental values are listed in the ESI,† Table S1. In line with the experimental values, MRCI predicted a4F3/2, a4F5/2, a4F7/2, and a4F9/2 ordering for the spin–orbit products of the a4F of Ta. Importantly, for these states, the maximum discrepancy between MRCI versus experiment is only 183 cm−1. The order of the spin–orbit constituents of the a4P at the MRCI level is a4P3/2 (at 6559 cm−1), a4P1/2 (at 6774 cm−1), and a4P5/2 (at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 112 cm−1) which deviates from their experimental placements by 490, 725, and 859 cm−1, respectively.85 The excitation energies for the J = 7/2 and 9/2 of a2G and J = 3/2 and 1/2 of a6D are also calculated and given in the ESI† Table S1. Overall, we observed the deviations between experiment versus MRCI become significant moving to high energy states of Ta. Then, we investigated the spin–orbit splitting of the TaB. At the MRCI level, the 10 lowest energy electronic states of TaB were included in the spin–orbit matrix. The several low-lying spin–orbit curves resulting from these states are shown in Fig. 3. As expected, the spin–orbit effects of TaB are significant. The spin–orbit ground state of TaB is an Ω = 0+ which carries 56% 15Δ + 31% 13Π + 5% 23Π + 7% 11Σ+ + 1% 13Σ− components. The ground Ω = 0+ of TaB has a 61.14 kcal mol−1De with respect to the lowest energy Ω state of TaB at r = 200 Å and its D0 (with the zero-point energy) is 60.40 kcal mol−1. The recently experimentally measured D0 of TaB by Merriles et al., is 2.700(3) eV (or ∼62.3 kcal mol−1) and only 1.9 kcal mol−1 higher than our D0.31 The re of the spin–orbit corrected ground state of TaB (Ω = 0+) is slightly shorter than the re of 15Δ of TaB (2.118 versus 2.155 Å). The calculated ωe (519 cm−1) and ωexe (2.3 cm−1) of the ground Ω = 0+ differ by 60 and 0.4 cm−1 from the corresponding values of the 15Δ. The second lowest energy Ω = 0− has a mixing of 81% 15Δ + 17% 13Π + 2% 23Π and lies approximately 1 kcal mol−1 above the ground Ω = 0+ state. The next several spin–orbit states of TaB are Ω = 1, 2, 1, 0+, 0−, 2, and 1 which span 1238–3599 cm−1. More information on the spin–orbit states of TaB is given in the ESI† Table S2.
112 cm−1) which deviates from their experimental placements by 490, 725, and 859 cm−1, respectively.85 The excitation energies for the J = 7/2 and 9/2 of a2G and J = 3/2 and 1/2 of a6D are also calculated and given in the ESI† Table S1. Overall, we observed the deviations between experiment versus MRCI become significant moving to high energy states of Ta. Then, we investigated the spin–orbit splitting of the TaB. At the MRCI level, the 10 lowest energy electronic states of TaB were included in the spin–orbit matrix. The several low-lying spin–orbit curves resulting from these states are shown in Fig. 3. As expected, the spin–orbit effects of TaB are significant. The spin–orbit ground state of TaB is an Ω = 0+ which carries 56% 15Δ + 31% 13Π + 5% 23Π + 7% 11Σ+ + 1% 13Σ− components. The ground Ω = 0+ of TaB has a 61.14 kcal mol−1De with respect to the lowest energy Ω state of TaB at r = 200 Å and its D0 (with the zero-point energy) is 60.40 kcal mol−1. The recently experimentally measured D0 of TaB by Merriles et al., is 2.700(3) eV (or ∼62.3 kcal mol−1) and only 1.9 kcal mol−1 higher than our D0.31 The re of the spin–orbit corrected ground state of TaB (Ω = 0+) is slightly shorter than the re of 15Δ of TaB (2.118 versus 2.155 Å). The calculated ωe (519 cm−1) and ωexe (2.3 cm−1) of the ground Ω = 0+ differ by 60 and 0.4 cm−1 from the corresponding values of the 15Δ. The second lowest energy Ω = 0− has a mixing of 81% 15Δ + 17% 13Π + 2% 23Π and lies approximately 1 kcal mol−1 above the ground Ω = 0+ state. The next several spin–orbit states of TaB are Ω = 1, 2, 1, 0+, 0−, 2, and 1 which span 1238–3599 cm−1. More information on the spin–orbit states of TaB is given in the ESI† Table S2.
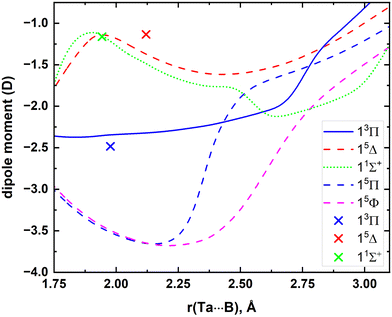
The MRCI DMCs calculated for the 5 lowest electronic states of TaB are illustrated in Fig. 4. The μ values of single-reference 13Π, 15Δ, and 11Σ+ states were also calculated at CCSD(T) and A5Z-C-CCSD(T) levels at their corresponding re values. Specifically, the CCSD(T) μ values of the aforementioned states are −2.54, −1.24, and −1.19 D, respectively, whereas those at the A5Z-C-CCSD(T) level are −2.48, −1.14, and −1.16 D. The calculated A5Z-C-CCSD(T) μ value is also marked in Fig. 4. The best harmony between MRCI versus A5Z-C-CCSD(T) was observed for the 11Σ+ state, whereas the μ values of 13Π and 15Δ under the two theories are also in reasonable agreement (Fig. 4).
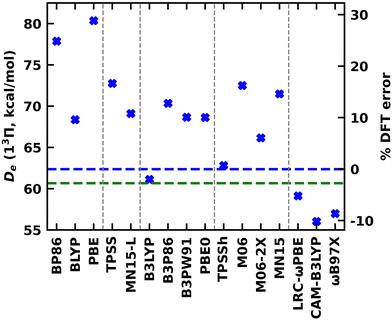
Going a step further, the single-reference 13Π electronic state of TaB was studied using a series of exchange–correlation functionals that span multiple rungs of the Jacob's ladder of DFA. The calculated De, re, ωe, and ωexe values under the GGA (BP86, BLYP, and PBE), MGGA (TPSS and MN15-L), global GGA hybrid (B3LYP, B3P86, B3PW91, and PBE0), MGGA hybrid (TPSSh, M06, M06-2X, and MN15), and RSH (LRC-ωPBE, CAM-B3LYP, and ωB97X) functionals are listed in the ESI,† Table S3. Generally, we expect the accuracy of the predictions to improve moving from less expensive GGA to more complex RSH functionals. As expected, the largest discrepancies between WFT Des versus DFT Des are displayed by the cheaper GGA PBE and BP86 (Fig. 5 and ESI,† Table S3). Specifically, these functionals overestimated the Des by 18.0 and 15.5 kcal mol−1 (or by 29 and 25%), with respect to MRCI De, respectively (Fig. 5 and ESI,† Tables S3 and S4). Comparatively, the performance of the GGA BLYP is better with an error of ∼10%. The De errors of MGGA TPSS and MN15-L are larger than GGA BLYP but significantly lower than the GGA PBE and BP86. The global GGA hybrids consistently overestimated the De of TaB(13Π) by 10–13% except for B3LYP which predicted a very similar De to the MRCI De (61.13 versus 62.37 kcal mol−1). The harmony of De between B3LYP vs the CCSD(T) is even better (61.13 versus 60.67 kcal mol−1). Among all the implemented functionals, the MGGA TPSSh carries the least error (less than 1%) for De. All RSH functionals underestimated the De of TaB(13Π) by ∼5–10%. All functionals predicted shorter res compared to the MRCI. Compared to MRCI, the largest deviation was observed for the LRC-ωPBE (2.012 versus 1.862 Å). All other functionals predicted res of 1.92–2.00 Å with less than 5% errors (ESI,† Tables S3 and S4). Similar to re, the largest mismatch of DFT ωeversus MRCI ωe was produced by the LRC-ωPBE (663 versus 844 cm−1), whereas all other functionals overestimated the ωe by 10–90 cm−1 (Table 3). The DFT ωexe values varied between 2.5–7.0 cm−1, and the expensive RSH CAM-B3LYP and ωB97X predicted identical values to the MRCI ωexe (Table 2 and ESI,† Table S3).
| Statea | Coefficientb | 1σ | 2σ | 3σ | 1πx | 1πy | 1δx2−y2 | 1δxy |
|---|---|---|---|---|---|---|---|---|
| a Only the B1 component of Π and Φ states and the A1 component of Δ states under C2v symmetry are listed. b Only the configuration interaction coefficients that are larger than 0.20 of the corresponding natural orbital representations are listed. | ||||||||
| 16Π | 0.91 | 2 | α | α | 2 | α | α | α |
| 16Σ+ | 0.92 | 2 | 2 | α | α | α | α | α |
| 14Δ | 0.89 | 2 | α | α | 2 | 2 | α | 0 |
| 12Σ+ | 0.84 | 2 | 2 | α | 2 | 2 | 0 | 0 |
| −0.21 | 2 | 0 | α | 2 | 2 | 0 | 2 | |
| −0.21 | 2 | 0 | α | 2 | 2 | 2 | 0 | |
| 14Π | 0.55 | 2 | 2 | α | 2 | α | 0 | α |
| −0.55 | 2 | 2 | α | α | 2 | α | 0 | |
| −0.24 | 2 | β | α | 2 | α | α | α | |
| 12Δ | 0.69 | 2 | α | β | 2 | 2 | α | 0 |
| −0.27 | 2 | β | α | 2 | 2 | α | 0 | |
| −0.42 | 2 | α | α | 2 | 2 | β | 0 | |
| 14Φ | 0.61 | 2 | 2 | α | 2 | α | 0 | α |
| 0.61 | 2 | 2 | α | α | 2 | α | 0 | |
| 24Π | 0.67 | 2 | α | β | 2 | α | α | α |
| −0.26 | 2 | α | α | 2 | α | β | α | |
| −0.26 | 2 | α | α | 2 | α | α | β | |
| 0.24 | 2 | 2 | 0 | 2 | α | α | α | |
| 26Σ+ | 0.87 | 2 | α | 2 | α | α | α | α |
| 12Φ | 0.47 | 2 | 2 | α | α | 2 | β | 0 |
| 0.47 | 2 | 2 | α | 2 | α | 0 | β | |
| −0.37 | 2 | 2 | β | 2 | α | 0 | α | |
| −0.37 | 2 | 2 | β | α | 2 | α | 0 | |
| 12Π | 0.33 | 2 | 2 | α | α | 2 | β | 0 |
| −0.33 | 2 | 2 | α | 2 | α | 0 | β | |
| 0.45 | 2 | 2 | β | 2 | α | 0 | α | |
| −0.45 | 2 | 2 | β | α | 2 | α | 0 | |
| 34Π | 0.53 | 2 | α | 2 | 2 | α | 0 | α |
| −0.53 | 2 | α | 2 | α | 2 | α | 0 | |
| −0.26 | 2 | 0 | 2 | 2 | α | α | α | |
| 24Δ | 0.81 | 2 | 2 | 2 | α | α | 0 | α |
| 22Δ | 0.79 | 2 | 2 | 0 | 2 | 2 | α | 0 |
III.B. WB
The spin–orbit splitting of W is quite substantial; for example the J = 1–4 components of its 5D (5d46s2) ground electronic state span from ∼4.8 to 17.8 kcal mol−1.85 The first electronically excited state of W (i.e., 7S) has a 5d56s1 electron configuration and rests in between J = 1 and J = 2 components of the 5D (specifically, the 7S is at 8.4 kcal mol−1).85 The following two states of W (i.e., 3P and 3H) carry the same electron configuration as the ground state and extend over 27.2–55.0 and 34.8–48.6 kcal mol−1, respectively.85In the present work, we have investigated the interaction of 5D, 7S, 3P and 3H electronic states of W with the B(2P). According to the Wigner–Witmer rules, the interaction between W(5D) + B(2P), W(7S) + B(2P), W(3P) + B(2P), and W(3H) + B(2P) produces 15(sextet + quartet), 3(octet + sextet), 9(quartet + doublet), and 33(quartet + doublet) spin states.89,90 First, at the CASSCF level, all PECs originating from W(5D) + B(2P), W(7S) + B(2P), and W(3P) + B(2P) and a few more curves resulting from W(3H) + B(2P) were analyzed. Similar to TaB, WB bears a plethora of closely lying electronic states (ESI,† Fig. S2). The PECs of the most stable 14 electronic states of WB were plotted at the MRCI level and are illustrated in Fig. 6. At this level W(7S) + B(2P) is ∼5 kcal mol−1 more stable compared to the W(5D) + B(2P) fragments. This is not surprising since W(7S) and W(5D) are rather close in energy and importantly the produced MRCI potential energy profile (Fig. 6) does not account for spin–orbit effects. Indeed the stabilization of W(7S) compared to W(5D) has also been observed before by Ma and Balasubramanian under the CASSCF/SOCI (SOCI = second-order configuration interaction) level.91
According to our MRCI potential energy profile, the ground state of WB is a 6Π originating from W(7S) + B(2P) fragments (Fig. 6). The 6Σ+ state resulting from the same fragments is the first excited state of WB which lies energetically closer to the 6Π state. The PEC of the second excited state of WB (i.e., 14Δ) dissociates to W(5D) + B(2P) but an avoided crossing was observed at ∼2.2 Å with the 24Δ PEC stemming from W(3P) + B(2P). The only 2Σ+ state produced by W(3P) + B(2P) is in fact the next electronic state of WB (i.e., 12Σ+). The proceeding 10 electronic states are amassed within ∼12 kcal mol−1 (Fig. 6) which clearly apprise of the complexity of the excited state spectrum of the molecule.
The dominant equilibrium electron configurations and the corresponding configuration interaction coefficients of the studied 14 electronic states of WB are listed in Table 3. The 16Π state carries the 1σ22σ13σ11π31δ2 electron distribution. The electron configuration of 16Σ+ can be formed by transferring an electron from the 16Π state's doubly occupied 1π to its singly occupied 2σ. On the other hand, transferring an electron from the 16Π state's 1δ to its singly occupied 1π orbital creates 14Δ. 12Σ+ has minor multireference characteristics but with a major allocation of 1σ22σ23σ11π4. Interestingly, among all studied states, 12Σ+ is the only state with a dominant configuration that does not host electrons in either of the δ orbitals (Table 3). Next 4 electronic states of WB (i.e., 14Π, 12Δ, 14Φ, 24Π) exhibit rich multireference characters. Notice that 24Π has a similar electronic configuration to the ground state, 16Π, where the spin up electrons in the 3σ and 1δ of the latter couple in different ways to produce the configuration of the former (note: only the three largest components of the 24Π were considered). The significant destabilization of the low spin 24Π compared to the 16Π (by ∼13 kcal mol−1; Fig. 6) is an example of the Hund's rule (recall that in the previous section we identified the 13Π and 11Π states of TaB as obeying the Hund rule). The heavy multireference nature of the low-spin open-shell electronic states is rather common especially for highly correlated systems with dense electronic spectra. The 12Φ and 12Π of WB are two such states made of 4 distinct electron distributions (Table 3).
Upon comparing electronic structures of WB with TaB, the electron configuration of WB(16Π) can be produced by attaching an electron to the vacant 1δ orbital of TaB(15Π) (Tables 1 and 3). Similarly, the electronic configuration of WB(16Σ+) is formed by adding an electron to the empty 1δ of TaB(15Δ). Since the additional electron is being attached to a nonbonding 1δ orbital of TaB, approximately similar re values can be expected for WB(16Π) versus TaB(15Π) and WB(16Σ+) versus 15Δ(TaB). Indeed, the re values of WB(16Σ+) and 15Δ(TaB) are very similar (i.e., 2.150 versus 2.155 Å, respectively) (Tables 2 and 4). On the other hand, the res of WB(16Π) and TaB(15Π) are 1.971 and 2.001 Å, respectively. This slightly longer re of the latter compared to the former (by 0.03 Å) might be a result of its multireference nature.
| State | Methoda | D e | re | T e | ω e | ω e x e |
|---|---|---|---|---|---|---|
| a Davidson corrected MRCI is given as MRCI+Q. The cc-pVQZ-PP (60ECP) of W and cc-pVQZ of B basis set was applied for all MRCI and MRCI+Q calculations. | ||||||
| 16Π | MRCI | 63.32 | 1.971 | 0 | 718 | 4.0 |
| MRCI+Q | 63.20 | 1.975 | 0 | 715 | 4.3 | |
| 16Σ+ | MRCI | 62.62 | 2.150 | 245 | 555 | 3.5 |
| MRCI+Q | 62.62 | 2.140 | 204 | 559 | 3.8 | |
| 14Δ | MRCI | 60.00 | 1.876 | 1160 | 823 | 3.3 |
| MRCI+Q | 60.16 | 1.877 | 1063 | 820 | 3.7 | |
| 12Σ+ | MRCI | 56.11 | 1.859 | 2523 | 807 | 4.8 |
| MRCI+Q | 56.20 | 1.861 | 2446 | 813 | 6.0 | |
| 14Π | MRCI | 53.92 | 1.983 | 3286 | 567 | 1.5 |
| MRCI+Q | 53.99 | 1.987 | 3219 | 573 | 1.9 | |
| 12Δ | MRCI | 53.75 | 1.879 | 3348 | 712 | 3.1 |
| MRCI+Q | 54.49 | 1.874 | 3047 | 705 | 2.3 | |
| 14Φ | MRCI | 51.77 | 1.970 | 4040 | 681 | 8.1 |
| MRCI+Q | 52.09 | 1.970 | 3886 | 693 | 7.7 | |
| 24Π | MRCI | 50.74 | 1.956 | 4401 | 629 | 8.3 |
| MRCI+Q | 50.66 | 1.962 | 4385 | 587 | 7.4 | |
| 26Σ+ | MRCI | 46.76 | 2.030 | 5790 | 738 | 6.3 |
| MRCI+Q | 47.16 | 2.034 | 5609 | 712 | 4.3 | |
| 12Φ | MRCI | 46.43 | 1.941 | 5906 | 740 | 3.9 |
| MRCI+Q | 46.47 | 1.943 | 5849 | 739 | 4.5 | |
| 12Π | MRCI | 45.77 | 1.940 | 6137 | 745 | 3.8 |
| MRCI+Q | 45.62 | 1.942 | 6148 | 744 | 3.7 | |
| 34Π | MRCI | 43.69 | 1.978 | 6864 | 824 | 5.3 |
| MRCI+Q | 44.59 | 1.976 | 6508 | 820 | 5.8 | |
| 24Δ | MRCI | 42.50 | 2.113 | 7281 | 680 | 5.0 |
| MRCI+Q | 42.94 | 2.112 | 7085 | 668 | 4.2 | |
| 22Δ | MRCI | 41.71 | 1.844 | 7559 | 863 | 4.8 |
| MRCI+Q | 42.61 | 1.845 | 7199 | 860 | 4.0 | |
The MRCI and MRCI+Q Des of the 14 electronic states of WB calculated with respect to W(7S) + B(2P) dissociation is reported in Table 4. The differences between MRCI and MRCI+Q Des are less than 1 kcal mol−1. At the MRCI level the De of WB (16Π) is 63.32 kcal mol−1 with respect to the W(7S) + B(2P) asymptote. The zero-point energy correction decreased this value to 62.38 kcal mol−1. The experimental D0 of the WB reported by Merriles et al., is 2.730(4) eV (or ∼63 kcal mol−1).31 Importantly, recall that the experimental ground state of W is 5D and hence we cannot make direct comparisons between our MRCI or MRCI+Q values versus the experimentally measured D0 by Merriles et al. However, a series of corrections can be made to predict its D0 with respect to W(5D) + B(2P) from the D0 calculated with reference to the W(7S) + B(2P) fragments. For example, an ab initio analysis reported for the first three electronic states of WB (i.e., 16Π, 16Σ+, 14Δ), incorporated a series of corrections (see ref. 12) to attain a D0 of 2.67 eV (or 61.57 kcal mol−1) for WB (16Π) with respect to the W(5D) + B(2P) fragments, which is in harmony with the experimental D0 by Merriles et al.31
The ∼0.2 Å long bond distance of 16Σ+ compared to 16Π (Table 4) can be rationalized by their electron arrangements or bond orders. Specifically, the approximate bond orders of these two states are 1.5 and 2, respectively. The approximate bond orders of both 14Δ and 12Σ+ are 2.5 and as expected their res (1.876 and 1.859 Å, respectively at MRCI) are shorter than both 16Π and 16Σ+. The CCSD(T) res reported for the 16Π, 16Σ+, and 14Δ states by Melo and Dixon are 1.952, 2.117, and 1.856 Å, respectively.12 For all three states our MRCI and MRCI+Q re values are ∼0.019–0.033 Å longer compared to their CCSD(T) values. This observation of slightly longer MRCI and MRCI+Q res compared to CCSD(T) res is in line with our findings of TaB.
For all states MRCI predicted 16–360 cm−1 higher excitation energies compared to MRCI+Q, except for the 12Π that has a slightly lower MRCI excitation energy (only by 11 cm−1) compared to the MRCI+Q (Table 4). Overall, at the MRCI level, the obtained order of the electronic states of WB is 16Π, 16Σ+, 14Δ, 12Σ+, 14Π, 12Δ, 14Φ, 24Π, 26Σ+, 12Φ, 12Π, 34Π, 24Δ, 22Δ. MRCI+Q follows the same order except for the 172 cm−1 stable 12Δ over the 14Π.
Next, we performed spin–orbit analysis for the W atom and the WB molecule. Our calculated spin–orbit splitting and the experimental literature values of W are given in the ESI† Table S5. The 5D ground state of W produces five spin–orbit products (J = 0, 1, 2, 3, 4). Experimentally the J = 3 of the first excited 7S falls in between the J = 1 and 2 of 5D.85 However, MRCI predicted the 7S3 to be in between 5D2 and 5D3 (ESI,† Table S5). The largest discrepancy observed between MRCI versus experiment is less than 460 cm−1. All 14 low-lying electronic states of WB were included in the spin–orbit matrix to study the spin–orbit effects of WB. At re = 1.971 Å (which is the re of 16Π at MRCI), the order of the lowest Ω states of WB is 7/2, 5/2, 3/2, 1/2, 1/2, 1/2, and 3/2. The ground Ω = 7/2 is dominantly 16Π (91%) with a minor fraction of 14Δ (9%). These values of Ω = 7/2 are in excellent agreement with the values reported in the recent work by Melo and Dixon.12 Our calculated compositions of all the Ω states are listed in the ESI† Table S6. Importantly, the spin–orbit coupling effects of WB are significant and for example, the first four spin–orbit states of WB are contained within 113 cm−1 (ESI,† Table S6). Another spin–orbit calculation was performed at re = 2.150 Å, which is the MRCI re of the 16Σ+ state of WB. At this distance, the lowest energy spin–orbit state of WB is an Ω = 5/2 with 90% 16Σ+ and 9% 14Π. The other two spin–orbit components of 16Σ+ (i.e., Ω = 3/2 and 1/2), lie 156 and 184 cm−1 above the 16Σ+1/2. Importantly, even though the 16Σ+ lies only 245 cm−1 above 16Π (Table 4) the 16Σ+5/2 lies 641 cm−1 above the 16Π7/2. This confirms that the ground state of WB is indeed the 16Π7/2.
To the best of our knowledge, the μ values or DMCs of WB are not available in the literature. Hence, at the MRCI level the DMCs were produced and plotted in Fig. 7. The A5Z-C-CCSD(T) μ values for the single-reference 16Π, 16Σ+, and 14Δ states were also calculated at their res and they are −2.67, −1.60, and −2.92 D, respectively (for comparison these values are also marked in Fig. 7). The MRCI and A5Z-C-CCSD(T) μ values of the 16Π and 14Δ states agree well with each other, but the discrepancy between the two levels for the 16Σ+ is ∼0.4 D.
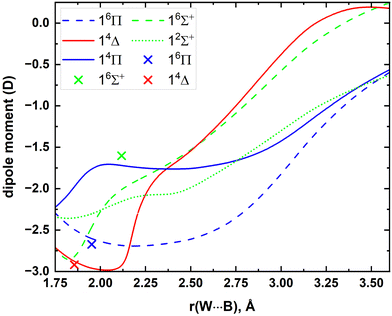 | ||
| Fig. 7 MRCI DMCs of the lowest 5 electronic states of WB as a function of W⋯B distance [r(W⋯B), Å]. The μ values of 16Π, 16Σ+, and 14Δ obtained under the A5Z-C-CCSD(T) level at their res are shown in blue (at −2.67 D), green (at −1.60 D), and red (at −2.92 D) cross marks, respectively. The CCSD(T) res reported by Melo and Dixon were used to calculate the A5Z-C-CCSD(T) μ values.12 | ||
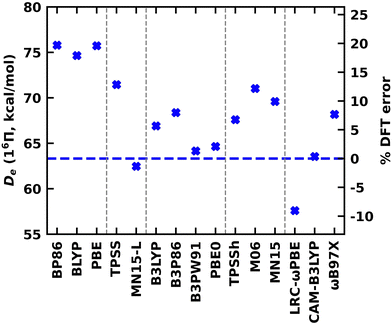
A DFT analysis was also conducted for the 16Π and 14Δ states of WB. The DFT values calculated under various exchange–correlation functionals are reported in the ESI† Table S7. The % DFT errors calculated with respect to the MRCI values are given in the ESI† Tables S8 and S9. Note that all DFT Des reported for the 16Π and 14Δ are with respect to the W(7S) + B(2P) dissociation. The DFT Des of the 16Π and 14Δ states of WB are also shown in Fig. 8 and the ESI† Fig. S3, respectively. Similar to TaB(13Π), all GGA functionals overestimated the De of the 16Π and 14Δ states of WB by 9–14 kcal mol−1 (with respect to MRCI De). Convergence issues were observed for the MGGA MN15-L calculation of 14Δ and are not reported here. The MN15-L performance for the 16Π De is exceptional with less than 2% deviation from the MRCI De. All global GGA hybrid functionals predicted less than 9% errors for both 16Π and 14Δ. Among the MGGA hybrids, the TPSSh carried the minimal errors for the Des for both states and specifically the TPSSh De of the 14Δ state is almost identical to the MRCI value (60.33 versus 60.00 kcal mol−1). Recall that we observed a better performance by the TPSSh for the De of TaB(13Π) as well. The RSH CAM-B3LYP predicted De for both states of WB are in excellent agreement with the MRCI, but the other two RSH functionals (i.e., LRC-ωPBE and ωB97X) carry errors of 7–19%. Overall, the global GGA hybrid B3LYP, MGGA hybrid TPSSh, and RSH CAM-B3LYP were found to represent the Des of 13Π of TaB and 16Π and 14Δ of WB accurately.
The DFT re values of 16Π and 14Δ of WB have less than 0.05 Å deviation from the corresponding MRCI values (Table 4 and the ESI,† Table S7). Similar to TaB(13Π), the deviation of LRC-ωPBE ωe from the MRCI value is 20% greater for WB(14Δ), but it is only ∼5% for the WB(16Π). The DFT ωexe values of WB varied within 3.7–6.7 cm−1. The better performing B3LYP, TPSSh, and CAM-B3LYP for De also showed smaller errors for ωe (ESI,† Tables S8 and S9). Interestingly, the less expensive GGA functionals carried minor errors on ωexe compared to the more expensive functionals.
IV. Conclusions
This work was devoted to investigating the low-lying electronic states of TaB and WB species. Specifically, 10 and 14 electronic states of TaB and WB respectively were analyzed utilizing high-level MRCI, MRCI+Q, and CCSD(T) levels of theory with the correlation-consistent basis sets. The full PECs, equilibrium electronic configurations, spectroscopic parameters, and several energy related properties for these states of TaB and WB are reported. All studied electronic states of TaB and WB lie close in energy (within ∼12 and 21 kcal mol−1, respectively) and several of these are multireference in nature. The lowest-lying 13Π and 15Δ states of TaB are energetically almost degenerate with ∼62 kcal mol−1De with reference to the Ta(4F) + B(2P) ground state fragments and their ordering is sensitive to the level of theory being utilized. Specifically, at the MRCI, MRCI+Q, and A5Z-C-CCSD(T) levels, 13Π (1σ22σ23σ11π3) is slightly stable over 15Δ (1σ22σ23σ11π21δ1) but the ordering is the opposite at the CCSD(T) and A5Z-CCSD(T) levels. The spin–orbit analysis made at the MRCI level predicted the 15Δ0 spin–orbit state to be the ground state of TaB. The zero-point energy corrected D0 of the 15Δ0 (i.e., 60.4 kcal mol−1) is in reasonable agreement with the experimentally measured D0 of the TaB by Merriles et al. (i.e., 62.3 kcal mol−1).31 Similar to TaB, the two most stable electronic states of WB are close in energy (i.e., 16Π and 16Σ+ are separated only by ∼0.6 kcal mol−1) but both MRCI and MRCI+Q levels predicted the 16Π to be the ground electronic state. This is consistent with a previous ab initio analysis reported by Melo and Dixon.12MRCI findings of the 13Π state of TaB and 16Π and 14Δ states of WB were used to evaluate DFT errors on a series of functionals spanning GGA, MGGA, global GGA hybrid, MGGA hybrid, and RSH classes of functionals. Many functionals predicted DFT res with minimal errors. As a family, the less expensive GGA displayed large deviations for Des with respect to MRCI. Among all functionals, the global GGA hybrid B3LYP, MGGA hybrid TPSSh, and RSH CAM-B3LYP predicted Des and ωes are in good agreement with the MRCI Des. The more expensive functionals displayed larger errors for ωexe compared to the cheaper GGAs. Our DFT analysis showcases the difficulty associated with choosing a specific functional for accurate representation of various properties of highly correlated inorganic species and that simply climbing the Jacob's ladder of DFA is not a guarantee for improved accuracy of the predictions for such systems.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of the Los Alamos National Laboratory (LANL) Laboratory Directed Research and Development program Project No. 20240737PRD1 is acknowledged. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001. Prof. Evangelos Miliordos is thanked for the useful discussions about spin–orbit coupling effects.References
- G. F. de Melo, M. Vasiliu, G. Liu, S. Ciborowski, Z. Zhu, M. Blankenhorn, R. Harris, C. Martinez-Martinez, M. Dipalo, K. A. Peterson, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 9392–9407 CrossRef CAS PubMed.
- G. Liu, Z. Zhu, S. M. Ciborowski, I. R. Ariyarathna, E. Miliordos and K. H. Bowen, Angew. Chem., Int. Ed., 2019, 58, 7773–7777 CrossRef CAS PubMed.
- G. Liu, I. R. Ariyarathna, S. M. Ciborowski, Z. Zhu, E. Miliordos and K. H. Bowen, J. Am. Chem. Soc., 2020, 142, 21556–21561 CrossRef CAS PubMed.
- G. Liu, I. R. Ariyarathna, Z. Zhu, S. M. Ciborowski, E. Miliordos and K. H. Bowen, Phys. Chem. Chem. Phys., 2022, 24, 4226–4231 RSC.
- D. M. Merriles, A. London, E. Tieu, C. Nielson and M. D. Morse, Inorg. Chem., 2023, 62, 9589–9601 CrossRef CAS PubMed.
- M. D. Morse, Chem. Rev., 2002, 86, 1049–1109 CrossRef.
- J. D. Mosley, J. W. Young, J. Agarwal, H. F. Schaefer, 3rd, P. Schleyer and M. A. Duncan, Angew. Chem., Int. Ed., 2014, 53, 5888–5891 CrossRef CAS PubMed.
- M. A. Duncan, Rev. Sci. Instrum., 2012, 83, 041101 CrossRef PubMed.
- J. F. Harrison, Chem. Rev., 2000, 100, 679–716 CrossRef CAS PubMed.
- E. E. Claveau and E. Miliordos, Phys. Chem. Chem. Phys., 2021, 23, 21172–21182 RSC.
- I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2019, 21, 24469–24477 RSC.
- G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2023, 127, 1588–1597 CrossRef CAS PubMed.
- I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2024 10.1039/d4cp01847h.
- Y. Gong, M. Zhou and L. Andrews, Chem. Rev., 2009, 109, 6765–6808 CrossRef CAS PubMed.
- E. E. Claveau, S. Sader, B. A. Jackson, S. N. Khan and E. Miliordos, Phys. Chem. Chem. Phys., 2023, 25, 5313–5326 RSC.
- Y. W. Ng, H. F. Pang and A. S. Cheung, J. Chem. Phys., 2011, 135, 204308 CrossRef CAS PubMed.
- D. Tzeli and A. Mavridis, J. Chem. Phys., 2008, 128, 034309 CrossRef PubMed.
- L. F. Ferrao, R. F. Spada, O. Roberto-Neto and F. B. Machado, J. Chem. Phys., 2013, 139, 124316 CrossRef PubMed.
- A. C. Borin and J. P. Gobbo, Int. J. Quantum Chem., 2011, 111, 3362–3370 CrossRef CAS.
- D. Tzeli and I. Karapetsas, J. Phys. Chem. A, 2020, 124, 6667–6681 CrossRef CAS PubMed.
- I. Cernusak, M. Dallos, H. Lischka, T. Muller and M. Uhlar, J. Chem. Phys., 2007, 126, 214311 CrossRef PubMed.
- C. Demetriou, C. E. Tzeliou, A. Androutsopoulos and D. Tzeli, Molecules, 2023, 28, 8016 CrossRef CAS PubMed.
- B. Welch, R. McLean and A. K. Wilson, Mol. Phys., 2023, 121, e2248292 CrossRef.
- D. M. Merriles, E. Tieu and M. D. Morse, J. Chem. Phys., 2019, 151, 044302 CrossRef PubMed.
- D. M. Merriles and M. D. Morse, J. Phys. Chem. Lett., 2023, 14, 7361–7367 CrossRef CAS PubMed.
- E. S. Goudreau, A. G. Adam, D. W. Tokaryk and C. Linton, J. Mol. Spectrosc., 2015, 314, 13–18 CrossRef CAS.
- W. J. Balfour, P. K. Chowdhury and R. Li, Chem. Phys. Lett., 2008, 463, 25–28 CrossRef CAS.
- J.-f Zhen, L. Wang, C.-b Qin, Q. Zhang and Y. Chen, Chin. J. Chem. Phys., 2010, 23, 626–629 CrossRef CAS.
- Y. W. Ng, H. F. Pang, Y. Qian and A. S. Cheung, J. Phys. Chem. A, 2012, 116, 11568–11572 CrossRef CAS PubMed.
- L. F. Cheung, T. T. Chen, G. S. Kocheril, W. J. Chen, J. Czekner and L. S. Wang, J. Phys. Chem. Lett., 2020, 11, 659–663 CrossRef CAS PubMed.
- D. M. Merriles, C. Nielson, E. Tieu and M. D. Morse, J. Phys. Chem. A, 2021, 125, 4420–4434 CrossRef CAS PubMed.
- A. C. Borin, J. P. Gobbo and C. A. Castro, J. Mol. Model., 2014, 20, 2285 CrossRef PubMed.
- L. F. Cheung, G. S. Kocheril, J. Czekner and L. S. Wang, J. Chem. Phys., 2020, 152, 174301 CrossRef CAS PubMed.
- J. Ye, H. F. Pang, A. M. Wong, J. W. Leung and A. S. Cheung, J. Chem. Phys., 2008, 128, 154321 CrossRef PubMed.
- Y. W. Ng, Y. S. Wong, H. F. Pang and A. S. Cheung, J. Chem. Phys., 2012, 137, 124302 CrossRef CAS PubMed.
- K. A. Gingerich, J. Chem. Phys., 1971, 54, 2646–2650 CrossRef CAS.
- I. R. Ariyarathna, C. Duan and H. J. Kulik, J. Chem. Phys., 2022, 156, 184113 CrossRef CAS PubMed.
- V. Kalamse, S. Gaikwad and A. Chaudhari, Bull. Mater. Sci., 2010, 33, 233–238 CrossRef CAS.
- H. Lischka, D. Nachtigallova, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453–2523 CrossRef CAS PubMed.
- I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 12278–12287 RSC.
- N. M. S. Almeida, I. R. Ariyarathna and E. Miliordos, J. Phys. Chem. A, 2019, 123, 9336–9344 CrossRef CAS PubMed.
- I. R. Ariyarathna, N. M. S. Almeida and E. Miliordos, Phys. Chem. Chem. Phys., 2020, 22, 16072–16079 RSC.
- I. R. Ariyarathna and E. Miliordos, J. Quant. Spectrosc. Radiat. Transfer, 2020, 255, 107265 CrossRef CAS.
- N. M. S. Almeida, I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 14578–14586 RSC.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- K. Burke, J. Chem. Phys., 2012, 136, 150901 CrossRef PubMed.
- H. S. Yu, S. L. Li and D. G. Truhlar, J. Chem. Phys., 2016, 145, 130901 CrossRef PubMed.
- W. Kohn, Rev. Mod. Phys., 1999, 71, 1253–1266 CrossRef CAS.
- I. R. Ariyarathna, Y. Cho, C. Duan and H. J. Kulik, Phys. Chem. Chem. Phys., 2023, 25, 26632–26639 RSC.
- L. R. Maurer, M. Bursch, S. Grimme and A. Hansen, J. Chem. Theory Comput., 2021, 17, 6134–6151 CrossRef CAS PubMed.
- J. P. Perdew, Presented in part at the AIP Conference Proceedings, 2001.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- K. R. Shamasundar, G. Knizia and H. J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 242–253 Search PubMed.
- H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Kohn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, 3rd, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- H.-J. Werner and P. J. Knowles, et al., MOLPRO, version 2023.2, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian Inc., Wallingford CT, 2016.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108 CrossRef PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed.
- D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2020, 152, 074102 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- F. J. Devlin, J. W. Finley, P. J. Stephens and M. J. Frisch, J. Phys. Chem., 1995, 99, 16883–16902 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241 Search PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (Version 5.3), National Institute of Standards and Technology, Gaithersburg, MD, 2015, https://physics.nist.gov/asd Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- Avogadro: an open-source molecular builder and visualization tool, Version 1.2.0 edn.
- I. R. Ariyarathna and E. Miliordos, J. Quant. Spectrosc. Radiat. Transfer, 2022, 280, 108074 CrossRef CAS.
- R. S. Mulliken, Rev. Mod. Phys., 1932, 4, 1–86 CrossRef CAS.
- E. Wigner and E. E. Witmer, Z. Phys., 1928, 51, 859–886 CrossRef CAS.
- Z. Ma and K. Balasubramanian, Chem. Phys. Lett., 1991, 181, 467–473 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1 lists MRCI Te and experimental Te values of Ta atom; Table S2 lists MRCI findings of spin–orbit states of TaB; Table S3 lists DFT findings of TaB(13Π); Table S4 lists % DFT errors of various properties of Tab(13Π); Table S5 lists MRCI Te and experimental Te values of W atom; Table S6 lists the % compositions of spin–orbit states of WB; Table S7 lists DFT findings of WB(16Π) and WB(14Δ); Tables S8 and S9 list % DFT errors of various properties of Wb(16Π) and Wb(14Δ); Fig. S1 and S2 illustrate the CASSCF PECs of TaB and WB; Fig. S3 illustrates the DFT De of WB(14Δ). See DOI: https://doi.org/10.1039/d4cp02202e |
| This journal is © the Owner Societies 2024 |