The valence electron affinity of uracil determined by anion cluster photoelectron spectroscopy

Abstract

The unoccupied π* orbitals of the nucleobases are considered to play important roles in low-energy electron attachment to DNA, inducing damage. While the lowest anionic valence state is vertically unbound in all neutral nucleobases, it remains unclear even for the simplest nucleobase, uracil (U), whether its valence anion (U⁻) is adiabatically bound, which has important implications on the efficacy of damage processes. Using anion photoelectron spectroscopy, we demonstrate that the valence electron affinity (EA_V) of U can be accurately measured within weakly solvating clusters, U⁻(Ar)_n and U⁻(N₂)_n. Through extrapolation to the isolated U limit, we show that EA_V = −2 ± 18 meV. We discuss these findings in the context of electron attachment to U and its reorganization energy, and more generally establish guidance for the determination of molecular electron affinities from the photoelectron spectroscopy of anion clusters.

---

Introduction

Low-energy electrons can induce strand breaks in DNA, even at electron energies below the ionization energy of individual components and below the dissociation energies of covalent bonds in the biopolymer.^1–3 The initial step is believed to involve the electron attachment to valence states of components of DNA, forming temporary negative ions that can then lead to bond-rupture through a long-range dissociative electron attachment process.^4–6 The nucleobases in particular have received much attention as the site for initial electron attachment via their low-lying valence states that are of π* character.^6–10 In the gas phase, electron transmission spectroscopic experiments have mapped out the location of these π* resonances.^11,12 However, such experiments are not sensitive to the subsequent dynamics that could stabilize the generated temporary negative ions. In particular, nuclear dynamics can compete with autodetachment to decrease the energy gap between the anion valence state and the neutral ground state, leading to a highly reactive radical anion that is long-lived, especially if the anion valence π* state is adiabatically bound. So, a natural question then arises: what is the adiabatic electron affinity of the lowest valence state, EA_V, of a nucleobase? Even for the simplest nucleobase, uracil (U), this remains a debated question. Here, we seek to answer this question by applying anion photoelectron spectroscopy to a range of uracil clusters to determine EA_V of U.

The U nucleobase forms a stable anion in the gas phase,^13,14 where the excess electron is very weakly bound in a diffuse orbital by the strong dipole moment of the molecule (μ ≈ 4.5 D). However, such a dipole-bound state (DBS)¹⁵ is not a valence state and, while non-valence states can partake in electron attachment at very low electron energies^16–23 and population can pass from valence to non-valence state and vice versa,^24,25 they are not thought to be relevant in the context of DNA damage because the environment will disrupt the orbital.²⁶ From electron transmission spectroscopy, the lowest-energy shape resonance, , is populated with incident electron energies around 220 meV.¹¹ Upon geometric relaxation, electronic states may stabilize by hundreds of meV, and the valence state was suspected to be adiabatically bound with respect to electron loss. However, anion photoelectron spectroscopic studies reported observation of only the DBS of U⁻.¹³ This was rationalized as the DBS being more stable than the state, and an upper-bound for the EA_V was found to be EA_V < EA_D ≈ +90 meV, where EA_D is the electron binding energy of the uracil anion in its DBS. On the other hand, long-lived U⁻ in its state was observed to form via Rydberg electron transfer to U(Ar)_n clusters, following evaporation of the solvating argon atoms.²⁷ This was presented as confirmation that the state is adiabatically bound with respect to electron loss, and they reported EA_V = +62 ± 32 meV.²⁷ Computationally, there have been a wide range of EA_V values reported ranging from negative^28–33 to positive.^6,34–40 The seemingly most comprehensive treatment has been performed by Gu et al., who followed the W1BD composite method⁴¹ and found EA_V = +24 ± 13 meV,⁴² suggesting a weakly adiabatically bound 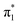valence state.

Solvation stabilizes valence-bound anions to a greater degree than dipole-bound anions.⁴³ Consequently, the ground state of uracil–water cluster anions, U⁻(H₂O)_n, is observed to be the valence state, as easily distinguished in photoelectron spectra by its greater spectral width compared to the signal arising from a DBS.^44–46 By plotting the n-dependent EA_V of these clusters, it therefore becomes possible to extrapolate towards n = 0 and obtain an estimate for the EA_V of U. Two studies have performed this procedure, both yielding relatively large positive adiabatic electron affinities: EA_V = +150 ± 120 meV⁴⁴ and EA_V = +159 meV⁴⁶ (uncertainty not stated). However, the 0–0 transition for photodetachment from the valence state could not be discerned clearly for any of the clusters, and moreover, the validity of performing such an extrapolation is questionable. Water molecules interact very strongly with the uracil anion through a multitude of interactions (e.g. hydrogen bonding and dipolar) so that a simple linear extrapolation is unlikely to be valid even for small clusters. In principle, these concerns can be alleviated through the study of uracil–solvent cluster anions with more weakly interacting solvent molecules. To this end, we performed anion photoelectron spectroscopy on two different series of uracil–solvent cluster anions: U⁻(Ar)_n and U⁻(N₂)_n, and compared our findings to results on U⁻(H₂O)_n. This approach, utilizing spectroscopic tags, also offers colder clusters and allowed us to unambiguously identify the 0–0 transition for photodetachment from the 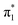valence state. Our determination for EA_V is broadly in line with the ‘best’ computational predictions,^6,42 and expands upon the results from Rydberg electron transfer experiments.²⁷ It also provides a rigorous assessment and establishes protocols for the determination of small (be they positive or negative) adiabatic electron affinities using photoelectron spectroscopy of anion clusters.

Methods

Experimental

The experimental apparatus has been described in detail elsewhere.⁴⁷ A solid sample of uracil (U) was placed inside a pulsed Even–Lavie valve⁴⁸ and heated to approximately 220 °C. The valve was backed with argon or nitrogen at ∼10 bar pressure to produce the desired series of molecular clusters, U(Ar)_n or U(N₂)_n. To induce formation of uracil–water clusters, U(H₂O)_n, a drop of water was added to the backing line. The molecular beam passed through a (thoriated tungsten) filament ring ionizer held at high current, attaching electrons and generating the corresponding progressions of cluster anions. A Wiley–McLaren time-of-flight mass spectrometer⁴⁹ separated the cluster anions by their mass-to-charge ratio (m/z), and the targeted anion packet was intersected with a delayed laser pulse at the center of a velocity map imaging electron spectrometer. Nanosecond laser pulses were sourced from an Nd:YAG laser (Quantel, Q-smart 450), at the fundamental (1064 nm) or second harmonic (532 nm) wavelengths. Photoelectron spectra and angular distributions were reconstructed from the resulting photoelectron images using the polar onion peeling (POP) algorithm.⁵⁰ The well-known energetics of atomic I⁻ were used for calibration, and full details on our calibration process are included in the ESI.†

Computational

Density functional theory (DFT) tends to produce a bound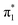 state of the uracil anion,⁴² making it an ideal choice for calculating the vibronic spectrum of valence U⁻. We opted for the long-range corrected CAM-B3LYP functional,⁵¹ with the diffuse aug-cc-pVDZ Dunning basis set.⁵² By omitting the extra-diffuse basis functions that are often added into calculations on U⁻, the optimized anion geometry settled into the buckled valence state, and a minimum was confirmed through vibrational frequency analysis. The planar equilibrium structure of neutral uracil was also calculated, allowing the vibronic spectrum associated with the S₀ ← 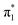transition to be computed. Each transition was broadened by a Gaussian function with standard deviation σ = 20 meV, and summed to produce a representative photoelectron spectrum. The simulated spectrum was shifted to align with the measured 0–0 transition of U⁻(Ar)₃. All calculations were performed with Gaussian 16.⁵³

Results and discussion

Photoelectron spectra of uracil–argon cluster anions

Photoelectron spectra of a series of uracil–argon cluster anions, U⁻(Ar)_n where n ≤ 25, were acquired using nanosecond laser pulses with photon energy hν = 1.165 eV. Fig. 1(a) shows a selection of the spectra corresponding to the smaller clusters, n ≤ 9. Photoelectron signal is plotted in terms of electron binding energy, defined as eBE = hν − eKE, where eKE is the measured electron kinetic energy. As found in earlier photoelectron spectroscopy experiments,^13,44,45 the photoelectron spectrum of U⁻ exhibits a single, sharp peak at low electron binding energy. This is the characteristic photoelectron signal arising from photodetachment of a DBS to reach the ground-state neutral, as the excess electron only weakly interacts with the neutral core. We additionally confirm that the electron emission is highly anisotropic (β₂ = +2.0, see Fig. 1(b)) as expected from an s-like non-valence orbital.^54,55 We determine that EA_D = +75 ± 6 meV (details of our calibration process in the ESI†).

Fig. 1 (a) Photoelectron spectra of uracil–argon cluster anions, U⁻(Ar)_n, acquired using nanosecond laser pulses with hν = 1.165 eV. Blue arrows highlight the electron binding energy (eBE) associated with the 0–0 transition from the valence state to the neutral ground state. (b) Corresponding photoelectron images from dipole-bound U⁻ (left) and valence-bound U⁻(Ar)₃ (right). The fixed direction of laser polarization vector is represented by ε.

The photoelectron spectra of U⁻(Ar)₁ and U⁻(Ar)₂ are similar to the spectrum of U⁻. The low-energy electrons (eBE > 0.5 eV) were produced from small contamination of uracil–water cluster anions of similar masses to U⁻(Ar)_1–2, but given this signal does not interfere with the low binding energy peak associated with the dipole-bound state, this signal has no impact on the current discussion. It is clear that formation of the DBS of U⁻ remains favorable in the presence of one or two argon atoms, and solvation appears to only increase EA_D by a few meV per argon atom. Upon the addition of a third solvating argon atom, the photoelectron spectrum changes drastically. U⁻(Ar)₃ exhibits a broad, structured photoelectron signal, with a far more isotropic photoelectron angular distribution (β₂ ≈ +0.4, see Fig. 1(b)). This arises from photodetachment of the 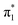valence state and suggests that it has become the ground electronic state of the anion due to stabilization from the solvating argon atoms and agrees well with an earlier photoelectron spectroscopic measurement of the valence state of U⁻(Xe)₁,⁴⁵ which also shows a broad feature with underlying vibrational structure (although the structured peak was partially obscured by photoelectron signal arising from some accompanying DBS). The considerable spectral width of the detachment feature arises from the substantially different equilibrium geometries between the anionic and neutral form of the uracil molecule: the neutral molecule is planar while the anion becomes non-planar.³³

Despite the disparate geometries, it appears that a peak corresponding to the 0–0 transition is resolved in Fig. 1 (blue arrows), which represents a direct measure of EA_V associated with the state of U⁻(Ar)_n. To reinforce assignment of the 0–0 transition peak, Fig. 2 recasts the photoelectron spectrum of U⁻(Ar)₃ with an overlay of a computed (DFT/(U)CAM-B3LYP/aug-cc-pVDZ) vibronic photodetachment spectrum of the valence state of U⁻. As the excess charge is expected to localize on the nucleobase, exclusion of the argon in the calculations was considered acceptable. Indeed, the vibrational structure displayed in photoelectron spectra of the larger U⁻(Ar)_n>3 clusters are very similar, demonstrating the negligible effect of the argon atoms. The calculated vibronic spectrum shows good overall agreement, although the vibrational structure of the experimental spectrum was not perfectly captured. Nevertheless, the dominant vibrational mode can be clearly identified as v₁₅, which corresponds to an out-of-plane motion (displacement vector shown in ESI†). Some disparity might be expected due to differences in anion–neutral geometries, which results in a broad Franck–Condon window made up of many combined excitations, and the neglect of anharmonicity. In the context of this study, it is more critical that we can conclude that the 0–0 transition is clearly distinguishable in the photoelectron spectra of U⁻(Ar)_n, and therefore the associated EA_V can be accurately determined for each cluster.

Fig. 2 Measured photoelectron spectrum of U⁻(Ar)₃ (black), overlaid with the calculated (CAM-B3LYP/aug-cc-pVDZ) vibronic photodetachment spectrum (red) of the valence state of U⁻.

With increasing cluster size, the 0–0 transition shifts to higher electron-binding energy. This demonstrates that EA_V increases with each incrementally added argon atom, directly reflecting the imposed anion-stabilizing effect. In particular, U⁻ is stabilized through favorable interactions between the excess negative charge and the polarizability of the argon atoms. From the measured 0–0 transition energies, it is possible to extrapolate the measured EA_V(n) to the isolated U⁻ limit (i.e. n = 0), obtaining an estimate for EA_V of U. However, in order to perform such an extrapolation, the behavior of EA_V(n) should be considered in detail.

Electron-binding energy extrapolation of valence-bound anions in solvating clusters

Fig. 3 compiles the argon-induced anion-stabilizing effect, E_stab(n) = EA_V(X(Ar)_n) − EA_V(X), from a number of photoelectron spectroscopic studies on valence-bound X⁻(Ar)_n clusters, where X = O,⁵⁶ NO,⁵⁷ Cl,⁵⁸ Br,⁵⁹ I,⁵⁹ I₂,⁶⁰ and pyrazine.⁶¹ It is apparent that the more electron-dense anions are stabilized to a greater degree by the clustered argon atoms. The trend in E_stab(n) (and therefore also EA_V) for each anion cluster appears approximately linear at small n, but curves slightly at larger n, where the E_stab(n) increases by a smaller amount per successive argon atom added. This curvature has been explained to be a result of various many-body interactions (mostly between the charged anion and the clustered argon atoms),^58,59 ultimately adding a small destabilizing effect to the anion with respect to the neutral form. Through least-squares fitting, we found the power function E_stab(n) ∼ n^0.95 to reproduce the exhibited curvature very well for each series of anion clusters. The only exception to this is O⁻(Ar)_n, which also interacts most strongly with the solvating Ar atoms. In the case of U, E_stab(n) for U⁻(Ar)_n is the most comparable to Br⁻(Ar)_n, suggesting that the U⁻–Ar interaction strength is similar to Br⁻–Ar and the above power function is appropriate to use for extrapolation purposes.

Fig. 3 Stabilization energy E_stab = EA_V(X(Ar)_n) − EA_V(X), associated with the clustering of n argon atoms to different anions, X. Circles and triangles are used to distinguish between atomic and molecular anions, respectively. The dotted lines show fitted power functions of n associated with each series of anion clusters. For errors on specific data points, the author is directed to the relevant studies. Adapted from ref. 56–61, with the permission of AIP publishing.

Determination of the electron affinity of the valence state of uracil

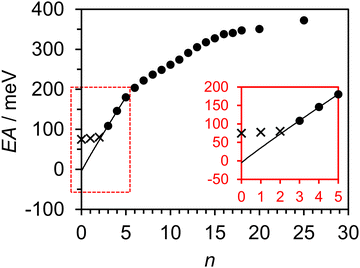
Fig. 4 presents the experimentally determined EA_V associated with each measured U⁻(Ar)_n cluster, demonstrating a slightly curved behavior at smaller cluster size. There is a clearly observable ‘kink’ in the trend around the U⁻(Ar)₁₂ cluster, which is indicative of the (partial) closing of a solvation shell around U⁻.^56,57 For now, we focus on the EA_V values of the small clusters. The EA_V values of U(Ar)_3–5 were fit to the empirical function EA_V(n) = k_Arn^0.95 + EA_V, where k_Ar was an optimized constant associated with the interaction strength between U⁻ and Ar. Only clusters consisting of up to five argons were included in the fit, since a second less-defined kink may be present at n = 6. The fitting function, extrapolated to n = 0, is shown in Fig. 4. Extrapolation to n = 2 suggests that the EA_V is below the electron binding energy of the DBS for this cluster, consistent with the absence of the valence state signal in the photoelectron spectrum of U⁻(Ar)₂. From the full extrapolation, we find that EA_V = −6 ± 24 meV, where the uncertainty in EA_V was determined by the combined contributions of our experimental resolution and the extrapolation process.⁶² Unfortunately, our results on the U⁻(Ar)_n clusters were unable to conclusively determine whether the 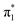state of U⁻ is adiabatically bound or not. Nevertheless, we can conclude that EA_V is very small. By directly observing the 0–0 transition associated with the valence state in weakly perturbed clusters, this extracted value is currently the most accurate experimentally-determined EA_V, and is lower than, but within the error of the most reliable theoretical determination.⁴²

Fig. 4 Adiabatic electron affinity (EA) of uracil–argon clusters, U(Ar)_n, extracted from photoelectron spectroscopy of the corresponding anions. Dots indicate EA_V(n) associated with the valence state of U⁻(Ar)_n, whereas the crosses show the measured electron binding energies of the DBS anions, EA_D. An extrapolation using the EA_V(n) of U(Ar)_3–5 is overlaid (black line). Inset is a magnified view for small n (red dashed area). Uncertainties in each data point were smaller than the size of the data point symbols, and were below ±10 meV for n = 0–5.

Comparison with other solvent clusters and the caveats of using strongly interacting solvents

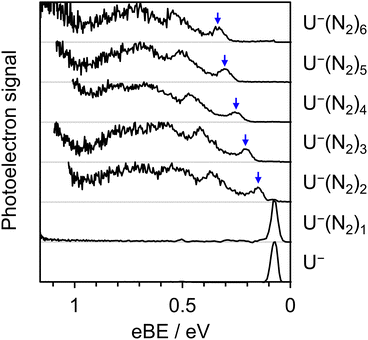
Further estimates for EA_V can be obtained by repeating the above procedure with different solvent molecules. Fig. 5 displays photoelectron spectra (hν = 1.165 eV) of U⁻(N₂)_n, with n ≤ 6. The vibrational structure in the detachment from the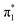 valence state is very similar to that observed from U⁻(Ar)_n, allowing EA_V(n) to be extracted from the distinct 0–0 transition feature in each spectrum. The nitrogen molecules interact more strongly with the uracil anion than do the argon atoms, as reflected in the greater degree of stabilization per added solvent molecule, as well as in the observation of the valence state for U⁻(N₂)₂. Despite the similar polarizabilities of N₂ and Ar,⁶³ the inherently anisotropic charge distribution of diatomic nitrogen allows for additional interactions with U⁻, e.g. through its significant quadrupole.⁶⁴ The observed 0–0 transitions in the photoelectron spectra of U⁻(N₂)_n are also broader than in the case of U⁻(Ar)_n, and so the uncertainty associated with finding the EA_V was slightly larger. This spectral broadening again correlates with stronger interactions between the anion and N₂, consistent with previous studies on NO⁻ cluster anions.⁵⁷ In particular, stronger interactions between U⁻ and N₂ (compared to U⁻ and Ar) can act to both: encourage excitation of lower-frequency vibrational modes which cannot be spectrally resolved; and increase the degree of structural rearrangement in the transition from anion to neutral, leading to a broader Franck–Condon window. Additionally, some of the broadening may be attributed to the presence of multiple structural isomers for each anion cluster, as the N₂ molecules preferentially bind to different sites of the uracil anion (with facile interchange), resulting in subtly different binding energies for the excess electron between isomers.

Fig. 5 Photoelectron spectra of uracil–nitrogen cluster anions, U⁻(N₂)_n, acquired using nanosecond laser pulses with hν = 1.165 eV. Blue arrows highlight the electron binding energy (eBE) associated with the 0–0 transition from the valence state to the neutral ground state.

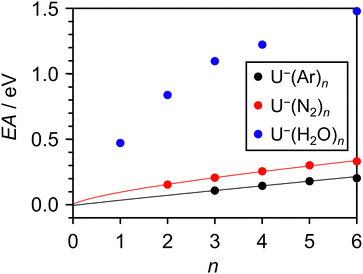
Fig. 6 presents the extracted EA_V(n) of the U(N₂)_n clusters, alongside the earlier results on U(Ar)_n. Over the range of small clusters measured, the curvature exhibited in the plot of EA_V(n) was exacerbated with the N₂ solvent. Once more, this follows from stronger intermolecular forces within the clusters. In fact, the strength of interaction between U⁻ and N₂ is comparable to the O⁻(Ar)_n anion clusters shown in Fig. 3, which also expressed a pronounced curvature (compared to the more weakly interacting anion–argon clusters). However, there is an important difference between the U⁻(N₂)_n and O⁻(Ar)_n: the latter series of clusters are comprised of atomic subunits, whereas both uracil and molecular nitrogen are polyatomic. Therefore, the many-body interactions that govern the exhibited curvature of the O⁻(Ar)_n clusters are completely absent in O⁻(Ar)₁, and so linear behavior is expected in the range 0 ≤ n ≤ 2 for these atomic clusters. In the case of U⁻(N₂)_n, the curvature results from a combination of many intermolecular interactions (e.g. between dipoles, quadrupoles, polarizabilities), which all remain present even in U⁻(N₂)₁. Consequently, there is no reason to suspect the exhibited curvature not to persist to the n = 0 limit. We found a relationship, EA_V(n) = k_N2n^0.7 + EA_V, to fit the data appropriately (fit included in Fig. 6), with the optimized coefficient k_N2 > k_Ar. A value EA_V = +1 ± 26 meV was extracted, consistent with the EA_V derived from the U⁻(Ar)_n series of clusters, and providing further evidence that the excess electron in the valence state of U⁻ is very weakly bound, if at all.

Fig. 6 Adiabatic electron affinities (EA) for a selection of uracil–solvent clusters, U(Ar)_n (black), U(N₂)_n (red), and U(H₂O)_n (blue), extracted from photoelectron spectroscopy of the corresponding anions. Extrapolations are overlaid as solid lines. Uncertainties in each data point were smaller than the size of the data point symbols for the U⁻(N₂)_n and U⁻(H₂O)₁ clusters. The uncertainties for U⁻(H₂O)_2–6 were larger (due to absence of the 0–0 transition), around 0.1 eV.

Solvation-induced stabilization of U⁻ has been the most extensively studied in uracil–water cluster anions,^44,46,65 where even a single water molecule sufficiently stabilizes the valence state to become the ground state of the uracil anion. A photoelectron spectrum of U⁻(H₂O)₁ is shown in Fig. 7 (hν = 1.165 eV), where the 0–0 transition peak arising from the valence state was distinct but broad. Through its characteristic spectral signature, the formation of the solvent-stabilized DBS of U⁻(H₂O)₁ in our ion source was also observed; it will be the subject of a forthcoming communication and is briefly discussed further below. From the 0–0 transition associated with the valence state, the solvating power of H₂O is demonstrably much greater than either Ar or N₂. Indeed, the anion-stabilizing effect of a single water molecule exceeded that of 25 argon atoms: EA_V(U(H₂O)₁) > EA_V(U(Ar)₂₅). It is unsurprising that the interactions of U⁻ with H₂O are so vastly stronger, as clustering with water is additionally supported by long-range charge–dipole interactions as well as hydrogen bonding.

Fig. 7 Photoelectron spectra of small uracil–water cluster anions, U⁻(H₂O)_n, acquired using nanosecond laser pulses with hν = 1.165 eV (n = 0, 1) and hν = 2.230 eV (n = 2, 3). Blue arrows highlight the electron binding energy (eBE) associated with the 0–0 transition from the valence state to the neutral ground state. The contribution from the DBS of U⁻(H₂O)₁ is highlighted in red.

Larger clusters of U⁻(H₂O)_n≥2 did not produce distinguishable 0–0 transition features due to further spectral broadening, and therefore each EA_V(n) associated with these clusters was estimated from the onset of the Gaussian-like photoelectron signal (taken as 10% of peak height). The resulting EA_V(n) values are also displayed in Fig. 6, and exhibit an even more pronounced curvature with n. We do not present an extrapolation to the monomeric limit (n = 0) using the uracil–water cluster EA_V(n) for several reasons: (i) there was no simple power function which suitably captured the experimental data; (ii) the 0–0 transition was not observable in all but one of the clusters, obscuring accurate determination of the EA_V; and (iii) water molecules are far more selective towards the binding site of U⁻ (or to other H₂O molecules in the cluster), largely due to their tendency for hydrogen bonding. Nonetheless, linearly extrapolating the EA_V(n) of the smallest U⁻(H₂O)_n clusters results in an estimated EA_V ≈ +177 meV, similar to the electron affinities obtained in earlier studies that performed this procedure.^44,46 Our results on the U⁻(Ar)_n and U⁻(N₂)_n clusters highlight the problems associated with performing such a linear extrapolation: in particular, the EA_V for some of the argon- and nitrogen-stabilized clusters are measurably lower than 177 meV. We conclude that, in general, linear behavior of the electron binding energy should not be assumed in clusters containing a polyatomic anion and a strongly solvating species such as water. In the case of U⁻, this leads to systematic errors up to hundreds of meV.

General discussion

The observed vibrational structure in the photoelectron spectra of U⁻(Ar)_n and U⁻(N₂)_n also provides insight into the nuclear rearrangement undergone by uracil in the transition from its neutral to anionic valence state. The vertical detachment energy (VDE) of each anion cluster was extracted from the eBE at which there was most (fitted) photoelectron signal, and it was found to decrease with smaller n at the same rate as EA_V(n). From the appropriate extrapolation, we find that VDE(U⁻) = +210 ± 30 meV. The extracted detachment energies of U⁻ (EA_D, EA_V, and VDE) can be used to draw a schematic of the relevant diabatic potential energy surfaces along the ring-buckling coordinate that connects the neutral (S₀) and anionic () equilibrium geometries (Fig. 8). Encouragingly, electron transmission spectroscopy has measured the vertical attachment energy (VAE) of the valence state of U to be very close to our extracted VDE:VAE = 220 meV.¹¹ Assuming the same harmonic diabatic surfaces for S₀ and valence states allows us to connect the buckling coordinate in a consistent picture as shown in Fig. 8. In the context of low-energy electron attachment into the 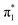resonance, U⁻ forms in the planar geometry, but will rapidly stabilize via the buckling distortion. With only the slightest buckling away from planarity, the valence state energy approaches that of the neutral S₀ state and then becomes vertically bound with respect to electron loss, greatly enhancing the lifetime of the generated anion. Regardless of whether the state is adiabatically bound in its minimum energy (fully-buckled) structure (i.e. EA_V < 0 or EA_V > 0), its vertical binding exceeds 200 meV and U⁻ formed by electron attachment via the resonance is expected to persist on a timescale greatly surpassing the sub-picosecond lifetimes associated with shape resonance autodetachment.^19,66,67

Fig. 8 Schematic showing diabatic potential energy surfaces of neutral (S₀) and anionic ( and DBS) uracil along the ring-buckling coordinate, Q, treated within a harmonic approximation. Energy gaps reflect the experimentally determined values, and the gray region represents the electron detachment continuum. Uncertainty in the measured value of EA_V is shown with blue bars.

A competing decay pathway for the state is through internal conversion to the DBS.²⁴ Within the harmonic approximation displayed in Fig. 8, an energetic barrier is expected to separate the two states, limiting the rate of internal conversion from the state to the DBS. Numerous computational studies have attempted to calculate the height of this barrier, with estimates ranging from tens to hundreds of meV.^32,38,68 Within our simple linear response model in Fig. 8, it appears the barrier height is on the order of 10 s of meV. This barrier may have held important consequences for the earlier Rydberg electron transfer experiments that had suggested a positive value for the EA_V.²⁷ These experiments attached electrons to U(Ar)_n clusters, and following evaporation of the clustered argon atoms, formed U⁻ in the state. U⁻ was kinetically trapped in the valence state for many microseconds (in order to be mass-separated), which is consistent with our combined observations of (i) a large vertical binding energy (VDE), and (ii) the suggested presence of a barrier between the valence- and dipole-bound states. We note that the lower threshold of their stated EA_V (+30 meV) was derived from the intermolecular binding energy between uracil and argon, which was explained to be less than EA_V such that even the smallest generated U⁻(Ar)_n clusters could then have sufficient internal energy to evaporate off the clustered argon atom(s), but not enough to undergo autodetachment. Our extracted EA_V for U⁻ is also consistent with this picture, despite being less than 30 meV. Our extrapolation predicts that EA_V ∼ 35 meV for U⁻(Ar)₁ so that both electron and argon loss result in similarly stable products. It should also be noted that these loss channels will differ in their kinetics. In particular, electron loss from the valence state of any U⁻(Ar)_n cluster is driven by a buckled-to-planar transformation of the uracil ring, which is expected to be inhibited by an energetic barrier. Therefore, we do not expect autodetachment to occur for up to many microseconds, giving sufficient time for competitive loss of the solvating argon.

Nuclear rearrangement associated with electron attachment to the state has been previously explored in U⁻(H₂O)_n clusters,^65,69 where the reorganization energy λ was estimated from the difference between the adiabatic and vertical detachment energies, λ = VDE − EA_V. Hydration of the uracil anion was found to significantly enhance the reorganization energy, since the preferred orientation of the water molecules is very sensitive to the overall charge state of the uracil. Extrapolation of λ(n) to the aqueous limit (n → ∞) culminated in an estimate of λ_(aq) ≈ 1.2 eV for U_(aq).⁶⁵ This can be decomposed into two separate contributions: λ_(aq) = λ_IS + λ_OS; where λ_IS represents the (inner-sphere) reorganization energy of the buckling uracil ring, and λ_OS represents the (outer-sphere) reorganization energy of the surrounding water molecules.⁶⁹ The first term, λ_IS, is independent of the solvent and can therefore be accurately extracted from the EA_V and VDE of U⁻, reported here (i.e.Fig. 8). We establish that λ_IS = 0.2 eV and conclude that the dominant contribution to the neutral-to-anion reorganization energy of U_(aq) arises from restructuring of the intermolecular hydration sphere (λ_OS ≈ 1.0 eV), i.e. from the solvent response, rather than the solute. This differs to our previous prediction that the inner- and outer-sphere reorganization energies were roughly equal, which we arrived at by approximating λ_IS as the λ of U⁻(H₂O)₁.⁶⁹ As clearly demonstrated here, even a single water molecule has a substantial effect on the reorganization energy of U⁻, and this approximation does not hold and underscores the dramatic limitations of cluster extrapolations using strongly-interacting solvent molecules.

Returning to our photoelectron spectrum of U⁻(H₂O)₁ shown in Fig. 7, signal arising from both the valence- and dipole-bound anions was present. This is in contrast to earlier photoelectron spectroscopic studies,^44–46 which observed detachment from only the valence state. Our observed ratio of DBS to valence state signal was sensitive to the ion source conditions, indicating that the DBS of U⁻(H₂O)₁ was generated in the source region of our experiment, and then persisted for the hundreds of microseconds that elapsed prior to photodetachment. But why was the DBS so long-lived in our experiment? From Fig. 7, the EA_D of U(H₂O)₁ was measured to exceed 200 meV and, thus, the DBS is clearly stable against autodetachment. On the other hand, EA_D < EA_V for U(H₂O)₁, such that internal conversion from the DBS to the valence state (through buckling of the uracil ring and reorganization of the water molecule) is energetically favorable. Hence, we conclude that there is a significant energetic barrier separating the DBS from the state, allowing the DBS to be kinetically trapped for the duration of our experiment (note that the initial electron attachment in the source is to a planar neutral U). We also observed a very small amount of DBS signal from U⁻(N₂)₂ (which also produced valence anions), indicating that some kinetic trapping was possible in the more weakly solvated clusters too. Since the relative DBS population of U⁻(N₂)₂ appeared to be much smaller than that of U⁻(H₂O)₁, it is likely that the barrier separating the DBS from the valence state is larger when the solvent is water, as may be expected from the strong hydrogen-bonding interactions that can act to inhibit the buckling motion. There is also an interesting question regarding the position of the clustered water molecule in the DBS of U⁻(H₂O)₁; if the water molecule were to solvate the DBS orbital rather than the uracil molecule, one may expect a greater reorganization between the dipole- and valence-bound states, and hence a greater dividing barrier. This will be considered further in a future study.

As demonstrated for U⁻, extrapolating adiabatic electron affinities of anion–solvent clusters must be performed with due consideration of the strength of the anion–solvent interaction. Strong interactions lead to significantly non-linear behavior, and a linear extrapolation to n = 0 is inappropriate. If the interactions are too weak, then many solvent molecules may be required to render the anion a bound (or kinetically-trapped metastable) state, causing greater uncertainty in the extrapolated EA. For instance, U⁻(He)_n and U⁻(Ne)_n anion clusters can also provide an estimate for the EA_V of U, but the weak solvating power of He and Ne means that the valence state is unlikely to be observed until n ≥ 4, necessitating a more extreme extrapolation that may lead to poorer determination of EA_V. Overall, the ideal solvent must strike a balance between strongly and weakly solvating the anion, permitting an approximately linear extrapolation from small clusters. In addition to argon and nitrogen, xenon also appears to be a suitable solvent probe for U⁻; as mentioned earlier, the valence state of U⁻(Xe)₁ had been measured with photoelectron spectroscopy, although with some obfuscation from the co-generated DBS.⁴⁵ From our clear characterizations of the 0–0 transition present in the photoelectron spectra of U⁻(Ar)_n and U⁻(N₂)_n, we can infer that EA_V(U(Xe)₁) ≈ 120 meV.⁴⁵ By then comparing the general anion solvating power of xenon with that of other solvent molecules,⁵⁷ which is stronger than argon but weaker than water, it appears that an extrapolation from the electron affinities of U⁻(Xe)_n is also likely to yield a value of EA_V close to zero.

Conclusions

The valence state of the uracil anion is significantly stabilized by clustered solvent molecules, even in the weakly-interacting case of U⁻(Ar)_n. Earlier estimates for the EA_V of isolated uracil utilized linear extrapolation techniques from the EA_V(n) of uracil–water clusters, in which the solvent interacts strongly with the nucleobase anion. We demonstrate that such linear extrapolations are, in general, not accurate and should not be applied in the context of a polyatomic anion and a strongly-interacting solvent. Instead, weakly-interacting solvent molecules induce a nearly linear increase in the EA_V(n), and can be used to perform a more suitable extrapolation. Our photoelectron spectroscopic measurements on U⁻(Ar)_n and U⁻(N₂)_n clusters distinguished the 0–0 transition corresponding to photodetachment of the valence state of U⁻, allowing for an accurate determination of the associated EA_V. With accountment for the subtle non-linearity in EA_V(n) with increasing cluster size, our extrapolated value for the adiabatic electron affinity associated with the state of bare uracil, EA_V = −2 ± 18 meV, using the combined values from U⁻(Ar)_n and U⁻(N₂)_n. Within the uncertainty of our experiment, we are unable to conclude that the state is adiabatically stable, which has elsewise been suggested by Rydberg electron transfer experiments,^27,70 and extrapolations from U⁻(H₂O)_n.^44,46 Nonetheless, our results demonstrate the magnitude of EA_V is very small and that any potential binding of the excess electron in the valence state of U⁻ must be very weak. This finding appears to reveal why computational attempts to calculate (the sign of) EA_V have shown such disagreement. Nevertheless, our reported value is close to the most rigorous computational efforts.⁴² We also offer insight into the barrier connecting the valence and non-valence states along the nuclear buckling coordinate. Our results are consistent with electron transmission spectroscopy, which, taken together with current insight, provides a direct measure of the intrinsic reorganization energy associated with U + e⁻ → U⁻ of λ_IS = 0.2 eV.

Data availability

The data which support the findings of this study will be available online at https://zenodo.org/10.5281/zenodo.12571786.

Conflicts of interest

The authors have no conflicts to declare.

Acknowledgements

This work was funded by the EPSRC under grant EP/V007971/1 (EMB, JRRV), the OP JAK project no. CZ.02.01.01/00/22_008/0004649 (QUEENTEC) (JRRV), and the Durham University for a Scholarship (CJC). For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising.

References

1. B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660.
2. F. Martin, P. D. Burrow, Z. Cai, P. Cloutier, D. Hunting and L. Sanche, Phys. Rev. Lett., 2004, 93, 068101.
3. C. Liu, Y. Zheng and L. Sanche, Photochem. Photobiol., 2022, 98, 546–563.
4. J. Simons, Acc. Chem. Res., 2006, 39, 772–779.
5. J. Gu, Y. Xie and H. F. Schaefer, J. Am. Chem. Soc., 2006, 128, 1250–1252.
6. J. Gu, J. Leszczynski and H. F. I. Schaefer, Chem. Rev., 2012, 112, 5603–5640.
7. M. A. Huels, I. Hahndorf, E. Illenberger and L. Sanche, J. Chem. Phys., 1998, 108, 1309–1312.
8. S. Denifl, S. Ptasińska, M. Probst, J. Hrušák, P. Scheier and T. D. Märk, J. Phys. Chem. A, 2004, 108, 6562–6569.
9. S. Denifl, S. Ptasińska, G. Hanel, B. Gstir, M. Probst, P. Scheier and T. D. Märk, J. Chem. Phys., 2004, 120, 6557–6565.
10. D. Svozil, P. Jungwirth and Z. Havlas, Collect. Czech. Chem. Commun., 2004, 69, 1395–1428.
11. K. Aflatooni, G. A. Gallup and P. D. Burrow, J. Phys. Chem. A, 1998, 102, 6205–6207.
12. A. M. Scheer, K. Aflatooni, G. A. Gallup and P. D. Burrow, Phys. Rev. Lett., 2004, 92, 068102.
13. J. H. Hendricks, S. A. Lyapustina, H. L. de Clercq, J. T. Snodgrass and K. H. Bowen, J. Chem. Phys., 1996, 104, 7788–7791.
14. C. Desfrançois, H. Abdoul-Carime and J. P. Schermann, J. Chem. Phys., 1996, 104, 7792–7794.
15. C. Desfrançois, H. Abdoul-Carime and J.-P. Schermann, Int. J. Mod. Phys. B, 1996, 10, 1339–1395.
16. T. Sommerfeld, J. Phys.: Conf. Ser., 2005, 4, 245.
17. M. A. Yandell, S. B. King and D. M. Neumark, J. Am. Chem. Soc., 2013, 135, 2128–2131.
18. J. P. Rogers, C. S. Anstöter and J. R. R. Verlet, Nat. Chem., 2018, 10, 341–346.
19. A. Kunin and D. M. Neumark, Phys. Chem. Chem. Phys., 2019, 21, 7239–7255.
20. J. N. Bull, C. S. Anstöter and J. R. R. Verlet, Nat. Commun., 2019, 10, 5820.
21. G. Liu, S. M. Ciborowski, J. D. Graham, A. M. Buytendyk and K. H. Bowen, J. Chem. Phys., 2020, 153, 044307.
22. D. H. Kang, J. Kim, H. J. Eun and S. K. Kim, J. Am. Chem. Soc., 2022, 144, 16077–16085.
23. D. H. Kang, J. Kim, H. J. Eun and S. K. Kim, Acc. Chem. Res., 2022, 55, 3032–3042.
24. J. R. R. Verlet, C. S. Anstöter, J. N. Bull and J. P. Rogers, J. Phys. Chem. A, 2020, 124, 3507–3519.
25. C. J. Clarke and J. R. R. Verlet, Annu. Rev. Phys. Chem., 2024, 75, 89–110.
26. M. Elena Castellani, C. S. Anstöter and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2019, 21, 24286–24290.
27. C. Desfrançois, V. Periquet, Y. Bouteiller and J. P. Schermann, J. Phys. Chem. A, 1998, 102, 1274–1278.
28. A. O. Colson, B. Besler, D. M. Close and M. D. Sevilla, J. Phys. Chem., 1992, 96, 661–668.
29. M. D. Sevilla, B. Besler and A.-O. Colson, J. Phys. Chem., 1995, 99, 1060–1063.
30. R. A. Bachorz, J. Rak and M. Gutowski, Phys. Chem. Chem. Phys., 2005, 7, 2116–2125.
31. P. Dedíková, L. Demovič, M. Pitoňák, P. Neogrády and M. Urban, Chem. Phys. Lett., 2009, 481, 107–111.
32. H. Motegi and T. Takayanagi, J. Mol. Struct., 2009, 907, 85–92.
33. C. S. Anstöter and S. Matsika, J. Phys. Chem. A, 2020, 124, 9237–9243.
34. N. Russo, M. Toscano and A. Grand, J. Comput. Chem., 2000, 21, 1243–1250.
35. S. D. Wetmore, R. J. Boyd and L. A. Eriksson, Chem. Phys. Lett., 2000, 322, 129–135.
36. N. J. Saettel and O. Wiest, J. Am. Chem. Soc., 2001, 123, 2693–2694.
37. S. S. Wesolowski, M. L. Leininger, P. N. Pentchev and H. F. Schaefer, J. Am. Chem. Soc., 2001, 123, 4023–4028.
38. T. Sommerfeld, J. Phys. Chem. A, 2004, 108, 9150–9154.
39. R. A. Bachorz, W. Klopper and M. Gutowski, J. Chem. Phys., 2007, 126, 085101.
40. D. Roca-Sanjuán, M. Merchán, L. Serrano-Andrés and M. Rubio, J. Chem. Phys., 2008, 129, 095104.
41. J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843–1856.
42. J. Gu, Y. Xie and H. F. Schaefer, J. Chem. Theory Comput., 2014, 10, 609–612.
43. I. Anusiewicz, P. Skurski and J. Simons, J. Phys. Chem. A, 2020, 124, 2064–2076.
44. J. Schiedt, R. Weinkauf, D. M. Neumark and E. W. Schlag, Chem. Phys., 1998, 239, 511–524.
45. J. H. Hendricks, S. A. Lyapustina, H. L. de Clercq and K. H. Bowen, J. Chem. Phys., 1998, 108, 8–11.
46. S. Eustis, D. Wang, S. Lyapustina and K. H. Bowen, J. Chem. Phys., 2007, 127, 224309.
47. J. P. Rogers, C. S. Anstöter, J. N. Bull, B. F. E. Curchod and J. R. R. Verlet, J. Phys. Chem. A, 2019, 123, 1602–1612.
48. U. Even, EPJ Techn. Instrum., 2015, 2, 17.
49. W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150–1157.
50. G. M. Roberts, J. L. Nixon, J. Lecointre, E. Wrede and J. R. R. Verlet, Rev. Sci. Instrum., 2009, 80, 053104.
51. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
52. R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
53. M. J. Frisch, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
54. R. N. Zare, Mol. Photochem., 1972, 4, 1–37.
55. J. Simons, J. Phys. Chem. A, 2020, 124, 8778–8797.
56. S. T. Arnold, J. H. Hendricks and K. H. Bowen, J. Chem. Phys., 1995, 102, 39–47.
57. J. H. Hendricks, H. L. de Clercq, C. B. Freidhoff, S. T. Arnold, J. G. Eaton, C. Fancher, S. A. Lyapustina, J. T. Snodgrass and K. H. Bowen, J. Chem. Phys., 2002, 116, 7926–7938.
58. T. Lenzer, I. Yourshaw, M. R. Furlanetto, N. L. Pivonka and D. M. Neumark, J. Chem. Phys., 2001, 115, 3578–3589.
59. I. Yourshaw, Y. Zhao and D. M. Neumark, J. Chem. Phys., 1996, 105, 351–373.
60. K. R. Asmis, T. R. Taylor, C. Xu and D. M. Neumark, J. Chem. Phys., 1998, 109, 4389–4395.
61. J. K. Song, N. K. Lee and S. K. Kim, J. Chem. Phys., 2002, 117, 1589–1594.
62. Note: Applying a linear extrapolation (n = 3–5) instead obtains EA_V = +2 meV, showing that the curvature has very little effect on the estimated energy.
63. T. N. Olney, N. M. Cann, G. Cooper and C. E. Brion, Chem. Phys., 1997, 223, 59–98.
64. A. Halkier, S. Coriani and P. Jørgensen, Chem. Phys. Lett., 1998, 294, 292–296.
65. G. A. Cooper, C. J. Clarke and J. R. R. Verlet, J. Am. Chem. Soc., 2023, 145, 1319–1326.
66. D. A. Horke, Q. Li, L. Blancafort and J. R. R. Verlet, Nat. Chem., 2013, 5, 711–717.
67. G. J. Schulz, Rev. Mod. Phys., 1973, 45, 423–486.
68. Y. Yokoi, K. Kano, Y. Minoshima and T. Takayanagi, Comput. Theor. Chem., 2014, 1046, 99–106.
69. G. A. Cooper, C. J. Clarke and J. R. R. Verlet, J. Phys. B: At., Mol. Opt. Phys., 2023, 56, 185102.
70. V. Periquet, A. Moreau, S. Carles, J. P. Schermann and C. Desfrançois, J. Electron Spectrosc. Relat. Phenom., 2000, 106, 141–151.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02146k

---