Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
All-atom molecular dynamics simulations showing the dynamics of small organic molecules in water–solvated polyelectrolyte brush layers†
Leon A.
Smook
 *a,
Raashiq
Ishraaq
b,
Tanmay Sarkar
Akash
b,
Sissi
de Beer
*a,
Raashiq
Ishraaq
b,
Tanmay Sarkar
Akash
b,
Sissi
de Beer
 a and
Siddhartha
Das
a and
Siddhartha
Das
 b
b
aDepartment of Molecules and Materials, MESA+ Institute, University of Twente, Enschede, The Netherlands. E-mail: l.a.smook@utwente.nl
bDepartment of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
First published on 27th September 2024
Abstract
Polyelectrolyte brushes can introduce functionality to surfaces and because of this, these brushes have been studied extensively. In many applications, these brushes are used in solutions that contain a variety of molecules. While the interaction between polyelectrolyte brushes and molecules has been studied via coarse-grained simulations and experiments, such interaction has not been studied in molecular detail. An understanding of interactions in such molecular detail may prove crucial in the design of future brush coatings that can enable desired adsorption of different organic and biological molecules. Therefore, we present a first all-atom molecular dynamics simulations study of poly(sodium acrylate) brushes in contact with a small organic molecule, γ-butyrolactone. Within this molecular framework, we study the interaction of this lactone molecule with the brush layer and study the ensuing absorption and dynamics of the lactone inside the brush layer. The lactone is found to prefer to remain in the bulk solution; however, when absorbed, lactone molecules are found to have significantly reduced mobilities as compared to that in the bulk solution and are able to massively influence the properties of the brush-entrapped water molecules. These findings provide unprecedented details about the absorption-driven changes to molecular structure and dynamics of the lactone molecules and the water molecules inside the brush layer and can only be uncovered by our all-atom MD simulations. Such explicit and atomistically-resolved information, taking into account the specific chemical nature of the interacting systems, is rare in the context of designing polymer and PE brush-based coatings. Thus, we anticipate that our findings will be crucial in the design of future brush coatings aimed at providing adsorption platforms for different organic and biomolecules.
1 Introduction
Polymer brushes are architectures where polymer chains are grafted onto a substrate with such high densities that interactions between neighboring chains make the chains deform from their unperturbed equilibrium configuration and stretch out in the form of ‘brushes’. These brushes are promising surface modifications since they resist bio-fouling1 and create low-friction surfaces.2,3 Due to these and other properties, the coatings created by grafting such polymer brushes to surfaces can be employed in a variety of applications. For instance, polymer brushes have been used to enhance the efficiency of sponges to recover oil after spills;4 to increase the selectivity of mixed-mode membranes;5 to create wound-disinfecting nanotubes;6 to functionalize nanoparticles that reduce dendrite formation in battery electrodes;7 to functionalize nanoparticles that can increase the water transport through membranes;8 to tune surface wettability;9,10 or to create biosensing field-effect transistors.11 Hence, these coatings find applications in fields ranging from separation technology to medicine and battery technology.Polyelectrolyte (PE) brushes are a subclass of polymer brushes where the grafted chains are polyions.12,13 Polyelectrolyte brushes by themselves have been theoretically researched extensively over the years using scaling theories and mean-field models,14–18 self-consistent field calculations,19–21 and coarse-grained molecular dynamics (MD) simulations.17,22–25 These works provide a good picture of the physics of these polyelectrolyte brushes and describe the effects of grafting density, linear charge density, external salt concentration, and external stimuli on these systems. Traditionally, research on polyelectrolyte brushes has been conducted from a polymer physics perspective considering generic interaction potentials. Such an approach, while it enables capturing very large polymeric systems, primarily considers a coarse-grained description of the PE system (thereby forbidding accounting for the influence of the individual polymer atoms) with additionally coarse-graining the effect of surrounding water. Under such circumstances, the influence of the individual polymer atoms as well as the behavior of brush-supported (or specifically, individual atoms of the polymer chain supported) water molecules and ions remain elusive. Identifying this significant gap, over the last years, there has been significant effort devoted in probing the behavior of polymer26–29 and PE brushes using all-atom MD simulations. These simulations unravel hitherto unknown properties of brush-supported water molecules and ions (e.g. identifying the “water-in-salt”-like responses of screening counterions inside brush layer,30 massive changes in the mobilities or counterions and water molecules inside the brush layer,31 significant changes in the factors determining the water–water hydrogen bonding inside brush layer,32,33 and many more). Therefore, such all-atom MD simulations provide excellent scope for studying the behavior of PE brushes, brush-supported water and ions, as well as PE-brush-other-moiety interactions in unprecedented details with exciting opportunities of several novel discoveries.
In this paper, we employ all-atom MD simulations to capture the absorption behavior of a small γ-butyrolactone molecule in water–solvated PE brushes. While the inclusion of small particles inside a polymer layer has been studied using theory and coarse-grained simulations34–40 and atomistically in neutral or zwitterionic brushes,41–47 to the best of our knowledge, this is the first study employing all-atom MD simulations for capturing the absorption behavior of a small organic molecule in a densely-grafted water-solvated PE brush layer. In these earlier studies, the investigated particles have sizes that tend to be large compared to the size of a chemical monomer in the polymer, making it difficult to directly translate results from these studies to experimental systems. The interaction between single molecules and polymer brushes has also been investigated experimentally via single-molecule tracking experiments.48 Some of the single-molecule studies use dyes like Rhodamines49–51 or carbocyanine dyes like DiIC18.52 These dyes often have a specific molecular structure including delocalized electrons and in some cases even an explicit positive charge. Other studies use larger molecules such as P2VP polyelectrolyte chains (110 kDa),53 dextran (10 kDa),54 or fluorescently labeled dodecanoic acid.54 These studies reveal that the diffusion of molecules in/on polymer brushes is slower than bulk diffusion, sometimes by 4 orders of magnitude. However, the observed effects cannot be decoupled from the molecular features of the used probes, so the molecules in these single-molecule tracking studies only provide limited insight into the interaction between polymer brushes and dissolved molecules. This is precisely why the ability to study the interactions of small molecules with PE brushes using an all-atom MD framework, as has been attempted in this study, becomes important.
To unravel the absorption behavior of small molecules in polyelectrolyte brushes, we study the interaction between a common water–solvated polyelectrolyte (in brush-like) configuration and a model solute in chemical detail will all-atom molecular dynamics simulations. Our model system consists of a poly(acrylic acid) derivative, namely poly(sodium acrylate) or PSA, which has been used as coating materials to enhance water flux55 and modulate ion transport56 in membrane materials, and γ-butyrolactone is a small flavor molecule in products as varied as beer and beans.57 While the lactone molecules prefer the bulk solution over the brush environment, the lactone molecules that do absorb are found to have significantly reduced mobilities as compared to those in the bulk solution. Additionally, the molecules massively influence the properties of the brush-entrapped water molecules as functions of their (lactone molecules) position with respect to the brush-absorbed water molecules. Such explicit modeling of the adsorption by the PE brushes, where we account for the atomistic specifics of the adsorbing molecule and the brush layer, will be important to understand the adsorption process and the consequent effects on the brush layer (and water molecules solvating such brush layer) for several situations58–62 where the brushes are used as preferred platforms for the adsorption of different organic and biomolecules.
2 Methods
We performed all-atom molecular dynamics (MD) simulations capturing the interaction (and subsequent absorption) of γ-buterolactone molecules in water–solvated poly(sodium acrylate) PE brushes. The γ-buterolactone molecules are introduced in water above the solvated brush layer. These molecules interact with the PE brush layer via diffusion and in the process some of these molecules get absorbed in the brush layer. These brushes are considered to have a degree of polymerization (N) of 25; the use of such short chains is commonplace for studying the behavior of PE brushes and brush-supported systems using all-atom MD simulations.21,30,31,63,64 The systems were simulated in a simulation box with periodic boundary conditions in the x and y directions and fixed boundary conditions in the z direction. The fixed boundary condition was enforced by using a wall of Lennard-Jones (LJ) particles (hexagonal closed packing arrangement, lattice constant 3.612 Å) with a purely repulsive potential. We studied systems with different grafting densities (0.3 nm−2 and 0.6 nm−2) and at different temperatures (300 K and 355 K). Our simulations consider a grafting density of 0.3 nm−2 and 0.6 nm−2. While such grafting densities are very high, grafting densities of around 0.5 nm−2 have been achieved experimentally for neutral PMMA brushes.65,66 We simulated the brushes and lactones using the OPLS-AA force field67 and water using the three-site SPC/E model.68 The values of the force-field parameters were taken from the OPLS database.67 The parameters for the sodium counterion were taken from Joung et al.69 The specific values of the different simulation parameters used in this work have been summarized in the ESI† (see Section S1).All non-bonded, non-electrostatic interactions were modeled using a combination of a truncated and shifted Lennard-Jones (LJ) potential with a cutoff of 13 Å. Interactions between dissimilar atom types have been modeled using geometrically mixed Lennard-Jones parameters (following Lorentz–Berthelot mixing rules in line with those used in Joung et al.69), except for interactions between the SPC/E water molecules and Na+ ions. Non-bonded electrostatic interactions were modeled using a Coulomb potential. The long-range portion of this potential was calculated using the particle–particle/particle-mesh (PPPM) solver.70 The bond-lengths and angles of the SPC/E water molecules were fixed using the SHAKE algorithm.71
The simulations were set up in a modular fashion. Fully-stretched poly(sodium acrylate) chains were placed in the simulation box using moltemplate72 in a 6 × 6 square array. SPC/E water molecules were placed in the available space between these chains. Simultaneously, a bulk mixture of lactone and SPC/E water was prepared and partially equilibrated using enhanced Monte Carlo.73 The lactone concentration of this initial solution was 1.0 M. These initial configurations were combined in one simulation box. This procedure resulted in the simulation systems summarized in Table 1. We remark that the samples with the lower grafting density have roughly twice the number of water and lactone molecules as a the simulation box varies in size to accommodate the 6 × 6 array of chains. First, the density of the simulation box was equilibrated in an NPz T ensemble (i.e. the walls are free to move towards each other in the out-of-plane z-direction) at a temperature of 300 K and a pressure of 1 atmosphere using a Nosé–Hoover thermostat and barostat with time constants of 200 ps (thermostat) and 2000 ps (barostat).74,75 Second, the volume was fixed at the equilibrium value and the simulation was continued in the NVT ensemble using a Langevin thermostat (time constant, 200 ps; temperature 300 K).76 The equilibration of the system was tracked by monitoring the convergence in the brush height (ESI,† Section S2) and the number of absorbed molecules in the brush. In other words, we identify that the system has equilibrated when the brush height and number of molecules no longer vary with time (see Section S3 in the ESI†). Also, from each simulation, we use the last 5 ns of the trajectory as the production run (i.e. to generate the results). The most efficient way for ascertaining whether a particular quantity (in this case, the brush height) has converged or not is to test the autocorrelation function of this quantity and quantify the autocorrelation decay time. If this decay time is significantly smaller than the total time for which the trajectory is probed, we can infer that the chosen quantity has converged. Accordingly, we have performed the autocorrelation analysis of the brush height (for different cases studied) for the 5 ns trajectory (production run is for 5 ns) (please see Fig. S2 in the ESI† document). For all the cases studied, we find an autocorrelation decay time of 0.32 ns or smaller. This means that the 5 ns simulation window is more than an order of magnitude larger than the autocorrelation decay time, indicating sufficient sampling.
| Code | Grafting density (nm−2) | Temperature (K) | # Water | # Lactone |
|---|---|---|---|---|
| 3R | 0.3 | 300 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 859 859 |
432 |
| 3H | 0.3 | 355 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 859 859 |
432 |
| 6R | 0.6 | 300 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541 541 |
234 |
| 6H | 0.6 | 355 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541 541 |
234 |
All simulations were run in LAMMPS.77,78 The positions of all atoms were dumped every 2 ps. The position data was subsequently analyzed in Python using MDAnalysis package for importing the data.79,80 Visualizations were performed with OVITO.81
3 Results and discussion
3.1 Poly(sodium acrylate) brush structure
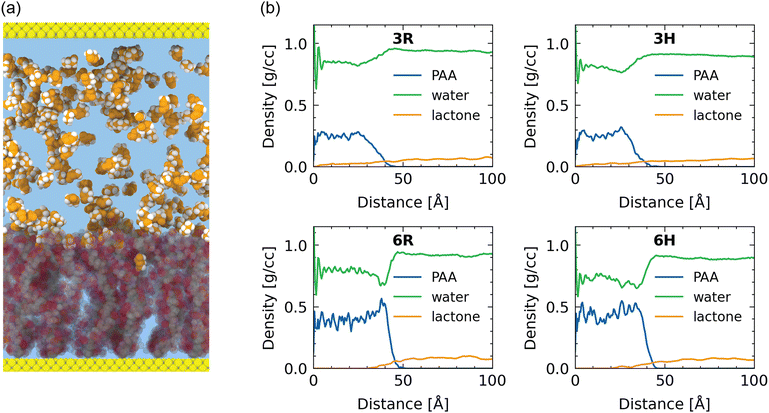
Before studying the behavior of the γ-butyrolactone and water, we first characterize the structure of the water–solvated poly(sodium acrylate) brush. We study these polyelectrolyte brushes at two grafting densities (0.3 nm−2 and 0.6 nm−2) and at two temperatures (300 K and 355 K) to see whether variations of the system conditions affect the brush configuration. For compactness, we refer to these samples using the following coding for grafting density (3–0.3 nm−2; 6–0.6 nm−2) and temperature (R/room temperature – 300 K; H/high temperature – 355 K). For instance, 3R refers to the brush with a grafting density of 0.3 nm−2 at a temperature of 300 K. For reference, we present this coding in Table 1. For visual reference, we provide a snapshot of the 6R-sample in Fig. 1(a).Polymer brushes are often characterized based on their height and monomer density profiles. Here, we define the brush height as the height below which 99% of the polymer resides. The polymer brush layers studied here have heights ranging from 39.0 Å (3H) to 44.8 Å (6R). In the summarized data in Table 2, we observe the following two trends: first, the brush height increases with the grafting density and second, the brush height decreases with increasing temperature. These trends are in line with observations in previous work.32,82 The temperature effect can be explained from the standpoint of an entropic effect: as temperature increases the contribution of entropy to the free energy becomes more pronounced since this contribution scales with temperature. This entropic effect promotes the collapse of the stretched chains; therefore, at higher temperatures the brush becomes more collapsed and compact.
| 3R | 3H | 6R | 6H | |
|---|---|---|---|---|
| Height [Å] | 39.9 | 39.0 | 44.8 | 42.1 |
| N lact,brush [−] | 81.6 | 80.4 | 13.2 | 15.0 |
| N wat,brush [−] | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 238 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
7230 | 6211 |
| f lact/wat,brush [−] | 5.73 × 10−3 | 6.10 × 10−3 | 1.83 × 10−3 | 2.42 × 10−3 |
| N lact,bulk [−] | 350.4 | 351.6 | 220.8 | 219.0 |
| N wat,bulk [−] | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 679 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 330 330 |
| f lact/wat,bulk [−] | 12.69 × 10−3 | 12.26 × 10−3 | 16.59 × 10−3 | 15.2 × 10−3 |
| c [nm−3] | 0.361 | 0.361 | 0.448 | 0.425 |
| D [Å2 ps−1] | 0.024 | 0.050 | 0.011 | 0.025 |
The brush height H increases with the grafting density. The grafting density is large enough to ensure that the brushes behave as non-linear osmotic brushes; accordingly, the brush height increases linearly (with an offset) with the grafting density. Following previous work30 based on Ahrens et al.83 and Nair,84 we can therefore write:
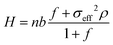 | (1) |
3.2 Absorption of γ-butyrolactone molecules in the brush layer
Understanding and capturing the absorption of γ-butyrolactone molecules in the brush layer is the main topic of interest of this paper. We start with a setting where γ-butyrolactone molecules are present in the water layer that is present above the water–solvated brush layer. The γ-butyrolactone molecules interact with the brush layer via diffusion and in the process some amount of the γ-butyrolactone molecules get trapped inside the brush layer. This is the absorption phenomenon.To quantify the absorption, we consider the ratio of lactone to water molecules inside the brush versus lactone to water molecules outside the brush. For the 3R case, the ratio of lactone to water outside the brush is 12.69 lactone molecules per 1000 water molecules, while the same ratio reduces to only 5.73 molecules per 1000 water molecules inside the brush. For the 6R case, this ratio changes even more from 16.59 to 1.83 γ-butyrolactone molecules per 1000 water molecules inside the brush.
This ratio reduction shows that the lactone molecules prefer more to stay outside the brush layer than inside the brush layer, which can readily be confirmed by looking at the density profiles in Fig. 1(b). As a consequence, the absorption is retarded but finite, as evident from the equilibrium values (per 1000 water molecules) of the number of lactone molecules present inside the brush layer. The size of the lactone molecules is much larger than the size of the water molecules: therefore, water will more easily penetrate into the densely grafted brush layer, as compared to the lactone molecules. This is a simple steric effect. This is even further evident for the more densely grafted brushes, justifying the progressive decrease in the number of lactone molecules (per 1000 water molecules) from the bulk to inside the brush layer with grafting density of 0.3 nm−2 and grafting density of 0.6 nm−2.
We obtain some additional insight by observing the trajectories of the lactone molecules that have absorbed in the brush layer. Fig. 2 shows the trajectories of the z-coordinate of the absorbed lactone molecules that remain inside the brush for the complete duration of the production run (5 ns). These trajectories reveal that the lactones penetrate much more deeply into the sparser brushes that have a grafting density of 0.3 nm−2, while they do not reach full depth in the denser brushes with a grafting density of 0.6 nm−2. This observation agrees with the absorption limitation as a result of the steric effects. Additionally, the trajectories reveal stationary periods (or periods of reduced mobilities), where the z-coordinate of the lactone remains rather constant. For instance, the lactone indicated with the red curve in 3H or the orange curve in 6H. These periods of reduced mobility characterize the lactone absorption in the PE brush layer.
3.3 Dynamics of γ-butyrolactone molecules in the brush layer
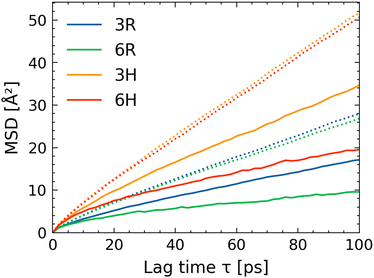
One of the key features of all-atom molecular dynamics (MD) simulations is the ability to investigate systems in molecular detail. In our simulations, we can differentiate between γ-butyrolactone molecules that are in the solution versus those that are within the brush layer. To distinguish between γ-butyrolactone molecules inside and outside the brush, we identify the locations of the γ-butyrolactone molecules relative to the equilibrated brush height; all γ-butyrolactone molecules with atoms below this height are considered to be inside the brush.To what extent do the dynamics of these molecules differ depending on their location in the system? In order to obtain the dynamics of these two types of the γ-butyrolactone molecules (γ-butyrolactone molecules inside the brush layer and γ-butyrolactone molecules outside the brush layer), we compute the mean squared displacements (MSDs) of the different types as a function of time and extract the corresponding diffusivities (see Fig. 3). The MSD-values of the lactones in the brush are lower than those in the bulk solution.
To obtain the diffusivity, we consider the MSD-vs.-time curve for lag times greater than 25 ps. For such times, the MSD-vs.-time curves are mostly linear and we obtain the diffusivity as 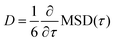 . As expected, the mean-squared displacements of the lactone molecules outside the brush layer depends only on temperature. At room temperature (300 K), the diffusivity of the lactone molecule in the bulk is 0.041 Å2 ps−1 and at elevated temperature (355 K) it is 0.080 Å2 ps−1. The diffusivities are calculated in all cartesian directions and no significant differences between directions have been found at the time scales evaluated.
. As expected, the mean-squared displacements of the lactone molecules outside the brush layer depends only on temperature. At room temperature (300 K), the diffusivity of the lactone molecule in the bulk is 0.041 Å2 ps−1 and at elevated temperature (355 K) it is 0.080 Å2 ps−1. The diffusivities are calculated in all cartesian directions and no significant differences between directions have been found at the time scales evaluated.
Inside the brush layer, however, the mobility of the lactone molecules is reduced. The diffusivity of the lactone decreases from 0.041 Å2 ps−1 (bulk value) to 0.024 Å2 ps−1 (3R) and to only 0.011 Å2 ps−1 (6R). At elevated temperature, this effect is slightly less pronounced but the diffusivities still decrease from 0.080 Å2 ps−1 (bulk value) to 0.049 Å2 ps−1 (3H) and 0.024 Å2 ps−1 (6H). Such reductions in diffusivities are not surprising. Interestingly, the directionality of the polymer seems to hardly affect the diffusivity of the lactone molecules; like for lactone molecules outside the brush, the diffusivity in all Cartesian directions is similar inside the brush. Previous all-atom simulations30,31 have shown that the large confinement effect imparted by the brush layer leads to a significant reduction in the mobility of the brush-supported counterions and water molecules. Here, we establish that this confinement effect also leads to a significant decrease in the diffusivity of the brush-absorbed small organic molecules (γ-butyrolactone molecules); there is even experimental evidence of such reduced mobility of molecules absorbed in the brush layer.49–51,53,54
3.4 Behavior of the water molecules
The presence of the PE brushes affects not only the properties of the lactone molecules, but also the water molecules. In our previous papers employing all-atom MD simulations for probing the PE brushes, we have provided extensive results on the manner in which the presence of the brushes drastically alter the properties of the brush-supported water molecules. Here we shall discuss the manner in which the properties of such brush-supported water molecules get further affected by the additional presence of the brush-absorbed lactone molecules. For this purpose, we shall employ different measures to quantify the water structure in the vicinity of the lactone molecules with the lactone molecules being either present in the bulk (outside the brush layer) or inside the brush layer. These measures include (1) orientation of water-dipoles around different parts of the lactone molecule (Fig. 4) and (2) the structural order of water molecules (around the lactone molecule) (Fig. 6).![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)], (2) the carbon in the carbonyl [–C(
C)], (2) the carbon in the carbonyl [–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)], (3) the alkoxy oxygen [–O(C)(C)], and (4) the aliphatic carbons [–C(H)(H)]. We compare the water-dipole distributions around these different atoms of the lactone molecules with those lactone molecules being either inside or outside the brush layer.
O)], (3) the alkoxy oxygen [–O(C)(C)], and (4) the aliphatic carbons [–C(H)(H)]. We compare the water-dipole distributions around these different atoms of the lactone molecules with those lactone molecules being either inside or outside the brush layer.
The distribution of dipole angles is shown in Fig. 4. In these distributions, we observe contributions of two main modes: one peaks around ∼75° and the other one around 120° (see Fig. 5 for the corresponding visual representation). The former mode corresponds to situations where the water dipole lies flat on the surface of the atom (see Fig. 5(a)); the latter corresponds to the situation where the O–H vector of the water molecule points to the atom (see Fig. 5(b)). In other words, the first mode is more representative of the hydrophobic behavior (i.e. the water is interacting with a hydrophobic solute) and the second mode is more representative of hydrophilic behavior with strong hydrogen bonds (i.e. the water is interacting with a hydrophilic solute). Furthermore, we find that the difference in water dipole distributions (around these four atoms) is not significant when comparing the cases of water hydrating the lactones inside versus outside the brush. At high temperatures (355 K), this difference is almost zero. At lower temperatures (300 K), however, this difference, which is mostly observed around the oxygen atoms, is weak but present. For water molecules around the lactone molecules in the solution (i.e. outside the brush layer), the mode centered around 120° is slightly more prevalent than the water molecules around the lactone molecules within the brush layer: this indicates that the lactones may be slightly less capable of forming hydrogen bonds with water when they enter the brush layer. However, this discrepancy is small and is therefore not expected to change the entropy of the lactone inside the brush significantly. In other words, the hydration shell of the lactone is mostly preserved upon absorption in the brush layer.
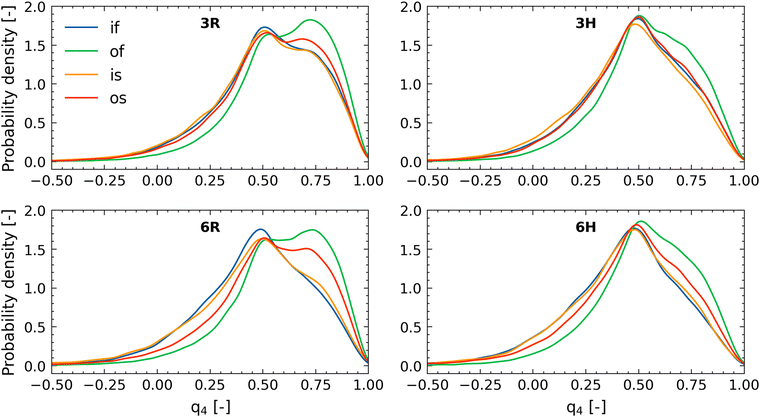
These probability density profiles (corresponding to different values of the order parameter q4) seem to have two peaks: one around q4 ≈ 0.78 and another around q4 ≈ 0.46. These peaks can be attributed to the regular tetrahedral order of water (〈q4〉 ≈ 0.78) and to tetrahedral order where a water molecule is located at an interstitial position (〈q4〉 ≈ 0.46).
Water inside the brush is always less structured than that in the bulk solution, stemming from the fact that the large confinement effect imparted by the PE brushes disrupts the water–water hydrogen bonding. For the case of 3R, we find that the structure of the free water (i.e., water that is more than 4 Å away from the lactone molecule) is much less ordered inside the brush as compared to that outside the brush: hence, if we compare the cases of “if” and “of” for all the four cases (3R, 3H, 6R, and 6H), we find that that probability density profiles corresponding to the “of” show greater values of the peaks (as compared to the “if” cases) at q4 ≈ 0.78 [see Fig. 6(a) and (d)]. The same dependence of the presence of the brush layer (in disrupting water structural order) is noted for the water molecules in close vicinity (within 4 Å) of the lactone molecules. Therefore, around the lactone molecules, the water structural order is more when the lactone molecules is outside the brush layer versus when the lactone molecules are inside the brush layer. This becomes obvious if one compares the cases of “os” and “is”: for all the four cases (3R, 3H, 6R, and 6H) we find that the probability density profiles corresponding to the “os” show greater values of the peaks (as compared to the “is” cases) at q4 ≈ 0.78 [see Fig. 6(a) and (d)]. We note that water structure could also be affected by the coordination number, but the trends in this property are qualitatively different and cannot explain the changing water structure (see ESI,† Section S5). The lactone molecules do not affect the water structure in the brush (compare is and if), but they make the water less structured outside the brush (compare os and of), indicating that the lactone molecules have a slight chaotropic character.
4 Conclusions
In this work, we have employed all-atom MD simulation for studying the interactions between lactone molecules and poly(sodium acrylate) brushes and captured the subsequent absorption and mobility of the lactone molecules (within the brush layer) and the resulting changes in the properties of the brush-supported water molecules (in the vicinity of such brush-absorbed lactone molecules).Using the capabilities of the all-atom MD simulations, we are able to point out the extent of absorption of the lactone molecules inside the brush layer. The numbers suggest that the lactone molecules prefer to remain in the bulk and have relatively weaker presence inside the brush layer. This can be primarily attributed to the significant steric effect imparted by the densely grafted brushes. However, even in the presence of such reduced number of absorbed lactone molecules, we are able to uncover highly intriguing dynamics of the lactone molecules inside the brush layer as well as interesting properties of the water molecules inside the brush layer as functions of their relative distances from the lactone molecules. For example, the diffusivities of the absorbed lactone molecules are reduced inside the brush layer, as compared to that in the bulk. This is in line with the ability of the brushes to significantly reduce the mobility of other entrained species (like water and ions). On the other hand, very interestingly, we find that while the dipole moments of water molecules show very weak variation as functions of their relative positions with respect to the lactone molecules (with the lactone molecules being either inside or outside the brushes), the water structural order parameter is significantly influenced depending on whether the corresponding lactone molecules are inside or outside the brushes (for all cases of grafting densities and temperatures, water molecules inside the brush layer have distinctly disrupted structural order as compared to water molecules outside the brush layer). We anticipate that this study will motivate several future studies that will employ all-atom MD simulations to better understand (with atomistically resolved information on water structure, structure of the polymers, and structure of interacting species) the absorption of a wide class of species on charged and uncharged polymer brush based coatings.
Data availability
The data that support the findings of this study are openly available in the 4TU. Research Data database at https://doi.org/10.4121/7b96bcc9-b5c1-4b47-a0b9-a970c3cb8972.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is part of Targets 1 and 5 of the TTW Perspectief research programme ReCoVR: Recovery and Circularity of Valuable Resources which is (partly) financed by the Dutch Research Council (NWO). The authors acknowledge the support of the Deepthought2 High-Performance Computing cluster at the University of Maryland. NWO and SURFsara are acknowledged for HPC resources and support (project ref EINF-9565).Notes and references
- Y. Higaki, M. Kobayashi, D. Murakami and A. Takahara, Polym. J., 2016, 48, 325–331 CrossRef CAS.
- C. Drummond, Phys. Rev. Lett., 2012, 109, 154302 CrossRef PubMed.
- M. A. Abdelbar, J. P. Ewen, D. Dini and S. Angioletti-Uberti, Biointerphases, 2023, 18, 010801 CrossRef CAS PubMed.
- Y. Liu, X. Wang and S. Feng, Adv. Funct. Mater., 2019, 29, 1902488 CrossRef.
- H. Wang, S. He, X. Qin, C. Li and T. Li, J. Am. Chem. Soc., 2018, 140, 17203–17210 CrossRef CAS PubMed.
- Y. Yang, L. Ma, C. Cheng, Y. Deng, J. Huang, X. Fan, C. Nie, W. Zhao and C. Zhao, Adv. Funct. Mater., 2018, 28, 1705708 CrossRef.
- S. Li, J. Huang, Y. Cui, S. Liu, Z. Chen, W. Huang, C. Li, R. Liu, R. Fu and D. Wu, Nat. Nanotechnol., 2022, 17, 613–621 CrossRef CAS PubMed.
- L. Dai, F. Xu, K. Huang, Y. Xia, Y. Wang, K. Qu, L. Xin, D. Zhang, Z. Xiong, Y. Wu, X. Guo, W. Jin and Z. Xu, Angew. Chem., Int. Ed., 2021, 60, 19933–19941 CrossRef CAS PubMed.
- V. Sénéchal, H. Saadaoui, J. Rodriguez-Hernandez and C. Drummond, Langmuir, 2017, 33, 4996–5005 CrossRef PubMed.
- V. Senechal, J. Rodriguez-Hernandez and C. Drummond, Macromolecules, 2022, 55, 2636–2648 CrossRef CAS.
- S. Klinghammer, S. Rauch, S. Pregl, P. Uhlmann, L. Baraban and G. Cuniberti, Micromachines, 2020, 11, 274 CrossRef PubMed.
- S. Das, M. Banik, G. Chen, S. Sinha and R. Mukherjee, Soft Matter, 2015, 11, 8550–8583 RSC.
- M. Geoghegan, Soft Matter, 2022, 18, 2500–2511 RSC.
- R. S. Ross and P. Pincus, Macromolecules, 1992, 25, 2177–2183 CrossRef CAS.
- P. Pincus, Macromolecules, 1991, 24, 2912–2919 CrossRef CAS.
- T. Yamamoto and P. A. Pincus, EPL, 2011, 95, 48003 CrossRef.
- H. Merlitz, C. Li, C. Wu and J.-U. Sommer, Soft Matter, 2015, 11, 5688–5696 RSC.
- F. Csajka, R. Netz, C. Seidel and J.-F. Joanny, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 505–513 CrossRef CAS.
- C. Tong, J. Chem. Phys., 2015, 143, 054903 CrossRef PubMed.
- B. M. Okrugin, R. P. Richter, F. A. M. Leermakers, I. M. Neelov, E. B. Zhulina and O. V. Borisov, Polymers, 2020, 12, 898 CrossRef CAS PubMed.
- H. S. Sachar, V. S. Sivasankar and S. Das, Soft Matter, 2018, 15, 559–574 RSC.
- Y.-F. Ho, T. N. Shendruk, G. W. Slater and P.-Y. Hsiao, Langmuir, 2013, 29, 2359–2370 CrossRef CAS PubMed.
- H. Ouyang, Z. Xia and J. Zhe, Nanotechnology, 2009, 20, 195703 CrossRef PubMed.
- S. Wang and C. Tong, J. Appl. Phys., 2020, 127, 074301 CrossRef CAS.
- F. Zhang, S. Wang, H. Ding and C. Tong, Soft Matter, 2019, 15, 2560–2570 RSC.
- D. E. S. Santos, D. Li, M. Ramstedt, J. E. Gautrot and T. A. Soares, Langmuir, 2019, 35, 5037–5049 CrossRef CAS PubMed.
- U. R. Dahal, Z. Wang and E. E. Dormidontova, Macromolecules, 2017, 50, 6722–6732 CrossRef CAS.
- G. Chen and E. Dormidontova, Macromolecules, 2022, 55, 5222–5232 CrossRef CAS.
- G. Chen and E. E. Dormidontova, Macromolecules, 2024, 57, 434–444 CrossRef CAS.
- H. S. Sachar, T. H. Pial, P. R. Desai, S. A. Etha, Y. Wang, P. W. Chung and S. Das, Matter, 2020, 2, 1509–1521 CrossRef.
- H. S. Sachar, T. H. Pial, B. S. Chava and S. Das, Soft Matter, 2020, 16, 7808–7822 RSC.
- H. S. Sachar, B. S. Chava, T. H. Pial and S. Das, Macromolecules, 2021, 54, 6342–6354 CrossRef CAS.
- T. H. Pial and S. Das, Soft Matter, 2022, 18, 8945–8951 RSC.
- T. Curk, F. J. Martinez-Veracoechea, D. Frenkel and J. Dobnikar, Nano Lett., 2014, 14, 2617–2622 CrossRef CAS PubMed.
- S. de Beer, L. I. S. Mensink and B. D. Kieviet, Macromolecules, 2016, 49, 1070–1078 CrossRef CAS.
- V. Ermilov, A. Lazutin and A. Halperin, Macromolecules, 2010, 43, 3511–3520 CrossRef CAS.
- J. Yaneva, D. Dimitrov, A. Milchev and K. Binder, J. Colloid Interface Sci., 2009, 336, 51–58 CrossRef CAS PubMed.
- J. Cheng, A. Vishnyakov and A. V. Neimark, J. Chem. Phys., 2015, 142, 034705 CrossRef PubMed.
- H. Merlitz, C.-X. Wu and J.-U. Sommer, Macromolecules, 2012, 45, 8494–8501 CrossRef CAS.
- L. A. Smook and S. de Beer, ChemPhysChem, 2023, 24, e202300003 CrossRef CAS PubMed.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, Macromolecules, 2018, 51, 4853–4864 CrossRef.
- M. Kanduč, R. Chudoba, K. Palczynski, W. K. Kim, R. Roa and J. Dzubiella, Phys. Chem. Chem. Phys., 2017, 19, 5906–5916 RSC.
- T. Yagasaki and N. Matubayasi, Langmuir, 2023, 39, 13158–13168 CrossRef CAS PubMed.
- T. Yagasaki and N. Matubayasi, Phys. Chem. Chem. Phys., 2022, 24, 22877–22888 RSC.
- Y. Xiang, R.-G. Xu and Y. Leng, Langmuir, 2016, 32, 4424–4433 CrossRef CAS PubMed.
- Y. Xiang, R.-G. Xu and Y. Leng, Langmuir, 2018, 34, 2245–2257 CrossRef CAS PubMed.
- Y. Liu, D. Zhang, B. Ren, X. Gong, L. Xu, Z.-Q. Feng, Y. Chang, Y. He and J. Zheng, J. Mater. Chem. B, 2020, 8, 3814–3828 RSC.
- S. Wang, B. Jing and Y. Zhu, J. Polym. Sci., Part B: Polym. Phys., 2014, 52, 85–103 CrossRef CAS.
- C. Reznik, Q. Darugar, A. Wheat, T. Fulghum, R. C. Advincula and C. F. Landes, J. Phys. Chem. B, 2008, 112, 10890–10897 CrossRef CAS PubMed.
- C. Reznik, N. Estillore, R. C. Advincula and C. F. Landes, J. Phys. Chem. B, 2009, 113, 14611–14618 CrossRef CAS PubMed.
- L. C. C. Elliott, M. Barhoum, J. M. Harris and P. W. Bohn, Langmuir, 2011, 27, 11037–11043 CrossRef CAS PubMed.
- L. C. C. Elliott, M. Barhoum, J. M. Harris and P. W. Bohn, Phys. Chem. Chem. Phys., 2011, 13, 4326–4334 RSC.
- W. Wang, C. Zhang, S. Wang and J. Zhao, Macromolecules, 2007, 40, 9564–9569 CrossRef CAS.
- H.-Y. Chin, D. Wang and D. K. Schwartz, Macromolecules, 2015, 48, 4562–4571 CrossRef CAS.
- L. G. Lopez and R. J. Nap, Phys. Chem. Chem. Phys., 2018, 20, 16657–16665 RSC.
- Y. Wang, L. Liu, J. Xue, J. Hou, L. Ding and H. Wang, AIChE J., 2018, 64(6), 2181–2188 CrossRef CAS.
- N. Garg, A. Sethupathy, R. Tuwani, R. NK, S. Dokania, A. Iyer, A. Gupta, S. Agrawal, N. Singh, S. Shukla, K. Kathuria, R. Badhwar, R. Kanji, A. Jain, A. Kaur, R. Nagpal and G. Bagler, Nucleic Acids Res., 2017, 46, D1210–D1216 CrossRef PubMed.
- K. Ishihara, K. Mitera, Y. Inoue and K. Fukazawa, Colloids Surf., B, 2020, 194, 111205 CrossRef CAS PubMed.
- C. Yoshikawa, S. Hattori, C.-F. Huang, H. Kobayashi and M. Tanaka, J. Mater. Chem. B, 2021, 9, 5794–5804 RSC.
- S. Sakata, Y. Inoue and K. Ishihara, Langmuir, 2015, 31, 3108–3114 CrossRef CAS PubMed.
- H. Wang, H. Zhang, S. Yuan, C. Liu and Z. Xu, J. Mol. Model., 2014, 20, 2267 CrossRef PubMed.
- M. Atif and A. Balasini, Mater. Adv., 2024, 5, 1420–1439 RSC.
- T. H. Pial, H. S. Sachar, P. R. Desai and S. Das, ACS Nano, 2021, 15, 6507–6516 CrossRef CAS PubMed.
- R. Ishraaq, T. S. Akash, A. Bera and S. Das, J. Phys. Chem. B, 2023, 128(1), 381–392 CrossRef PubMed.
- R. R. Patil, S. Turgman-Cohen, J. Šrogl, D. Kiserow and J. Genzer, Langmuir, 2015, 31, 2372–2381 CrossRef PubMed.
- Z. He, W. J. Xie, Z. Liu, G. Liu, Z. Wang, Y. Q. Gao and J. Wang, Sci. Adv., 2016, 2, e1600345 CrossRef PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- R. W. Hockney and J. W. Eastwood, Computer Simulations Using Particles, McGraw-Hill, New York, 1989 Search PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- P. J. in’T Veld and G. C. Rutledge, Macromolecules, 2003, 36, 7358–7365 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- T. Schneider and E. Stoll, Phys. Rev. B: Solid State, 1978, 17, 1302–1322 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- R. Gowers, M. Linke, J. Barnoud, T. Reddy, M. Melo, S. Seyler, J. Domański, D. Dotson, S. Buchoux, I. Kenney and O. Beckstein, Python in Science Conference, Austin, Texas, 2016, pp. 98–105 Search PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- A. E. Nasrabad, R. Laghaei and R. D. Coalson, Int. J. Mol. Sci., 2023, 24, 832 CrossRef PubMed.
- H. Ahrens, S. Förster, C. A. Helm, N. A. Kumar, A. Naji, R. R. Netz and C. Seidel, J. Phys. Chem. B, 2004, 108, 16870–16876 CrossRef CAS.
- A. Nair, PhD thesis, Universität Potsdam, 2006.
- J. R. Errington and P. G. Debenedetti, Nature, 2001, 409, 318–321 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: OPLS-AA force field parameters; brush height convergence; lactone absorption along trajectory; water structure of non-solvating water; water coordination number. See DOI: https://doi.org/10.1039/d4cp02128b |
| This journal is © the Owner Societies 2024 |