Description of an original molecular ordering process into a disordered crystalline form: the atypical low-temperature transformation of the disordered form III of linezolid

Abstract

Form III of linezolid was prepared by heating the commercial form above 150 °C and subsequently analyzed upon cooling down to −160 °C, by low- and high-frequency Raman spectroscopy, differential scanning calorimetry and powder X-ray diffraction (PXRD). It was observed that form III was preserved down to 0 °C. At lower temperatures a soft mode was clearly detected by low-frequency Raman spectroscopy associated with the detection of additional Raman bands distinctive of additional intermolecular H-bond interactions. Raman spectroscopy investigations performed in a wide frequency range revealed a continuous transformation characterized by both displacive and order–disorder signatures. By contrast, PXRD highlighted the absence of symmetry breaking, Bragg peaks being still indexed in the same unit cell from room temperature down to −160 °C. Additionally, a significant broadening of Bragg peaks was observed with decreasing temperature interpreted as being a consequence of a distribution of frozen molecular conformations.

---

1. Introduction

Molecular materials are characterized by the strong discrepancy between intra and intermolecular forces. The weak intermolecular interactions via van der Waals, electrostatic forces or H-bonding are responsible for the rich polymorphism of these types of materials.^1,2 It is also recognized that the solid-state form of molecular materials has a significant impact on their water solubility.³ This consideration is crucial for active pharmaceutical ingredients (APIs), since water solubility is closely related to bioavailability.⁴ As a consequence, solid-state transformation should impact their polymorphs. In particular, polymorphic transformations can change their dosage form. In this context, detailed knowledge of the phase diagram is required for using molecular materials as drugs.⁴

Linezolid (C₁₆H₂₀FN₃O₄, LIN) is well known as a commonly used oxazolidinone antibiotic, and is also characterized by rich polymorphism since 4 crystalline forms have been reported.⁵ However, more recent works report the existence of two well-defined crystalline forms,^6,7 namely forms II⁸ and III.⁹ Form III can be prepared from a solution of toluene/o-xylene and form II, or merely by heating.⁷ The crystalline symmetry of form II is orthorhombic (P2₁2₁2₁).⁵ Form II transforms upon heating above 150 °C into a disordered high-temperature phase via the transient liquid state.⁵ Intriguingly, the symmetry of the disordered form III (triclinic, P1̄)⁵ is lower than that of the ordered form II. These uncommon features have drawn our attention and motivated detailed investigations of form III in a wide temperature range.

The present work focuses on the detailed analysis of the dynamics of forms II and III, mostly from Raman investigations in a wide spectral range (5–3800 cm⁻¹) and in a wide temperature range (−160 to 120 °C). Differential scanning calorimetry (DSC) and powder X-ray diffraction (PXRD) experiments were used as complementary data for interpreting changes in the dynamics observed upon cooling form III down to −160 °C.

2. Experimental

2.1. Materials

Linezolid form II was purchased from ABCR GmbH (Germany) and used as was. Form III was systematically prepared in situ upon heating above 150 °C, before Raman, DSC and PXRD investigations carried out in this study.

2.2. Methods

Low-frequency Raman spectra were collected using a high-resolution Raman XY-Dilor spectrometer to analyze the non-polarized back-scattered light. The spectrometer is composed of three gratings, i.e. a double monochromator and a spectrograph in a configuration characterized by a focal length of 800 mm. The choice of experimental conditions (incident radiation, entrance and exit slit width of the opening at 200 μm) gives a spectral resolution of about 1 cm⁻¹ in the 5–250 cm⁻¹ region and allows the rejection of excitation light (the 660 nm line of a solid diode laser) down to 5 cm⁻¹. The spectrometer is equipped with a liquid nitrogen cooled charge coupled device detector. The high sensitivity of the detector and the large analyzed scattered volume (∼0.5 cm³) allow us to record low-wavenumber Raman spectra in the 5–250 cm⁻¹ range in 60 seconds. Powder samples were loaded in spherical Pyrex cells and hermetically sealed. The temperature of the samples was regulated using an Oxford nitrogen flux device that keeps temperature fluctuations within 0.1 °C. Spectra were collected during heating ramps in steps of 10 degrees with an acquisition time of 60 seconds.

The low-frequency Raman intensity I_Raman(ω,T) was transformed into reduced intensity I_r(ω) for correcting the spectrum distortion from temperature fluctuation according to ref. 10

where n(ω,T) is the Bose–Einstein factor. Low-frequency spectra were systematically analyzed in this representation.

High-frequency Raman investigations were performed using the InVia Renishaw Raman microscope in the 800–4000 cm⁻¹ range equipped with a solid diode laser emitting 514.5 nm radiation. An achromatic lens was used for analyzing a large volume of the powder sample. The sample temperature was controlled by placing the sample in a THMS 600 Linkam temperature device. Spectra were collected during heating ramps carried out in steps of ten degrees under the same conditions as those used in the low-frequency region.

In both the low- and high-frequency Raman investigations the laser power was 200 mW and estimated to 160 mW minimum on samples.

X-Ray diffraction was performed on form III of LIN using a Panalytical X’pert PRO MPD diffractometer. The Bragg–Brentano geometry was used, operated with the CuKα_1,2 radiation selected using a hybrid monochromator. Form III of LIN was cooled down to −140 °C by placing the powder in an Anton Paar TTK 450 chamber under vacuum. The PXRD pattern was analyzed above 2θ ∼ 6°. The PXRD patterns were collected from −140 °C up to room temperature in steps of 10 degrees with an acquisition time of 10 minutes. Data were analyzed after removing the background. The unit cell parameters were determined at room temperature and at −150 °C using a peak search method in WinPLOTR.¹¹ Dicvol06 software¹² was used for determining the lattice parameters. These unit cell and width parameters of Bragg peaks described using the pseudo-Voigt function were refined using the profile matching option¹³ of the FullProf program.¹⁴

Differential scanning calorimetry (DSC) experiments were carried out using a DSC Q10 (TA Instruments, Guyancourt, France) equipped with a liquid nitrogen cooling system, between −150 °C and 100 °C, at heating rate of 5 °C min⁻¹. A sample of 3.2 mg was encapsulated in aluminum hermetic pans. During all measurements, the calorimeter head of Q10 was flushed with highly pure helium gas (flow rate of 25 mL min⁻¹). Temperature and enthalpy (cell constant) calibrations were based on the melting peak of the indium standard (T_m = 156.6 °C) supplied by TA Instruments, using the same experimental conditions (cell environment, type of pan and heating rate) as for the sample.

3. Results and discussion

3.1. Raman investigations

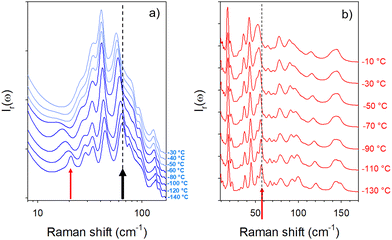
The low-frequency Raman spectrum of molecular materials is composed of two types of bands,¹⁰ corresponding to external vibrational modes i.e. the lattice modes, and semi-external motions which are overlapping in the very low-frequency region (<50 cm⁻¹). The lattice modes provide the crystalline fingerprint of a polymorphic form, while semi-external motions give a contribution to the very low-frequency intensity distinctive of the degree of molecular disorder. This very low-frequency intensity is called quasielastic intensity. It corresponds to large-amplitude motions of a group of atoms within the molecule or global motions (usually rotations) of the entire molecule. Low-frequency Raman spectra of forms II and III are compared in Fig. 1 at room temperature and −140 °C.

Fig. 1 Comparison of low-frequency Raman spectra of forms II and III (a) at room temperature; below 100 cm⁻¹ the spectrum of form III corresponds to the envelope of the phonon peaks in form II, except in the region below 20 cm⁻¹ where no phonon peak is detected whilst a double peak is observed in form II; (b) at −140 °C, one peak is observed in form III in the region where the double peak is observed in form II, see the arrow.

Fig. 1a shows that the spectrum of form III at room temperature appears as the envelope of the phonon peaks of form II in the 25–100 cm⁻¹ region. In the very low-frequency region (<25 cm⁻¹), 2 sharp bands are detected in form II, while an enhanced intensity is observed in form III without the presence of phonon peaks. This low-frequency intensity can be interpreted as quasielastic intensity inherent to dynamical disorder in form III. By contrast, a phonon peak is clearly observed around 20 cm⁻¹ in the spectrum of form III cooled down to −140 °C and collected at this temperature, in the region of the 2 low-frequency phonon peaks of form II. It is worth noting that the presence of the additional peak in the spectrum of form III collected at −140 °C can be associated with the intensity decrease in the low-frequency region below 25 cm⁻¹. It is clearly observed in Fig. 1b that at −140 °C, the spectrum of form III can no longer be considered as the envelope of phonon peaks in form II. Consequently, the temperature dependences of the low-frequency spectra of forms II and III were analyzed. They are plotted in the low-temperature region for better clarity in Fig. 2.

Fig. 2 Temperature dependence of the low-frequency spectrum of LIN (a) in form III in the logarithm X-scale for clear observation of the low-frequency band; the arrows highlight the soft mode and the Raman band which exhibits a strong temperature dependence; (b) in form II; the arrow localizes the Raman band which exhibits a temperature dependence similar to that of the Raman band localized by the thick black arrow above 0 °C.

Fig. 2a clearly reveals the typical temperature dependence of a soft mode, characterized by the significant broadening of the 20 cm⁻¹ band associated with the shift towards the low frequencies upon heating. Above −60 °C the phonon is clearly overdamped and the band progressively disappears into the Rayleigh wing to make a contribution to the quasielastic intensity. At higher frequencies, it can be observed that some phonon peaks are merging into broad Raman bands, leading to the envelope of phonon peaks of form II observed at room temperature in Fig. 1a. The temperature dependence of form II doesn’t exhibit drastic changes. Only 3 bands detected between 50 and 65 cm⁻¹ localized by the arrow at −130 °C in Fig. 2b merge into a broad band upon heating. Spectra of forms II and III are fitted at various temperatures between −140 and 110 °C. Fitting procedures are described in the ESI† in Fig. S2 and S3 for form III and form II respectively. The temperature dependences of the frequencies of Raman bands detected between 0 and 65 cm⁻¹ are plotted in Fig. 3 for both crystalline forms.

Fig. 3 Temperature dependence of frequencies of low-frequency modes in form II and form III; (a) for Raman bands detected below 25 cm⁻¹; it is clearly observed that in the very low-temperature range the soft mode in form III is localized at the position of the barycenter of the double peak in form II, while the temperature dependence of its position is drastically stronger than those of both peaks in form II; (b) for Raman bands detected between 35 and 65 cm⁻¹. Dashed blue lines correspond to the fitting procedures in the framework of the hard-core model. This temperature dependence is also clearly stronger than those of other peaks. It is also noticeable that above 0 °C the temperature dependence of this peak is significantly less marked and is rigorously superimposed with that of a peak in form II. The vertical black dashed lines localize the temperature of the phase transition.

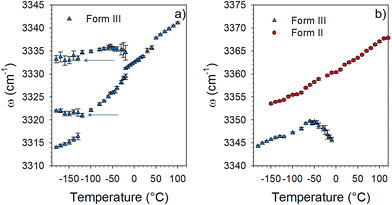
Fig. 3 shows that two Raman bands exhibit a strong temperature dependence in form III. The first corresponds to the soft mode which disappears into the Rayleigh wing around −50 °C. The softening of this phonon peak observed in Fig. 2a and 3a is accompanied by a significant broadening. Fig. 3b shows that the Raman band detected at about 65 cm⁻¹ at −140 °C (localized by the thick black arrow in Fig. 2a) also exhibits a strong frequency downshift upon heating up to about −10–0 °C. Above 10 °C, the temperature dependence of the frequency is significantly less pronounced, and is rigorously superimposed with that of a Raman band active in form II (localized by the arrow in Fig. 2b). It can be observed in Fig. 2b and 3b that this band splits in 3 bands below −10 °C in form II while no other change can be detected, suggesting the absence of phase transition in the low-temperature region of form II. Only this band has the same frequency in the two different forms above −10 °C. Given the high flexibility of the molecule this band could be attributed to internal vibrations involving the oxazolidine-amide branches, recognized as highly flexible.⁵ Torsion motions represented by arrows in Fig. S1 (ESI†) could be involved in this Raman band. Density functional theory (DFT) calculations were performed using the software TmoleX (TURBOMOLE). These calculations have shown that torsional motions (see the ESI† movie files) are actually involved in low-frequency bands. The temperature dependence of these internal motions could be driven by an order–disorder process induced by the freezing of these motions. These motions are thermally activated, and could trigger the order–disorder transition, as a soft mode triggers a displacive transition. They can represent the motions in a double well described by the hard-core model in the disordered form III. The temperature dependence of this band frequency was then fitted using the following equation:¹⁵

ω = ω₀²[1 + γ(T − T_C)]

where T_C ≈ 0 °C is the transition temperature, ω₀ is the hard-core frequency at T_C and γ the thermal coefficient is directly related to the energy barrier of the double well potential. The good agreement between the fitting curve and experimental frequencies observed in Fig. 3b strongly suggests the order–disorder mechanism. On the other hand, the softening of the very low-frequency mode cannot be described by the classical temperature dependence of a soft mode.¹⁶ By contrast, the temperature dependence of the hard-core mode satisfactorily fits the experimental frequencies, as shown in Fig. 3a. This model predicts that this mode shifts to 11.6 cm⁻¹ at T_C = 0 °C, not to zero as could be expected for lattice mode softening and disappearing in the Rayleigh wing.

Beyond the region of lattice modes extends the domain of internal modes. The number of internal modes is directly related to the number of atoms within the molecule. Additionally, the number of active Raman bands depends both on symmetries of the molecule and the lattice. This domain can be divided in two regions, i.e. the 800–1800 cm⁻¹ and 2800–3800 cm⁻¹ regions.

Medium frequency region (800–1800 cm⁻¹). The medium frequency range lying between 800 and 1800 cm⁻¹ corresponds to the vibrations of the molecular skeleton,¹⁰ and thus can be considered as distinctive of the molecular fingerprint. The 1500–1800 cm⁻¹ region was specifically investigated for analyzing the C=O stretching vibration, since this bond is commonly involved in C=O⋯H hydrogen-bonding molecular associations.¹⁰ The spectra of forms II and III collected in this region at −140 and 20 °C are plotted in Fig. 4.

Fig. 4 Raman spectra in the C=O stretching region at room and low temperatures in forms II and IV; the arrows localize Raman bands which exhibit opposite frequency shift vs. temperature.

It can be observed in Fig. 4 that two bands (localized by arrows) have a frequency dependence on temperature. The temperature dependences of these frequencies are plotted in Fig. 5 from the fitting procedure described in Fig. S4 in the ESI.† The Raman band around 1730 cm⁻¹ shifts towards the high frequencies upon heating while the band located at 1630 cm⁻¹ exhibits an opposite temperature dependence in both forms of LIN. Such a positive frequency increase upon heating is distinctive of bonds involved in H-bonding. Consequently, this band can be assigned to the C=O stretching vibration, involved in C=O⋯H hydrogen bonding. Fig. 5b clearly shows that the temperature dependence of the frequency is stronger in form III. The lower position of this band in form III cooled below 0 °C than in form II, indicates that intermolecular H-bonds are stronger in form III than in form II, while upon heating above 0 °C it's the converse. In Fig. 5a, a similar temperature dependence can be observed in the two forms for the frequency of the band located around 1630 cm⁻¹. The lowest frequency of this band in form III can be considered as reflecting the higher flexibility of the molecule in form III.

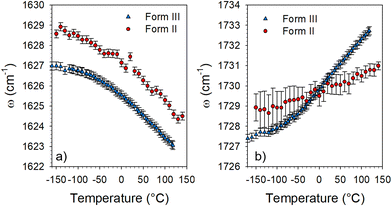Fig. 5 Temperature dependence of the frequency of two Raman bands detected in the 1550–1750 cm⁻¹ region.

The high-frequency range lying between 2800 and 3800 cm⁻¹ is the domain of X–H stretching vibrations (X = C, O, and N). It was investigated for obtaining additional information about molecular associations via C–H⋯O, O–H⋯O and N–H⋯O H-bonding in forms II and III. The spectra collected in each form at low (−140 °C) and high temperature (100 °C) were plotted in Fig. 6.

Fig. 6 High-frequency Raman spectra collected at low and high temperatures in forms II and III. The arrow localizes a C–H stretching band considered as the signature of C–H⋯O H-bonding; the green box defines N–H stretching bands showing the existence of N–H⋯O H-bonding.

The low-frequency region of spectra plotted in Fig. 6 is usually attributed to C–H stretching vibrations, while the 3300–3400 cm⁻¹ region is assigned to N–H stretching vibrations. Intriguingly, the N–H stretching spectrum of form III contains a greater number of bands in the low-temperature range of the disordered phase (form III) than on form II. In the high-temperature range only one band is detected as being significantly more broadened than in form II, as it can be expected for a disordered phase. This spectral range was carefully analyzed from the fitting procedure described in Fig. S5 in the ESI.† The temperature dependences of the band frequencies are plotted in Fig. 7.

Fig. 7 Temperature dependence of the frequency of N–H stretching bands collected in forms II and III; (a) between 3310 and 3340 cm⁻¹ (the arrows show additional components detected upon cooling which are frequency temperature independent) and (b) between 3340 and 3370 cm⁻¹.

Fig. 7 shows that the broad band detected around 3340 cm⁻¹ at 100 °C in form III (see the green box in Fig. 6) splits in several components between 0 and −130 °C. Two components emerging in the low-temperature range exhibit a positive temperature dependence of the frequency. This indicates the existence in the low-temperature range of two different types of H-bonding involving N–H bonds. Additionally, the quasi temperature independence, below −100 °C of the frequency of two components (see arrows in Fig. 7a) indicates that some N–H bonds are not involved in H-bonding. The very different frequencies of these two Raman bands suggest different molecular neighboring inherent to various molecular configurations. Consequently, the coexistence of different H-bonded via N–H bonds and non-H-bonded molecules clearly reveals the disordered configuration of LIN molecules upon cooling form III below 0 °C. In contrast, only one relatively sharp band is detected in the spectrum of form II over the whole temperature range. The positive temperature dependence of its frequency clearly indicates the existence of only one type of H-bonding via N–H bonds. Given that the frequency of this band is significantly higher in form II than in form III, molecular interactions can be considered as weaker in form II. Additionally, the analysis of the C–H stretching spectrum in Fig. 6 reveals significant changes in the 2900–3020 cm⁻¹ range between low and high temperatures. The arrow localizes a Raman band shifting towards the high frequencies upon heating which indicates H-bonding involving C–H bonds not existing in form II. The analysis of the high-frequency spectrum clearly indicates the existence of a variety of H-bonds in form III, while only one type of H-bond was detected in form II. This can be related to a greater flexibility of the molecule as can be expected in the high-temperature phase. By lowering the temperature in the metastability domain of form III (T < 150 °C), the slowing down of the dynamics of the molecule generates a distribution of molecular conformations slightly different from that existing in form II. This can explain the Raman band-shape observed in the low-frequency spectrum of form III which can be described as resulting from the broadening of phonon peaks in form II.

In view of Raman investigations, form III is more stable at high temperature because of additional and stronger H-bonding interactions. Low-frequency investigations have revealed the disordered character of form III, which can be preserved to be deeply metastable from 150 °C down to 0 °C. A phase transformation of phase III was detected via a soft mode well detected below −30 °C, which usually considered as a signature of a displacive transition.^16–20 Consequently, DSC and powder X-ray diffraction experiments were carried out in the low-temperature range in order to better describe this transformation.

3.2. DSC experiments

The DSC trace was collected upon heating (5 °C min⁻¹) and plotted in Fig. 8. This trace reveals a low energy endothermic feature spreading over around hundred degrees, between 0 and −100 °C.

Fig. 8 DSC trace collected upon heating form III previously cooled from 160 °C down to −160 °C; the thick dashed line highlights the endothermic feature and the vertical dashed line defines the upper limit of the endotherm.

The observation of this widespread endothermic feature agrees with the spectral modifications detected upon cooling form III, indicating a phase transformation of form III into another form called III′. The enthalpy of transformation was estimated to be ΔH(III′ → III) = 1.35 kJ mol⁻¹, which can be compared to those corresponding to the polymorphic transformation via melting of form II ΔH(II → liquid) = 11.53 kJ mol⁻¹,⁵ and ΔH(liquid → III) = 1.66 kJ mol⁻¹ determined in a previous study⁵ upon heating form II at 10 °C min⁻¹.

3.3. Powder X-ray diffraction experiments

PXRD patterns are plotted in Fig. 9 at room temperature and −150 °C. Intriguingly, this figure reveals the merging of Bragg peaks into a broad peak by lowering the temperature in 2θ-regions localized by red frames. The PXRD pattern collected at −150 °C can be interpreted as reflecting a distribution of slightly distorted molecular conformations.

Fig. 9 PXRD patterns of form III at room temperature and form III cooled down to −150 °C. Both boxes define 2θ-regions which were more deeply investigated.

The temperature dependence of the PXRD pattern in these 2θ-regions are more clearly presented in Fig. 10.

Fig. 10 Temperature dependence of two 2θ-regions: (a) 12–20°; (b) 20–28°; thick arrows highlight broad Bragg peaks at low temperature splitting in several Bragg peaks (thin arrows) upon heating.

Fig. 10a shows that the broad Bragg peak localized by the thick arrow gradually splits in 4 peaks upon heating up to room temperature. Splitting is also observed in Fig. 10b around 2θ = 22.5 and 26°. These observations point out the disordered character of the low-temperature form III′.

The X-ray diffraction patterns collected at several temperatures between 30 and −160 °C were refined using the ‘profile matching’ option¹³ of the FullProf program¹⁴ from the cell parameters determined at 20 °C using the DICVOL program.

The results of XRD pattern refinements obtained at 20 and −160 °C are presented in Table S1 in the ESI.† The corresponding refined diffraction patterns are plotted in Fig. S6 in the ESI.† The results obtained at 20 °C are found in good agreement with those previously obtained by Maccaroni et al.⁵ The unit cell parameters were determined using the profile matching options at various temperatures from room temperature down to −160 °C. Each diffraction pattern was successfully refined from the unit cell parameters determined at room temperature. The temperature dependence of the volume of the triclinic unit cell is plotted in Fig. 11a. It can be observed that the volume decreases with temperature decreasing only in the low-temperature range below 0 °C. Fig. 11a shows a reduction of the unit cell volume of about 3% over more than 100 °C. By contrast to the size reduction of the unit cell volume, Fig. 11b shows the increase of the c parameter with decreasing temperature between room temperature and −100 °C. The temperature dependence of the two other cell parameters is plotted in Fig. S7 in the ESI.† However, the broadening of Bragg peaks appears as the most striking feature highlighted by PXRD analyses. The temperature dependence of the full width at half-maximum (FWHM) of the isolated (110) Bragg peak is plotted in Fig. 11c. This peak detected at 2θ ∼ 13.5° at room temperature, appears as one of the most intense peaks in the PXRD pattern of form III plotted in Fig. 9. A drastic broadening can be observed via temperature decrease from −50 °C down to −160 °C. Consequently Fig. 11 indicates modifications in the molecular organization below 0 °C.

Fig. 11 Temperature dependence of structural data resulting from profile matching refinements: (a) volume of the unit cell; (b) c parameter of the triclinic unit cell; (c) full width at half-maximum of the (110) Bragg peak detected at 2θ = 13.5° at 20 °C.

3.4. Synthesis and contribution of Raman, DSC and PXRD investigations to the understanding of the low-temperature phase transformation of linezolid

A low-temperature phase transition was mostly revealed by low-frequency Raman spectroscopy investigations via the detection of a soft mode. It was confirmed by the detection of a low energy endothermic feature spread over a hundred degrees (Fig. 8). The softening of the lattice mode is clearly related to the temperature behavior of the Raman band located around 50 cm⁻¹. This band is detected at the same frequency and exhibits the same temperature dependence in forms II and III above 0 °C. It was therefore assigned to the same internal distortion of the flexible molecule in both forms. Below 0 °C this band splits into three bands in form II, while a significant and unusual temperature dependence of its frequency, mimicking the softening of the lattice mode, is observed in form III. Intriguingly, the softening of the very low-frequency lattice mode does not follow the classical temperature dependence of a soft mode (∝(T_C − T)^1/2).¹⁶ Both bands located at 20 and 50 cm⁻¹ show temperature dependence distinctive of hard-core modes. In molecular materials order–disorder transitions are mostly triggered by intramolecular motions.^21,22 It can be understood that torsional motions of the very flexible molecule can be coupled with very low-frequency lattice vibration characterized by very low interaction potential energy. This order–disorder process is only observed in the disordered form III, described by two molecules with different conformations, while the unit cell of form II is composed of only one molecular conformation.

In addition to these low-frequency features, extra N–H stretching bands are detected by lowering temperature in form III, indicating the existence of non H-bonded molecules and two different N–H⋯O molecular associations while only one band is detected in form III above 0 °C and in form II over the whole temperature range, interpreted as the signature of only one type of N–H⋯O molecular association. Consequently, the phase transformation of form III into form III′ below 0 °C could be driven by a freezing of the molecular distortions (internal motions) coupled to the freezing of a lattice mode, triggering an order–disorder mechanism. The existence of various molecular conformations in form III′ can explain the broadening of Bragg peaks in the low-temperature range (in form III′), progressively sharpening and splitting upon heating into form III. The detection of a lattice mode mimicking a softening recognized as the criterion of a displacive phase transformation^16,23 and the existence of a distribution of molecular conformations at low-temperature could suggest the description of the low-temperature phase transformation of form III as a hybrid displacive – order/disorder transition, as previously observed in several compounds.^19,24 However, the absence of symmetry breaking, the evidence of a distribution of molecular conformations and the temperature dependence of two vibrational modes indicate an order–disorder mechanism. This uncommon III → III′ transformation can be reported in a Gibbs diagram in Fig. 12, showing the thermal route for reaching form III′ from room temperature.

Fig. 12 Gibbs diagram of linezolid. Thin red arrows show the thermal route for reaching from room temperature (RT) the newly revealed form III′. The thick red arrow highlights the temperature region corresponding to the III → III′ transformation.

4. Conclusions

The present study describes an original low-temperature phase transformation in linezolid, a molecular material which is an active pharmaceutical ingredient. It was shown that form II transforms into a lower symmetric form III upon heating above 150 °C via powder melting. Low-frequency Raman investigations highlighted the very disordered character of this low symmetric phase, the spectrum of form III between 20 and 150 cm⁻¹ mimicking the envelope of the phonon peaks of form II. A phase transformation was detected in the low-temperature range mostly via Raman spectroscopy which is very sensitive to detect molecular disordering processes both in the low- and high-frequency regions. The analyses of the temperature of the Raman spectrum collected in a wide spectral region have revealed an order–disorder mechanism triggered by torsional vibrations. PXRD analyses have shown the loss of the long-range order via strong Bragg peaks broadening without detectable change in the unit cell, i.e. without symmetry breaking. Intriguingly, the ordering process induced by the freezing of torsional motions results in a very disordered state.

Data availability

Data supporting this article have been included as part of the manuscript and the ESI.†

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The generous financial support provided by the French Embassy in Poland to the first author under the SSHN scholarship for a high-level scientific visit to UMET, grant number 148767Z, is sincerely appreciated.

References

1. A. D. Bond and Curr Opin, Solid State Mater. Sci., 2009, 13, 91–97.
2. L. Yu, Acc. Chem. Res., 2010, 43, 1257–1266.
3. R. Censi and P. Di Martino, Molecules, 2015, 20, 18759–18776.
4. D. Singhal and W. Curatolo, Adv. Drug Delivery Rev., 2004, 56, 335–347.
5. E. Maccaroni, E. Alberti, L. Malpezzi, N. Masciocchi and C. Vladiskovic, Int. J. Pharm., 2008, 351, 144–151.
6. J. Frelek, M. Gorecki, M. Laszcz, A. Suszczynska, E. Vass and W. Szczepek, Chem. Commun., 2012, 48, 5295–5297.
7. E. Wielgus, P. Paluch, J. Frelek, W. Szczepek and M. Potrzebowski, J. Pharm. Sci., 2015, 104, 3383–3392.
8. M. S. Bergren, Linezolid-crystal form, US 6559305 B1, 2003.
9. D. Mohan Rao and P. Krishna Reddy, WO 2007/026369 A1, 2007.
10. A. Hédoux, Adv. Drug Delivery Rev., 2016, 100, 133–146.
11. T. Roisnel and J. Rodriguez-Carvajal, Mater. Sci. Forum, 2001, 378–383.
12. A. Boutlif and D. Louer, J. Appl. Cryst., 2004, 37, 724–731.
13. A. Le Bail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447–452.
14. J. Rodriguez-Carvajal, LLB, CEA/SACLAY France, 2001.
15. P. da R. Andrade and S. P. S. Porto, Solid State Commun., 1974, 14, 547–550.
16. R. Currat and T. Janssen, Solid State Phys., 1988, 41, 201–302.
17. M. T. Dove, Am. Mineral., 1997, 82, 213–244.
18. Y. Vysochanskii and A. Drobnich, Condens. Matter Phys., 2002, 4, 669–683.
19. J. T. Wang, S. Hall, Y. Zhen and Z. W. Sun, Ferroelectrics, 2009, 386, 94–104.
20. S. Aubry and R. Pick, J. Phys. France, 1971, 32, 657–670.
21. M. Asher, M. Bardini, L. Catalano, R. Jouclas, G. Schweicher, J. Liu, R. Korobko, A. Cohen, Y. Geerts, D. Beljonne and O. Yaffe, J. Phys. Chem. Lett., 2023, 14, 1570–1577.
22. S. Forss, J. Raman Spectr., 1982, 12, 266–273.
23. A. Grunebohm, A. Hutten, A. Bohmer, J. Frenzel, I. Eremin, R. Drautz, I. Ennen, L. Caron, T. Kuschel, F. Lechermann, D. Anselmetti, T. Dahm, F. Weber, K. Rossnagel and G. Schierning, Adv. Energy Mater., 2023, 13, 2300754.
24. S. Aubry, J. Chem. Phys., 1975, 643, 3217.

---

Footnote

† Electronic supplementary information (ESI) available: Structural description of linezolid (Fig. S1); description of the fitting procedure of the low-frequency Raman spectra collected upon cooling form III (Fig. S2); description of the fitting procedure of the low-frequency Raman spectra collected upon cooling form II (Fig. S3); description of the fitting procedure of the mid-frequency spectra (1550–1800 cm⁻¹) collected at low temperature after cooling forms II and III down to −150 °C (Fig. S4); description of the fitting procedure of the high-frequency Raman spectra (N–H stretching mode region between 3300 and 3400 cm⁻¹) (Fig. S5); description of the refinements of the X-ray powder diffraction patterns at 293 K and 373 K (Fig. S6); temperature dependence of a and b parameters obtained from Le Bail refinements (Fig. S7); and results of XRPD pattern refinements with profile matching option of the FullProf program (Table S1). Movies showing three internal molecular motions giving a contribution to the Raman spectrum below 100 cm⁻¹. See DOI: https://doi.org/10.1039/d4cp02104e

---