Enantiopure molecules form apparently racemic monolayers of chiral cyclic pentamers

Abstract

Ultra-high vacuum scanning tunneling microscopy (UHV-STM) was used to investigate two related molecules pulse-deposited onto Au(111) surfaces: indoline-2-carboxylic acid and proline (pyrrolidine-2-carboxylic acid). Indoline-2-carboxylic acid and proline form both dimers and C₅-symmetric “pinwheel” pentamers. Enantiomerically pure S-(−)-indoline-2-carboxylic acid and S-proline were used, and the pentamer structures observed for both were chiral. However, the presence of apparently equal numbers of ‘right-‘ and ‘left-handed‘ pinwheels is contrary to the general understanding that the chirality of the molecule dictates supramolecular chirality. A variety of computational methods were used to elucidate pentamer geometry for S-proline. Straightforward geometry optimization proved difficult, as the size of the cluster and the number of possible intermolecular interactions produced an interaction potential with multiple local minima. Instead, the Amber force field was used to exhaustively search all of phase space for chemically reasonable pentamer structures, producing a limited number of candidate structures that were then optimized as gas-phase clusters using density functional theory (DFT). The binding energies of the two lowest-energy pentamers on the Au(111) surface were then calculated by plane-wave DFT using the VASP software, and STM images predicted. These calculations indicate that the right- and left-handed pentamers are instead two different polymorphs.

---

1 Introduction

Studies of molecular chirality at surfaces benefit a wide range of fields, including enantioselective heterogeneous catalysts,^1–3 2D chiral crystal engineering,^4–6 chirality in 2D nanomaterials,^7,8 and determination of the fundamental role of chirality in crystallization.^9,10 Understanding enantioselective crystallization has significant practical applications, for instance, the development of single-enantiomer active pharmaceutical compounds.^11,12 Chiral molecular self-assemblies on metal surfaces have been studied via a variety of surface science techniques,¹³ particularly scanning tunneling microscopy (STM),^1,13–26 as the submolecular resolution affords insight into the structural details of two-dimensional crystal structures.

Any arrangement of enantiopure molecules necessarily remains chiral; this includes monolayer or other structures formed when molecules adsorb onto a surface.^6,17,27–29 Indeed, many examples exist where enantiopure adsorbates transfer their molecular chirality to the surface, which then exhibits global chirality.^16,30–35 So far, we have only read of two exceptions to this phenomenon. In the first, Walba et al. observed apparently heterochiral domains forming when depositing the enantiopure samples of the chiral liquid crystalline 4-[(S)-2-ethoxypropoxy]phenyl 4-(decyloxy)benzoate; they determined these were instead “quasi-enantiomorphous” domains resulting from different monolayer structures.³⁶ In the second, the S-enantiomer of a chiral diacetylene isophthalic acid forms an enantiomorphous lamella structure that is not correlated to the surface. Zhang et al. explained that the self-assembled monolayers did not follow the molecular chirality due to the stereocenter being forced away from interacting with the surface, which was believed to drive the organization.³⁷ In both systems, chirality appears to be lost in STM images, ultimately because the chiral center does not propagate to form structures that are apparent to the microscope.

Much of the work in our group revolves around studying molecular “families,” or studying many derivatives of the same molecular backbone to probe the effect different functional groups have on the intermolecular interactions that drive self-assembly.³⁸ One such molecule, the achiral indole-2-carboxylic acid, adsorbed to the surface of Au(111) in chiral cyclic pentamers after pulse deposition.^39,40 However, under vapor deposition conditions it forms catemer chains, thus showing that pulse deposition can lead to interesting metastable assemblies on surfaces.⁴¹ In this study, we look at another molecule in the same family, S-(−)-indoline-2-carboxylic acid (S-ICA), the chiral analog of indole-2-carboxylic acid. We found that the chirality of S-ICA does not clearly transfer to the monolayer, but instead forms a monolayer that appears to be a racemic mixture of chiral pinwheel-like pentamers. We continue the study by investigating a similar family of molecules (related by removing the fuzed benzene ring) that include S-(−)-pyrrolidine-2-carboxylic acid (S-proline). Structures of these molecules are shown in Fig. 1. The S-proline molecule also did not pass chirality to the monolayer, instead showing the same mixture of left- and right-handed pinwheel pentamers.

Fig. 1 Molecular structures of the molecules used in this study: (a) S-indoline-2-carboxylic acid (S-ICA) and (b) S-proline.

2 Methods

2.1 Experimental

Au(111)-on-mica thin films were cleaned in high vacuum with two cycles of Ar⁺ sputtering (0.55 kV for 15 min) and subsequent annealing at 350–400 °C, which we found to yield flat, clean surfaces of Au(111) with the characteristic “herringbone” reconstruction. Cleaned samples were allowed to cool before being transferred to a load-lock chamber for preparation of the monolayer. All molecules used in this study were purchased from Sigma Aldrich and used without further purification: S-(−)-indoline-2-carboxylic acid (S-ICA) ≥99%, L-proline (S-proline) ReagentPlus® ≥99%. Solutions with a concentration of 10 mM were prepared in methanol (unless otherwise noted). Droplets of solutions of interest were delivered via a pulsed-solenoid valve (Parker Instruments, Series 9, Iota One Driver, 0.5 mm diameter nozzle) onto the cleaned Au(111) substrate kept at room temperature in a load-lock chamber. Before the deposition, the load-lock chamber was at pressures <5 × 10⁻⁶ Torr. During the deposition, the pressure rose significantly and then returned to the baseline within a minute. The sample was then transferred to an Omicron LT-STM, kept at a base pressure of 5 × 10⁻¹⁰ Torr, and was cooled to 77 K. All images were acquired with a Pt/Ir tip in constant current mode with a tunneling current of 10 pA and a tip-sample bias of +1.0 V unless otherwise noted.

2.2 Computational

Because the clusters we are studying are quite large, DFT became computationally expensive. To narrow the size of the problem, we used a less accurate but much more affordable force-field method to achieve reasonable starting points for the more expensive electronic-structure calculations. This dramatically lowered our computational cost while still allowing us to probe tens of thousands of pentamer configurations.

The simulations of proline pentamers used the Amber22 force field in the Gaussian 16 software package.^42,43 A single zwitterionic proline monomer was first geometrically optimized, then used as the building block to generate pentamers. As a C₅-symmetric pentamer can be defined by three angles and a distance, a script was used to produce ∼18 000 starting configurations for proline pentamers that covered all of geometric phase space. An initial single-point energy calculation allowed us to rank each cluster by starting energy. Geometric optimization of the lowest 3000 starting configurations in the Amber force field resulted in 60 unique configurations. These configurations were then geometrically optimized using DFT at the B3LYP/6-31g(d) level of theory.

All pentamer-on-gold calculations were performed utilizing VASP.^44–47 A slab of Au(111) was constructed with the dimensions of 6 × 5 × 3 gold atoms with 10 Å of vacuum above and below the slab. The lattice constant was found to be 4.2 Å. All calculations were conducted with a PBE functional with an energy cutoff (encut) of 500 eV. The k points used were [7, 7, 1] with an energy difference of 1 × 10⁻⁵ eV.

Pentamer configurations were placed on the surface of the gold and single-point calculations were performed for both nitrogen-up and nitrogen-down orientations of the pentamer. The pentamer was raised off the surface at varying heights. For the nitrogen-up orientation, the height is defined as the height of the top of the surface to the lowest oxygen in the pentamer. As for the nitrogen-down orientation, the height is defined as the height of the top of the surface to the lowest carbon atom. Single-point calculations were conducted for the gold slab, each pentamer, and the pentamer on the gold slab. All binding energies were calculated by:

E_{binding energy} = E_{slab & pentamer} − E_slab − E_pentamer (1)

3 Results and discussion

3.1 Indoline-2-carboxylic acid monolayers

Fig. 2 shows an STM image of the S-ICA monolayer after pulse deposition. The majority species cluster on the surface was the tightly packed pinwheel-like structures seen in Fig. 2. These pentamers are similar in structure to those we observed previously in the monolayer of indole-2-carboxylic acid and isatin.^39,48 These pentameric clusters are quite stable, remaining on the surface after thermal annealing to 30–40 °C, but desorbing when annealed to 65–70 °C. S-ICA pentamers also form via vapor deposition, so they are not preparation-method dependent as previously observed for indole-2-carboxylic acid pentamers.^39,41

Fig. 2 STM image (139 × 139 Å) of S-ICA pulse deposited in methanol on the Au(111) surface, with red (R-) and blue (S-) circles indicating the handedness of each pentamer. The pentamers appear to be approximately hexagonally packed, with the unit cell rhombus measuring 17.2 ± 1.4 and 60 ± 6.0°.

Fig. 3(A) and (B) shows pulsed deposited S-ICA onto Au(111) using acetonitrile as the solvent. Fig. 3(A) shows that the pentamer structure is still present on the surface of the gold, so the pentamer structure is observed using at least two different solvents. However, when acetonitrile is used as the pulse-deposition solvent, a new phase is observed: parallel dimer chains, highlighted in Fig. 3(A) and (B). Dimer chains were not observed for S-ICA using methanol as the solvent for pulse deposition, but are a common structural motif for carboxylic acids.⁴⁹ X-ray crystallography data for S-ICA confirms a zwitterionic dimer-based crystal structure (see ESI†). The parallel chains observed in Fig. 3(A) and (B) are similar to those in the crystal structure of S-ICA.

Fig. 3 (A) and (B) Monolayer of S-ICA pulse deposited in acetonitrile consists of both phases of pentamers and dimer chains; representative pentamers are colored in light blue and dimer chains are colored in green and blue (200 × 200 Å and 148 × 148 Å, respectively).

In our previous studies of clusters and monolayers produced through pulse deposition, the choice of solvent has been shown to affect the range of structures formed, though the mechanism by which this occurs remains uncertain.^48,50–52 Simple chemical intuition (e.g., zwitterions favored in polar solvents) does not have strong predictive power.^53–58

Analysis of STM images was done in an automated fashion with minimal user input. First, the centroid of each pentameric cluster was determined, and the molecular features in the STM image fit to a function of the form sin 5θ + ϕ. The chirality can then be measured by the dependence of ϕ on radius (distance from the centroid)—that is, for left-handed pentamers ϕ increases with radius, while ϕ decreases for right-handed pentamers. The calculated chirality is shown in Fig. 2, with pentamers circled in red and blue for R- and S-pentamers, respectively. Once the orientation and chirality of every pentamer in the image have been determined in this fashion, clusters of like chirality can be overlapped (and reoriented as necessary), and the numerical average of the STM image calculated. These composites are what is shown in Fig. 4(A) and (B). Fig. 4(C) is a tight zoom on the S pentamer with a line drawn from the centroid of the pentamer cluster through the top molecule. As all mirror planes must contain the C₅ axis, the lack of mirror symmetry in Fig. 4(C) makes the chirality of the cluster evident. We automated a count, Fig. 2, of 226 pentamer clusters over 5 scanned areas and determined the chirality split to be 118 : 108 (R : S). This is indistinguishable from a binomial distribution that assumes equal probabilities, which gives a most likely result of 113 with a standard deviation of 7.5 (see ESI†).

Fig. 4 (A) Composite of left-handed pentamers shown in the image in Fig. 2 (25 × 25 Å). (B) Composite of right-handed pentamers shown in the image in Fig. 2. The pentamer is distinct from that in (A). (C) One lobe of the composite left-handed pentamer with a line drawn from the centroid of the pentamer cluster through the centroid of a single lobe. As there is a clear imbalance of electron density on either side of the line, it does not constitute a mirror plane, defining the structure as chiral.

The mixing of the R- and S-pentamers of the S-ICA monolayer shown in Fig. 2 is peculiar. In addition to the equal total numbers of R- and S-pentamers, there is no obvious segregation of homochiral pentamers into separate domains. This is analyzed quantitatively, showing only a slight deviation from a random mixture for nearest-neighbor and next-nearest-neighbor pentamers (see ESI,† Fig. S1). This implies that there are no significant short-range interactions between left- and right-hand pinwheels, so that one geometry does not seed the growth of a domain; or, alternately, there must be a very large number of “seeds” such that many domains grow and merge. As we do observe the characteristic “herringbone” reconstruction of the gold surface underneath the monolayer, the kinks that accompany this reconstruction could be one source of such nucleation sites. Diffusion of pentamers may also be limited because of their size, the high surface coverage, or the peculiar condition that result during the pulse-deposition process.⁵⁹ In contrast, most of the extant literature reports that when mirror-image enantiomorphs are present on the surface, they phase separately into two homochiral domains (conglomerates).^16,60–62 These conglomerates typically consist of homochiral molecular adsorbates, in which both enantiomers self-assemble in different domains.⁶²

A racemic mixture of pentameric structures is surprising given that the deposited molecule is purely the S-enantiomer. Typically, for a racemic mixture of 2D crystals to form, a racemic mixture of the starting molecule must be adsorbed.⁶¹S-ICA should not racemize during or after deposition as the energetic barrier to switch to R-ICA is far higher than kT, especially at our operating temperatures.^63,64 Supramolecular chirality usually results from the chirality of the starting molecule,⁶⁵ except in limited cases.^36,37 Because S-ICA is a small molecule, the stereocenter would be forced to interact with the surface, so we would expect the chirality of the molecule to be passed to the surface, forming an enantiomorphous monolayer.^16,17

3.2 S-Proline monolayers

S-Proline and S-ICA have very similar chemical structures, Fig. 1(a) and (b), S-proline differing only in the absence of the benzene ring fused to the five-membered heterocycle. Because the amine and carboxylic acid groups remain in the same positions, we expected the chemical interactions to be quite similar to those of S-ICA. Indeed, when we scan S-proline after pulse deposition, Fig. 5, we find both the pentamer and dimer phases present in the image. Additionally, we observe that the proline pentamers are chiral and form an apparently racemic mixture, just as the S-ICA pentamers do.

Fig. 5 STM images of S-proline pulse deposited on Au(111). (A) Pentamers and dimer chains are observed (450 × 450 Å). (B) Representative pentamers are colored in light blue, and right-handed and left-handed pentamers are present in the monolayer. The pentamers appear to be approximately hexagonally packed, with the unit cell rhombus measuring 18.4 ± 1.6 Å and 60 ± 8.8° (169 × 169 Å).

The adsorption of amino acids on metal surfaces has been well studied. The copper surface is more reactive and commonly results in the deprotonation of carboxylic acids, resulting in adsorption in the anionic form.^66–74S-Proline adsorbes on Pd(111) in the zwitterionic form,⁷⁵ but zwitterionization does not typically occur on the less reactive gold surface^76,77 (except at elevated temperatures).⁷⁸ However, monolayers of proline have been observed on the Au(111) surface⁷⁹ that consisted of a motif reminiscent of the crystal structure of proline, in which zwitterionic molecules are bound by NH⋯O hydrogen bonds to form a two-dimensional network.⁸⁰ Given this evidence, we believe it likely that at our experimental conditions—in which molecules are deposited on the gold surface at room temperature upon adsorption—proline adsorbs on the gold surface in the zwitterionic form.

A significant difference between the current study and the aforementioned studies of amino acids on metal surfaces is the incorporation of the solution to deliver the molecule to the surface. Previous work from our group has resulted in the formation of kinetically-locked structures that have been attributed to the non-equilibrium solvent evaporation conditions present in the pulse deposition process.^39,51,81 It is possible that pentamer formation can occur independent of the non-equilibrium adsorption kinetics of solution deposition.^48,82 Nonetheless, for the case of S-proline pentamers, non-equilibrium adsorption kinetics are likely the cause of pentamer formation in our experiments because Seljamae-Green et al. do not observe pentamers of S-proline on a vapor-deposited monolayer.⁷⁹

In addition to there being no measurable preference for right-handed or left-handed pinwheels, both for the S-ICA and the S-proline, there is also no evidence for separation of these pinwheels into homochiral domains. In Fig. S1 (ESI†), the likelihood of neighboring left- and right-handed pentamers is very close to what would be expected from a random distribution. This implies that there are no significant short-range interactions between left- and right-hand pinwheels, so that one geometry does not seed the growth of a domain; or, alternately, there must be a very large number of “seeds” such that many domains grow and merge.

Fig. 6(A) and (B) shows the composite images for the S- and R-pentamers of proline. In exactly the same way as the S-ICA pentamers, the line in Fig. 6(C) does not define a mirror plane, causing the pentamer structure to be chiral.

Fig. 6 Composite of (A) left- and (B) right-handed pentamers shown in the image in Fig. 5(A) (25 × 25 Å). (C) One lobe of the composite left-handed pentamer with a line drawn from the centroid of the pentamer cluster through the centroid of a single lobe. As there is a clear imbalance of electron density on either side of the line, it does not constitute a mirror plane, defining the structure as chiral.

3.3 Molecular modeling

We used proline in our computational approach to simplify calculations and lower computational cost. S-ICA and proline are identical except for the aforementioned fused benzene ring, so the strongly interacting functional groups (carboxylic acid, amine) are shared. We expect that, if undertaken, the S-ICA calculations would yield similar results.

In the solid state, proline is in the zwitterionic form.⁸⁰ The zwitterion is also the majority species adsorbed on the surface of Au(111), though XPS of a monolayer does reveal small amounts of co-existing neutral and anionic species.⁷⁹ In our observations, proline pentamers are C₅ symmetric, which is not consistent with a mixture of different charge states. Based on the XPS data, we modeled all prolines as zwitterionic.

Gas phase DFT optimizations for systems of this size are feasible. However, we found that a geometry optimization procedure produced different solutions depending on the starting geometry used, so we could not be confident that the global minimum-energy structure or all local minima had been found. An exhaustive search of phase space was not possible, given the time required for each individual electronic structure calculation. Instead, we used Amber force-field calculations to find the type of structural configurations of proline that made physical and chemical sense, and thus to narrow down the number of starting configurations to test with DFT.

To identify all potential configurations, and thus probe phase space for these pentamers, we exhaustively sampled starting geometries of C₅ symmetric pentamer clusters. We forced all clusters to be C₅ symmetric to match our observation of C₅ symmetric pentamers in the STM images. For C₅-symmetric clusters, only three angles and one distance are needed to fully specify the internal cluster geometry, so a grid covering all values of the angles and a physically reasonable range of distances was generated, translating to ∼18 000 potential pentamer geometries. We performed single-point energy calculations on each geometry using the Amber22 force field.⁴² The 3000 lowest energy configurations were then geometrically optimized using the same force field. Our study of the optimized clusters found that all of the original 18 000 structures had either broken symmetry or converged to one of 60 C₅-symmetric clusters. Each of these clusters corresponds to a local minimum in the potential energy, as defined using Amber. The six lowest-energy clusters are shown in Fig. 7.

Fig. 7 Six lowest-energy stable or metastable C₅-symmetric S-proline pentamer structures predicted using the AMBER force field.

It is important to note that a classical force field will not produce quantitatively accurate results, especially given the importance of hydrogen bonding in these molecular clusters. The results are also necessary qualitative in nature as they are performed on gas-phase clusters; that is, in the absence of a surface. Au(111) is, however, both flat and non-reactive, and in several previous studies, we have found that gas-phase calculations provide good predictions for observed self-assembled structures.³⁸ Additional evidence for a molecule-based model of self-assembly is that molecules adsorb incommensurately, and with clusters in random orientations. This is emphatically not the case for other crystal faces of gold or other metals. For Au(111) specifically, the self-assembly of molecules can often be substantively understood based on molecule–molecule interactions while ignoring the molecule–surface interactions. This can be true even if the molecule–surface interactions are large in magnitude (as we would expect given the polarizability of gold and the large molecular dipole of proline); all that is required is that these interactions do not have significant lateral corrugation, whether directly or through substrate-mediated interactions.^83–85

3.4 DFT

Unlike 18 000 starting configurations, 60 configurations are not computationally prohibitive for DFT calculations. Using the results of the Amber calculations as starting points, we optimized the geometry of the clusters using the B3LYP/6-31g(d) level of theory. All 60 configurations optimized to one of three results, which are shown in Fig. 8(A)–(C). We believe that this approach is the most practical way to identify multiple local energy minima, though it can not guarantee it will find all of them. The geometry of the cluster in Fig. 8(C) is significantly different from the other two and is much less stable, so we consider only Fig. 8(A) (configuration A) and Fig. 8(B) (configuration B) to explain the pentamers observed experimentally.

Fig. 8 The three pentamer configurations that all DFT optimizations conformed to. In all three cases, nitrogen is on the far side of the cluster. Configurations (A) and (B) are apparently opposite chiralities, but are not mirror images, and so are diastereomers. NH⋯O hydrogen-bond contact distances are 1.63 Å in configuration A and 1.57 Å in configuration B. (C) is ignored as it is qualitatively unlike the other two, and because of its significantly less favorable binding energy. Binding energies were calculated by subtracting five times the total monomer energy from each pentamer energy. (D) Configurations A and B from an axial view with the nitrogen-up and -down sides labeled.

While configurations A and B appear qualitatively similar, they are not mirror images. This can be seen by comparing the top view, that is with respect to the C₅ axis of symmetry, of both clusters in Fig. 8(A) and (B). Then, the NH₂-to-CO₂ axis of each proline is oriented differently: clockwise for configuration A and counterclockwise for B. The clusters should be described as diastereomeric rather than enantiomeric as they have opposite handedness but are not mirror images.

The experimental images of proline and ICA show equal numbers of opposite-handedness pentamers. One hypothesis is that this results from a mixture of A and B diastereomers, with the two configurations appearing as near-mirror images due to the specifics of STM contrast. Alternately, either or both could be flipped over, adsorbed with the oxygen atoms (instead of nitrogen) in proximity to the surface, which, of course, also flips the perceived handedness of the cluster. To address these questions, we turned to DFT calculations of the surface-adsorbed clusters using VASP software.

3.5 VASP

A proline pentamer adsorbed on a gold slab is large enough that using DFT to perform a full geometry optimization is prohibitively expensive. Instead, calculations with VASP were aimed at answering specific questions important to understanding the experimental results: (1) what is the difference in binding energy when a pentamer is flipped over, nitrogen-up vs. nitrogen-down; (2) would STM be able to distinguish between clusters in nitrogen-up and nitrogen-down orientations; and (3) are configurations A and B predicted to appear as mirror images when observed using STM?

Using the DFT-optimized pentamer clusters, a series of single-point energy calculations was performed while varying the cluster–surface distance to determine the energy minimum of absorption. The potential curves for both orientations are shown in Fig. 9 for configurations A and B. We initially expected to find a strong preference for the nitrogen-down orientation because we hypothesized a nitrogen–surface interaction, but we instead see that the minimum energies in Fig. 9 are similar for both configurations A and B in both the nitrogen-up and -down orientations.

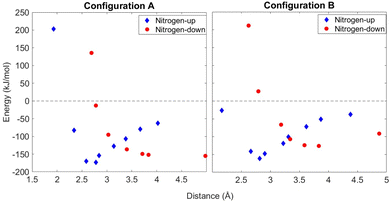Fig. 9 Calculations for both accepted clusters from Fig. 8. Single-point energy calculations were taken of both clusters from varying distances and at nitrogen-up and nitrogen-down orientations.

The formation of any pentamers at all is likely due to kinetic factors at play in the pulse deposition process, as they have not been reported in early observations of this system.^71,86 On the sole basis of calculated energies, then, all four possibilities (both configurations and both orientations) could be present in a mixture on the surface. To discriminate between them, we simulated constant-current STM images using the output of the VASP calculations, and these images are shown in Fig. 10. From these, we conclude that despite not being true enantiomers, configurations A and B are predicted to appear as mirror images in STM measurements, in both the nitrogen-down (Fig. 10(A) and (B)) and nitrogen-up (Fig. 10(C) and (D)) orientations. However, for both configurations, there is a large contrast between the two orientations. Of the two, the simulated images of the nitrogen-up orientations of configuration A and B, as seen in Fig. 10(C) and (D), are a better match to the experimental data. Fig. 11 shows the same simulated images as Fig. 10 with models of the molecules overlaid on the images. The main contrast seems to originate from the carboxyl oxygens, particularly when those atoms are in proximity to the surface (in the nitrogen-up orientation).

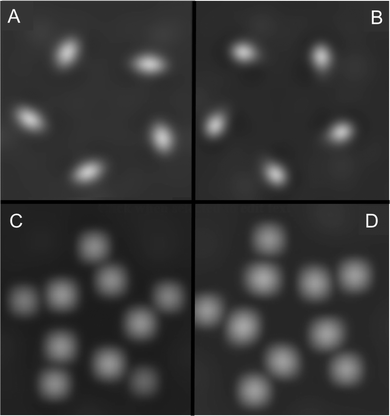Fig. 10 Simulated STM images using VASP for both accepted cluster configurations from Fig. 8 in both nitrogen-down and nitrogen-up orientations. (A) Configuration A/nitrogen-down, (B) configuration B/nitrogen-down, (C) configuration A/nitrogen-up, (D) configuration B/nitrogen-up.

Fig. 11 Simulated STM images from Fig. 10 with overlaid molecular models. (A) Configuration A/nitrogen-down, (B) configuration B/nitrogen-down, (C) configuration A/nitrogen-up, (D) configuration B/nitrogen-up.

In comparing the experimental STM images (Fig. 6) and calculated images (Fig. 10) for proline, we note that agreement is by no means quantitative: the experimentally observed molecular features are larger and less well resolved than what is predicted from the calculations. This could be the effect of limited experimental resolution, but another likely confounding factor is the simplifications made in the VASP calculation, most importantly that the geometry of the surface-adsorbed cluster was not fully optimized. However, we propose that the qualitative findings of the calculations are what is most significant: that nitrogen-up and nitrogen-down oriented clusters would be readily distinguished in STM images, while different diastereomeric configurations can appear very similar in structure, but with apparently opposite chirality.

4 Conclusion

The adsorption of both S-indoline-2-carboxylic acid and S-proline on the Au(111) surface creates pinwheel-shaped cyclic pentamers. Even though both molecules were enantiomerically pure, upon adsorption both left- and right-handed pinwheels form in an apparently racemic mixture. Electronic structure calculations confirm two C₅-symmetric diastereomers with comparable binding energies and predict that STM images of the two look nearly identical, but are mirror-imaged. Calculated STM images also rule out that there is a mixture of adsorption orientations. We conclude that the observed loss of chirality results from a near-equal mixture of diastereomeric clusters, where the apparent chirality of a pentamer on the surface is not derived from the molecular stereocenter.

Considering the relatively small NH⋯O hydrogen bond distances for both proposed pentamer configurations, we conclude that molecule–molecule interactions, specifically hydrogen bonding, drive pentamer formation for these molecules instead of being stabilized by molecule–surface interactions.

These results show that even for small organic molecules, the intermolecular interaction potential can be complex, leading to multiple local energy minima and ultimately structural polymorphism during self-assembly. This study presents one computational approach to investigate the complexities of these interactions. In addition, it highlights the importance of polymorphism in the propagation of chiral structure in self-assembly. A better fundamental understanding of chiral self-assembly may inform efforts to more effectively realize directed enantioselective crystallization, which has important implications in the development of single-enantiomer pharmaceuticals and enantioselective heterogeneous catalysts.

Data availability

CCDC 2356146 contains the supplementary crystallographic data for this paper.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support for this work has been provided by the National Science Foundation NSF grants no. CHE-1807313 and CHE-2108186. The authors would like to thank Professor William Schneider for helpful discussions.

Notes and references

1. F. Zaera, J. Phys. Chem. C, 2008, 112, 16196–16203.
2. C. Baddeley, T. E. Jones, A. G. Trant and K. E. Wilson, Top. Catal., 2011, 25, 17–28.
3. G. Kyriakou, S. K. Beaumont and R. M. Lambert, Langmuir, 2011, 27, 9687–9695.
4. J. Huan, X. Zhang and Q. Zeng, Phys. Chem. Chem. Phys., 2019, 21, 11537–11553.
5. Y. Zheng, W. Luo, L. Yu, S. Chen, K. Mao, Q. Fang, Y. Yang, C. Wang, H. Zhu and B. Tu, J. Phys. Chem. B, 2022, 126, 723–733.
6. A. Bera, S. Henkel, J. Mieres-Perez, Y. Andargie Tsegaw, E. Sanchez-Garcia, W. Sander and K. Morgenstern, Angew. Chem., Int. Ed., 2022, 61, e202212245.
7. F. Purcell-Milton, R. McKenna, L. J. Brennan, C. P. Cullen, L. Guillemeney, N. V. Tepliakov, A. S. Baimuratov, I. D. Rukhlenko, T. S. Perova, G. S. Duesberg, A. V. Baranov, A. V. Fedorov and Y. K. Gun'Ko, ACS Nano, 2018, 12, 954–964.
8. L. Ji, Y. Zhao, M. Tao, H. Wang, D. Niu, G. Ouyang, A. Xia and M. Liu, ACS Nano, 2020, 14, 2373–2384.
9. I. Kuzmenko, H. Rapaport, K. Kjaer, J. Als-Nielsen, I. Weissbuch, M. Lahav and L. Leiserowitz, Chem. Rev., 2001, 101, 1659–1696.
10. B. Sung, A. de la Cotte and E. Grelet, Nat. Commun., 2018, 9, 1405.
11. H. Caner, E. Groner, L. Levy and I. Agranat, Drug Discovery Today, 2004, 9, 105–110.
12. A. Calcaterra and I. D'Acquarica, J. Pharm. Biomed. Anal., 2018, 147, 323–340.
13. F. Zaera, Chem. Soc. Rev., 2017, 46, 7374–7398.
14. N. Jiang, Y. Wang, Q. Liu, Y. Zhang, Z. Deng, K.-H. Ernst and H.-J. Gao, Phys. Chem. Chem. Phys., 2010, 12, 1318–1322.
15. R. Raval, Chem. Soc. Rev., 2009, 38, 707–721.
16. J. A. A. W. Elemans, I. De Cat, H. Xu and S. De Feyter, Chem. Soc. Rev., 2009, 38, 722–736.
17. K.-H. Ernst, Phys. Status Solidi B, 2012, 249, 2057–2088.
18. A. Bauer, M. Maier, W. M. Schosser, J. Diegel, F. Paschke, Y. Dedkov, F. Pauly, R. F. Winter and M. Fonin, Adv. Mater., 2020, 32, 1907390.
19. J. C. Martín Romano, P. Casado Aguilar, A. L. Vázquez de Parga, M. Garnica, O. Rodríguez de la Fuente, J. M. Rojo and M. A. Niño, Phys. Chem. Chem. Phys., 2022, 24, 8022–8031.
20. L. Xie, Y. Ding, D. Li, C. Zhang, Y. Wu, L. Sun, M. Liu, X. Qiu and W. Xu, J. Am. Chem. Soc., 2022, 144, 5023–5028.
21. H. Liu, H. Li, Y. He, P. Cheng, Y.-Q. Zhang, B. Feng, H. Li, K. Wu and L. Chen, Nat. Commun., 2023, 14, 2100.
22. M.-X. Shi, J. Xu, K. Sun, M.-L. Tao, J.-Y. Yang, D.-X. Yang, Z.-L. Wang, Z. Li, J.-Z. Wang, Q.-K. Xue and S. Meng, Nano Res., 2022, 15, 5316–5321.
23. I. Baltaci, M. G. H. Schulte and C. Westphal, J. Phys. Chem. C, 2020, 124, 23648–23656.
24. L. M. Rodríguez, P. Gómez, M. Más-Montoya, J. Abad, A. Tárraga, J. I. Cerdá, J. Méndez and D. Curiel, Angew. Chem., Int. Ed., 2020, 60, 1782–1788.
25. Y. Cao, J. Mieres-Perez, J. F. Rowen, E. Sanchez-Garcia, W. Sander and K. Morgenstern, Nat. Commun., 2023, 14, 4500.
26. Z. Tessari, K. Tahara and S. De Feyter, J. Phys. Chem. C, 2023, 127, 9248–9256.
27. J. Lipton-Duffin, M. Abyazisani and J. MacLeod, Chem. Commun., 2018, 54, 8316–8319.
28. K. Tahara, Y. Kubo, S. Hashimoto, T. Ishikawa, H. Kaneko, A. Brown, B. E. Hirsch, S. De Feyter and Y. Tobe, J. Am. Chem. Soc., 2020, 142, 7699–7708.
29. Q. Han, Z. Li, K. Sun, M.-L. Tao, M.-X. Shi, D.-X. Yang, J.-X. Xia, J.-J. Wan and J.-Z. Wang, Phys. Chem. Chem. Phys., 2022, 24, 10292–10296.
30. D. G. Yablon, J. Guo, D. Knapp, H. Fang and G. W. Flynn, J. Phys. Chem. B, 2001, 105, 4313–4316.
31. S. De Feyter, A. Gesquière, P. C. M. Grim, F. C. De Schryver, S. Valiyaveettil, C. Meiners, M. Sieffert and K. Müllen, Langmuir, 1999, 15, 2817–2822.
32. A. Miura, P. Jonkheijm, S. De Feyter, A. Schenning, E. Meijer and F. De Schryver, Small, 2004, 1, 131–137.
33. M. M. Knudsen, N. Kalashnyk, F. Masini, J. R. Cramer, E. Lægsgaard, F. Besenbacher, T. R. Linderoth and K. V. Gothelf, J. Am. Chem. Soc., 2011, 133, 4896–4905.
34. M. L. Liriano, A. M. Larson, C. Gattinoni, J. Carrasco, A. E. Baber, E. A. Lewis, C. J. Murphy, T. J. Lawton, M. D. Marcinkowski, A. J. Therrien, A. Michaelides and E. C. H. Sykes, J. Chem. Phys., 2018, 149, 034703.
35. M. Maeda, K. Sato, S. De Feyter and K. Tahara, Nanoscale, 2023, 15, 19569–19576.
36. D. M. Walba, F. Stevens, N. A. Clark and D. C. Parks, Acc. Chem. Res., 1996, 29, 591–597.
37. J. Zhang, A. Gesquière, M. Sieffert, M. Klapper, K. Müllen, F. C. De Schryver and S. De Feyter, Nano Lett., 2005, 5, 1395–1398.
38. B. R. Heiner, A. M. Pittsford and S. A. Kandel, Chem. Commun., 2023, 59, 170–178.
39. N. A. Wasio, R. C. Quardokus, R. D. Brown, R. P. Forrest, C. S. Lent, S. A. Corcelli, J. A. Christie, K. W. Henderson and S. A. Kandel, J. Phys. Chem. C, 2015, 119, 21011–21017.
40. M. Wolf, V. Hayes, C. R. Gerber, P. G. Quardokus, J. J. Ortiz-Garcia, C. Plummer and R. C. Quardokus, J. Vac. Sci. Technol., A, 2020, 38, 022413.
41. F. De Marchi, D. Cui, J. Lipton-Duffin, C. Santato, J. M. MacLeod and F. Rosei, J. Chem. Phys., 2015, 142, 101923.
42. D. Case, H. Aktulga, K. Belfon, I. Ben-Shalom, J. Berryman, S. Brozell, D. Cerutti, T. I. Cheatham, G. Cisneros, V. Cruzeiro, T. Darden, R. Duke, G. Giambasu, M. Gilson, H. Gohlke, A. Goetz, R. Harris, S. Izadi, S. Izmailov, K. Kasavajhala, M. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. O'Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. Simmerling, N. Skrynnikov, J. Smith, J. Swails, R. Walker, J. Wang, J. Wang, H. Wei, R. Wolf, X. Wu, Y. Xiong, Y. Xue, D. York, S. Zhao and P. Kollman, Amber, 2022.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
44. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
45. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
46. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
47. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
48. A. M. Silski, R. D. Brown, J. P. Petersen, J. M. Coman, D. A. Turner, Z. M. Smith, S. A. Corcelli, J. C. Poutsma and S. A. Kandel, J. Phys. Chem. C, 2017, 121, 21520–21526.
49. T. Beyer and S. L. Price, J. Phys. Chem. B, 2000, 104, 2647–2655.
50. J. P. Petersen, R. D. Brown, A. M. Silski, S. A. Corcelli and S. A. Kandel, J. Phys. Chem. C, 2019, 123, 13610–13614.
51. A. M. Silski-Devlin, J. P. Petersen, J. Liu, G. A. Turner, J. C. Poutsma and S. A. Kandel, J. Phys. Chem. C, 2020, 124, 5213–5219.
52. A. M. Silski, J. P. Petersen, R. D. Brown, S. A. Corcelli and S. A. Kandel, J. Phys. Chem. C, 2018, 122, 25467–25474.
53. R. Gatti, J. M. MacLeod, J. A. Lipton-Duffin, A. G. Moiseev, D. F. Perepichka and F. Rosei, J. Phys. Chem. C, 2014, 118, 25505–25516.
54. W. Mamdouh, H. Uji-I, J. S. Ladislaw, A. E. Dulcey, V. Percec, F. C. De Schryver and S. De Feyter, J. Am. Chem. Soc., 2005, 128, 317–325.
55. T. Sirtl, W. Song, G. Eder, S. Neogi, M. Schmittel, W. M. Heckl and M. Lackinger, ACS Nano, 2013, 7, 6711–6718.
56. S. Lei, et al. , Angew. Chem., Int. Ed., 2008, 47, 2964–2968.
57. M. Lackinger, S. Griessl, W. M. Heckl, M. Hietschold and G. W. Flynn, Langmuir, 2005, 21, 4984–4988.
58. L. Kampschulte, M. Lackinger, A.-K. Maier, R. S. K. Kishore, S. Griessl, M. Schmittel and W. M. Heckl, J. Phys. Chem. B, 2006, 110, 10829–10836.
59. R. C. Quardokus, N. A. Wasio, R. D. Brown, J. A. Christie, K. W. Henderson, R. P. Forrest, C. S. Lent, S. A. Corcelli and S. Alex Kandel, J. Chem. Phys., 2015, 142, 101927.
60. T. Balandina, M. W. van der Meijden, O. Ivasenko, D. Cornil, J. Cornil, R. Lazzaroni, R. M. Kellogg and S. De Feyter, Chem. Commun., 2013, 49, 2207–2209.
61. S. Dutta and A. J. Gellman, Chem. Soc. Rev., 2017, 46, 7787–7839.
62. Y. Fang, B. D. Lindner, I. Destoop, T. Tsuji, Z. Zhang, R. Z. Khaliullin, D. F. Perepichka, K. Tahara, S. D. Feyter and Y. Tobe, J. Am. Chem. Soc., 2020, 142, 8662–8671.
63. R. H. Janke, G. Haufe, E. U. Würthwein and J. H. Borkent, J. Am. Chem. Soc., 1996, 118, 6031–6035.
64. J. Weckesser, A. De Vita, J. V. Barth, C. Cai and K. Kern, Phys. Rev. Lett., 2001, 87, 961011.
65. M. Liu, L. Zhang and T. Wang, Chem. Rev., 2015, 115, 7304–7397.
66. T. Eralp, A. Shavorskiy and G. Held, Surf. Sci., 2011, 605, 468–472.
67. T. Eralp, A. Shavorskiy, Z. V. Zheleva, G. Held, N. Kalashnyk, Y. Ning and T. R. Linderoth, Langmuir, 2010, 26, 18841–18851.
68. S. Barlow, K. Kitching, S. Haq and N. Richardson, Surf. Sci., 1998, 401, 322–335.
69. S. M. Barlow, S. Louafi, D. Le Roux, J. Williams, C. Muryn, S. Haq and R. Raval, Langmuir, 2004, 20, 7171–7176.
70. V. Humblot, C. Méthivier and C.-M. Pradier, Langmuir, 2006, 22, 3089–3096.
71. M. Forster, M. S. Dyer, M. Persson and R. Raval, J. Am. Chem. Soc., 2009, 131, 10173–10181.
72. S. Stepanow, T. Strunskus, M. Lingenfelder, A. Dmitriev, H. Spillmann, N. Lin, J. V. Barth, C. Wöll and K. Kern, J. Phys. Chem. B, 2004, 108, 19392–19397.
73. T. Schmitt, L. Hammer and M. A. Schneider, J. Phys. Chem. C, 2016, 120, 1043–1048.
74. M. Abyazisani, J. Bradford, N. Motta, J. Lipton-Duffin and J. MacLeod, Langmuir, 2019, 35, 7112–7120.
75. F. Gao, Y. Wang, L. Burkholder and W. Tysoe, Surf. Sci., 2007, 601, 3579–3588.
76. S. Clair, S. Pons, A. P. Seitsonen, H. Brune, K. Kern and J. V. Barth, J. Phys. Chem. B, 2004, 108, 14585–14590.
77. N. Zhu, T. Osada and T. Komeda, Surf. Sci., 2007, 601, 1789–1794.
78. D. Schwarz, R. van Gastel, H. J. Zandvliet and B. Poelsema, J. Phys. Chem. C, 2013, 117, 1020–1029.
79. R. T. Seljamäe-Green, G. J. Simpson, F. Grillo, J. Greenwood, S. M. Francis, R. Schaub, P. Lacovig and C. J. Baddeley, Langmuir, 2014, 30, 3495–3501.
80. J. J. Koenig, J.-M. Neudörfl, A. Hansen and M. Breugst, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2018, 74, 1067–1070.
81. R. D. Brown, J. M. Coman, J. A. Christie, R. P. Forrest, C. S. Lent, S. A. Corcelli, K. W. Henderson and S. A. Kandel, J. Phys. Chem. C, 2017, 121, 6191–6198.
82. S. Karan, Y. Wang, R. Robles, N. Lorente and R. Berndt, J. Am. Chem. Soc., 2013, 135, 14004–14007.
83. E. Hansen, A. R. Rosales, B. Tutkowski, P.-O. Norrby and O. Wiest, Acc. Chem. Res., 2016, 49, 996–1005.
84. J. Wyrick, D.-H. Kim, D. Sun, Z. Cheng, W. Lu, Y. Zhu, K. Berland, Y. S. Kim, E. Rotenberg, M. Luo, P. Hyldgaard, T. L. Einstein and L. Bartels, Nano Lett., 2011, 11, 2944–2948.
85. E. C. H. Sykes, P. Han, S. A. Kandel, K. F. Kelly, G. S. McCarty and P. S. Weiss, Acc. Chem. Res., 2003, 36, 945–953.
86. R. T. Seljamäe-Green, G. J. Simpson, F. Grillo, J. Greenwood, S. M. Francis, R. Schaub, J. E. Gano, H. A. Früchtl, P. Lacovig and C. J. Baddeley, Langmuir, 2015, 31, 262–271.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2356146. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cp02094d

---