Open Access Article
Open Access ArticleCharacterisation of the ground X+ 2ΠΩ and first excited A+ 2Σ+ electronic states of MgO+ by high-resolution photoelectron spectroscopy
C.
Kreis†
,
J. R.
Schmitz†
and
F.
Merkt
 *
*
Institute of Molecular Physical Sciences, ETH Zurich, CH-8093 Zurich, Switzerland
First published on 25th June 2024
Abstract
Despite the importance of MgO+ for understanding the electronic structure and chemical bonds in alkaline-earth metal oxides and its potential astrophysical relevance, hardly any spectroscopic information is available on this molecular cation. We report on a high-resolution photoelectron spectroscopic study of MgO using a resonant (1 + 1′) two-photon excitation scheme in combination with PFI-ZEKE photoelectron spectroscopy. By carrying out the resonant excitation via selected rotational levels of several intermediate states of different electronic configurations, total electronic spins, and internuclear distances, a broad range of vibrational levels of the X+ 2ΠΩ (Ω = 3/2, 1/2) ground and A+ 2Σ+ first excited states of MgO+ were observed for the first time. The new data provide a full characterisation of the rovibronic level structure of MgO+ up to 2 eV (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) of internal energy. A full set of vibrational, rotational and spin–orbit-coupling molecular constants were extracted for these two electronic states. The adiabatic ionisation energy and the singlet–triplet interval of 24Mg16O were determined to be 64
000 cm−1) of internal energy. A full set of vibrational, rotational and spin–orbit-coupling molecular constants were extracted for these two electronic states. The adiabatic ionisation energy and the singlet–triplet interval of 24Mg16O were determined to be 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.65(20) cm−1 and 2492.4(3) cm−1, respectively.
577.65(20) cm−1 and 2492.4(3) cm−1, respectively.
1 Introduction
This article presents a study of the structure and dynamics of the ground and first excited electronic states of MgO+, the X+ 2ΠΩ and A+ 2Σ+ states, by high-resolution pulsed-field-ionisation zero-kinetic-energy photoelectron (PFI-ZEKE-PE) spectroscopy using resonant two-photon excitation via several singlet (S = 0) and triplet (S = 1) excited states of MgO, as depicted schematically in Fig. 1. | ||
| Fig. 1 Resonant (1 + 1′) two-photon excitation scheme to access the X+ 2ΠΩ and A+ 2Σ+ states of MgO+ from the X 1Σ+ ground state (dashed black arrows) and the a 3Π2 metastable state (solid blue arrows) of MgO. The potential curves are taken from ref. 1, 2 and 3 and the triplet states of MgO are shown in blue. | ||
Alkaline-earth metal oxides (MOs) exhibit a complex electronic structure with significant configuration interaction already at low energies and a dominant role played by configurations involving M2+ and O− (2p5) centres and a single electron in orbitals centred on the M2+ ion.4,5 Molecular states arise from different combinations of such orbitals with the p-hole orbitals on O−, which can be oriented toward the metal atom (σ) or perpendicular to the internuclear axis (π).4–14 Among alkaline-earth metal oxides, MgO stands out because of particularly pronounced configurational mixing of closed (6σ)2(2π)4 and open-shell (6σ)1(2π)4(7σ)1 configurations,1,15,16 where (2π), (6σ) and (7σ) orbitals have dominant O(2pπ), O(2pz) and Mg(3s) character, respectively. This mixing leads to a formal-charge distribution intermediate between Mg+O− and Mg2+O2−, whereas the ground-state of the other alkaline-earth metal oxides primarily corresponds to a M2+O2− formal-charge distribution.5,7,17 This difference results in a much smaller energy separation between the X 1Σ+ ground and a 3Π metastable states in MgO (2492.5 cm−1 or 0.309 eV18) than in BeO (0.73 eV19) and CaO (1.0 eV5,7,13).
Strong configurational mixing also affects the valence electronically excited states of MgO,1,2,15,16,20,21 which have been studied experimentally by laser18,22–24 and microwave24,25 spectroscopy. Particularly noteworthy are the detailed investigations of the F 1Π, E 1Σ+ and G 1Π electronic states26–29 and the 3Π2 states30 at term values in the range of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–40
000–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the ground state. Breckenridge and coworkers have used these excited states to determine the adiabatic ionisation energy of MgO (64
000 cm−1 above the ground state. Breckenridge and coworkers have used these excited states to determine the adiabatic ionisation energy of MgO (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578(7) cm−1) by resonance-enhanced two-photon ionisation (R2PI) spectroscopy.27 The Rydberg states of MgO are also expected to be affected by unusually strong configurational mixing because the X+ 2Σ+ ground state of the MgO+ ion core is itself configurationally mixed, with dominant contributions of the (6σ)2(2π)3 and (6σ)1(2π)3(7σ)1 open-shell configurations.3,15
578(7) cm−1) by resonance-enhanced two-photon ionisation (R2PI) spectroscopy.27 The Rydberg states of MgO are also expected to be affected by unusually strong configurational mixing because the X+ 2Σ+ ground state of the MgO+ ion core is itself configurationally mixed, with dominant contributions of the (6σ)2(2π)3 and (6σ)1(2π)3(7σ)1 open-shell configurations.3,15
In contrast to MgO, which has been well characterised experimentally and theoretically, the current knowledge of the electronic structure of MgO+ almost exclusively stems from ab initio quantum-chemical calculations.3,15 The lack of experimental data on MgO+ is surprising given the special position of MgO among alkaline-earth metal oxides and its potential significance in planetary atmospheres and the interstellar medium. MgO and CaO have been observed in the atmosphere of the planet Mercury,31,32 in meteoroids,33,34 and CaO and BaO have been identified in stars.35,36 MgO is also believed to be present in interstellar dust although spectroscopic searches for MgO have been unsuccessful so far.37
Through the spectroscopic characterisation of the low-lying electronic states of MgO+, we provide important data that fill current knowledge gaps and may assist in searches for MgO+ in planetary atmospheres and the interstellar medium. These new data also complement data obtained by high-resolution photoelectron spectroscopy in other alkaline-earth metal oxides.38–40
2 Experimental setup and procedure
The experimental setup used for this work is shown schematically in Fig. 2. It has been previously described in ref. 41–44 and only the main aspects are repeated here. MgO was produced in the gas phase by combining laser-ablation and supersonic-expansion techniques. The frequency-doubled output of a Nd:YAG laser (532 nm) was used to ablate magnesium (Mg) atoms off a rotating Mg rod. MgO molecules were generated by expanding the vaporised Mg in a He/N2O (1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) supersonic jet using a pulsed valve, as described in ref. 45. Approximately 26 cm downstream from the valve orifice, the supersonic expansion passed through a 3-mm-diameter skimmer serving the purpose of reducing the transverse velocity of the molecular jet. The beam then entered a resistively coupled 5.8-cm-long cylindrical electrode stack consisting of five equally spaced electrodes inside the magnetically shielded photoexcitation chamber.
1) supersonic jet using a pulsed valve, as described in ref. 45. Approximately 26 cm downstream from the valve orifice, the supersonic expansion passed through a 3-mm-diameter skimmer serving the purpose of reducing the transverse velocity of the molecular jet. The beam then entered a resistively coupled 5.8-cm-long cylindrical electrode stack consisting of five equally spaced electrodes inside the magnetically shielded photoexcitation chamber.
MgO was photoexcited from the ground X 1Σ+ or the metastable a 3Π2 state, which are both populated in the supersonic beam, to selected intermediate states of the neutral molecule using the output of a Nd:YAG-pumped dye laser of frequency ν1, which was frequency-tripled to the UV (νUV = 3ν1, pulse length ∼5 ns, and bandwidth ≈0.15 cm−1) using two successive beta-barium-borate (BBO) crystals. The intermediate states were selected for the large Franck–Condon factors and large electric-dipole transition moments from the initial states. To avoid saturation and line broadening, the energy of the photoexcitation pulse was reduced to below 50 μJ. To either photoionise MgO in the (1 + 1′) R2PI experiments or to excite MgO to high-lying Rydberg states in the PFI-ZEKE-PE measurements, the frequency-doubled or frequency-tripled output ν2 of a second Nd:YAG-pumped pulsed dye laser was employed, again using either a single or two successive BBO crystals for frequency doubling or tripling. The pulsed laser beams (νUV and ν2) were spatially overlapped before entering the photoexcitation chamber, where they crossed the molecular beam at right angles. The fundamental frequencies of both dye lasers were calibrated using a wavemeter with a specified accuracy of 0.02 cm−1. The pulses from the second laser were delayed by ∼5 ns with respect to those of the first laser to minimise contributions to the ion signal from nonresonant ionisation processes.
In the (1 + 1′) R2PI measurements, a pulsed electric field of + 172 V cm−1 was applied across the electrode stack to extract the MgO+ cations for mass-selective detection at a microchannel-plate (MCP) detector located at the end of a 15-cm-long linear time-of-flight (TOF) mass spectrometer. (1 + 1′) R2PI spectra were measured by monitoring the MgO+ ion signal as a function of the wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) UV of the first laser. 24MgO+, 25MgO+, and 26MgO+, with 0.7899(4), 0.1000(1), and 0.1101(3) natural abundances,46 respectively, were resolved in the TOF spectra and their (1 + 1′) R2PI spectra recorded separately.
UV of the first laser. 24MgO+, 25MgO+, and 26MgO+, with 0.7899(4), 0.1000(1), and 0.1101(3) natural abundances,46 respectively, were resolved in the TOF spectra and their (1 + 1′) R2PI spectra recorded separately.
For the PFI-ZEKE-PE measurements, electric-field pulse sequences were applied to the electrode stack, consisting of a first pulse with positive polarity to sweep prompt electrons out of the photoexcitation volume, followed by multiple pulses of negative polarity used to field ionise high Rydberg states lying just below the ionisation thresholds. A low-resolution electric-field pulse sequence [(+0.17, −0.69, −1.72) V cm−1] was used to record PFI-ZEKE-PE spectra of weak transitions and a high-resolution electric-field pulse sequence [(+0.09, −0.09, −0.17, −0.26, −0.34, −0.43, −1.72) V cm−1] was employed to resolve the rotational structure of stronger bands. The photoelectrons were extracted down the TOF tube and detected at the MCP detector. Spectra were measured by monitoring the field-ionisation signals induced by each of the negative-field pulses of the sequence as a function of the wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 of the second laser. To correct for the shifts of the ionisation thresholds induced by the electric-field pulses, PFI-ZEKE-PE spectra of the Mg(3s3p) 3PJ → Mg+ (3s) 2S1/2 photoionising transition were recorded using the same electric-field pulse sequences and the line positions were compared with the precisely known field-free ionisation threshold of Mg.47 The differences were then used to correct for the field-induced shifts.
2 of the second laser. To correct for the shifts of the ionisation thresholds induced by the electric-field pulses, PFI-ZEKE-PE spectra of the Mg(3s3p) 3PJ → Mg+ (3s) 2S1/2 photoionising transition were recorded using the same electric-field pulse sequences and the line positions were compared with the precisely known field-free ionisation threshold of Mg.47 The differences were then used to correct for the field-induced shifts.
3 Results
3.1 (1 + 1′) R2PI spectra of electronically excited states of MgO
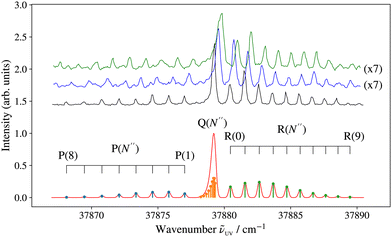
In order to confirm the production of MgO as well as to characterise the rotational temperature of the MgO sample in the gas expansion, we recorded the (1 + 1′) R2PI spectrum of the MgO F 1Π (v′ = 0)–X 1Σ+ (v′′ = 0) origin band. This band was chosen because its rotational structure had been previously characterised by Bellert et al.,27 who used the F 1Π (v′ = 0) state as an intermediate state in their measurement of the ionisation energy of MgO. We recorded the (1 + 1′) R2PI spectra of 24Mg16O, 25Mg16O and 26Mg16O, fixing the wavenumber![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 of the ionisation laser to 26
2 of the ionisation laser to 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900.00 cm−1, well above the adiabatic ionisation threshold. The corresponding spectra are displayed in Fig. 3 in black, blue, and green, respectively. The rotational structure of 24MgO was analysed using standard expressions for 1Π–1Σ+ transitions. To obtain the spectrum displayed in red colour in Fig. 3, the stick spectrum calculated using the energy expression and Hönl-London factors48 for Hund's case (b) ← Hund's case (b) transitions, with the resulting P-, Q-, and R-branch lines marked in blue, orange, and green colours, respectively, was convoluted with a Gaussian lineshape function with a full width at half maximum of 0.3 cm−1. The ground-state rotational quantum number N′′ is given in parentheses in Fig. 3. Rotational constants determined by a least-squares fit agree with those determined by Bellert et al.27 within the combined experimental uncertainties and the experimental spectrum is well described by assuming a rotational temperature Trot of 15 K. The isotopic shifts in the F 1Π (0)–X 1Σ+ (0) band are large enough to allow the ionisation from selected rotational levels of 24MgO and 25MgO, which turned out to be useful for the assignment of the rovibrational structure of the PFI-ZEKE-PE spectra.
900.00 cm−1, well above the adiabatic ionisation threshold. The corresponding spectra are displayed in Fig. 3 in black, blue, and green, respectively. The rotational structure of 24MgO was analysed using standard expressions for 1Π–1Σ+ transitions. To obtain the spectrum displayed in red colour in Fig. 3, the stick spectrum calculated using the energy expression and Hönl-London factors48 for Hund's case (b) ← Hund's case (b) transitions, with the resulting P-, Q-, and R-branch lines marked in blue, orange, and green colours, respectively, was convoluted with a Gaussian lineshape function with a full width at half maximum of 0.3 cm−1. The ground-state rotational quantum number N′′ is given in parentheses in Fig. 3. Rotational constants determined by a least-squares fit agree with those determined by Bellert et al.27 within the combined experimental uncertainties and the experimental spectrum is well described by assuming a rotational temperature Trot of 15 K. The isotopic shifts in the F 1Π (0)–X 1Σ+ (0) band are large enough to allow the ionisation from selected rotational levels of 24MgO and 25MgO, which turned out to be useful for the assignment of the rovibrational structure of the PFI-ZEKE-PE spectra.
To allow a broader choice of intermediate states for PFI-ZEKE-PE measurements, the R2PI spectrum of MgO was recorded from 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to 40
000 cm−1 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1. Fig. 4 shows a survey R2PI spectrum from 37
400 cm−1. Fig. 4 shows a survey R2PI spectrum from 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 to 39
500 to 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, with the vibronic transitions labelled as
000 cm−1, with the vibronic transitions labelled as  . In this region, one primarily observes transitions from the X 1Σ+ electronic ground state to the E 1Σ+, F 1Π, and G 1Π electronic states previously assigned and characterised by Bellert et al.26,27 and Wang et al.28 In the case of the G 1Π state, no vibrational assignment could be derived so far, and we have adopted the labels “A”, “B”, “C”, “D”, etc. introduced by Bellert et al.26,27 and Wang et al.28 to designate the observed vibrational levels in the order of increasing wavenumber. Surprisingly, vibrational levels up to v′′ = 6 in the ground X 1Σ+ state are significantly populated in the supersonic beam, indicating that hardly any cooling of the vibrational degree of freedom takes place in the supersonic expansion. These levels allow access to highly-excited vibrational levels of the G 1Π (up to the level denoted as “E”) and E 1Σ+ (up to v′ = 8) electronic states, which was used to reach a broad range of vibrational levels of the ground and first excited electronic states of MgO+.
. In this region, one primarily observes transitions from the X 1Σ+ electronic ground state to the E 1Σ+, F 1Π, and G 1Π electronic states previously assigned and characterised by Bellert et al.26,27 and Wang et al.28 In the case of the G 1Π state, no vibrational assignment could be derived so far, and we have adopted the labels “A”, “B”, “C”, “D”, etc. introduced by Bellert et al.26,27 and Wang et al.28 to designate the observed vibrational levels in the order of increasing wavenumber. Surprisingly, vibrational levels up to v′′ = 6 in the ground X 1Σ+ state are significantly populated in the supersonic beam, indicating that hardly any cooling of the vibrational degree of freedom takes place in the supersonic expansion. These levels allow access to highly-excited vibrational levels of the G 1Π (up to the level denoted as “E”) and E 1Σ+ (up to v′ = 8) electronic states, which was used to reach a broad range of vibrational levels of the ground and first excited electronic states of MgO+.
 | ||
Fig. 4 Overview (1 + 1′) R2PI spectrum of 24Mg16O in the region between 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 39 000 and 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, acquired using an ionisation-laser wavenumber 000 cm−1, acquired using an ionisation-laser wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 of 26 2 of 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900.00 cm−1. The assignments of the E 1Σ+–X 1Σ+, F 1Π–X 1Σ+, and G 1Π–X 1Σ+ transitions are based on previous work by Breckenridge and coworkers.26–28 The progressions marked in green and orange colours are assigned in Table 1. Unassigned bands are marked with asterisks. 900.00 cm−1. The assignments of the E 1Σ+–X 1Σ+, F 1Π–X 1Σ+, and G 1Π–X 1Σ+ transitions are based on previous work by Breckenridge and coworkers.26–28 The progressions marked in green and orange colours are assigned in Table 1. Unassigned bands are marked with asterisks. | ||
In our R2PI spectrum, we also observed eight (Ω′ = 2)–(Ω′′ = 2) transitions, in agreement with the earlier observation of multiple (Ω′ = 2)–(Ω′′ = 2) transitions in the R2PI spectrum of MgO.30 The analysis of the rotational structure of these eight bands using the PGOPHER® software49 led to the results presented in Table 1, where the term values T′ of the upper states are given relative to the X 1Σ+ (0) ground state. The lower electronic state of all eight transitions can be unambiguously assigned to the a 3Π2 metastable state because the rotational-structure analysis resulted in values of  (0.497(3) cm−1) and
(0.497(3) cm−1) and  (0.493(3) cm−1), which agree within the experimental uncertainties with the rotational constants reported in ref. 25 and 30. Comparing the vibrational intervals observed in our spectrum with the fundamental interval of the a 3Π2 state reported by Bellert et al.,30 we could assign the lower levels of the observed bands to the first two vibrational levels (v = 0, 1) of the a 3Π2 state. In the analysis of the rotational structure, we fixed the rotational constants to the values determined for these states by microwave spectroscopy.25Table 1 reports the results of this analysis and groups the transitions according to the electronic assignment of the upper state.
(0.493(3) cm−1), which agree within the experimental uncertainties with the rotational constants reported in ref. 25 and 30. Comparing the vibrational intervals observed in our spectrum with the fundamental interval of the a 3Π2 state reported by Bellert et al.,30 we could assign the lower levels of the observed bands to the first two vibrational levels (v = 0, 1) of the a 3Π2 state. In the analysis of the rotational structure, we fixed the rotational constants to the values determined for these states by microwave spectroscopy.25Table 1 reports the results of this analysis and groups the transitions according to the electronic assignment of the upper state.
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0. All values in cm−1
0. All values in cm−1
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0
0
|
B′ | B′′ | T′ | ΔG′ | |
|---|---|---|---|---|---|
| 4 3Π2 (0)–a 3Π2 (0) | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474.91(3) 474.91(3) |
0.4761(20) | 0.5003 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969.31(10) 969.31(10) |
699.51(15) |
| 4 3Π2 (1)–a 3Π2 (0) | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174.38(4) 174.38(4) |
0.432(3) | 0.5003 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668.61(11) 668.61(11) |
|
| 3Π2 (v)–a 3Π2 (1) | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 257.839(21) 257.839(21) |
0.3746(20) | 0.4957 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393.54(13) 393.54(13) |
|
| 3Π2 (v)–a 3Π2 (0) | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899.60(3) 899.60(3) |
0.3760(20) | 0.5003 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393.60(11) 393.60(11) |
|
| 3Π2 (v)–a 3Π2 (0) | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792.37(3) 792.37(3) |
0.465(3) | 0.5003 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 286.73(11) 286.73(11) |
704.57(16) |
| 3Π2 (v + 1)–a 3Π2 (0) | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496.97(5) 496.97(5) |
0.457(3) | 0.5003 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991.30(12) 991.30(12) |
635.35(16) |
| 3Π2 (v + 2)–a 3Π2 (0) | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132.54(3) 132.54(3) |
0.4131(20) | 0.5003 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626.67(10) 626.67(10) |
|
| 3Π2 (v + 1)–a 3Π2 (1) | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855.30(4) 855.30(4) |
0.455(20) | 0.4957 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991.32(13) 991.32(13) |
|
| 1Π–X 1Σ+ (0) | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936.23(3) 936.23(3) |
0.4911(20) | 0.5722 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936.72(4) 936.72(4) |
|
| 1Π–X 1Σ+ (6) | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 948.81(3) 948.81(3) |
0.4920(10) | 0.5402 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450.35(10) 450.35(10) |
|
| 1Π–X 1Σ+ (4) | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 083.010(19) 083.010(19) |
0.511(2) | 0.5511 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984.79(3) 984.79(3) |
|
In the first section of Table 1, we report two transitions, the first of which has been reported by Bellert et al.30 and assigned by Maatouk et al.1 as the 3 3Π2 (0)–a 3Π2 (0) origin transition. In a later study, Bauschlicher and Schwenke2 argued that the upper 3Π2 state actually is the fourth state of 3Π2 symmetry and should therefore be assigned as 4 3Π2. We thus assign the second transition to 4 3Π2 (1)–a 3Π2 (0), which results in a fundamental vibrational interval ΔG1/2 of 699.51(15) cm−1 for the upper 3Π2 state. The term values of the 4 3Π2 (0,1) states in the first section in Table 1 as well as those of another two 3Π2 states (second and third sections of Table 1) agree with the results previously reported by Wang and Breckenridge.29 In addition, transitions to a 1Π state were observed for the first time (see the bottom section of Table 1). Our analysis confirms their analysis and provides, in addition, slightly more precise band origins and new information on the vibrational structure of the 4 3Π2 states. Observing these 3Π2 states proved useful for the PFI-ZEKE-PE measurements, because they allowed access to a broad range of internuclear separations. Single-photon, single-electron photoionisation selection rules from these 3Π2 electronic states also provide access to a broad range of electronic states of MgO+.
We did not observe transitions from the 3Π0 and 3Π1 components of the a 3ΠΩ state in our spectra. We do not have a full explanation for the dominance of the a 3Π2 state in our supersonic ablation source. A possible reason is that the 3Π0 and 3Π1 components of the a 3ΠΩ state can decay radiatively to the X 1Σ0+ ground state because of singlet–triplet mixing induced by the spin–orbit interaction. Alternatively, the dominance of the a 3Π2 state may be the result of the collisional relaxation in the high-pressure zone of the expansion, as suggested by Bellert et al.27
3.2 The ground X+ 2ΠΩ state of MgO+
An overview of the level structure of the X+ 2ΠΩ electronic ground state of MgO+ as measured by PFI-ZEKE-PE spectroscopy using a resonant (1 + 1′) two-photon excitation scheme is presented in Fig. 5. The wavenumber scale in the figure is relative to the X 1Σ+g (v′′ = 0, N′′ = 0) ground state of MgO. The spectrum consists of a regular progression of 11 vibrational levels (v+ = 0–10), each split into two spin–orbit components. To observe these levels, it was necessary to use several intermediate states, as indicated by the legend and the colour code in the figure and by the second column of Table 2. Consequently, the relative intensities of the different bands cannot be directly compared.| v + | 2S+1Λ′(v′) | 2S+1Λ′′(v′′) | E v + /(hc)a (Ω = 3/2, J+ = 3/2) | E v + /(hc)a (Ω = 1/2, J+ = 1/2) | A v + | B v + |
|---|---|---|---|---|---|---|
| a The uncertainties correspond to one standard deviation and do not include a 0.2 cm−1 systematic uncertainty arising from the compensation of the field-induced shift of the ionisation thresholds. b In order to accurately describe the potential at the v+ = 18–20 levels, Dunham coefficients Y40 and Y50 (fourth- and fifth-order in (v+ + 1/2)) were added to the vibrational energy expression to reproduce the experimental positions of the X+ 2Π3/2 (v+ = 19, 20) [Y40 = 2.39(24) × 10−4 cm−1, Y50 = −2.19(12) × 10−5 cm−1] and X+ 2Π1/2 (v+ = 18) states [Y40 = 2.29(16) × 10−4 cm−1, Y50 = −2.35(9) × 10−5 cm−1]. The reported values of A18–20+ were calculated from these high-order vibrational-energy expressions and their uncertainties are dominated by the extrapolation. | ||||||
| 0 | F 1Π (0) | X 1Σ+ (0) | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.654(23) 577.654(23) |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 706.973(22) 706.973(22) |
−129.846(14) | 0.5330(10) |
| 1 | F 1Π (1) | X 1Σ+ (1) | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307.39(4) 307.39(4) |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436.91(4) 436.91(4) |
−130.020(16) | 0.5290(10) |
| 2 | G 1Π (A) | X 1Σ+ (2) | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027.07(7) 027.07(7) |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156.65(7) 156.65(7) |
−130.107(14) | 0.5246(10) |
| 3 | G 1Π (B) | X 1Σ+ (3) | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736.64(3) 736.64(3) |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866.33(3) 866.33(3) |
−130.217(14) | 0.5199(10) |
| 4 | G 1Π (B) | X 1Σ+ (3) | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436.08(3) 436.08(3) |
67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565.94(3) 565.94(3) |
−130.315(15) | 0.5146(10) |
| 5 | E 1Σ+ (6) | X 1Σ+ (4) | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 125.201(22) 125.201(22) |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255.165(22) 255.165(22) |
−130.422(14) | 0.5106(10) |
| 6 | E 1Σ+ (6) | X 1Σ+ (4) | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803.958(22) 803.958(22) |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934.000(23) 934.000(23) |
−130.527(14) | 0.5050(10) |
| (25MgO) | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793.48(4) 793.48(4) |
0.4975(22) | ||||
| 7 | E 1Σ+ (6) | X 1Σ+ (4) | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472.148(22) 472.148(22) |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602.266(23) 602.266(23) |
−130.601(14) | 0.5007(10) |
| (25MgO) | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458.58(4) 458.58(4) |
0.4933(16) | ||||
| 8 | E 1Σ+ (6) | X 1Σ+ (4) | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129.572(23) 129.572(23) |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 259.780(23) 259.780(23) |
−130.699(14) | 0.4929(10) |
| (25MgO) | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111.41(5) 111.41(5) |
0.4885(10) | ||||
| 9 | E 1Σ+ (6) | X 1Σ+ (4) | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775.977(23) 775.977(23) |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 906.210(24) 906.210(24) |
−130.738(16) | 0.4897(10) |
| 10 | E 1Σ+ (6) | X 1Σ+ (4) | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411.274(3) 411.274(3) |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541.673(23) 541.673(23) |
−130.877(16) | 0.4816(11) |
| 18 | 4 3Π2 (1) | a 3Π2 (0) | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186.86(3) 186.86(3) |
−129(10)b | 0.444(3) | |
| 19 | 4 3Π2 (1) | a 3Π2(0) | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579.60(3) 579.60(3) |
−128(10)b | 0.4280(15) | |
| 20 | 4 3Π2 (1) | a 3Π2(0) | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085.61(4) 085.61(4) |
−127(10)b | 0.4211(15) | |
Rotationally resolved photoelectron spectra were recorded from selected rotational levels (N′) of the intermediate states and Fig. 6 shows, as representative examples, the rotational structures of the Ω = 3/2 (left) and Ω = 1/2 (right) spin–orbit components of the X+ 2ΠΩ (v+ = 0, J+) ← F 1Π (v′ = 0, N′) ionising transition recorded from low (N′ = 1; top panels) and high (N′ = 7, 8; bottom panels) F 1Π state rotational levels. These spectra reveal that photoionisation processes with |J+–N′| values up to 5.5 dominate the intensity distribution.
The lowest rotational level in a 2ΠΩ state has J+ = Ω. Consequently, the presence or absence of a transition to the J+ = 1/2 rotational level in the spectra recorded from low-N′ intermediate states enables the unambiguous assignment of the lower and upper spin–orbit components of the X+ 2ΠΩ state to the 2Π3/2 and 2Π1/2 states, respectively. To model the relative intensities in these spectra, we used an empirical model describing the relative photoionisation cross section as a superposition of contributions from different orbital-angular momentum (l) components of the outermost valence orbital of the dominant electronic configuration of the intermediate state:51,52
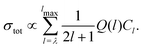 | (1) |
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) on the molecular axis. In eqn (1), Cl values are adjustable coefficients, as explained in ref. 53 and:
on the molecular axis. In eqn (1), Cl values are adjustable coefficients, as explained in ref. 53 and: | (2) |
The fourth and fifth columns of Table 2 list the ionisation energies corresponding to the lowest rotational levels of each observed vibrational level of the X+ 2Π3/2 and 2Π1/2 states with respect to the X 1Σ+ (v′′ = 0, N′′ = 0) ground state of MgO. The uncertainties are purely statistical and do not include a systematic contribution of 0.2 cm−1 originating from the uncertainty in the determination of the shifts of the ionisation thresholds induced by the pulsed electric fields. The adiabatic ionisation energy of 24Mg16O, corresponding to the X+ 2Π3/2 (v+ = 0, J+ = 3/2) ← X 1Σ+ (v′′ = 0, N′′ = 0) ionising transition, is thus 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.65(20) cm−1 (8.00661(3) eV), and agrees with the earlier experimental value of 64
577.65(20) cm−1 (8.00661(3) eV), and agrees with the earlier experimental value of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578(7) cm−1 reported by Bellert et al.54
578(7) cm−1 reported by Bellert et al.54
To determine the spin–orbit-coupling constants Av+ and the rotational constants Bv+ of the X+ 2Π3/2 and 2Π1/2 states, we used the expression:50
 | (3) |
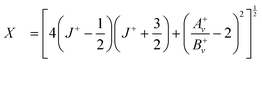 | (4) |
Table 3 presents the equilibrium molecular constants B+e, α+e, ω+e, ωex+e and ωey+e extracted from separate analyses of the 2Π3/2 and 2Π1/2 spin–orbit components based on the standard power-series expansion in v+ + 1/2 and J+(J+ + 1).48 To reach a satisfactory description of the rovibrational structure, it was necessary to include anharmonicity terms up to the third order (ωey+e) as well as the first-order correction of the rotational constant (Bv+ = B+e − α+e(v+ + 1/2)).48
| T 0 | ω e | ω e x e | ω e y e | B e | α e | Ref. | |
|---|---|---|---|---|---|---|---|
| a With respect to the X 1Σ+ (v′′ = 0, N′′ = 0) ground state of 24Mg16O. This value corresponds to the adiabatic ionisation energy for the specified ionic electronic state. The uncertainty does not include a systematic contribution of 0.2 cm−1 originating from the correction of the field-induced shift of the ionisation thresholds but the uncertainties coming from the fits of the vibrational constants. | |||||||
| a 3Π2 | 2492.4(3) | This work | |||||
| 2492.5 | 649.1(2) | 4.0(2) | 0.496(2) | 0.005(6) | 18 | ||
| X+ 2Π3/2 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.65(5)a 577.65(5)a |
739.32(8) | 4.825(16) | −0.0246(10) | 0.5352(13) | 0.00485(23) | This work |
| 738.2 | 4.5(2.0) | 0.529(10) | 0.0040(10) | 3 | |||
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578(7) 578(7) |
27 | ||||||
| X+ 2Π1/2 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 706.97(5)a 706.97(5)a |
739.47(9) | 4.840(19) | −0.0239(11) | 0.5400(12) | 0.00502(21) | This work |
| A+ 2Σ+ | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091.905(14)a 091.905(14)a |
848.6(4) | 4.46(3) | 0.6090(25) | 0.0062(4) | This work | |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215(400) 215(400) |
832.5 | 2.60(2.0) | 0.590(10) | 0.0050(10) | 3 | ||
The absolute vibrational assignment was confirmed in a standard analysis of the isotopic shifts determined from the spectra of the v+ = 6–8 levels of the X+ 2Π3/2 state of 25Mg16O+ based on the molecular constants reported in Table 3. In the range of v+ values up to 10, the observed dependence of the spin–orbit coupling constant on the vibrational quantum number (see the inset of Fig. 5) could be accurately described by the quadratic function:
 | (5) |
The molecular equilibrium constants reported in Table 3 are in good agreement with the results of previous ab initio calculations.2,3,15 These calculations predict that the X+ 2ΠΩ ground state of MgO+ near the equilibrium internuclear distance is well described by two dominant configurations ((6σ)2(2π)3; c1 = 0.865 and (6σ)1(2π)3(7σ)1; c2 = 0.446),3 which imply a mixed O(2p)4 3P0,1 + Mg+(3s) and Mg2+ + O−(2p)5 2P1/2,3/2 character in the separated-atom limit. Maatouk et al.3 predicted a value of 133.6 cm−1 for the spin–orbit-constant A+ at the internuclear separation (Re = 3.445(15)a0), close to the Av+ values determined experimentally (see Table 2).
3.3 The A+ 2Σ+ excited state of MgO+
An overview of the vibrational structure of the A+ 2Σ+ state of 24MgO+ measured by PFI-ZEKE-PES following (1 + 1′) two-photon excitation via different intermediate states (indicated by the legend and the colour code) is presented in Fig. 7. In this figure, the horizontal scale corresponds to the term values of the A 2Σ+ (v+) levels with respect to the X 1Σ+ (v′′ = 0) ground state of 24MgO. Excitation from the a 3Π2 (v′′ = 0) via the 4 3Π2 (v′ = 1) intermediate level turned out to be ideal to access a broad range of A+ 2Σ+ vibrational levels (v+ = 4–10) and also several high-lying vibrational levels of the X+ 2ΠΩ state, with v+ values in the range of 18–20. In many cases, the isotopic shifts in the spectra of 24MgO, 25MgO and 26MgO could be measured, as illustrated in the inset of Fig. 7 for the A+ 2Σ+ (v+ = 4) level. These shifts enabled us to unambiguously determine the absolute vibrational assignment in a standard isotopic-shift analysis.48Rotationally resolved PFI-ZEKE-PE spectra of most vibrational bands were recorded at high resolution from individual rotational levels of the intermediate states. As illustrations, Fig. 8a and b depict the spectra of the A+ 2Σ+ (v+ = 0) and A+ 2Σ+ (v+ = 6) levels measured from the F 1Π (v′ = 0, N′ = 1) and 4 3Π2 (v′ = 1, J′ = 3) intermediate levels, respectively. The rotational structures in the spectra of the different vibrational levels of the A+ 2Σ+ state all display the pronounced asymmetry between transitions associated with negative and positive N+–J′ (or N+–N′) values already noted in the analysis of the X+ 2ΠΩ state, the former being systematically stronger than the latter. We therefore conclude that the rotational intensity distributions are strongly influenced by rotational channel interactions.53 These interactions effectively mask effects that would originate from the different electronic configurations of the intermediate states. The term values of all ionic levels observed in the spectrum displayed in Fig. 7 are listed in Table 4 for the A+ 2Σ+ state and in the lower part of Table 2 for the X+ 2ΠΩ (v+ = 18–20) levels. Table 4 also lists the initial and intermediate states used to record the respective PFI-ZEKE-PE spectra. The adiabatic ionisation energies of the 24MgO A+ 2Σ+← 24MgO X 1Σ+ and 24MgO A+ 2Σ+← 24MgO a 3Π2 transitions were determined to be 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091.9(3) cm−1 and 69
091.9(3) cm−1 and 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599.5(3) cm−1, respectively, from which we determined the interval between the X 1Σ+ (v′′ = 0, N′′ = 0) and the a 3Π2 (v = 0, J = 2) state to be 2492.4(3) cm−1. This value is in good agreement with the values determined earlier by Bellert et al. from the photoionisation spectrum (2488(5) cm−1)30 and Kagi et al. from the pure rotational spectrum of the a 3ΠΩ (Ω = 0–2) states (2491.86 cm−1).25
599.5(3) cm−1, respectively, from which we determined the interval between the X 1Σ+ (v′′ = 0, N′′ = 0) and the a 3Π2 (v = 0, J = 2) state to be 2492.4(3) cm−1. This value is in good agreement with the values determined earlier by Bellert et al. from the photoionisation spectrum (2488(5) cm−1)30 and Kagi et al. from the pure rotational spectrum of the a 3ΠΩ (Ω = 0–2) states (2491.86 cm−1).25
| v + | 2S+1Λ′(v′) | 2S+1Λ′′(v′′) | E v + /(hc)(N+ = 0) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc–
calc–![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp exp |
B v + |
|---|---|---|---|---|---|
| a Perturbed level. The least-squares fit of the rotational structure also yielded a spin-rotation constant of γ = −0.208(5) cm−1. b Estimated using the values of Be and αe listed in Table 3, which were determined from a least-squares fit to the experimental B0–9 values. | |||||
| 0 | F 1Π (0) | X 1Σ+ (0) | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091.905(14) 091.905(14) |
0.132 | 0.6043(17) |
| 25MgO | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091.8(5) 091.8(5) |
0.592(5) | |||
| 26MgO | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091.6(5) 091.6(5) |
0.583(4) | |||
| 1 | F 1Π (1) | X 1Σ+ (1) | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931.26(14) 931.26(14) |
0.175 | 0.6065(15) |
| 2 | E 1Σ+ (0) | X 1Σ+ (0) | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761.655(14) 761.655(14) |
0.539 | 0.5900(10) |
| 25MgO | F 1Π (1) | X 1Σ+ (1) | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748.4(5) 748.4(5) |
||
| 26MgO | F 1Π (1) | X 1Σ+ (1) | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 737.8(5) 737.8(5) |
||
| 3 | E 1Σ+ (4) | X 1Σ+ (2) | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583.51(14) 583.51(14) |
0.530 | 0.589(4) |
| 4 | 3 3Π2 (1) | a 3Π2 (0) | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395.92(14) 395.92(14) |
1.569 | 0.579(3) |
| E 1Σ+ (5) | X 1Σ+ (3) | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 396.05(14) 396.05(14) |
|||
| G 1Π (B) | X 1Σ+ (3) | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395.82(14) 395.82(14) |
|||
| 25MgO | G 1Π (B) | X 1Σ+ (3) | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374.2(5) 374.2(5) |
||
| 26MgO | G 1Π (B) | X 1Σ+ (3) | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348.7(5) 348.7(5) |
||
| 5 | 3 3Π2 (1) | a 3Π2 (0) | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202.13(14) 202.13(14) |
1.138 | 0.5608(11)a |
| 26MgO | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135.0(5) 135.0(5) |
||||
| 6 | 4 3Π2 (1) | a 3Π2 (0) | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 994.98(14) 994.98(14) |
1.119 | 0.566(4) |
| 26MgO | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927.8(5) 927.8(5) |
||||
| 7 | 4 3Π2 (1) | a 3Π2 (0) | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782.14(14) 782.14(14) |
0.162 | 0.559(3) |
| 8 | 4 3Π2 (1) | a 3Π2 (0) | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558.48(14) 558.48(14) |
1.105 | 0.5604(3) |
| 9 | 4 3Π2 (1) | a 3Π2 (0) | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328.32(14) 328.32(14) |
0.351 | 0.5521(8) |
| 10 | 4 3Π2 (1) | a 3Π2 (0) | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087.88(14) 087.88(14) |
0.440 | 0.545(3)b |
Table 3 summarises the vibrational and rotational constants determined from the X+ 2ΠΩ and A+ 2Σ+ states. Overall, the fits that led to these constants were more satisfactory for the X+ 2ΠΩ (v+ = 0–10) states (weighted rms deviation of 1.05, see Section 3.2) than for the A+ 2Σ+ states (weighted rms deviation of 4). We attribute this difference to potential slight perturbations of the vibrational structure of the X+ 2ΠΩ and A+ 2Σ+ states in the spectral regions above the X+ 2ΠΩ (v+ = 10) ionic state, where both states overlap. However, in none of the observed bands could we detect significant perturbations, with the exception of the close-lying A+ 2Σ+ (v+ = 5) and X+ 2Π1/2 (v+ = 18) states. The PFI-ZEKE-PE spectrum in the region of these levels, recorded from the 4 3Π2 (v′ = 1, J′ = 3) intermediate state, is displayed in Fig. 9 and shows a weak transition at the position expected for the X+ 2Π1/2 (v+ = 18) state and a stronger transition at the position of the A+ 2Σ+ (v+ = 5). To see whether we could expect any other perturbations in the A+ 2Σ+ state from nearby X+ 2Π1/2 levels, term energies for the X+ 2Π1/2 (v+ = 11–28) levels were calculated using the molecular constants in Table 3. The X+ 2Π1/2 (v+ = 18) level was the only one to be within 20 cm−1 of an A+ 2Σ+ (v+ = 0–10) level.
In the A+ 2Σ+ (v+ = 5) ← 4 3Π2 (v′ = 1, J′ = 3) band, we observe that the rotational levels of the A+ 2Σ+ (v+ = 5) are split into doublets for N+ ≥ 2 and that the splittings increase with increasing N+ values, corresponding to an unusually large value of the spin-rotation coupling constant γ of −0.205(5) cm−1. We attribute this observation to a large contribution to γ from a second-order spin–orbit coupling that is enhanced by the close proximity of the X+ 2Π1/2 (v+ = 18) state. Such effects were observed in similar systems and are discussed in detail in Section 3.5.4 of ref. 55. An estimate of the magnitude of γ based on their equations (3.5.33) and (3.5.40) yield |γ| values between 0.02 and 0.06 cm−1 on the assumption of pure-precession with l = 1 and 2, respectively, which can be considered to be in agreement with the experimental observation given that the pure-precession approximation is not expected to be accurate in the present case. This interaction between the A+ 2Σ+ (v+ = 5) and X+ 2Π1/2 (v+ = 18) states would also affect the X+ 2Π1/2 (v+ = 18) level by causing an unusually large Λ-doubling. The corresponding splittings of the 2Π rotational levels could unfortunately not be observed because of the weakness of the X+ 2Π1/2 (v+ = 18) band and the limited spectral resolution (0.3 cm−1) (see Fig. 9).
4. Conclusions
In this article, we have reported on a measurement of the spin-rovibronic level structure of MgO+ by PFI-ZEKE photoelectron spectroscopy using a resonant two-photon excitation sequence via selected rotational levels of several electronically excited states of MgO. The new data include rovibronic term values for the levels of MgO+ up to 2 eV of internal energy, from which sets of vibrational, rotational and spin–orbit-coupling molecular constants were derived for the X+ 2ΠΩ ground and A+ 2Σ+ first excited electronic states of MgO+. The adiabatic ionisation energies of 24Mg16O associated with the formation of the X+ 2Π3/2 and A+ 2Σ+ states were determined to be 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.65(20) cm−1 and 72
577.65(20) cm−1 and 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091.91(20) cm−1, respectively, and the energy difference between the lowest singlet (X 1Σ+ (v′′ = 0, N′′ = 0)) and the lowest triplet (a 3Π2 (v = 0, J = 2)) states of MgO was found to be 2492.4(3) cm−1. The rotationally state-resolved photoionisation dynamics are dominated by the couplings of different rotational ionisation channels which strongly favour photoionising transitions associated with a reduction of the rotational quantum number upon photoionisation. These couplings masked potential differences in the rotational-intensity distributions arising from the different electronic structures of the selected intermediate states. A perturbation of the rotational structure of the A+ 2Σ+ (v+ = 5) level was detected through the observation of anomalously large spin-rotational splittings. It was attributed to an interaction with the almost degenerate X+ 2Π1/2 (v+ = 18) level. The molecular constants derived for the X+ 2ΠΩ state of MgO+ may be helpful in searches for this ion in planetary atmospheres and the interstellar space.
091.91(20) cm−1, respectively, and the energy difference between the lowest singlet (X 1Σ+ (v′′ = 0, N′′ = 0)) and the lowest triplet (a 3Π2 (v = 0, J = 2)) states of MgO was found to be 2492.4(3) cm−1. The rotationally state-resolved photoionisation dynamics are dominated by the couplings of different rotational ionisation channels which strongly favour photoionising transitions associated with a reduction of the rotational quantum number upon photoionisation. These couplings masked potential differences in the rotational-intensity distributions arising from the different electronic structures of the selected intermediate states. A perturbation of the rotational structure of the A+ 2Σ+ (v+ = 5) level was detected through the observation of anomalously large spin-rotational splittings. It was attributed to an interaction with the almost degenerate X+ 2Π1/2 (v+ = 18) level. The molecular constants derived for the X+ 2ΠΩ state of MgO+ may be helpful in searches for this ion in planetary atmospheres and the interstellar space.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Josef A. Agner and Hansjürg Schmutz for their technical assistance. This work is supported financially by the Swiss National Science Foundation (grant No. 200020B-200478).References
- A. Maatouk, A. Ben Houria, O. Yazidi, N. Jaidane and M. Hochlaf, J. Chem. Phys., 2010, 133, 144302 CrossRef CAS PubMed.
- C. W. Bauschlicher Jr. and D. W. Schwenke, Chem. Phys. Lett., 2017, 683, 62–67 CrossRef PubMed.
- A. Maatouk, A. Ben Houria, O. Yazidi, N. Jaidane and M. Hochlaf, J. Phys. B: At. Mol. Phys., 2011, 44, 225101 CrossRef.
- S. F. Rice, H. Martin and R. W. Field, J. Chem. Phys., 1985, 82, 5023–5034 CrossRef CAS.
- J. B. Norman, K. J. Cross, H. S. Schweda, M. Polak and R. W. Field, Mol. Phys., 1989, 66, 235–268 CrossRef CAS.
- S. R. Langhoff, C. W. Bauschlicher Jr. and H. Partridge, J. Chem. Phys., 1986, 84, 4474–4480 CrossRef CAS.
- C. W. Bauschlicher Jr. and D. R. Yarkony, J. Chem. Phys., 1978, 68, 3990–3997 CrossRef.
- J. N. Allison, R. J. Cave and W. A. Goddard III, J. Phys. Chem., 1984, 88, 1262–1268 CrossRef CAS.
- J. N. Allison and W. A. Goddard III, J. Chem. Phys., 1982, 77, 4259–4261 CrossRef CAS.
- D. P. Baldwin, E. J. Hill and R. W. Field, J. Am. Chem. Soc., 1990, 112, 9156–9161 CrossRef CAS.
- S. M. Bresler, J. R. Schmitz, M. C. Heaven and R. W. Field, J. Mol. Spectrosc., 2020, 370, 111293 CrossRef CAS.
- J. F. Harrison, R. W. Field and C. C. Jarrold, Low-Lying Potential Energy Surfaces, 2002, ch. 11, pp. 238–259 Search PubMed.
- R. F. Marks, R. A. Gottscho and R. W. Field, Phys. Scr., 1982, 25, 312–328 CrossRef CAS.
- D. P. Baldwin, J. B. Norman, R. A. Soltz, A. Sur and R. W. Field, J. Mol. Spectrosc., 1990, 139, 39–67 CrossRef CAS.
- J. Schamps and H. Lefebvre-Brion, J. Chem. Phys., 1972, 56, 573–585 CrossRef CAS.
- H. Thümmel, R. Klotz and S. D. Peyerimhoff, Chem. Phys., 1989, 129, 417–430 CrossRef.
- H. Partridge, S. R. Langhoff and C. W. Bauschlicher Jr., J. Chem. Phys., 1986, 84, 4489–4496 CrossRef CAS.
- P. C. F. Ip, K. J. Cross, R. W. Field, J. Rostas, B. Bourguignon and J. McCombie, J. Mol. Spectrosc., 1991, 146, 409–436 CrossRef CAS.
- P. K. Pearson, S. V. O'Neil and H. F. Schaefer III, J. Chem. Phys., 1972, 56, 3938–3942 CrossRef CAS.
- A. I. Boldyrev, I. L. Shamovskii and P. von R. Schleyer, J. Am. Chem. Soc., 1992, 114, 6469–6475 CrossRef CAS.
- D. R. Yarkony, J. Chem. Phys., 1983, 78, 6763–6772 CrossRef CAS.
- P. Mürtz, S. Richter, C. Pfelzer, H. Thümmel and W. Urban, Mol. Phys., 1994, 82, 989–1007 CrossRef.
- P. Mürtz, H. Thümmel, C. Pfelzer and W. Urban, Mol. Phys., 1995, 86, 513–534 Search PubMed.
- Y. Azuma, T. R. Dyke, G. K. Gerke and T. C. Steimle, J. Mol. Spectrosc., 1984, 108, 137–142 CrossRef CAS.
- E. Kagi and K. Kawaguchi, J. Mol. Struct., 2006, 795, 179–184 CrossRef CAS.
- D. Bellert and W. H. Breckenridge, Chem. Rev., 2002, 102, 1595–1622 CrossRef CAS PubMed.
- D. Bellert, K. L. Burns, N.-T. Van-Oanh, J. Wang and W. H. Breckenridge, Chem. Phys. Lett., 2003, 381, 725–728 CrossRef CAS.
- J. Wang, N.-T. Van-Oanh, D. Bellert, W. H. Breckenridge, M.-A. Gaveau, E. Gloaguen, B. Soep and J.-M. Mestdagh, Chem. Phys. Lett., 2004, 392, 62–67 CrossRef CAS.
- J. Wang and W. H. Breckenridge, J. Chem. Phys., 2006, 124, 124308 CrossRef PubMed.
- D. Bellert, K. L. Burns, N.-T. Van-Oanh, J. Wang and W. H. Breckenridge, Chem. Phys. Lett., 2003, 381, 381–384 CrossRef CAS.
- S. Z. Weider, L. R. Nittler, R. D. Starr, T. J. McCoy, K. R. Stockstill-Cahill, P. K. Byrne, B. W. Denevi, J. W. Head and S. C. Solomon, J. Geophys. Res. Planets, 2012, 117, E00L05 CrossRef.
- R. M. Killen, A. E. Potter, R. J. Vervack Jr., E. T. Bradley, W. E. McClintock, C. M. Anderson and M. H. Burger, Icarus, 2010, 209, 75–87 CrossRef CAS.
- A. A. Berezhnoy, Adv. Space Res., 2010, 45, 70–76 CrossRef CAS.
- A. A. Berezhnoy, J. Borovička, J. Santos, J. F. Rivas-Silva, L. Sandoval, A. V. Stolyarov and A. Palma, Planet. Space Sci., 2018, 151, 27–32 CrossRef CAS.
- I. Dubois, Astronomy Astrophys., 1977, 57, 51–54 CAS.
- Y. Kimura and J. A. Nuth III, Astrophys. J., 2005, 630, 637–641 CrossRef CAS.
- S. Sakamoto, G. J. White, K. Kawaguchi, M. Ohishi, K. S. Usuda and T. Hasegawa, Mon. Not. R. Astron. Soc., 1998, 301, 872–880 CrossRef CAS.
- J. H. Bartlett, R. A. VanGundy and M. C. Heaven, J. Chem. Phys., 2015, 143, 044302 CrossRef PubMed.
- R. A. VanGundy, J. H. Bartlett and M. C. Heaven, J. Mol. Spectrosc., 2018, 344, 17–20 CrossRef CAS.
- J. M. Dyke, M. Feher, B. W. J. Gravenor and A. Morris, J. Phys. Chem., 1987, 91, 4476–4481 CrossRef CAS.
- C. Kreis, M. Holdener, M. Génévriez and F. Merkt, Mol. Phys., 2023, 121, e2152746 CrossRef.
- M. Génévriez, D. Wehrli and F. Merkt, Mol. Phys., 2020, 118, e1703051 CrossRef.
- D. Wehrli, M. Génévriez, C. Kreis, J. A. Agner and F. Merkt, J. Phys. Chem. A, 2020, 124, 379–385 CrossRef CAS PubMed.
- M. Génévriez, D. Wehrli, J. A. Agner and F. Merkt, Int. J. Mass Spectrom., 2019, 435, 209–216 CrossRef.
- T. D. Persinger, D. J. Frohman, W. M. Fawzy and M. C. Heaven, J. Phys. Chem., 2020, 153, 054308 CrossRef CAS PubMed.
- M. Berglund and M. E. Wieser, Pure Appl. Chem., 2011, 83, 397–410 CrossRef CAS.
- W. C. Martin and R. Zalubas, J. Phys. Chem. Ref. Data, 1980, 9, 1–58 CrossRef CAS.
- G. Herzberg, Molecular Spectra and Molecular Structure, Volume I, Spectra of Diatomic Molecules, Krieger Publishing Company, Malabar, 2nd edn, 1989 Search PubMed.
- C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242 CrossRef CAS.
- R. N. Zare, Angular momentum, John Wiley & Sons, New York, 1988 Search PubMed.
- A. D. Buckingham, B. J. Orr and J. M. Sichel, Philos. Trans. R. Soc. London, Ser. A, 1970, 268, 147–157 CrossRef CAS.
- S. Willitsch and F. Merkt, Int. J. Mass Spectrom., 2005, 245, 14–25 CrossRef CAS.
- F. Merkt and T. P. Softley, Int. Rev. Phys. Chem., 1993, 12, 205–239 Search PubMed.
- D. Bellert, K. L. Burns, R. Wampler and W. H. Breckenridge, Chem. Phys. Lett., 2000, 322, 41–44 CrossRef CAS.
- H. Lefebvre-Brion and R. W. Field, The spectra and dynamics of diatomic molecules, Elsevier, Amsterdam, 2004 Search PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2024 |