Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oscillations in delayed positive feedback systems
Christopher J.
Ryzowicz
 a,
Richard
Bertram
a,
Richard
Bertram
 abc and
Bhargav R.
Karamched†
abc and
Bhargav R.
Karamched†
 *abc
*abc
aDepartment of Mathematics, Florida State University, Tallahassee, FL 32306, USA
bProgram in Molecular Biophysics, Florida State University, Tallahassee, FL 32306, USA
cProgram in Neuroscience, Florida State University, Tallahassee, FL 32306, USA
First published on 11th September 2024
Abstract
Positive feedback loops exist in many biological circuits important for organismal function. In this work, we investigate how temporal delay affects the dynamics of two canonical positive feedback models. We consider models of a genetic toggle switch and a one-way switch with delay added to the feedback terms. We show that long-lasting transient oscillations exist in both models under general conditions and that the duration depends strongly on the magnitude of the delay and initial conditions. We then show the existence of long-lasting oscillations in specific biological examples: the Cdc2-Cyclin B/Wee1 system and a genetic regulatory network. Our results challenge fundamental assumptions underlying oscillatory behavior in biological systems. While generally delayed negative feedback systems are canonical in generating oscillations, we show that delayed positive feedback systems are a mechanism for generating oscillations as well.
1 Introduction
Positive feedback loops are a prominent network motif in many biophysical and biochemical circuits. They appear at multiple different scales ranging from gene regulatory networks through hormone secretion. Well-known examples of this motif include platelet activation during blood coagulation,1–3 the Ferguson reflex during human child birth,4,5 the Cdc2-Cyclin B/Wee1 network for cell cycle regulation,6–8 the interaction between the central nervous system and hypothalamus-pituitary-adrenal axis,9,10 and the Mos/MEK/p42 MAPK cascade.6,11Models of positive feedback systems have been studied extensively and many display bistability, a feature where two stable steady states exist simultaneously.12–14 Beyond bistability, models of positive feedback often do not exhibit more complicated dynamics such as oscillations. A very common motif for the generation of oscillations is delayed negative feedback, which is a control motif used in homeostatic systems such as the pancreas and its regulation of blood sugar.15,16 Models of delayed negative feedback are well-known to generate limit cycles emerging from a delay-dependent supercritical Hopf bifurcation. The effect of temporal delay on positive feedback systems has received much less attention. This article is a first step in delineating the effect of delay on positive feedback systems.
We study the effect of delays on positive feedback models by incorporating explicit delay into feedback terms of two well-known models: a genetic toggle switch and a one-way switch.7,12,17 Both models describe two proteins that undergo production governed by a Hill function and linear degradation. In parameter regimes that facilitate bistability, we show that these models exhibit long-lasting transient oscillations before reaching a steady state. These findings suggest a mostly unexplored mechanism for generating oscillatory behavior in a biological system. Under certain conditions, the duration of these oscillations is so long as to be indistinguishable from true limit cycle oscillations. From the viewpoint of biology, the transient oscillations could last longer than the lifespan of the cell or organism that generates them.
Our findings challenge fundamental understanding of mechanisms that drive oscillations in biological and biochemical systems. Historically, when oscillations were observed in an experimental setting, it was assumed that they were most likely caused by delayed negative feedback. We argue against this assumption.
We begin by giving a preliminary overview of the positive feedback systems that we investigate. For completeness, we also describe how delays facilitate pulsatile dynamics in delayed negative feedback systems. Thereafter, we incorporate explicit delay in positive feedback systems and describe the means by which long-lasting but transient oscillations emerge.
2 Preliminaries
2.1 Genetic toggle switch, one-way switch, and bistability
We begin with a review of minimal models of canonical positive feedback systems that exhibit bistability. The dynamics of these models with time delay in the feedback are analyzed later in the manuscript. | (1) |
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) measures the cooperativity between the repressors13 and is positive for the mutual inhibition case. Because each molecule inhibits the production of its inhibitor, the feedback provides positive feedback of x onto x and y onto y. That is, x inhibits its inhibitor y (and vice versa), so the cumulative effect is positive feedback of x onto x and y onto y. For n ≥ 2 the system admits three real steady states (x*,y*): two stable nodes and one saddle point. The existence of two stable steady states classifies system (1) as bistable, a feature that can emerge in positive feedback systems.7,12Fig. 1A–C depicts dynamics of this system. The two stable nodes in Fig. 1B (black circles) are characterized by the dominance of one protein over the other
measures the cooperativity between the repressors13 and is positive for the mutual inhibition case. Because each molecule inhibits the production of its inhibitor, the feedback provides positive feedback of x onto x and y onto y. That is, x inhibits its inhibitor y (and vice versa), so the cumulative effect is positive feedback of x onto x and y onto y. For n ≥ 2 the system admits three real steady states (x*,y*): two stable nodes and one saddle point. The existence of two stable steady states classifies system (1) as bistable, a feature that can emerge in positive feedback systems.7,12Fig. 1A–C depicts dynamics of this system. The two stable nodes in Fig. 1B (black circles) are characterized by the dominance of one protein over the other  and the saddle point (black triangle) describes coexistence (x* = y*). The basins of attraction of each stable steady state are separated by the stable manifold of the saddle point, which for this system is
and the saddle point (black triangle) describes coexistence (x* = y*). The basins of attraction of each stable steady state are separated by the stable manifold of the saddle point, which for this system is ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI = {(x,y)|y = x}.13
SI = {(x,y)|y = x}.13
 | ||
Fig. 1 Reaction network diagram, phase space, and time series for system (1) when α = 10, n = 2 (A)–(C) and α = 2.15, n = −2 (D)–(F). Leftmost column: schematics of biomolecular feedback structures studied. Middle column: phase portrait of eqn (1) with sample trajectories (color). The dashed lines are the separatrices ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI (top) and SI (top) and ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA (bottom). Right column: sample time series for the trajectories shown in the middle panels. SA (bottom). Right column: sample time series for the trajectories shown in the middle panels. | ||
The Hill function§ used for the feedback is a modeling choice but is not necessary for the results in this work, which hold for more general functional choices for the feedback. With a feedback function g(u) that describes inhibition, we require that g(u) ≥ 0 for all u, g should be monotonically decreasing, and g → 0 as u → ∞. Similarly, if g describes activation, we require g(u) ≥ 0 for all u, g should be monotonically increasing, and g → A ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) ≥0 as u → ∞, for some constant A. For n > 0, it is straightforward to see that g(u) = (1 + un)−1 satisfies the inhibition conditions. Similarly, for n < 0, g(u) = (1 + un)−1 satisfies the activation conditions.
≥0 as u → ∞, for some constant A. For n > 0, it is straightforward to see that g(u) = (1 + un)−1 satisfies the inhibition conditions. Similarly, for n < 0, g(u) = (1 + un)−1 satisfies the activation conditions.
One alternative popular function used for modeling biochemical systems is the Boltzmann function,  , where a,b are constants. For b > 0, this equation satisfies the inhibition conditions. Similarly, for b < 0, the equation satisfies the activation conditions. Another example is the hyperbolic tangent function,
, where a,b are constants. For b > 0, this equation satisfies the inhibition conditions. Similarly, for b < 0, the equation satisfies the activation conditions. Another example is the hyperbolic tangent function,  , where a, b are constants. When b < 0 (b > 0), the equation satisfies the inhibition (activation) conditions. Using such functions would not alter the qualitative results of our work.
, where a, b are constants. When b < 0 (b > 0), the equation satisfies the inhibition (activation) conditions. Using such functions would not alter the qualitative results of our work.
![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA = {(x,y)|y = K − x}, with K ≈ 1.36 when α = 2.15, n = −2.
SA = {(x,y)|y = K − x}, with K ≈ 1.36 when α = 2.15, n = −2.
2.2 Delayed negative feedback
A canonical example of a biomolecular feedback system is a protein inhibiting its own production after some temporal delay, τ > 0 (see Fig. 2A). Mathematically, this system can be represented by the delay differential equation (DDE)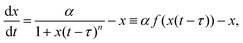 | (2) |
 | ||
| Fig. 2 Delayed negative feedback. (A) Schematic of the delayed negative feedback biomolecular system. (B) Oscillations emerge in system (2) as the delay is increased from τ = 1 (blue curve) to τ = 3 (orange curve). (C) Bifurcation diagram for eqn (2) when varying the delay τ. Solid and dashed black lines correspond to stable and unstable stationary steady states, respectively. The red curve shows the minimum and maximum values of x on the periodic branch, and the green circle is a supercritical Hopf bifurcation point with τc ≈ 1.7 and α = 10, n = 2. | ||
Although this system is comprised of a single equation, it contains limit cycles in its phase space that are generated by the delay. The role delays play in the onset of oscillations in delayed negative feedback systems is well-understood: the amount of delay, τ, in feedback determines the onset of oscillations via a supercritical Hopf bifurcation.19–21 Furthermore, the frequency of the delay-induced oscillation decreases as τ is increased and the amplitude scales as  near the bifurcation point. Linear stability analysis of eqn (2) about the steady state x = x* yields the following conditions for a Hopf bifurcation:
near the bifurcation point. Linear stability analysis of eqn (2) about the steady state x = x* yields the following conditions for a Hopf bifurcation:
| ω = −αf′(x*)sin(ωτ) 1 = αf′(x*)cos(ωτ) ω = −tan(ωτ), |
For τ > 0, however, there exist critical values (ωc,τc) satisfying the bifurcation conditions. When τ is increased past τc, a pair of complex conjugate eigenvalues crosses the imaginary axis. Although this is not sufficient to guarantee the emergence of a stable periodic solution via a supercritical Hopf bifurcation for τ > τc, the existence of stable oscillations beyond the Hopf bifurcation point can be verified numerically (see Fig. 2B and C).
We next discuss how the network motifs and dynamics presented in this section produce pulsatility in delayed positive feedback systems.
3 Delayed positive feedback
To investigate the role delay plays in producing oscillations in the toggle switch and one-way switch systems, we implement explicit delay, τ, into both feedback terms of system (1). This yields the set of DDEs | (3) |
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) can be adjusted to model delayed mutual inhibition or delayed mutual activation by letting n > 0 or n < 0, respectively. Importantly, the set of possible steady states for system (3) is identical to system (1). In all simulations, we use constant history functions for initial data.
can be adjusted to model delayed mutual inhibition or delayed mutual activation by letting n > 0 or n < 0, respectively. Importantly, the set of possible steady states for system (3) is identical to system (1). In all simulations, we use constant history functions for initial data.
In this section, we discuss dynamics of system (3) and how they change with τ and different history functions. In particular, we discuss how the presence of delay facilitates onset of pulsatile dynamics. DDEs are infinite-dimensional structures, so illustrating dynamics in their true phase space is not possible. We therefore present results by projecting the phase portrait into a two-dimensional subspace of the phase space.
3.1 Delayed mutual inhibition
We set n > 0 in eqn (3) to model delayed mutual inhibition. To see that oscillations are indeed present in the phase space of this delayed positive feedback system, observe that taking system (3) with initial data satisfying x(t) = y(t) = a ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) for t ∈ [−τ,0] constrains the dynamics to the stable manifold of the saddle point,
for t ∈ [−τ,0] constrains the dynamics to the stable manifold of the saddle point, ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI, which is the seperatrix partitioning the basins of attraction of the two stable steady states in the system without delay (eqn (1)). The resulting differential equation is exactly eqn (2), which is a model for delayed negative feedback and exhibits stable oscillations for sufficiently large values of τ. Thus, eqn (3) admits pulsatile dynamics along
SI, which is the seperatrix partitioning the basins of attraction of the two stable steady states in the system without delay (eqn (1)). The resulting differential equation is exactly eqn (2), which is a model for delayed negative feedback and exhibits stable oscillations for sufficiently large values of τ. Thus, eqn (3) admits pulsatile dynamics along ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI in the xy-plane. Although this is a limiting circumstance, it illustrates that limit cycles are indeed possible in delayed positive feedback systems. In more complicated mutual inhibition systems, choosing history functions precisely on an invariant manifold is very difficult. For that reason, we investigate dynamics of (3) starting near, but not on,
SI in the xy-plane. Although this is a limiting circumstance, it illustrates that limit cycles are indeed possible in delayed positive feedback systems. In more complicated mutual inhibition systems, choosing history functions precisely on an invariant manifold is very difficult. For that reason, we investigate dynamics of (3) starting near, but not on, ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI.
SI.
Numerical solutions suggest that limit cycles do not arise with initial data off ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI. However, the system exhibits transient but long-lasting oscillations that eventually contract to a steady state. Fig. 3B shows two sample trajectories of system (3) starting on opposite sides of
SI. However, the system exhibits transient but long-lasting oscillations that eventually contract to a steady state. Fig. 3B shows two sample trajectories of system (3) starting on opposite sides of ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI. Superimposed on top are the trajectories of the ODE system (1) with the same initial conditions. The ODE solutions (black) approach their respected steady states without oscillatory dynamics. In contrast, the DDE system trajectories (red and blue) oscillate for many cycles before eventually reaching their respective steady states.
SI. Superimposed on top are the trajectories of the ODE system (1) with the same initial conditions. The ODE solutions (black) approach their respected steady states without oscillatory dynamics. In contrast, the DDE system trajectories (red and blue) oscillate for many cycles before eventually reaching their respective steady states.
 | ||
Fig. 3 Dynamics of eqn (3) for α = 10, n = 2, τ = 6 (A)–(C) and α = 2.15, n = −2, τ = 8 (D)–(F). Left column: schematics of the biomolecular feedback system. Middle column: dynamics in the xy-plane with actual or approximate separatrices ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI (top) and SI (top) and ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA (bottom) superimposed as dashed lines and sample trajectories from eqn (3) plotted (color). Black trajectories are solutions of eqn (1) for the same initial conditions. Right column: sample time series. The abscissa shows the oscillation number, using the fact that the period T ≈ 2τ to scale time. SA (bottom) superimposed as dashed lines and sample trajectories from eqn (3) plotted (color). Black trajectories are solutions of eqn (1) for the same initial conditions. Right column: sample time series. The abscissa shows the oscillation number, using the fact that the period T ≈ 2τ to scale time. | ||
Because the trajectory initially oscillates near the stable manifold of the ODE system, we refer to the long lasting oscillations as “remnants of the delayed negative feedback oscillator”, which is present exactly on ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI. Numerical time series show that the period, T, of the transient oscillations is related to the delay by T ≈ 2τ. Thus, during the period of transient oscillations, t ≈ NT ≈ N(2τ) so time can be replaced by
SI. Numerical time series show that the period, T, of the transient oscillations is related to the delay by T ≈ 2τ. Thus, during the period of transient oscillations, t ≈ NT ≈ N(2τ) so time can be replaced by  , where N is the oscillation number. The time series in Fig. 3C shows oscillations in x graphed as a function of oscillation number. From a biological viewpoint, it is possible that the transient oscillations last longer than the lifespan of the cell or organism. In such a case, there is little distinction between “long-lasting transient” oscillations and “stable limit cycle” oscillations.
, where N is the oscillation number. The time series in Fig. 3C shows oscillations in x graphed as a function of oscillation number. From a biological viewpoint, it is possible that the transient oscillations last longer than the lifespan of the cell or organism. In such a case, there is little distinction between “long-lasting transient” oscillations and “stable limit cycle” oscillations.
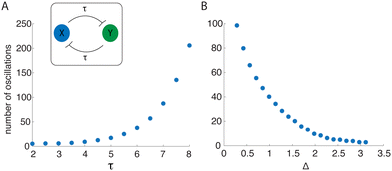
There appear to be two main factors that contribute to the duration of the transient oscillations in the delayed mutual inhibition system: (1) the magnitude of the delay, τ, and (2) the distance of the initial conditions from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI. To quantify how these factors affect oscillation duration, we simulated the mutual inhibition system (3) and recorded the number of cycles in the x variable. The results are given in Fig. 4A. The number of oscillations increases super-linearly with τ.
SI. To quantify how these factors affect oscillation duration, we simulated the mutual inhibition system (3) and recorded the number of cycles in the x variable. The results are given in Fig. 4A. The number of oscillations increases super-linearly with τ.
We next numerically investigated the delayed mutual inhibition system under varying initial conditions. To see how distance from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI influenced the number of oscillations produced, we extended a line orthogonal to
SI influenced the number of oscillations produced, we extended a line orthogonal to ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI and sampled pairs of initial conditions for x and y on this normal line. We then simulated the delay system with each initial condition pair. The number of oscillations is shown as a function of the Euclidean distance (Δ) to
SI and sampled pairs of initial conditions for x and y on this normal line. We then simulated the delay system with each initial condition pair. The number of oscillations is shown as a function of the Euclidean distance (Δ) to ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI in Fig. 4B. This decreases monotonically with distance from
SI in Fig. 4B. This decreases monotonically with distance from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI, suggesting that the transient oscillations are driven by flow near
SI, suggesting that the transient oscillations are driven by flow near ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI.
SI.
3.2 Delayed mutual activation
We set n < 0 in system (3) to model delayed mutual activation (Fig. 3D). Similar to the previous model, this system displays bistability and sample trajectories on either side of![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA are shown in Fig. 3E. As in the delayed mutual inhibition case, we superimposed the trajectories from the ODE system (1) with identical parameters and initial conditions. The results show that the trajectories without delay (black) approach the stable steady states without oscillation, but the trajectories with delay (color) oscillate roughly parallel to
SA are shown in Fig. 3E. As in the delayed mutual inhibition case, we superimposed the trajectories from the ODE system (1) with identical parameters and initial conditions. The results show that the trajectories without delay (black) approach the stable steady states without oscillation, but the trajectories with delay (color) oscillate roughly parallel to ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA before eventually approaching a steady state. A sample time series for the state variable x is given in Fig. 3F and exhibits long-lasting oscillations before reaching a steady state.
SA before eventually approaching a steady state. A sample time series for the state variable x is given in Fig. 3F and exhibits long-lasting oscillations before reaching a steady state.
As in the previous model, we simulated the delayed mutual activation model for varying delay values τ to explore how oscillation duration changed. Results are summarized in Fig. 5A. For small τ the system displays a small number of transient oscillations. However, increasing τ to sufficiently large value leads to a rapid rise in the number of oscillations, which continues to increase for larger delays. To understand the origin of this rapid increase in oscillation number, it is helpful to view the dynamics in the xy-plane (Fig. 6A and B). The trajectory in Fig. 6A corresponds to the parameters and delay value of the red point in Fig. 5A. With these parameters, the trajectory oscillates as it moves towards the upper steady state. However, when the delay is increased from 4 to 6, as in Fig. 6B, the trajectory first moves towards the upper steady state before changing direction to the lower steady state. This flow reversal generates many more oscillations, and there appears to be a critical delay value at which this dynamic behavior occurs.
 | ||
Fig. 6 Dynamics of the mutual activation model depend critically on τ and Δ. (A) and (B) Two trajectories with the same starting points (black stars), but with two different delays, τ = 4 (A) and τ = 6 (B) corresponding to the red and green points in Fig. 5A. (C) and (D) Two trajectories with the same delays (τ = 6) but starting at two different distances from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA, Δ = 0.07 (C) and Δ = 0.09 (D), corresponding to the red or green points in Fig. 5B. SA, Δ = 0.07 (C) and Δ = 0.09 (D), corresponding to the red or green points in Fig. 5B. | ||
In addition to varying delay values, we simulated the delayed mutual activation model with varying initial conditions. As with the previous model, we extended a normal line from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA and sampled initial condition pairs along that line. Next, we simulated the system for each initial condition and recorded oscillation duration. The results for the number of oscillations as a function of the distance (Δ) to
SA and sampled initial condition pairs along that line. Next, we simulated the system for each initial condition and recorded oscillation duration. The results for the number of oscillations as a function of the distance (Δ) to ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA are given in Fig. 5B. The plot suggests that, initially, as you get farther away from
SA are given in Fig. 5B. The plot suggests that, initially, as you get farther away from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA, the number of oscillations increases monotonically. However, when Δ is sufficiently large there is a sharp downwards jump and the number of oscillations monotonically decreases as Δ is increased further. Looking again in the xy-plane (Fig. 6C and D) we plot two trajectories with identical parameter values, but starting at different distances from
SA, the number of oscillations increases monotonically. However, when Δ is sufficiently large there is a sharp downwards jump and the number of oscillations monotonically decreases as Δ is increased further. Looking again in the xy-plane (Fig. 6C and D) we plot two trajectories with identical parameter values, but starting at different distances from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA. In one case (Fig. 6C), the trajectory begins to travel toward the upper steady state, but then turns around and crosses over
SA. In one case (Fig. 6C), the trajectory begins to travel toward the upper steady state, but then turns around and crosses over ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA to eventually end at the origin. Initial conditions satisfying Δ < 0.07 in Fig. 5B show similar dynamics in phase space to that of Fig. 6C. Taking an initial condition a small distance farther away (green point) yields a trajectory that oscillates directly towards the upper steady state. Similarly, all starting points satisfying Δ > 0.09 in Fig. 5B show similar dynamics in phase space to that of Fig. 6D.
SA to eventually end at the origin. Initial conditions satisfying Δ < 0.07 in Fig. 5B show similar dynamics in phase space to that of Fig. 6C. Taking an initial condition a small distance farther away (green point) yields a trajectory that oscillates directly towards the upper steady state. Similarly, all starting points satisfying Δ > 0.09 in Fig. 5B show similar dynamics in phase space to that of Fig. 6D.
3.3 Asymmetric networks
Thus far, we assumed that the dynamics of both of the interacting species are the same, described by eqn (3) with identical parameter values for x and y. We now explore the effects of breaking the symmetry, using the set of DDEs | (4) |
 | ||
| Fig. 7 Dynamics of eqn (4) when the symmetry between the two cells is broken. (A) Toggle switch with n1,2 > 0 and α = 10, and (B) one-way switch with n1,2 < 0, α = 2.15. First column: schematics of the biomolecular feedback systems. Second column: time series of species x when |n1| = |n2| = 2, τ1 = 8 and τ2 = 12. Third column: time series of x when |n1| = 3, |n2| = 5, and τ1 = τ2 = 8. Fourth column: time series of x when |n1| = 3, |n2| = 5, τ1 = 8, and τ2 = 12. | ||
3.4 Single equation example
The long-lasting oscillations in Fig. 3 and 7 come from models which describe the evolution of two species. However, we found that long lasting transient oscillations can occur in models of a single species. Consider the following DDE | (5) |
 | ||
| Fig. 8 Delayed positive autoregulation of a single species. (A) Schematic of biomolecular feedback structure. (B) Long lasting transient oscillations occur over time in system (5). Parameter values were α = 2.15, n = −2, τ = 14. | ||
4 Biological examples
Here we present two, more complicated biological models of delayed mutual inhibition and delayed mutual activation. We show they are capable of displaying similar dynamics to system (3).4.1 The Cdc2-Cyclin B/Wee1 system
Cdc2 is one member of a class of enzymes coded by cell-division-cycle (cdc) genes that is required to move through the cell division cycle.22 In preparation for progressing into the M phase of the cycle, cyclin B is synthesized and binds with free Cdc2 to form an inactive M-phase promoting factor (MPF). Only when this MPF is phosphorylated on threonine-167 by a cyclin-dependent activating kinase (CAK) is it in an active state. Once the concentration of active MPF is sufficiently high, the cell can progress to the M phase.23 Wee1 is a protein that helps mitigate this process by phosphorylating the MPF at the tyrosine-15 site, rendering it inactive. Conversely, the MPF phosphorylates Wee1, rendering Wee1 inactive. This is a clear example of mutual inhibition, and mathematical models have shown this system to be bistable (high MPF, low Wee1 or high Wee1, low MPF).7,8,24 When Wee1 is high, the cell remains in interphase.We extend the equations in a previous model for this system6 to include explicit delays in the relevant feedback terms. The equations to model the interaction between the active Cdc2-Cyclin B and active Wee1 molecules are given by the dimensionless DDEs
 | (6) |
![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SCdc2. Fig. 9B displays a phase portrait of the system projected onto the xy-plane with sample trajectories (color) starting with initial conditions on either side of
SCdc2. Fig. 9B displays a phase portrait of the system projected onto the xy-plane with sample trajectories (color) starting with initial conditions on either side of ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SCdc2. The black trajectories are the solutions to the system without delay starting at the same initial points. These trajectories exhibit similar behavior to those in Fig. 3B, demonstrating that it is possible to achieve transient oscillations in more complex delayed mutual inhibition models for biological systems. A sample scaled time series showing how active Cdc2-Cyclin B evolves is shown in Fig. 9C, exhibiting over 30 oscillations before reaching equilibrium, similar to system (3).
SCdc2. The black trajectories are the solutions to the system without delay starting at the same initial points. These trajectories exhibit similar behavior to those in Fig. 3B, demonstrating that it is possible to achieve transient oscillations in more complex delayed mutual inhibition models for biological systems. A sample scaled time series showing how active Cdc2-Cyclin B evolves is shown in Fig. 9C, exhibiting over 30 oscillations before reaching equilibrium, similar to system (3).
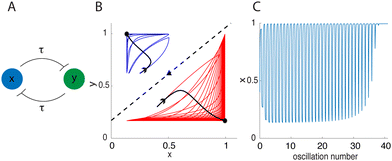 | ||
Fig. 9 (A) Schematic of the delayed Cdc2-Cyclin B/Wee1 biomolecular system. (B) Phase space with approximate seperatix ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SCdc2 superimposed (dashed line) and sample trajectories from eqn (6) plotted (color). The black trajectories are solutions to system (6) without delay under identical starting conditions. (C) Sample time series exhibiting long-lasting transient oscillations. Parameter values are μ = 1, β1 = 200, β2 = 10, γ = 4, K1 = 30, K2 = 1, ν = 1, and τ = 8. SCdc2 superimposed (dashed line) and sample trajectories from eqn (6) plotted (color). The black trajectories are solutions to system (6) without delay under identical starting conditions. (C) Sample time series exhibiting long-lasting transient oscillations. Parameter values are μ = 1, β1 = 200, β2 = 10, γ = 4, K1 = 30, K2 = 1, ν = 1, and τ = 8. | ||
4.2 Genetic regulatory networks
Genetic regulatory networks (GRNs) illustrate the interaction and relations of genes, proteins, and other molecules inside cells and are an active area of study in mathematical biology research.25–30 Here we consider a simple delayed mutual activation model between a gene and protein shown schematically in Fig. 10A. A typical non-dimensional model for such a GRN, but incorporating a time delay in the feedback terms, is | (7) |
![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SGRN. The trajectories of the system with time delay have a behavior that is similar to trajectories in Fig. 3E of the delayed one-way switch model. This illustrates that very long transient oscillations can occur in delayed mutual activation GRN models. A sample time course of protein concentration is shown in Fig. 10C. We observed long lasting oscillations in the protein concentration up until the trajectory converged to steady state.
SGRN. The trajectories of the system with time delay have a behavior that is similar to trajectories in Fig. 3E of the delayed one-way switch model. This illustrates that very long transient oscillations can occur in delayed mutual activation GRN models. A sample time course of protein concentration is shown in Fig. 10C. We observed long lasting oscillations in the protein concentration up until the trajectory converged to steady state.
 | ||
Fig. 10 (A) Schematic of the delayed gene/protein system. (B) Phase space with seperatix ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SGRN superimposed (dashed line). Trajectories from eqn (7) plotted (color) along with those starting at the same location but without delay (black). (C) Sample time series showing extensive oscillations before reaching steady state. The parameter values are ρ = 0.1, σ = 2, λ = 9, δ = 1, κ = 2, n = 3, and τ = 10. SGRN superimposed (dashed line). Trajectories from eqn (7) plotted (color) along with those starting at the same location but without delay (black). (C) Sample time series showing extensive oscillations before reaching steady state. The parameter values are ρ = 0.1, σ = 2, λ = 9, δ = 1, κ = 2, n = 3, and τ = 10. | ||
The major implication of this result for GRNs is that the mechanism underlying protein production at the genetic level may manifest as a delayed positive feedback system. Historically, oscillatory protein production has been interpreted as a result of delayed negative feedback. With the sheer number of oscillatory genes in biology, our findings suggest the likelyhood that delayed positive feedback is an underlying mechanism in many cases.
As an example, gene expression of over 1000 proteins during development in C. elegans have been identified as undergoing oscillatory dynamics. Cuticular collagen genes, hedgehog receptors, and metallopeptidase, amongst many others, have been observed to oscillate.31 Since only a few cycles are typically observed, it is unclear whether these are true sustained limit cycle oscillations or if they are simply long-lasting. In the latter case, delayed positive feedback could be the driving mechanism.
5 Discussion
We presented two canonical examples for positive feedback, the toggle switch and the one-way switch, and explored their dynamics when adding temporal delay to the feedback terms. We showed that they are capable of generating long-lasting oscillatory dynamics under certain conditions. We verified our results using a two-dimensional projected phase space for comparison against the model dynamics without a time delay. Finally, we showed that qualitatively similar oscillatory dynamics occur when applying temporal delay to previously studied biological models of the toggle switch and one-way switch. Because of the large number of cycles produced, the transient oscillations in the delayed positive feedback systems may be indistinguishable from true limit cycle oscillations. Although our models used Hill function formulations for the feedback, we found similar long-lasting oscillations when either Boltzmann or hyperbolic tangent formulations were used (not shown).We found that two main factors contribute to the duration of these transient oscillations: (1) the magnitude of the delay (τ) and (2) the Euclidean distance (Δ) of the initial conditions from ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SI or
SI or ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) SA. The delayed mutual inhibition system showed that the oscillation duration increases super-linearly with delay and decreases super-linearly with Δ. The delayed mutual activation model showed oscillation duration increases with the delay value, but a sharp jump occurs at some critical τ value. We showed in Fig. 6A and B the trajectories with τ values on either side of the jump approach different steady states. We believe this may be due to a shift in the DDE seperatrix when changing the delay value τ. This would explain why the trajectories approach different steady states even though the initial conditions are the same. The oscillation duration as a function of Δ shows initial increase in oscillation duration with a sharp decrease in oscillation duration at some critical distance. Similarly, we hypothesize that the critical Δ value in Fig. 5B could mark the location of the DDE seperatrix, and that on the true seperatrix a limit cycle exists. Thus, as initial data is taken further away from the critical Δ value, we observe fewer oscillations. We hope to explore these phenomena in the future to get a better idea of the shape of the true DDE seperatrix and determine the mechanisms responsible for these interesting transitions in the dynamics.
SA. The delayed mutual inhibition system showed that the oscillation duration increases super-linearly with delay and decreases super-linearly with Δ. The delayed mutual activation model showed oscillation duration increases with the delay value, but a sharp jump occurs at some critical τ value. We showed in Fig. 6A and B the trajectories with τ values on either side of the jump approach different steady states. We believe this may be due to a shift in the DDE seperatrix when changing the delay value τ. This would explain why the trajectories approach different steady states even though the initial conditions are the same. The oscillation duration as a function of Δ shows initial increase in oscillation duration with a sharp decrease in oscillation duration at some critical distance. Similarly, we hypothesize that the critical Δ value in Fig. 5B could mark the location of the DDE seperatrix, and that on the true seperatrix a limit cycle exists. Thus, as initial data is taken further away from the critical Δ value, we observe fewer oscillations. We hope to explore these phenomena in the future to get a better idea of the shape of the true DDE seperatrix and determine the mechanisms responsible for these interesting transitions in the dynamics.
We observed that within parameter regimes which enable bistability, the long lasting oscillations in models of delayed positive feedback oscillated “orthogonally” to their equilibria. For example, with delayed mutual inhibition the equilibria are characterized by either x ≫ y or x ≪ y. However, x ≈ y during most of the transient oscillation. In the delayed mutual activation case, the opposite occurs. The equilibria are characterized by both species completely extinct or maximally expressed. However, in the oscillation, the trajectories flip between states where x ≫ y and x ≪ y, which is reminiscent of mutual inhibition. This is significant, especially to experimentalists, because it gives an inference strategy for determining which mechanism produced the oscillations (if they occur due to delayed positive feedback). In-phase oscillations indicate delayed mutual inhibition, while anti-phase oscillations indicate delayed mutual activation.
Many previously studied biological systems have shown oscillatory behavior.31–33 Models for these behaviors would most likely contain a delayed negative feedback motif or a combination of negative and positive feedback, as these two systems are canonical generators of pulsatile dynamics. However, our results argue that the mechanism behind oscillations in such systems can potentially be explained by delayed positive feedback alone, as long as there is delay in the feedback and as long as the system has strong non-linearity.
Finally, although the examples shown here were based on biochemical or biological examples, the concept of oscillations driven by delayed positive feedback is applicable in other areas as well. Any mechanism that exhibits bistability must have an inherent positive feedback loop; thus, any system exhibiting bistability and strong non-linearity has the potential for long-lasting oscillatory dynamics. Examples include optical bistability34 in condensed matter physics, physical biogeochemistry of sediments and oceans as a means to understand anoxic marine systems,35 and astrochemical bistability arising from autocalatyic oxygen chemistry.36
Author contributions
Christopher J. Ryzowicz: methodology, software, writing – original draft. Richard Bertram: methodology, writing – review & editing, funding acquisition. Bhargav R. Karamched: conceptualization, methodology, writing – review & editing, funding acquisition.Data availability
The code used to generate the figures in this manuscript are available at https://cryzowicz.wixsite.com/chris-ryzowicz/general-5.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was partially supported by the National Science Foundation, grant number DMS 2324926 to R. Bertram and by the FSU Council on Research and Creativity SEED grant to B. Karamched. C. Ryzowicz would like to thank his family and fellow graduate student colleagues for their unending support during the writing of this manuscript. B. Karamched would like to thank his wife, Hajra Habib, for her love and unending support.Notes and references
- K. A. Abdel-Sater, Physiological positive feedback mechanisms, Am. J. Biomed. Sci., 2011, 3, 145–155 CrossRef.
- E. Beltrami and J. Jesty, Mathematical analysis of activation thresholds in enzyme-catalyzed positive feedbacks: application to the feedbacks of blood coagulation, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 8744–8748 CrossRef CAS.
- J. Jesty and E. Beltrami, Positive feedbacks of coagulation: their role in threshold regulation, Arterioscler., Thromb., Vasc. Biol., 2005, 25, 2463–2469 CrossRef CAS PubMed.
- K. Uvnäs-Moberg, A. Ekström-Bergström, M. Berg, S. Buckley, Z. Pajalic, E. Hadjigeorgiou, A. Kotłowska, L. Lengler, B. Kielbratowska and F. Leon-Larios, et al., Maternal plasma levels of oxytocin during physiological childbirth-a systematic review with implications for uterine contractions and central actions of oxytocin, BMC Pregnancy Childbirth, 2019, 19, 1–17 CrossRef.
- K. Uvnäs-Moberg, The physiology and pharmacology of oxytocin in labor and in the peripartum period, Am. J. Obstet. Gynecol., 2024, 230(3), S740–S758 CrossRef PubMed.
- D. Angeli, J. E. Ferrell Jr and E. D. Sontag, Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 1822–1827 CrossRef CAS PubMed.
- J. J. Tyson, K. C. Chen and B. Novak, Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell, Curr. Opin. Cell Biol., 2003, 15, 221–231 CrossRef CAS.
- J. Keener and J. Sneyd, Mathematical Physiology 1: Cellular Physiology, 2009 Search PubMed.
- B. Ron Mizrachi, A. Tendler, O. Karin, T. Milo, D. Haran, A. Mayo and U. Alon, Major depressive disorder and bistability in an HPA-CNS toggle switch, PLoS Comput. Biol., 2023, 19, e1011645 CrossRef CAS.
- N. J. Lasikiewicz, PhD thesis, University of Leeds, 2006.
- C. P. Bagowski and J. E. Ferrell, Bistability in the JNK cascade, Curr. Biol., 2001, 11, 1176–1182 CrossRef CAS PubMed.
- U. Alon, An Introduction to Systems Biology: Design Principles of Biological Circuits, Chapman and Hall/CRC, 2019 Search PubMed.
- R. Bertram, Mathematical modeling in neuroendocrinology, Compr. Physiol., 2015, 5, 911–927 Search PubMed.
- T. S. Gardner, C. R. Cantor and J. J. Collins, Construction of a genetic toggle switch in Escherichia coli, Nature, 2000, 403, 339–342 CrossRef CAS.
- I. Marinelli, B. M. Thompson, V. S. Parekh, P. A. Fletcher, L. Gerardo-Giorda, A. S. Sherman, L. S. Satin and R. Bertram, Oscillations in K (ATP) conductance drive slow calcium oscillations in pancreatic β-cells, Biophys. J., 2022, 121, 1449–1464 CrossRef CAS.
- N. Bruce, I.-A. Wei, W. Leng, Y. Oh, Y.-C. Chiu, M. G. Roper and R. Bertram, Coordination of pancreatic islet rhythmic activity by delayed negative feedback, Am. J. Physiol.: Endocrinol. Metab., 2022, 323, E492–E502 CrossRef CAS.
- D. Del Vecchio and R. M. Murray, Biomolecular Feedback Systems, Princeton University Press, Princeton, NJ, 2015 Search PubMed.
- T. Tian and K. Burrage, Stochastic models for regulatory networks of the genetic toggle switch, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8372–8377 CrossRef CAS.
- F. Bai, R. Bertram and B. R. Karamched, A closed-loop multi-scale model for intrinsic frequency-dependent regulation of axonal growth, Math. Biosci., 2022, 344, 108768 CrossRef CAS PubMed.
- B. R. Karamched, G. Hripcsak, R. L. Leibel, D. Albers and W. Ott, Delay-induced uncertainty in the glucose-insulin system: Pathogenicity for obesity and type-2 diabetes mellitus, Front. Physiol., 2022, 13, 936101 CrossRef.
- B. R. Karamched and C. E. Miles, Stochastic switching of delayed feedback suppresses oscillations in genetic regulatory systems, J. R. Soc., Interface, 2023, 20, 20230059 CrossRef.
- S. Dalton, Cell cycle regulation of the human cdc2 gene, EMBO J., 1992, 11, 1797–1804 CrossRef CAS.
- T. R. Coleman and W. G. Dunphy, Cdc2 regulatory factors, Curr. Opin. Cell Biol., 1994, 6, 877–882 CrossRef CAS PubMed.
- J. M. Raleigh and M. J. O’Connell, The G2 DNA damage checkpoint targets both Wee1 and Cdc25, J. Cell Sci., 2000, 113, 1727–1736 CrossRef CAS.
- A. Y. Mitrophanov and E. A. Groisman, Positive feedback in cellular control systems, BioEssays, 2008, 30, 542–555 CrossRef CAS PubMed.
- G. Karlebach and R. Shamir, Modelling and analysis of gene regulatory networks, Nat. Rev. Mol. Cell Biol., 2008, 9, 770–780 CrossRef CAS PubMed.
- T. Schlitt and A. Brazma, Current approaches to gene regulatory network modelling, BMC Bioinf., 2007, 8, 1–22 CrossRef.
- A. Polynikis, S. Hogan and M. Di Bernardo, Comparing different ODE modelling approaches for gene regulatory networks, J. Theor. Biol., 2009, 261, 511–530 CrossRef CAS PubMed.
- M. J. Schilstra and H. Bolouri, Modelling the regulation of gene expression in genetic regulatory networks, BioComputation group, University of Hertfordshire., Tech. Rep, 2002 Search PubMed.
- M. Hecker, S. Lambeck, S. Toepfer, E. Van Someren and R. Guthke, Gene regulatory network inference: data integration in dynamic models—a review, BioSystems, 2009, 96, 86–103 CrossRef CAS PubMed.
- G.-J. Hendriks, D. Gaidatzis, F. Aeschimann and H. Großhans, Extensive oscillatory gene expression during C. elegans larval development, Mol. Cell, 2014, 53, 380–392 CrossRef CAS PubMed.
- S. Zambrano, I. De Toma, A. Piffer, M. E. Bianchi and A. Agresti, NF-κB oscillations translate into functionally related patterns of gene expression, eLife, 2016, 5, e09100 CrossRef.
- B. Zhu and S. Liu, Preservation of 12-h ultradian rhythms of gene expression of mRNA and protein metabolism in the absence of canonical circadian clock, Front. Physiol., 2023, 14, 1195001 CrossRef PubMed.
- H. Gibbs, S. McCall, T. Venkatesan, A. Gossard, A. Passner and W. Wiegmann, Optical bistability in semiconductors, Appl. Phys. Lett., 1979, 35, 451–453 CrossRef CAS.
- S. J. van de Velde, C. T. Reinhard, A. Ridgwell and F. J. Meysman, Bistability in the redox chemistry of sediments and oceans, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 33043–33050 CrossRef CAS.
- G. Dufour and S. B. Charnley, Astrochemical Bistability: Autocatalysis in Oxygen Chemistry, Astrophys. J., 2019, 887, 67 CrossRef CAS.
Footnotes |
| † Correspondence to: LOV Building, Rm 317, 1017 Academic Way, Tallahassee, FL 32306, United States. E-mail: bkaramched@fsu.edu |
| ‡ All models presented and described in this manuscript are nondimensionalized. |
| § This is also referenced as a Langmuir function in some biochemical literature. |
| This journal is © the Owner Societies 2024 |