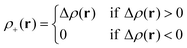Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Benchmarking DFT-based excited-state methods for intermolecular charge-transfer excitations†
Nicola
Bogo
 *ab and
Christopher J.
Stein
*ab and
Christopher J.
Stein
 b
b
aFaculty of Physics, University of Duisburg-Essen, 47057 Duisburg, Germany
bDepartment of Chemistry and Catalysis Research Center, TUM School of Natural Sciences, Technische Universität München, Lichtenbergstr. 4, 85748 Garching, Germany. E-mail: christopher.stein@tum.de
First published on 24th July 2024
Abstract
Intermolecular charge-transfer is a highly important process in biology and energy-conversion applications where generated charges need to be transported over several moieties. However, its theoretical description is challenging since the high accuracy required to describe these excited states must be accessible for calculations on large molecular systems. In this benchmark study, we identify reliable low-scaling computational methods for this task. Our reference results were obtained from highly accurate wavefunction calculations that restrict the size of the benchmark systems. However, the density-functional theory based methods that we identify as accurate can be applied to much larger systems. Since targeting charge-transfer states requires the unambiguous classification of an excited state, we first analyze several charge-transfer descriptors for their reliability concerning intermolecular charge-transfer and single out the charge-transfer distance calculated based on the variation of electron density upon excitation (DCT) as an optimal choice for our purposes. In general, best results are obtained for orbital-optimized methods and among those, the maximum overlap method proved to be the most numerically stable variant when using the initial MOs as reference orbitals. Favorable error cancellation with optimally-tuned range-separated hybrid functionals and a rather small basis set can provide an economical yet reasonable wavefunction when using time-dependent density functional theory, which provides relevant information about the excited-state character to be used in the orbital-optimized methods. The qualitative agreement makes these fast calculations attractive for high-throughput screening applications.
1 Introduction
Charge-transfer (CT) excitations between two molecules where one molecular unit serves as the donor and the other as the acceptor of the transferred electron are classified as intermolecular charge transfer (ICT) if these units are individual molecules or moieties sufficiently far apart. Biological molecular devices exploit these transfer properties to move excess energy in the excited state through different locations in space and perform complex operations.1,2 Naturally, chemists strive to understand the properties of such molecular systems to engineer novel, artificial devices with accurately predicted CT properties.In supramolecular chemistry, large multi-component systems are synthesized starting from separate molecular units. The key benefit of the assembled structure is that the characteristics of the isolated components are preserved, whereas novel properties emerge that arise due to the arrangement of the individual units in the nanostructure. Supramolecular cage molecules hence provide a blueprint for such artificial CT devices, and since donor and acceptor moieties are well separated due to the presence of linkers, spacers, and connecting metal ions, we focus our investigation on molecular dimers with a donor and acceptor unit as prototypes for the study of ICT processes. Unfortunately, accurate wavefunction methods are plagued by a prohibitively steep scaling of the computational cost, and the typical size of supramolecular cages forces us to apply more economic electronic-structure methods. Developments in DFT-based electronic-structure theory3,4 shed light on the failures and successes of DFT methods on intra-molecular CT excitations, testing the performance of modern exchange–correlation functionals against accurate wavefunction-based methods.5–9 On the other hand, fewer reference data are available for inter-molecular CT excitations, and it is crucial to test how DFT-based methods reproduce their electronic surface. Hence, in this work, we benchmark DFT-based methods to identify the most accurate methods suitable for calculations on systems with more than a hundred atoms. Specifically, we apply time-dependent DFT (TD-DFT) within the Tamm–Dancoff approximation (TDA), and orbital-optimized DFT methods (OO-DFT), and benchmark them against highly accurate wavefunction theory on small dimer systems to investigate their accuracy for ICT excitations.
In the following, we first review a selection of descriptors for CT states and several DFT-based excited-state methods. We then discuss the strengths and weaknesses of these methods in describing ICT for molecular dimers at different distances.
2 Charge-transfer descriptors
In organic photochemistry, excitations are frequently divided into 4 classes: valence excitations, core excitations, Rydberg excitations, and charge-transfer excitations. The identification of the CT character of a given excited state is a crucial prerequisite for any study of CT properties. Many approaches were proposed for this problem, resulting in a diverse set of CT descriptors. Here, we will divide them into two major classes: density-based and wavefunction-based descriptors. Appropriate descriptors are expected to yield a consistent classification, while quantitative results may differ. Obviously, only descriptors with the same unit and range can be directly compared quantitatively.2.1 Fragment localized-orbital-based descriptors
Plasser et al.10,11 defined two sets of CT descriptors, both derived from the analysis of the CIS-like wavefunction produced by a TD-DFT calculation under the TDA and the resulting 1-particle transition-density matrix (1TDM). The first set10 originates from the construction of an approximate 1TDM in a two-fragment model for each excited state.In a basis of localized molecular orbitals, all orbitals can be assigned to a predefined fragment A or B. For the sake of simplicity, we consider a molecular dimer system consisting of two separate molecular units which constitute the two fragments. Excited states dominated by a singly-excited configuration can be produced from the ground state by applying a spin-averaged excitation operator12Êsr on the ground state |0〉
 , s = f and only the ionic contributions |A−〉 and |B+〉 arising from a CT transition are shown. The Êsr operators are spin-averaged excitation operators and the normalization
, s = f and only the ionic contributions |A−〉 and |B+〉 arising from a CT transition are shown. The Êsr operators are spin-averaged excitation operators and the normalization 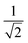 comes from the spin averaging (see ref. 12).
comes from the spin averaging (see ref. 12).
The 1TDM D0α for each excited state |α〉 can be written in the localized basis of MOs centered on fragment A {i, f} and B {i′, f′}, where transitions occur from row to column. Each element of D0α is the amplitude of a spin-averaged de-excitation operator Êrs
| D0αrs = 〈0|Êrs|α〉 |
Once the 1TDM for an excited state α has been constructed under a given partitioning scheme, a 2-by-2 charge-transfer number matrix Ωα can be constructed by summing over its squared elements. An element of Ωα is hence defined as
The off-diagonal elements of this matrix then quantify the weight of CT excitations in the excited state.13 The elements of Ω are then used to compute CT descriptors characterizing the locality of the excitation from the ground state to the target excited state. Based on this, the charge transfer descriptor CT is defined by simply summing over the off-diagonal elements of Ω
Two limitations apply to this approach. One is related to the fact that the 1TDM analysis works with a CIS-like wavefunction; this is the form characterizing the results of linear-response (LR) TD-DFT, but higher-order response TD-DFT includes contributions from higher-order excitations to some extent. Another limitation arises for the application of the 1TDM analysis to methods that approximate excited states with a single configuration and subsequently relax the density of such a configuration. This is the case for the OO-DFT methods we apply in this study. In these methods, since the MOs for the ground and excited states are different, it is not trivial to apply the 1TDM analysis. Moreover, neither the partitioning of a molecular system into two fragments nor the orbital localization is unique. This is particularly problematic when the excited-state analysis is applied to single chromophores, while it is admittedly rather trivial when the CT-numbers matrix is computed for a molecular dimer.
2.2 Electron–hole distance descriptor
The second set of parameters from Plasser et al.11 is focused on the interpretation of the 1TDM as a 2-particle excitonic wavefunction. In many-body Green's function theory, the 1TDM is a 2-body wavefunction χ, describing the correlated motion of hole and electron quasi-particles in the excited state α | (1) |
 | (2) |
Since χexc is a two-particle wavefunction, its square χexc2 computed for given re and rh returns the probability of having the electron in position re, while the hole is in position rh. χμ(rh)2 and χν(re)2 can be studied separately like the density-accumulation and depletion functions by Le Bahers et al.14 covered in the next paragraph, providing similar information as for their density-based parameters.
The advantage of χexc depending explicitly on the electron and hole positions is that parameters characterizing the electron–hole correlation can be computed. One example is the calculation of the dexc parameter,15 also termed RMSdeh in ref. 16:
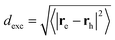 | (3) |
2.3 Density-based descriptors
Le Bahers, Adamo, and Ciofini14 provide an alternative characterization of the changes happening in the electron density upon excitation. The ground-state electron density ρGS(r) is subtracted from the excited-state electron density ρEX(r) producing the density-difference function Δρ(r), and its positive and negative co-domains ρ+(r) and ρ−(r) are characterized separately.| Δρ(r) = ρEX(r) − ρGS(r) | (4) |
In areas where the density-difference function is positive, charge accumulates upon excitation, whereas in areas where the density-difference function is negative, charge is depleted upon excitation. Each density-accumulation and depletion distribution can be characterized by studying its center of charge
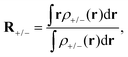 | (5) |
 | (6) |
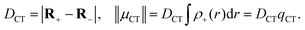 | (7) |
Ellipsoid functions can be defined at the centers of charge accumulation and depletion (R+ and R−) with axis length equal to the variance of the electron density-accumulation/depletion distributions along each direction,
 | (8) |
This dimensionless descriptor S+− is 1 for local excitations and drops to 0 by displacing the C+ and C− far from one another in an ICT state.
The obvious advantage of applying density-based CT quantifiers is that they can be computed using normalized electron density cube files, easily produced by a variety of electronic-structure codes. We would like to point out, however, that parameters based on the center of charge like DCT are prone to fail for charge-resonance excitations.
2.4 Earth-mover distance
A novel density-based CT descriptor,16 inspired by the solution of the earth-mover distance (EMD) optimal transport problem, has been introduced by Wang, Liang, and Head-Gordon. Interestingly, a similar CT descriptor was proposed around the same time in two other publications, respectively by Lieberherr, Gori-Giorgi and Giesbertz,19 and Fraiponts, Maes and Champagne.20The approach is based on the notion that changes in the electron density happening shortly after the excitation are similar to transport problems of discrete distributions. The EMD problem, extensively discussed in the field of computer vision, can be explained with the following analogy: assume a hole is dug in the ground, and the moved soil lies close by. The problem of transferring the soil back into the hole while minimizing the performed work is an optimal transport problem. The transportation simplex algorithm21 can be applied to solve it. By mapping the displacement of electron density happening after the excitation to an optimal transport problem, the charge-depletion and charge-accumulation distributions (eqn (4)) appear as analogous to the hole (ρ−(r)) and soil (ρ+(r)) piles, denoted as the demand (D) and supply (S) piles. Operating with discrete density distributions computed on a three-dimensional grid, the density-difference distributions are characterized by point charges q for a set of Cartesian coordinates r of the grid points.
| ρ−(r) = {(rj,qDj)} = D and ρ+(r) = {(ri,qSj)} = S | (9) |
 | (10) |
In the optimal transport problem, the transmission matrix F is defined and its elements fij are optimized such that
 | (11) |
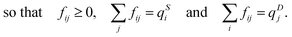 | (12) |
Finally, the charge-transfer descriptors μEMD and dEMD are defined based on that matrix
 | (13) |
Due to the scaling of the transportation simplex algorithm, one should employ a relatively coarse grid for the density analysis. Because of that, μEMD and dEMD are computed on an Euler–MacLaurin grid. On the other hand, the density produced by a quantum-chemical calculation is interpolated on a quadrature grid, and the use of a thin mesh for the real-space grid is necessary to get accurate results. The calculation of EMD-based CT descriptors is available in the ChargeEMD open-source package for μEMD and dEMD on GitHub.16
More charge-transfer descriptors of various nature were proposed in the literature,22–29 but are not included in this work since some can be proven to be equivalent to the parameters introduced above.
In our study of ICT excitations, we will combine the descriptors that were introduced in the previous paragraph aiming to unravel the following information:
• Find out if the computed excited state is a CT excitation, as this is not trivial for some methods like TD-DFT. Frequently, when setting up a TD-DFT calculation the user does not know if a CT state is included in the requested lowest n roots. If one or more CT states are present, it is not trivial to identify which roots show a strong CT character by simply looking at the dominant singly-excited configurations through visual inspection of the contributing orbitals.
• Classify the computed CT state as an inter-molecular CT state or an intra-molecular CT excitation centered on a single monomer. Excited states characterized by a moderate CT character centered on one single molecule (intra-molecular CT excitations) are standard in organic photochemistry. Their calculation is a very different problem compared to ICT, as the donor and acceptor MOs often overlap. This study focuses on ICT, and the best-performing methods for ICT are not necessarily the best-performing for intra-molecular CT. In the case of ICT, since the donor and acceptor molecular orbitals in the dominant configuration of a CT state are dislocated far in space, their overlap is expected to vanish; this overlap appears in the expression for the Kab term in Hartree–Fock theory and is responsible for the singlet–triplet energy gap in electronic excitations. In the case of methods based on the ΔSCF approach, a spin-broken determinant is computed, whose energy is the arithmetic average between the singlet and the triplet states.
• Analyze the dependence of the CT descriptors on the distance separating the donor and acceptor moieties in space. In the limit of CT happening over a large distance, the magnitude of CT descriptors with distance units is expected to scale proportional to the distance between the centers of electronic charge of the monomers, while the adimensional descriptors should stay constant. This is a crucial point when assessing the performance of OO-DFT methods, as we analyze and explain later in the manuscript.
3 Excited-state electronic-structure methods for the prediction of intermolecular charge-transfer
Before briefly reviewing electronic-structure methods for the description of ICT, it is necessary to point out a set of requirements necessary to describe CT properly in a supramolecular system. We take Clever's cages30 as a prototypical supramolecular system for which we aim to compute CT properties. In these supramolecules, the chromophore units are integrated in banana-shaped ligands forming the walls of the cage. By means of spectro-electrochemical methods31 and time-resolved ultrafast IR spectroscopy,32 it has been deduced that charge-transfer states are formed upon excitation, where one electron is transferred from the donor moiety (effectively oxidizing it) to an acceptor moiety, which is reduced. Photo-induced CT involving a chromophore integrated into the structure of a supramolecular cage as a donor and a molecular guest as an acceptor has been investigated previously33 and has been shown to switch the charge-transfer properties of the material upon host–guest binding. On the one hand, the application of highly accurate, wavefunction-based electronic-structure methods to such a system is a rather prohibitive task; on the other hand, TD-DFT is capable of achieving accuracy in the range of tenths of eV for the prediction of excitation energies,34 and OO-DFT methods35,36 display similar accuracy,37 also for cases known to be problematic for general-purpose TD-DFT like core-excited states or doubly-excited configurations. We assessed the suitability of OO-DFT methods for large systems by performing a single-point calculation on the HOMO–LUMO excitation of a coordination cage based on banana-shaped ligands by Clever et al. This system was previously investigated employing spectro-electro chemical methods to detect CT excitations where one electron is transferred between the chromophore moieties integrated into the walls of the cage.31 The system size is considerably large for an all-electrons calculation, counting 190 atoms, amongst which 128 are heavy atoms and 62 are hydrogens. The system is +4 charged, and there are 444 alpha and 444 beta electrons, totaling 1666 shells and 4370 basis functions using the def2-TZVP basis set. The unrestricted IMOM calculation on the HOMO–LUMO excitations converged in 10 iterations to tight convergence (10−8 Hartree) using the DIIS SCF algorithm implemented in Q-Chem. The calculation took 33.5 total CPU hours and 3.5 CPU hours per iteration. Our calculations were performed on an HPC cluster node with Intel Xeon Platinum 8380 Processor and 500 GB of memory. Since range-separated hybrid XCFs can be efficiently parallelized over multiple CPU cores (we used 16 physical cores), a single XCF iteration took around 12.5 min per iteration. The scaling of the presented OO-DFT methods for the single iteration is similar than the ground-state DIIS method since IMOM and MOM are just changing the occupation criteria in the Fock matrix construction step of the algorithm. The single SGM iteration scales with a prefactor of 3, which yields reasonable timings. Unfavorable, slow convergence of SCF towards the saddle points in the MO rotation space affects OO-DFT methods in some instances and leaves room for improvement in future work.A requirement for the predicted ICT excitation energy ECT is to follow approximately the trend defined by Mulliken's formula38 for the distance dependence of the CT energy:
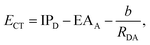 | (14) |
Multiple studies40–42 aimed to identify the adequate exchange–correlation functional form and parametrization for the accurate prediction of CT energies. In this work, we focus on range-separated hybrid exchange–correlation functionals (XCFs). We benchmark TD-DFT43 within the TDA44 and compare the results to the maximum overlap method45 (MOM), initial MOM46 (IMOM), and squared-gradient minimization35 (SGM) DFT47 methods, which all belong to the class of OO-DFT excited-state electronic-structure methods (also known as ΔSCF methods). In addition to standard TDA calculations, we applied the non-empirical optimal tuning procedure proposed by Baers et al.40 and implemented in Q-Chem48 for various XCFs to test their performance on ICT excitations. We also applied the Z-vector method49 to the TDA excited-state electron densities to obtain relaxed excited-state electron densities,50 using the libwfa51 interface integrated in Q-Chem 6.
While TD methods analyze an approximation of the response function of the system to an external field to retrieve the excitation energies, the OO-DFT approach variationally optimizes the excited-state density, much like SCF algorithms do for the ground state. The key difference to ground-state electronic-structure theory is that the ground-state energy is a minimum of the electronic energy hypersurface in the occupied-virtual MO rotations, while excited determinants are saddle points. Convergence of saddle points on hyperdimensional surfaces instead of minima is a far more complicated task, so the SCF algorithms need to be adjusted to converge excited states. Two major approaches were proposed over the last 20 years, based on the (geometric) direct minimization ((G)DM52,53) and direct inversion of the iterative subspace (DIIS54,55) SCF algorithms. SGM exploits the GDM algorithm, changing the minimized objective function to converge the SCF on the closest saddle point, while IMOM and MOM are coupled to the DIIS algorithm instead, changing the Fock matrix construction step to always compute the same excited configuration in each iteration. The default DIIS subspace size is 15 in Q-Chem, which was not altered for the OO-DFT calculations reported in this study. In the Fock matrix construction step of a ground-state SCF algorithm, the new MOs are occupied according to the Aufbau principle which is not desirable for OO-DFT SCF algorithms, as it would mean re-coupling the excited electrons to the ground-state configuration. The MOM and IMOM methods therefore change the Fock matrix construction step to occupy the MOs that have the maximum overlap with a reference MO set, which can be either fixed (IMOM) or updated during the calculation (MOM). An alternative excited-state SCF algorithm is SGM, which works by minimizing the square of the gradient of the electronic energy in the MO rotations through a Newton-like optimizer. Since OO-DFT methods use local optimization methods, their convergence is highly sensitive to the initial guess. In our experience with the application of OO-DFT methods to the calculation of ICT excitations, using the restricted closed-shell ground state MOs is not always the optimal choice. An alternative guess for calculating low-lying CT excitations is to use the ground-state MOs from an unrestricted calculation for a mono-cationic system and add one electron to the target virtual orbital. All OO-DFT methods investigated compute a spin-broken determinant, which is neither a singlet state nor a triplet state but whose energy lies halfway between the singlet and triplet energy. Usually, it is not recommended to use such an ansatz to calculate singlet excited state energies, as it is not a spin eigenfunction and typically yields a wrong energy. However, for CT excitations, the singlet–triplet energy gap is small and in the extreme case of pure ICT excitations, the singlet–triplet energy gap is negligible. Hence, it is not necessary to use a spin-purification formula to retrieve the singlet energy (see the ESI† for an extensive discussion).
Highly accurate reference excitation energies were computed using the EOM-CCSD(fT) method.56 They serve as reference data in this benchmark study alongside data points extracted from the literature computed with other coupled-cluster methods or second-order perturbation theory corrections, and experimental measurements (please see the ESI† for a detailed discussion of the reference data used).
4 Computational methods
Our benchmark study is organized into three sections. In Section 5, we study ICT in a prototypical organic dimer system, the ammonia–fluorine dimer, at various donor–acceptor separations. The reference results in this section were computed with the EOM-CCSD(fT) method56 and the cc-pVTZ basis set,57 while all DFT methods (TDA,44 MOM,45 IMOM,46 and SGM35) employ the LRC-ωPBE58 XCF and def2-TZVP59 basis. The charge-transfer descriptors were computed with Multiwfn,18 TheoDORE,17 and the ChargeEMD package.16 In Section 6, we benchmark the distance-dependence of ICT excitations in 4 molecular dimers of various sizes in the RDA-dataset. All data points in the RDA-dataset were computed with the EOM-CCSD(fT) method and the cc-pVTZ basis set, apart from the data points belonging to the ammonia–nitrous acid molecular dimer, which were taken from the literature.60 Again, all DFT methods (TDA and IMOM) in this section employ the LRC-ωPBE XCF and def2-TZVP basis. Finally, in Section 7, we benchmark TDA and IMOM against a set of chemically diverse reference data from the literature (both from wavefunction-based calculations and experiments). All IMOM calculations were performed using the LRC-ωPBE XCF and def2-TZVP basis, while the TDA method was tested with the CAM-B3LYP,61 LC-VV10,62 LC-rVV10,63 LRC-ωPBE, LRC-ωPBEh,64 LRC-BOP,65 and ωB97M-V66 XCFs and their optimally-tuned reparametrizations. All TDA results were computed both with the def2-SVP59 and def2-TZVP bases. The non-empirical optimal-tuning procedure of the RSH XCF from Baer et al.40 was applied throughout the manuscript, and all electronic-structure calculations were performed with Q-Chem 6.485 Calculation of the CT energy and CT descriptors for a small model system: ammonia–fluorine dimer
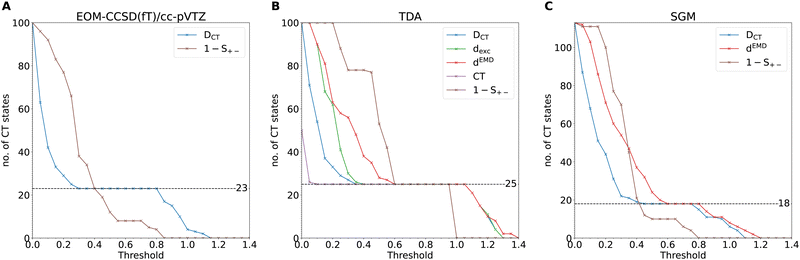
According to Mulliken's formula (eqn (14)), the ICT excitation energy is expected to change by displacing the donor (D) and acceptor (A) units in space. We require CT descriptors for all distances to distinguish ICT from intra-molecular CT and local excitations. In this section, we will test the abovementioned requirements for several electronic-structure models and compare to highly accurate benchmark data from wavefunction theory computed for a small model system, the ammonia–fluorine dimer, over a range of donor–acceptor separations (3.5, 4.25, 5, 8 and 10 Å). The excited-state electronic-structure reference data is computed with the EOM-CCSD method56 and the cc-pVTZ basis set,57 yielding rather accurate electron densities and excitation energies. The excitation energies are then adjusted, computing the perturbative contribution from triple-excited configurations, using the EOM-CCSD(fT) method67 implemented in Q-Chem.48 We will first analyze the trends observed for the reference data and the performance of density-based CT descriptors on the accurate EOM-CCSD densities. Then, the performance of DFT-based excited-state methods using the LRC-ωPBE58 XCF and the def2-TZVP59 basis set is discussed. The 20 lowest-lying excitations are computed with each method, leading to a total of 100 single-point excited states for the EOM-CCSD(fT) and TDA methods for the five donor–acceptor distances. The SGM, IMOM, and MOM calculations are set up using the closed-shell ground-state MOs as the initial guess, and all configurations with a weight greater than 0.3 in the CIS-like wavefunction from the TDA calculation are recomputed with the various OO-DFT calculations. All OO-DFT calculations employ unrestricted open-shell orbitals. Due to the selected threshold on the amplitudes, each CIS wavefunction can be dominated by up to three excited configurations, each potentially a CT excitation. This is the reason why in panel C of Fig. 1 the total number of states exceeds 100, as more than 1 OO-DFT calculation was performed per each TDA state, on average. Additionally, it is essential to underline that the number of CT states identified by the descriptors can vary when comparing TDA to the other OO-DFT methods. OO-DFT calculations are frequently prone to variational collapse which means that the number of CT states in the OO-DFT calculations varies for different methods or initial guesses. Hence, the number of assigned CT states can change substantially for the SGM, IMOM, and MOM results because some configurations with strong CT character in the TDA results converge to local excitations or vice versa. We analyze the ability of CT descriptors to identify convergence failure for CT excitations in OO-DFT methods. Since TD-DFT produces a CIS-like wavefunction, both wavefunction-based and density-based CT descriptors can be calculated.In Fig. 1, we plot the number of identified CT excitations against the selected assignment threshold spanning a range from 0 to 1.4 for each method. For descriptors with distance units, the assignment threshold is defined as the ratio between the CT descriptor and the donor–acceptor distance RDA, while no such rescaling is necessary for dimensionless CT descriptors. Since S+− is expected to vanish with increasing RDA, CT states are detected when 1 − S+− is greater than the assignment threshold; all other parameters assign a CT state when they are greater than the threshold.
 | (15) |
All wavefunction-based parameters are computed with TheoDORE, and the molecular structure is automatically divided into two fragments with the OpenBabel68 package. For all DFT methods, density-based parameters are computed. DCT and S+− are computed with Multiwfn18 by processing density cube-files generated with the electronic-structure program. To compute the EMD-based parameters, a development branch of Q-Chem was used to write the density data to an SG-1 quadrature grid.69 The resulting density was fitted to a “(19, 26)” grid with the ChargeEMD16 package, where 19 is the number of grid points in the radial part, and 26 is the number of grid points in the angular part for each atom. The ChargeEMD package then uses this coarser grid to solve the EMD problem.
As reported in panel A of Fig. 1, the number of ICT states identified by the DCT diagnostic for the EOM-CCSD(fT) calculations is constant over a large range of specified assignment thresholds, leading to a plateau with 23 CT states. This is not the case for the S+− descriptor, where no such plateau is observed signaling an undesired strong dependence of the CT assignment on the threshold. All descriptors consistently detect 25 CT excitations for the TDA calculations (panel B). The descriptor giving the most consistent results over the largest assignment threshold range is CT, which is either close to 1 or 0, depending on whether or not the corresponding state is a CT excitation. DCT and dEMD consistently match 21, 22, and 18 CT excitations for MOM, IMOM, (see ESI† for both plots), and SGM (panel C), respectively. For all OO-DFT methods, S+− shows the same undesired behavior as for the EOM-CCSD densities, limiting its applicability. Since the density-based DCT descriptor shows good agreement with other CT descriptors and minor sensitivity to the assignment threshold, it will be used exclusively in the remainder of our study.
In Fig. 2, we compare only the lowest-energy CT excited state to the reference data. As predicted by Mulliken's formula (eqn (14)), the EOM-CCSD(fT) CT excitation energy (panel A) increases monotonously upon displacing the donor and acceptor units. While the standard TDA results (blue line) capture the asymptotic trend of the CT excitation energy, it is strongly red-shifted. In this example, the error is greater than 3 eV, making the predicted energy of little use for the rational design of supramolecular assemblies. However, TDA benefits from the optimal tuning procedure of the XCF proposed by Baer et al.40 (denoted with TDA-OT in Fig. 2, red line), as the error on the excitation energies reduces by about 50% to 1.5 eV while retaining the correct asymptotic trend. Amongst the OO-DFT methods (SGM, MOM, and IMOM), SGM shows consistent asymptotic behavior, and the predicted CT excitation energy is red-shifted by only about 0.5 eV, except for the data point calculated at 5 Å separation. To converge the calculations, we started from cationic MOs for one data point in the IMOM curve and two data points for the MOM and SGM curve. All the OO-DFT calculations performed in Sections 6 and 7 were computed by using the neural ground-state MOs as initial guess. As a check, we recomputed the data points with  using the MOs belonging to a cationic system (charge 1 and multiplicity 2, using unrestricted orbitals), but this did not improve our results.
using the MOs belonging to a cationic system (charge 1 and multiplicity 2, using unrestricted orbitals), but this did not improve our results.
 | ||
Fig. 2 Panel A: CT excitation energy belonging to the lowest-lying CT state of the ammonia–fluorine dimer vs. donor–acceptor separation distance (Å) computed with the EOM-CCSD(fT) (ref.), TDA, optimally-tuned TDA (TDA-OT), IMOM, MOM, and SGM methods, respectively. Data points characterised by  are connected with a solid lines. The reference data is fitted to Mulliken's equation for the CT excitation energy (eqn (14)), using the 2-parameter expression are connected with a solid lines. The reference data is fitted to Mulliken's equation for the CT excitation energy (eqn (14)), using the 2-parameter expression  , where a = IPD − EAA and b is a system-specific parameter with unit of energy times distance. Panel B: DCT parameter (Å) computed on the lowest-lying CT state vs. donor–acceptor separation distance (Å) computed with the EOM-CCSD(fT) (ref.), TDA, optimally-tuned TDA (TDA-OT), relaxed TDA (TDA-rlx), IMOM, MOM, and SGM densities. Panel C: S+− diagnostic computed for the lowest-lying CT state vs. donor–acceptor separation distance (Å). Inset: Isosurface plot of the normalized C+ and C− ellipsoids produced by Multiwfn, using TDA and EOM-CCSD densities at 10 Å separation. The isovalue is ±0.0001 for C+ and C−. , where a = IPD − EAA and b is a system-specific parameter with unit of energy times distance. Panel B: DCT parameter (Å) computed on the lowest-lying CT state vs. donor–acceptor separation distance (Å) computed with the EOM-CCSD(fT) (ref.), TDA, optimally-tuned TDA (TDA-OT), relaxed TDA (TDA-rlx), IMOM, MOM, and SGM densities. Panel C: S+− diagnostic computed for the lowest-lying CT state vs. donor–acceptor separation distance (Å). Inset: Isosurface plot of the normalized C+ and C− ellipsoids produced by Multiwfn, using TDA and EOM-CCSD densities at 10 Å separation. The isovalue is ±0.0001 for C+ and C−. | ||
The maximum-overlap methods (IMOM and MOM) show errors similar to those of SGM. For the OO-DFT methods there are obvious convergence problems at short donor–acceptor distances, e.g. the data point produced with MOM at 3.5 Å is the result of convergence to a state with smaller CT character (see panel B), and IMOM computes the same excitation energy. The SGM algorithm is not immune to similar errors (see abovementioned data point at 5 Å separation) due to convergence to other roots or to regions of the MO rotations hypersurface that are not saddle points of the electronic energy, so they do not belong to the electronic structure of excited configurations.70 The data points computed using OO-DFT methods and the default ω parameter for large separation distances are indistinguishable from one to another, blue-shifted by only about 0.5 eV compared to the reference. While the TDA method benefits greatly from tuning the range-separation parameter of the XCF, IMOM gives a larger error of around 1 eV when using the optimal ω parameter (pink line in Fig. 2). Due to the more stable convergence behavior over SGM, we will use IMOM for all OO-DFT calculations in the following part of the study.
The DCT diagnostic (panel B) increases linearly with the donor–acceptor separation RDA for the reference results. The OO-DFT calculations that converged reliably onto true ICT states (circle markers connected by the solid lines), as well as the relaxed densities calculated with the Z-vector method (green line, cross markers), are characterized by a DCT diagnostic very close to the reference. In stark contrast, the unrelaxed TDA densities (red and blue plots, cross marker) return a more pronounced CT character than the reference EOM-CCSD density. As expected, S+− (panel C) gives 0 overlap for the density depletion and accumulation volumes in the CT state for the unrelaxed TDA densities, while its value stays rather large for all methods providing an accurate density. In general, density-based CT descriptors are enhanced when applying the TDA: the molecular orbitals are unchanged in the excited state, so the charge separation does not polarize the approximate excited-state density. On the opposite, for the reference calculations as well as for orbital-optimized methods, the electrons belonging to the acceptor unit are attracted toward the cationic donor unit, and the resulting density is accumulated at shorter distances. Accordingly, the C+ and C− ellipsoids are elongated along the direction of the Coulomb attraction, to the point where they exceed the volume of the cube file used for the electron density calculation. This is observed in the inset in panel C, where the localized ellipsoids from the TD-DFT density are displayed alongside the elongated, cut-off ellipsoids computed using the accurate density.
In conclusion, the density-based CT descriptors calculated with the OO-DFT densities agree substantially better with the reference than the TDA results for the lowest-lying ICT excitation in the ammonia–fluorine dimer. Relating density-based CT descriptors like DCT and dEMD to RDA helps to identify convergence failure of the OO-DFT calculations.
6 Benchmarking the distance dependence of ICT excitations
We benchmarked the performance of DFT-based excited-state methods to accurately describe ICT on a small variety of small molecular dimers. To generate accurate reference data, we computed the 20 lowest-lying singlet excited states of the beryllium–fluorine dimer and the tetrafluoroethylene-ethylene dimer with EOM-CCSD(fT) and the cc-pVTZ basis at 3.5, 4.25, 5, 8 and 10 Å distance between the molecular center of mass. The same number of lowest-lying excitations was computed with the TDA method and IMOM using the LRC-ωPBE XCF and the def2-TZVP basis. To test a wider range of donor–acceptor separation distances, a set of data points with the lowest-lying ICT excitations of the ammonia–nitrous acid dimer computed with the SA2-MS-CAS(2,2)PT2 method and the jul-cc-pVTZ basis at nine separation distances (3.7, 6.1, 8.6, 11, 13.5, 15.9, 18.4, 23.3 and 25.8 Å) was taken from the literature.60 This system was included in our reference dataset, which we will refer to as the RDA-dataset from here on. All states with a DCT greater than half of the donor–acceptor distance RDA were classified as ICT states.Table 1 summarizes the performance of DFT-based excited-state methods for the prediction of ICT excitation energies over the RDA-dataset. For the tetrafluoroethylene-ethylene dimer, many excited states show intermediate DCT values, close to half RDA, especially at short donor–acceptor separation (3.5, 4.25, 5 Å). For all of these states, the examination of the CIS-like wavefunction produced by TDA showed no single dominant excited configuration; instead, several singly-excited determinants exhibited similar amplitudes. The data points belonging to the three lowest-lying ICT states were selected using information from adjacent separation distances. Amongst the states with significant DCT character, the data points reproducing the monotonous trend predicted by Mulliken's formula (eqn (14)) were classified as ICT, such that the energy of each CT root was increasing by displacing donor and acceptor far in space.
| Dimer | TDA | TDA-OT | IMOM | Nr. | |||
|---|---|---|---|---|---|---|---|
| MSE | MSV | MSE | MSV | MSE | MSV | ICTs | |
| Be–F2 | −2.71 | 1.21 | −1.71 | 0.57 | −1.23 | 0.01 | 1(5) |
| NH3–F2 | −3.36 | 0.4 | −1.45 | 0.32 | −0.53 | 0.08 | 4(17) |
| NH3–HNO3 | −1.64 | 0.01 | −0.22 | 0.00 | 0.07 | 0.00 | 1(9) |
| C2F4–C2H4 | −0.74 | 0.08 | −0.74 | 0.08 | −0.16 | 0.12 | 3(15) |
| All | −2.09 | 1.52 | −1.03 | 0.47 | −0.55 | 0.49 | 9(46) |
| D CT > 0.5RDA | −2.13 | 1.55 | −0.93 | 0.42 | −0.27 | 0.14 | 8(37) |
TDA (column 2) tends to underestimate the energy of ICT states by several eV. The generally poor performance on the whole dataset (5th row) is manifested in a large variance, meaning the error is not a simple offset in energy, but is due to systematic scattering in the range of several eV in the worst cases, like the beryllium–fluorine (first line of Table 1). In the case of organic systems like the tetrafluoroethylene-ethylene dimer (second line), the MSE drops below 1 eV. This is reasonable since the LRC-ωPBE XCF was parametrized with the Minnesota Database/3,71 which is mainly composed of small organic molecules, and a set of ionization potentials, electron affinities, and excitation energies.58 In fact, LRC-ωPBE has been shown to successfully estimate the excitation energy of CT states in polycyclic aromatic hydrocarbons.22 Still, the variance increases dramatically when the data points from all molecular dimers are combined. This means the method's performance is system-dependent and cannot be corrected by a universal shift or offset. In supramolecules, multiple ICT excitations are possible, and electronic structure methods must be capable of computing all ICT excitations with negligible or small transferable error. TDA is clearly not capable of that with the default LRC-ωPBE XCF, and we therefore investigated the performance of other methods.
Column 3 in Table 1 shows the performance of the TDA method with an optimally-tuned range-separation parameter ω in the LRC-ωPBE XCF. It has been shown that the range-separated BNL XCF72 proved to benefit from optimal tuning for the description of ICT excitations in small organic molecules73 and optimal tuning also significantly improves the performance of LRC-ωPBE with the TDA method in our study, lowering the MSE by up to 1.5 eV. The fact that the tetrafluoroethylene-ethylene dimer is largely unaffected can be explained by considering that the default ω parameter was selected by benchmarking against data including redox properties of organic systems. Yet, the error and the variance of the combined dataset remain significant, and hence the results from TDA cannot be directly compared to experimental data for ICT.
In the last column of Table 1, we show the results obtained with IMOM for the same RDA-dataset. The default value of the ω parameter was used in these calculations since, as we have observed for the ammonia–fluorine dimer in the previous section, optimal tuning does not yield an improvement for ICT states with IMOM. Some calculations on the tetrafluoroethylene-ethylene dimer converged on electron densities with small DCT and electronic energies far from the reference, hinting at a numerical issue for this high-dimensional problem,74 and we excluded them from this benchmark study. Without these data points, IMOM produces the best results for the calculation of ICT excitation energies for all molecular dimer systems, with MSE in the order of tenths of eV, with the exception of the beryllium–fluorine system. This system proved to be the most challenging to compute using an RSH XCF and is not representative of the ICT states that are likely to be formed in supramolecular assemblies. For this reason, the error statistics excluding this system are shown in the last line of Table 1, which, in our opinion, gives the most representative picture for the error of all DFT-based methods discussed here.
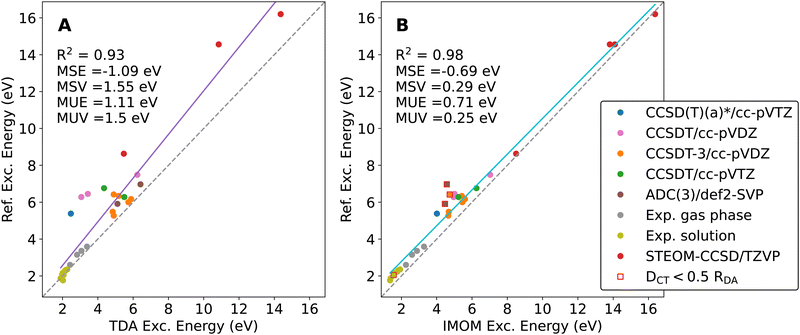
In Fig. 3, we show the explicit data points and linear correlations for all methods. Clearly, IMOM (panel C) produces the smallest errors with little variance. It is also evident that optimally-tuned LRC-ωPBE improves considerably over the results obtained with the default ω parameter.
7 Benchmarking TDA and OO-DFT methods in a larger set of small molecular dimers
While the RDA-dataset includes CT excitation energies for several donor–acceptor separation distances, the dimers included in this dataset are chemically not very diverse. We therefore conducted an extensive literature search to test the selection of TDA and OO-DFT methods for a diverse set of molecular dimers with ICT states.60,73,75–87 We selected the most accurate electronic-structure results obtained with the largest basis sets in our reference data. More information on this benchmark set and the selected reference methods can be found in the ESI.† We followed the same computational protocol and ICT classification scheme as for the RDA-dataset. In Fig. 4, the correlation of the DFT results with the reference data is plotted with specified color coding for different reference methods and data sources.Again, IMOM outperforms TDA with the default ω parameter, achieving both a significantly lower error and reduced variance. On top of that, IMOM yields much better results for large excitation energies. Both methods perform well on the experimental data for low-lying ICT states as well.
The goal of this study is not a thorough theory to experiment benchmark, which would come with its own challenges especially for dimers in solution, where solvent rearrangement has a major effect on the CT states. We rather seek to identify a suitable electronic-structure method that describes these states reliably at low computational cost. In that sense, a comparison to accurate theoretical reference data is most meaningful. In Fig. 5, we hence compare the accuracy of TDA, OT-TDA and IMOM on a subset of our dataset, where we excluded experimental data and those data points where IMOM did not converge to a CT state (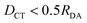 ).
).
As we have seen before, optimal tuning (panel B) considerably reduces the error compared to TDA, but IMOM shows the best overall performance. While the MSE on this subset of the dataset from the literature is still considerably high (an underestimation of the ICT excitation energy by 0.7 eV), the variance of the IMOM data is less than half that of the optimally-tuned TDA method. This points to a systematic and system-independent underestimation of the ICT energies. While the improvement obtained using the optimal-tuning procedure over the default ω parameter for the LRC-ωPBE XCF is noteworthy, the variance is still quite large and the error is hence more system-dependent.
Although we demonstrated the limitations of TDA regarding the calculation of ICT excitations, the method plays a crucial role in the computational protocol employed to set up IMOM calculations for low-lying ICT states. In addition, the performance of TDA critically depends on the choice of an adequate XCF and basis set. Obviously, a plethora of XCFs were developed over the years using various combinations of functional form and parameterization. Therefore, we analyzed several XCF and basis set combinations on the reduced data set used in Fig. 5, applying the optimal tuning procedure. The results are summarized in Tables 2 and 3.
| Method | XCF | Basis | MSE | MSV | MUE | MUV |
|---|---|---|---|---|---|---|
| TDA | LRC-ωPBE | def2-SVP | −1.66 | 1.50 | 1.66 | 1.50 |
| TDA | OT LRC-ωPBE | def2-SVP | −0.53 | 0.50 | 0.77 | 0.18 |
| TDA | LRC-ωPBE | def2-TZVP | −1.75 | 1.57 | 1.75 | 1.57 |
| TDA | OT LRC-ωPBE | def2-TZVP | −1.14 | 0.46 | 1.14 | 0.46 |
| TDA | LRC-ωPBEh | def2-SVP | −1.92 | 1.39 | 1.92 | 1.39 |
| TDA | OT LRC-ωPBEh | def2-SVP | −0.64 | 0.67 | 0.91 | 0.23 |
| TDA | LRC-ωPBEh | def2-TZVP | −2.04 | 1.37 | 2.04 | 1.37 |
| TDA | OT LRC-ωPBEh | def2-TZVP | −1.07 | 0.61 | 1.09 | 0.57 |
| IMOM | LRC-ωPBE | def2-TZVP | −0.72 | 0.20 | 0.74 | 0.17 |
| XCF | MSE | MSV | MUE | MUV | ||||
|---|---|---|---|---|---|---|---|---|
| def2-TZVP | def2-SVP | def2-TZVP | def2-SVP | def2-TZVP | def2-SVP | def2-TZVP | def2-SVP | |
| LRC-ωPBE58 | −1.75 | −1.64 | 1.57 | 1.42 | 1.66 | 1.64 | 1.50 | 1.42 |
| OT LRC-ωPBE | −1.14 | −0.45 | 0.46 | 0.62 | 1.14 | 0.78 | 0.46 | 0.18 |
| LRC-ωPBEh64 | −2.04 | −1.92 | 1.37 | 1.39 | 2.04 | 1.92 | 1.37 | 1.39 |
| OT LRC-ωPBEh | −1.07 | −0.64 | 0.61 | 0.67 | 1.09 | 0.91 | 0.57 | 0.23 |
| LRC-BOP65 | −0.34 | −0.16 | 0.75 | 0.66 | 0.72 | 0.68 | 0.33 | 0.20 |
| OT LRC-BOP | −0.90 | −0.41 | 0.34 | 0.56 | 0.92 | 0.72 | 0.30 | 0.19 |
| LC-VV1062 | −0.39 | 0.21 | 0.65 | 0.67 | 0.68 | 0.69 | 0.32 | 0.21 |
| OT LC-VV10 | −1.17 | −0.44 | 0.43 | 0.62 | 1.17 | 0.78 | 0.43 | 0.18 |
| LC-rVV1063 | −0.40 | −0.21 | 0.65 | 0.67 | 0.68 | 0.69 | 0.33 | 0.21 |
| OT LC-rVV10 | −1.17 | −0.44 | 0.43 | 0.62 | 1.17 | 0.78 | 0.43 | 0.18 |
| CAM-B3LYP61 | −2.07 | −1.98 | 1.43 | 1.31 | 2.07 | 1.98 | 1.43 | 1.31 |
| OT CAM-B3LYP | −1.11 | −0.87 | 0.73 | 0.70 | 1.11 | 0.89 | 0.73 | 0.67 |
| ωB97M-V66 | −1.22 | −1.07 | 0.72 | 0.71 | 1.22 | 1.07 | 0.72 | 0.71 |
| OT ωB97M-V | −0.77 | −0.31 | 0.24 | 0.40 | 0.77 | 0.58 | 0.24 | 0.15 |
Table 2 shows the dependence of the results on the basis set size for the TDA method, using both the default range-separation parameter and an optimally tuned value for the LRC-ωPBE and LRC-ωPBEh XCFs. Notably, the benefit from the optimal tuning procedure is more pronounced for the smaller def2-SVP basis set than for def2-TZVP, lowering the error by up to 1.2 eV. The MSE is similar to the one obtained with IMOM and a large basis set. However, the variance is rather large, indicating a more system-dependent performance. The inverted basis set dependence is, in principle, undesired since it compromises the systematic improvement of results, but has practical relevance, since it motivates the use of small basis sets for cost-efficient calculation of the CIS-like wavefunction that can be refined with orbital-optimized methods. In Table 3, we report error statistics for several common XCFs for the same reduced dataset employing TDA calculations and the small def2-TZVP and def2-SVP basis sets. The MSE depends strongly on the XCF; when the default ω is used, LRC-ωPBE, LRC-ωPBEh, CAM-B3LYP, and ωB97M-V perform poorly, but their performance does improve with optimal tuning. In stark contrast, LRC-BOP and the VV10 family of XCFs achieve errors within tenths of eV, and optimal tuning worsens the results. None of these XCFs were parametrized against CT energies, ionization potentials, or electron affinities. The VV10-based XCFs were previously shown62 to yield good performance on ground-state energies of molecular dimers, as they accurately compute van-der-Waals interactions but were not designed for the calculation of the redox properties. Isolated optimal tuning of the range-separation parameter is generally not advised for XCFs where all parameters were simultaneously optimized, like CAM-B3LYP and ωB97M-V. Yet, the predicted ICT excitation energies benefit from tuning. This is to be expected since the improved approximate IP and EA values produced by an XCF directly enter the Mulliken expression for the ICT energy (eqn (14)). The improvement is remarkable and we highlight the excellent performance of the optimally-tuned LRC-ωPBE functional both in terms of error and variance for the def2-TZVP basis set. For the smaller def2-SVP basis, fortuitous error compensation yields more accurate statistics for the ICT energy. While the use of a small basis usually results in an inaccurate description of the electron density and introduces basis set superposition errors88 which affects properties such as calculated molecular geometries, economic TDA calculations can provide an approximate wavefunction for subsequent refinements with the OO-DFT methods. The LRC-BOP XCF provides a reliable performance for this task, with no need for a system-specific reparametrization.
8 Conclusions
We analyzed a diverse set of charge-transfer descriptors for ICT excitations in small molecular dimers, and found that especially DCT is well-suited to reliably identify the CT character for these systems. We then compared several DFT-based excited-state methods with highly accurate reference data from wavefunction theory for ICT excitation energies. Among these, IMOM provides the most robust performance among the OO-DFT methods. A new dataset containing reference data with several donor–acceptor separations, termed RDA-dataset, was then established using the EOM-CCSD(fT) method and a cc-pVTZ basis. All DFT methods were then tested against the reference data in the RDA-dataset (see Table 1), using the LRC-ωPBE XCF and the def2-TZVP basis set. Standard TDA calculations showed the worst performance, with both MSE and MSV significantly larger than 1 eV. The non-empirical optimal-tuning procedure from Baer et al.40 was then applied, yielding a significant improvement over the results obtained with the default range-separation parameter. Yet, the performance of optimally-tuned TDA is not satisfactory for the general calculation of ICT states, as its variance is in the range of 0.5 eV. In stark contrast, IMOM showed satisfying performance, with sub-eV errors and a variance also on the order of tenths of eVs. We emphasize that this result was obtained by excluding data points where IMOM failed to converge on the ICT excitations, underlining the need for robust SCF algorithms for OO-DFT methods to be suitable for semi-automated calculations, e.g. in screening applications. In a recent publication,89 a similar method from the ΔSCF family of excited-state electronic-structure theory was applied to the ICT excitation of a Flavin molecule in a biomatrix, where one electron is transferred from a tyrosine moiety, with the mediation of an adjacent glutamine group. ΔSCF methods are characterized by a low computational cost, which makes them ideal for excited-states electronic-structure calculations of complex systems like this, and the ΔSCF/AMOEBA90 QM/MM method proved capable to describe the PES of the ICT state with satisfactory results. Yet, 10 out of 30 excited state dynamics simulations failed due to SCF convergence issues. More work is going in the direction of improving the stability and reliability of OO-DFT methods,91,92 with special care for cases where DFT is known to be a problematic choice, like intra-molecular CT excitations,74 Rydberg excitations,93 conical intersections and avoided crossings.94 With more robust SCF algorithms, it will be possible to systematically benchmark XCFs in OO-DFT against reference data, since we have shown in this study that they outperform even optimally-tuned TDA methods. Ongoing work in our lab is focused on improving the stability of the SCF convergence.We further benchmarked the TDA and IMOM methods with the LRC-ωPBE and the def2-TZVP basis for a large dataset of reference data from the literature, with similar conclusions. As discussed above, general-purpose RSH XCFs give errors on the order of 1 eV and variances of almost equal magnitude, while IMOM achieved superior results with sub-eV MSE and an MSV on the order of tenths of eV. Further testing on a subset of the data, in a pure theory-to-theory comparison, showed how optimal tuning of the ω parameter again improves the results obtained with the TDA method. However, IMOM still outperforms TDA. Finally, several RSH XCFs were benchmarked in TDA calculations with the smaller def2-SVP and def2-TZVP basis sets and an optimally-tuned range-separation parameter. Interestingly, a smaller basis set benefits from error compensation, improving the predicted ICT excitation energies to a sub-eV MSE for optimally-tuned XCFs. We conclude that IMOM is capable of providing the most accurate ICT energies among all methods tested. To obtain an economic guess wavefunction for the orbital-optimized method, we recommend TDA with the LRC-BOP range-separated hybrid XCF, which yields the most accurate results using the small def2-SVP basis set. All the reference data and results obtained with different DFT-based excited-state electronic structure methods are available on Zenodo under record 1272965612729656.
Data availability
Data for this article, including ICT excitation energies and density-based descriptors are available at Zenodo at https://doi.org/10.5281/zenodo.12802816.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Rasma Sandra Knipše for the contribution of several data points in Fig. 3. This work is funded by the Deutsche Forschungsgemeinschaft (DFG) through the Research Training Group “Confinement Controlled Chemistry” (GRK 2376).References
- D. J. Vinyard, G. M. Ananyev and G. Charles Dismukes, Annu. Rev. Biochem., 2013, 82, 577–606 CrossRef CAS PubMed.
- A. Sirohiwal and D. A. Pantazis, Acc. Chem. Res., 2023, 56, 2921–2932 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS.
- M. Casanova-Páez and L. Goerigk, J. Chem. Theory Comput., 2021, 17, 5165–5186 CrossRef PubMed.
- M. Casanova-Páez and L. Goerigk, J. Comput. Chem., 2021, 42, 528–533 CrossRef PubMed.
- É. Brémond, A. Ottochian, Á. J. Pérez-Jiménez, I. Ciofini, G. Scalmani, M. J. Frisch, J. C. Sancho-Garca and C. Adamo, J. Comput. Chem., 2021, 42, 970–981 CrossRef PubMed.
- D. Mester and M. Kállay, J. Chem. Theory Comput., 2021, 17, 4211–4224 CrossRef CAS PubMed.
- D. Mester and M. Kállay, J. Chem. Theory Comput., 2022, 18, 1646–1662 CrossRef CAS PubMed.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- F. Plasser, B. Thomitzni, S. A. Bäppler, J. Wenzel, D. R. Rehn, M. Wormit and A. Dreuw, J. Comput. Chem., 2015, 36, 1609–1620 CrossRef CAS PubMed.
- A. L. East and E. C. Lim, J. Chem. Phys., 2000, 113, 8981–8994 CrossRef CAS.
- A. Luzanov and O. Zhikol, Int. J. Quantum Chem., 2010, 110, 902–924 CrossRef CAS.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS PubMed.
- S. A. Mewes, J.-M. Mewes, A. Dreuw and F. Plasser, Phys. Chem. Chem. Phys., 2016, 18, 2548–2563 RSC.
- Z. Wang, J. Liang and M. Head-Gordon, J. Chem. Theory Comput., 2023, 19, 7704–7714 CrossRef CAS PubMed.
- F. Plasser, J. Chem. Phys., 2020, 152, 084108 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- A. Z. Lieberherr, P. Gori-Giorgi and K. J. Giesbertz, arXiv, 2023, preprint, arXiv:2308.09118, DOI:10.48550/arXiv.2308.09118.
- M. Fraiponts, W. Maes and B. Champagne, J. Chem. Theory Comput., 2024, 20(7), 2751–2760 CrossRef PubMed.
- Y. Rubner, C. Tomasi and L. J. Guibas, Sixth international conference on computer vision (IEEE Cat. No. 98CH36271), 1998, 59-66.
- R. M. Richard and J. M. Herbert, J. Chem. Theory Comput., 2011, 7, 1296–1306 CrossRef CAS PubMed.
- M. J. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- C. A. Guido, P. Cortona, B. Mennucci and C. Adamo, J. Chem. Theory Comput., 2013, 9, 3118–3126 CrossRef CAS PubMed.
- C. A. Guido, P. Cortona and C. Adamo, J. Chem. Phys., 2014, 140, 104101 CrossRef PubMed.
- T. Etienne, X. Assfeld and A. Monari, J. Chem. Theory Comput., 2014, 10, 3896–3905 CrossRef CAS PubMed.
- E. Ronca, M. Pastore, L. Belpassi, F. De Angelis, C. Angeli, R. Cimiraglia and F. Tarantelli, J. Chem. Phys., 2014, 140, 054110 CrossRef PubMed.
- H. Ma, T. Qin and A. Troisi, J. Chem. Theory Comput., 2014, 10, 1272–1282 CrossRef CAS PubMed.
- T. Etienne, J. Chem. Theory Comput., 2015, 11, 1692–1699 CrossRef CAS PubMed.
- M. Han, D. M. Engelhard and G. H. Clever, Chem. Soc. Rev., 2014, 43, 1848–1860 RSC.
- M. Frank, J. Ahrens, I. Bejenke, M. Krick, D. Schwarzer and G. H. Clever, J. Am. Chem. Soc., 2016, 138, 8279–8287 CrossRef CAS PubMed.
- J. Ahrens, M. Frank, G. H. Clever and D. Schwarzer, Phys. Chem. Chem. Phys., 2017, 19, 13596–13603 RSC.
- S. Ganta, J.-H. Borter, C. Drechsler, J. J. Holstein, D. Schwarzer and G. H. Clever, Org. Chem. Front., 2022, 9, 5485–5493 RSC.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS.
- D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2020, 16, 1699–1710 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2021, 12, 4517–4529 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2020, 11, 775–786 CrossRef CAS PubMed.
- R. S. Mulliken, J. Am. Chem. Soc., 1952, 74, 811–824 CrossRef CAS.
- S. Juber, S. Wingbermühle, P. Nuernberger, G. H. Clever and L. V. Schäfer, Phys. Chem. Chem. Phys., 2021, 23, 7321–7332 RSC.
- R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109 CrossRef CAS PubMed.
- G. Prokopiou, M. Hartstein, N. Govind and L. Kronik, J. Chem. Theory Comput., 2022, 18, 2331–2340 CrossRef CAS PubMed.
- S. Klawohn and H. Bahmann, J. Chem. Theory Comput., 2020, 16, 953–963 CrossRef CAS PubMed.
- E. Runge and E. K. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- A. T. Gilbert, N. A. Besley and P. M. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- G. M. Barca, A. T. Gilbert and P. M. Gill, J. Chem. Theory Comput., 2018, 14, 1501–1509 CrossRef CAS PubMed.
- L. J. Sham and W. Kohn, Phys. Rev., 1966, 145, 561 CrossRef CAS.
- E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al. , J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- E. Ronca, C. Angeli, L. Belpassi, F. De Angelis, F. Tarantelli and M. Pastore, J. Chem. Theory Comput., 2014, 10, 4014–4024 CrossRef CAS PubMed.
- P. Kimber and F. Plasser, Phys. Chem. Chem. Phys., 2020, 22, 6058–6080 RSC.
- T. Van Voorhis and M. Head-Gordon, Mol. Phys., 2002, 100, 1713–1721 CrossRef CAS.
- Y. L. Schmerwitz, G. Levi and H. Jónsson, J. Chem. Theory Comput., 2023, 19(12), 3634–3651 CrossRef CAS PubMed.
- P. Pulay, J. Comput. Chem., 1982, 3, 556–560 CrossRef CAS.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393–398 CrossRef CAS.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- T. H. Dunning Jr., J. Chem. Phys., 1971, 55, 716–723 CrossRef.
- M. A. Rohrdanz and J. M. Herbert, J. Chem. Phys., 2008, 129, 034107 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Ghosh, A. L. Sonnenberger, C. E. Hoyer, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 3643–3649 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- N. Mardirossian, L. Ruiz Pestana, J. C. Womack, C.-K. Skylaris, T. Head-Gordon and M. Head-Gordon, J. Phys. Chem. Lett., 2017, 8, 35–40 CrossRef CAS PubMed.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed.
- J.-W. Song, T. Hirosawa, T. Tsuneda and K. Hirao, J. Chem. Phys., 2007, 126, 154105 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- P. U. Manohar and A. I. Krylov, J. Chem. Phys., 2008, 129, 194105 CrossRef PubMed.
- N. M. O’Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 1–14 Search PubMed.
- P. M. Gill, B. G. Johnson and J. A. Pople, Chem. Phys. Lett., 1993, 209, 506–512 CrossRef CAS.
- H. G. Burton, J. Chem. Theory Comput., 2022, 18, 1512–1526 CrossRef CAS PubMed.
- B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 3898–3906 CrossRef CAS.
- E. Livshits and R. Baer, Phys. Chem. Chem. Phys., 2007, 9, 2932–2941 RSC.
- T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818–2820 CrossRef CAS PubMed.
- E. Selenius, A. E. Sigurarson, Y. L. Schmerwitz and G. Levi, arXiv, 2023, preprint, arXiv:2311.01604, DOI:10.48550/arXiv.2311.01604.
- C. Zuluaga, V. A. Spata and S. Matsika, J. Chem. Theory Comput., 2020, 17, 376–387 CrossRef PubMed.
- D. Bokhan, D. N. Trubnikov and R. J. Bartlett, J. Chem. Phys., 2015, 143, 074111 CrossRef PubMed.
- J. Masnovi, E. Seddon and J. Kochi, Can. J. Chem., 1984, 62, 2552–2559 CrossRef CAS.
- I. Hanazaki, J. Phys. Chem., 1972, 76, 1982–1989 CrossRef CAS.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- M. Musiał and R. J. Bartlett, J. Chem. Phys., 2011, 134, 034106 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130 CrossRef CAS PubMed.
- B. Kozma, A. Tajti, B. Demoulin, R. Izsák, M. Nooijen and P. G. Szalay, J. Chem. Theory Comput., 2020, 16, 4213–4225 CrossRef CAS PubMed.
- A. Solovyeva, M. Pavanello and J. Neugebauer, J. Chem. Phys., 2014, 140, 164103 CrossRef PubMed.
- A. K. Dutta, M. Nooijen, F. Neese and R. Izsák, J. Chem. Theory Comput., 2018, 14, 72–91 CrossRef CAS PubMed.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS PubMed.
- F. Plasser, S. A. Bäppler, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024107 CrossRef PubMed.
- D. Manna, J. Blumberger, J. M. Martin and L. Kronik, Mol. Phys., 2018, 116, 2497–2505 CrossRef CAS.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed.
- P. Mazzeo, S. Hashem, F. Lipparini, L. Cupellini and B. Mennucci, J. Phys. Chem. Lett., 2023, 14, 1222–1229 CrossRef CAS PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht and R. A. DiStasio Jr., et al. , J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- Y. L. A. Schmerwitz, N. U. Ollé, G. Levi and H. Jónsson, arXiv, 2024, preprint, arXiv:2402.16601, DOI:10.48550/arXiv.2402.16601.
- G. Levi, A. V. Ivanov and H. Jónsson, J. Chem. Theory Comput., 2020, 16, 6968–6982 CrossRef CAS PubMed.
- A. E. Sigurdarson, Y. L. Schmerwitz, D. K. Tveiten, G. Levi and H. Jónsson, J. Chem. Phys., 2023, 159, 214109 CrossRef CAS PubMed.
- Y. L. Schmerwitz, A. V. Ivanov, E. O. Jónsson, H. Jónsson and G. Levi, J. Phys. Chem. Lett., 2022, 13, 3990–3999 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01866d |
| This journal is © the Owner Societies 2024 |