Substituent effects and electron delocalization in five-membered N-heterocycles

Abstract

Five-membered N-heterocycles are principal constituents of many compounds of vital importance in various fields of chemistry, biochemistry or pharmaceutical chemistry. For this reason, unequivocal identification of structural factors determining electron donating/withdrawing properties of specific groups attached to the heterocyclic moiety becomes an utmost need together with elucidation of the substitution-induced changes in cyclic and noncyclic electron delocalization. Thus, quantum-chemical calculations were performed for pyrrole, imidazole, pyrazole, 1,2,3- and 1,2,4-triazole, and their C-substituted mono-derivatives (X = NO₂, CN, Br, Cl, F, SH, OH, NH₂). The obtained dataset contains information on substituent properties (cSAR – charge of the substituent active region method), delocalization (EDDB – electron density of delocalized bonds) and geometry. It follows that the positions of endocyclic N atoms relative to the substituent influence in the most profound manner its properties. N atoms in ortho positions significantly boost the electron-donation and weaken the electron-withdrawal by induction. Another factor is the resonance charge transfer from the substituents to N atoms, and then inductive interactions with further (non-ortho) N atoms. While substituent constants correctly describe the changes of their properties (including those attached to the heterocycles), a testimony to Hammett's genius, quantum chemical models must be used to quantify the exact properties. In most heterocycles, electron-donating substituents hinder the cyclic delocalization, except 4-pyrazole. The applied recent EDDB method allows to study this phenomenon in detail. It follows that changes in aromaticity originate from the π-electronic effects of substituents on the ring bonds, changing the localization and delocalization of particular bonds in a correlated manner.

---

Introduction

Heterocycles are the largest and one of the most important classes of organic compounds. They are of great biological and industrial importance, and even for the functioning of every developed human society.^1,2 For example, the most preferred and significant structures among pharmaceuticals are small molecule drugs containing a nitrogen heterocycle (59% of drugs approved by the US FDA), mainly six- and five-membered ones.³ Due to the variety of applications, one of the most important systems seems to be the aromatic five-membered N-heterocycles shown in Fig. 1. Their incorporation into the azo dye scaffold improved the bioactive properties of the target derivatives⁴ and, moreover, also enabled the development of fluorescent probes for the detection of biologically relevant species.^5–7 The main fields of application of polypyrrole (obtained by oxidative polymerization of pyrrole), a representative of conductive polymers, are electronic devices, chemical sensors and electrochemistry.⁸ Imidazole and pyrazole units are used as organic linkers in drug delivery MOFs and for the generation of reactive oxygen species.^9–11 Imidazolium salts, formed by protonation or substitution at the basic nitrogen atom, are used as ionic liquids and precursors of N-heterocyclic carbenes (NHC).¹² The latter, in turn, are used as ligands in molecular chemistry, which have found applications in organometallic catalysis, in metallodrugs, in luminescent and polymeric materials, as well as in surface and nanomaterial chemistry.^13–17

Fig. 1 Studied five-membered N-heterocycles and their abbreviations in bold. Substitution positions marked with red numbers. In the case of triazoles, two tautomeric forms of each derivative were considered, with NH group in positions marked with blue numbers.

However, the use of biological activities of pyrazole, pyrrole, imidazole and triazole derivatives should not be overestimated.¹⁸ In recent years, many publications have appeared summarizing their biological significance.^19–27 Pyrrole does not occur naturally, but many of its derivatives can be found in various cofactors and natural products, for example, vitamin B12 or bile pigments such as bilirubin and biliverdin. The first natural pyrazole, pyrazole-1-alanine, was isolated from watermelon seeds.²⁸ Pyrazole moieties are listed by the US FDA among frequently used ring systems in small molecule drugs. The imidazole moiety, which has two nonadjacent nitrogen atoms, is incorporated into many important biological compounds (nucleobases, histidine, histamine). Triazole, containing three nitrogen atoms, exists as two isomers 1,2,3-triazole and 1,2,4-triazole, each of which has two tautomers, as shown in Fig. 1. The latest (2024) review focuses on current progress in the biological use and preparation of triazole derivatives, highlighting their role in pharmaceutical chemistry.²⁹ Tetrazole, in addition to its biological activity,^30,31 due to its unique properties and practical importance, is considered an important precursor for the development of a wide range of energetic compounds.³²

All of the above-mentioned five-membered heterocycles, shown in Fig. 1, are aromatic, as documented below (Table 1). The systems whose properties and applications are outlined above contain these units. Therefore, they can be regarded as substituted systems in which one or more functional groups (substituents) are attached to the heterocyclic ring. Undoubtedly, this is a great simplification, but it can be very helpful in understanding and planning subsequent compounds with the desired properties. In this case, it is very helpful to use studies on the substituent effect, one of the most important concepts in chemistry, biochemistry and related fields.³³ Many such studies have been performed, computationally and experimentally, for example for pyrroles,^34,35 pyrazoles,³⁶ imidazoles^37,38 and triazoles^39–41 and references therein. However, they mainly concern the influence of the substituent on the tautomeric stability, the geometric and electronic structure of the ring and their aromaticity, while the substituents are characterized by the σ Hammett constants.^42,43 The use of σ constants implies the assumption that the properties of the substituent attached to the benzene and the five-membered heterocyclic ring are similar. However, it has been shown that the properties of the substituent depend both on the place of its attachment and on the substituted system,³⁵ the so-called reverse substituent effect. For this purpose, quantum-chemical descriptors calculated specifically for each molecule, such as cSAR (charge of the substituent active region),⁴⁴ should be used. One of the goals of this work is to determine the properties (and their changes) of substituents attached to pyrrole, pyrazole, triazoles and their tautomers (Fig. 1). For this purpose, a wide set of substituents was selected (X = NO₂, CN, Br, Cl, F, SH, OH, NH₂) with properties ranging from electron withdrawing to electron donating. By analyzing all possible five-membered N-heterocycles with many substituents, our aim is to unravel the general principles determining the properties of substituents, geometry of individual systems and the electron delocalization – cyclic associated with aromaticity, and non-cyclic. HOMA (Harmonic Oscillator Model of Aromaticity) is undoubtedly the most popular geometric aromaticity index.⁴⁵ HOMA compares the bond lengths with those of the reference aromatic system, whilst taking into account the lengths of the reference single and double bonds encoded in the normalization constant. For fully aromatic reference systems, HOMA = 1, while lower values indicate lower aromatic character of a ring. Originally, it was formulated in 1972 and included parametrization only for CC bonds.⁴⁵ In 1993 Krygowski extended HOMA by adding parameters for CC, CN, CO, CP, CS, NN, and NO bonds, thus expanding its applicability to heterocycles.⁴⁶ However, it has been noticed that this parametrization suffers from inconsistent choice of reference systems. For example, the parameters for the C=C and C=O bonds are based on (Z)-1,3-butadiene and formic acid, respectively, two systems in which resonance of the double bond is present, whereas the C=N bond was parametrized from methylimine, where only marginal resonance is present by hyperconjugation. This sometimes causes strange results, for example, furan is classified as non-aromatic (HOMA = 0.298). Another consequence is that HOMA has different scales depending on the bonds found in the molecule. For example, for systems with CC bonds it can vary from highly negative values to 1, while for CN, only from 0 to 1. This problem of different scales of HOMA is discussed in detail by Raczyńska.⁴⁷ The shortcomings of HOMA were addressed in its new parametrization, called HOMED (Harmonic Oscillator Model of Electron Delocalization).⁴⁸ HOMED attempts to describe various resonance effects (conjugation, hyperconjugation, aromaticity) and has a fixed scale from 0 to 1. It greatly improves the description of electron delocalization in small heteroaromatic systems. However, the parametrization procedure, which requires a choice of a single Lewis structure, is unclear for macrocycles (e.g. porphyrins), where the ground state electronic structure is described as superposition of many Lewis structures. It should also be remembered that the values of HOMA and HOMED are influenced by noncyclic delocalization. On the one hand, it allows to assess delocalization also in non-aromatic systems, but on the other, contributions of cyclic and non-cyclic delocalization (e.g. resonance between atoms in considered delocalization pathway and other atoms) cannot be separated as with the novel EDDB (electron density of delocalized bonds) method, which is the main tool used in this study.^49–52

Table 1 Values of aromaticity indices of selected five-membered N-heterocycles. Green shading corresponds to a high absolute value of the aromaticity index, red to a low value

a Isosurfaces of EDDBP(π) (0.02 electron) superimposed onto Lewis structures and below the number of cyclically delocalized π-electrons. b Normalized multicenter index in NAO basis. c Aromatic stabilization energies in kcal mol⁻¹, taken from ref. 53. d Low absolute value results from the ring size extensivity of NICS. e Bottleneck for cyclic delocalization – the bond at which connection between EDDB_P(π) isosurfaces first breaks when increasing isovalue.

---

As shown in Table 1, HOMED, unlike HOMA, correctly describes the sequence of increasing aromaticity of five-membered N-heterocycles with one or two N atoms: imidazole > pyrrole > pyrazole. The sequence agrees with ASE (aromatic stabilization energy) and EDDB_P(π) results. Tautomeric forms also differ in aromaticity. Furthermore, more aromatic tautomers are also more stable (in the gas phase), in agreement with B3LYP/6-311+G(d,p) calculations by Raczyńska.⁴⁷ However, it should be remembered that in solution, tautomeric equilibria may shift, for example, in polar solvents like DMSO, tetrazole exists mostly in N1H form, as evidenced by NMR studies.^54,55 Among the aromaticity indices shown, ASE, MCI and EDDB_P(π) allow to directly compare the aromaticity of heterocycles with benzene, since they do not depend on parametrization (HOMA/HOMED), nor on the ring size (NICS). Generally, heterocycles with fewer C–N(H) bonds are more aromatic. There is a decent correlation (R² = 0.733) between EDDB_P(π) and the number of C–N(H) bonds in the ring (Fig. S1, ESI†). No correlation is observed between EDDB_P(π) and the total number of N atoms or the number of other C–N bonds. The bond at which the connection between the isosurfaces first breaks when increasing EDDB_P(π) value, is the bottleneck for cyclic delocalization.

Results and discussion

In order to study the influence of substituents on electron delocalization, a set of substituents with properties ranging from strongly electron-withdrawing to electron-donating (X = NO₂, CN, Br, Cl, F, SH, OH, NH₂) was selected. First, electron delocalization and associated changes in geometry are analyzed, and then the focus is on the properties of substituents. The latter were quantitatively assessed using the cSAR method.⁴⁴ The interpretation of the cSAR values is shown in Fig. 2. The last part of the paper is devoted to keto (=O), thioketo (=S) and imino (=NH) tautomeric forms of SH, OH and NH₂ substituted heterocycles.

Fig. 2 Relations between the number of cyclically delocalized π-electrons evaluated by EDDB_P(π) function and substituent properties evaluated with cSAR(X) method. Unsubstituted systems not included in the correlations.

Electron delocalization

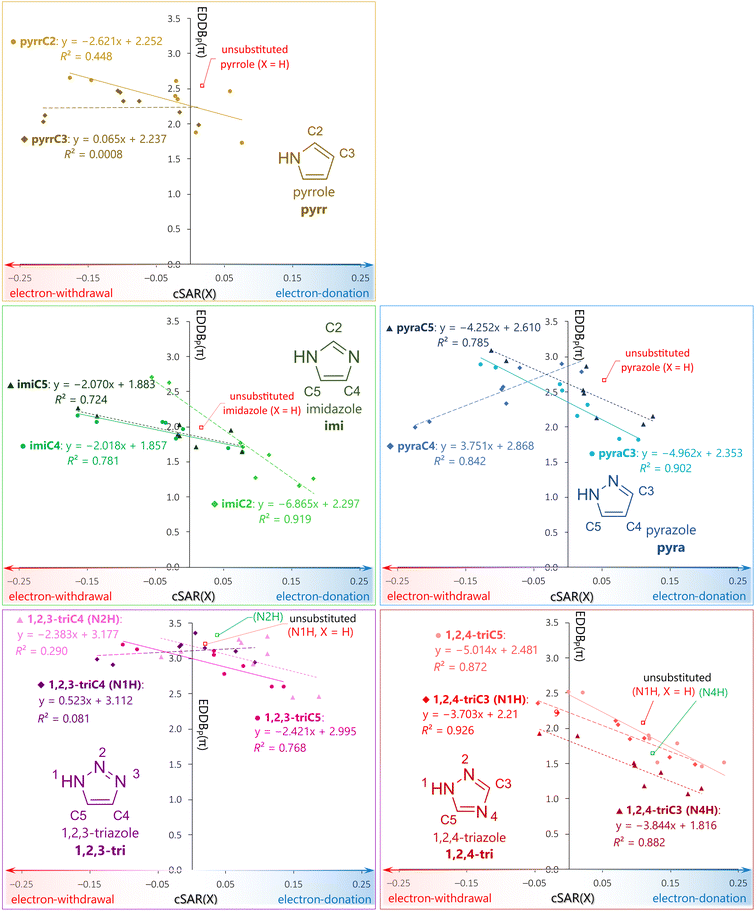
For many systems, the correlation between aromaticity and substituent properties is clear. Generally, the slopes of EDDB_P(π) vs. cSAR(X) correlations are negative, which indicates that the aromaticity decreases with the electron-donating properties of substituent. The only exception to this rule is pyraC4, which has a positive slope and relatively good determination coefficient: a = 3.751, R² = 0.842. There are also two systems (pyrrC3 and 1,2,3-triC4(N1H)) in which the slopes are positive but the R² values are close to zero, indicating that there is no correlation between aromaticity and the properties of substituent. Particularly interesting is that in pyrazoles, imidazoles and 1,2,4 triazoles, it is possible to boost aromaticity with strongly electron-withdrawing groups so that it surpasses the unsubstituted heterocycle.

The slope values of EDDB_P(π) vs. cSAR(X) relations (collected in Table S1, ESI†) indicate that the cyclic delocalization in imiC2 is the most sensitive to the change in substituent properties. In this system, the number of cyclically delocalized π-electrons increases 2.3 times when changing from the strongly electron donating to the withdrawing group. Other systems with slopes lower than −3.7 and high R² values are all 1,2,4-triazoles and two pyrazoles: pyraC3 and pyraC5. Systems with moderate changes (slope between −1.8 and −2.6) and lower R² values (0.290 to 0.781) are pyrrC2, 1,2,3-triC5, 1,2,3-triC4(N2H), imiC5 and imiC4. It should be noted that for the imiC4 and imiC5 systems the slope is approximately −2 (R² > 0.72), so their aromaticity is 3.4 times less sensitive to the substituent effect than in the imiC2 derivatives. Fig. 3 presents electron delocalization in derivatives with electron-withdrawing X = NO₂, slightly π-donating but withdrawing by induction X = Cl, and strongly π-donating X = OH groups. As for Cl, its π-donating properties are more important, since we consider the π-electron structure. Similar visualizations for all substituents are shown in ESI† (Table S2). It should be mentioned that the conclusions drawn from NO₂, Cl and OH extend to other π-electron withdrawing and donating groups, as confirmed by the data for all substituents (Table S2, ESI†). The OH group gives better assessment of how π-electron donation changes aromaticity because the other strongly donating group, X = NH₂, rotates in some derivatives due to interaction between its hydrogens and endocyclic N atoms. Rotation weakens π-donating effect of NH₂, as it decreases overlap between the π orbitals of substituted system and the lone electron pair orbital of NH₂. Such effects in aminopyrazoles (pyraC5 and N-substituted) have already been reported in the literature.^36,56 Therefore, the OH group is simpler and adds no additional effects to consider. In pyrrC2, the NO₂ group enhances the total cyclic delocalization by increasing delocalization through two single bonds (C3–C4 and N1–C5), which in unsubstituted pyrrole have a larger localized character. Bond lengths follow changes in the electronic structure – these single bonds are shorter for X = NO₂ than for Cl and OH. In pyrrC2–OH derivative, the C4–C5 double bond is more localized and shorter, which is pictured by separated EDDB_P(π) isosurfaces (Fig. 3). In pyrrC3, both the donating and withdrawing substituents disrupt the cyclic delocalization, but weaker electron donors, such as Cl, disrupt it to a much smaller extent (the points in Fig. 2 form an inverse ‘v’ shape). Adding another N atom to the ring in the C2 position (pyrazole), enhances cyclic delocalization. PyraC3 and pyraC5 derivatives are characterized by similar changes in aromaticity due to the substituent effect, although the C5 derivatives have slightly better cyclic delocalization. PyraC5–NO₂ is the most aromatic of the systems studied with two endocyclic N atoms. On the contrary, pyraC4 is the only system in which electron-donating substituents increase aromaticity, and electron-withdrawing groups reduce it. Comparing the shapes of EDDB_P(π) isosurfaces (Fig. 3), the NO₂ group increases the localization of N2–C3 and adjacent bonds. The N2–C3 double bond is the shortest for the least aromatic X = CN and NO₂ and the longest for the most aromatic X = OH; the correlation between EDDB_P(π) and its length is remarkable (R² = 0.96) (Fig. 4). The increase in localization of this bond along with the electron-withdrawing properties of X may be responsible for the inverse correlation between aromaticity and substituent properties in pyraC4. In no other system does the electron-withdrawal by substituent cause such a large shortening of the N2–C3 double bond, for X = CN down to 1.3265 Å which is below the optimal value of the CN aromatic bond, 1.3337 Å (Fig. 4). In the pyraC4–CN derivative, this bond, rather than N1–N2 as in unsubstituted pyrazole (Table 1), is the bottleneck for cyclic delocalization. This is further confirmed by the high R² of the N2–C3 bond length vs. EDDB_P(π) relation (Fig. 4).

Fig. 3 Isosurfaces of the EDDB_P(π) function (0.02 electrons) and the number of cyclically delocalized π-electrons in the ring for selected systems (X = H, NO₂, Cl, OH).

Fig. 4 (a) Schematic representation of changes in bond lengths due to the substituent effect and relations between ring bond lengths and resonance constants, R, of X substituents (example: pyraC4). (b) Relations between ring bond lengths and number of cyclically delocalized π-electrons; calculated reference aromatic bond lengths are marked. Isosurfaces of EDDB_P(π) for X = CN and OH derivatives. Data for all systems in Fig. S3 (ESI†).

Imidazole, with the second endocyclic N atom in the 3-position is less aromatic than pyrrole. However, this is the most labile system when it comes to aromaticity, as already shown by the slope of EDDB_P(π) vs. cSAR(X) plot (Fig. 2). Changing the substituents in the C2 position may increase (X = NO₂) or decrease (X = OH) the effectiveness of cyclic delocalization by ∼40% relative to the unsubstituted system. The shapes of isosurfaces change uniformly around the ring, so that disruption of aromaticity by electron-donating groups cannot be attributed to changes in one or two bonds. The aromaticity of imiC4 and C5 derivatives is less prone to change due to the substituent effect than imiC2 ones.

The results of previous studies on imidazole derivatives indicate that the ranges of variability of HOMA due to the substituent effect are larger for imiC2 than for imiC4 and imiC5, which agrees with the above conclusion; similarly, electron-withdrawing groups boost aromaticity.³⁸ Interestingly, if the N position of imidazole and pyrazole is substituted, the aromaticity decreases with increasing electron-withdrawing properties of the substituent, as shown by Curutchet et al.⁵⁷ Thus, the N-substitution effect on aromaticity of pyrazoles and imidazoles is similar to that in the pyraC4 systems. In addition, linear regressions between aromaticity indices HOMA, NICS, FLU, MCI, and the resonance constants (R), had similar slope values for pyrazole and imidazole N-derivatives, indicating similar sensitivity to the substituent effect in both cases. This cannot be said for the C-derivatives, since the slopes for the “imi” and “pyra” systems in relations EDDB_P(π) vs. cSAR(X) (Fig. 2) and R (Fig. S2, ESI†) vary.

Among the systems with three endocyclic N atoms, 1,2,4-triazoles are less aromatic than 1,2,3-triazoles, while the N4H tautomer of 1,2,4- is the least aromatic of all the N-heterocycles studied (Table 1). The aromaticity of 1,2,4-triC3(N4H) shows a similar sensitivity to the substituent effect as 1,2,4-triC3(N1H) (a = −3.8 and −3.7, respectively, Fig. 2). These systems behave similarly to imiC4 and imiC5, but the changes in aromaticity are higher. 1,2,4-triC5 and imiC2 are the two systems with the greatest sensitivity of the cyclic delocalization to the substituent effect (a = −5.0 and −6.8, respectively, Fig. 2), but in this case, imidazole is characterized by larger changes in aromaticity.

In highly aromatic 1,2,3-triazole derivatives (EDDB_P(π) = 3.2 and 3.3 for N1H and N2H tautomers, respectively), all substituents but one (X = F in 1,2,3-triC4(N1H)) disrupt the cyclic delocalization. The F-substituted molecule is characterized by the most extensive cyclic delocalization among all studied. In 1,2,3-triC4(N1H) derivatives, the smallest changes in the cyclic delocalization occur compared to the other substituted systems. Moreover, the points for this system in Fig. 2 form an inverse ‘v’ shape, similar to the pyrrC3 systems. However, in 1,2,3-triC5(N1H) and 1,2,3-triC4(N2H), the NO₂ group disrupts cyclic delocalization only slightly, while the OH group significantly. It can be noticed that the N1(H)–N2 or N2(H)–N3 bonds in these two systems are more localized for X = OH (and also longer, Fig. S3, ESI†), than for X = NO₂. Since our study did not include tetrazole derivatives, it is worth mentioning Sadlej-Sosnowska's study on C-substituted tetrazoles (X = BH₂, NO₂, CN, Br, Cl, F, H, CH₃, OCH₃, NH₂).⁵⁸ The obtained results showed that for derivatives of the N2H tautomer the variation in aromaticity is small, while for the N1H tautomer the aromaticity is the highest for π-electron withdrawing substituents (BH₂, NO₂, CN).

The structure of a molecule is a valuable source of information about its properties. Considering the series of substituted X-derivatives for each heterocycle, the bond lengths in the ring correlate well with the number of cyclically delocalized π-electrons (Fig. 4 and Fig. S3, ESI†). In systems with more efficient delocalization, bonds approach the reference lengths for aromatic systems. In general, no correlation is observed in systems with small changes in aromaticity and for two bonds with a substituted ring atom. However, it is important to mention here that the substituents influence the three other bonds in a consistent manner. As the π-withdrawing properties of substituent increase, the bond opposite to the substituent (e.g., N1–N2 in pyraC4) is elongated, while the two bonds ‘parallel’ to the C–X bond (N1–C5 and N3–C4 in pyraC4) are shortened. The regularity of these changes is reflected in the good correlations between the bond lengths and the resonance substituent constants, R (Fig. 4a). Interestingly, the lengthening and shortening of these bonds are observed regardless of their double or single character in the primary Lewis structure. This trend is also observed in the crystallographic data found for monosubstituted compounds (Table S3, ESI†). Moreover, the trend also applies to N-substituted pyrazoles, which is evident from the MP2/6-31G(d,p) results presented by Mó et al.,⁵⁶ thus, it appears to be a universal characteristic of N- and C-substituted five-membered N-heterocycles. However, the effect is discussed by Mó et al. only qualitatively, in terms of hybridization changes and resonance effects by substituents. Our NBO results do not reveal any correlations between hybridization of natural hybrid orbitals forming particular bonds and their lengths (Fig. S4, ESI†), as suggested in the article, so the interpretation in terms of π-electronic effects is more valid (which is further supported by good correlations between bond lengths and R constants). Regularity in ring bond length changes are due to the fact that the shapes of the π orbitals are similar in all monoderivatives of five-membered N-heterocycles (Fig. S5, ESI†), regardless of the substituent, the number of N atoms, and the positions of both. Therefore, it appears that the changes in aromaticity come from the interplay between how the substituent resonance properties influence the ring bond lengths and the bond lengths in the unsubstituted system. In most cases, π-electron withdrawing groups enhance cyclic delocalization by affecting particular bonds, while π-electron donating groups create bottlenecks for cyclic delocalization by shortening double bonds or elongating single. This can be noticed by comparing the slopes of the linear equations correlating the bond length and R or EDDB_P(π) (Fig. 4 and Fig. S3, ESI†) – both have the same sign. As mentioned above, the only systems in which electron-donating substituents increase and electron-withdrawing groups decrease aromaticity in a correlated manner are pyraC4 derivatives (slopes have opposite signs, Fig. 4), and N-substituted imidazoles and pyrazoles.⁵⁷

The relationships between the number of cyclically delocalized electrons (EDDB_P(π)) and HOMA or HOMED (Fig. S6, ESI†) are curvilinear due to the harmonic oscillator model used in the HOMA definition. The points in HOMED relation are more condensed than in HOMA due to the fixed 0 to 1 scale of HOMED, and the position of three deviating points is improved. The system with almost zero cyclically delocalized electrons is the imino (=NH) form of pyraC3–NH₂. However, the HOMED value indicates some electron delocalization (HOMED = 0.59). This is because EDDB_P(π) only accounts for cyclic delocalization, while HOMED also accounts for non-cyclic delocalization. A variant of EDDB that takes into account all delocalization (cyclic and non-cyclic, EDDB_F) gives a value of 1.16 delocalized π-electrons for atoms in the ring.

Non-cyclic electron delocalization

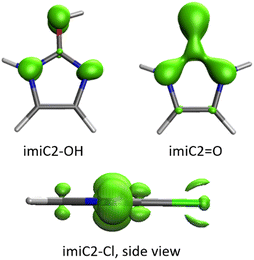
The EDDB_G–P function (difference between global and cyclically delocalized electron densities) accounts only for non-cyclic delocalization within the molecules. EDDB_G–P isosurfaces mainly show delocalization associated with substituent effects and charge delocalization from endocyclic N(H) groups onto other N atoms (Fig. 5). Around non-pyrrolic endo-N atoms, a σ-delocalization of the in-plane lone electron pair can be observed. Furthermore, in some systems, for example imiC2–Cl (Fig. 5), the densities of delocalized σ and π electrons can be clearly distinguished; more extensive delocalization is observed in the π cloud. Much stronger non-cyclic delocalization effects occur in keto/thioketo/imino tautomeric forms than in forms with one pyrrolic NH group in the ring (Fig. 5). This is a consequence of the strong electron-withdrawing ability of =O/=S/=NH groups by resonance, as evidenced by high negative cSAR(X) values – these groups are by far the strongest electron-acceptors. The low aromaticity of the substituted ring in the keto/thioketo/imino forms can contribute to this – systems with extensive cyclic delocalization are resistant to changes in their electronic structure due to the stabilization associated with it.⁵⁹ Keto, thioketo and imino forms are discussed in detail in the last section of the article.

Fig. 5 Isosurfaces of EDDB_G–P function (0.02 electrons) for selected systems – a visual representation of non-cyclic electron delocalization. Data for all systems in Table S4 (ESI†).

Substituent properties

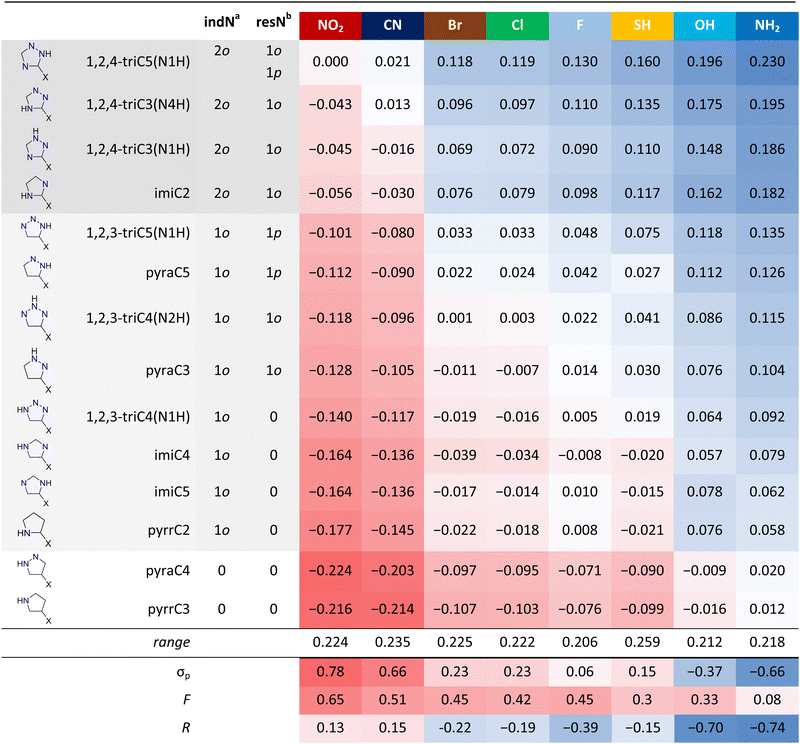
The cSAR(X) values for all systems (Table 2) evidence a large variability in the substituent properties in studied heterocycles. First of all, the heterocycles that promote the electron-donation of substituents also disrupt the electron-withdrawal of the NO₂ and CN groups. This could already be noticed in Fig. 2, as shifts of the data points for some series of derivatives toward electron-donating (right) or electron-withdrawing (left) part of the substituent electronic properties spectrum. For example, the points for imiC2 are on the right relative to imiC4 and imiC5, or the points for pyrr derivatives are much to the left relative to the points for 1,2,4-tri (Fig. 2). Therefore, the type of system determines how much electron density can be transferred from or onto substituents. Because of that, the ruling factor appears to be the inductive electron-withdrawing strength of rings rich in electronegative N atoms. The most important here is the number of endocyclic N atoms (both N and NH) in the ortho positions. Two such groups, one on each side (‘double ortho’ systems), promote the electron-donation and disrupt the electron-withdrawal by substituents. One ortho N atom has similar, but weaker, effect, and when there are no ortho N atoms, electron-withdrawing properties are the most pronounced and electron-donating properties are weak. This is caused by the fact that electronegative N atoms are capable of withdrawing electrons by induction from the nearby substituent. The second factor, although less important than the number of ortho N atoms, is the number of ring N atoms which can accept the charge transferred by resonance with the substituent. This number depends on the structure of heterocycle, namely the position of NH group relative to substituent. As illustrated by singly excited resonance structures (Table S5, ESI†), π-electron donating substituents (Br, Cl, F, SH, OH and NH₂) delocalize the negative charge, while π-electron withdrawing positive (NO₂ and CN). Importantly, due to the electronegativity of nitrogen, the endocyclic N atoms accept the negative charge delocalization more readily than C atoms, while delocalization of positive charge is less effective compared to C atoms.⁶⁰ For this reason, the systems with more resonance interactions between substituents and ring N atoms have higher cSAR values, indicating stronger electron-donation or weaker electron-withdrawal by substituents (Table 2). To sum up, inductive effect of ortho N atoms is the most important factor in determining electron-donating and withdrawing properties of substituents in five-membered N-heterocycles, while resonance between substituents and ring N atoms is the second most important factor. A similar effect of ortho N atoms and the resonance between substituents and N atoms has been observed in our study of six-membered N-heterocycles (Table S6, ESI†).⁶⁰ Interestingly, within 1o (indN column) subgroup, two systems with one para-like resonance interaction (1p in resN column, Table 2) between substituent and the ring N atom have higher cSAR values than systems with one ortho resonance interaction (1o). This suggests that para-like resonance interactions in five-membered N-heterocycles are stronger than ortho ones. The ranges of variability of cSAR(X) for substituents show that SH is the most labile when it comes to electronic properties, while F and OH are the least. The SH group easily changes conformation from planar to perpendicular to the ring plane with low energy barriers (0.1–1.7 kcal mol⁻¹). All cases when SH is electron-withdrawing (with negative cSAR) refer to when the perpendicular conformation is preferred. Rotation disrupts the resonance effect, which for SH is donating (R = −0.15), so the inductive withdrawal effect (F = 0.30) dominates. It should be mentioned that in heterocycles which are strong electron-acceptors, e.g. double ortho systems, SH never rotates. It shows that rotation occurs only in systems where the heterocycle is a weak electron acceptor, so that the energy gain from the resonance interaction between weakly donating SH and this heterocycle is lower than the energy difference between coplanar (less stable) and perpendicular (more stable) conformers. In Table 2, Hammett (σ_p), as well as the inductive (F) and resonance (R) constants, are included, but it should be stressed that they describe the properties of substituents in para-benzoic acid derivatives. Thus, for other systems, they are only an approximate measure of how the given substituent behaves.

Table 2 Values of cSAR(X) in all studied five-membered heterocycles and their ranges of variation for each substituent and heterocycle. Hammett's σ_p constants and their inductive (F) and resonance (R) components are given.⁴³ Shading intensity proportional to the substituent effect descriptor value, blue indicates electron donating, while red electron withdrawing properties

a indN – the number of endocyclic N atoms in ortho positions relative to substituent, 2o – grey shading of compound name, 1o – light grey shading, 0 – no shading. b resN – the number of endocyclic N atoms interacting via resonance (singly excited structures) with substituent and their position relative to substituent: o – ortho, p – para-like.

---

On the graph between cSAR(X) and σ_p substituent constants, it can be noticed that these two parameters correlate well and series for different heterocycles are almost parallel – they differ mostly by the intercept (b) of cSAR(X) = a·σ_p + b linear equations (Fig. 6). This indicates that the nature of the substituent effect is similar for different heterocycles; in other words, none of the heterocycles interacts with the substituents in a specific way, for example by much stronger resonance effect like a charged substituent would.⁴³ The source of differences in the intercepts is mainly the inductive electron withdrawal by ortho-N atoms as discussed earlier (Table 2). Interestingly, heterocycles with 0 indN are better electron donors to the substituents compared to benzene, while all the others are better electron acceptors (Fig. 6).

Fig. 6 Relationships between cSAR(X) and the substituent constants σ_p. Parameters of fitted functions cSAR(X) = a·σ_p + b in table.

Points for the SH group regularly lie above the fitted lines in systems where the SH conformation is coplanar relative to the ring plane. It indicates that in this conformation SH is more electron donating relative to other substituents than according to its σ_p substituent constant. Indeed, the coplanar conformation of SH allows for stronger electron donation by resonance due to the larger 3p-π orbital overlap. The resonance between the substituent and the heterocycle is associated with shortening of the C–X bond connecting them. For this reason, in the d_CXvs. cSAR(X) plot (Fig. 7) we can see a correlated series for each substituent – π-electron donating groups (Br, Cl, F, SH, OH, NH₂) have negative slope values, while π-electron withdrawing (NO₂, CN) have positive slope values. This is another example of how changes in the electronic structure shift the positions of atomic centers and change molecular geometry. The worst R² values are observed for X = CN and SH, since the C–X bond in these derivatives is the least susceptible to changes in length (both have range of variation ∼0.014 Å). For the bulky NO₂ substituent, systems with ortho NH group form a series with slightly shorter C–X bonds due to the lack of repulsive steric interaction (with CH or N) as in the case of other systems. It should be mentioned that the analysis of non-covalent interactions with NCI method⁶¹ does not detect through space interactions between substituent atoms and endocyclic N/NH groups in ortho positions (for example NO⋯HN for X = NO₂ and NH⋯N for X = NH₂). Some very weak interactions are detected only in NO₂ derivatives (Fig. S7, ESI†). This indicates the weakness of such interactions, mainly due to the sharp angles between the atoms involved, imposed by the five-membered ring geometry.

Fig. 7 Correlations between C–X bond lengths and cSAR(X) for each substituent.

Imino, keto and thioketo tautomeric forms

Most of the =NH/=O/=S tautomeric forms of heterocycles with two pyrrolic N(H) groups in the ring are less stable than their NH₂/OH/SH counterparts with one N(H) group (Fig. 8). However, the derivatives with two ortho N(H) groups, one in each adjacent position to the =O/=S substituent, are actually the most stable tautomeric forms of respective heterocycles (more stable than –OH/–SH by 6.6–9.0 kcal mol⁻¹). These derivatives are imiC2 and 1,2,4-triC3(N2H,N4H) (Fig. 8). In the case of =NH, these forms are somewhat more stable than the other =NH forms; they are less stable than –NH₂ by 11–13 kcal mol⁻¹, in contrast to similar forms with N and N(H) in ortho positions, which are less stable by 30–33 kcal mol⁻¹ (Table S7, ESI†). In 1,2,4-triC3, moving one of the hydrogens from the N2 or N4 to the N1 position, gives forms less stable by over 20 kcal mol⁻¹! (compare 1,2,4-triC3(N2H,N4H) and (N1H,N4H), Fig. 8).

Fig. 8 Keto and thioketo forms of studied five-membered heterocycles with their EDDB_P(π), cSAR(X), d_CX and ΔE values. ΔE is the energy (in kcal mol⁻¹) of keto or thioketo form relative to the OH (enol) or SH (thiol) form. Shading intensity is proportional to the aromaticity index value (green-yellow-red), electron-withdrawing properties (red) or bond length (green-yellow).

Therefore, there must be a substantially stabilizing (by approximately 20 kcal mol⁻¹) effect associated with the interaction between =NH/=O/=S and ortho N(H) groups. A possible explanation is the strong resonance interactions between the substituent and two ortho N(H) groups, exemplified by two zwitterionic resonance forms with O⁻ and N(H)⁺. Endocyclic N(H) groups have a 2p_z electron pair that can be delocalized onto nearby electron withdrawing =NH/=O/=S groups. This resonance is clearly visible on the EDDB_G–P plots (Fig. 5). Such interaction is stronger than that between the substituent and the endocyclic N atom with only one 2p_z electron.

Generally, the =NH/=O/=S forms have poor cyclic delocalization (EDDB_P(π) < 1.0), due to the possible π-electron excess in the ring – from the Lewis structure there are formally seven 2p_z electrons, each N(H) group provides two, each C and N one. However, some of these forms have good cyclic delocalization; five systems have EDDB_P(π) between 1.0 and 2.0, and four systems between 2.05 and 2.23 (Table S7, ESI†). Interestingly, the anisotropy of the induced current density (AICD)⁶² plot of pyraC4=O, the most aromatic keto form (EDDB_P(π) = 2.05), reveals diatropic ring current, whereas in imiC2=O the lack of diatropic ring current suggests its nonaromatic character in agreement with low EDDB_P(π) value, 0.605 (Fig. S8, ESI†). Among the =NH/=O/=S forms, =S are always the most aromatic, followed by =O and the least aromatic =NH. From Fig. 8 and Table S7 (ESI†) it can be noticed that HOMED values do not correlate well with EDDB_P(π) in the =NH/=O/=S forms; unlike EDDB_P(π), HOMED also accounts for non-cyclic delocalization effects, which are significant in these forms, as visualized by voluminous EDDB_G–P isosurfaces (Fig. 5 and Table S4, ESI†). The highly negative cSAR(X) values (Fig. 8 and Table S7, ESI†) indicate a strong electron-withdrawal via resonance by =NH/=O/=S groups.

This particularly strong resonance between the substituent and heterocycle can be noticed in EDDB_G–P plots (Table S4, ESI†). Furthermore, the EDDB_G–P plots of four heterocycles with the lowest cSAR(X) values of =O, =S and =NH (pyraC4, 1,2,3-triC4(N1H,N2H), 1,2,3-triC4(N1H,N3H), imiC4) clearly show more extensive resonance than in the other six. It should be remembered here that, depending on the N/N(H) positions, the rings themselves have different inductive electron withdrawing strength, and that =O/=S/=NH withdraw electrons both by induction and resonance. Moreover, the four most aromatic systems among the =O, =S and =NH forms have the lowest cSAR(X) values and longer CX bonds (Fig. 8 and Table S7, ESI†). This indicates a large contribution of zwitterionic forms with O⁻ and N(H)⁺ to their ground state. Such resonance forms formally have six delocalizable 2p_z electrons in the ring, which contribute to their higher aromaticity.

Furthermore, the CX bond lengths (C=O, C=S and C=NH) are well correlated with electronic properties of X (Fig. 7); elongating the bond increases the electron-withdrawing ability of X. This indicates that with an increase in the electron-withdrawal by X, also increases the contribution of X⁻ and N(H)⁺ zwitterionic resonance forms with a single bond between C and X⁻. Nonetheless, despite relatively high aromaticity, =NH/=O/=S forms of pyraC4, 1,2,3-triC4(N1H,N2H), 1,2,3-triC4(N1H,N3H) and imiC4 are not stable, as shown by large ΔE values (Fig. 8 and Table S7, ESI†). Interestingly, there is a decent correlation (R² = 0.738) between EDDB_P(π) and cSAR(X) of =NH, =O and =S (Fig. S9, ESI†). This indicates that the systems in which these substituents withdraw more electrons from the rings (with π-electron excess relative to aromatic sextet) have better cyclic delocalization. It resembles the situation in heptafulvenes, which are non-aromatic conjugated molecules with exocyclic double bond and π-electron excess in the ring; similarly, strongly electron-withdrawing exocyclic substituent can enhance the cyclic delocalization.⁶³ The HOMO and LUMO orbital energies of all studied heterocycles correlate with the properties of substituents evaluated by cSAR(X) (Fig. S10, ESI†). In all cases, the energies increase with electron-donating ability of X. However, the HOMO–LUMO gaps do not correlate with cSAR(X).

Conclusions

A systematic quantum-chemical study of five-membered N-heterocycles (pyrrole, pyrazole, imidazole, 1,2,3- and 1,2,4-triazole) and their monosubstituted derivatives (X = NO₂, CN, Br, Cl, F, SH, OH, NH₂) allowed to describe in detail the influence of substituents on aromaticity and non-cyclic delocalization (EDDB method), and to identify structural factors determining the electron-donating/withdrawing properties (cSAR method) of groups attached to heterocycles. The obtained results can be useful in molecular property prediction and can be summarized as follows:

Substituents influence the π-electron structure and geometry of heterocycles in an orderly manner due to the fact that the π orbitals in all derivatives have a similar shape and node location. The length of the bond opposite the substituent increases with π-electron withdrawing strength of the substituent (R constant), while the two bonds adjacent to the opposite one are shortened.

Interplay between ring bond lengths and substituent resonance properties determines the aromaticity of heterocycle. For example, when short, highly localized double bonds are further shortened by substituents, bottlenecks for cyclic delocalization are created. In most cases, this effect causes that π-electron withdrawing groups enhance, while π-donating groups disrupt the cyclic delocalization in a correlated manner. The exceptions are 4-substituted pyrazoles, in which opposite correlation is observed; the same was found for N-substituted pyrazoles and imidazoles. In the case of 3-substituted pyrrole and 4-substituted 1,2,3-triazole derivatives, no correlation is observed. However, the 4-F-1,2,3-triazole(N1H) molecule is characterized by the most intense cyclic delocalization among all studied systems, while pyrrole is the most aromatic of the pyrrC3 series. Moreover, changing the substituent to a more electron-donating or electron-withdrawing one disrupts cyclic delocalization.

The properties of the substituents depend on the number and positions of the endocyclic N-atoms. For example, cSAR values for NO₂ vary from 0.00 to −0.216, while for NH₂ from 0.230 to 0.012. The most important is the number of N atoms in ortho positions, which withdraw electrons from the substituents by induction, increasing their electron-donation or weakening their electron-withdrawal. The second, less important factor, is the number of ring N-atoms which interact with the substituent via resonance. Every such N-atom increases the electron-donating or weakens the electron-withdrawing properties of substituent. This is because the ring N-atoms more readily accept the negative charge delocalized by electron-donating groups than less electronegative C-atoms, and less readily the positive charge delocalized by electron-withdrawing groups.

Each series of heterocyclic derivatives forms a linear relationship between the quantum-chemical descriptor of substituent properties, cSAR(X), and the Hammett constants σ_p. Relationships for different heterocycles are parallel and differ only in their intercept, according to the structural features discussed in the previous point. This indicates that the nature of the substituent effect and the variability of substituent properties are similar for different heterocycles. The unique utility of substituent constants should also be emphasized. Hammett's choice of the acid–base equilibrium constants of benzoic acids to determine the substituent constants was a clever idea. These constants describe well the changes in the properties of substituents also in heterocycles, but to quantify the exact properties, quantum-chemical models should be used, or the structural features should be considered in e.g. multivariate model.

The tautomeric keto and thioketo forms are more stable than their OH and SH counterparts only in systems with two endocyclic ortho-NH groups (3-substituted 1,2,4-triazole(N2H,N4H) and 2-imidazole derivatives). This is explained by the strong resonance interaction between =O/=S and NH, which stabilizes these keto and thioketo forms by ∼20 kcal mol⁻¹.

Author contributions

Conceptualization, T. M. K. and H. S.; formal analysis, P. A. W. and H. S.; funding acquisition, H. S.; investigation, P. A. W.; methodology, P. A. W. and H. S.; supervision, H. S.; validation, H. S. and P. A. W.; visualization, P. A. W.; writing – original draft, P. A. W. and H. S.; writing – review & editing, H. S. and T. M. K.

Data availability

All computational details and data are added to the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Warsaw University of Technology within the Excellence Initiative: Research University (IDUB) programme (no. 1820/107/Z01/2023). The authors would like to thank the Wrocław Center for Networking for providing computer time and facilities.

Notes and references

1. A. F. Pozharskii, A. T. Soldatenkov and A. R. Katritzky, Heterocycles in Life and Society: An Introduction to Heterocyclic Chemistry, Biochemistry and Applications, Wiley, 1st edn, 2011.
2. A. R. Katritzky, Chem. Rev., 2004, 104, 2125–2126.
3. E. Vitaku, D. T. Smith and J. T. Njardarson, J. Med. Chem., 2014, 57, 10257–10274.
4. K. Mezgebe and E. Mulugeta, RSC Adv., 2022, 12, 25932–25946.
5. M. Kaur and D. H. Choi, Chem. Soc. Rev., 2015, 44, 58–77.
6. S. Gond, P. Yadav, A. Singh, S. Garai, A. Shekher, S. C. Gupta and V. P. Singh, Org. Biomol. Chem., 2023, 21, 4482–4490.
7. S. Yokoyama and N. Nishiwaki, J. Org. Chem., 2019, 84, 1192–1200.
8. T. V. Vernitskaya and O. N. Efimov, Russ. Chem. Rev., 1997, 66, 443–457.
9. S. He, L. Wu, X. Li, H. Sun, T. Xiong, J. Liu, C. Huang, H. Xu, H. Sun, W. Chen, R. Gref and J. Zhang, Acta Pharm. Sin. B, 2021, 11, 2362–2395.
10. H. D. Lawson, S. P. Walton and C. Chan, ACS Appl. Mater. Interfaces, 2021, 13, 7004–7020.
11. K. Wu, X.-Y. Liu, P.-W. Cheng, Y.-L. Huang, J. Zheng, M. Xie, W. Lu and D. Li, J. Am. Chem. Soc., 2023, 145, 18931–18938.
12. I. Nawaz, M. Bashir, R. S. Z. Saleem and G. A. Chotana, Tetrahedron Lett., 2023, 128, 154696.
13. I. Omae, Coord. Chem. Rev., 2016, 310, 154–169.
14. C. A. Smith, M. R. Narouz, P. A. Lummis, I. Singh, A. Nazemi, C.-H. Li and C. M. Crudden, Chem. Rev., 2019, 119, 4986–5056.
15. M. Virant and J. Košmrlj, J. Org. Chem., 2019, 84, 14030–14044.
16. R. S. Ghadwal, Angew. Chem., Int. Ed., 2023, 62, e202304665.
17. C. Yoo, S. Bhattacharya, X. Y. See, D. W. Cunningham, S. Acosta-Calle, S. T. Perri, N. M. West, D. C. Mason, C. D. Meade, C. W. Osborne, P. W. Turner, R. W. Kilgore, J. King, J. H. Cowden, J. M. Grajeda and A. J. M. Miller, Science, 2023, 382, 815–820.
18. C. T. Walsh, Tetrahedron Lett., 2015, 56, 3075–3081.
19. A. Ansari, A. Ali, M. Asif and S. Shamsuzzaman, New J. Chem., 2017, 41, 16–41.
20. V. Kumar, K. Kaur, G. K. Gupta and A. K. Sharma, Eur. J. Med. Chem., 2013, 69, 735–753.
21. L. Zhang, X.-M. Peng, G. L. V. Damu, R.-X. Geng and C.-H. Zhou, Med. Res. Rev., 2014, 34, 340–437.
22. P. N. Kalaria, S. C. Karad and D. K. Raval, Eur. J. Med. Chem., 2018, 158, 917–936.
23. O. Ebenezer, M. Shapi and J. A. Tuszynski, Biomedicines, 2022, 10, 1124.
24. M. Dhameja and P. Gupta, Eur. J. Med. Chem., 2019, 176, 343–377.
25. Z. Xu, S.-J. Zhao and Y. Liu, Eur. J. Med. Chem., 2019, 183, 111700.
26. K. Bozorov, J. Zhao and H. A. Aisa, Bioorg. Med. Chem., 2019, 27, 3511–3531.
27. E. Bonandi, M. S. Christodoulou, G. Fumagalli, D. Perdicchia, G. Rastelli and D. Passarella, Drug Discovery Today, 2017, 22, 1572–1581.
28. F. F. Noe and L. Fowden, Nature, 1959, 184, BA69–BA70.
29. U. Salma, S. Ahmad, M. Zafer Alam and S. A. Khan, J. Mol. Struct., 2024, 1301, 137240.
30. L. V. Myznikov, S. V. Vorona and Y. E. Zevatskii, Chem. Heterocycl. Compd., 2021, 57, 224–233.
31. R. K. Uppadhayay, A. Kumar, J. Teotia and A. Singh, Russ. J. Org. Chem., 2022, 58, 1801–1811.
32. S. Manzoor, Q. Tariq, X. Yin and J.-G. Zhang, Def. Technol, 2021, 17, 1995–2010.
33. H. Szatylowicz, O. A. Stasyuk and T. M. Krygowski, Advances in Heterocyclic Chemistry, Elsevier, 2015, vol. 116, pp. 137–192.
34. K. Zborowski, I. Alkorta and J. Elguero, Struct. Chem., 2007, 18, 797–805.
35. K. K. Zborowski, H. Szatylowicz, O. A. Stasyuk and T. M. Krygowski, Struct. Chem., 2017, 28, 1223–1227.
36. M. Jarończyk, J. C. Dobrowolski and A. P. Mazurek, J. Mol. Struct. THEOCHEM, 2004, 673, 17–28.
37. M. Kurzepa, J. C. Dobrowolski and A. P. Mazurek, J. Mol. Struct., 2001, 565–566, 107–113.
38. A. N. Chermahini, B. Hosseinzadeh, A. S. Beni and A. Teimouri, Comput. Theor. Chem., 2012, 994, 97–104.
39. W. P. Ozimiński, J. Cz Dobrowolski and A. P. Mazurek, J. Mol. Struct., 2003, 651–653, 697–704.
40. W. P. Ozimiński, J. Cz Dobrowolski and A. P. Mazurek, J. Mol. Struct. THEOCHEM, 2004, 680, 107–115.
41. M. F. Shibl, S. A. K. Elroby and R. H. Hilal, Mol. Simul., 2011, 37, 11–17.
42. L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103.
43. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
44. N. Sadlej-Sosnowska, Chem. Phys. Lett., 2007, 447, 192–196.
45. J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 13, 3839–3842.
46. T. M. Krygowski, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78.
47. E. Raczyńska, Symmetry, 2019, 11, 146.
48. E. D. Raczyńska, M. Hallman, K. Kolczyńska and T. M. Stępniewski, Symmetry, 2010, 2, 1485–1509.
49. D. W. Szczepanik, M. Andrzejak, K. Dyduch, E. Żak, M. Makowski, G. Mazur and J. Mrozek, Phys. Chem. Chem. Phys., 2014, 16, 20514–20523.
50. D. W. Szczepanik, Comput. Theor. Chem., 2016, 1080, 33–37.
51. D. W. Szczepanik, M. Andrzejak, J. Dominikowska, B. Pawełek, T. M. Krygowski, H. Szatylowicz and M. Solà, Phys. Chem. Chem. Phys., 2017, 19, 28970–28981.
52. D. W. Szczepanik and M. Solà, Aromaticity, Elsevier, 2021, pp. 259–284.
53. M. K Cyrański, Chem. Rev., 2005, 105, 3773–3811.
54. D. S. Wofford, D. M. Forkey and J. G. Russell, J. Org. Chem., 1982, 47, 5132–5137.
55. J. Elguero, C. Marzin and J. D. Roberts, J. Org. Chem., 1974, 39, 357–363.
56. O. Mó, M. Yáñez, A. L. Llamas-Saiz, C. Foces-Foces and J. Elguero, Tetrahedron, 1995, 51, 7045–7062.
57. C. Curutchet, J. Poater, M. Solà and J. Elguero, J. Phys. Chem. A, 2011, 115, 8571–8577.
58. N. Sadlej-Sosnowska, J. Org. Chem., 2001, 66, 8737–8743.
59. T. M. Krygowski, M. Palusiak, A. Płonka and J. E. Zachara-Horeglad, J. Phys. Org. Chem., 2007, 20, 297–306.
60. P. A. Wieczorkiewicz, H. Szatylowicz and T. M. Krygowski, Molecules, 2021, 26, 6543.
61. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
62. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758.
63. P. A. Wieczorkiewicz, K. K. Zborowski, T. M. Krygowski and H. Szatylowicz, J. Org. Chem., 2023, 88, 14775–14780.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details, data and additional figures. See DOI: https://doi.org/10.1039/d4cp01709a

---